Похожие презентации:
Уравнение и неравенства с двумя переменными
1. Уравнение и неравенства с двумя переменными
mathvideourok.moy.su2. Уравнения с двумя переменными
Решением уравнения с двумя переменныминазывают всякую пару чисел (х ; у), которая
обращает уравнение в верное числовое
равенство
Например :1) 2 х 6 3 у 12 0
2
4
(3; 4) единтвенное решение этого уравнения
Так как сумма двух неотрицательных чисел равна
нулю когда каждое слагаемое равно нулю.
3.
2) х 2 у 2 9имеет много решений
х у 9
2
2
Изобразим их графически
Это Окр (О;3)
Переход к графику уравнения
является одним из
наиболее удобных приемов
решения уравнения с двумя
переменными
4. Решение неравенств с двумя переменными
Решением неравенства с двумяпеременными называется пара значений
этих переменных, обращающее данное
неравенство в верное числовое
неравенство
Но таких пар, точек, очень много. Значит на
координатной плоскости это целая
область.
5.
Решить неравенство:а) у 2 х 1
Строим у 2 х 1
Если ; , то линия прерывистая
Если ; , то линия сплошная
Эта линия разбивает плоскость
на две области.Точки какой области
удовлетворяют этому неравенству ,
то та область и является решением
этого неравенства
6.
у 2х 1у 2х 1
линейная функция, график прямая
(0; 1)(1;1)
Возьмем точку (0;0)
0 2 0 1 верно
у 2х 1
7.
б) у ( х 2)у ( х 2)2
2
у ( х 2)
квадратичная функция
у х2
у ( х 2)2
Берем (2; 2)
2
2 (2 2) верно
2
8.
в) х у 162
2
х 2 у 2 16
окружность (0;0); r 4
Берем (0;0)
0 0 16 неверно
2
х 2 у 2 16
2
9.
г) ху 66
у
х
6
у
ху 6
х
обратная пропорциональность,
график гипербола I;IIIк.ч.
Берем (6;6)
6 6 6 верно
(0;0)
0 0 6 неверно
( 6; 6)
6 ( 6) 6 верно
10. Системы неравенств с двумя переменными
Множеством решений системы неравенств сдвумя переменными является пересечение
множеств решений входящих в нее
неравенств.
11.
Решите систему неравенств2
2
2
2
1) х у 4
х у 4
а)
х у 1
х у 1
окружность (0;0) r 2
берем (0;0)
02 02 4 верно
2) х у 1
у 1 х линейная функция,
х2 у 2 4
график прямая
(0;1);(1;0)
берем (3;3)
3 3 1 верно
Решение системы пересечение
показанное на рисунке
12.
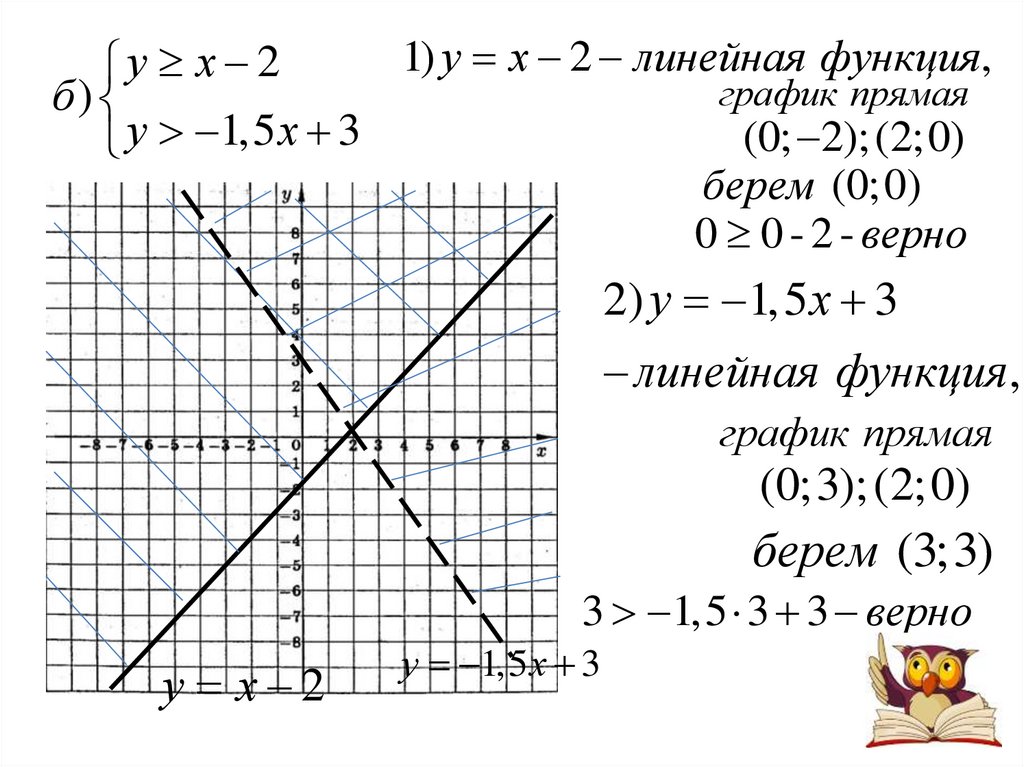
1) у х 2 линейная функция,у х 2
график прямая
б)
(0; 2);(2;0)
у 1,5 х 3
берем (0;0)
0 0 - 2 - верно
2) у 1,5 х 3
линейная функция,
график прямая
(0;3);(2;0)
берем (3;3)
3 1,5 3 3 верно
у х 2
у 1,5 х 3











 Математика
Математика








