Понятие множества. Операции над множествами

1. Понятие множества. Операции над множествами.

2.

«Множество
есть многое,
мыслимое
нами как
единое».
Основоположник
теории множеств
немецкий
математик
Георг Кантор
(1845-1918)

3. Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Множество – набор, совокупность, собрание

каких-либо объектов (элементов), обладающих
общим для всех их характеристическим
свойством.
Примеры множеств:
множество учащихся в данной аудитории;
множество людей, живущих на нашей планете в данный
момент времени;
множество точек данной геометрической фигуры;
множество чётных чисел;

4.

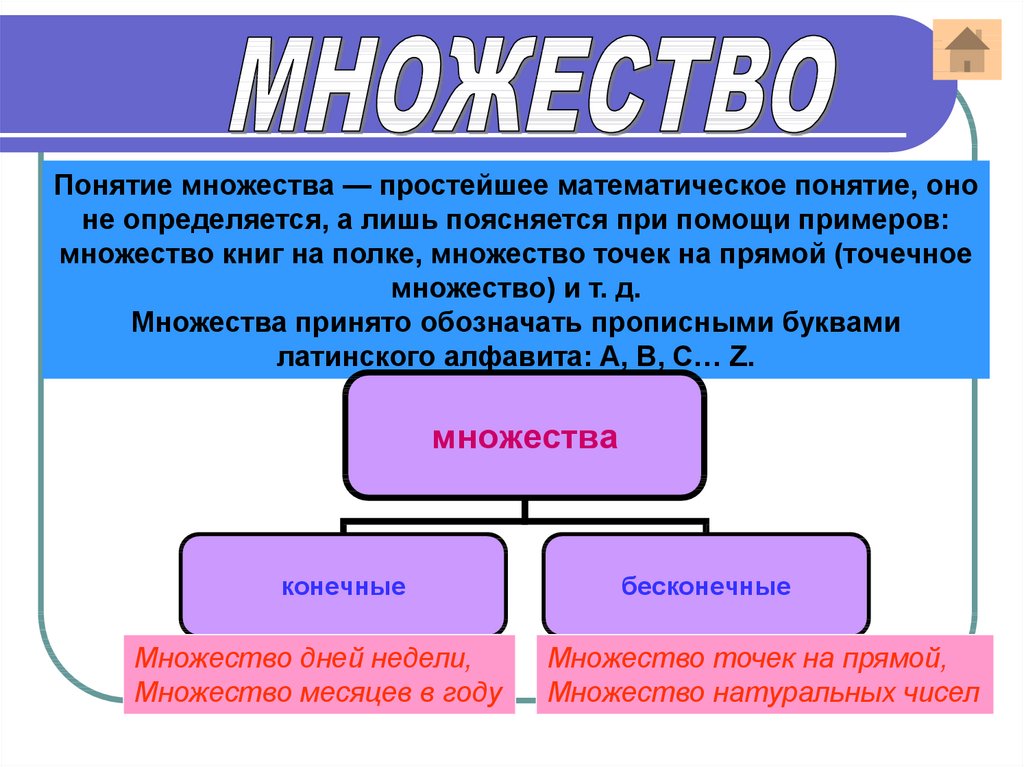
Понятие множества — простейшее математическое понятие, оно
не определяется, а лишь поясняется при помощи примеров:
множество книг на полке, множество точек на прямой (точечное
множество) и т. д.
Множества принято обозначать прописными буквами
латинского алфавита: A, B, C… Z.
множества
конечные
Множество дней недели,
Множество месяцев в году
бесконечные
Множество точек на прямой,
Множество натуральных чисел

5. Объекты, составляющие данное множество, называют его элементами. Множество обычно обозначают большими латинскими буквами (А, В,

С,..) , а элементы множества − малыми
латинскими буквам (a. b. c…).
Если элемент, а принадлежит множеству А, то пишут:
а
А
Если а не принадлежит А, то пишут:
а
А.

6. В математике часто исследуются так называемые числовые множества, т.е. множества, элементами которых являются числа. Для самых

основных числовых множеств утвердились
следующие обозначения:
N - множество всех натуральных чисел;
Z - множество всех целых чисел;

7.

Среди множеств выделяют особое
множество - пустое множество.
Обозначение пустого множества ∅
Пустое множество- множество, не
содержащее ни одного элемента.
Пустое множество является частью любого
множества.
Примеры пустых множеств.
1) множество простых делителей числа 1;
2) множество точек пересечения двух параллельных прямых;
3) множество прямых углов равностороннего треугольника;
4) множество людей на Солнце;

8. Способы задания множества

перечисление элементов множества;
А={a; b; c; …;d}
указание характеристического
свойства элементов множества, т.е.
такого свойства, которым обладают
все элементы данного множества и
только они.
Например: Множество цифр, то есть
{1; 2; 3; …;9}

9. Поставьте вместо звездочки знак (принадлежит или не принадлежит) так, чтобы получить правильное утверждение: 1) 5 * N; 2) 0 *

N;
3) − 12 * Z;
4) π * Z;

10. Действия над множествами

Включение и равенство множеств
Пусть Х и У – два множества. Если каждый
элемент х множества Х является
элементом множества У, то говорят, что
множество Х содержится во множестве У и
пишут: Х У. Говорят также, что Х
включено в У или У включает Х, или что Х
является подмножеством множества У.

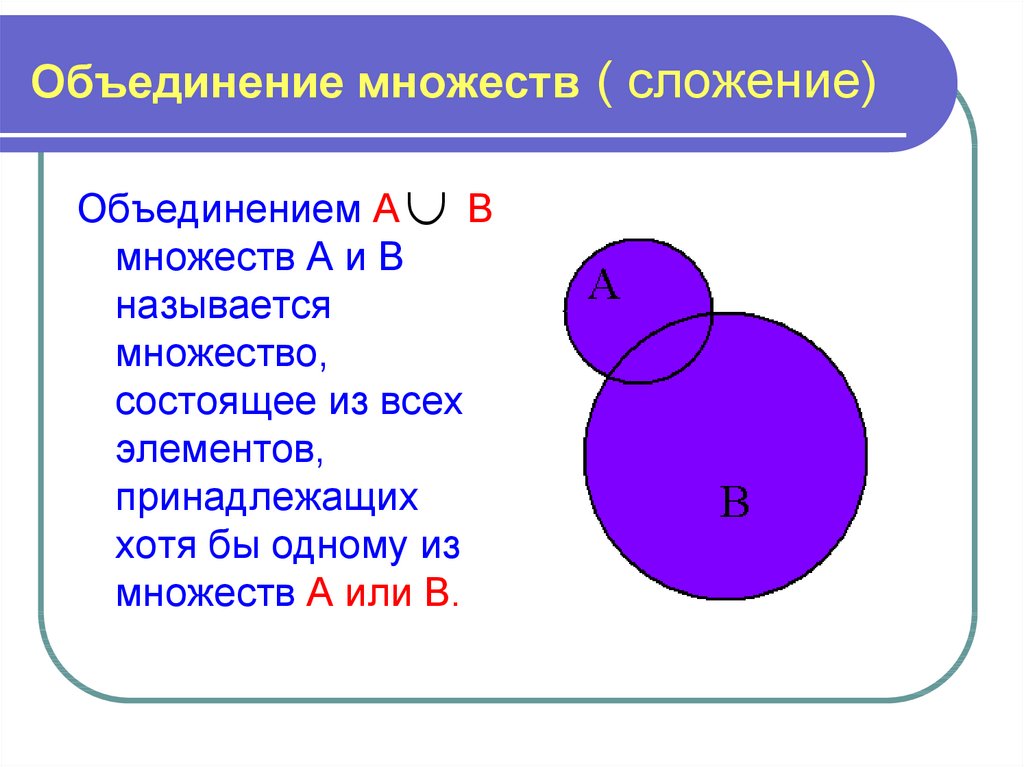
11. Объединение множеств ( сложение)

Объединением А
В
множеств А и В
называется
множество,
состоящее из всех
элементов,
принадлежащих
хотя бы одному из
множеств А или В.

12.

Объединение множеств обозначается
На диаграмме Эйлера-Венна объединение двух
множеств выглядит так
П р и м е р : {1,2,3} {2,3,4} = {1,2,3,4}.

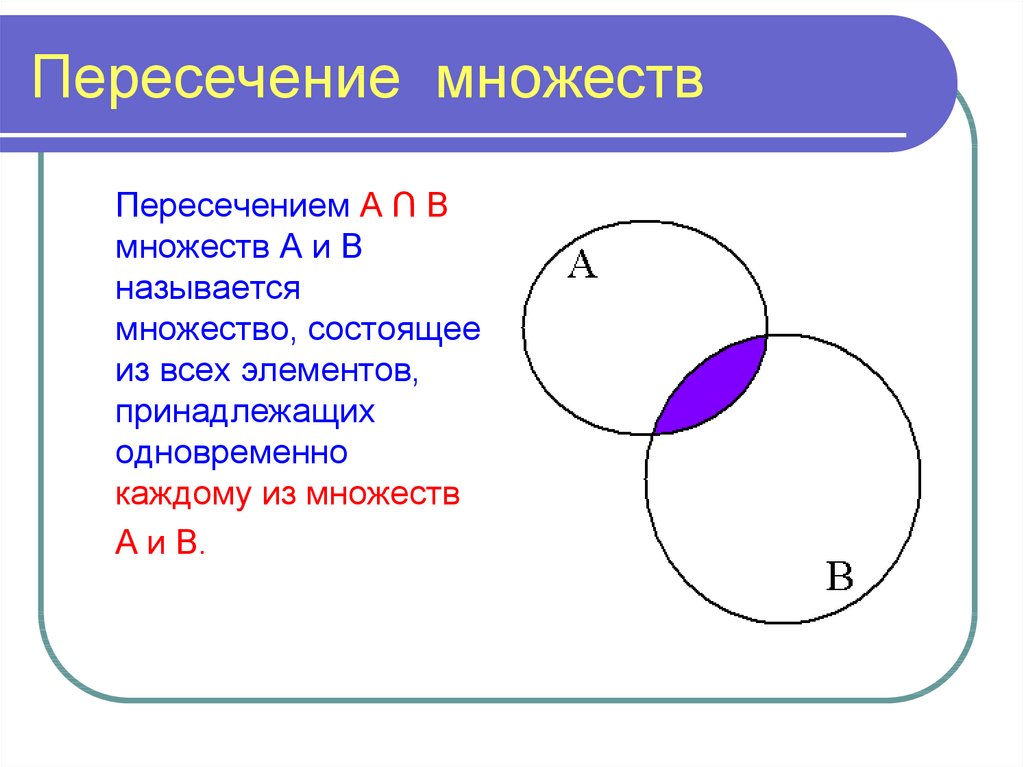
13. Пересечение множеств

Пересечением А ∩ В
множеств А и В
называется
множество, состоящее
из всех элементов,
принадлежащих
одновременно
каждому из множеств
А и В.

14.

На диаграмме Эйлера-Венна пересечение двух
множеств выглядит так
Пересечение двух множеств
обозначается так
Пример:
{1,2,3} {2,3,4} = {2,3}

15. Решение задач с помощью кругов Эйлера

Задача 1
Расположите 4 элемента в двух множествах так, чтобы в
каждом из них было по 3 элемента.
15

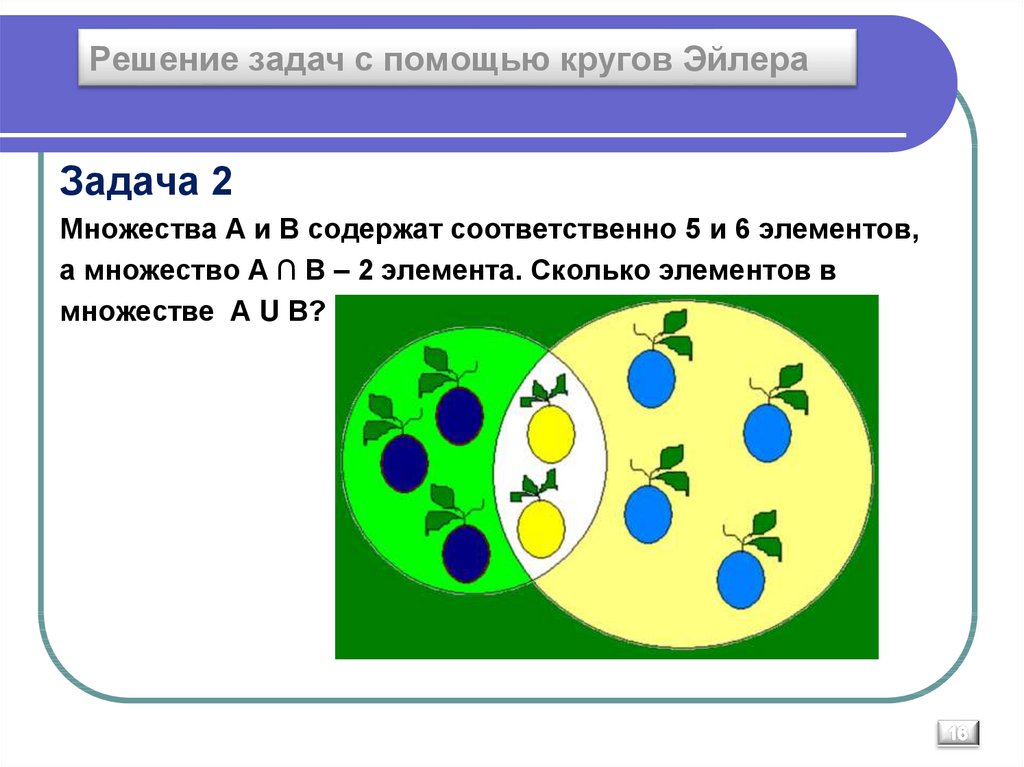
16. Решение задач с помощью кругов Эйлера

Задача 2
Множества А и В содержат соответственно 5 и 6 элементов,
а множество А ∩ В – 2 элемента. Сколько элементов в
множестве А U В?
16

17. Учебник:

№805, №806, №818(а), №833.

18. Домашнее задание:

п.п. 10.1 – 10.3
(внимательно прочитать)
№ 804, №818(б), №836, №797.