Похожие презентации:
Умножение. Основные алгоритмы
1.
1эвм
2.
2эвм
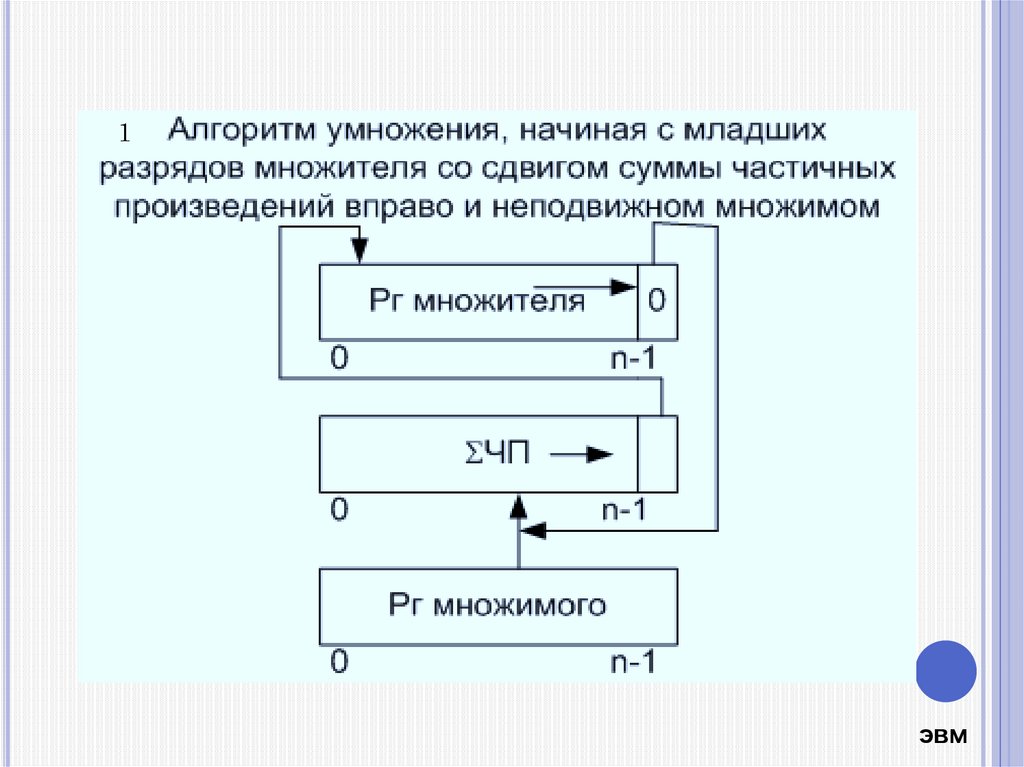
3.
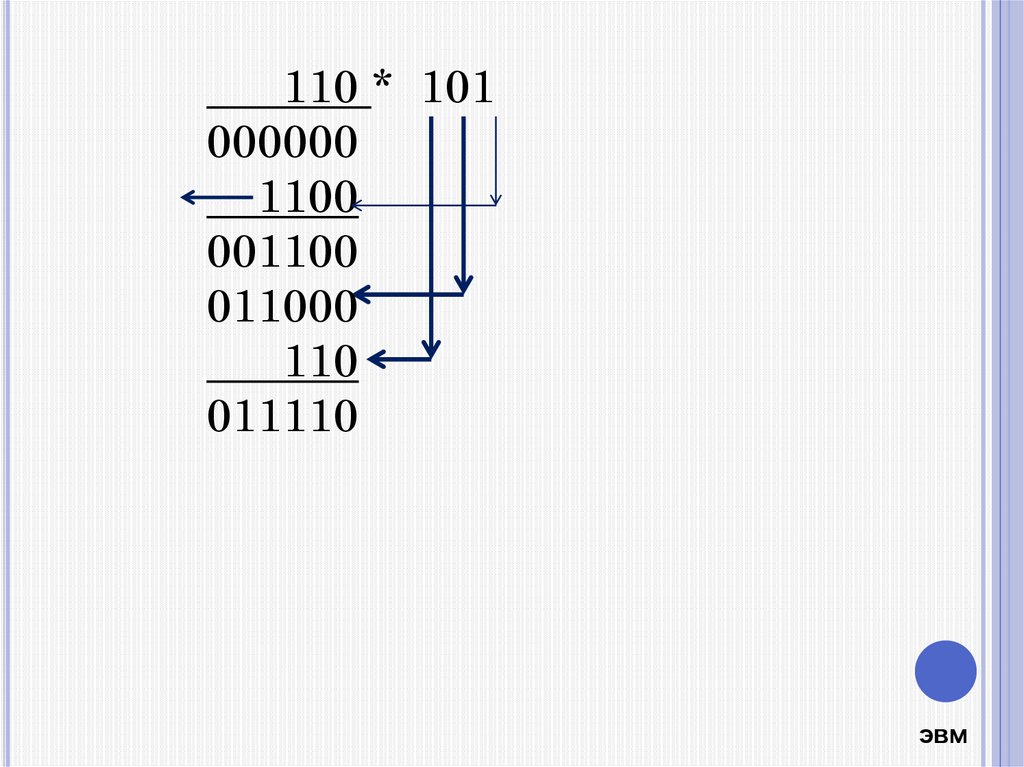
110 * 101000000
1100
001100
011000
110
011110
эвм
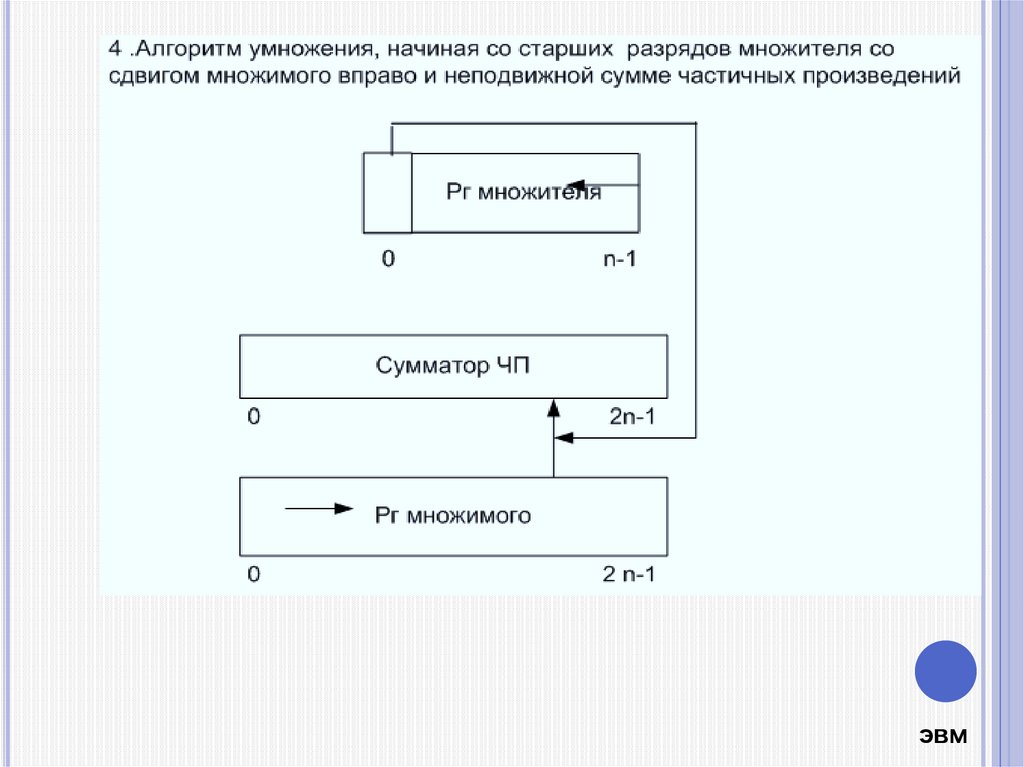
4.
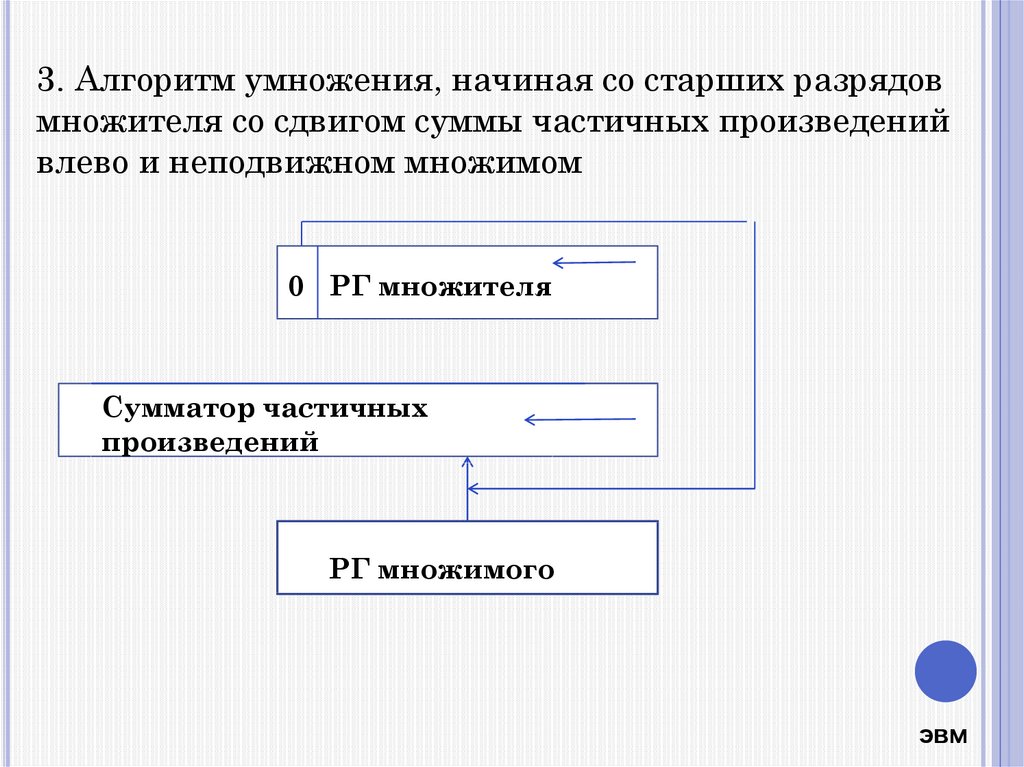
3. Алгоритм умножения, начиная со старших разрядовмножителя со сдвигом суммы частичных произведений
влево и неподвижном множимом
000000
0 РГ множителя
Сумматор частичных
произведений
РГ множимого
эвм
5.
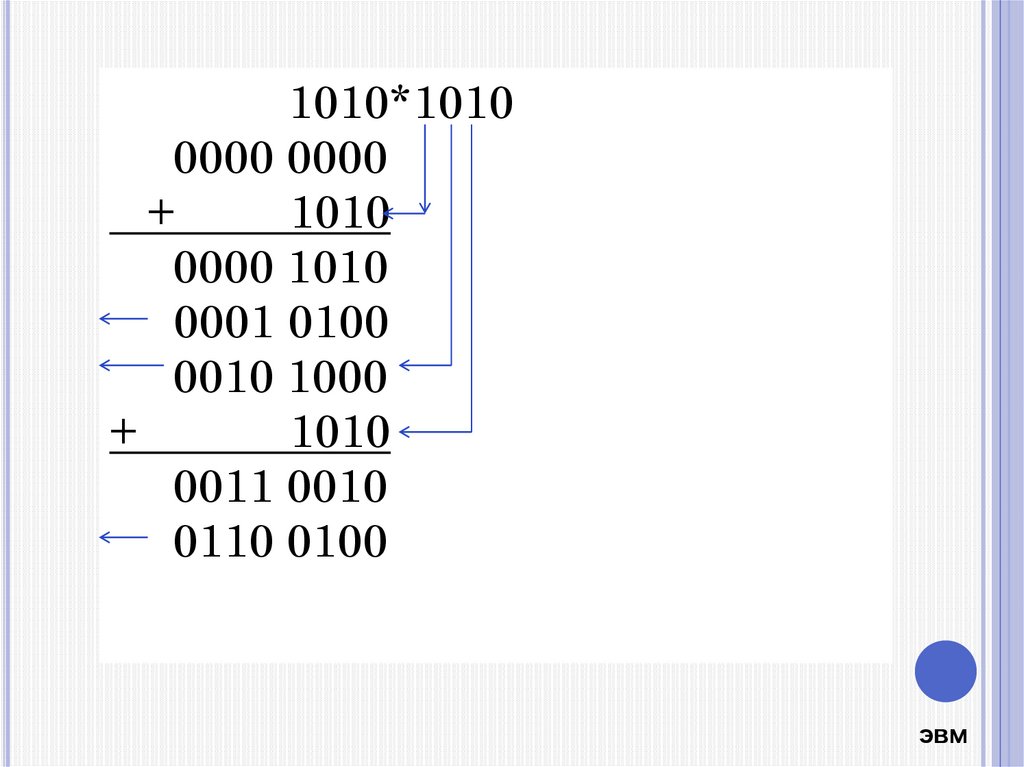
1010*10100000 0000
+
1010
0000 1010
0001 0100
0010 1000
+
1010
0011 0010
0110 0100
эвм
6.
эвм7.
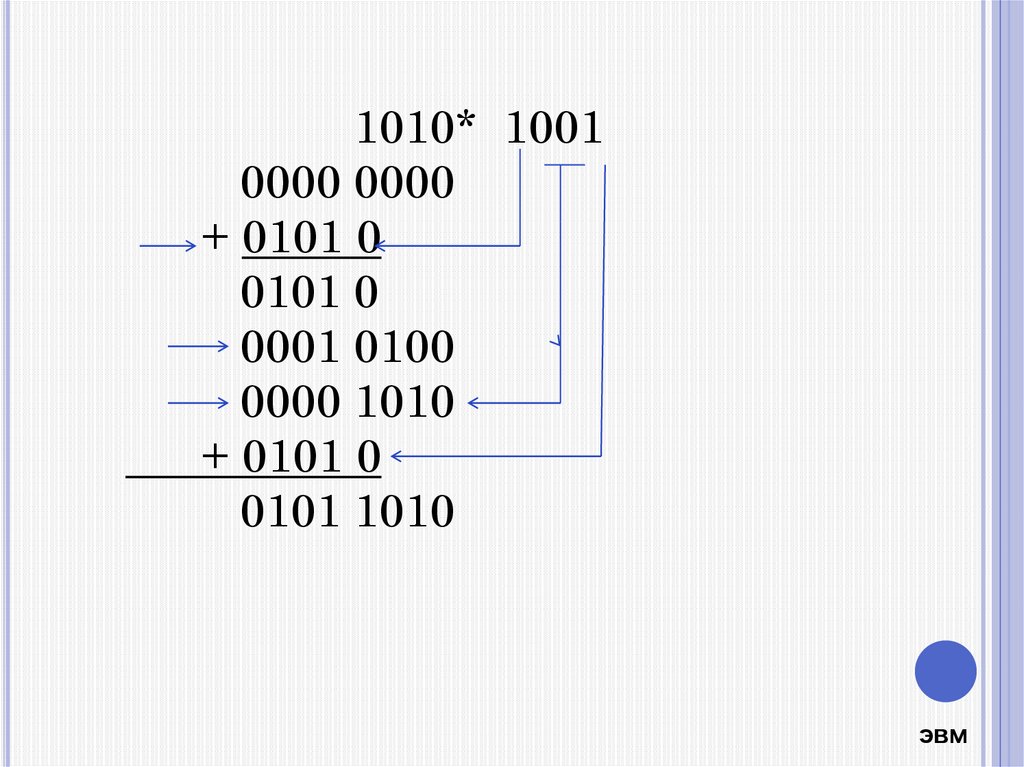
1010* 10010000 0000
+ 0101 0
0101 0
0001 0100
0000 1010
+ 0101 0
0101 1010
эвм
8.
Z XY X y1 22
n 1
xy 2
1
1
n 2
y2 2
n 3
... yn 1 2
xy2 2 ... xyn 1 2
2
0
( n 1 )
Используя схему Горнера, получим:
2n 1 ... 0 xyn 1 2 1 xyn 2 2 1 ... y1 2 1 2n 1 A
2
n 1
дополнительный сдвиг, который выполняется при
умножении целых чисел, для правильного расположения
числа в разрядной сетке.
-
,
где x – множимое, y – множитель, А – сумма частичных произведений,
эвм
9.
эвм10.
Алгоритм умножения целых чисел с младших разрядов множителя.Умножению подвергаются сомножители представленные в прямом коде с
фиксированной точкой.
1. Берутся модули от сомножителей, запоминаются значения знаков.
2. Исходное значение суммы частичных произведений равно нулю.
3. Если анализируемая цифра множителя равна 1, то к сумме
прибавляется множимое.
4. Производится сдвиг суммы частичных произведений вправо на 1
разряд.
5. Пункты 3 и 4 последовательно выполняются для всех цифровых
разрядов множителя.
6. Произведению присваивается знак “+” если сомножители имеют
одинаковые знаки, в противном случае “-”.
7. В алгоритме необходимо производить проверку сомножителей на
ноль.
эвм
11.
Алгоритм умножения, начиная с младших разрядов множителя, сосдвигом суммы частичных произведений и использованием
сумматора дополнительного кода.
1.Исходное значение суммы частичных произведений принимается
равным 0.
2.Если анализируемая цифра множителя равна 1, то к сумме
частичных произведений прибавляется множимое, в том коде, в
котором оно представлено, если эта цифра равна 0, прибавление не
производится.
3.Сумма частичных произведений сдвигается на 1 разряд вправо, при
этом,
если
множимое
отрицательно,
осуществляется
модифицированный сдвиг.
4.Пункты 2 и 3 последовательно выполняются для всех цифровых
разрядов множителя, начиная с младшего.
5.Если
множитель
положителен,
полученный
результат
–
произведение. Если множитель отрицателен, то для получения
произведения к результату необходимо прибавить множимое с
обратным знаком. Произведение получается в дополнительном коде.
эвм




 Информатика
Информатика








