Четыре замечательные точки треугольника. Блиц-опрос. Найдите угол МАВ

1.

2.

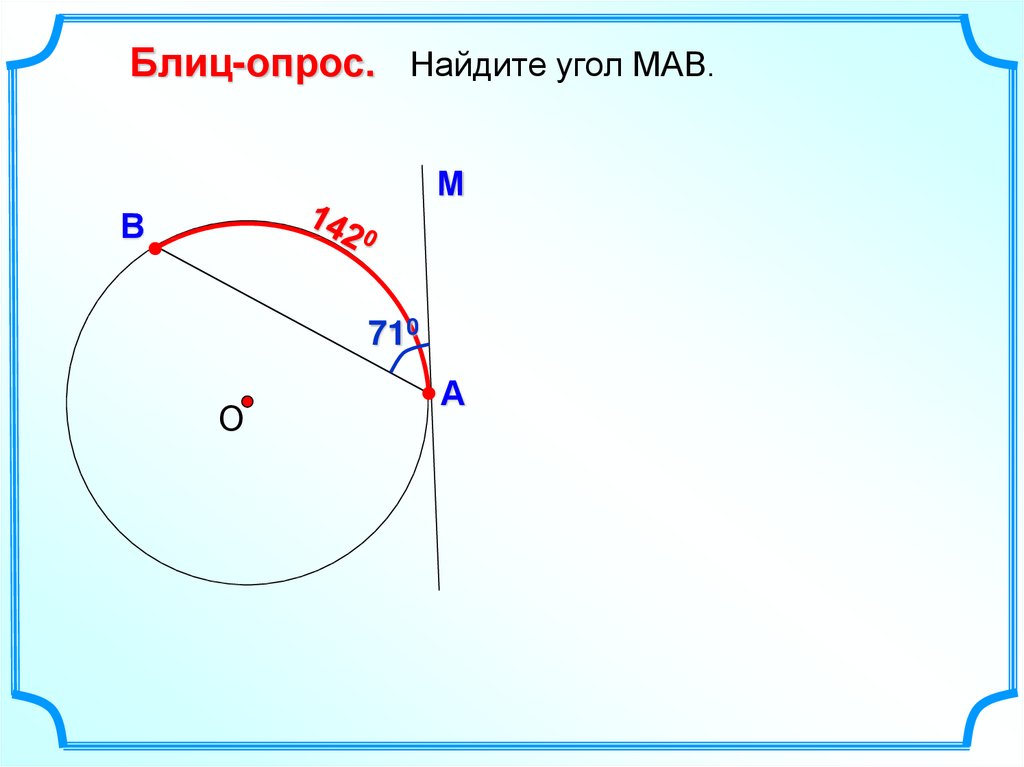
Блиц-опрос. Найдите угол МАВ.
М
В
710
О
А

3.

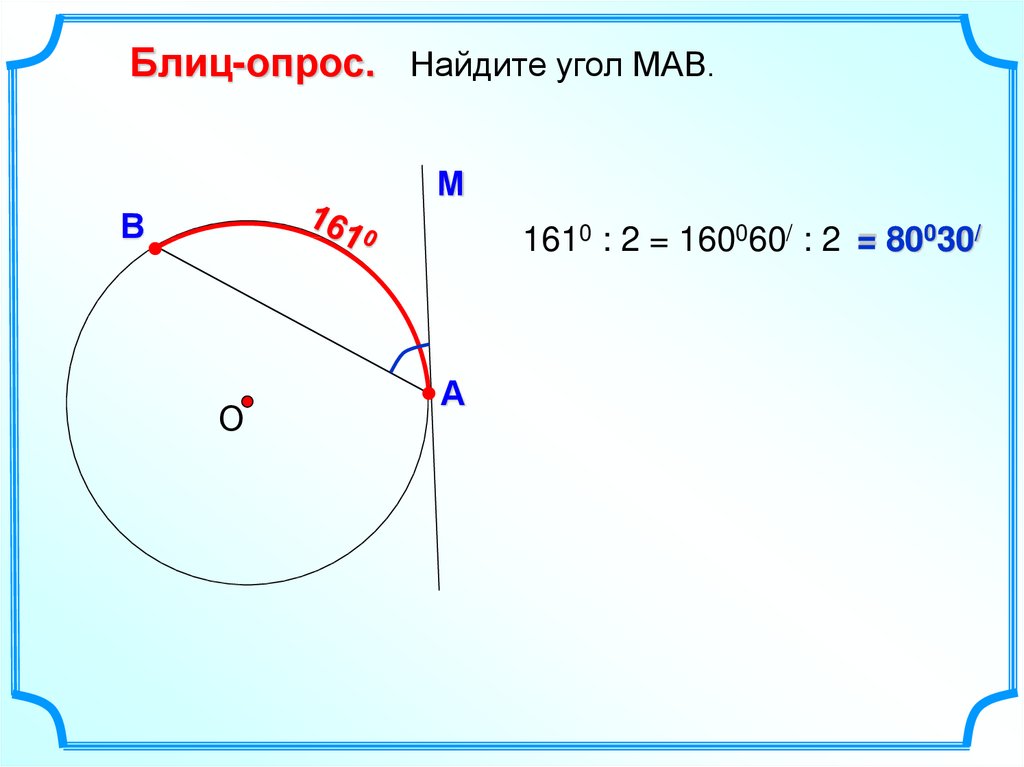
Блиц-опрос. Найдите угол МАВ.
М
В
1610 : 2 = 160060/ : 2 = 80030/
О
А

4.

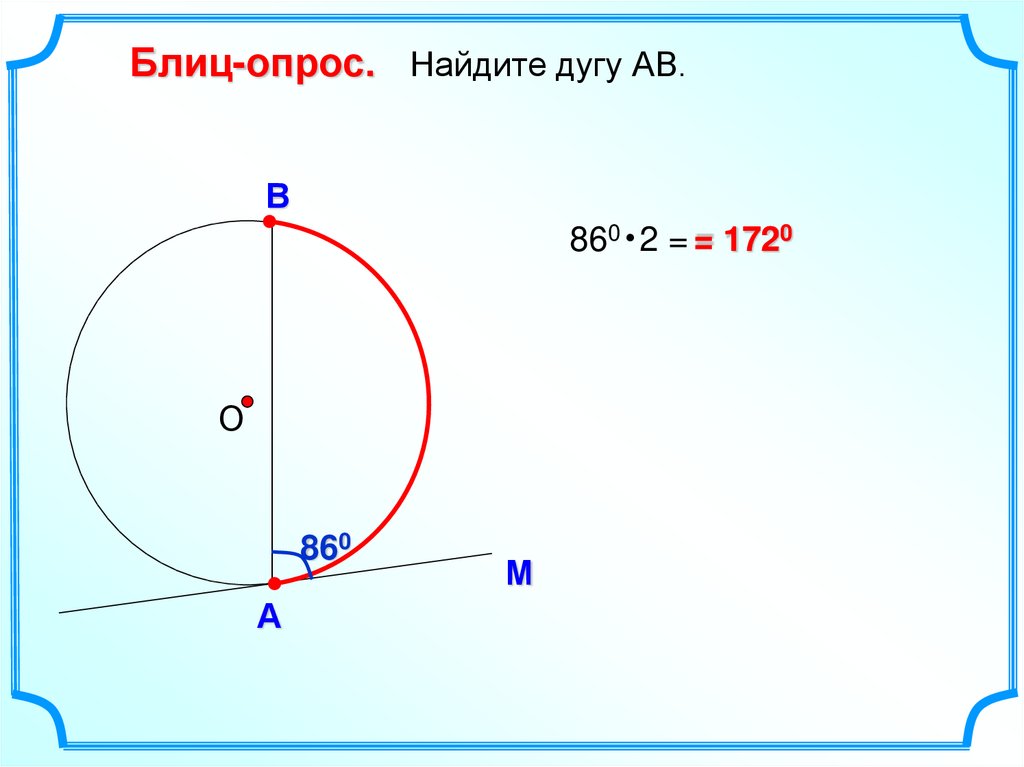
Блиц-опрос. Найдите дугу АВ.
В
860 2 = = 1720
О
860
А
М

5.

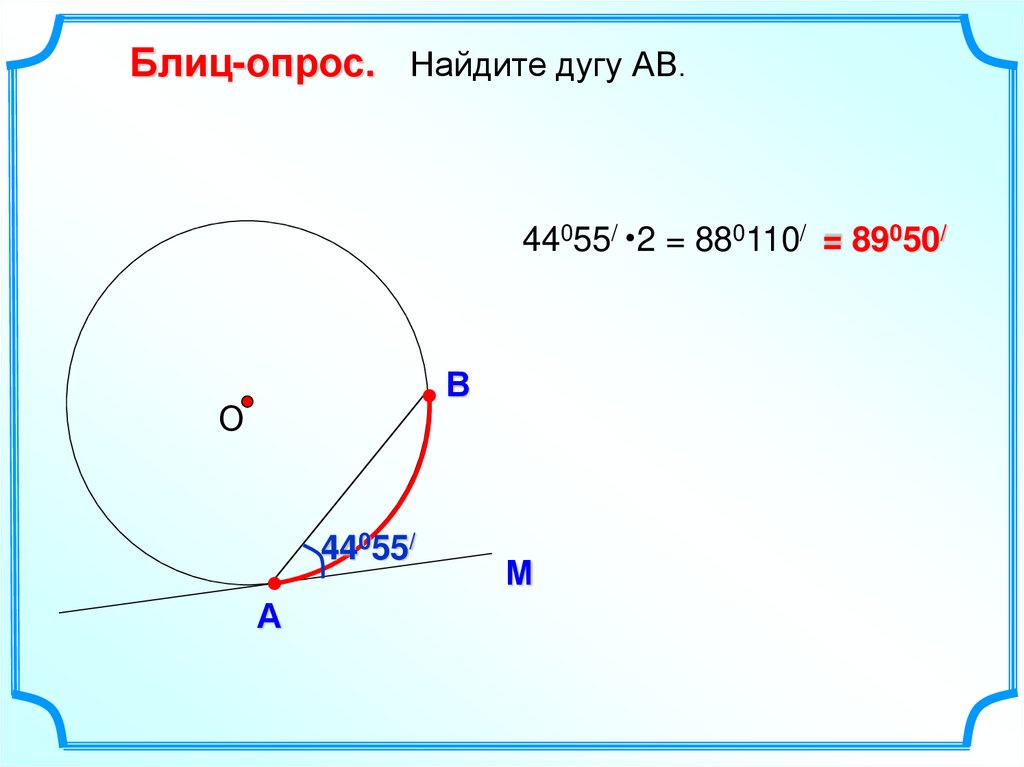
Блиц-опрос. Найдите дугу АВ.
44055/ 2 = 880110/ = 89050/
В
О
44055/
А
М

6.

Свойство медиан треугольника.
Медианы треугольника пересекаются в одной точке,
которая делит каждую медиану в отношении 2:1, считая
от вершины.
С
2
АО
СО
ВО
=
=
=
1
В О А1О С1О
1
В1
А1
О
А
1
С1
В

7.

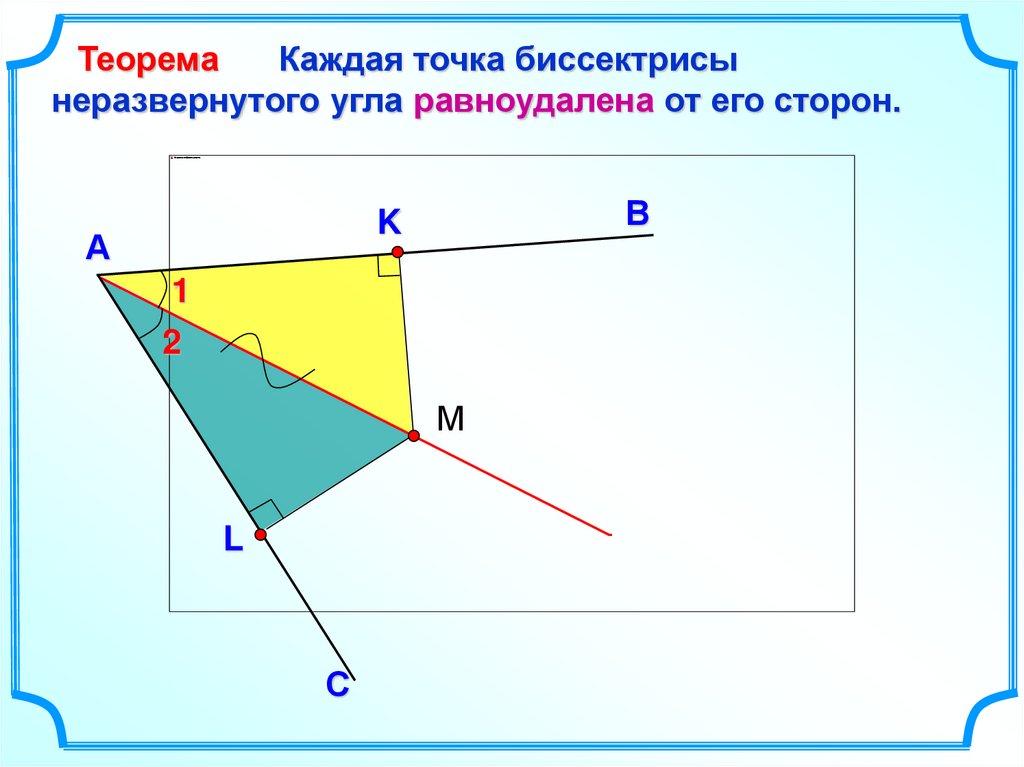
Теорема
Каждая точка биссектрисы
неразвернутого угла равноудалена от его сторон.
В
K
А
1
2
М
L
С

8.

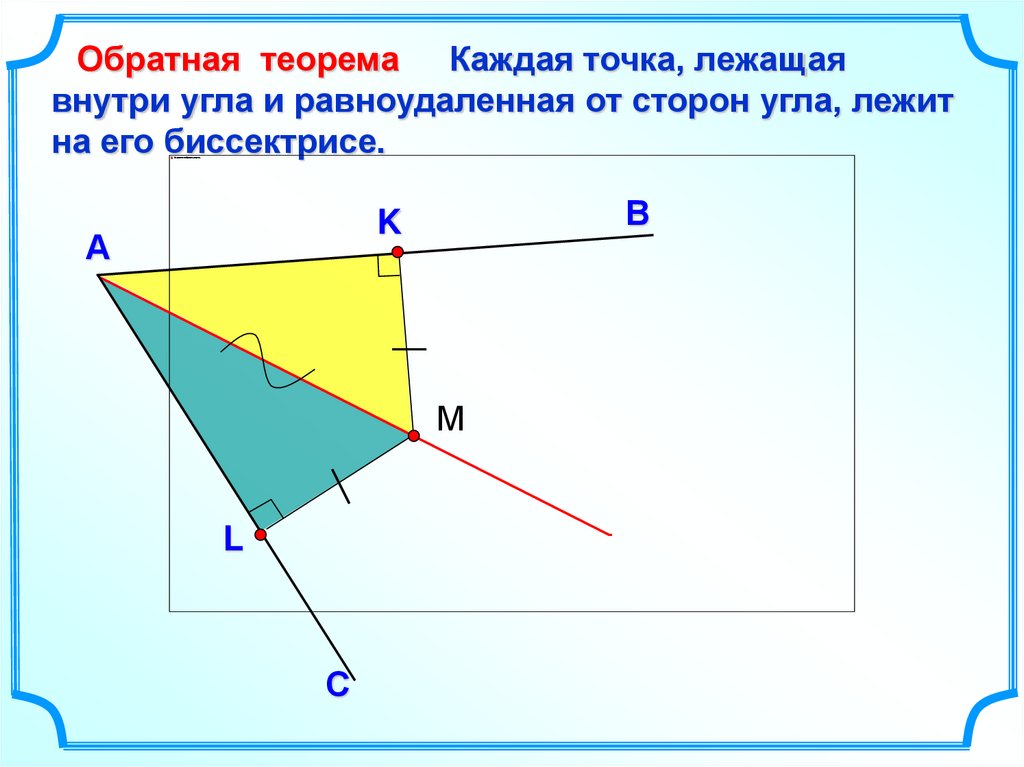
Обратная теорема Каждая точка, лежащая
внутри угла и равноудаленная от сторон угла, лежит
на его биссектрисе.
В
K
А
М
L
С

9.

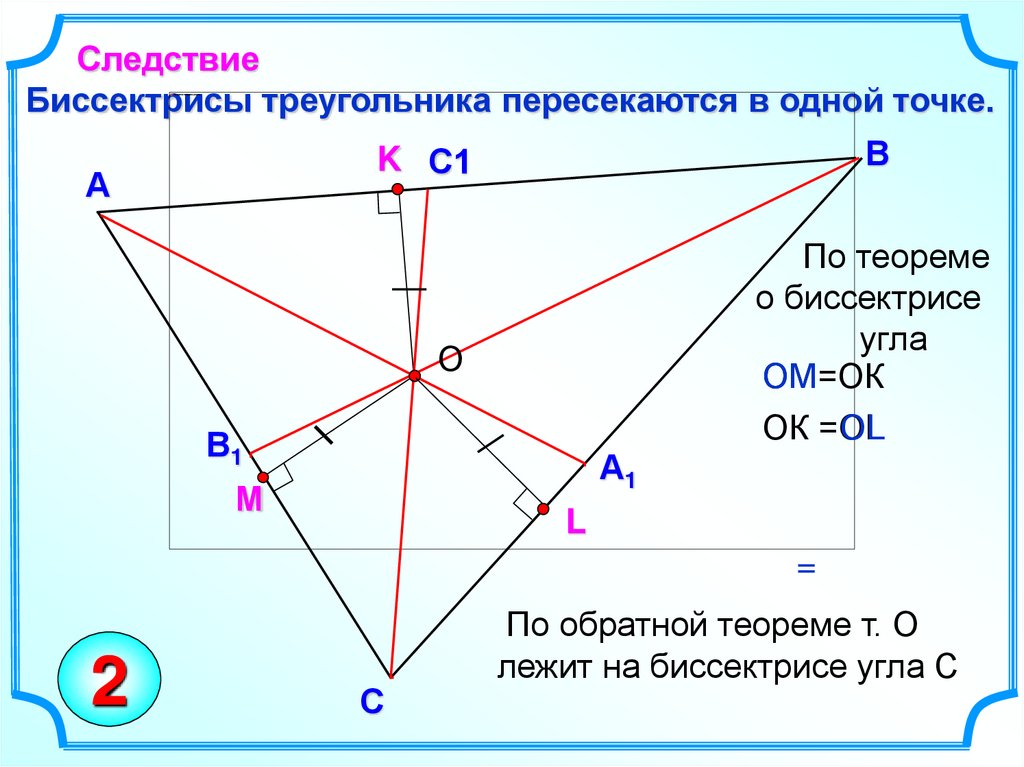
Следствие
Биссектрисы треугольника пересекаются в одной точке.
В
K С1
А
По теореме
о биссектрисе
угла
ОМ=ОК
ОМ
ОК =ОL
ОL
О
В1
А1
М
L
=
2
С
По обратной теореме т. О
лежит на биссектрисе угла С

10.

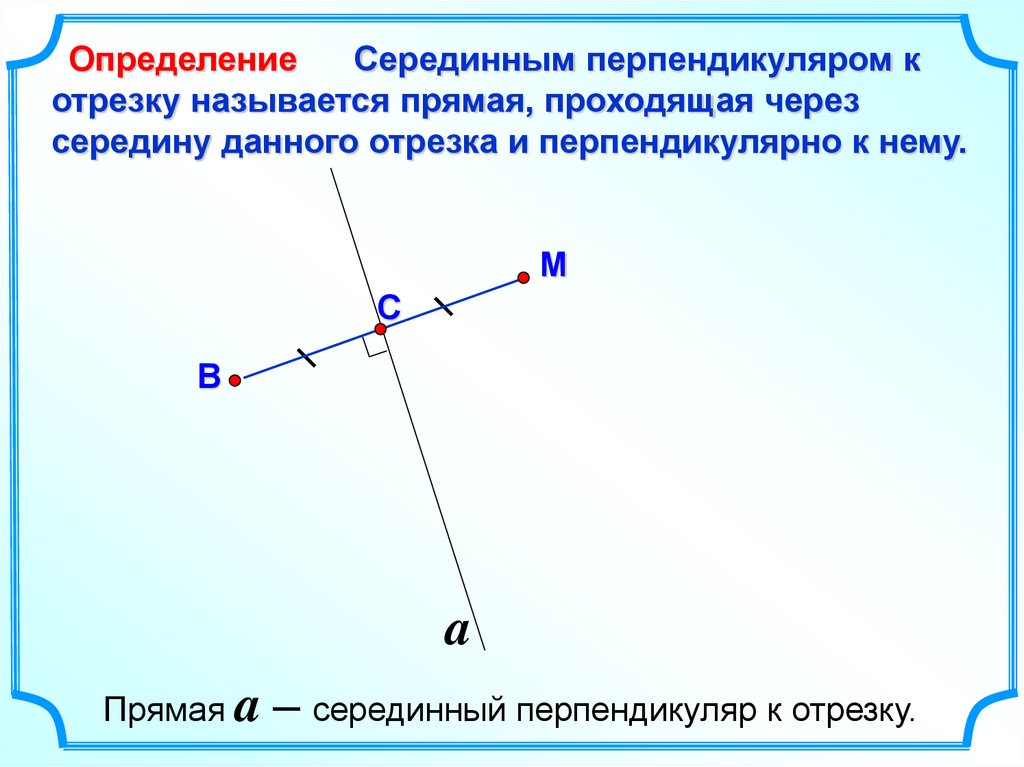
Определение
Серединным перпендикуляром к
отрезку называется прямая, проходящая через
середину данного отрезка и перпендикулярно к нему.
М
С
В
a
Прямая a
– серединный перпендикуляр к отрезку.

11.

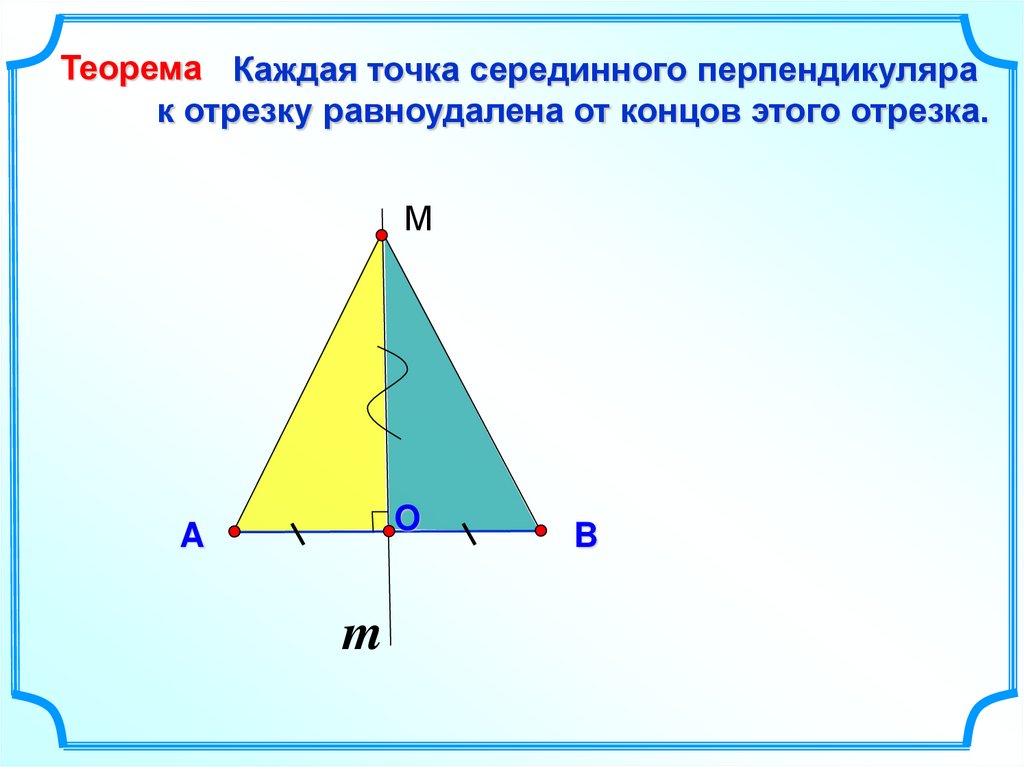
Теорема Каждая точка серединного перпендикуляра
к отрезку равноудалена от концов этого отрезка.
М
O
A
m
B

12.

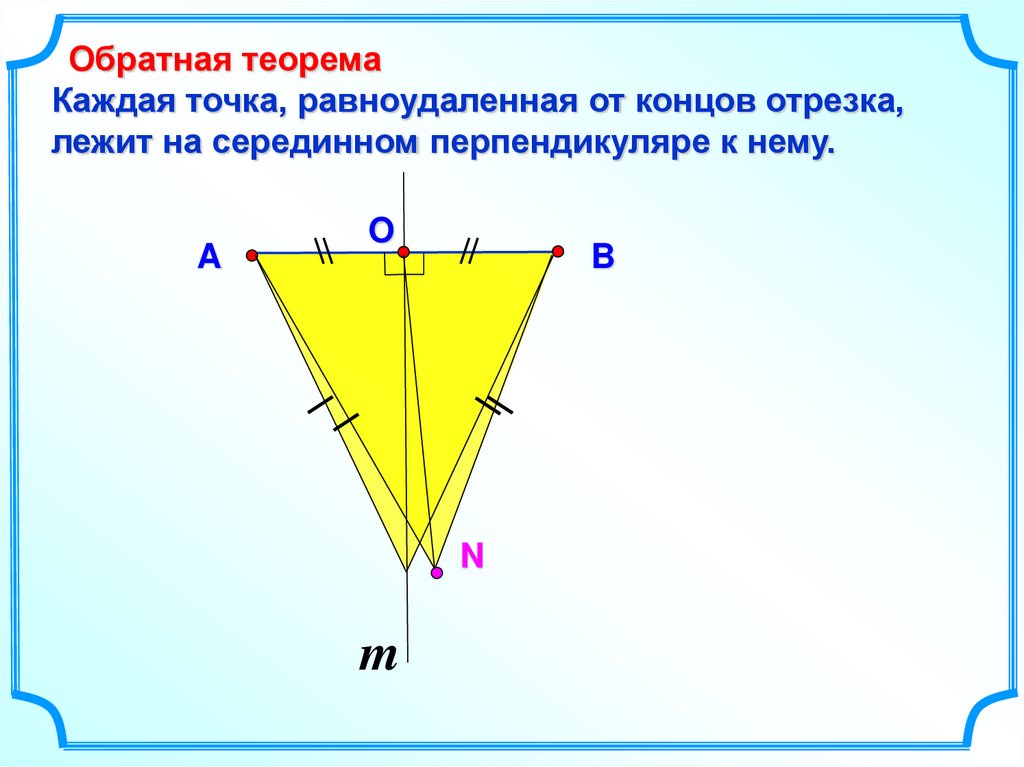
Обратная теорема
Каждая точка, равноудаленная от концов отрезка,
лежит на серединном перпендикуляре к нему.
A
O
B
N
m

13.

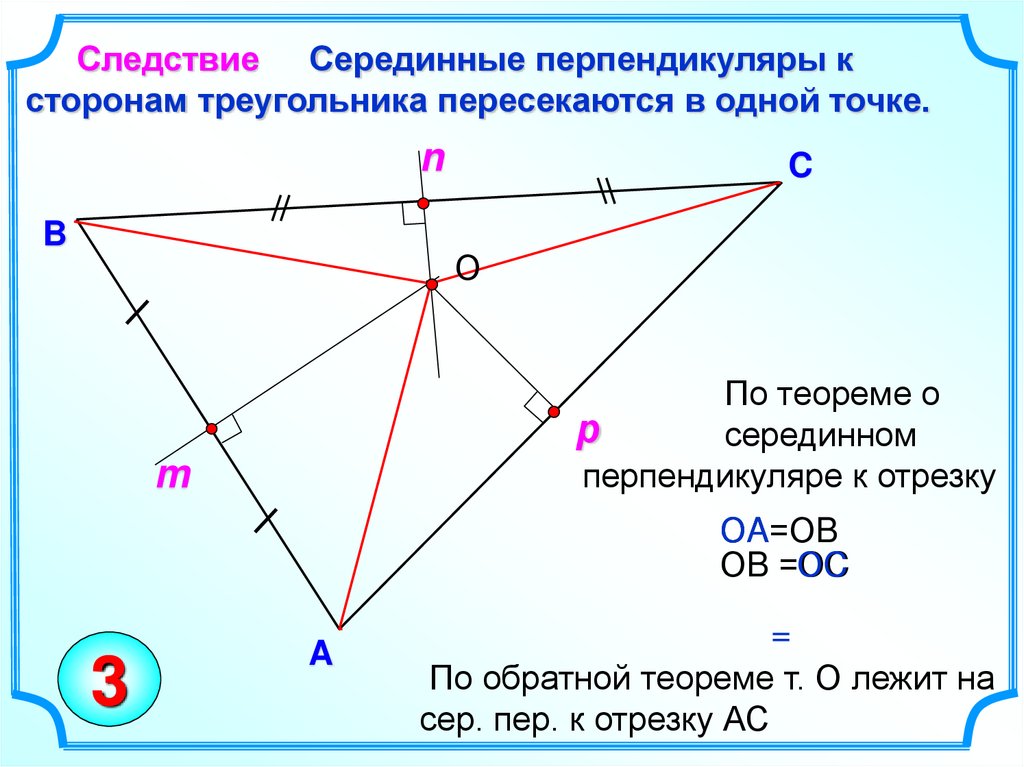
Следствие Серединные перпендикуляры к
сторонам треугольника пересекаются в одной точке.
n
B
C
О
По теореме о
р
серединном
перпендикуляре к отрезку
m
ОA
ОA=ОB
ОB =ОC
ОC
3
A
=
По обратной теореме т. О лежит на
сер. пер. к отрезку АС

14.

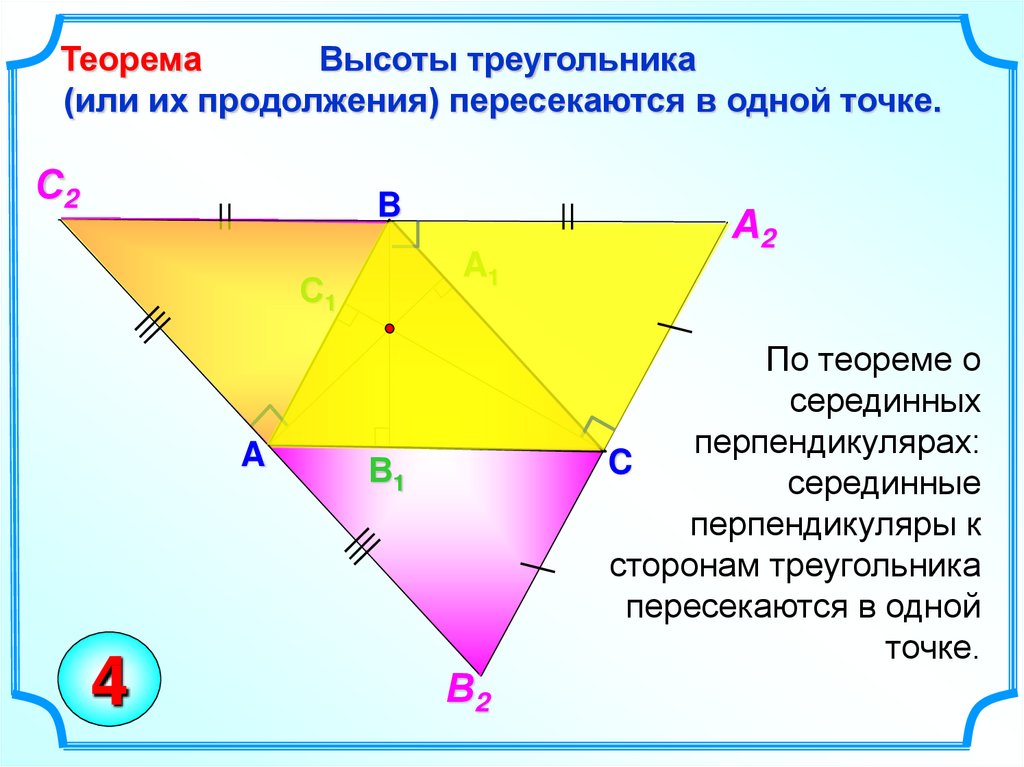
Теорема
Высоты треугольника
(или их продолжения) пересекаются в одной точке.
С2
B
A1
С1
A
4
В1
В2
А2
По теореме о
серединных
перпендикулярах:
C
серединные
перпендикуляры к
сторонам треугольника
пересекаются в одной
точке.

15.

Точка
пересечения
Точка
пересечения
Замечательные
точки
треугольника.
Точка
пересечения
Точка
пересечения
серединных

16.

Треугольник, который опирается на острие иглы в точке
пересечения медиан, находится в равновесии!
Точка, обладающая таким свойством, называется
центром тяжести треугольника.

17.

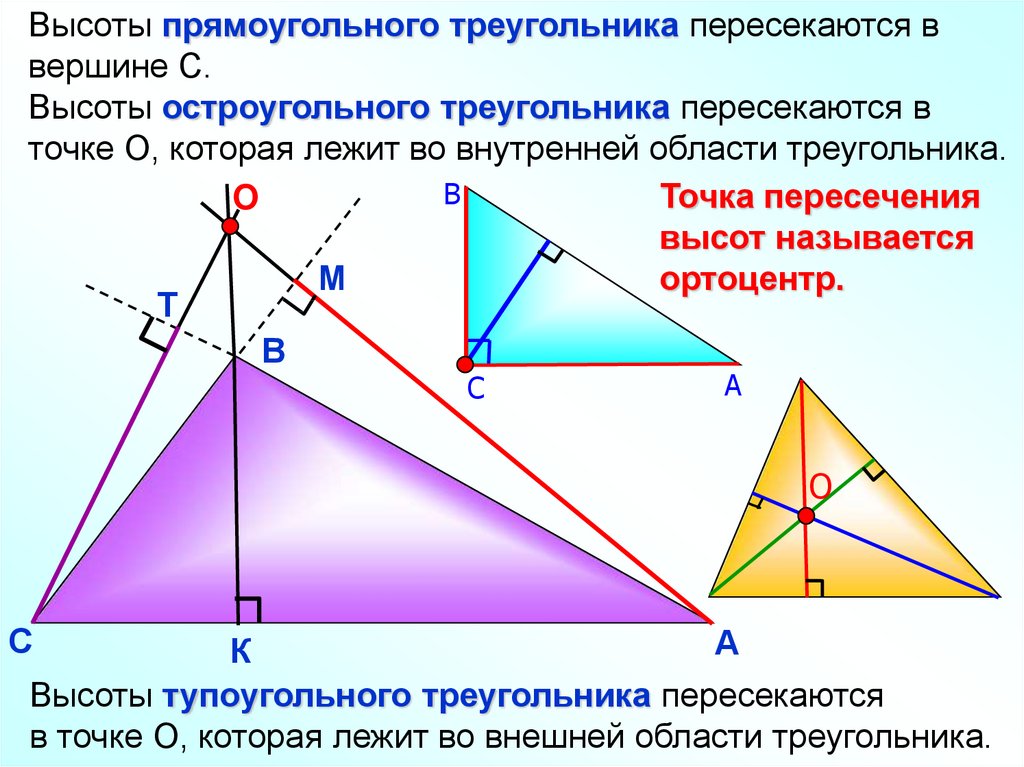
Высоты прямоугольного треугольника пересекаются в
вершине С.
Высоты остроугольного треугольника пересекаются в
точке О, которая лежит во внутренней области треугольника.
В
Точка пересечения
O
высот называется
М
ортоцентр.
Т
В
С
А
O
С
А
К
Высоты тупоугольного треугольника пересекаются
в точке О, которая лежит во внешней области треугольника.

18.

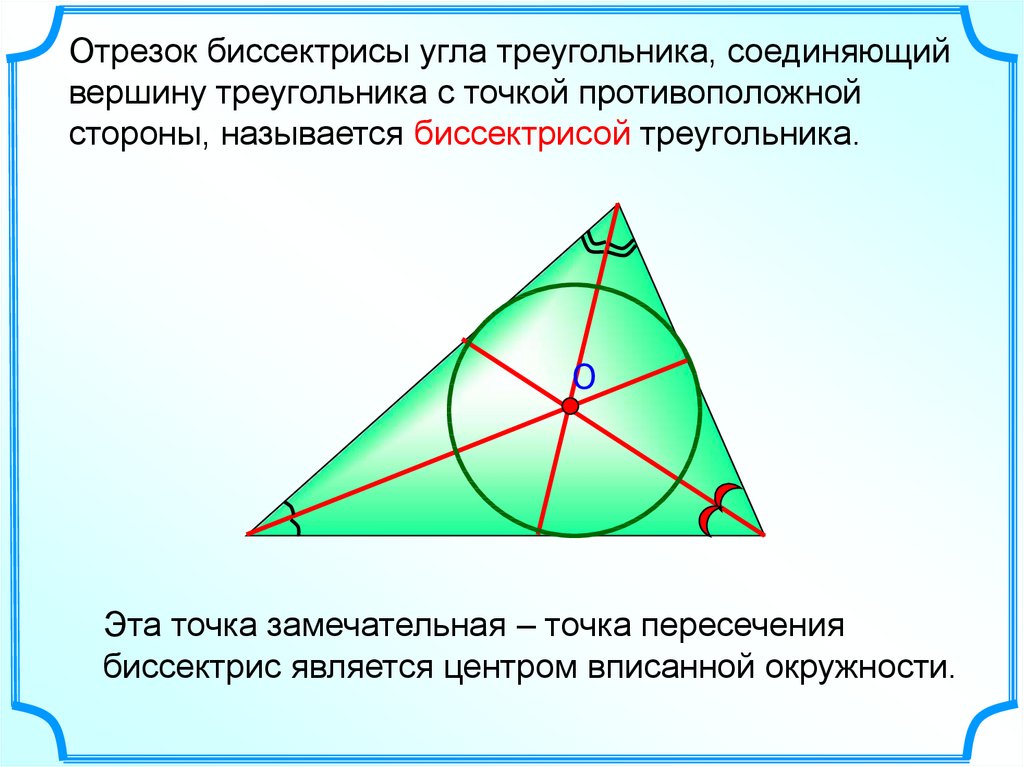
Отрезок биссектрисы угла треугольника, соединяющий
вершину треугольника с точкой противоположной
стороны, называется биссектрисой треугольника.
O
Эта точка замечательная – точка пересечения
биссектрис является центром вписанной окружности.

19.

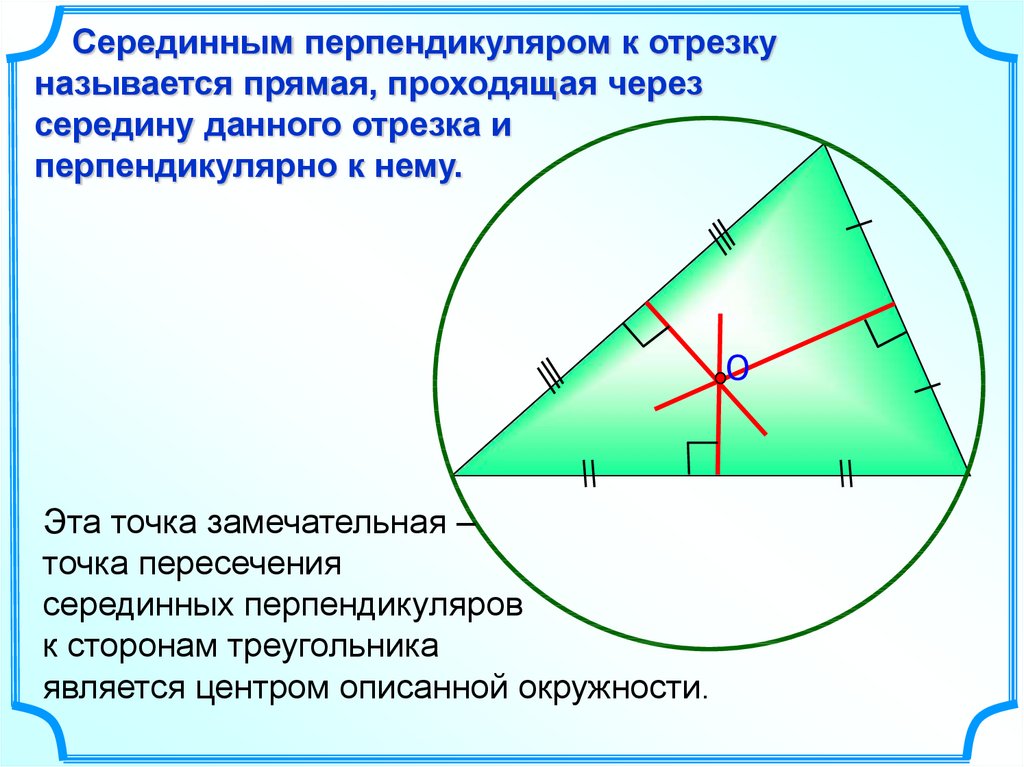
Серединным перпендикуляром к отрезку
называется прямая, проходящая через
середину данного отрезка и
перпендикулярно к нему.
O
Эта точка замечательная –
точка пересечения
серединных перпендикуляров
к сторонам треугольника
является центром описанной окружности.

20.

21.

22.

23.

24.

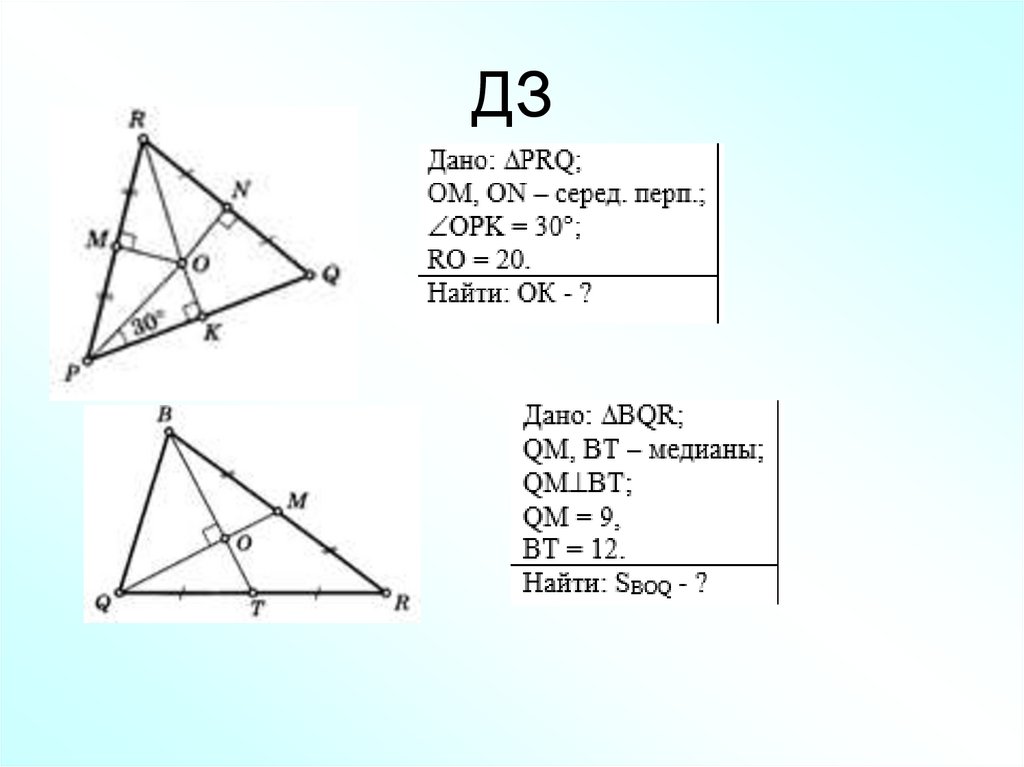
25. ДЗ

26.

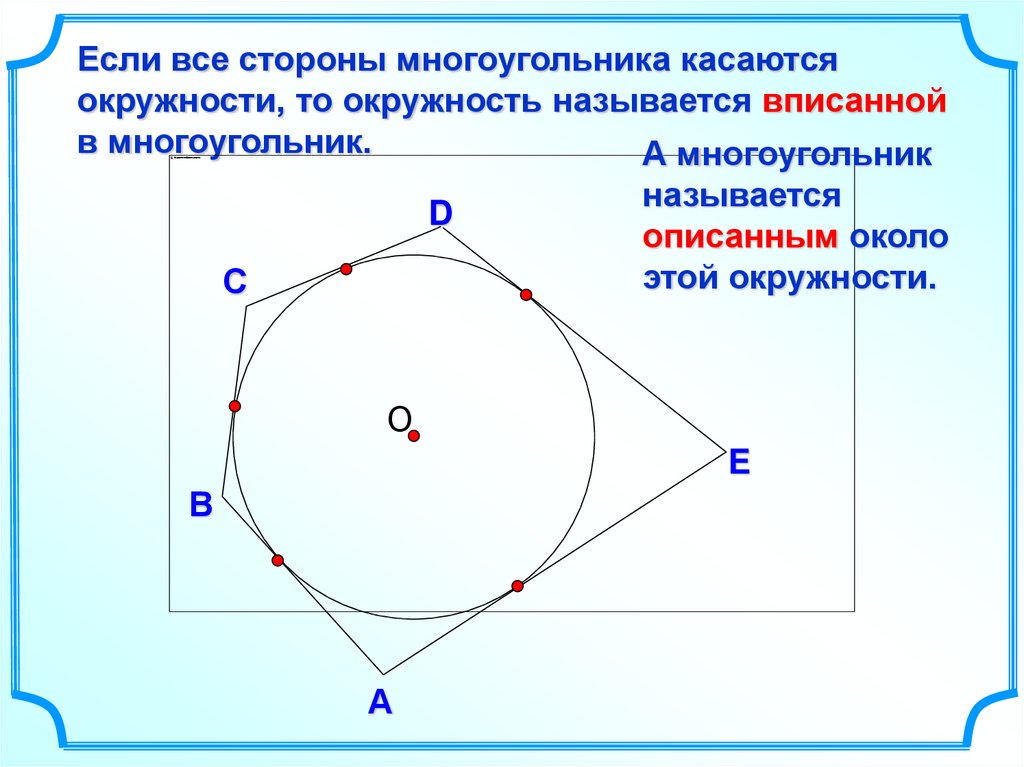
Если все стороны многоугольника касаются
окружности, то окружность называется вписанной
в многоугольник.
А многоугольник
D
С
называется
описанным около
этой окружности.
О
E
В
А

27.

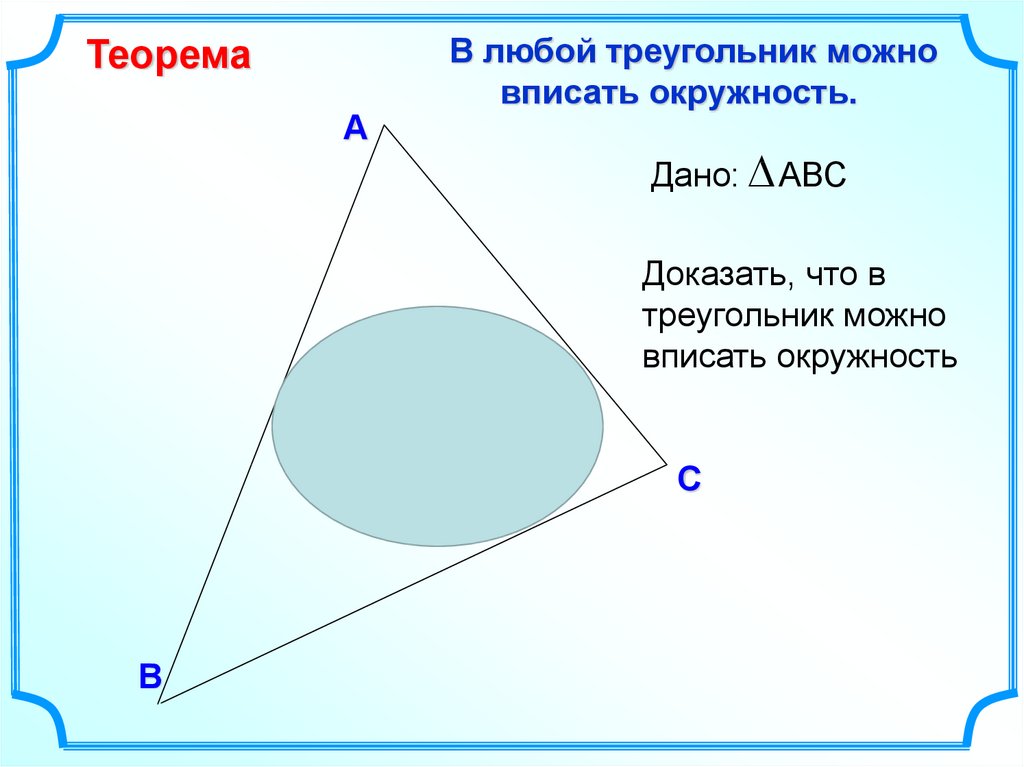
Теорема
А
В любой треугольник можно
вписать окружность.
Дано: АВС
Доказать, что в
треугольник можно
вписать окружность
С
В

28.

29.

Какой из двух четырехугольников АВСD или АЕКD
является описанным?
К
С
E
В
О
D
А

30.

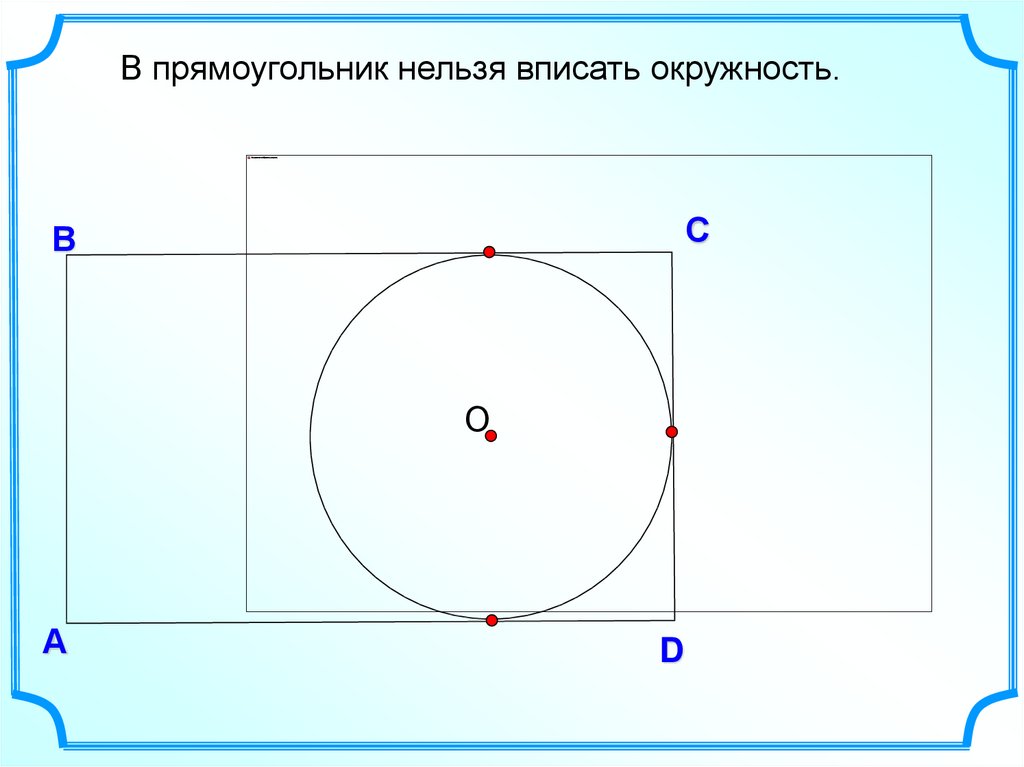
В прямоугольник нельзя вписать окружность.
С
В
О
А
D

31.

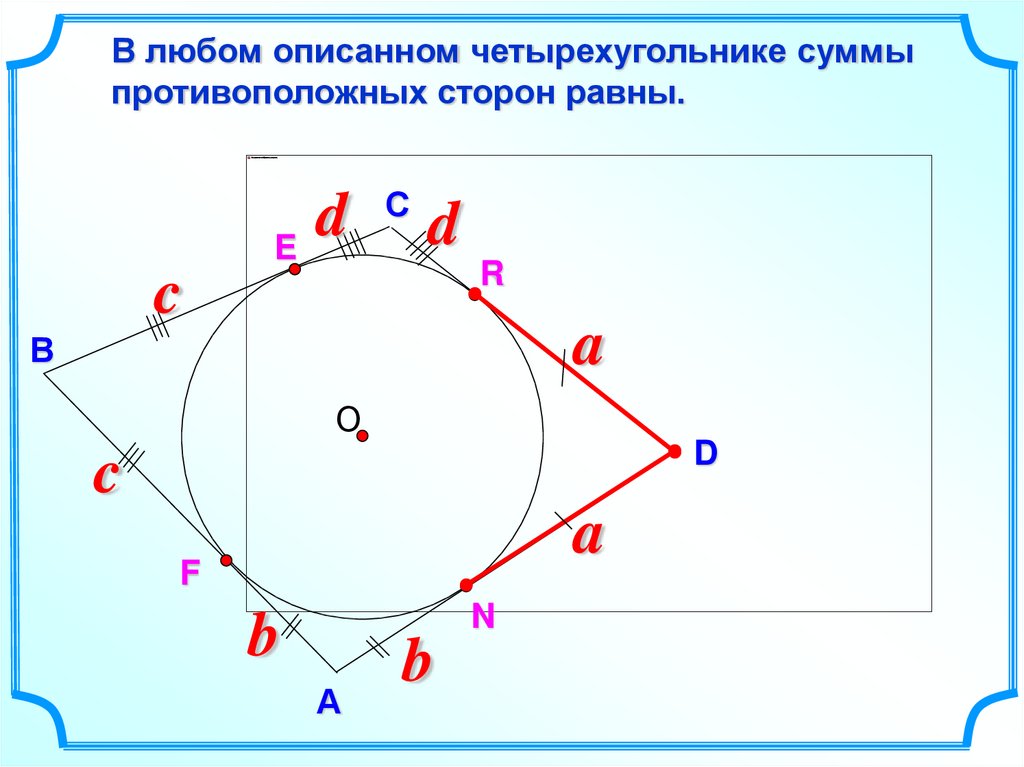
В любом описанном четырехугольнике суммы
противоположных сторон равны.
E
d
С
d
R
c
a
В
О
D
c
a
F
N
b
А
b

32.

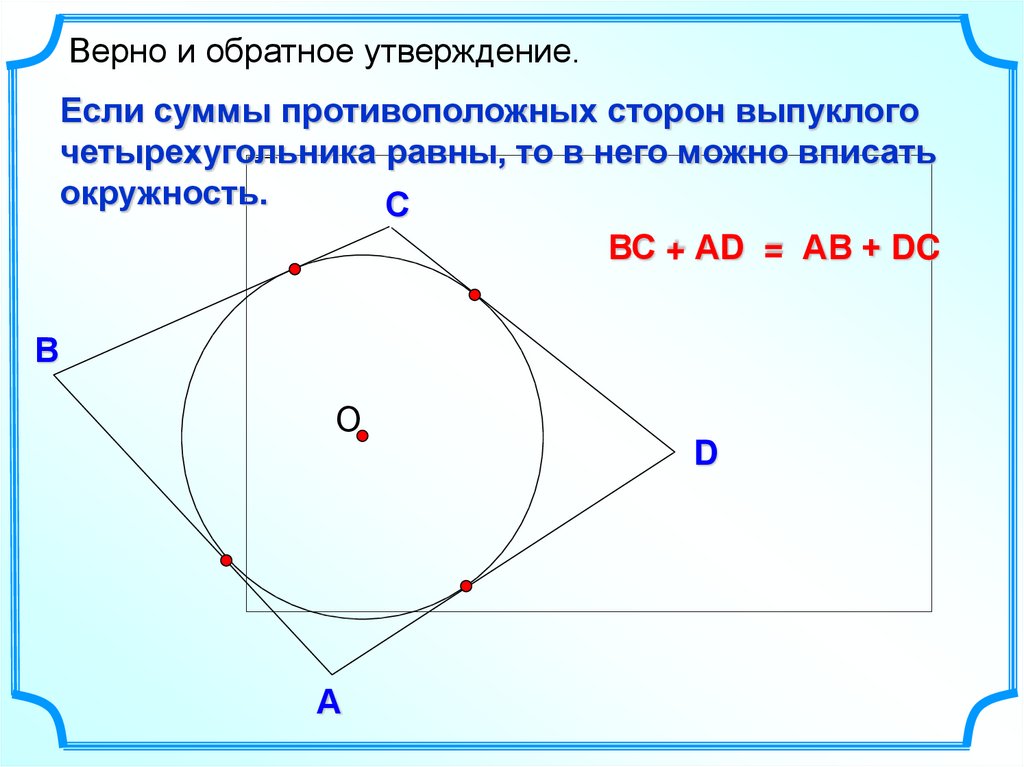
Верно и обратное утверждение.
Если суммы противоположных сторон выпуклого
четырехугольника равны, то в него можно вписать
окружность.
С
ВС + АD = АВ + DC
В
О
D
А

33.

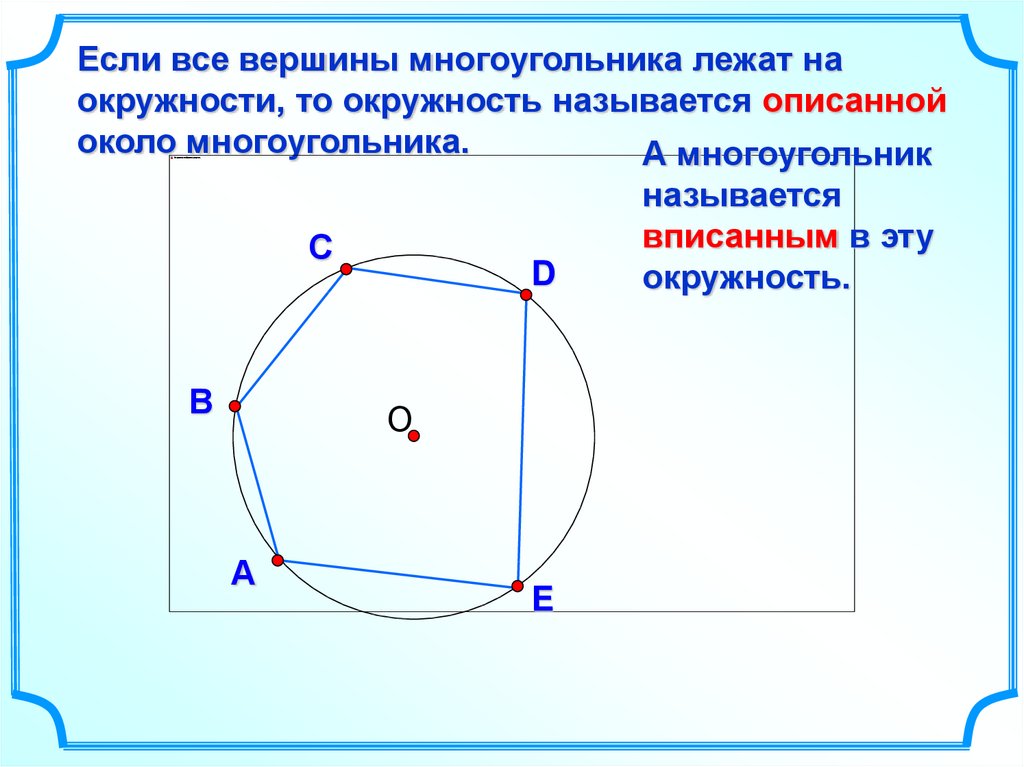
Если все вершины многоугольника лежат на
окружности, то окружность называется описанной
около многоугольника.
А многоугольник
С
В
D
О
А
E
называется
вписанным в эту
окружность.

34.

Теорема
А
Около любого треугольника
можно описать
окружность.
M
K
О
С
L
В

35.

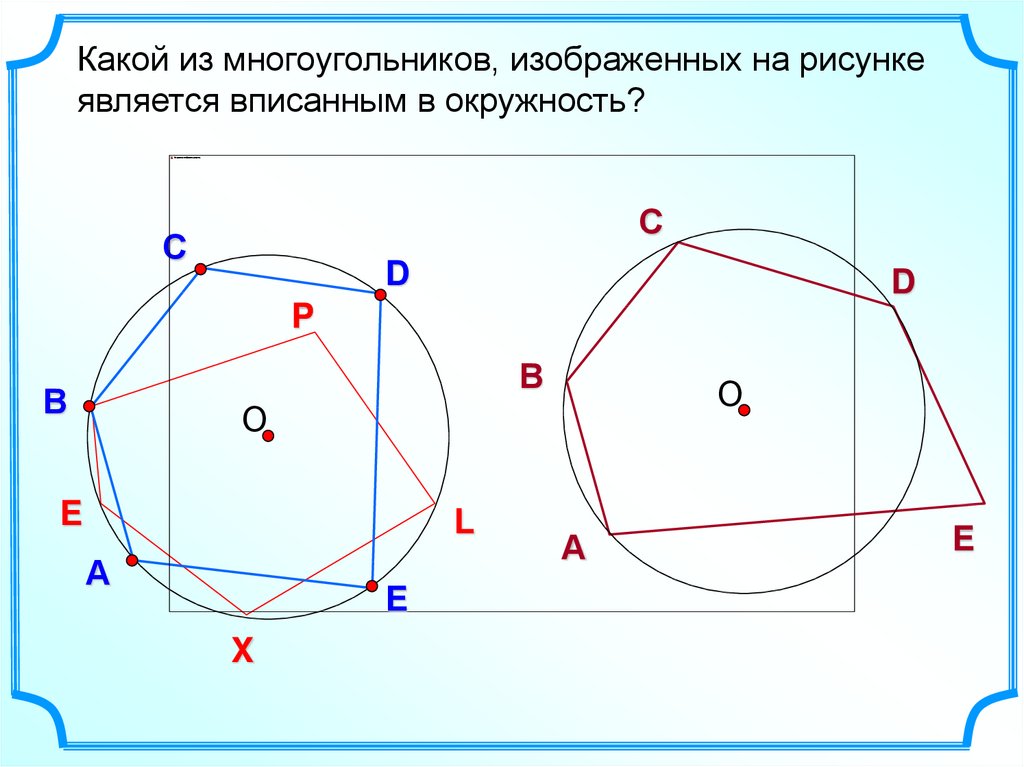
Какой из многоугольников, изображенных на рисунке
является вписанным в окружность?
С
С
D
D
P
В
В
О
О
E
L
А
E
X
А
E

36.

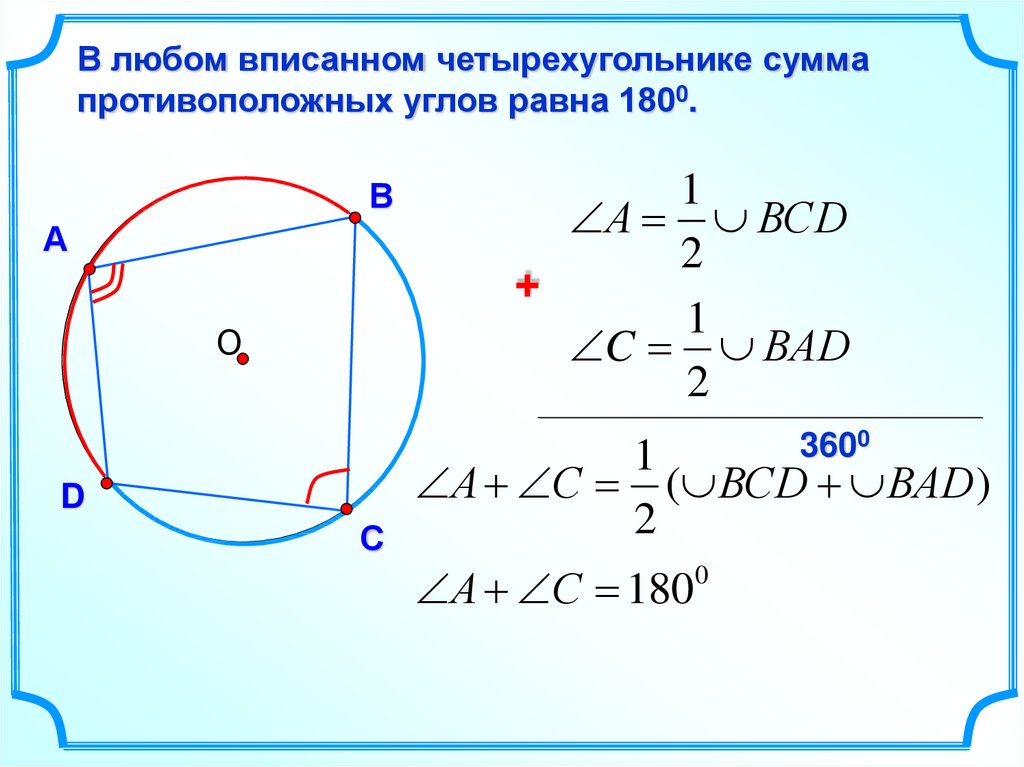
В любом вписанном четырехугольнике сумма
противоположных углов равна 1800.
В
А
О
1
А ВCD
2
+
1
C ВAD
2
3600
D
С
1
А С ( ВСD ВАD )
2
А С 1800

37.

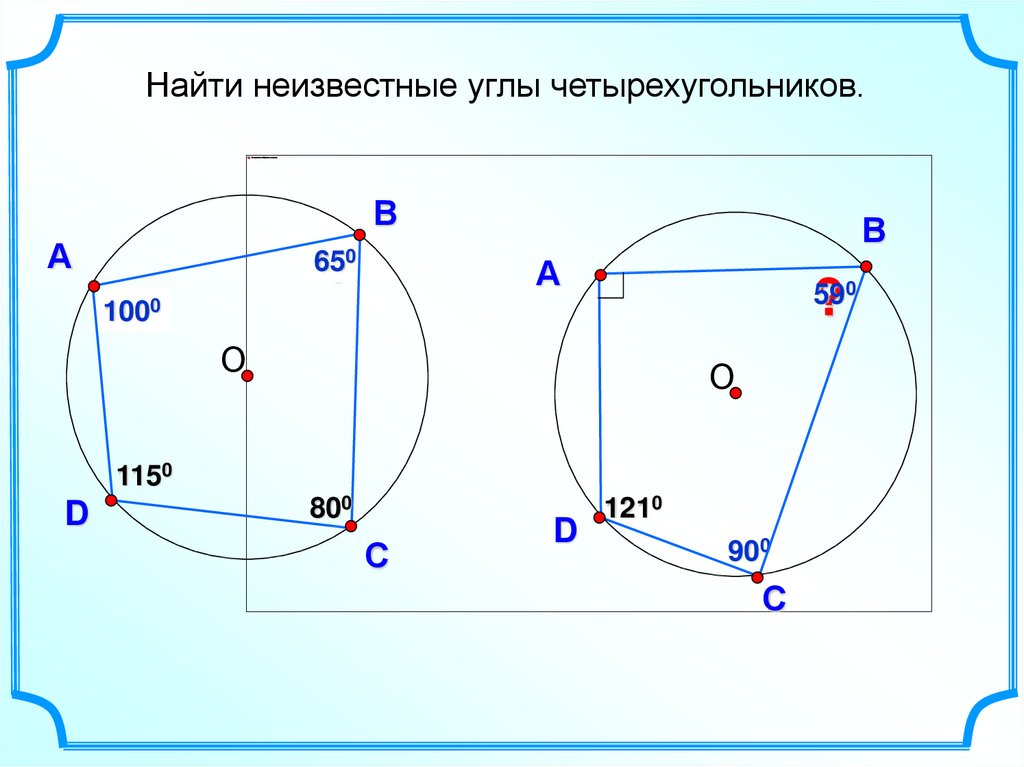
Найти неизвестные углы четырехугольников.
В
А
?
650
?
В
А
?
590
1000
О
О
1150
D
800
С
D
1210
?
9 00
С

38.

Верно и обратное утверждение.
Если сумма противоположных углов
четырехугольника равна 1800, то около него можно
вписать окружность.
В
А
670
А
1000
D
В
990
О
1130
770
О
800
1230
С
D
790
С