Исследование функций и построение графиков с помощью производной

1. Исследование функций и построение графиков с помощью производной

2. Цели обучения:

10.4.1.33
исследовать свойства функции с помощью
производной и строить её график;
Критерии оценивания:
Учащийся достиг цели обучения, если:
• знает алгоритм исследования функции
• исследует функцию с помощью производной
• выполняет эскизы графиков, используя свойства функций

3. Актуализация знаний

Кроссворд
Тест

4. План исследования

• Найти область определения. Область значений (если возможно найти)
• Исследовать на четность и нечетность, периодичность (для
тригонометрических) функцию.
• Найти точки пересечения графика с осями координат(осью Ох (х;0) и
осью Оу (0;у) )
• Непрерывность, асимптоты
• Найти критические точки.
• Найти промежутки монотонности (возрастания и убывания)
• Найти точки экстремума и экстремум функции(хmax, xmin, ymax, ymin)
• Построить график.
• Если необходимо вычислить дополнительные точки.

5. Область определения функции

Определение. Областью определения
функции называется множество значений
независимой переменной, при которых
функция определена.
Пример
y
2
x 3
2
D f R \ 3

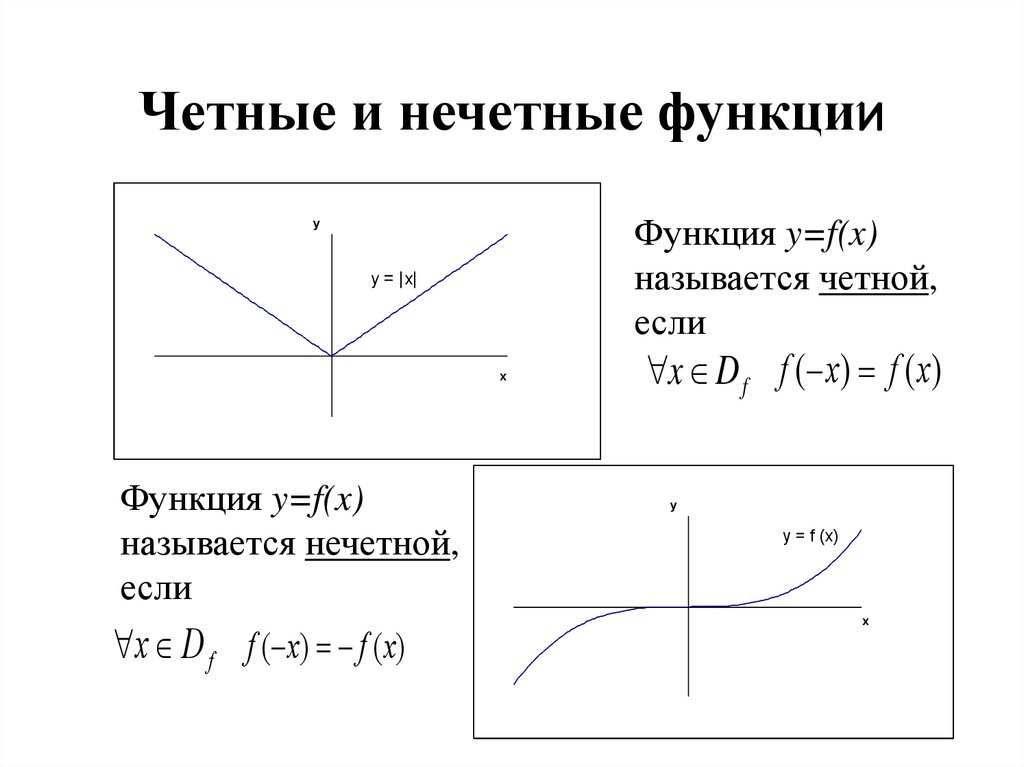
6. Четные и нечетные функции

Функция y=f(x)
называется четной,
если
y
y = |x|
x
Функция y=f(x)
называется нечетной,
если
x D f f ( x) f ( x)
x D f f ( x) f ( x)
y
y = f (x)
x

7. Периодичные функции

Определение. Функция y=f(x) называется
периодической, если существует такое
положительное число Т, что если х принадлежит Df ,
то х±Т также принадлежит Df и f(x+T)=f(T).
y
y=cosx
x

8. Точки пересечения с осями координат

При исследовании функции необходимо найти
координаты точек пересечения графика функции с
осями координат.
Абсциссы точек пересечения графика функции
с осью Ох находятся из системы уравнений у=f(x)
и у=0, а ординаты точек пересечения графика
функции с осью Оу находятся из системы
уравнений у=f(x) и х=0.

9. Непрерывность

Функция у=f(x) называется непрерывной в
точке х0, если функция определена в точке х0 и
предел функции в точке х0 равен значению функции
в точке х0.
x0 D f
lim f ( x) f ( x )
x x0
0
Функции, непрерывные в каждой точке из
области определения функции, называются
непрерывными функциями.
Примеры непрерывных функций: y=cosx,
y=sinx, y=ex , y=Pn(x) (многочлен степени n).

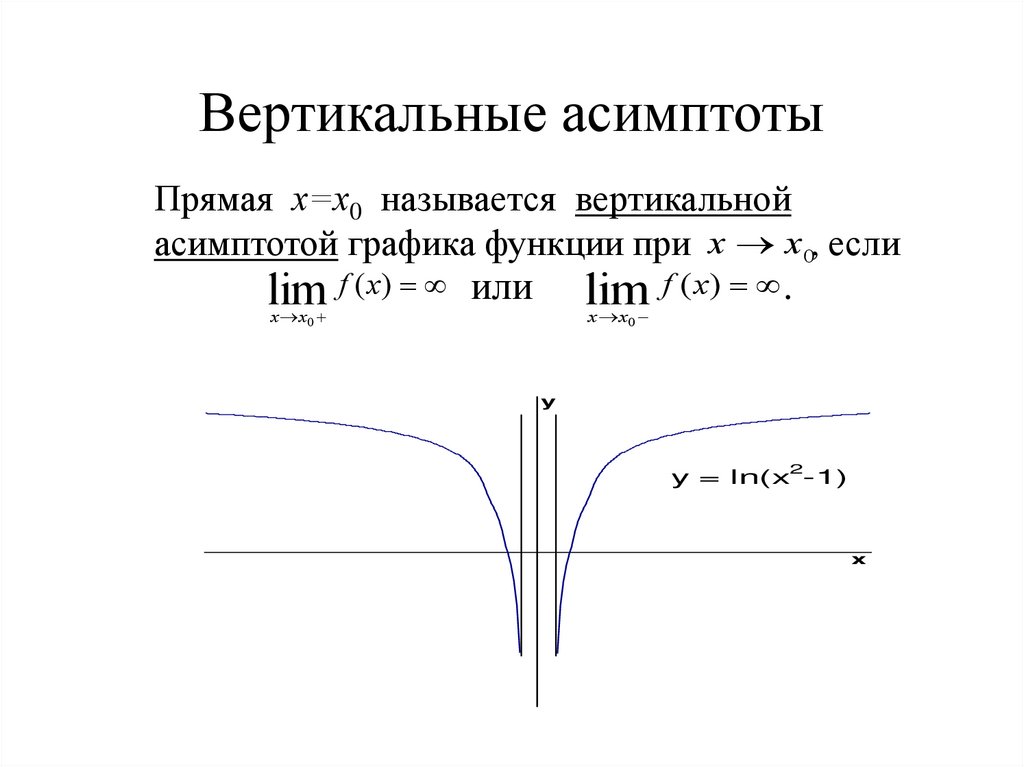
10. Вертикальные асимптоты

Прямая х=х0 называется вертикальной
асимптотой графика функции при х х0, если
lim f ( x)
x x0
x x0
.
lim f ( x) или
y
y = ln(x2-1)
x

11. Точки разрыва функции

Определение. Точкой разрыва функции
называется точка из области определения
функции, в которой функция не является
непрерывной.
Пример. Функция
sin x
, если x 0;
f ( x) x
0, если x 0
разрывна в 0, так как
lim
x 0
f ( x) lim
x 0
sin x
1, f (0) 0
x

12. Наклонные асимптоты

Если существует прямая y=kx+b такая, что
lim ( f ( x) kx b) 0 , то эта прямая называется
x
асимптотой графика функции f при x .
Для того чтобы прямая y=kx+b была асимптотой,
необходимо и достаточно, чтобы выполнялись
следующие условия:
lim
x
f ( x)
k,
x
lim ( f ( x) kx) b .
x

13. Экстремумы функции

Пусть функция f (x) определена и непрерывна на
интервале (а, b). Точка х0 интервала (а, b) называется
точкой строгого максимума (минимума) функции f (x),
если в некоторой проколотой окрестности точки х0 f
(x)< f (x0) ( f (x) > f (x0) ).
Точки минимума и точки максимума функции
называются точками экстремума функции.
Необходимое условие экстремума. Пусть
точка х0 - точка экстремума функции. Тогда либо
производная функции в этой точке равна 0, либо
не существует.

14. Исследование функции на монотонность

Известно, что если f '(x)>0 (f '(x)>0) в (а, b), то
функция f (x) строго возрастает (строго убывает)
в (а, b).
Рассмотрим функцию f(x) = x + 1|x
1
1
f ( x) x 1 2
x
x
Критические точки функции х=±1. f '(x)>0 при х<-1
и при х>1; f '(x)<0 при -1<x<0 и при 0<x<1.
x , 1 ; 1,
x , 1 ; 1,
функция возрастает
функция убывает

15. Выпуклость функции

Функция у=f(х), определенная на интервале (а, b),
называется выпуклой вверх (вниз) в интервале (а, b), если
для любых х1и х2 из интервала (а, b) из того, что х1<х2,
следует, что часть графика функции между точками
(х1,f(х1)) и (х2,f(х2)) лежит выше (ниже) хорды,
соединяющей эти точки.
а
x1
x2 b
функция выпукла вверх
a
x1
x2 b
функция выпукла вниз

16. Выпуклость функции. Точки перегиба

Также говорят, что график функции f (x) имеет
на интервале (a, b) выпуклость, направленную вниз
(вверх), если график этой функции в пределах (a, b)
лежит не ниже (не выше) любой своей касательной.
Если график функции в точке (х0, f(x0))
переходит с одной стороны касательной на другую,
то точка х0 называется точкой перегиба функции
f(x).

17. Достаточные условия выпуклости функции и существования точек перегиба

Достаточное условие строгой выпуклости функции
Если на интервале (а,b) f ''(x)>0, то на интервале (а,b)
функция выпукла вниз, и если на интервале f ''(x)<0, то
на интервале (а,b) функция выпукла вверх.
Достаточное условие строгой выпуклости
функции
Если в левой и правой полуокрестностях
некоторой точки х0 f ''(x) имеет противоположные
знаки, то точка х0 – точка перегиба функции.

18. Исследуем функцию и построим её график.

1) Поскольку знаменатель положителен при всех ,
область определения функции - вся ось ох
2) Функция f(x) - нечётная, поскольку при смене знака x
числитель меняет знак, а знаменатель остаётся без
изменения, откуда f(-x) = - f(x). Следовательно, график
функции симметричен относительно начала координат.
Периодической функция не является.
3) Поскольку область определения этой элементарной
функции -- вся вещественная ось, вертикальных
асимптот график не имеет.

19.

4) Найдём наклонные асимптоты при
. Имеем:
Таким образом, асимптотой как при
служит прямая
.
в виде
, так и при

20.

5) Найдём точки пересечения с осями координат. Имеем:
f(0) = 0, причём x=0 - единственное решение
уравнения f(x) = 0. Значит, график y = f(x) пересекает
сразу и ось Ox, и ось Oy в начале координат.
Очевидно, что f(x)>0 при x>0 и f(x)<0 при x<0.
6) Найдём производную:
Очевидно, что f´(x) ≥ 0 при всех
; единственная точка, в
которой f´(x) = 0 - это x=0. Значит, функция f(x) возрастает на всей
оси Ox, а в стационарной точке x=0 имеет горизонтальную
касательную.

21.

7) Найдём вторую производную:
Знаменатель этой дроби положителен при всех x.
Числитель имеет корни x=0 и x=±√3, при этом f’’(x)>0
на интервалах
и
- на этих интервалах
функция выпукла. На интервалах
и
выполняется обратное неравенство f’’(x)<0, здесь
функция вогнута. Все три точки, в которых f’’(x)=0, то
есть точки - √3, 0, √3, являются точками перегиба.

22.

8) Теперь мы можем построить график с учётом всех
предыдущих пунктов исследования функции. График
имеет такой вид:

23.

1. Область определения: R. Функция непрерывна.
2. Вычисляем производную : y’=6x²-6x-36.
3. Находим критические точки: y’=0.
x²-x-6=0
Д=1-4*(-6)*1=1+24=25
4. Делим область определения на интервалы:
+
-
-2
5. Функция возрастает при
функция убывает при xϵ[-2;3].
+
3
xϵ(-∞;-2]υ[3;+∞),

24.

1. Область определения: R. Функция непрерывна.
2. Вычисляем производную : y’=-6x²-6x+12.
3. Находим критические точки: y’=0.
-x²-x+2=0
Д=1-4*(-1)*2=1+8=9
x1=1; x2=-2
4. Делим область определения на интервалы:
+
-2
1
5. x=-2 – точка минимума. Найдём минимум функции
ymin=-24. x=1 – точка максимума.
Найдём максимум функции: ymax=3.

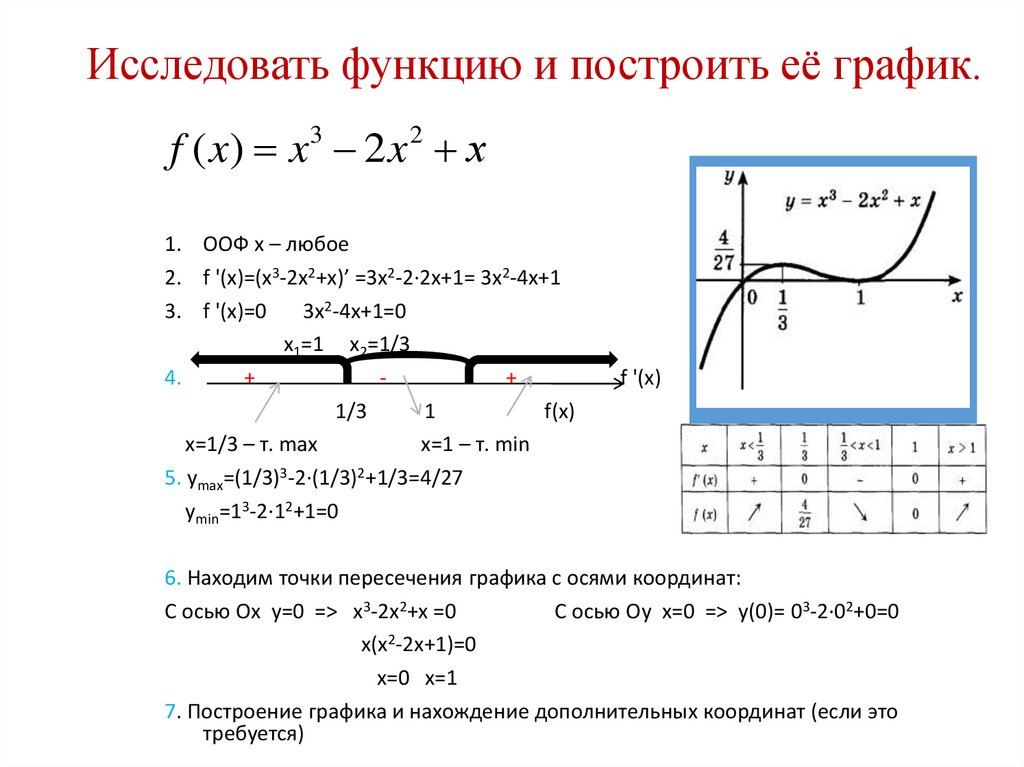
25. Исследовать функцию и построить её график.

f ( x) x 3 2 x 2 х
1. ООФ x – любое
2. f '(x)=(x3-2x2+x)’ =3x2-2∙2x+1= 3x2-4x+1
3. f '(x)=0
3x2-4x+1=0
x1=1 x2=1/3
4.
+
+
1/3
1
f(x)
x=1/3 – т. max
x=1 – т. min
5. ymax=(1/3)3-2∙(1/3)2+1/3=4/27
ymin=13-2∙12+1=0
f '(x)
6. Находим точки пересечения графика с осями координат:
С осью Ох у=0 => x3-2x2+x =0
С осью Оу х=0 => у(0)= 03-2∙02+0=0
х(х2-2х+1)=0
х=0 х=1
7. Построение графика и нахождение дополнительных координат (если это
требуется)

26. Домашняя работа

Исследуйте функцию и постройте график:
f ( x) x 3x х 5
3
2
1 x2
f ( x)
х 1

27.

Исследовать функцию и построить график
у=
x3
–
3x2 +
x+5
у = (x2 – 1)2

28. Разноуровневые задания

• Исследовать функцию и построить график
Уровень А
f ( x) x 3 2 x 2 х
УровеньВ
f ( x)
х
3
( х 1)
2
УровеньС
f ( x) x 2arctgx

29.

Рефлексия
Было не понятно
Не
уверен в
себе
Все понятно