Похожие презентации:
Геометрическая прогрессия. 9 класс
1. Классная работа
21 апреляКЛАССНАЯ РАБОТА
2.
3.
Определение. Геометрической прогрессиейназывается последовательность
отличных от нуля чисел, каждый член
которой, начиная со второго, равен
предыдущему члену, умноженному на
одно и то же число.
Иначе, последовательность ( b )- геометрическая
n
прогрессия, если для любого натурального n
bn 0 и , bn 1 bn q
выполняется условие
где
вn 1
q
вn
4.
Примеры геометрической прогрессии:а) 2; 4; 8; 16; 32; 64; …
×2
×2
×2
×2
q=2
×2
б) -10; 100; -1000; 10000; -100000…..
q = - 10
× (-10)
× (-10)
× (-10)
× (-10)
5.
Формула n-го членав2 в1q
в3 в2 q (в1q )q в1q
в4 в3 q (в1q )q в1q
2
………
в5 в4 q (в1q )q в1q
3
вn в1q
n 1
3
4
2
6.
ПримерыВ геометрической прогрессии b1 = 13, 4 и
q=0,2. Найти
b6
Решение.
По формуле n-ого члена геометрической
прогрессии
b6 13,4 0,2 13,4 0,00032 0,004288
5
7.
Дано: (bn ) - геометрическая прогрессияb1= 5 q = 3
Найти: b3 ; b5.
Решение: используя формулу bn = b1 q n-1
b3 =b1q2 = 5 . 32 =5 . 9=45
b5 =b1q4 = 5 . 34 =5 . 81=405
Ответ:45; 405.
8.
Найти пятый член геометрическойпрогрессии: 2; -6…
Решение.
Зная первый и второй члены
геометрической прогрессии, можно
найти её знаменатель.
q= -6:2= -3.
Таким образом
b5 2 3 162.
4
9.
Дано: (bn ) - геометрическая прогрессияb4= 40 q = 2
Найти: b1.
Решение: используя формулу bn = b1 q n-1
b4 =b1q3 ; b1 = b4 : q3 =40:23 =40 :8=5
Ответ: 5.
10. Решить в классе (работа по учебнику, стр. 229
№ 817 (1 столбец)
№ 818
№ 820




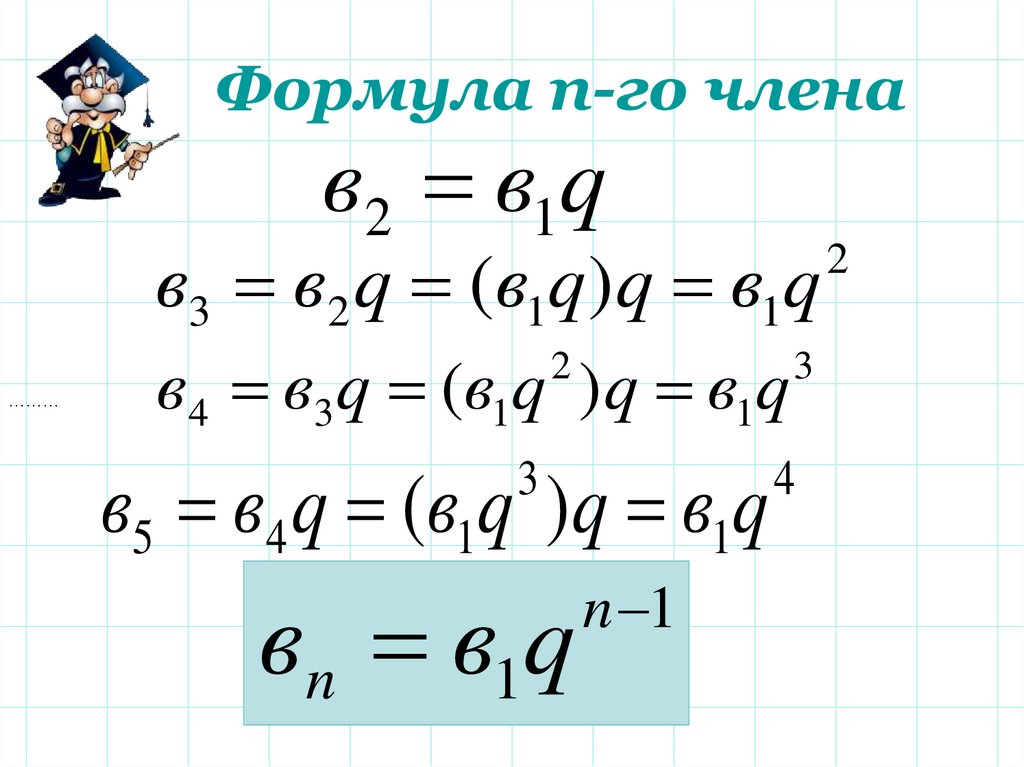






 Математика
Математика








