Многогранники

1.

2. Школьный курс геометрии состоит из двух частей:

•ПЛАНИМЕТРИИ
Планиметрия-это
раздел геометрии, в
котором изучаются
свойства
геометрических фигур
на плоскости.
•СТЕРЕОМЕТРИИ
Стереометрия-это
раздел геометрии, в
котором изучаются
свойства фигур
в пространстве.

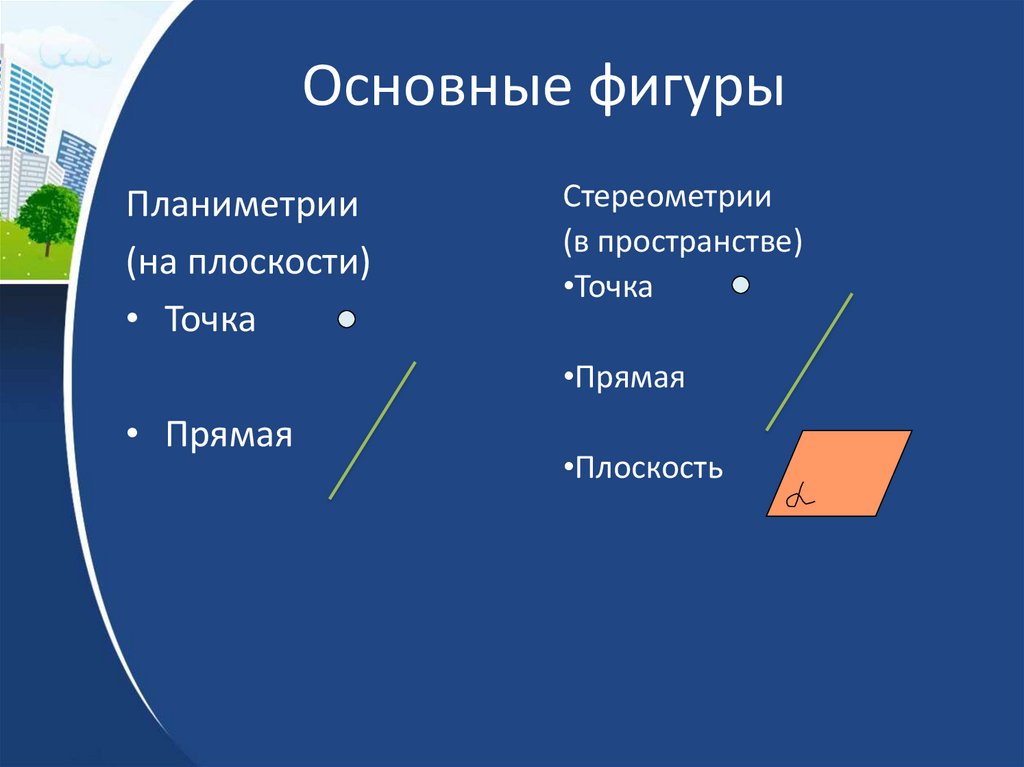
3. Основные фигуры

Планиметрии
(на плоскости)
• Точка
Стереометрии
(в пространстве)
•Точка
•Прямая
• Прямая
•Плоскость

4. Точки обозначаются прописными латинскими буквами А, В, С, D, Е, К,…

А
В
С
Е
Прямые обозначаются строчными
латинскими буквами a, b, c, d, e, k,…
b
d
a
Плоскости обозначаются греческими
буквами α, β, γ, λ, π, ω,…
β
γ
α
4

5.

Что такое многогранник?
Многогранник-это поверхность,
составленная из многоугольников
и ограничивающая некоторое тело.
Это тело также называется
многогранником
Приведите примеры многогранников
куб
параллелепипед
пирамида

6. Основные элементы многогранника

Что такое грани многогранника?
Грани - это многоугольники, из которых
составлен многогранник
Что такое ребра многогранника?
Ребра многогранника-это стороны
граней многогранника
Что такое вершины многогранника?
Вершины-это концы ребер
многогранника

7.

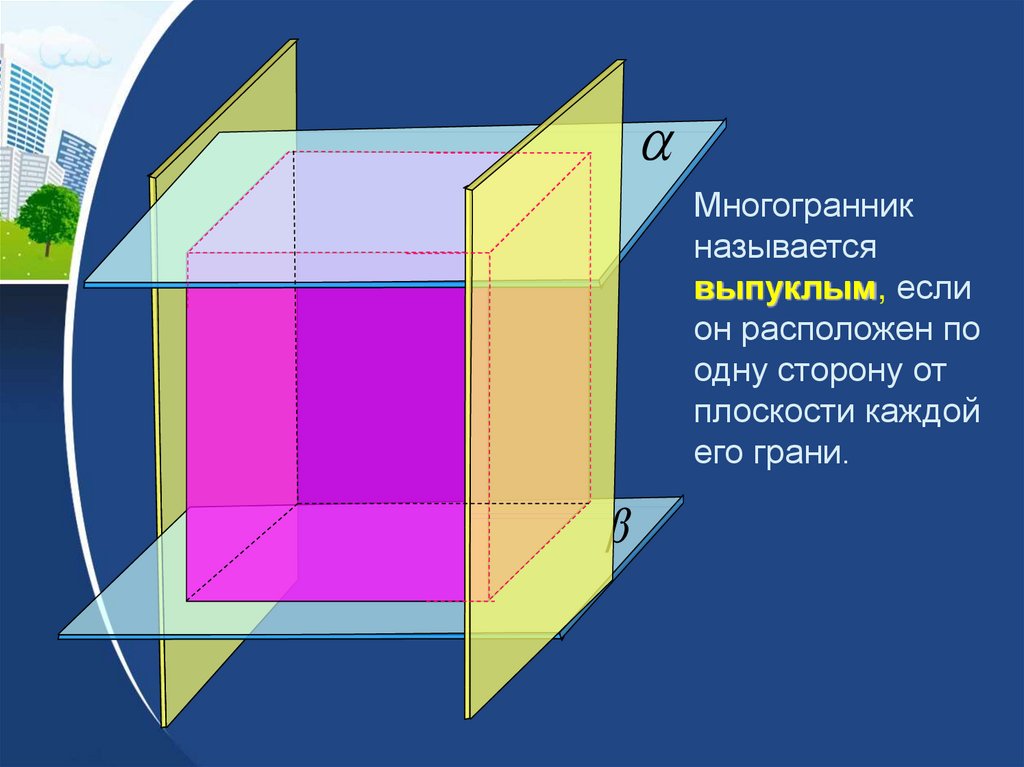
Многогранник
называется
выпуклым, если
он расположен по
одну сторону от
плоскости каждой
его грани.

8.

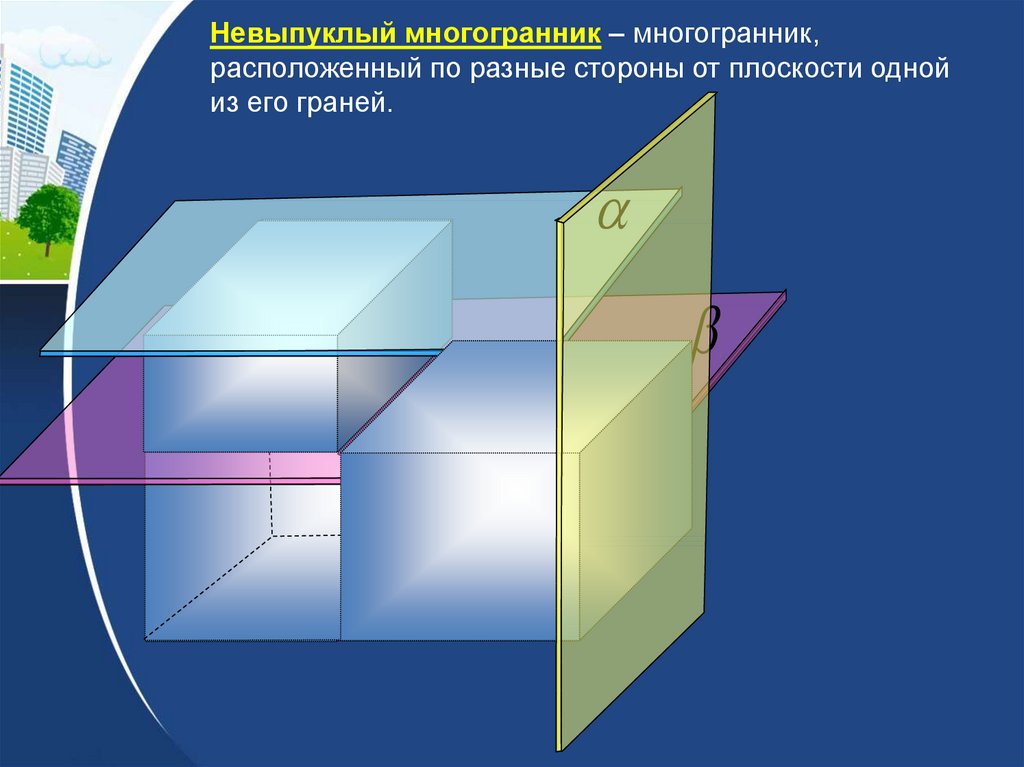
Невыпуклый многогранник – многогранник,
расположенный по разные стороны от плоскости одной
из его граней.

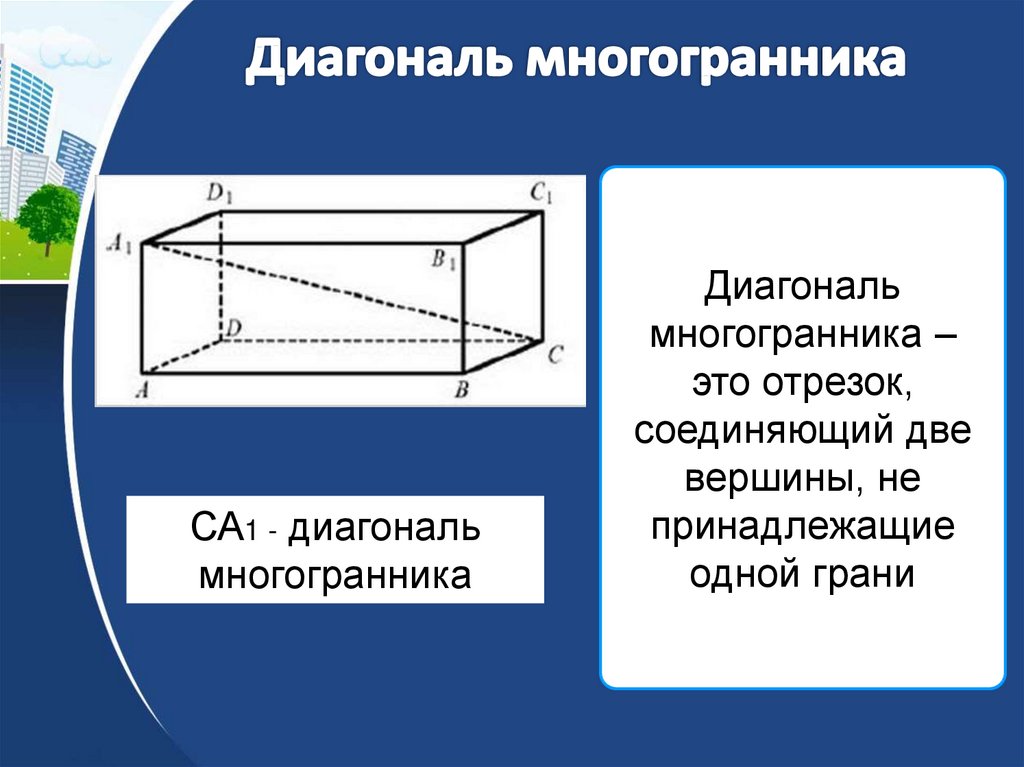
9. Диагональ многогранника

СА1 - диагональ
многогранника
Диагональ
многогранника –
это отрезок,
соединяющий две
вершины, не
принадлежащие
одной грани

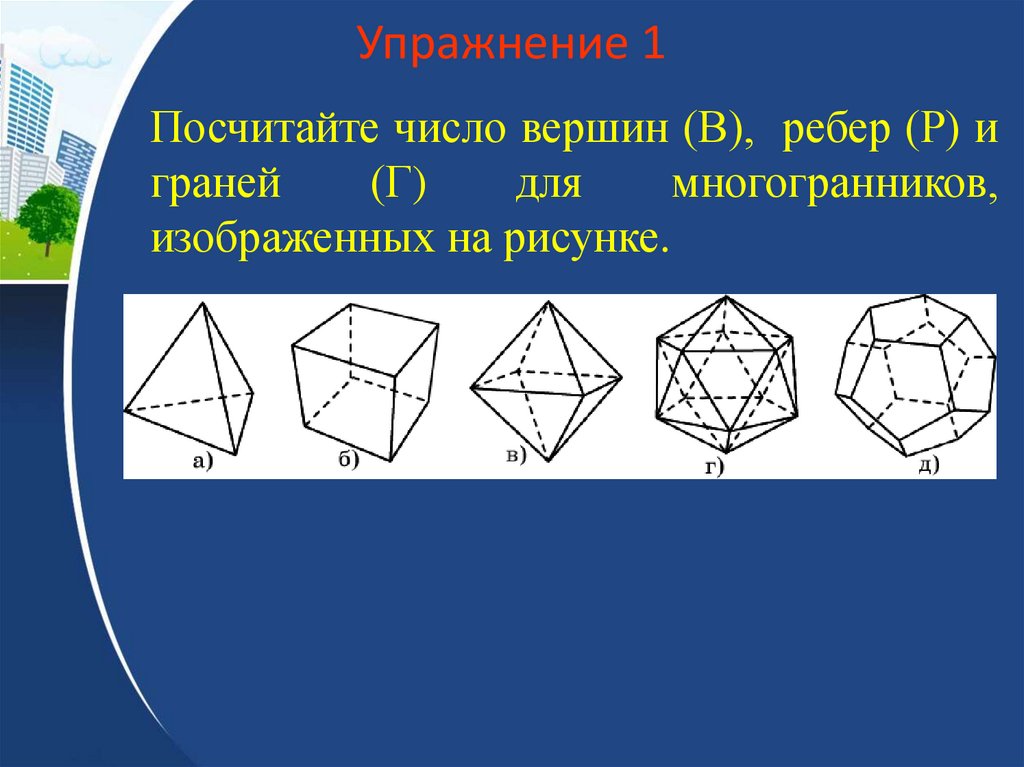
10. Упражнение 1

Посчитайте число вершин (В), ребер (Р) и
граней
(Г)
для
многогранников,
изображенных на рисунке.

11.

12.

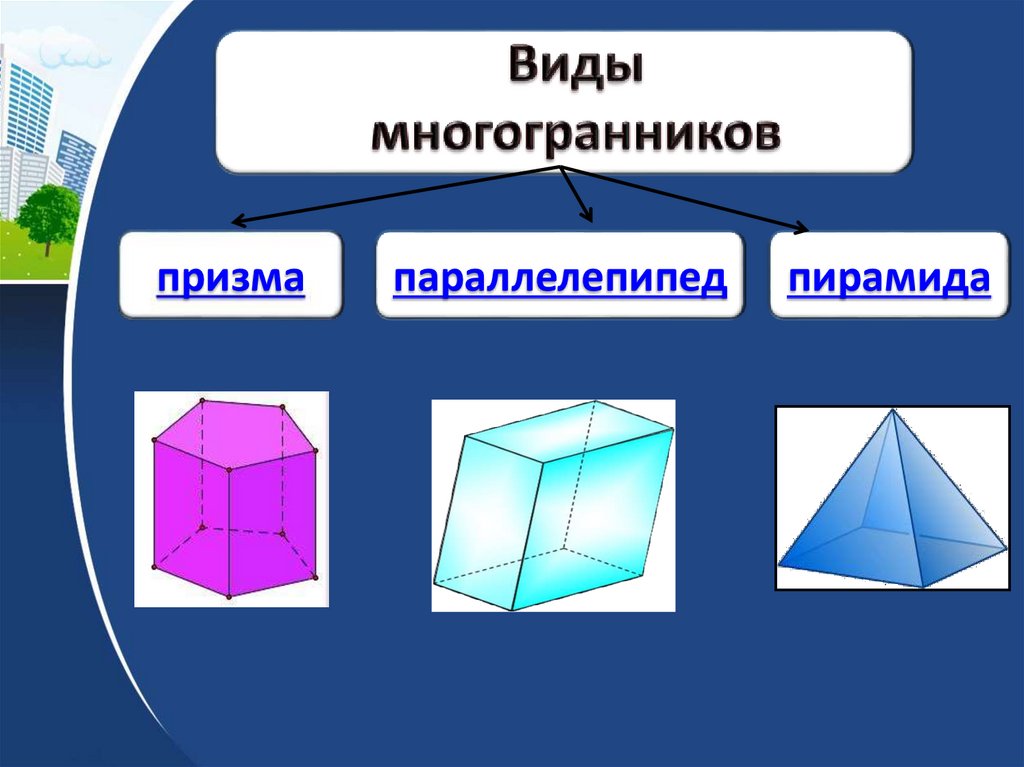
призма
параллелепипед
пирамида

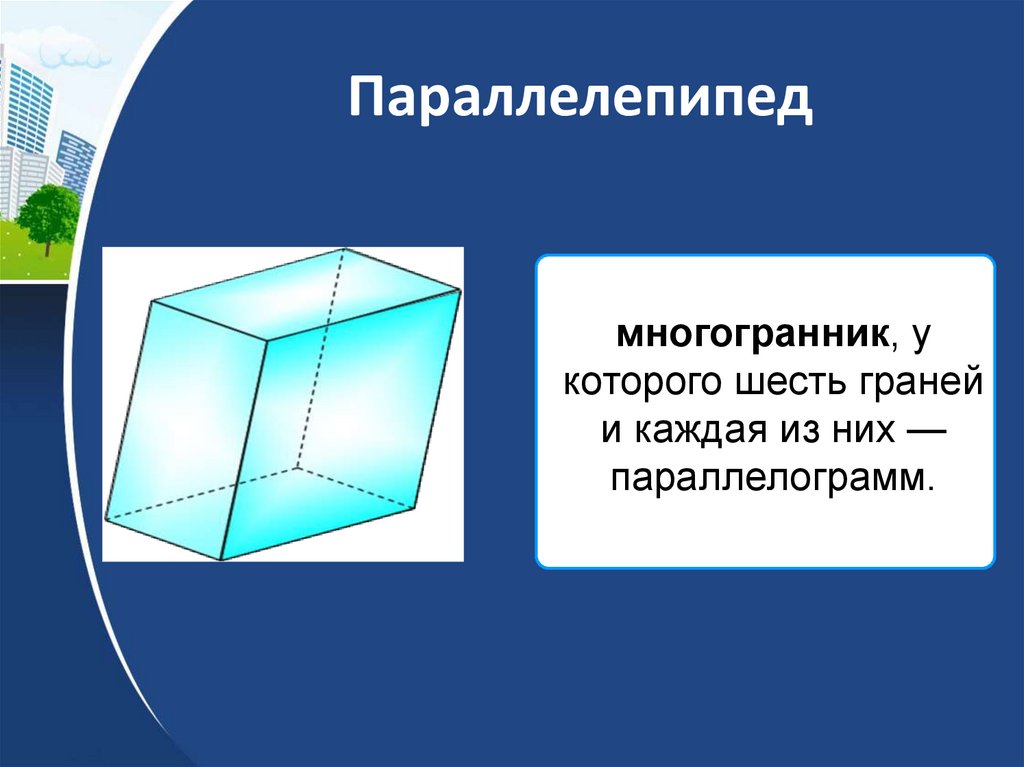
13. Параллелепипед

многогранник, у
которого шесть граней
и каждая из них —
параллелограмм.

14.

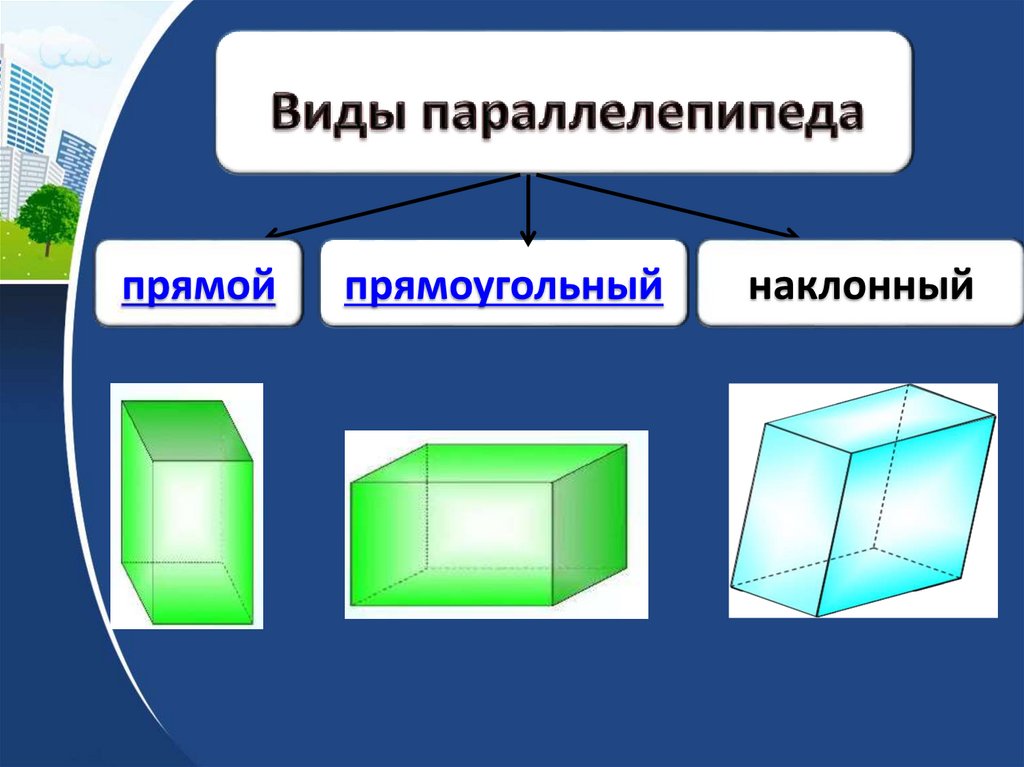
прямой
прямоугольный
наклонный

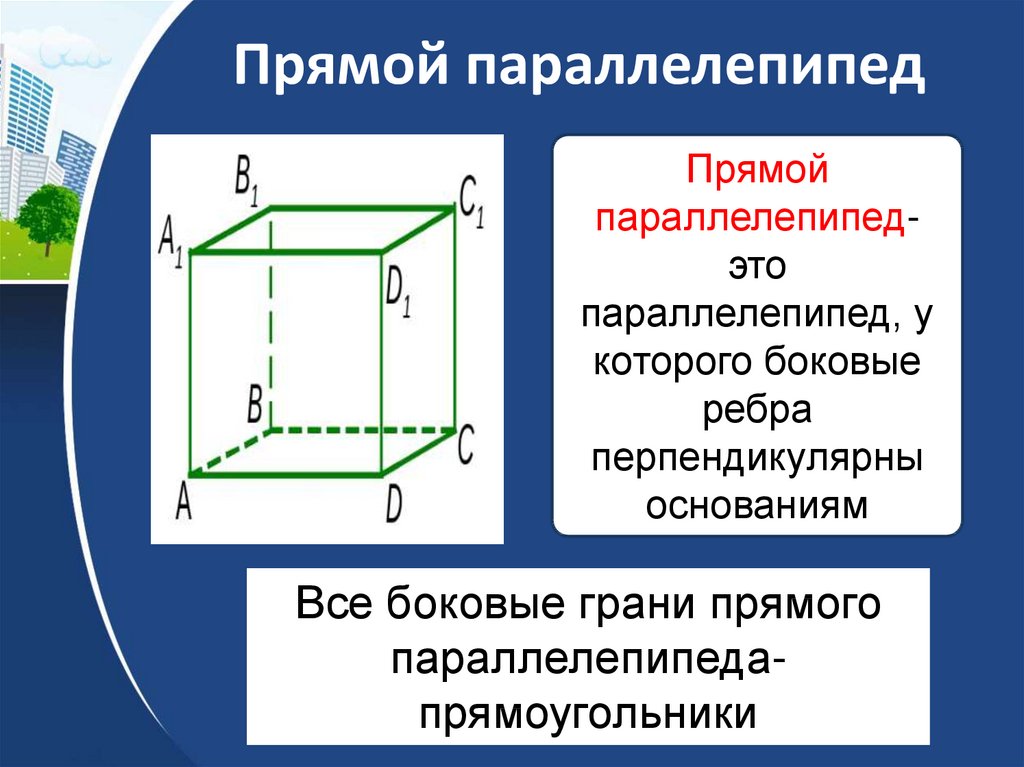
15. Прямой параллелепипед

Прямой
параллелепипедэто
параллелепипед, у
которого боковые
ребра
перпендикулярны
основаниям
Все
Чембоковые
являютсяграни
все боковые
прямого
параллелепипедаграни прямого
параллелепипеда?
прямоугольники

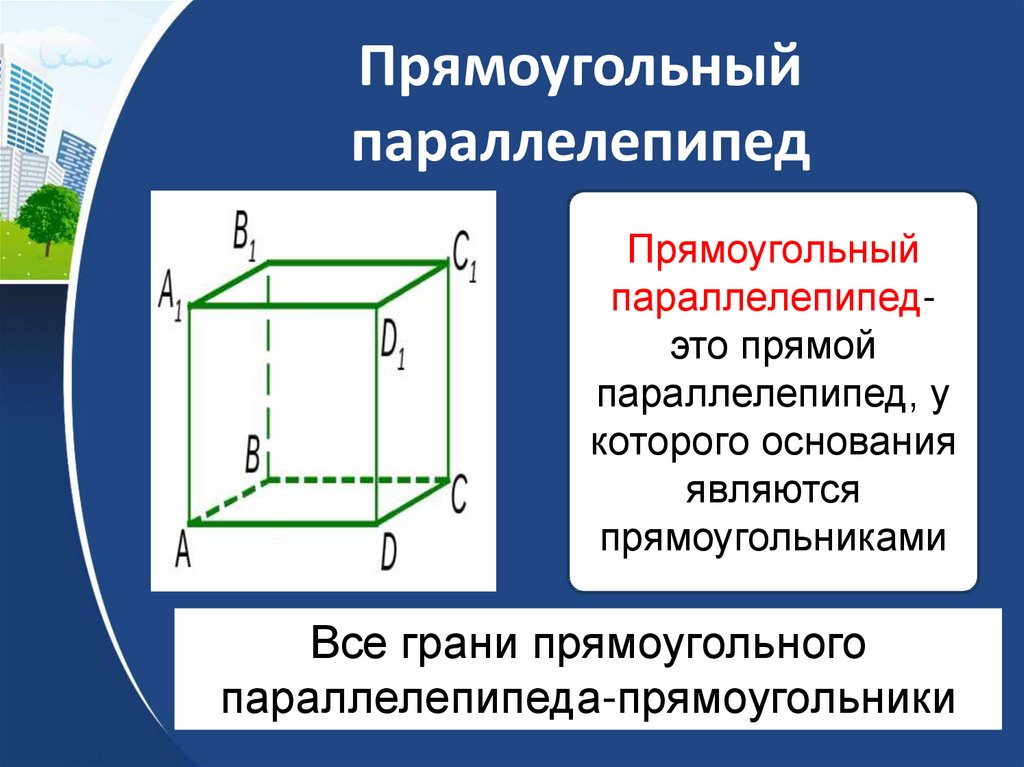
16. Прямоугольный параллелепипед

Прямоугольный
параллелепипедэто прямой
параллелепипед, у
которого основания
являются
прямоугольниками
ЧтоВсе
можно
грани
сказать
прямоугольного
о всех гранях
прямоугольного
параллелепипеда-прямоугольники
параллелепипеда?

17. Свойство прямоугольного параллелепипеда

Квадрат диагонали
прямоугольного
параллелепипеда
равен сумме квадратов
трех его измерений

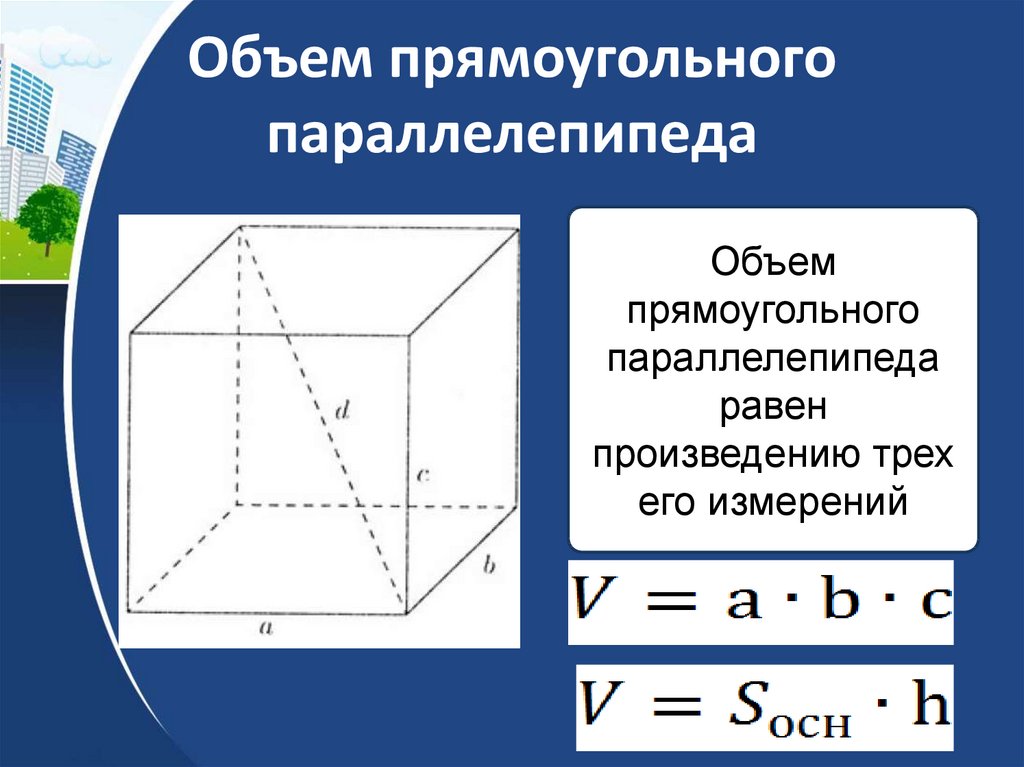
18. Объем прямоугольного параллелепипеда

Объем
прямоугольного
параллелепипеда
равен
произведению трех
его измерений

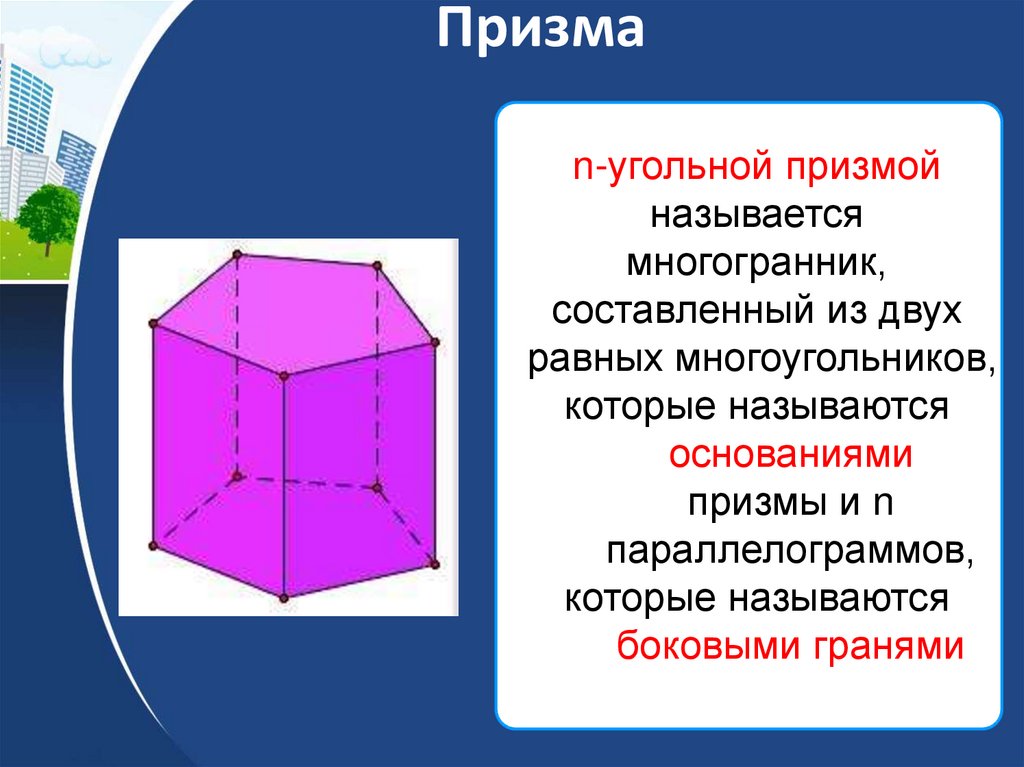
19. Призма

n-угольной призмой
называется
многогранник,
составленный из двух
равных многоугольников,
которые называются
основаниями
призмы и n
параллелограммов,
которые называются
боковыми гранями

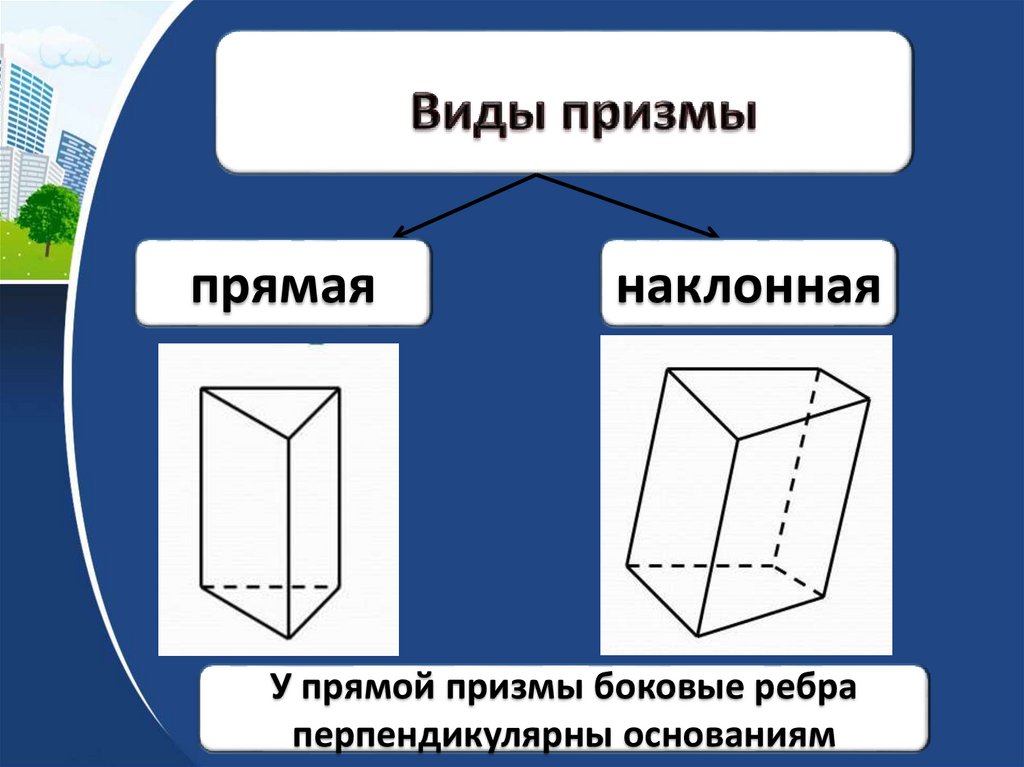
20.

прямая
наклонная
У прямой призмы боковые ребра
перпендикулярны основаниям

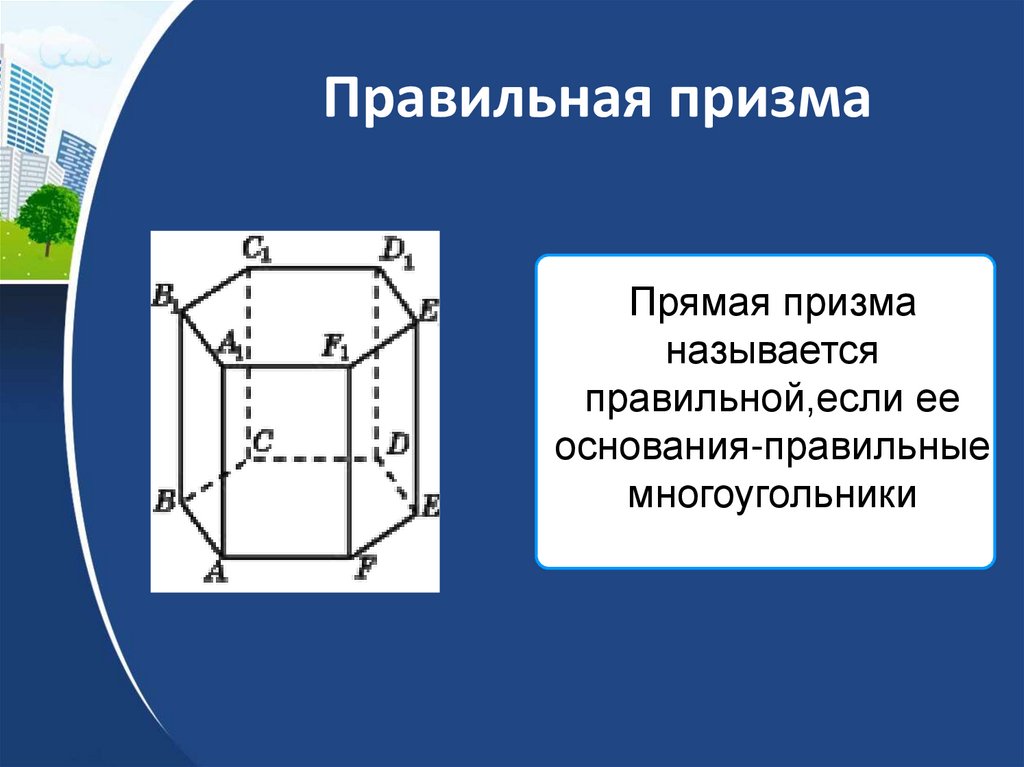
21.

Правильная призма
Прямая призма
называется
правильной,если ее
основания-правильные
многоугольники

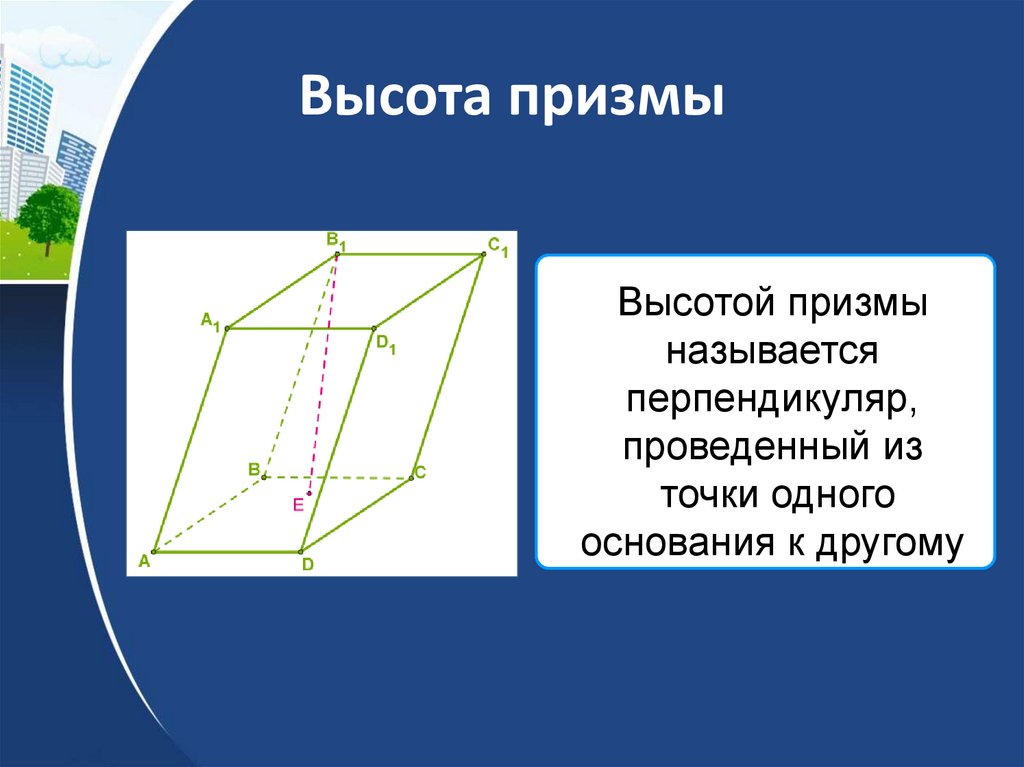
22. Высота призмы

Высотой призмы
называется
перпендикуляр,
проведенный из
точки одного
основания к другому

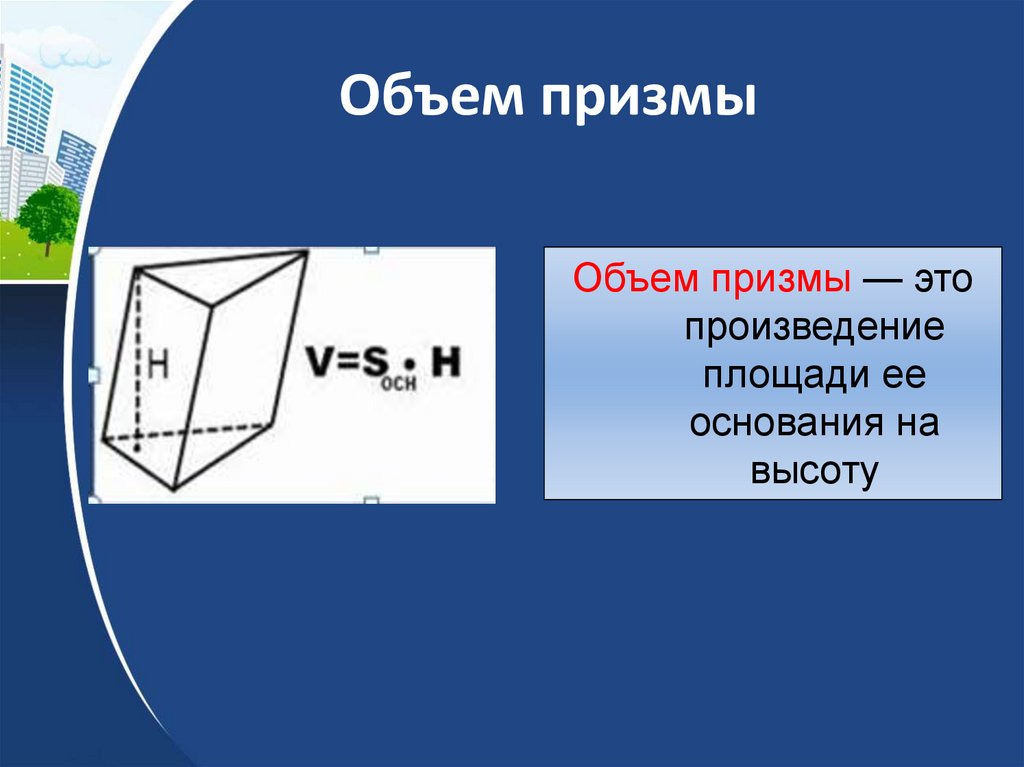
23. Объем призмы

Объем призмы — это
произведение
площади ее
основания на
высоту

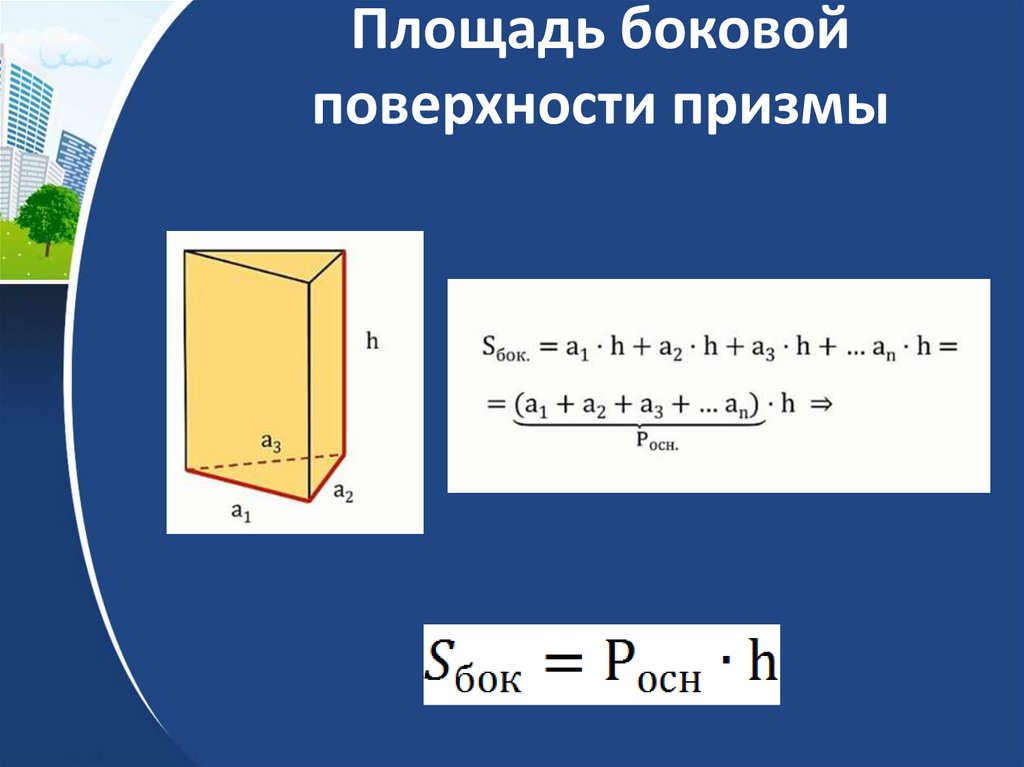
24. Площадь боковой поверхности призмы

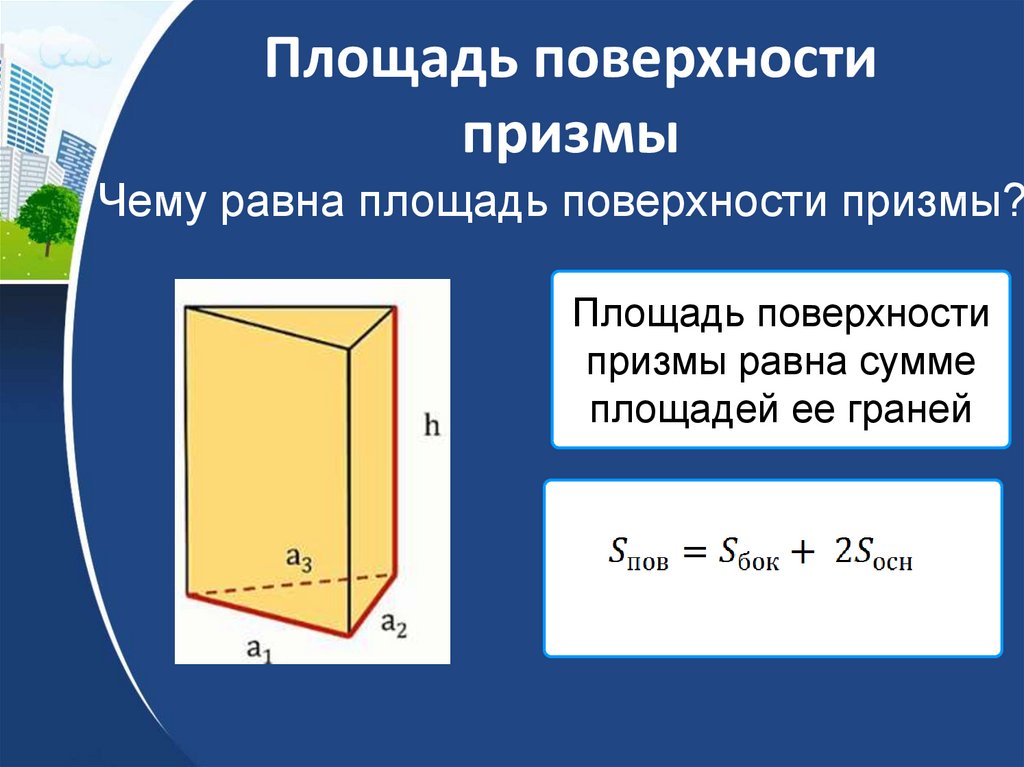
25. Площадь поверхности призмы

Чему равна площадь поверхности призмы?
Площадь поверхности
призмы равна сумме
площадей ее граней

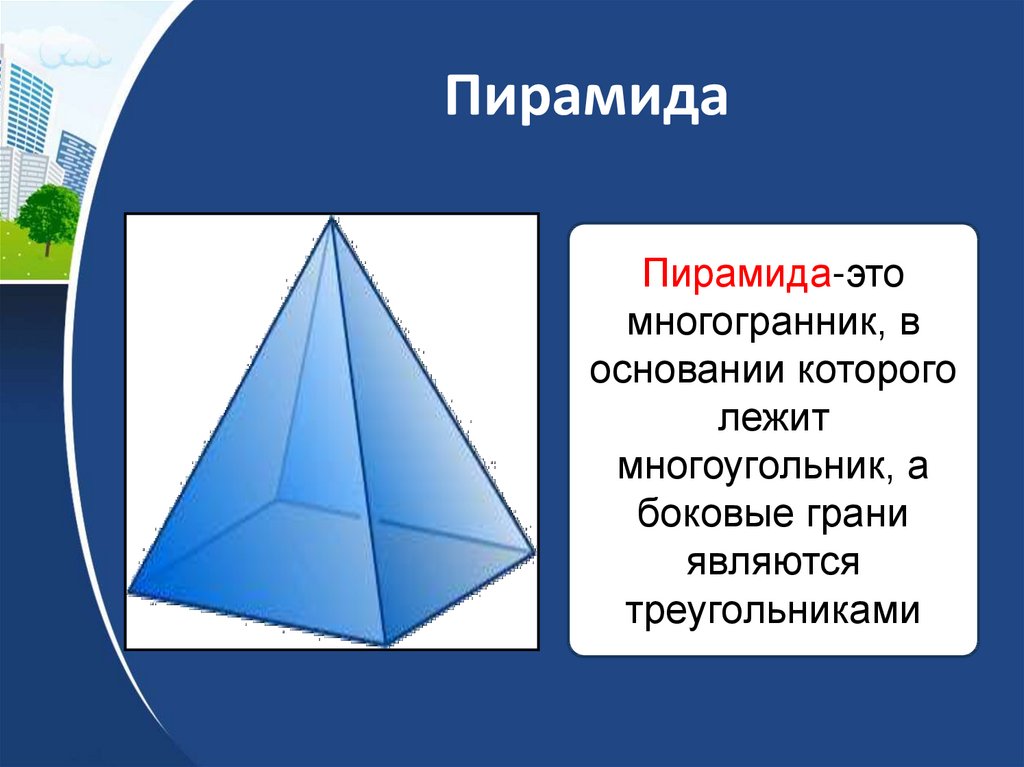
26. Пирамида

Пирамида-это
многогранник, в
основании которого
лежит
многоугольник, а
боковые грани
являются
треугольниками

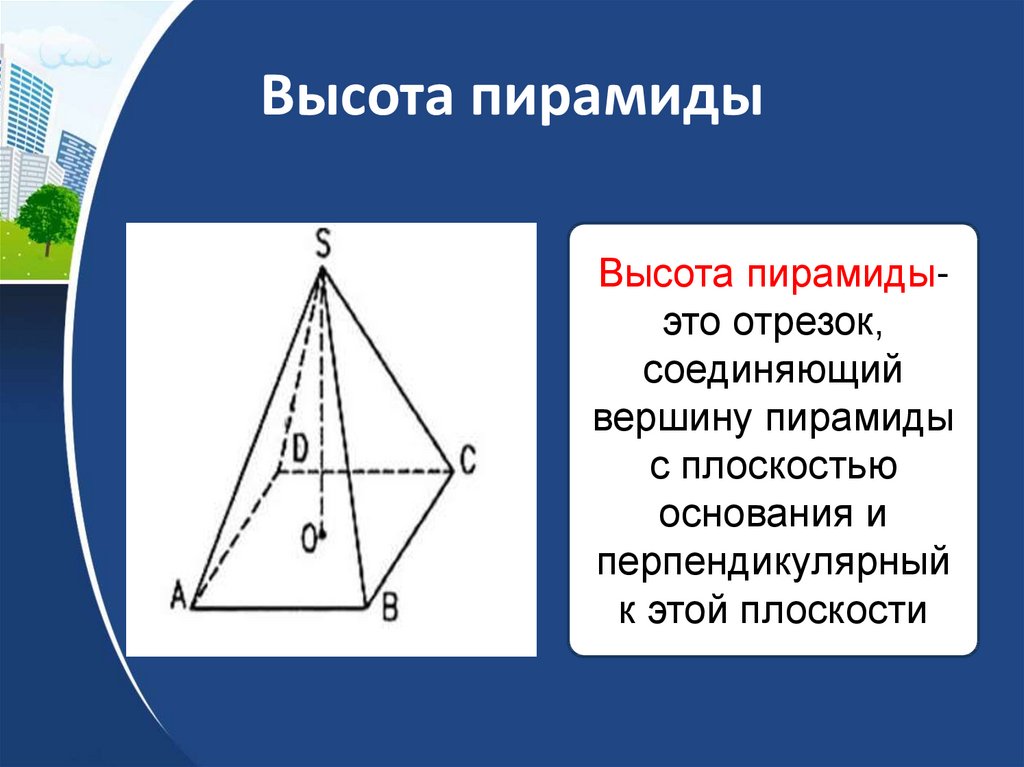
27. Высота пирамиды

Высота пирамидыэто отрезок,
соединяющий
вершину пирамиды
с плоскостью
основания и
перпендикулярный
к этой плоскости

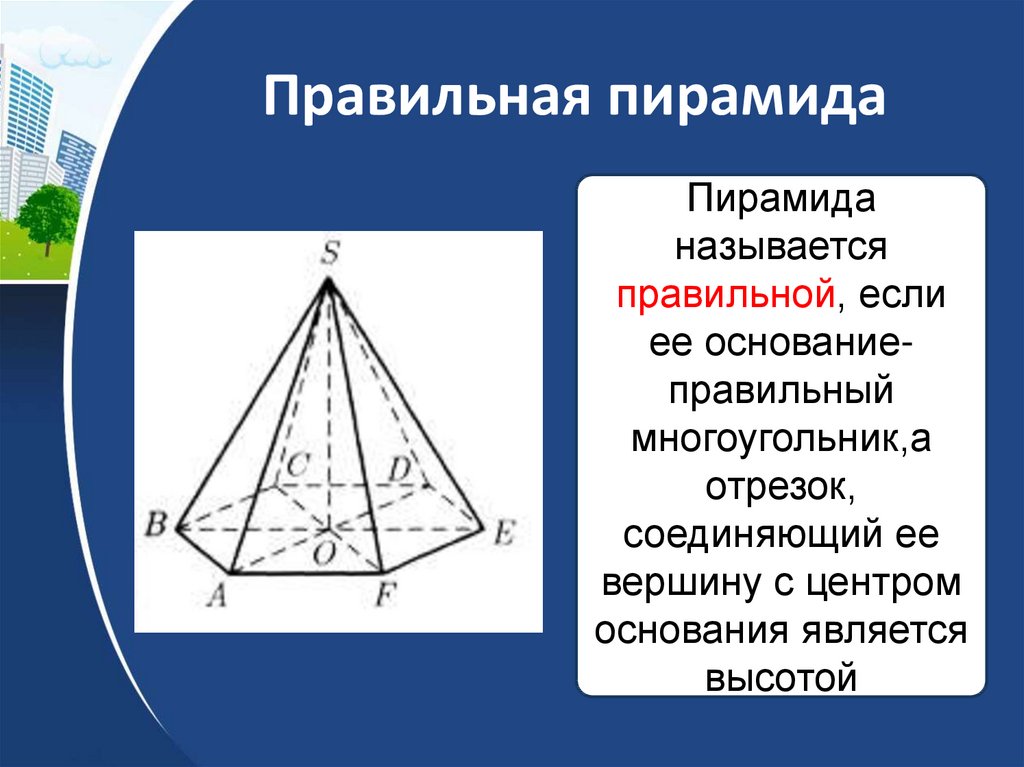
28. Правильная пирамида

Пирамида
называется
правильной, если
ее основаниеправильный
многоугольник,а
отрезок,
соединяющий ее
вершину с центром
основания является
высотой

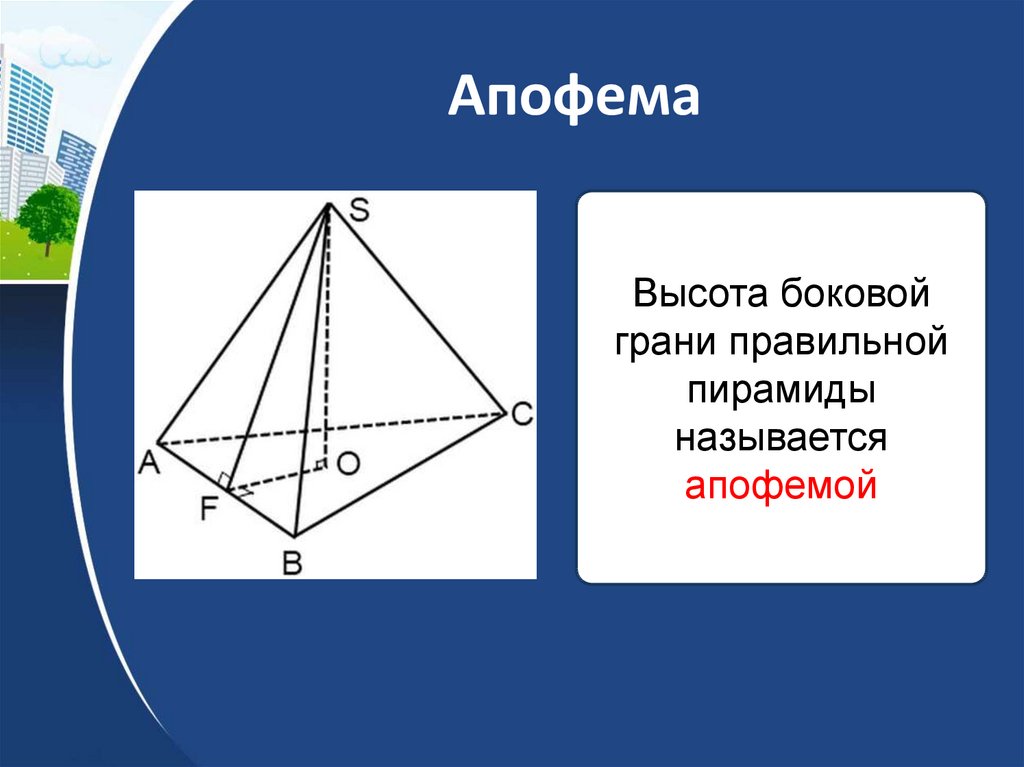
29. Апофема

Высота боковой
грани правильной
пирамиды
называется
апофемой

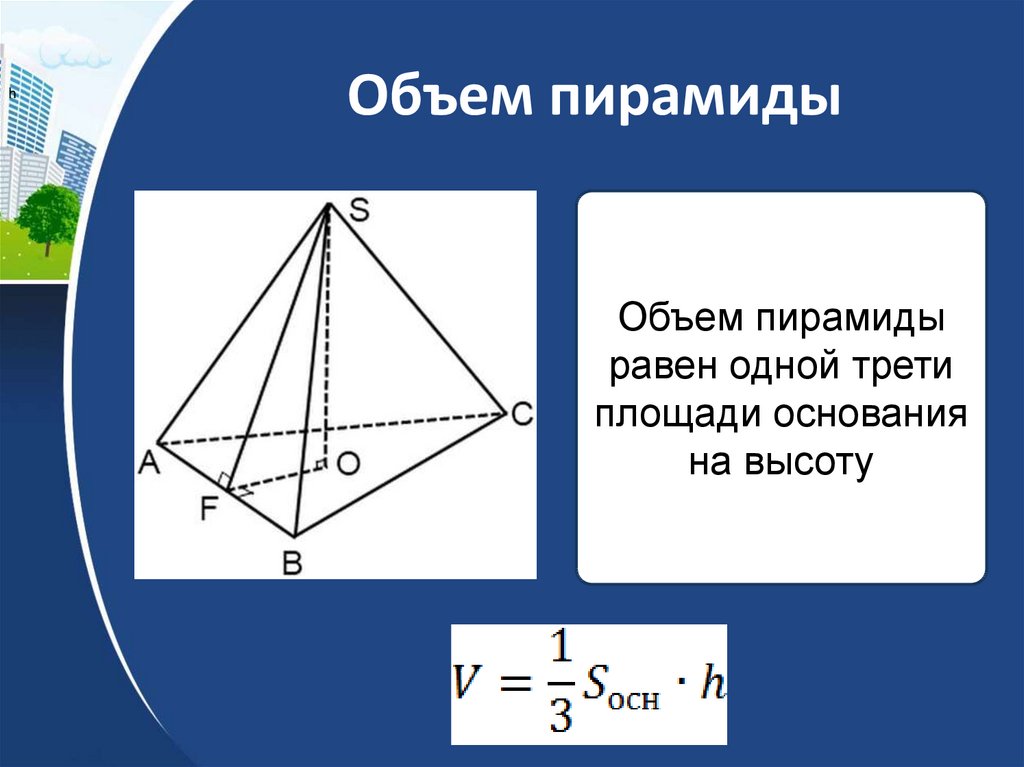
30. Объем пирамиды

h
Объем пирамиды
Объем пирамиды
равен одной трети
площади основания
на высоту

31.

Цилиндром называется тело, полученное при
вращении прямоугольника вокруг оси,
проходящей через одну из его сторон.

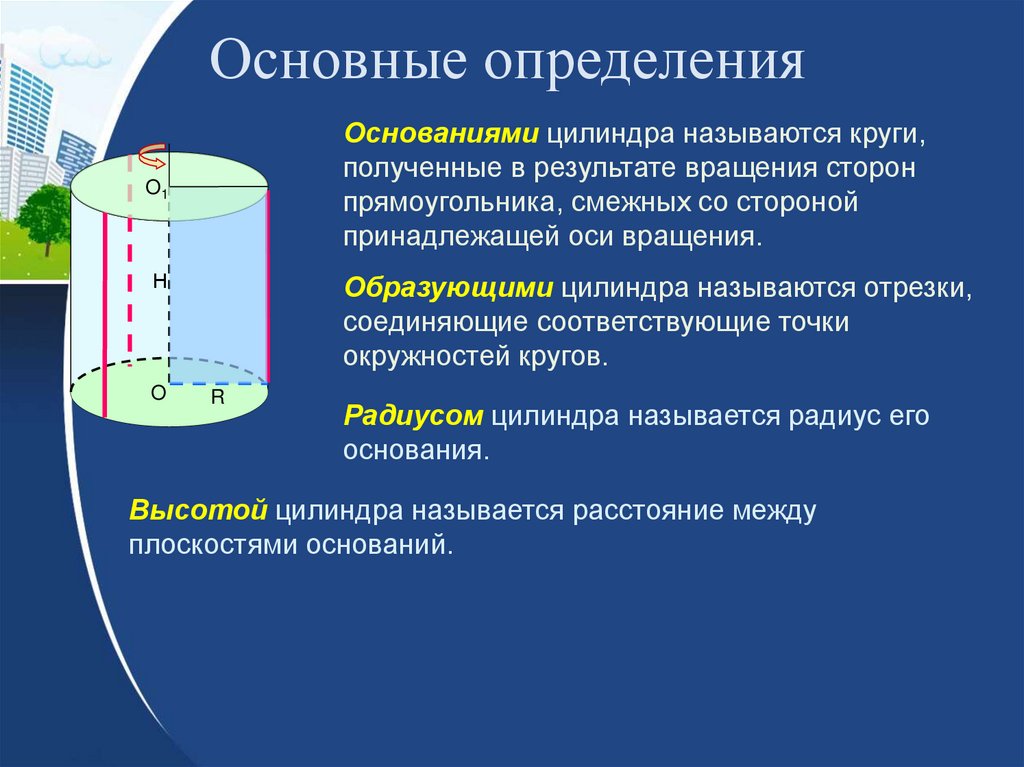
32.

Основные определения
Основаниями цилиндра называются круги,
полученные в результате вращения сторон
прямоугольника, смежных со стороной
принадлежащей оси вращения.
O1
Н
O
Образующими цилиндра называются отрезки,
соединяющие соответствующие точки
окружностей кругов.
R
Радиусом цилиндра называется радиус его
основания.
Высотой цилиндра называется расстояние между
плоскостями оснований.

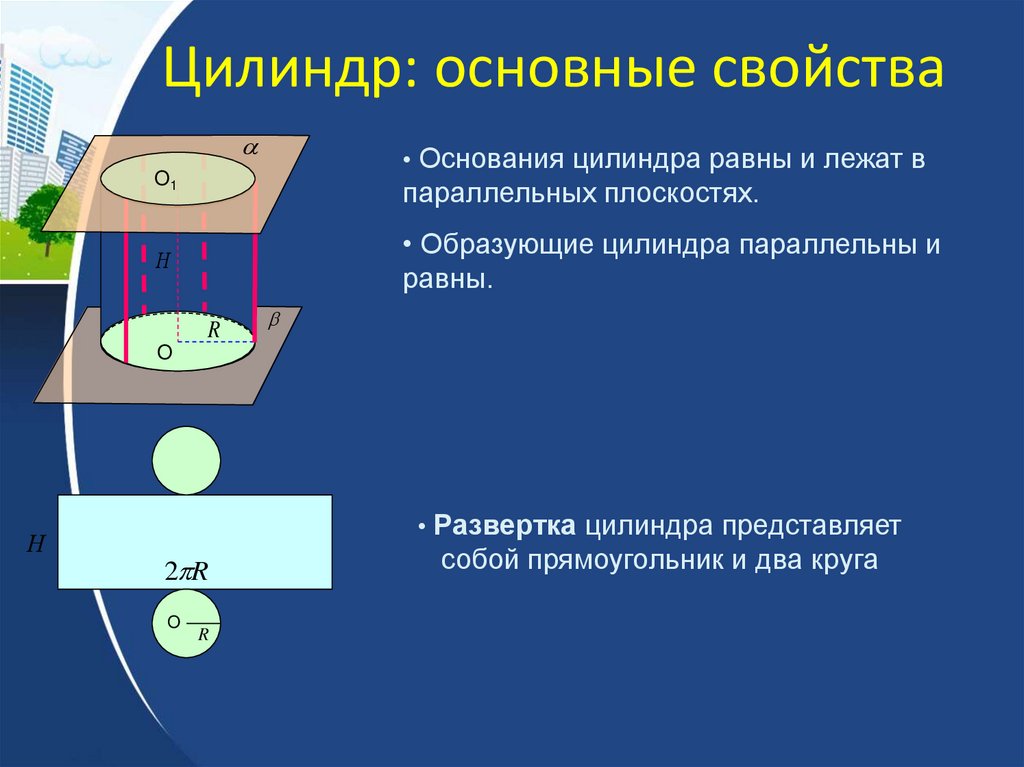
33. Цилиндр: основные свойства

• Основания цилиндра равны и лежат в
O1
параллельных плоскостях.
• Образующие цилиндра параллельны и
равны.
Н
R
O
Н
• Развертка цилиндра представляет
2 R
O
R
собой прямоугольник и два круга

34.

Конусом называется тело, полученное при
вращении прямоугольного треугольника вокруг
оси, содержащей его катет.

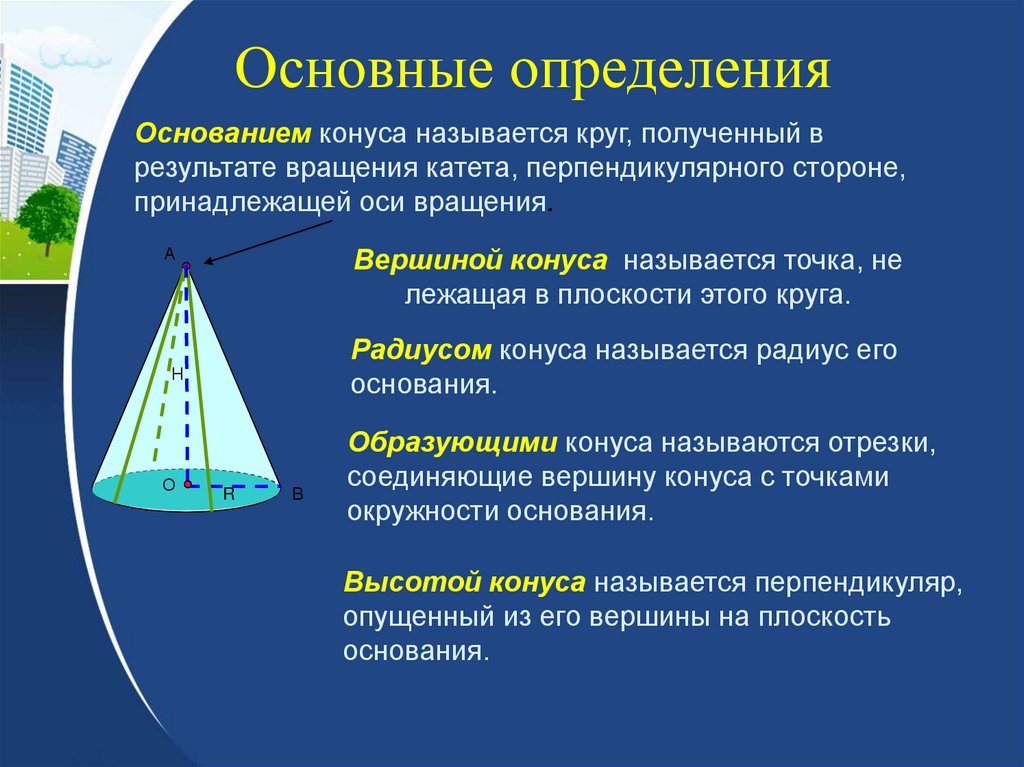
35.

Основные определения
Основанием конуса называется круг, полученный в
результате вращения катета, перпендикулярного стороне,
принадлежащей оси вращения.
Вершиной конуса называется точка, не
лежащая в плоскости этого круга.
А
Радиусом конуса называется радиус его
основания.
Н
О
R
В
Образующими конуса называются отрезки,
соединяющие вершину конуса с точками
окружности основания.
Высотой конуса называется перпендикуляр,
опущенный из его вершины на плоскость
основания.

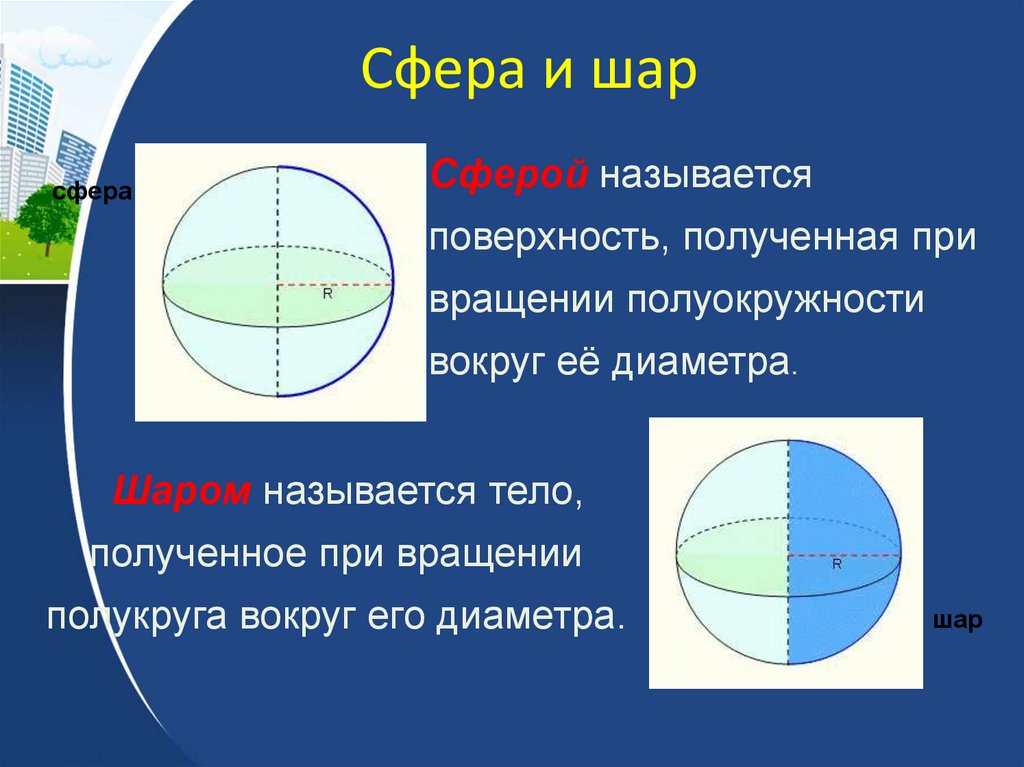
36. Сфера и шар

сфера
Сферой называется
поверхность, полученная при
вращении полуокружности
вокруг её диаметра.
Шаром называется тело,
полученное при вращении
полукруга вокруг его диаметра.
шар