Похожие презентации:
Расстояние от точки до прямой в пространстве
1. РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ
Расстоянием от точки до прямой в пространственазывается длина перпендикуляра, опущенного из
данной точки на данную прямую.
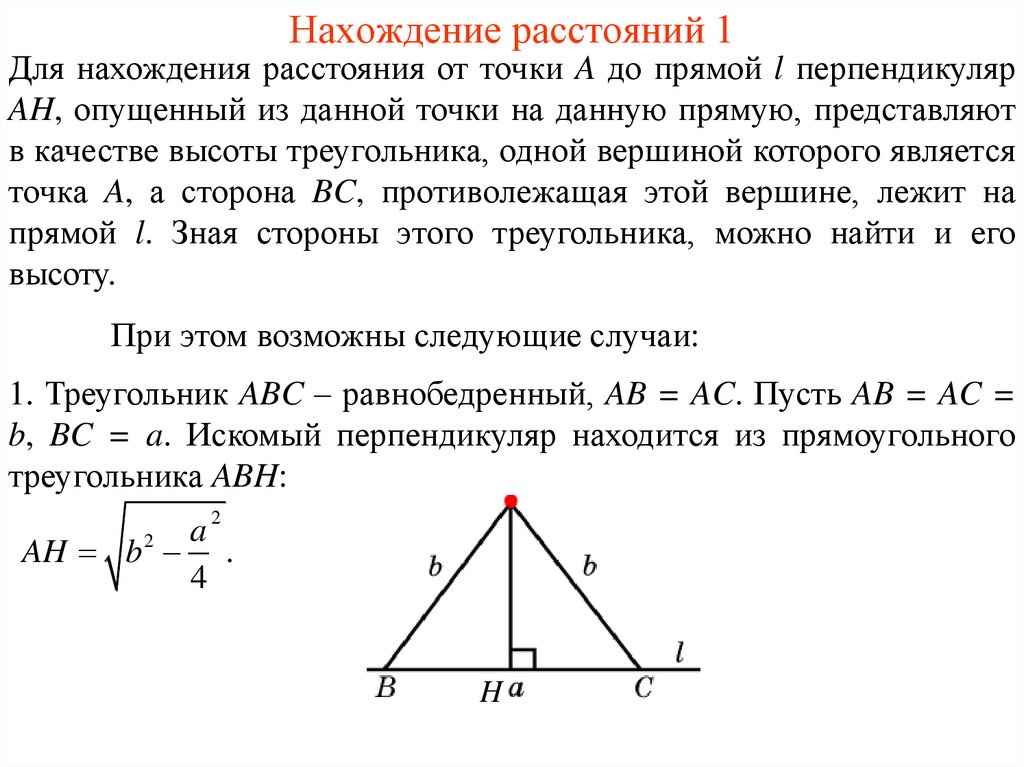
2. Нахождение расстояний 1
Для нахождения расстояния от точки A до прямой l перпендикулярAH, опущенный из данной точки на данную прямую, представляют
в качестве высоты треугольника, одной вершиной которого является
точка A, а сторона BC, противолежащая этой вершине, лежит на
прямой l. Зная стороны этого треугольника, можно найти и его
высоту.
При этом возможны следующие случаи:
1. Треугольник ABC – равнобедренный, AB = AC. Пусть AB = AC =
b, BC = a. Искомый перпендикуляр находится из прямоугольного
треугольника ABH:
2
AH b 2
a
.
4
H
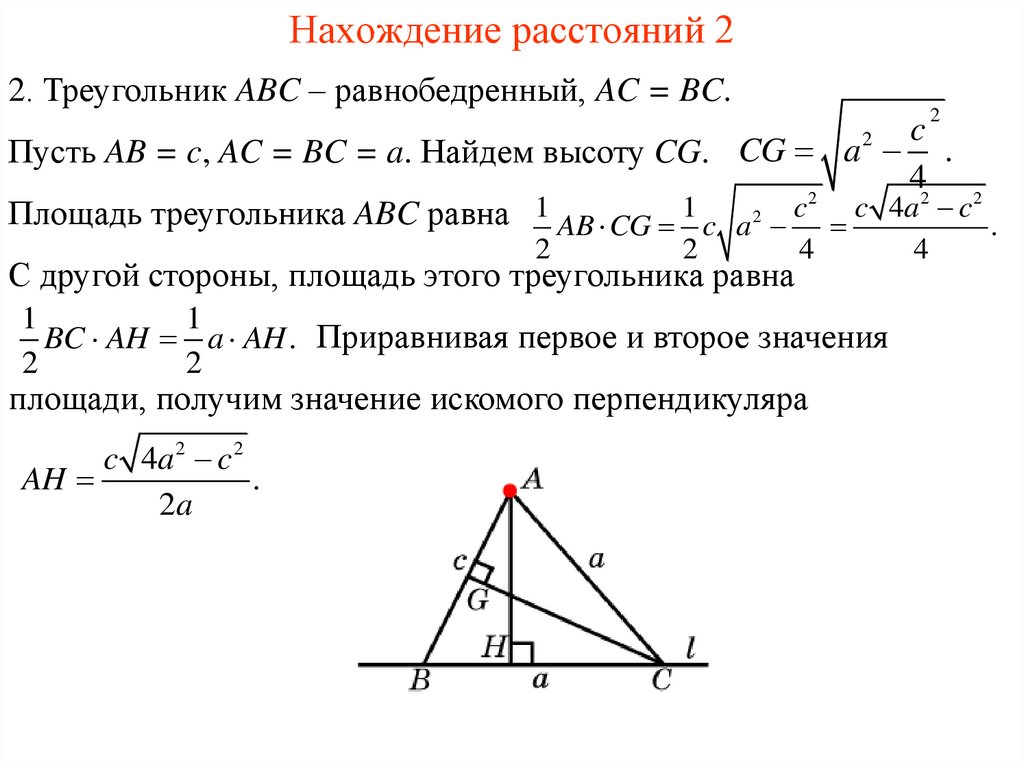
3. Нахождение расстояний 2
2. Треугольник ABC – равнобедренный, AC = BC.2
c
2
Пусть AB = c, AC = BC = a. Найдем высоту CG. CG a .
42 2
2
Площадь треугольника ABC равна 1 AB CG 1 c a 2 c c 4a c .
2
2
С другой стороны, площадь этого треугольника равна
4
1
1
BC AH a AH . Приравнивая первое и второе значения
2
2
площади, получим значение искомого перпендикуляра
c 4a 2 c 2
AH
.
2a
4
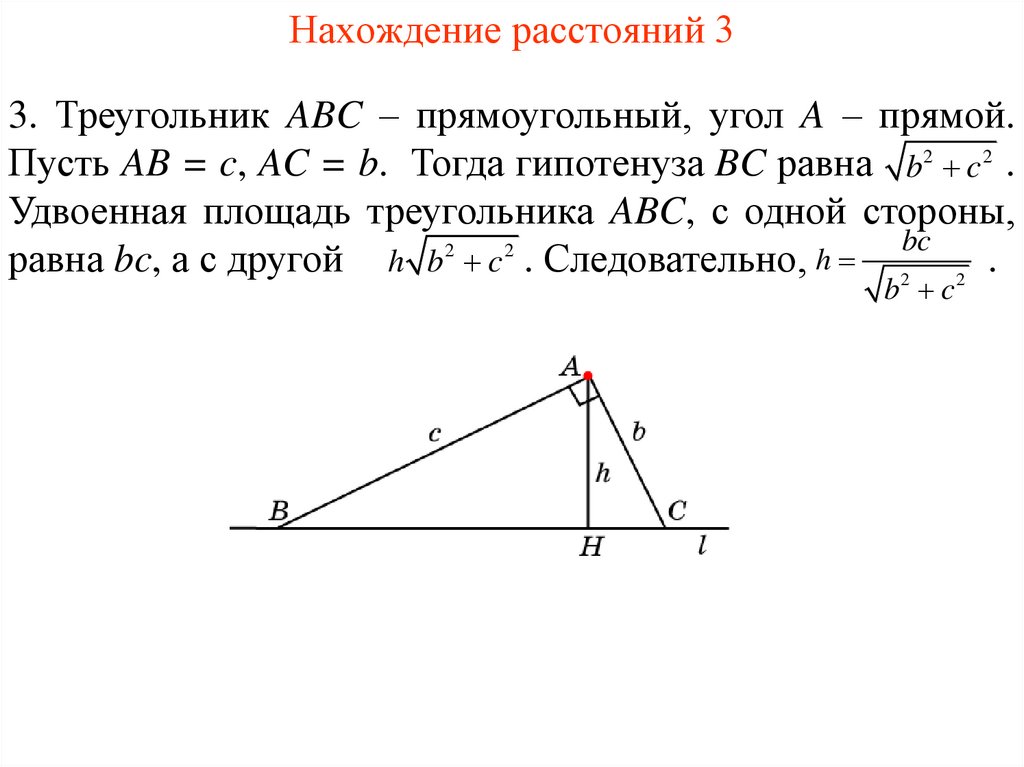
4. Нахождение расстояний 3
3. Треугольник ABC – прямоугольный, угол A – прямой.Пусть AB = c, AC = b. Тогда гипотенуза BC равна b2 c 2 .
Удвоенная площадь треугольника ABC, с одной стороны,
bc
равна bc, а с другой h b 2 c 2 . Следовательно, h 2 2 .
b c
5. Нахождение расстояний 4
4. Треугольник ABC – произвольный.Пусть AB = c, AC = b, BC = a, ACB . По теореме косинусов
имеет место равенство c2 a2 b2 2ab cos . Откуда
a 2 b2 c 2 Зная косинус угла, можно найти его синус
cos
.
2ab
sin 1 cos 2 , а зная синус , можно найти высоту AH b sin .
6. Куб 1
В единичном кубе A…D1 найдите расстояние отточки A до прямой BC.
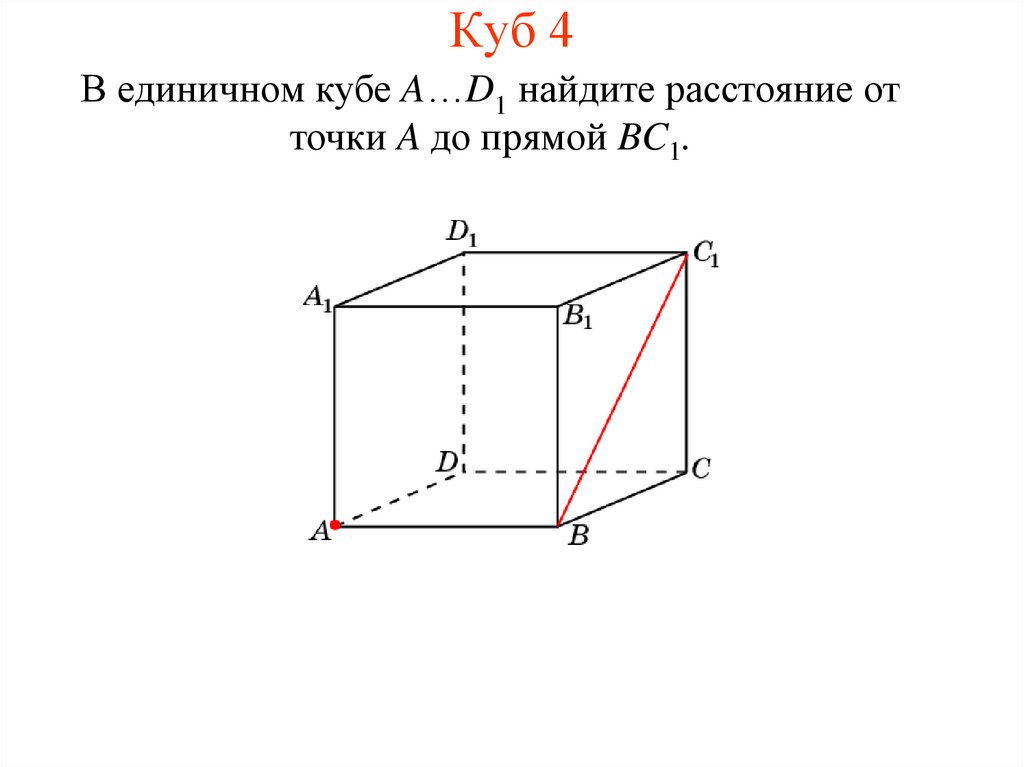
7. Куб 4
В единичном кубе A…D1 найдите расстояние отточки A до прямой BC1.
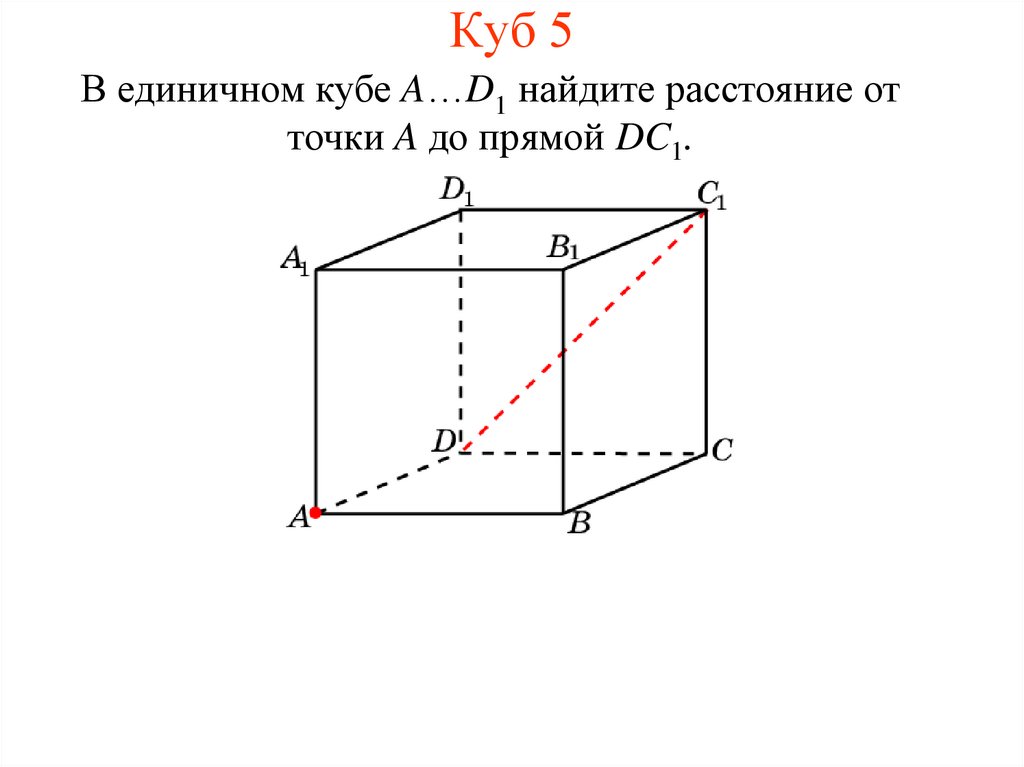
8. Куб 5
В единичном кубе A…D1 найдите расстояние отточки A до прямой DC1.
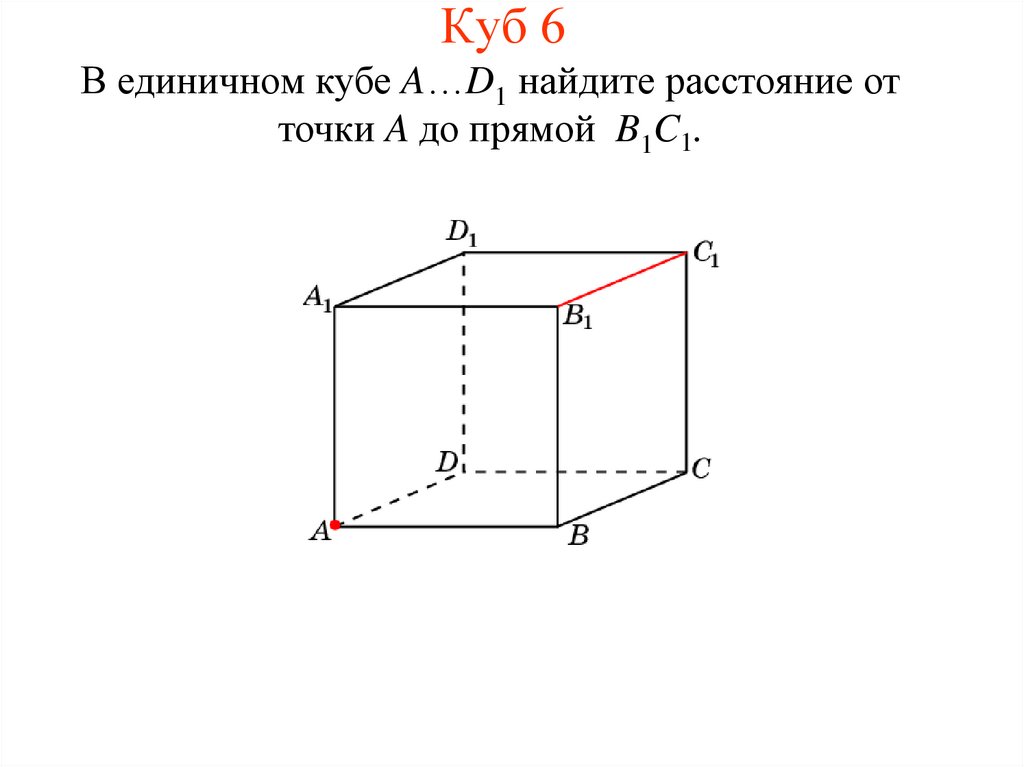
9. Куб 6
В единичном кубе A…D1 найдите расстояние отточки A до прямой B1C1.
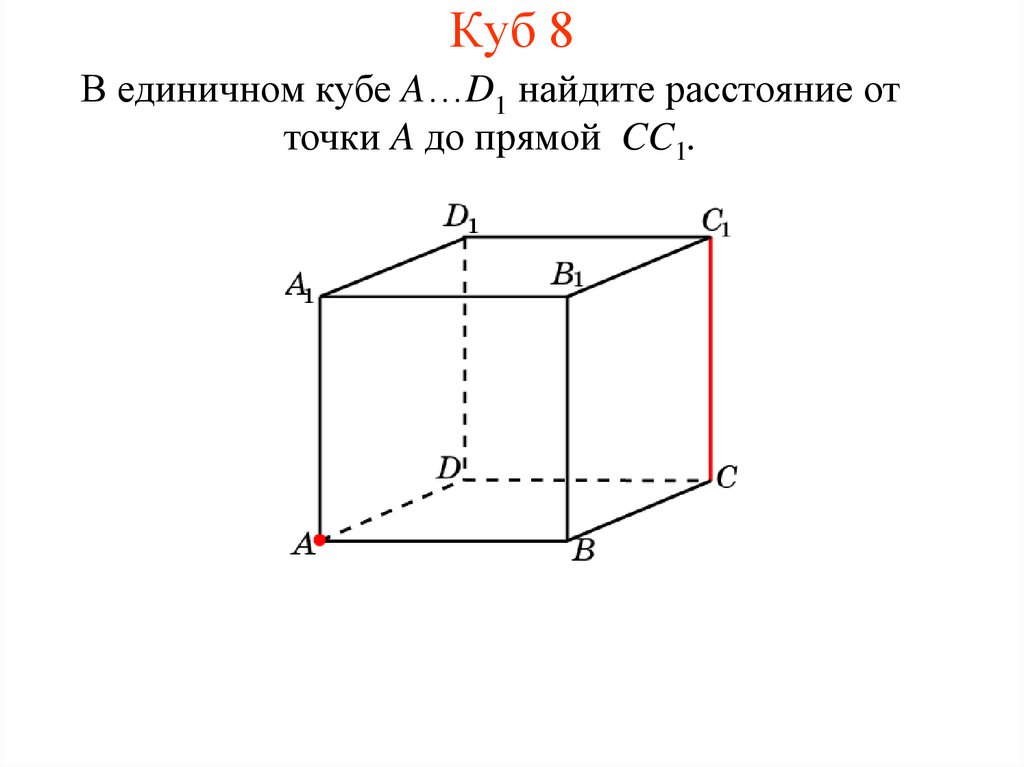
10. Куб 8
В единичном кубе A…D1 найдите расстояние отточки A до прямой CC1.
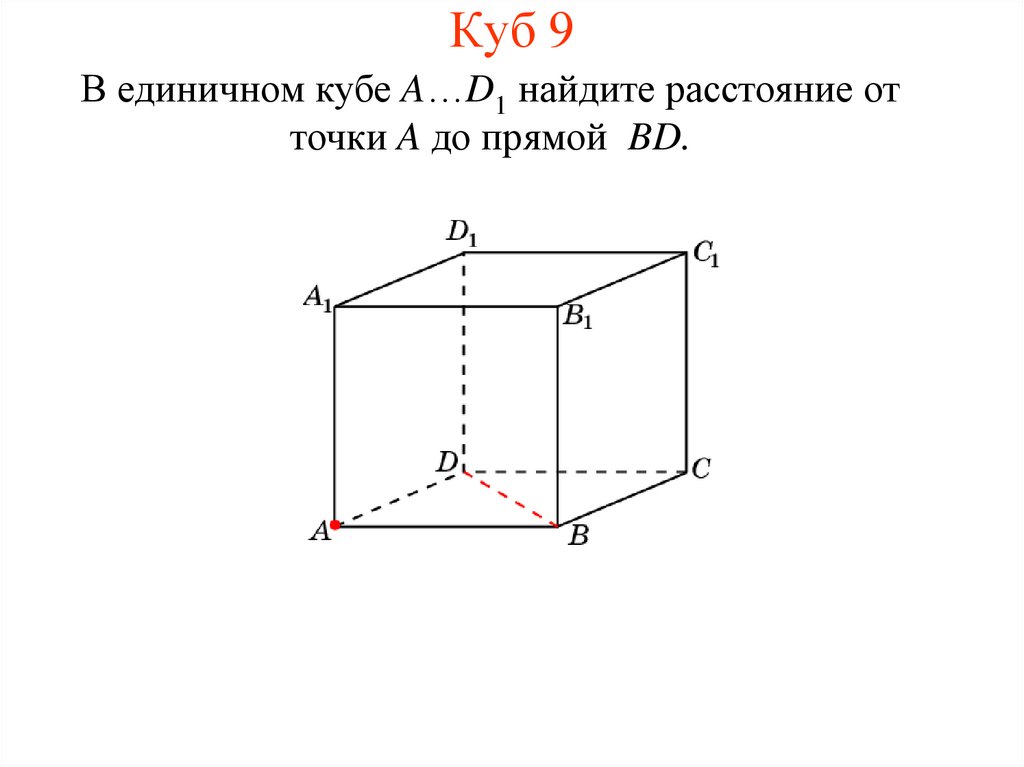
11. Куб 9
В единичном кубе A…D1 найдите расстояние отточки A до прямой BD.
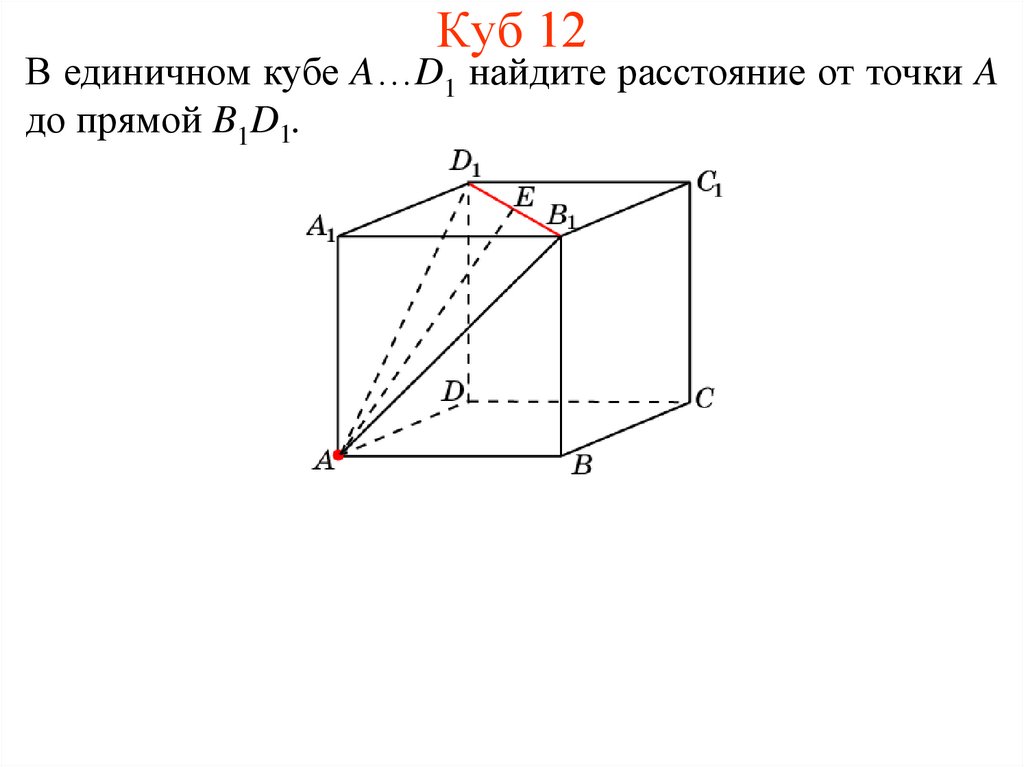
12. Куб 12
В единичном кубе A…D1 найдите расстояние от точки Aдо прямой B1D1.
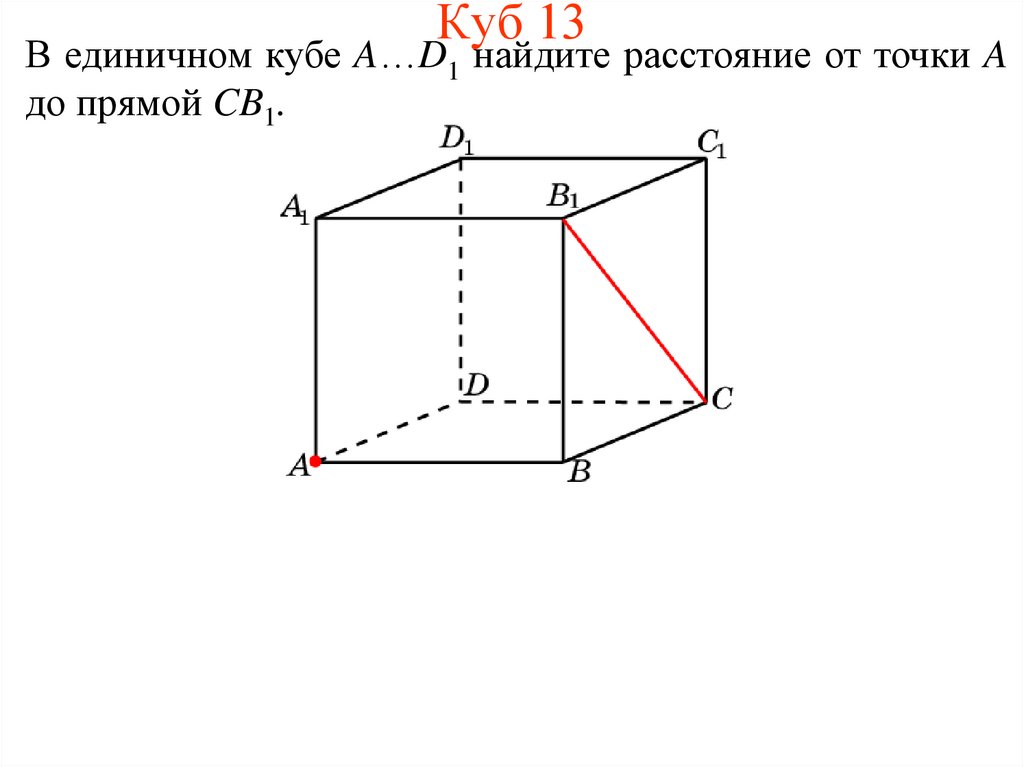
13. Куб 13
В единичном кубе A…D1 найдите расстояние от точки Aдо прямой CB1.
14. Куб 16
В единичном кубе A…D1 найдите расстояние отточки A до прямой BD1.
15. Куб 18
В единичном кубе A…D1 точка E – середина ребра C1D1.Найдите расстояние от точки A1 до прямой BE.
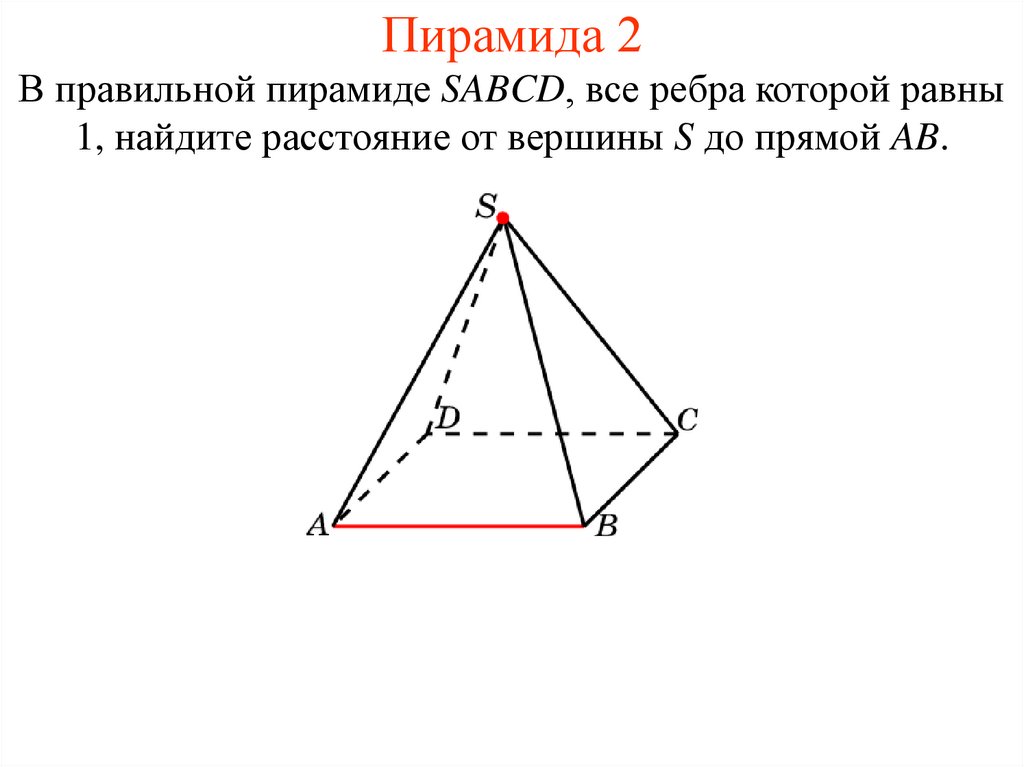
16. Пирамида 2
В правильной пирамиде SABCD, все ребра которой равны1, найдите расстояние от вершины S до прямой AB.
17. Пирамида 3
В правильной пирамиде SABCD, все ребра которой равны1, найдите расстояние от вершины A до прямой SB.
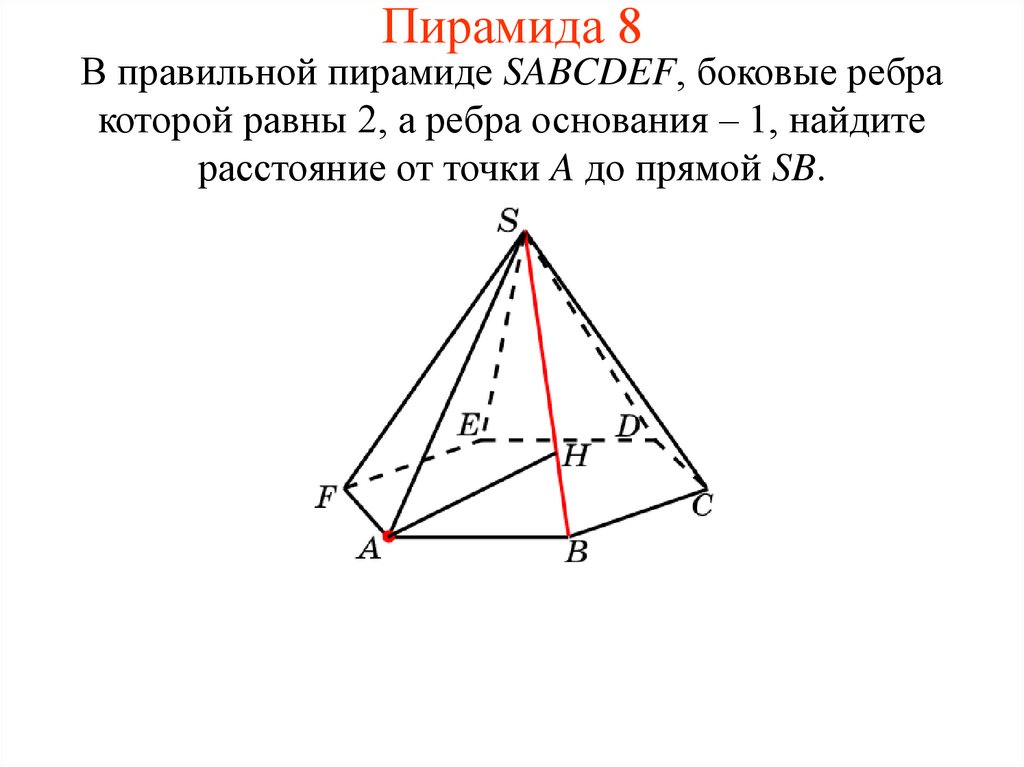
18. Пирамида 8
В правильной пирамиде SABCDEF, боковые ребракоторой равны 2, а ребра основания – 1, найдите
расстояние от точки A до прямой SB.
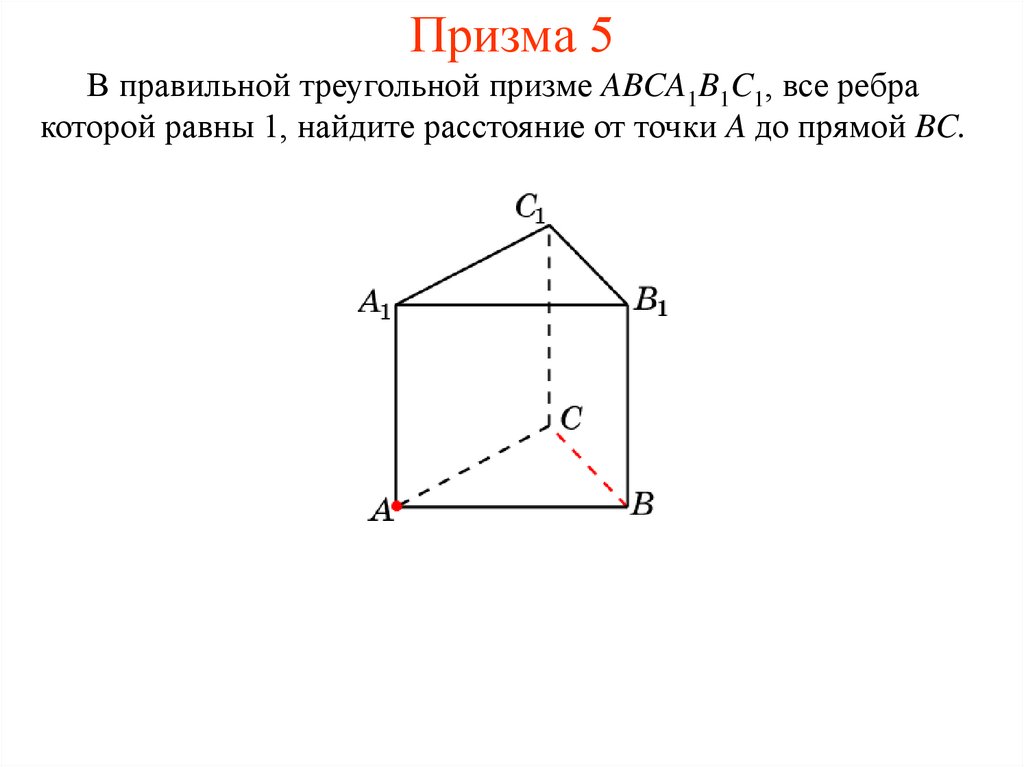
19. Призма 5
В правильной треугольной призме ABCA1B1C1, все ребракоторой равны 1, найдите расстояние от точки A до прямой BC.
20. Призма 10
В правильной треугольной призме ABCA1B1C1, все ребра которойравны 1, найдите расстояние от точки A до прямой BD1, где D1 –
середина ребра A1C1.







 Математика
Математика








