Сложение и вычитание векторов

1.

2.

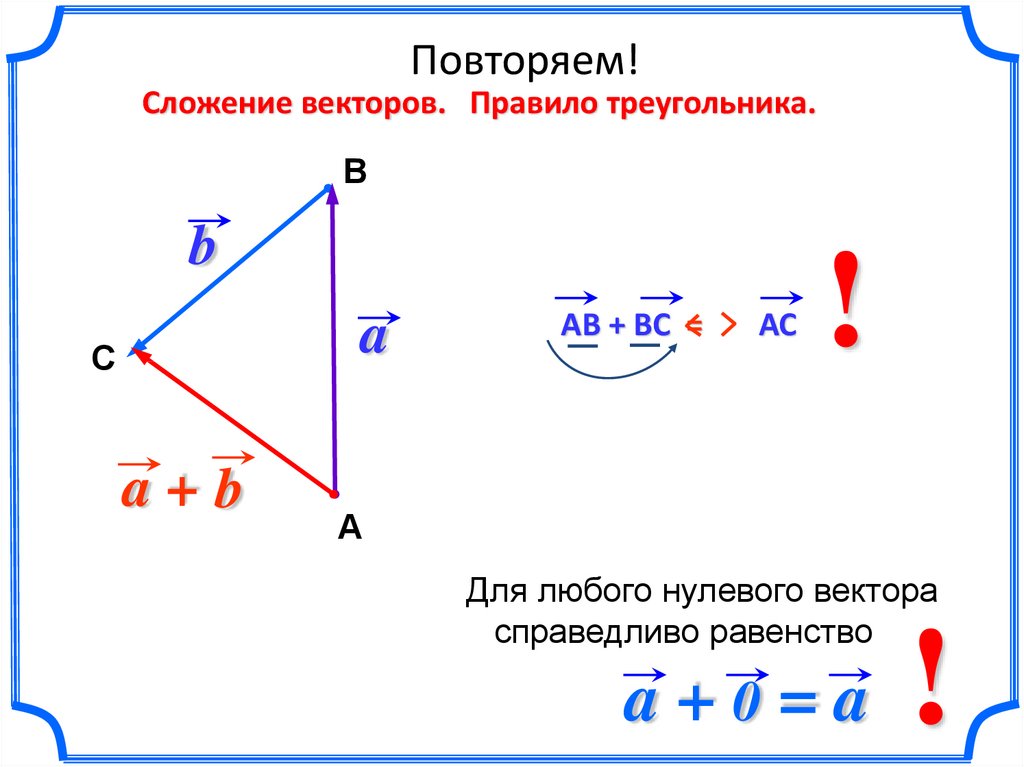
Повторяем!
Сложение векторов. Правило треугольника.
В
b
a
С
a+b
АВ + ВС =
АС
!
А
Для любого нулевого вектора
справедливо равенство
a+0=a
!

3.

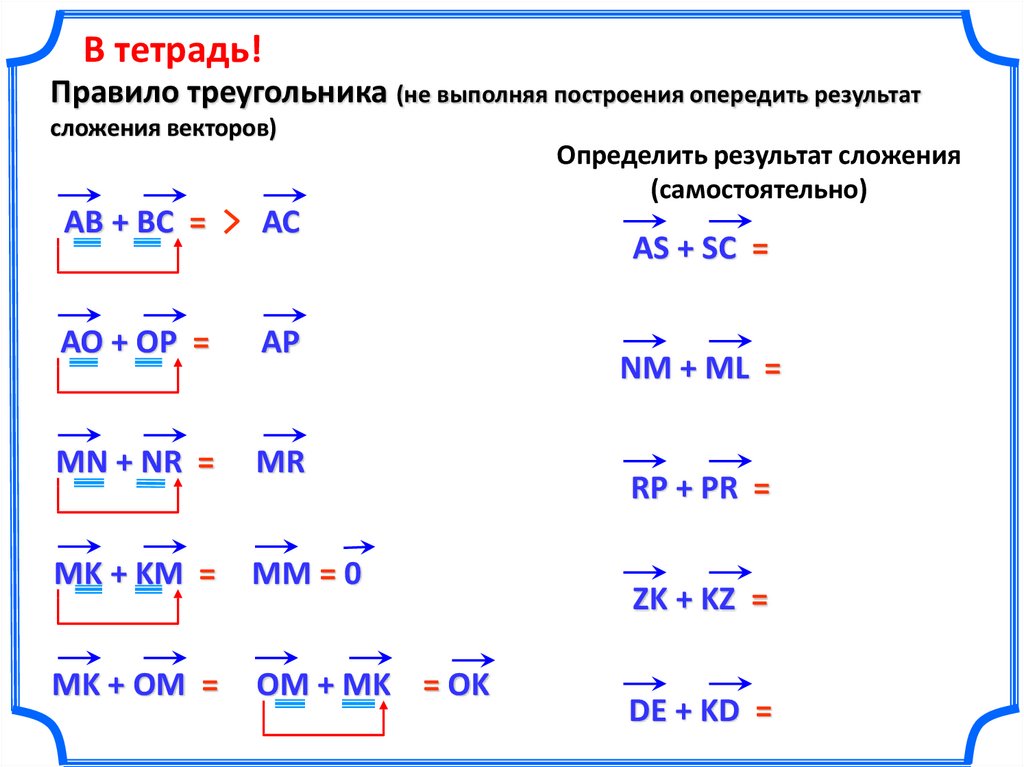
В тетрадь!
Правило треугольника (не выполняя построения опередить результат
сложения векторов)
Определить результат сложения
(самостоятельно)
АВ + ВС =
АС
АО + ОР =
АР
MN + NR =
MR
MK + KM =
MM = 0
MK + OM =
OM + MK = OK
АS + SС =
NM + ML =
RP + PR =
ZK + KZ =
DE + KD =

4.

В тетрадь!
Правило треугольника (постройте треугольники)
АС =
Расписать в виде суммы векторов
(самостоятельно)
АВ + ВС
из ОВN
ON =
OB + ВN
OB =
из ASR
AS =
AR + RS
RA =
из XKH
XH =
XK + KH
KX =
из АMD
MD = MA + AD
AD =
из FPO
OP =
FO =
OF + FP

5.

Законы сложения векторов
Теорема
Для любых векторов
1
2
a, b, c
a+b=b+a
справедливы равенства:
!
переместительный закон
(a + b) + c = a + (b + c)
сочетательный закон
!

6.

a называется противоположным В тетрадь!
a1 , если векторы a и a1 имеют равные
Вектор
вектору
длины и противоположно направлены.
a1
a
А
-b
А
Вектор ВА, противоположный
вектору АВ
ВА = – АВ
В
a1
-b, противоположный вектору b
Вектор
b
a = a1 ; a
В
a + (-a) = 0

7.

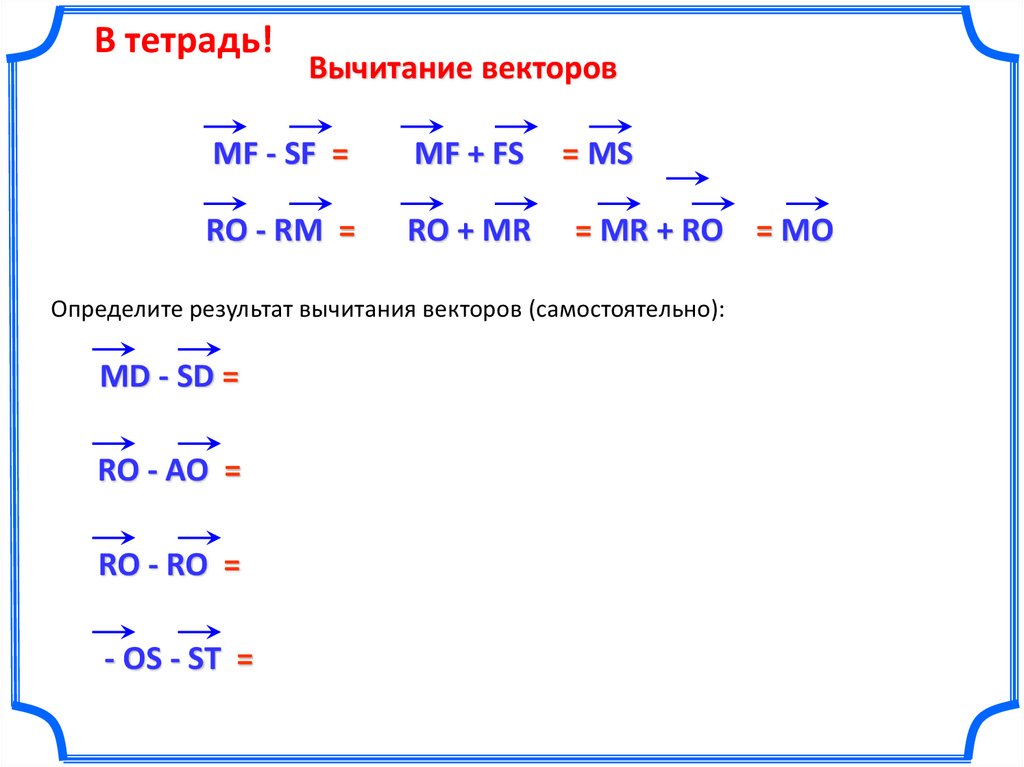
В тетрадь!
Вычитание векторов.
a – b = a +(–b)
b
-b
a
a- b
a
-b

8.

В тетрадь!
Вычитание векторов
MF - SF =
MF + FS
RO - RM =
RO + MR
= MS
= MR + RO = MO
Определите результат вычитания векторов (самостоятельно):
MD - SD =
RO - AO =
RO - RO =
- OS - ST =

9.

В тетрадь!
№ 766 На рисунке изображены векторы
a, b, c, d
ХУ. Представьте вектор ХУ в виде суммы остальных или им
противоположных векторов.
–b
–a
c
Х
d
–a–b+c+d=
ХУ
У

10.

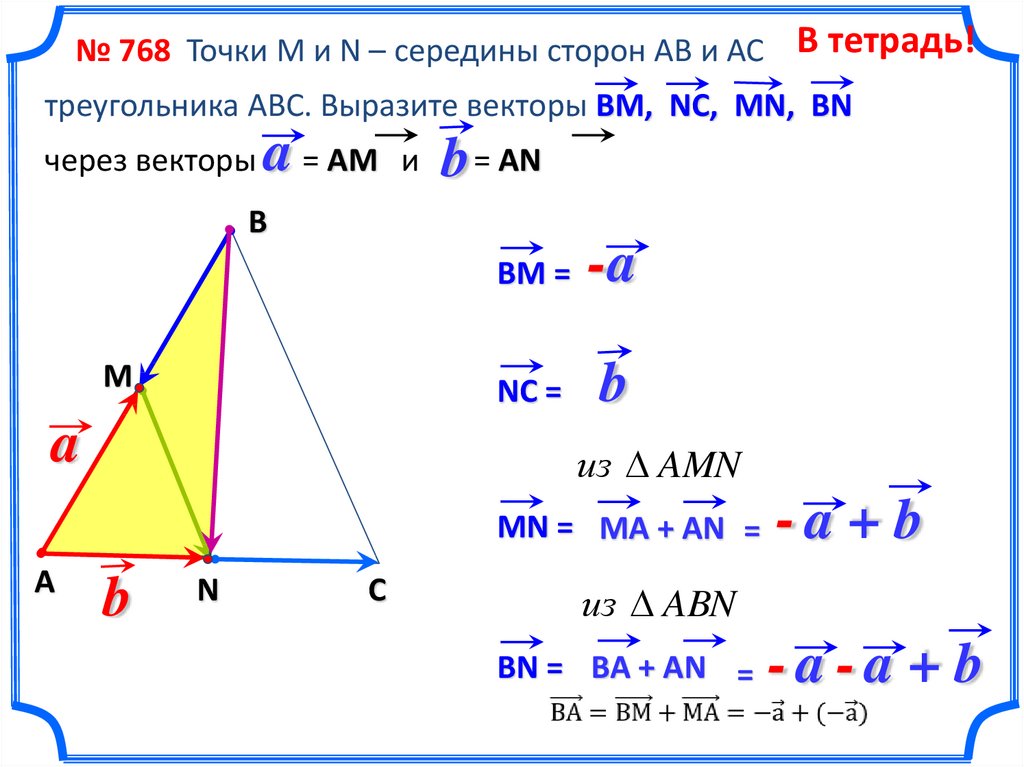
№ 768 Точки М и N – середины сторон АВ и АС В тетрадь!
треугольника АВС. Выразите векторы ВМ, NC, MN, BN
через векторы
a = АМ
и
b = АN
В
М
a
ВМ =
-a
NC =
b
из AMN
MN = MA + AN =
А
b
N
С
-a + b
из ABN
BN = BA + AN =
-a-a + b