Похожие презентации:
Решение вычислительных задач на компьютере
1. Решение вычислительных задач на компьютере
1Решение
вычислительных
задач на компьютере
§ 69. Точность вычислений
§ 70. Решение уравнений
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
2. Решение вычислительных задач на компьютере
2Решение
вычислительных
задач на компьютере
§ 69. Точность вычислений
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
3. Погрешности измерений
Решение вычислительных задач, 10 класс3
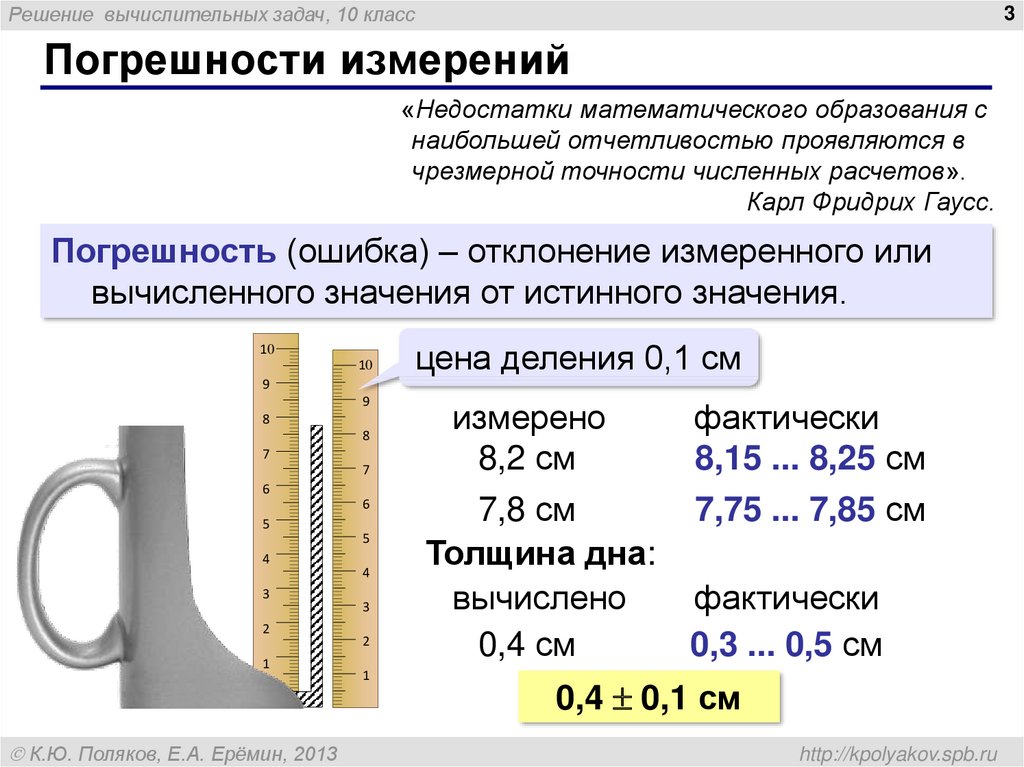
Погрешности измерений
«Недостатки математического образования с
наибольшей отчетливостью проявляются в
чрезмерной точности численных расчетов».
Карл Фридрих Гаусс.
Погрешность (ошибка) – отклонение измеренного или
вычисленного значения от истинного значения.
10
10
цена деления 0,1 см
9
9
8
8
7
7
6
6
5
5
4
3
2
1
К.Ю. Поляков, Е.А. Ерёмин, 2013
4
3
2
1
измерено
8,2 см
7,8 см
Толщина дна:
вычислено
0,4 см
фактически
8,15 ... 8,25 см
7,75 ... 7,85 см
фактически
0,3 ... 0,5 см
0,4 0,1 см
http://kpolyakov.spb.ru
4. Погрешности измерений
Решение вычислительных задач, 10 класс4
Погрешности измерений
абсолютная
погрешность x
0,4 0,1
0,1 см
?
Можно ли оценить
точность измерений?
Относительная погрешность:
x
x *
x*
измеренное
истинное
значение
0,1
x
0,25 25%
0,4
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
5. Погрешности вычислений
Решение вычислительных задач, 10 класс5
Погрешности вычислений
D 1,2 0,1 см
S
D2
Smin
S ?
1,1309733552923255658465516179806...
4
1,12
0,950...
4
S 1,1 0,2 см
Smax
1,32
4
1,327...
0,2
x
100% 18%
1,1
Все практические расчеты выполняются неточно.
Погрешность результата вычислений определяется
погрешностью исходных данных.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
6. Погрешности вычислений
Решение вычислительных задач, 10 класс6
Погрешности вычислений
a 1000 0,001; b 0,002 0,001;
a c
x
c 1000 0,001; d 0,003 0,001.
b d
0,001
0,001
0,001
50% b
33%
a c
0,01% b
0,002
0,003
1000
1000 1000
неточные числа
x
166667
0,002 0,003
в знаменателе
1000 1000
xmax
750000
0,001 0,004
750000 166667
x
352%
1000 1000
166667
xmin
166667
0,003 0,002
Метод вычислительно неустойчив: малые погрешности
в исходных данных могут привести к большим
погрешностям в решении.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
7. Источники погрешностей
Решение вычислительных задач, 10 класс7
Источники погрешностей
• неточность исходных данных
• неточность записи вещественных чисел в двоичном
коде конечной длины
• погрешности приближенного вычисления некоторых
стандартных функций (sin, cos, …)
• накопление погрешностей при арифметических
действиях с неточными данными
• погрешность метода
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
8. Решение вычислительных задач на компьютере
8Решение
вычислительных
задач на компьютере
§ 70. Решение уравнений
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
9. Методы решения уравнений
Решение вычислительных задач, 10 класс9
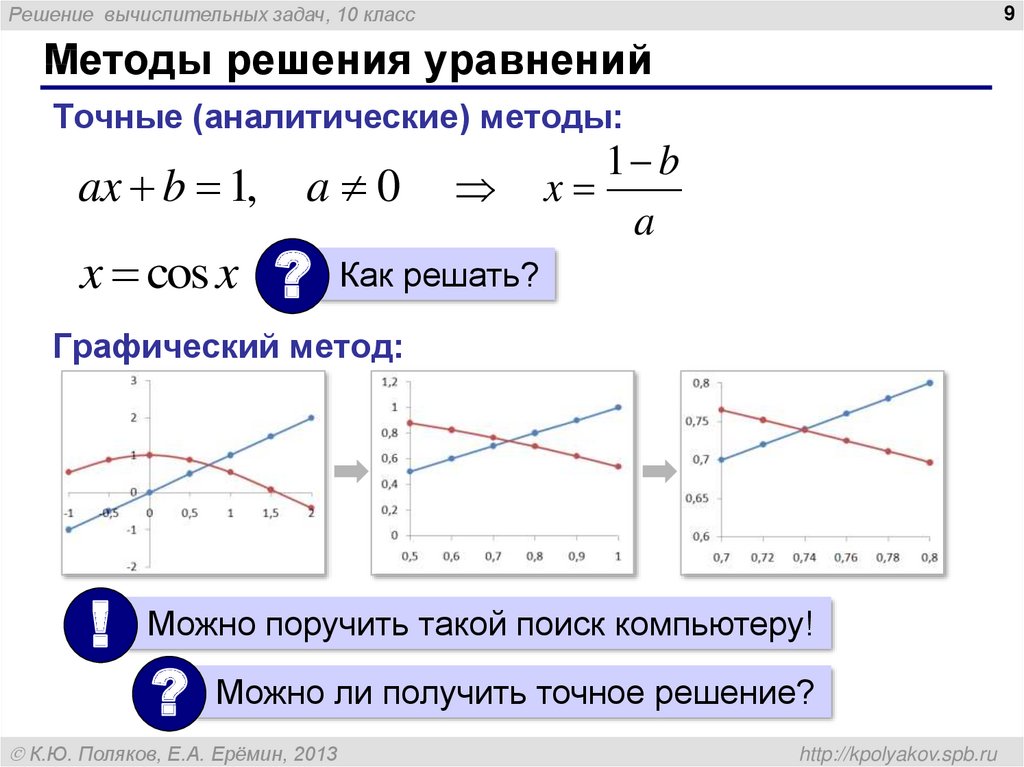
Методы решения уравнений
Точные (аналитические) методы:
ax b 1,
x cos x
a 0
?
1 b
x
a
Как решать?
Графический метод:
!
Можно поручить такой поиск компьютеру!
?
Можно ли получить точное решение?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
10. Приближённые методы
Решение вычислительных задач, 10 класс10
Приближённые методы
Сжатие отрезка:
1) выбрать начальный отрезок [a0, b0] (одно решение!)
2) уточнить решение с помощью некоторого
алгоритма: [a, b]
3) повторять шаг 2, пока длина отрезка [a, b] не станет
достаточно мала
a
?
x
a b
2
?
b
Как оценить ошибку?
Завершение работы:
К.Ю. Поляков, Е.А. Ерёмин, 2013
Что лучше выбрать в
качестве решения?
b a
x x
2
b a 2
*
допустимая
ошибка
http://kpolyakov.spb.ru
11. Приближенные методы
Решение вычислительных задач, 10 класс11
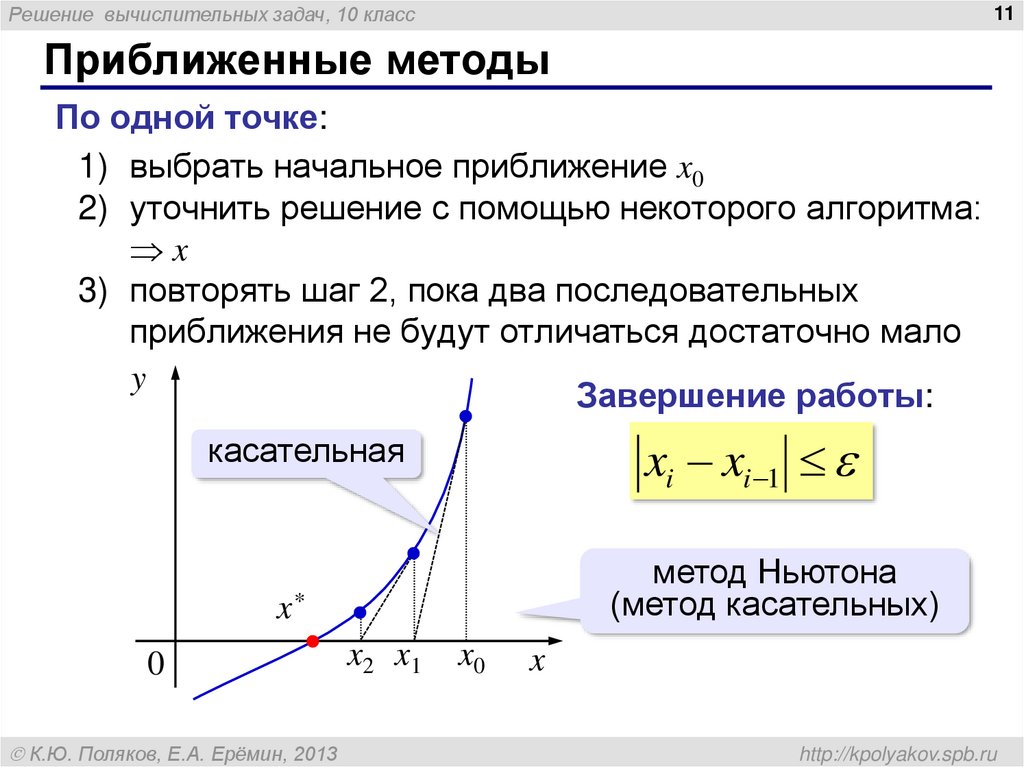
Приближенные методы
По одной точке:
1) выбрать начальное приближение x0
2) уточнить решение с помощью некоторого алгоритма:
x
3) повторять шаг 2, пока два последовательных
приближения не будут отличаться достаточно мало
y
Завершение работы:
xi xi 1
касательная
метод Ньютона
(метод касательных)
x*
0
К.Ю. Поляков, Е.А. Ерёмин, 2013
x2 x1
x0
x
http://kpolyakov.spb.ru
12. Приближенные методы
Решение вычислительных задач, 10 класс12
Приближенные методы
Итерационные методы (лат. iteratio – повторение) –
основаны на многократном выполнении одинаковых
шагов, каждый из которых уточняет решение.
xk 1 f ( xk )
следующее
приближение
предыдущее
приближение
дают какое-то решение, если точное неизвестно
могут давать меньшие ошибки, чем вычисления по
точным формулам
решение приближенное: x
= 1,23345
ответ – число (зависимость от параметра?)
большой объем вычислений
не всегда просто оценить погрешность
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
13. Метод перебора
Решение вычислительных задач, 10 класс13
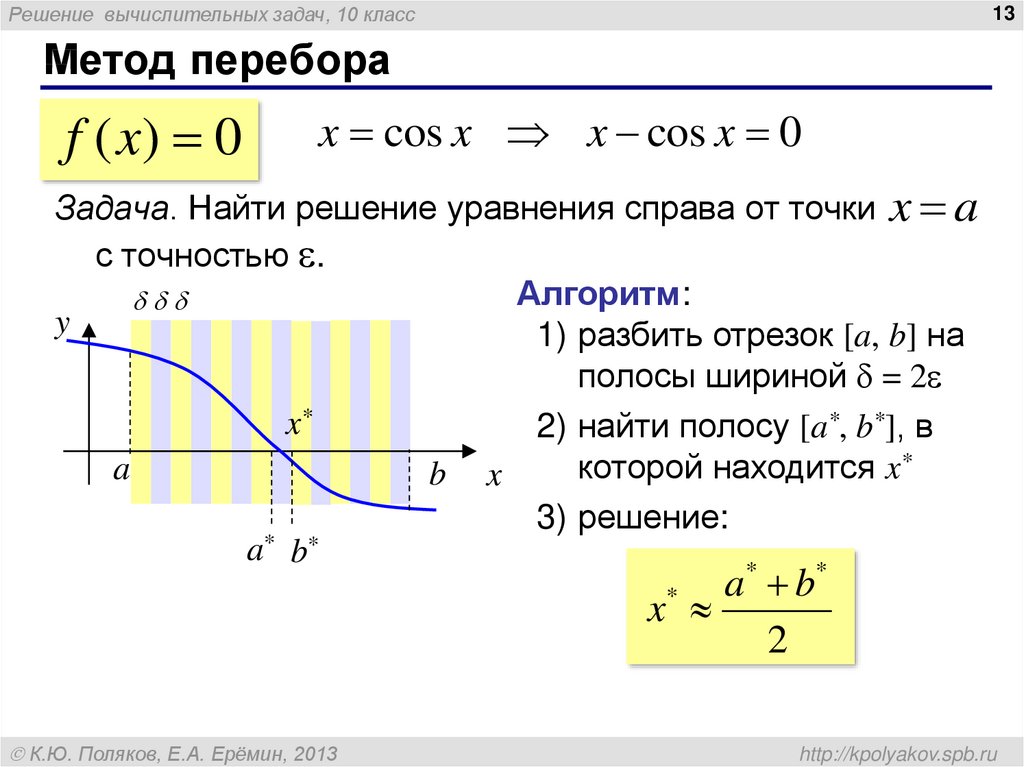
Метод перебора
f ( x) 0
x cos x x cos x 0
Задача. Найти решение уравнения справа от точки x a
с точностью .
Алгоритм:
y
1) разбить отрезок [a, b] на
полосы шириной = 2
x*
2) найти полосу [a*, b*], в
которой находится x*
a
b x
3) решение:
a* b*
*
*
a b
x
2
*
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
14. Есть ли решение на [x, x+ ]?
Решение вычислительных задач, 10 класс14
Есть ли решение на [x, x+ ]?
нет решения
y
есть решение!
y
x*
0
x
x+
x
f ( x) 0
f (x ) 0
0
x*
x
нет решения
y
x+
x
x*
0
x
x
?
f ( x) 0
В чём отличие?
f (x ) 0
x+
f ( x) 0
f (x ) 0
f ( x) f ( x ) 0
!
Если непрерывная функция f (x) имеет разные знаки
на концах интервала [a, b], то в некоторой точке x*
внутри [a, b] она равна 0, то есть f (x* ) = 0!
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
15. Метод перебора (a = 0)
Решение вычислительных задач, 10 класс15
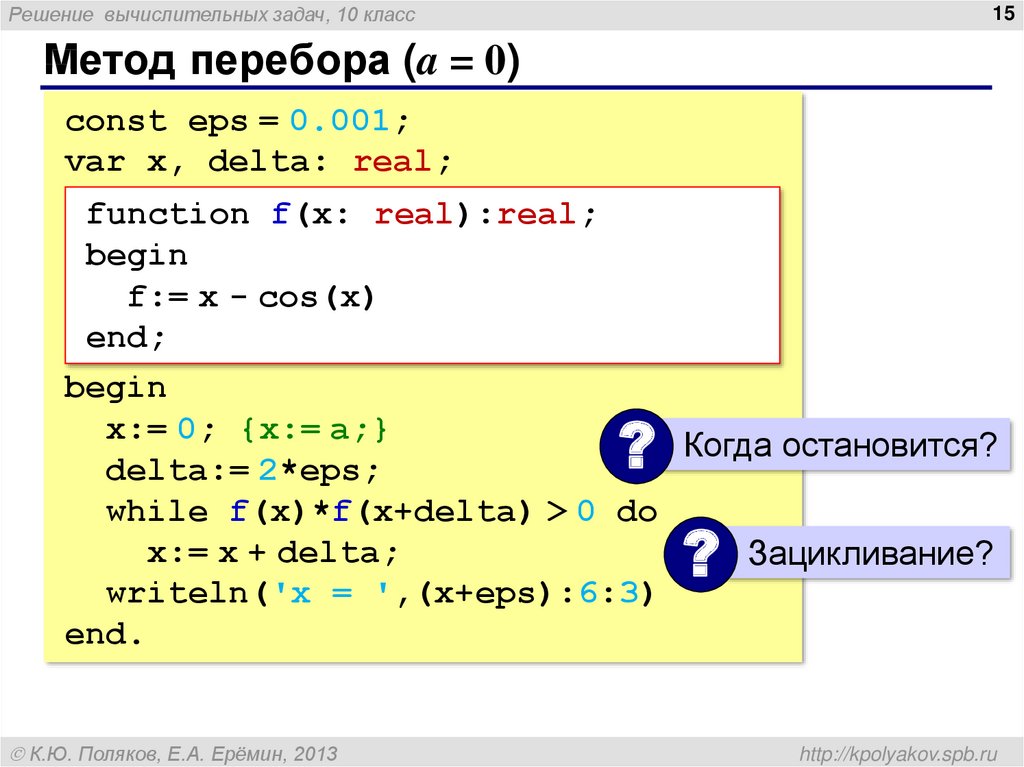
Метод перебора (a = 0)
const eps = 0.001;
var x, delta: real;
function f(x: real):real;
begin
f:= x - cos(x)
end;
begin
x:= 0; {x:= a;}
Когда остановится?
delta:= 2*eps;
while f(x)*f(x+delta) > 0 do
x:= x + delta;
Зацикливание?
writeln('x = ',(x+eps):6:3)
end.
?
?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
16. Метод перебора
Решение вычислительных задач, 10 класс16
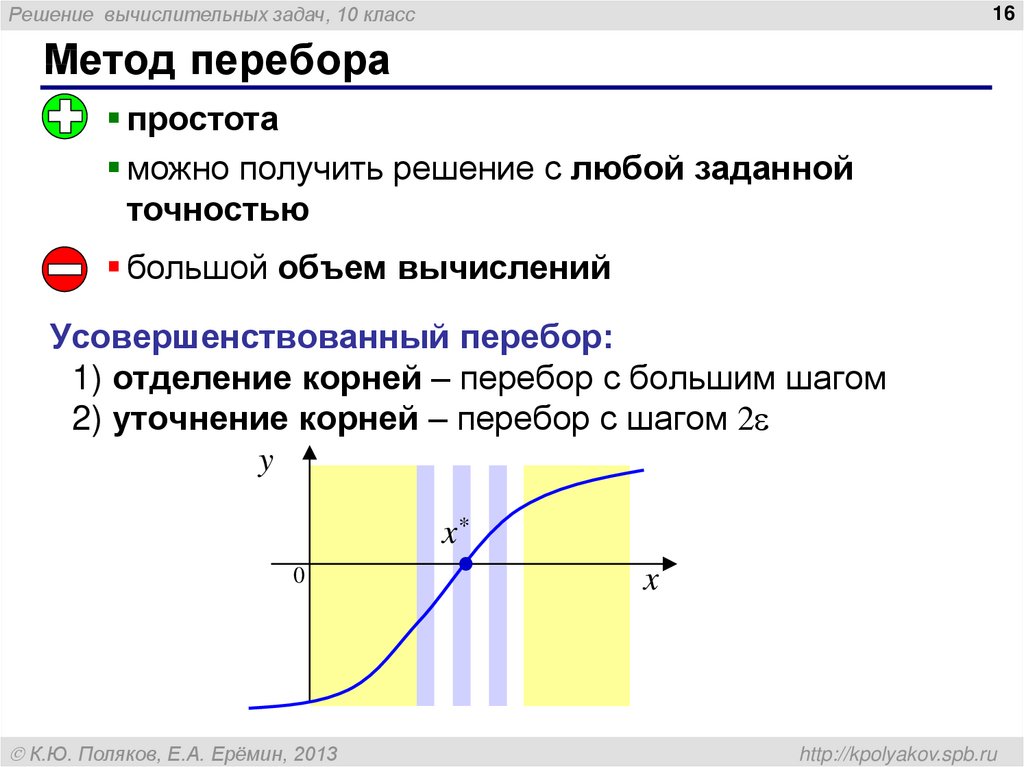
Метод перебора
простота
можно получить решение с любой заданной
точностью
большой объем вычислений
Усовершенствованный перебор:
1) отделение корней – перебор с большим шагом
2) уточнение корней – перебор с шагом 2
y
x*
0
К.Ю. Поляков, Е.А. Ерёмин, 2013
x
http://kpolyakov.spb.ru
17. Метод деления отрезка пополам
Решение вычислительных задач, 10 класс17
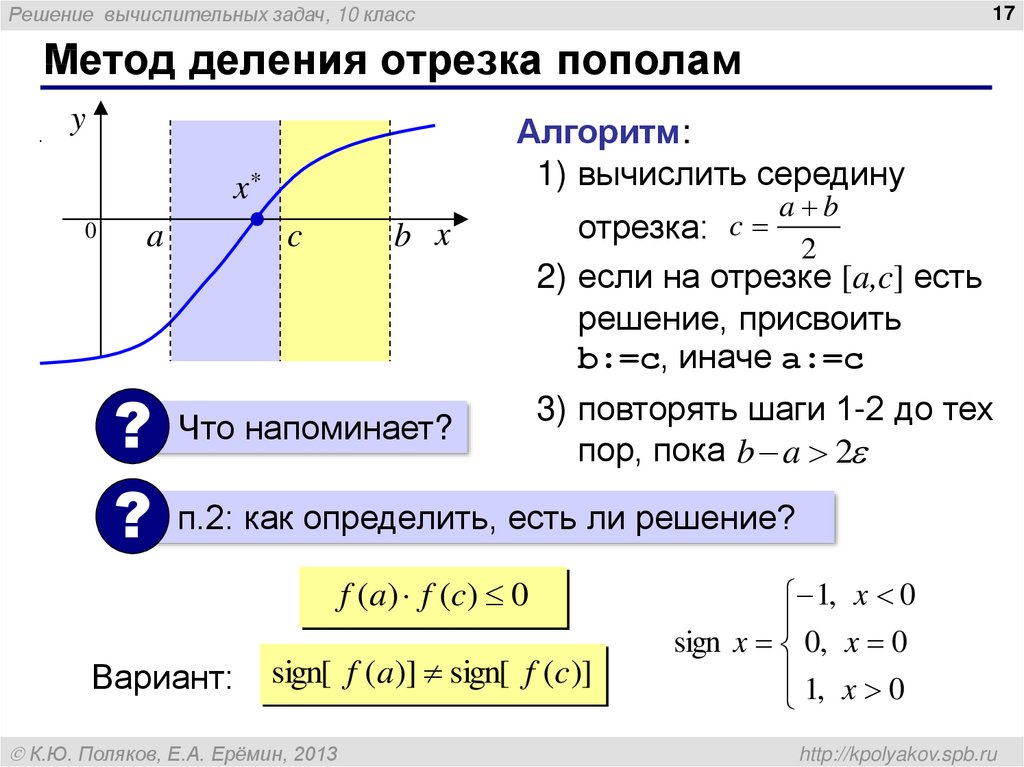
Метод деления отрезка пополам
.
y
Алгоритм:
1) вычислить середину
x*
0
c
a
b x
отрезка: c
a b
2
2) если на отрезке [a,c] есть
решение, присвоить
b:=c, иначе a:=c
?
?
Что напоминает?
3) повторять шаги 1-2 до тех
пор, пока b a 2
п.2: как определить, есть ли решение?
f ( a ) f (c ) 0
Вариант:
sign[ f (a)] sign[ f (c)]
К.Ю. Поляков, Е.А. Ерёмин, 2013
1, x 0
sign x 0, x 0
1, x 0
http://kpolyakov.spb.ru
18. Метод деления отрезка пополам
Решение вычислительных задач, 10 класс18
Метод деления отрезка пополам
.
Паскаль:
delta:= 2*eps;
while b - a > delta do begin
c:= (a + b) / 2;
if f(a)*f(c) <= 0 then
b:= c
else a:= c;
end;
writeln('x = ', (a+b)/2:6:3);
?
Как меняется длина отрезка?
?
За сколько шагов уменьшится в 1000 раз?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
19. Полёт мяча
Решение вычислительных задач, 10 класс19
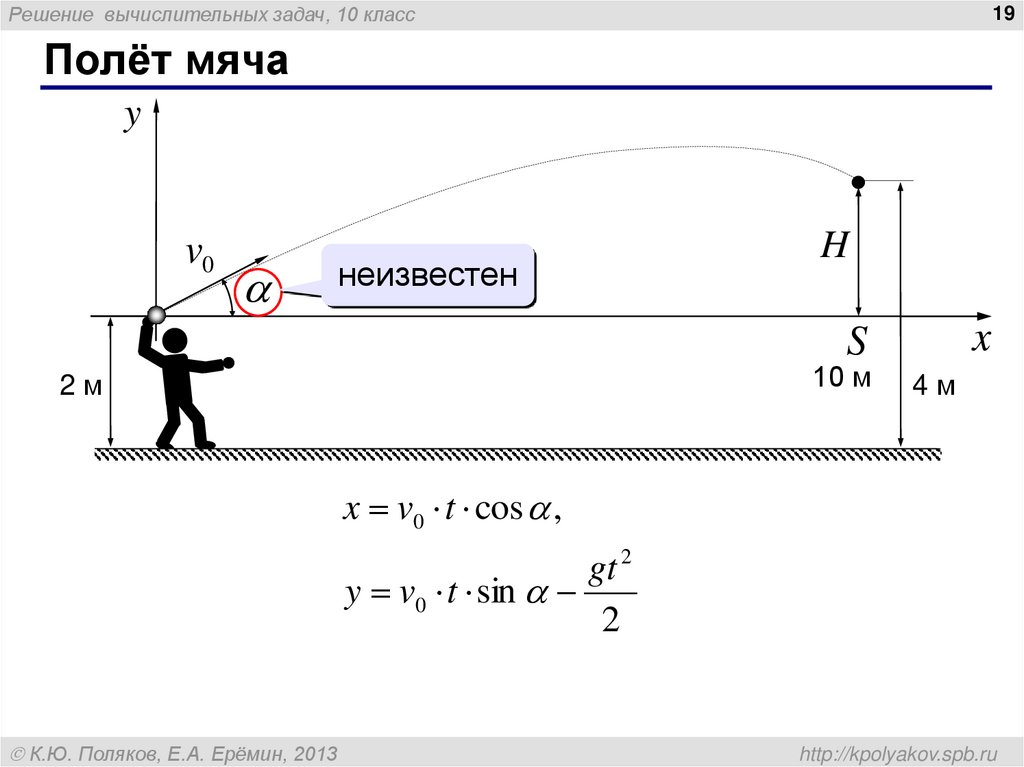
Полёт мяча
y
v0
неизвестен
H
x
S
10 м
2м
4м
x v0 t cos ,
gt 2
y v0 t sin
2
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
20. Полёт мяча
Решение вычислительных задач, 10 класс20
Полёт мяча
Задача. Найти угол (и время t) при котором x = S и y = H:
gt 2
S v0 t cos , H v0 t sin
2
Решение:
S
t
v0 cos
v0 S sin
g S2
H
2
v0 cos
2v0 cos 2
g S2
f ( ) S tg 2
H 0
2
2v0 cos
Диапазон углов для поиска: [0 ...90 ] 0...
2
Как уточнить?
?
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
21. Уточнение диапазона углов
Решение вычислительных задач, 10 класс21
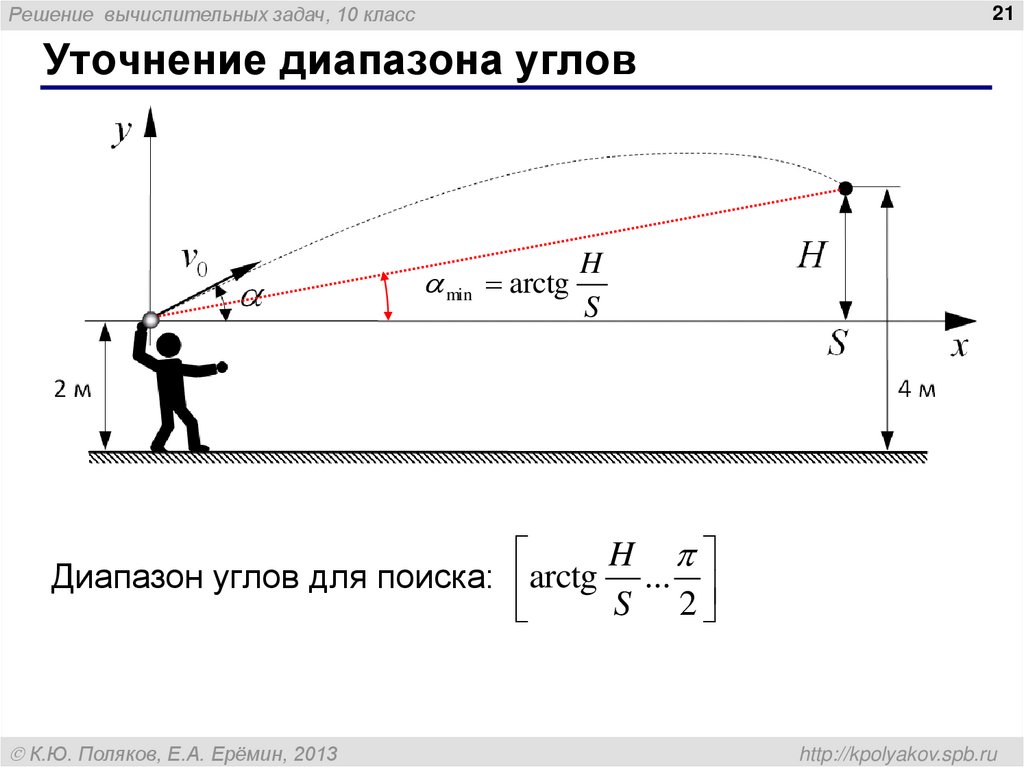
Уточнение диапазона углов
min arctg
H
S
H
Диапазон углов для поиска: arctg ...
S 2
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
22. Полёт мяча
Решение вычислительных задач, 10 класс22
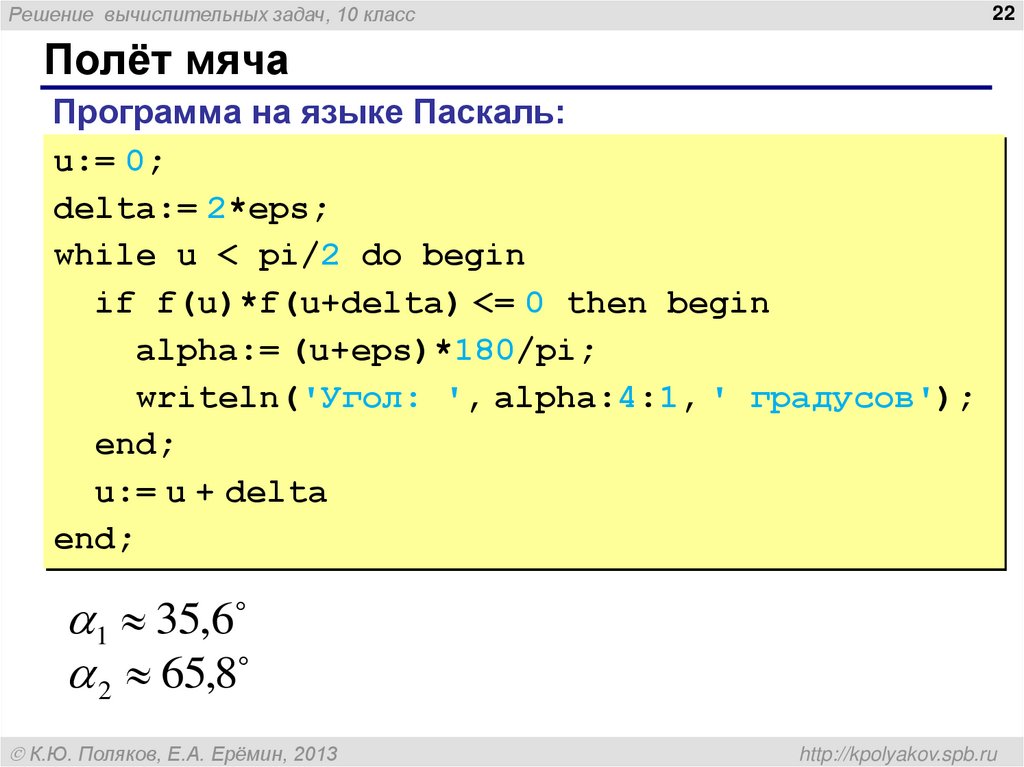
Полёт мяча
Программа на языке Паскаль:
u:= 0;
delta:= 2*eps;
while u < pi/2 do begin
if f(u)*f(u+delta) <= 0 then begin
alpha:= (u+eps)*180/pi;
writeln('Угол: ', alpha:4:1, ' градусов');
end;
u:= u + delta
end;
1 35,6
2 65,8
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
23. Полёт мяча
Решение вычислительных задач, 10 класс23
Полёт мяча
Использование табличного процессора:
имя ячейки
или диапазона
Диапазон углов:
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
24. Полёт мяча
Решение вычислительных задач, 10 класс24
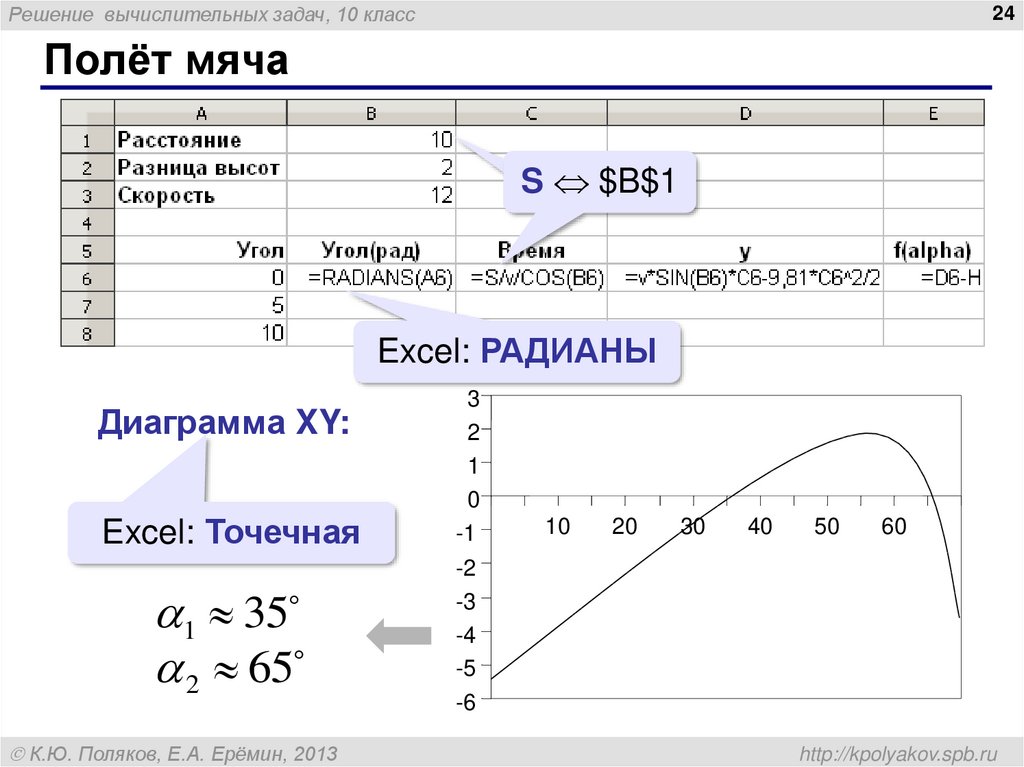
Полёт мяча
S $B$1
Excel: РАДИАНЫ
Диаграмма XY:
Excel: Точечная
1 35
2 65
К.Ю. Поляков, Е.А. Ерёмин, 2013
3
2
1
0
-1
10
20
30
40
50
60
-2
-3
-4
-5
-6
http://kpolyakov.spb.ru
25. Полёт мяча
Решение вычислительных задач, 10 класс25
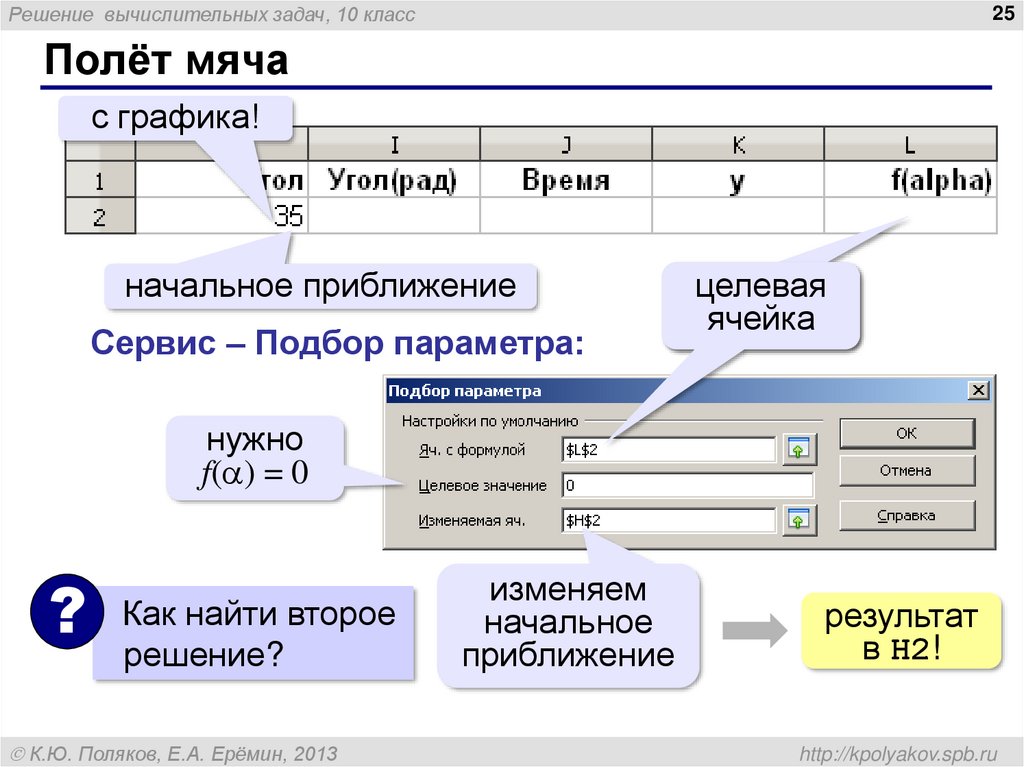
Полёт мяча
с графика!
начальное приближение
Сервис – Подбор параметра:
целевая
ячейка
нужно
f( ) = 0
?
Как найти второе
решение?
К.Ю. Поляков, Е.А. Ерёмин, 2013
изменяем
начальное
приближение
результат
в H2!
http://kpolyakov.spb.ru









![Есть ли решение на [x, x+ ]? Есть ли решение на [x, x+ ]?](https://cf2.ppt-online.org/files2/slide/i/iH6wD1Ot2Ke4SPLxpMR7XqJz9dBafWvEoZbG8T/slide-13.jpg)



 Информатика
Информатика








