Применение производной

1.

2.

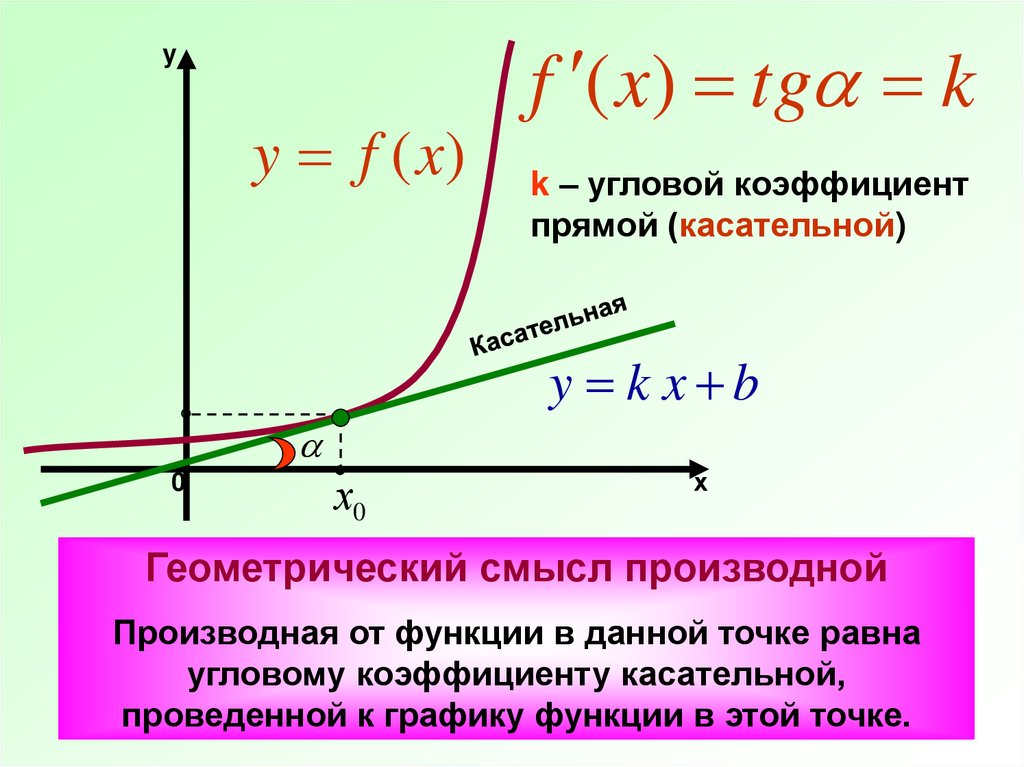
y
y f (x)
f ( x) tg k
k – угловой коэффициент
прямой (касательной)
y k x b
0
х0
х
Геометрический смысл производной
Производная от функции в данной точке равна
угловому коэффициенту касательной,
проведенной к графику функции в этой точке.

3.

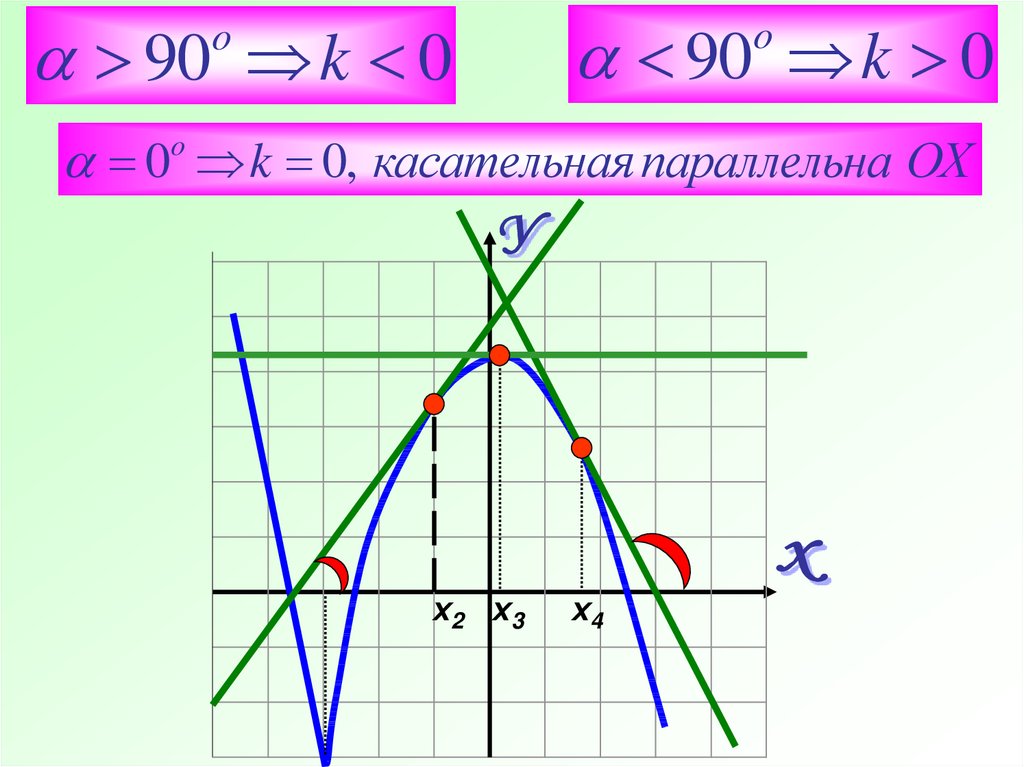
90 k 0
o
90 k 0
o
0 k 0, касательная параллельна ОХ
o
х2 х3
х4

4.

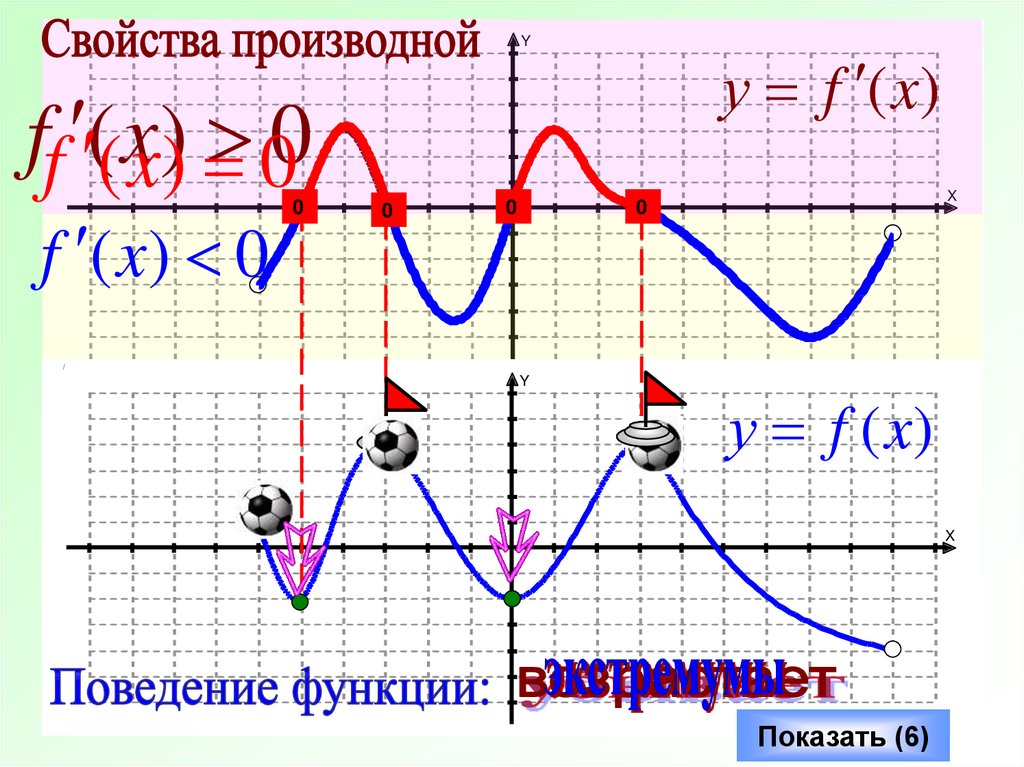
Y
ff ((xx)) 00
f ( x) 0
0
0
0
у f (x)
X
0
Y
у f (x)
X
Показать (6)

5.

У
у f (x)
хо
1
-1 0
-1
Х
1
В7
f ( xo )
-
3
10 х
х
Показать (2)

6.

k f ( xo )
Ищу наименьше
значение
производной
наименьший
В7
-
3
10 х
х
Показать (2)

7.

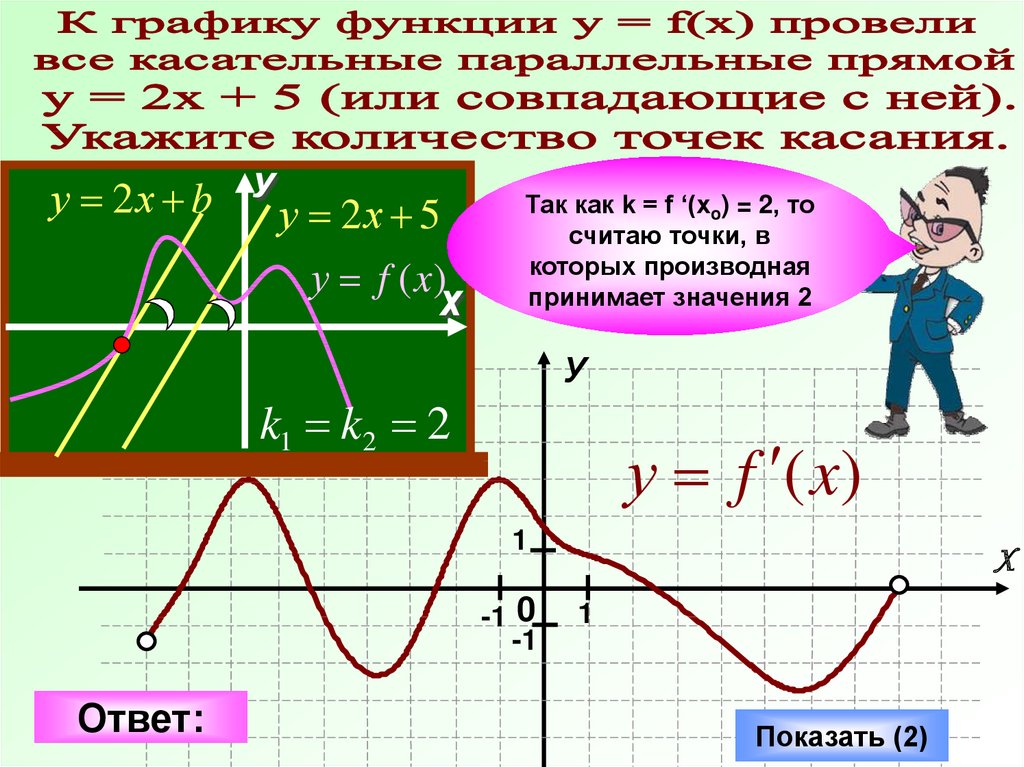
у 2х b
у 2х 5
у f (x)
Так как k = f ‘(xo) = 2, то
считаю точки, в
которых производная
принимает значения 2
У
k1 k2 2
у f (x)
1
-1 0
-1
Ответ:
Х
1
Показать (2)

8.

У
у f (x)
1
-1 0
-1
k f ( xo ) 2
В7
-4
3
10 х
х
Х
1

9.

У
1
-1
0
-1
1
хо
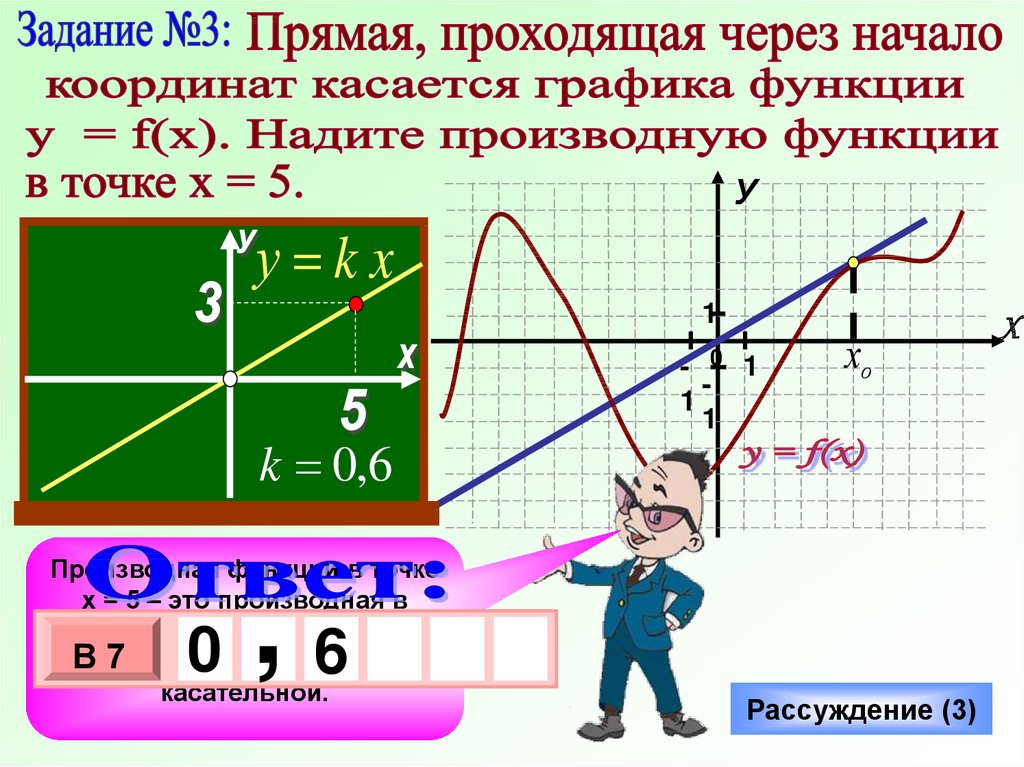
Х

10.

У
у kx
1
- 0 1
1
1
k 0,6
Производная функции в точке
х = 5 – это производная в
точке касания хо, а она 3равна
1 0 х
Вугловому
7
коэффициенту
касательной.
,
- 6
0
хо
х
Рассуждение (3)
Х

11.

уугол
наклона
f (x)
У
касательной1 к оси ОХ :
tg k f -1(-1xo 1)
0
tg 135 1 f ( xo )
o
7В
7
-4
Ответ (2)
3
10 х
х
Рассуждение (2)
Х

12.

y
у f ( x) возрастает,
y = f (x) f ( x ) 0
если
у f ( x) убывает,x
b
a
1
если f ( x) 0
0
В7
-7
3
10 х
х

13.

f/(x)
-
f(x)
+
-4
-2
+
0
У
3
+
4
Из двух точек
максимума
наибольшая хmax =
3
y = f /(x)
+
-
-4 -3 -2 -1-
1
+2
3
-
4
+
5
х
В7
3
3
10 х
х

14.

f/(x)
-
f(x)
+
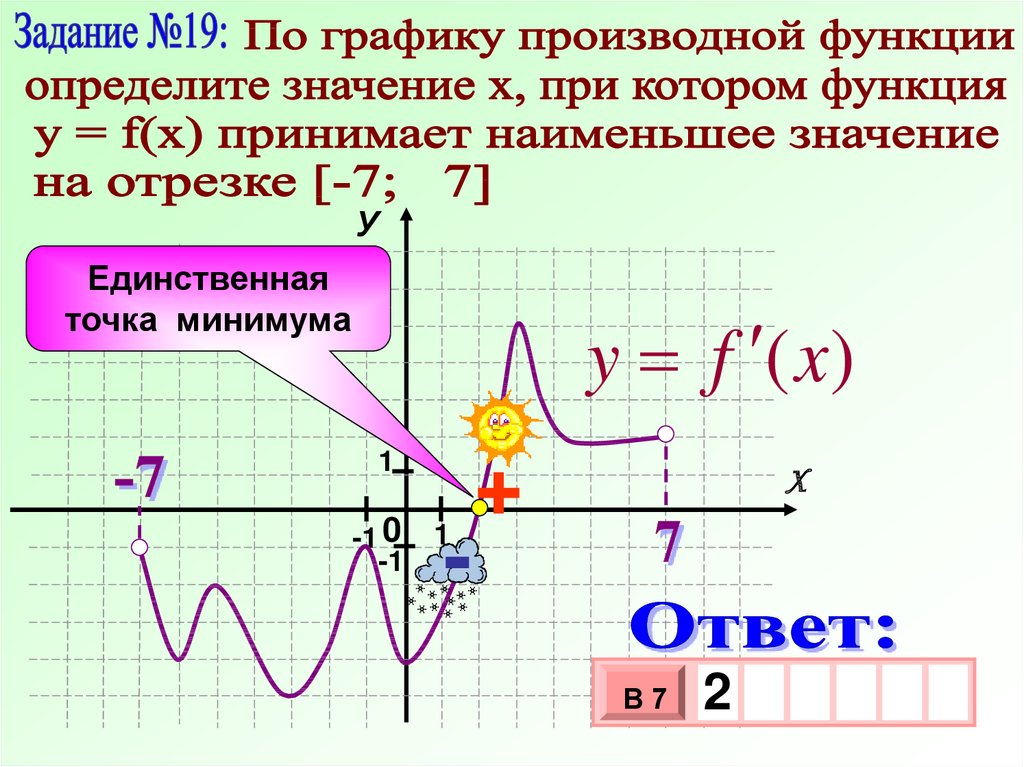
хmin = 2 - единственная
В этой точке функция
у = f (x) примет
наименьшее значение
2
У
y = f /(x)
-4 -3 -2 -1
1
+
2
-
3
4
5 х
В7
2
3
10 х
х

15.

поведение f (x)
y
При переходе через
y = f (x)
точку максимума
a
f ( x)
0
меняет свой
знак bс x на
В7
2
3
10 х
х

16.

f (а ) y tg
В7
y=g(x)
угол наклона
1 йa к
касательно
0
1
x
положитель
ному
-1
направлению оси ОХ
0
,
5
3
10 х
х

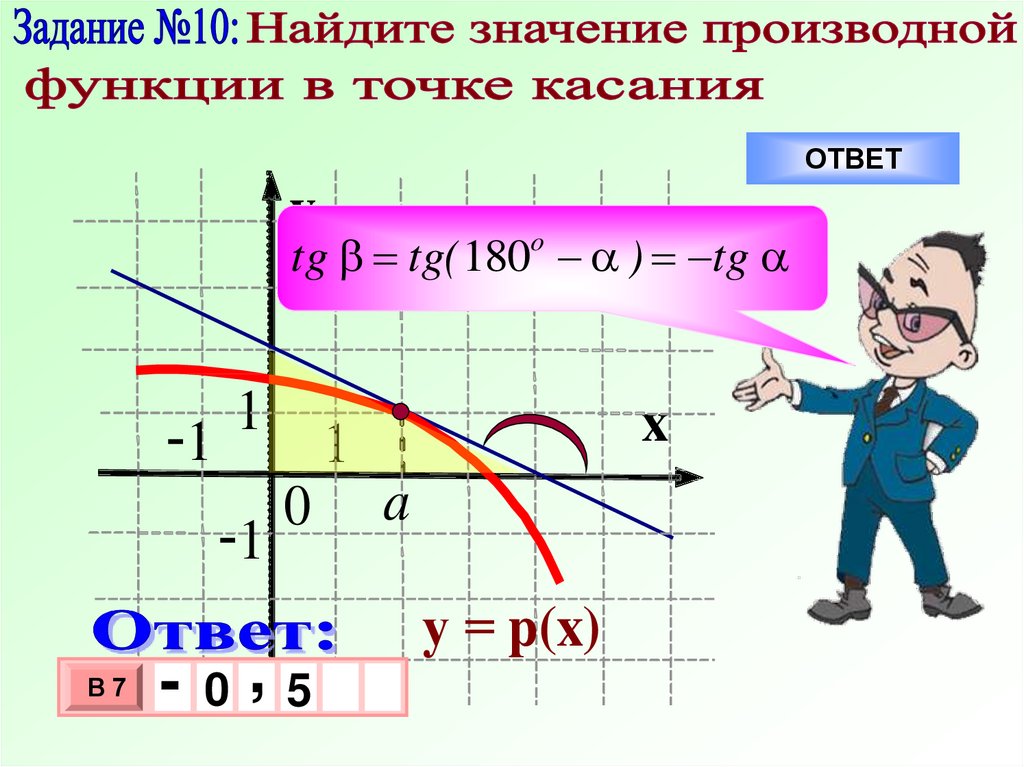
17.

ОТВЕТ
y
tg tg( 180o ) tg
1
-1
-1
В7
-
0
,
x
1
a
0
у = p(x)
5
3
10 х
х
–
–
Ри

18.

f ( x) 3x C
f (5) 0
3
0 3 -25 С
С 15
-3
2
5
f ( x) 3
у f ( x )
f (2) 3 2 15 9
В7
9
3
10 х
х

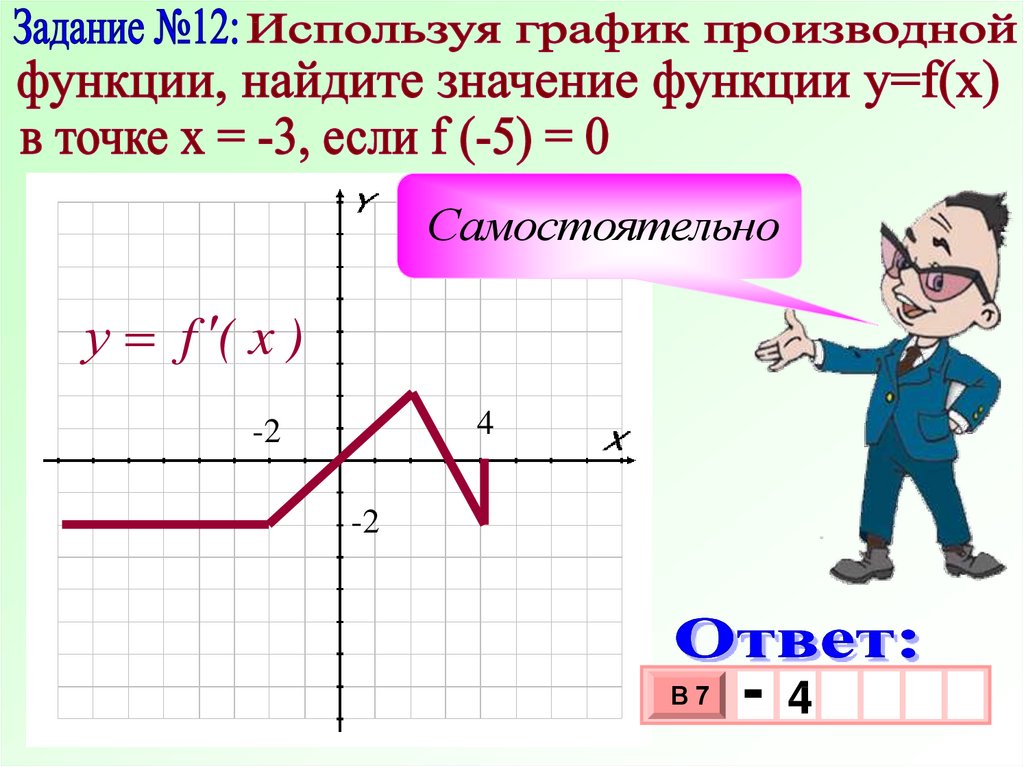
19.

Самостоятельно
у f ( x )
4
-2
-2
В7
-
4
3
10 х
х

20.

У
y f (x)
f ( 3) 1 tg
1
4
В7
-4 5
-1 0
-1
3
10 х
х
4
Х
1
Показать (2)

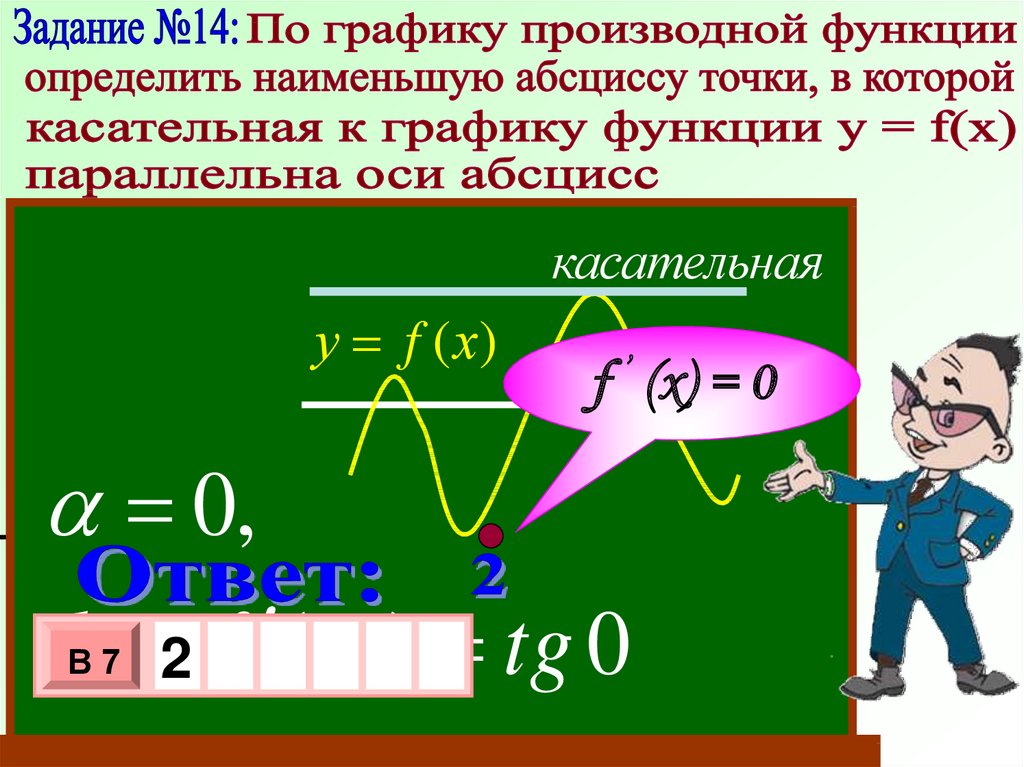
21.

У
y f (x)у f (х)
касательная
f ’ (x) = 0х
0,
k -2 f ( xo ) tg 0
1
-1 0
-1
В7
3
10 х
х
1
Х

22.

У
y f (x)
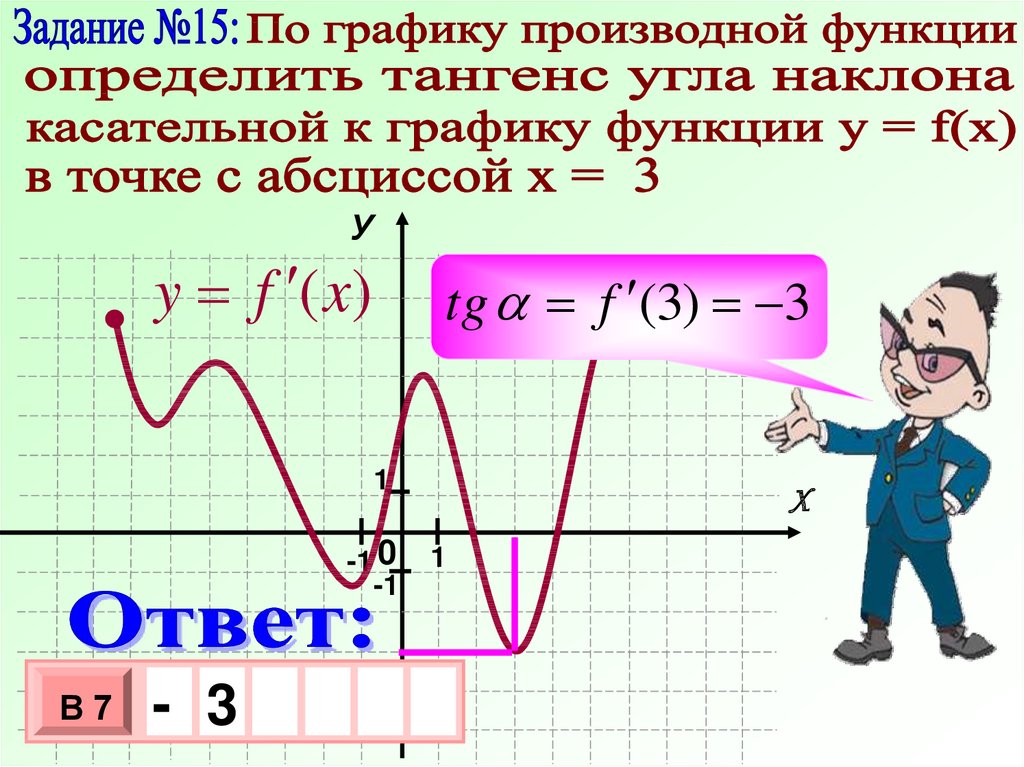
tg f (3) 3
1
-1 0
-1
В7
-- 3
3
10 х
х
Х
1

23.

уугол
наклона
f (x)
У
касательной1 к оси ОХ :
tg k f -1(-1xo 1)
0
tg 60 3 1,7 f ( xo )
o
В7
-4
Ответ
3
10 х
х
Рассуждение (2)
Х

24.

У
y f (x)
-
+
В7
1
+
0
-
-1
1
-1
-6
+
-
3
10 х
Х
х

25.

У
y f (x)
+
-
1
-1 0
-1
1
-
+
Х
В7
-1
3
10 х
х

26.

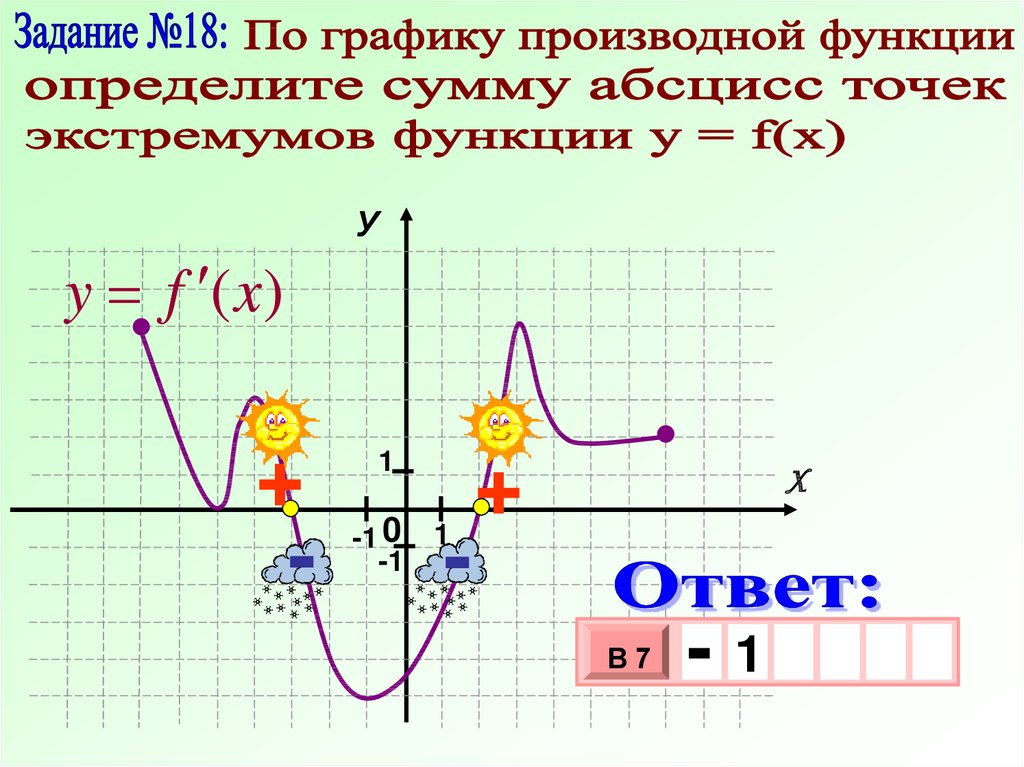
У
Единственная
точка минимума
y f (x)
1
-1 0
-1
1
-
+
Х
В7
2
3
10 х
х

27.

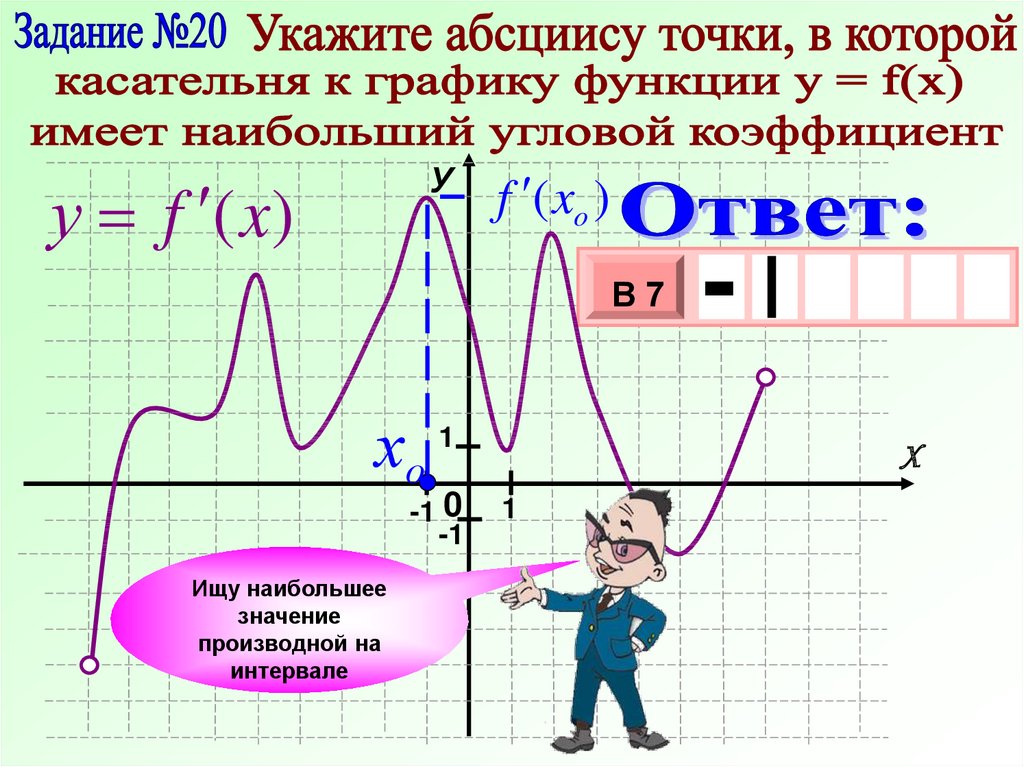
У
у f (x)
f ( xo )
В7
хо
1
-1 0
-1
Ищу наибольшее
значение
производной на
интервале
-
х
3
10 х
Х
1