Похожие презентации:
Элементы теории вероятности. События. Классическое определение вероятности
1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТИ.
2. СОБЫТИЕ
Под СОБЫТИЕМ понимаетсяявление, которое происходит в
результате осуществления какоголибо определенного комплекса
условий.
ПРИМЕР. Бросаем шестигранный игральный кубик.
Определим события:
А {выпало четное число очков};
В {выпало число очков, кратное 3};
С {выпало более 4 очкков}.
3. Эксперимент (опыт)
ЭКСПЕРИМЕНТ (или опыт)заключается в наблюдении за
объектами или явлениями в строго
определенных условиях и
измерении значений заранее
определенных признаков этих
объектов (явлений).
4. ПРИМЕРЫ
• сдача экзамена,• наблюдение за дорожно-транспортными
происшествиями,
• выстрел из винтовки,
• бросание игрального кубика,
• химический эксперимент,
• и т.п.
5. СТАТИСТИЧЕСКИЙ
Эксперимент называютСТАТИСТИЧЕСКИМ, если он
может быть повторен в
практически неизменных
условиях неограниченное
число раз.
6. СЛУЧАЙНОЕ СОБЫТИЕ
СЛУЧАЙНЫМ называют событие, котороеможет произойти или не произойти в
результате некоторого испытания (опыта).
Обозначают заглавными буквами А, В, С,
Д,… (латинского алфавита).
7. Рассмотрим несколько наиболее «излюбленных» в теории вероятностей примеров случайных экспериментов.
8. Опыт 1:
Подбрасывание монеты.Испытание – подбрасывание
монеты; события – монета упала
«орлом» или «решкой».
«решка» - лицевая
«орел» - обратная
сторона монеты (аверс) сторона монеты (реверс)
9. Опыт 2:
Подбрасывание кубика.Это следующий по популярности
после монеты случайный
эксперимент.
Испытание – подбрасывание
кубика; события – выпало 1, 2, 3,
4, 5 или 6 очков (и другие).
10. Опыт 3:
Выбор перчаток. В коробке лежат 3 парыодинаковых перчаток. Из нее, не глядя,
вынимаются две перчатки.
Опыт 4:
«Завтра днем – ясная погода».
Здесь наступление дня – испытание, ясная погода
– событие.
11. Типы событий
СОБЫТИЕДОСТОВЕРНОЕ
НЕВОЗМОЖНОЕ
СЛУЧАЙНОЕ
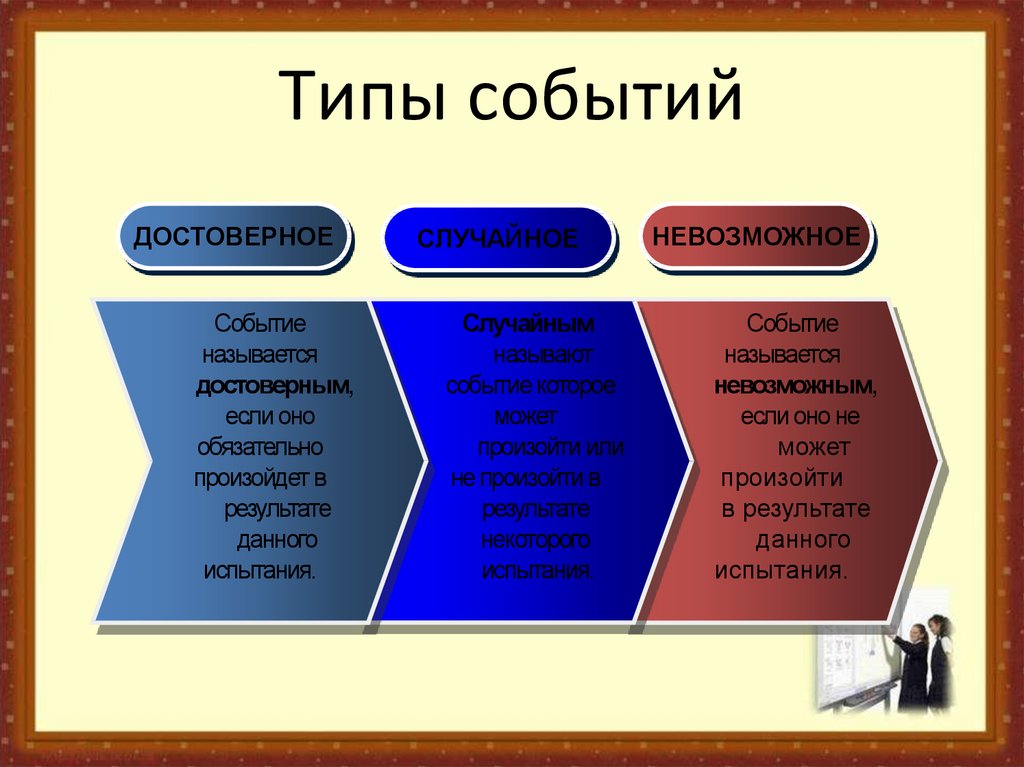
12. Типы событий
ДОСТОВЕРНОЕСобытие
называется
достоверным,
если оно
обязательно
произойдет в
результате
данного
испытания.
СЛУЧАЙНОЕ
Случайным
называют
событие которое
может
произойти или
не произойти в
результате
некоторого
испытания.
НЕВОЗМОЖНОЕ
Событие
называется
невозможным,
если оно не
может
произойти
в результате
данного
испытания.
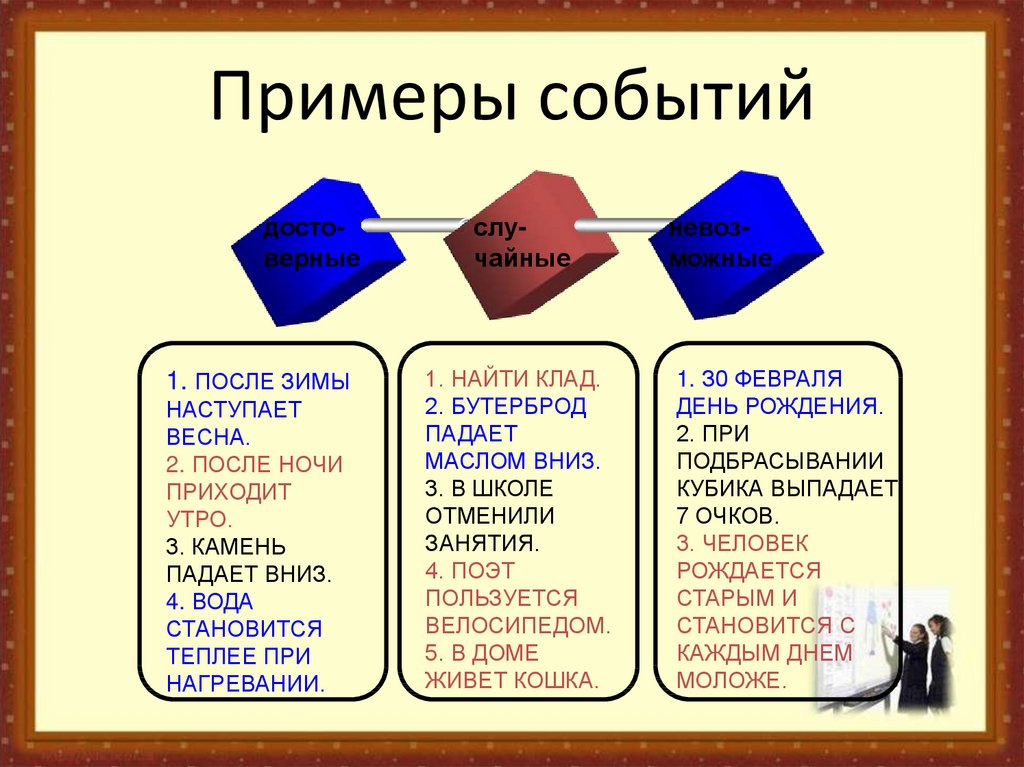
13. Примеры событий
достоверные1. ПОСЛЕ ЗИМЫ
НАСТУПАЕТ
ВЕСНА.
2. ПОСЛЕ НОЧИ
ПРИХОДИТ
УТРО.
3. КАМЕНЬ
ПАДАЕТ ВНИЗ.
4. ВОДА
СТАНОВИТСЯ
ТЕПЛЕЕ ПРИ
НАГРЕВАНИИ.
случайные
1. НАЙТИ КЛАД.
2. БУТЕРБРОД
ПАДАЕТ
МАСЛОМ ВНИЗ.
3. В ШКОЛЕ
ОТМЕНИЛИ
ЗАНЯТИЯ.
4. ПОЭТ
ПОЛЬЗУЕТСЯ
ВЕЛОСИПЕДОМ.
5. В ДОМЕ
ЖИВЕТ КОШКА.
невозможные
1. З0 ФЕВРАЛЯ
ДЕНЬ РОЖДЕНИЯ.
2. ПРИ
ПОДБРАСЫВАНИИ
КУБИКА ВЫПАДАЕТ
7 ОЧКОВ.
3. ЧЕЛОВЕК
РОЖДАЕТСЯ
СТАРЫМ И
СТАНОВИТСЯ С
КАЖДЫМ ДНЕМ
МОЛОЖЕ.
14.
Задание 1Охарактеризуйте события, о которых идет речь в
приведенных заданиях как достоверные, невозможные или
случайные.
Петя задумал натуральное число. Событие состоит в
следующем:
а) задумано четное число;
б) задумано нечетное число;
в) задумано число, не являющееся ни четным, ни нечетным;
г) задумано число, являющееся четным или нечетным.
15.
Задание 2В мешках лежит 10 шаров: 3 синих, 3 белых и 4
красных.
Охарактеризуйте следующее событие:
а) из мешка вынули 4 шара и они все синие;
б) из мешка вынули 4 шара и они все красные;
в) из мешка вынули 4 шара, и все они оказались разного
цвета;
г) из мешка вынули 4 шара, и среди них не оказалось шара
черного
цвета.
16. ИСХОД
ИСХОДОМ (или элементарнымисходом, элементарным событием)
называется один из
взаимоисключающих друг друга
вариантов, которым может
завершиться случайный
эксперимент.
17. Число возможных исходов в каждом из рассмотренных выше опытах.
Опыт 1. – 2 исхода: «орел», «решка».Опыт 2. – 6 исходов: 1, 2, 3, 4, 5, 6.
Опыт 3. – 3 исхода: «обе перчатки на левую
руку», «обе перчатки на правую руку»,
«перчатки на разные руки».
18.
• Однозначные исходыпредполагают
единственный
результат того или
иного события: смена
дня и ночи, смена
времени года и т.д.
19.
Неоднозначные исходы предполагают несколькоразличных результатов того или иного события:
при подбрасывании кубика выпадают разные
грани; выигрыш в Спортлото; результаты
спортивных игр.
20.
Задание 3Запишите множество исходов для следующих
испытаний.
а) В урне четыре шара с номерами два, три, пять,
восемь. Из урны наугад извлекают один шар.
б) В копилке лежат три монеты достоинством в 1
рубль, 2 рубля и 5 рублей. Из копилки достают одну
монету.
в) В доме девять этажей. Лифт находится на первом
этаже. Кто-то из жильцов дома вызывает лифт на
свой этаж. Лифтовый диспетчер наблюдает, на
каком этаже лифт остановится.
21.
Задание 4Найдите количество возможных исходов.
а) За городом N железнодорожные станции расположены
в следующем порядке: Луговая, Сосновая, Озёрная,
Дачная, Пустырь. Событие А – пассажир купил билет не
далее станции Озёрная.
б) Один ученик записал целое число от 1 до 5, а другой
ученик пытается отгадать это число. Событие В – записано
чётное число.
в) Вини Пух думает, к кому бы пойти в гости: к Кролику,
Пяточку, ослику Иа-Иа или Сове? Событие А – Вини Пух
пойдёт к Пяточку; событие В – Вини Пух не пойдёт к
Кролику.
22.
Задание 5В каждом из следующих опытов найдите количество
возможных исходов:
а) подбрасывание двух монет;
б) подбрасывание двух кнопок;
в) подбрасывание двух кубиков;
г) подбрасывание монеты и кубика;
д) подбрасывание монеты, кнопки и кубика.
23. Комбинаторные правила для решения задач по теории вероятностей
24.
2425.
2526.
Классическое определение вероятностиСтохастическим называют опыт, если заранее нельзя предугадать
его результаты. Результаты (исходы) такого опыта называются
событиями.
Пример: выбрасывается игральный кубик (опыт);
выпадает двойка (событие).
Событие, которое обязательно произойдет в результате испытания,
называется достоверным, а которое не может произойти, невозможным.
Пример: В мешке лежат три картофелины.
Опыт – изъятие овоща из мешка.
Достоверное событие – изъятие картофелины.
Невозможное событие – изъятие кабачка.
26
27.
Классическое определение вероятностиРавновозможными называют события, если в результате опыта ни
одно из них не имеет большую возможность появления, чем другие.
Примеры: 1) Опыт - выбрасывается монета.
Выпадение орла и выпадение решки –
равновозможные события.
2) В урне лежат три шара. Два белых и синий.
Опыт – извлечение шара.
События – извлекли синий шар и извлекли
белый шар - неравновозможны.
Появление белого шара имеет больше шансов..
27
28.
Классическое определение вероятностиНесовместимыми (несовместными) называют события, если
наступление одного из них исключает наступление других.
Пример: 1) В результате одного выбрасывания выпадает
орел (событие А) или решка (событие В).
События А и В - несовместны.
2) В результате двух выбрасываний выпадает
орел (событие А) или решка (событие В).
События А и В - совместны.
Выпадение орла в первый раз
не исключает выпадение решки во
второй
28
29.
Классическое определение вероятностиПолной группой событий называется множество всех событий
рассматриваемого опыта, одно из которых обязательно произойдет,
а любые два других несовместны.
События образующие полную группу называют элементарными.
Пример: 1) Опыт – один раз выбрасывается монета.
Элементарные события: выпадение орла
и выпадение решки образуют полную группу.
29
30.
Классическое определение вероятностиВероятностью случайного события А называется отношение числа
элементарных событий, которые благоприятствуют этому событию, к
общему числу всех элементарных событий, входящих в данную
группу .
P(A) = m/n
30
31.
Для конечных множеств событий принахождении m и n широко используют
правила комбинаторики.
Задача №1: Сколько двузначных чисел можно
составить используя цифры 7; 8; 9
(цифры могут повторяться)?
В данном случае легко перебрать все комбинации.
77
78
79
88
87
89
99
97
98
9 вариантов
31
32.
Задача №2: Сколько пятизначных можносоставить используя цифры 7; 8; 9
(цифры могут повторяться)?
Как видим, в этой задаче перебор довольно
Решим задачу иначе.
затруднителен.
На первом месте может стоять
любая из трех цифр – 3 варианта.
На втором месте может стоять
любая из трех цифр – 3 варианта.
На третьем месте может стоять
любая из трех цифр – 3 варианта.
3 3 3 3 3 243
На четвертом месте может стоять
любая из трех цифр – 3 варианта.
На пятом месте может стоять
любая из трех цифр – 3 варианта.
Комбинаторное правило умножения
32
33. Задача №3: чемпионате по гимнастике участвуют 50 спортсменок: 24 из России, 13 из США, остальные — из Канады. Порядок, в
Задача №3: чемпионате по гимнастике участвуют 50 спортсменок: 24из России, 13 из США, остальные — из Канады. Порядок, в котором
выступают гимнастки, определяется жребием. Найдите вероятность
того, что спортсменка, выступающая первой, окажется из Канады.
Благоприятное событие А: первой выступает
спортсменка из Канады
К-во всех событий группы: n=?
К-во благоприятных
событий: m=?
Соответствует
количеству
гимнасток
из Канады.
m=50-(24+13)=13
12.05.2020
Соответствует количеству всех гимнасток.
n=50
m 13
Р ( А)
0,26
n 50
33
34. Задача №4: В среднем из 1400 садовых насосов, поступивших в продажу, 14 подтекают. Найдите вероятность того, что один случайно
выбранный для контроля насос не подтекает.Благоприятное событие А: выбранный насос
не подтекает.
К-во всех событий группы: n=?
К-во благоприятных
событий: m=?
Соответствует
количеству
исправных
насосов
m=1400-14=1386
12.05.2020
Соответствует количеству всех насосов.
n=1400
m 1386
Р ( А)
0,99
n 1400
34
35. Задача №5: Фабрика выпускает сумки. В среднем на 190 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите
вероятность того, что купленная сумка окажетсякачественной. Результат округлите до сотых.
Благоприятное событие А: купленная сумка
оказалась качественной.
К-во всех событий группы: n=?
К-во благоприятных
событий: m=?
Соответствует
количеству
качественных
сумок.
m=190
12.05.2020
Соответствует количеству всех сумок.
n=190+8
m 190
Р ( А)
0,959... 0,96
n 198
35
36. Задача №6: В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков.
Результатокруглите до сотых.
Опыт: выпадают три игральне кости.
Благоприятное событие А: в сумме выпало 7 очков.
К-во благоприятных
событий m=?
331
313
133
К-во всех событий группы n=?
1-я кость - 6 вариантов
2-я кость - 6 вариантов
3-я кость - 6 вариантов
223 511
232 151
322 115
18
412
421
124
12.05.2020
142
214
241
6 6 6 216
m 18
Р ( А)
0,08
n 216
36
37.
Задача №7: случайном эксперименте симметричную монету бросаютчетырежды. Найдите вероятность того, что орел не выпадет ни разу.
Условие можно трактовать так: какова вероятность того,
что все четыре раза выпадет решка?
К-во всех событий группы n=?
К-во благоприятных
событий m=?
m=1
Четыре раза выпала
решка.
12.05.2020
1-й раз - 2 варианта
2-й раз - 2 варианта
3-й раз - 2 варианта
4-й раз - 2 варианта
Р( А)
2 2 2 2 16
m 1
0,0625
n 16
37


































 Математика
Математика








