Похожие презентации:
Модели популяции. Часть 1
1. Модели популяции. Часть 1
Гирко КристинаГруппа 34
2. Модель внутривидовой конкуренции при дискретном размножении
Модель описывается уравнением:Nt R
N t 1
b
1 (a N t )
где
R — скорость воспроизводства популяции
в отсутствии внутривидовой конкуренции
N0 — начальная численность популяции,
a и b — параметры модели,
t – время (поколение популяции).
3. Задача №1
Изучить характер эволюциипопуляции, описываемый
рассматриваемой моделью, при
значении параметра b = 1, в
зависимости от значения
параметра а.
Населенность
100
10
В качестве начальных значений
задавалось: N0=100, R=1,2.
120
100
80
60
40
20
0
В Excel построена таблица и
рассчитаны графики развития
популяции.
1
Поколение
0,1
4. Так выглядит модель
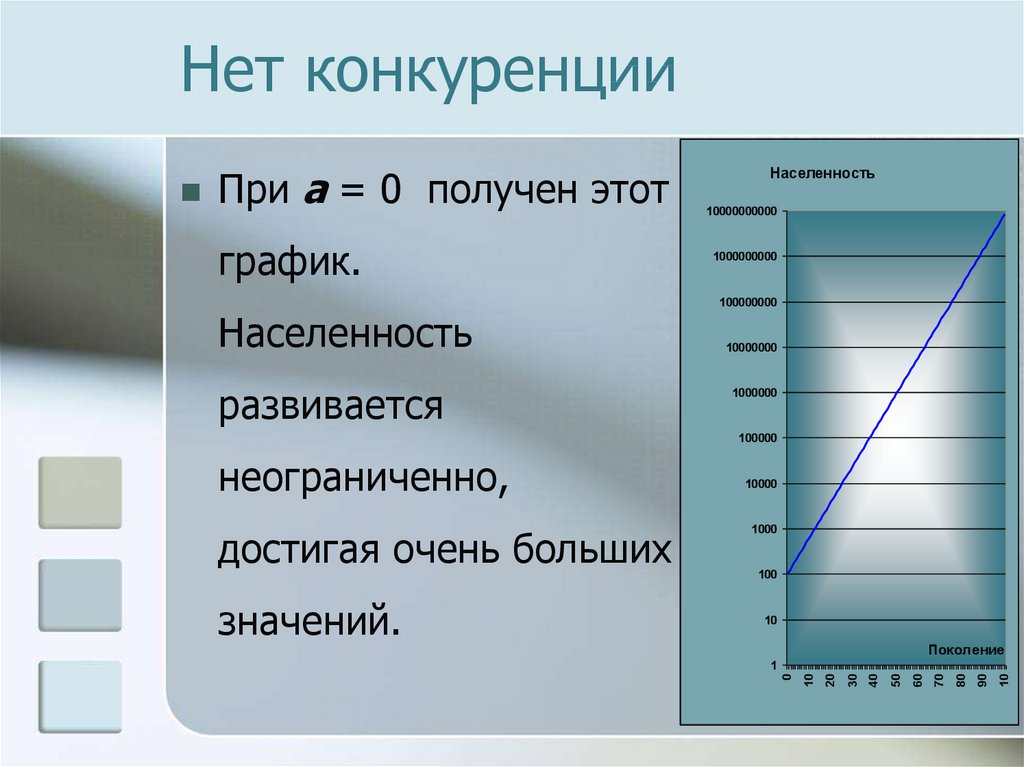
5. Нет конкуренции
При a = 0 получен этотграфик.
Населенность
развивается
10000000000
1000000000
100000000
10000000
1000000
100000
100
10
Поколение
10
90
80
70
60
50
40
1
30
значений.
1000
20
достигая очень больших
10000
10
неограниченно,
0
Населенность
6. Конкуренция началась!
10010
Поколение
120
100
80
60
40
1
20
Населенность быстро
спадает и дальше
остается постоянной.
Населенность
0
Уже при значении a =
0,01 получается такой
график.
7. Сомнения в модели…
10010
120
100
80
60
40
1
20
Это сомнительно! Не
может быть население
меньше единицы и
продолжать
существовать
Населенность
0
Уже при значении a=0,21
стационарное значение
становится меньше 1 и
уменьшается при
дальнейшем увеличении
a. Например, при a=0.3
получается такой график:
Поколение
0,1
8. Объяснение сомнений
Населенность100
10
120
100
80
60
40
20
1
0
Кривая опускается ниже
значения N = 1 при t = 7.
Биологическая
разумность говорит, что
доля особи не может
размножаться.
Модель при t 7 стала
неадекватной и ее
использование для этого
интервала времени
невозможно.
Поколение
0,1
9. Анализ адекватности
Углубленный анализ показал такиерезультаты:
поколение
20
y = -4,237Ln(x) + 16,469
15
R2 = 0,9838
10
5
0,37
0,35
0,33
0,31
0,29
0,27
0,25
0,23
0,21
0,39
a
0
Поколение, начиная с которого модель становится
неадекватной
Логарифмический (Поколение, начиная с которого
модель становится неадекватной)
10. Выводы по модели
Модель можно считать адекватнойтолько в интервале условий,
описанном в отчете.
Этот интервал достаточно узок.
Модель практической пользы не
имеет и может быть использована
как инструмент для изучения
процессов моделирования с
помощью Excel.









 Биология
Биология Информатика
Информатика








