Глобальные переменные, отладка кода, матрицы. Лекция 8

1. Глобальные переменные, отладка кода, матрицы

Лекция 8

2. Глобальные переменные и глобальное присваивание в документе Mathcad

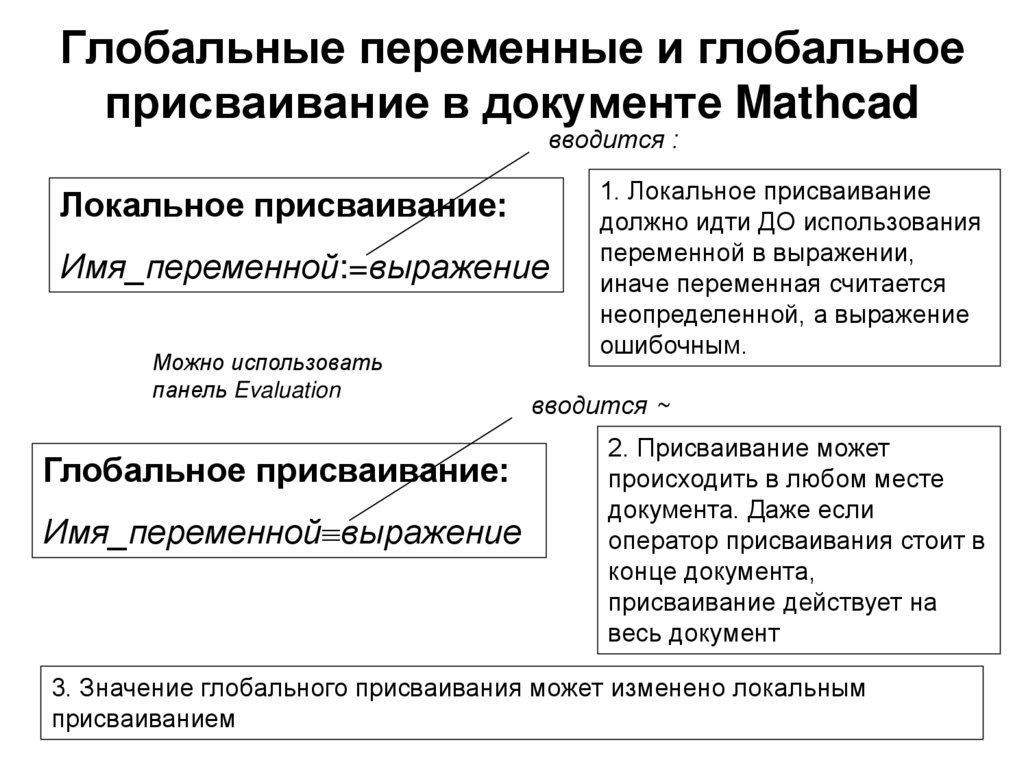
вводится :
Локальное присваивание:
Имя_переменной:=выражение
Можно использовать
панель Evaluation
Глобальное присваивание:
Имя_переменной выражение
1. Локальное присваивание
должно идти ДО использования
переменной в выражении,
иначе переменная считается
неопределенной, а выражение
ошибочным.
вводится ~
2. Присваивание может
происходить в любом месте
документа. Даже если
оператор присваивания стоит в
конце документа,
присваивание действует на
весь документ
3. Значение глобального присваивания может изменено локальным
присваиванием

3. Примеры локального и глобального присваивания

x=
ln(x)=
This variable or function
is not defined above/
Переменная х не определена и поэтому
недоступна для применения.
x:=5
Переменной x присвоено значение, теперь она
ln(x)=1.609
доступна.
ln(y)=2.303
Переменная y доступна, так как ей присвоено
глобальное значение в конце документа.
y:=123
Значение переменной y может быть
y=123
переопределено локально.
e=2.718
Системная переменная e – основание
натурального
логарифма.
e:=10
Системная переменная может быть
e=10
переопределена, но это не рекомендуется.
y 10
y присвоено глобальное значение 10.

4. Порядок выполнения присваивания

Mathcad анализирует документы на предмет присваивания
переменных в два прохода: сначала распознаются все
операторы глобального присваивания, и все выражения в
документе сверху вниз и слева направо вычисляются в
соответствии с ними, а при втором проходе в том же
порядке анализируются операторы локального
присваивания, и все выражения вычисляются с поправкой
на них.

5. Примеры локального и глобального присваивания

При вычислении y используется
глобальное значение x, так как y было
определено глобальным
присваиванием.

6. Глобальное определение пользовательской функции

Распространяется на весь документ:
Использование
функции выше ее
определения

7. Системные (встроенные) переменные Mathcad

Переменная
Ввод
Назначение
Ctrl+Shift+p
Число (3.1415…)
e
e
Основание натурального логарифма
Ctrl+Shift+z
Символ бесконечности и максимальное
вещественное значение
%
%
Процент (0.01)
i, j
1i, 1j
Мнимая единица
TOL
Погрешность численных методов (0.001)
CTOL
Погрешность некоторых численных методов
(0.001)
ORIGIN
Начальное значение индекса массива
PRNCOLWIDTH
Число столбцов оператора WRITEPRN (8)
PRNPRECISION
Число десятичных знаков оператора
WRITEPRN (4)
CWD
Строка, содержащая путь к текущей папке
…

8. Локальные и глобальные переменные относительно описания программы-функции

Внутреннее, локальное присваивание:
Имя_переменной ←выражение
Переменная сохраняет присвоенное значение только в
теле функции. За пределами функции значение
переменной или не определено, или имеет значение.
заданное локальным := или глобальным
присваиванием.
Обратите внимание:
Пример.
X:=5
F:= X X+1
X
F=6
X=5
программа-функция
может не иметь
формальных (входных)
параметров, так как она
может использовать
глобальные
относительно функции
переменные.

9. Оператор on error и функция error

Кнопка панели инструментов
Программирование
Выражение_1 on error Выражение_2
Пример:
1
f(x):= on error 2 x
f(2)=1×10307
Здесь может быть текст в “ ”
Функция error(S) - выводит маленькое желтое окно, в котором
отображается S (строка-константа (любая фраза в кавычках)
или значение строковой переменной S). Окошко появляется
только после щелчка мыши на выделенном красном вызове
подпрограммы-функции.
X 5
Пример 1:
2
G( i) error( "No value" ) on error b B
i
B 3
b
4
G( 1) 3
G(3)=
No value

10. Тестирование и отладка программ в пакете MathCAD

• В ранних версиях пакета MathCAD (до 13
версии) отсутствуют какие-либо инструменты
отладки.
• Начиная с версий MathCAD 13-14, появились
следующие инструменты отладки программы:
• две встроенных функции trace и pause;
• окно трассировки программы;
• панель с четырьмя кнопками отладки.

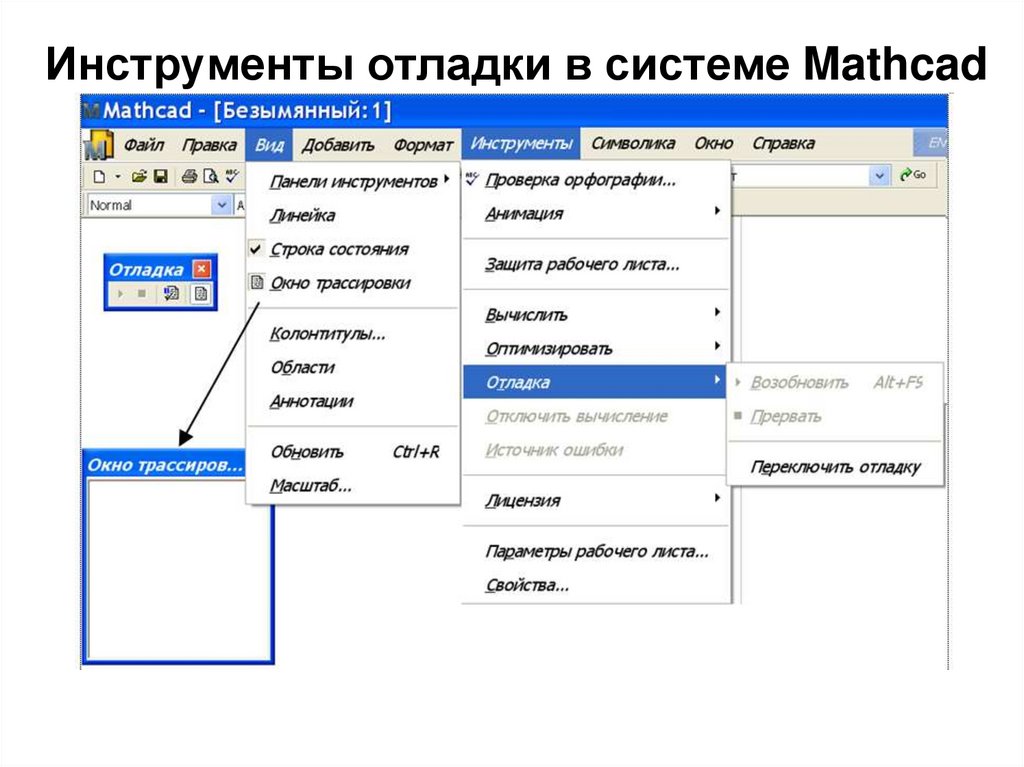
11. Инструменты отладки в системе Mathcad

12. Встроенная функция trace

• Функция возвращает строку, содержащую
значения аргументов x, y, z, которая
выводится в Окне трассировки. Обращение к
этой функции имеет вид:
trace(S,x,y,z)
• Параметр S задает очередность вывода
информации в окне трассировки и
сопровождающий текст. Если выводится
значение только одной переменной, то
параметр S в обращении к функции можно
опустить.

13. Пример работы функции trace

14. Особенности работы функции trace

• для получения данных в Окне трассировки
необходимо пересчитать весь документ MathCAD
(нажать клавиши [Ctrl+F9] даже при установленном
автоматическом режиме вычислений);
• для работы с данными Окна трассировки можно
использовать команды контекстного меню;
• в параметре S порядковый номер вывода значений
(номер задается в фигурных скобках {}) обязательно
должен начинаться с нулевого значения (независимо
от значения системной переменной ORIGIN);
• пояснения к выводимым значениям, задаваемые в
параметре S, могут содержать пробелы и другие
символы (включая русские буквы), что повышает
читаемость информации, выводимой в Окне
трассировки.

15. Встроенная функция pause

• Функция возвращает строку (также как
функция trace), но после этого выполнение
вычисления прерывается. Для продолжения
вычислений необходимо нажать кнопку Run
(зеленый треугольник) палитры инструментов
Отладка
• Обращение к функции имеет вид:
pause(S,x,y,z)
• Формальные параметры имеют то
назначение, что и параметры функции trace.

16. Инструменты палитры Отладка

1. Возобновить вычисления (при нажатии
кнопки процесс вычисления продолжается –
часто используется с функцией pause).
2. Прервать вычисления (прекращается
процесс вычисления – для продолжения
нажать клавиши [Ctrl+F9]).
3. Переключение режима отладки (нажать на
кнопку для включения режима отладки).
4. Включение или выключение окна
трассировки (при нажатии кнопки
появляется окно трассировки).

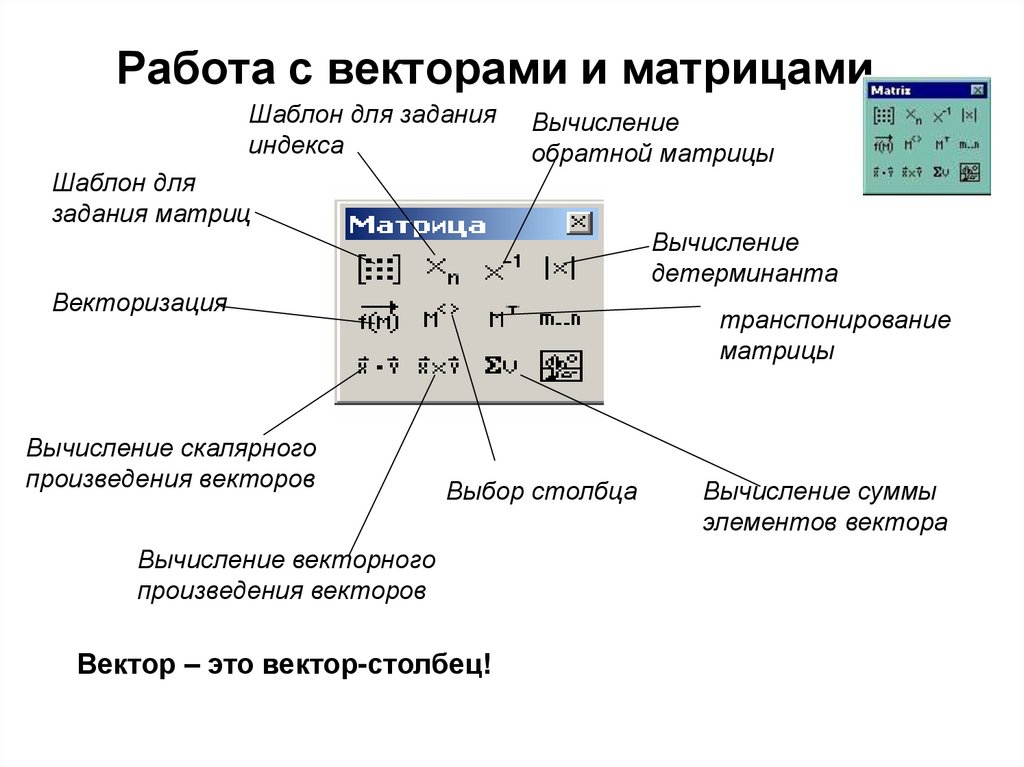
17. Работа с векторами и матрицами

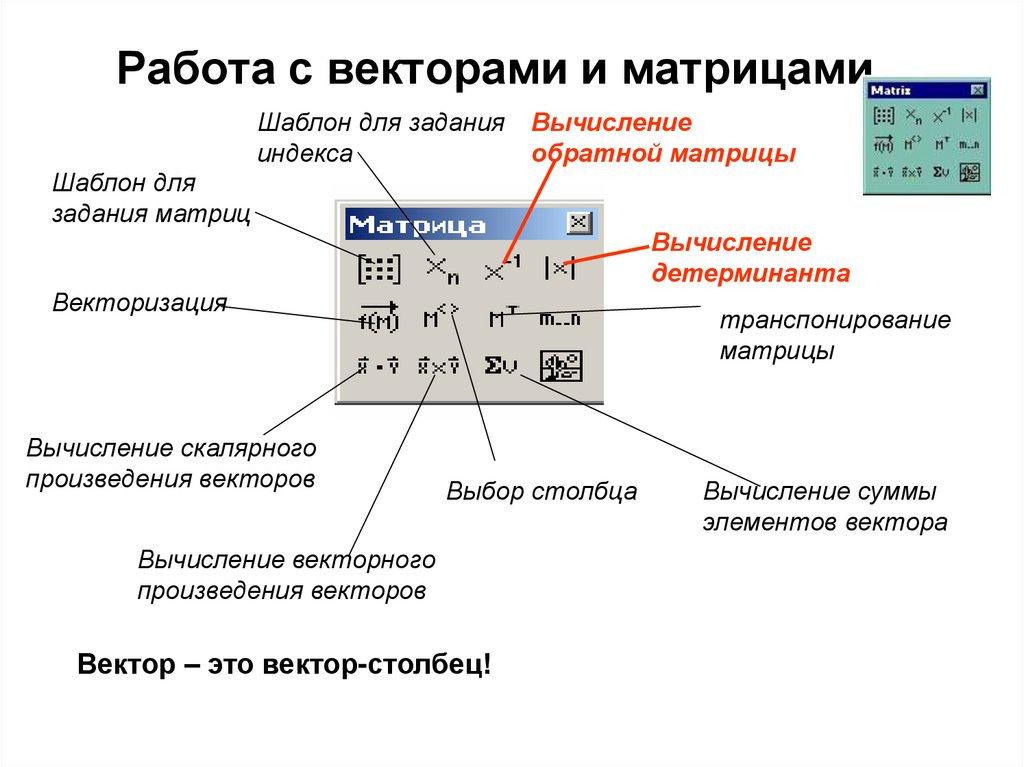
18. Работа с векторами и матрицами

Шаблон для задания
индекса
Вычисление
обратной матрицы
Шаблон для
задания матриц
Вычисление
детерминанта
Векторизация
Вычисление скалярного
произведения векторов
транспонирование
матрицы
Выбор столбца
Вычисление векторного
произведения векторов
Вектор – это вектор-столбец!
Вычисление суммы
элементов вектора

19. Задание матрицы

1 способ – использование шаблона. Его вызов: Главное
меню /Вставка /Матрица или кнопка панели «Матрица».
1 2 3
1 2 3
1 2 3

20. Задание матрицы

2 способ – задание значений некоторым элементам
матрицы (индексированным переменным). Индексы
элементов матрицы – нижние индексы.
Нижние индексы можно ввести:
1. Используя шаблон с панели «Матрица»
2. Используя шаблон с панели инструментов
«Форматирование»
3. Набором символа [
Индексы строки и столбца отделяются запятой.

21. Работа с векторами и матрицами

Шаблон для задания Вычисление
индекса
обратной матрицы
Шаблон для
задания матриц
Вычисление
детерминанта
Векторизация
Вычисление скалярного
произведения векторов
транспонирование
матрицы
Выбор столбца
Вычисление векторного
произведения векторов
Вектор – это вектор-столбец!
Вычисление суммы
элементов вектора

22. Примеры использования индексированных переменных

1. Набираем:
Пробел указывает, что набор индекса закончен
v[0 =
Если вектор v существует, то в документе Mathcad будет выведено,
например:
v0=2
2. Пусть вектор w не существует. Набираем:
w[2 :2
На экране отображается:
w2:=2
Набираем:
w[5 :8
На экране отображается:
w5:=8
Набираем:
w=
Получаем:
0
0
2
w
0
0
8
Неопределенные элементы
массива заполняются нулями

23. Примеры использования индексированных переменных

3. Набираем:
M0,0:=1
M0,1:=3
M0,1:=2
M1,1:=6
M0,2:=5
M=
Получаем:
M 1
3
3
6
5
0
4. Набираем
M2,2=
индекс вне границ
Здесь используется значение
ORIGIN=0 по умолчанию

24. Примеры использования индексированных переменных

набираем ~
5. В новом документе устанавливаем ORIGIN в значение 1 (Origin 1 или с
помощью команды TOOLS / BUILT-IN Variables главного меню –см.
следующий слайд). Задаем матрицу M:
1 3 7
M 2 4 6
5 8 1
Выводим значения элементов матрицы:
M2,2=4
M3,1=5
M0,0=
индекс вне границ
M3,3=1
ORIGIN=1

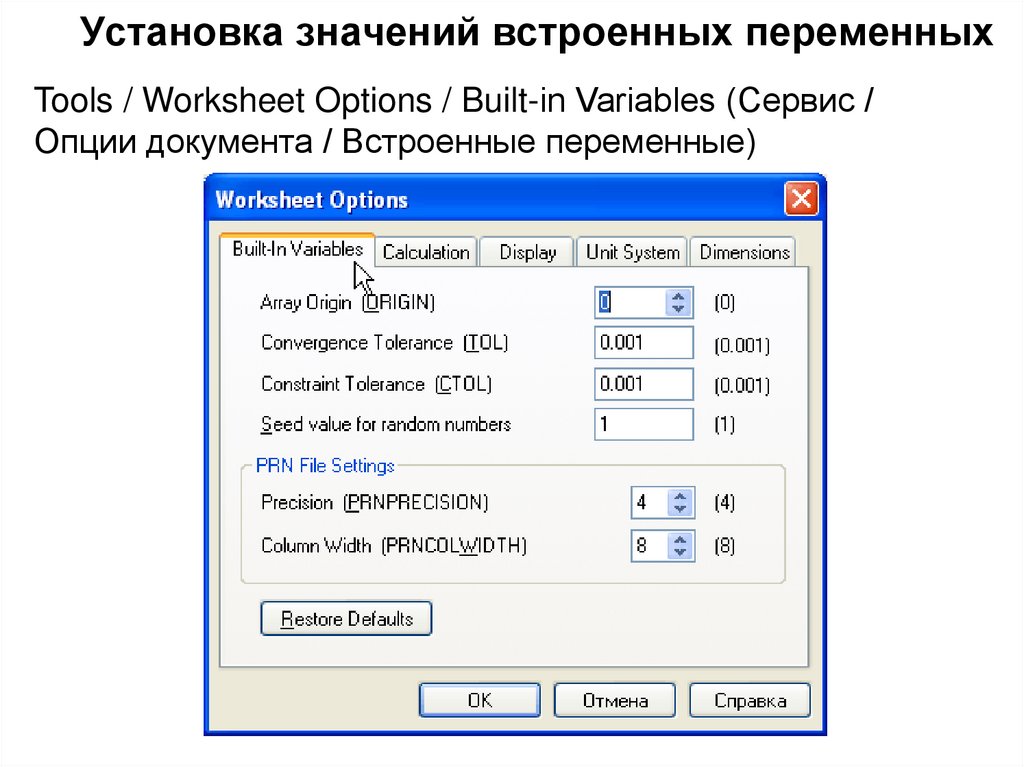
25. Установка значений встроенных переменных

Tools / Worksheet Options / Built-in Variables (Сервис /
Опции документа / Встроенные переменные)

26. Особенности переопределения ORIGIN

• Если ORIGIN определяется в рабочем документе, а не с помощью
команды Встроенные переменные, используйте одно глобальное
определение. Хотя можно переопределять ORIGIN с помощью :=,
это приведет к путанице. Если изменить ORIGIN в середине
рабочего документа, Mathcad будет показывать, что массивы
имеют n элементов, где n — разница между старым и новым
значением ORIGIN.
• Когда ORIGIN устанавливается в диалоговом окне Встроенные
переменные, его значение применяется ко всем массивам
документа. Невозможно сделать так, чтобы одни массивы
использовали один ORIGIN, а другие — другой.
• Если сослаться на элемент массива с нижним индексом меньшим,
чем ORIGIN, Mathcad отмечает обращение к массиву сообщением
об ошибке “индекс вне границ”. Это же сообщение выводится при
выходе индекса за верхнюю границу массива.
• Если неосторожно определить массив, начиная с первого элемента,
когда ORIGIN установлен на своё значение по умолчанию, равное
нулю, будут получаться неожиданные ответы от функций массива,
подобных mean. Дело в том, что Mathcad будет автоматически
определять x0 = 0 для всех этих массивов. Этот дополнительный
элемент искажает значения, возвращаемые функциями массива.
Чтобы избежать этой проблемы, выберите Встроенные
переменные из меню Математика и установите ORIGIN равным 1
в диалоговом окне “Встроенные переменные”.

27. Некоторые функции Mathcad, работающие с массивами

•mean(A) - возвращает среднее арифметическое
элементов массива A.
•max(A) - возвращает самый большой элемент в
массиве A. Если A имеет комплексные элементы,
возвращает наибольшую вещественную часть плюс i,
умноженную на наибольшую мнимую часть.
•min(A) - возвращает самый маленький элемент в
массиве A. Если A имеет комплексные элементы,
возвращает наименьшую вещественную часть плюс i,
умноженную на наименьшую мнимую часть.

28. Примеры работы функций mean, max, min

1 2
A 3 4
5 6
max( A) 6
1 i 1 5i 2i
B 1 2i 5 i 3i
8
i
1
max( B) 8 5i
mean( A) 3.5
min( B) 1
mean( B) 1.667 1.667i

29. Некоторые функции Mathcad, работающие с массивами

•tr(A) - возвращает сумму диагональных элементов
(след) матрицы A (только для квадратных матриц).
•rank(A) - возвращает ранг вещественной матрицы A.
Примеры работы функций tr, rank
1 2
A 3 4
5
6
tr( A)
matrix must be square
rank( A) 2
1 i 1 5i 2i
B 1 2i 5 i 3i
8
i
1
C
1 1
0 2
tr( C) 1
tr( B) 6 3i
rank( B)
This value must be a
matrix of real numbers
1 2
1 2
D
rank( D) 1

30. Некоторые функции Mathcad, работающие с массивами

•Re(A) - возвращает массив, состоящий из элементов, которые
являются вещественными частями элементов A.
•Im(A) - возвращает массив, состоящий из элементов, которые
являются коэффициентами при мнимых частях элементов A.
• augment (A, B) - возвращает массив, сформированный
расположением массивов A и B бок о бок. Массивы A и B должны
иметь одинаковое число строк.
•stack (A, B) - возвращает массив, сформированный
расположением A над B. Массивы A и B должны иметь одинаковое
число столбцов.
•submatrix (A, i1, i2, j1, j1) - возвращает подматрицу, состоящую из
всех элементов, содержащихся в строках с i1 по i2 и столбцах
с j1 по j1. Чтобы поддерживать порядок строк и-или столбцов,
удостоверьтесь, что i1<=i2 и j1<=j2, иначе порядок строк и-или
столбцов будет обращен.

31. Примеры работы функций Re, Im, augment, stack, submatrix

1 i 1 5i 2i
B 1 2i 5 i 3i
8
i
1
1 1 0
Re( B) 1 5 0
1
8
0
1
A 3
5
1 5 2
Im( B) 2 1 3
0
0
1
1 2 1 i 1 5i 2i
augment( A B) 3 4 1 2i 5 i 3i
1
8
i
5 6
1 5i 2i
submatrix( B 0 1 1 2)
5
i
3i
2
4
6
T
A
1 3 5
2 4 6
3
1
2
4
T
stack A B 1 i 1 5i
1 2i 5 i
8
1
6
2i
3i
i
5

32. Функции генерации матриц

• identity(n) – возвращает единичная матрица
размером n x n (все диагональные элементы равны
1, остальные элементы равны 0).
• diag(v) - возвращает диагональную матрицу,
содержащую на диагонали элементы вектора v.
• matrix(n,m,f) – возвращает матрицу, в которой
элемент с индексами i,j равен f(i,j), где i=0,1, …, n,
j=0,1, …, m, f(i,j) – некоторая функция.

33. Примеры работы функций identity, diag и matrix

34. Вычисление обратной матрицы

• С помощью кнопки панели инструментов «Матрица».
• С помощью операции возведения в степень,
допустимой для квадратных матриц. Выражение Mn
набирается с помощью клавиши ^. При n=-1
получаем обращение матрицы.
• Использование функции geninv(A). Она вычисляет
левую обратную к A матрицу L такую, что:
L A = I,
где I - единичная матрица, имеющая то же самое
число столбцов, что и A.
Матрица А - n x m вещественная матрица, где n>=m.
Соответственно L имеет размер m x n, I - m x m.

35. Работа с векторами и матрицами

Шаблон для задания
индекса
Вычисление
обратной матрицы
Шаблон для
задания матриц
Вычисление
детерминанта
Векторизация
Вычисление скалярного
произведения векторов
транспонирование
матрицы
Выбор столбца
Вычисление векторного
произведения векторов
Вектор – это вектор-столбец!
Вычисление суммы
элементов вектора

36. Решение системы линейных алгебраических уравнений

Ax=b
1. Использование обратной матрицы
d:=|A|
x:=if (d 0, A-1 b, ″матрица вырождена ″)
x:=if (|d|>TOL, A-1 b, ″ матрица почти вырождена ″)
2. Использование функции lsolve(A,b)
решения СЛАУ.

37. Примеры решения СЛАУ

A : 3
2
d A
6
0.54
v : 9
4
d 10.38
x1 lsolve( A v)
x A
1
v
1.844
x1
0.578
1.844
0.578
x

38. Функции сортировки для векторов и матриц

• sort(v) – сортировка вектора в порядке
возрастания их значений.
• reverse(v) – перестановка элементов вектора
в обратном порядке (например, после sort)/
• csort(M,n) – перестановка строк матрицы
таким образом, чтобы отсортированным
оказался n-й столбец.
• rsort(M,n) – перестановка столбцов матрицы
таким образом, чтобы отсортированной
оказалась n-я строка.

39. Выбор столбца из матрицы

• Выбор столбца из матрицы осуществляется
использованием верхнего индекса.
• Значение верхнего индекса – номер столбца.
• Верхний индекс заключается в угловые
скобки.
• Набор верхнего индекса осуществляется с
помощью панели «Матрица» или
комбинацией клавиш Ctrl+6.

40. Работа с векторами и матрицами

Шаблон для задания
индекса
Вычисление
обратной матрицы
Шаблон для
задания матриц
Вычисление
детерминанта
Векторизация
Вычисление скалярного
произведения векторов
транспонирование
матрицы
Выбор столбца
Вычисление векторного
произведения векторов
Вектор – это вектор-столбец!
Вычисление суммы
элементов вектора

41. Примеры выбора столбца

1 i 1 5i 2i
B 1 2i 5 i 3i
8
i
1
1 i
0
B 1 2i
1
3
B
This array index is invalid for
this array

42. Векторные и матричные операторы

Оператор
Набор на
клавиатуре
Назначение
V1+V2
V1+V2
Сложение векторов V1и
V2
-V
-V
Смена знака у всех
элементов вектора
-M
-M
Смена знака у всех
элементов матрицы
V+Z
V+Z
Сложение вектора V со
скаляром Z
Z*V,V*Z
Z*V,V*Z
Умножение вектора V
на скаляр Z
Z*M,M*Z
Z*M,M*Z
Умножение Матрицы М
на скаляр Z
V1*V2
V1*V2
Умножение двух
векторов
M*V
M*V
Умножение матрицы М
на вектор V

43. Векторные и матричные операторы (продолжение)

Оператор
Набор на
клавиатуре
Назначение
M1*M2
M1*M2
Умножение двух матриц М1
и М2
V/Z
Деление вектора V на скаляр
Z
M/Z
Деление матрицы М на
скаляр Z
M^-1
Обратная матрица М
M^n
Возведение матрицы М в
степень n
\V
Вычисление квадратного
корня из V
|M
Вычисление определителя
матрицы
V Ctrl!
Транспонирование вектора V

44. Векторные и матричные операторы (продолжение)

Оператор
V1*V2
Набор на
клавиатуре
Назначение
M Ctrl!
Транспонирование матрицы М
V1 Ctrl*V2
Скал-умножение векторов V1и
V2
V”
Получение комплексно
скалярного вектора
M”
Получение комплексно
скалярной матрицы
Alt $ V
Вычисление суммы элементов
вектора V
V Ctrl -
Векторизация вектора V
M Ctrl -
Векторизация матрицы М
M Ctrl ^ n
Выделение n-го столбца
матрицы М
V[n
Выделение n-го элемента
вектора V
M[m,n
Выделение элементов (m,n)
матрицы М

45. Использование массивов в скалярных выражениях

Допустимо использование матриц (векторов) вместо
скалярных выражений: в этом случае предполагается,
что указанные действия должны быть применены к
каждому элементу матрицы (вектора), и результат также
представляется в виде матрицы (вектора):
Вектор подставляется в скалярное выражение, результат - вектор

46. Векторизация

Векторизация – одновременное проведение некоторой
скалярной математической операции над всеми элементами
вектора или матрицы, помеченными знаком векторизации.
Векторизация
В системе MATLAB: скалярные операции.

47. Пример: XD сравните с

A
Пример: X D сравните с ( X D)
1 3
X
2
1
1 4
X D
3
3
2 1
D
1
1
2 3
( X D)
2
1

48. Код, эквивалентный

P(A,B) i1 ORIGIN
j1 ORIGIN
n rows(A) - ORIGIN-1
m cols(A) - ORIGIN-1
for i i1 ..n
for j j1 ..m
Ci,j Ai,j Bi,j
C
( A B)
Предположение: матрицы
имеют одинаковые
размеры.
Преимущества векторизации:
1. Краткость и универсальность записи.
2. Запись с векторизацией, показывает что над элементами
массивов с одинаковыми номерами выполняются одинаковые
действия. Таким образом, векторизация – первый шаг к
распараллеливанию вычислений. В системе MATLAB
параллельные вычисления – это реальность.