Корреляционно-регрессионный анализ: статистическое моделирование зависимостей

1. Теория статистики

Корреляционно-регрессионный анализ:
статистическое моделирование
зависимостей
Часть 1.
1

2. Задача изучения зависимостей

• Исследование объективно существующих
связей между явлениями и их
показателями – одна из важнейших задач
анализа
• Различают классы статистических
признаков:
- независимые (факторные)
- и зависимые (результативные)
• Причинность, корреляция, регрессия
2

3. Виды зависимости

• Зависимости бывают функциональными и
нет, т.е. с элементом случайности
• При Функциональной зависимости
каждому значению независимой
переменной соответствует определенное
значение зависимой
3

4. Балансовая зависимость

• Пример функциональной связи –
балансовая:
Он П Р Ок
0н – остаток средств на начало изучаемого
периода;
П – поступление средств в течении данного
периода;
Р – расход средств за период;
0к – остаток средств на конец периода
4

5. Статистическая зависимость

• В социально-экономических
исследованиях в большинстве случаев
наблюдается связь, при которой каждому
значению одной переменной
соответствует некоторое множество
возможных значений другой переменной
• Такая зависимость называется
статистической
5

6. Корреляционная связь – частный случай статистической зависимости

• Корреляционной зависимостью между
двумя переменными величинами
называется функциональная зависимость
между значениями одной из них и средним
значением другой
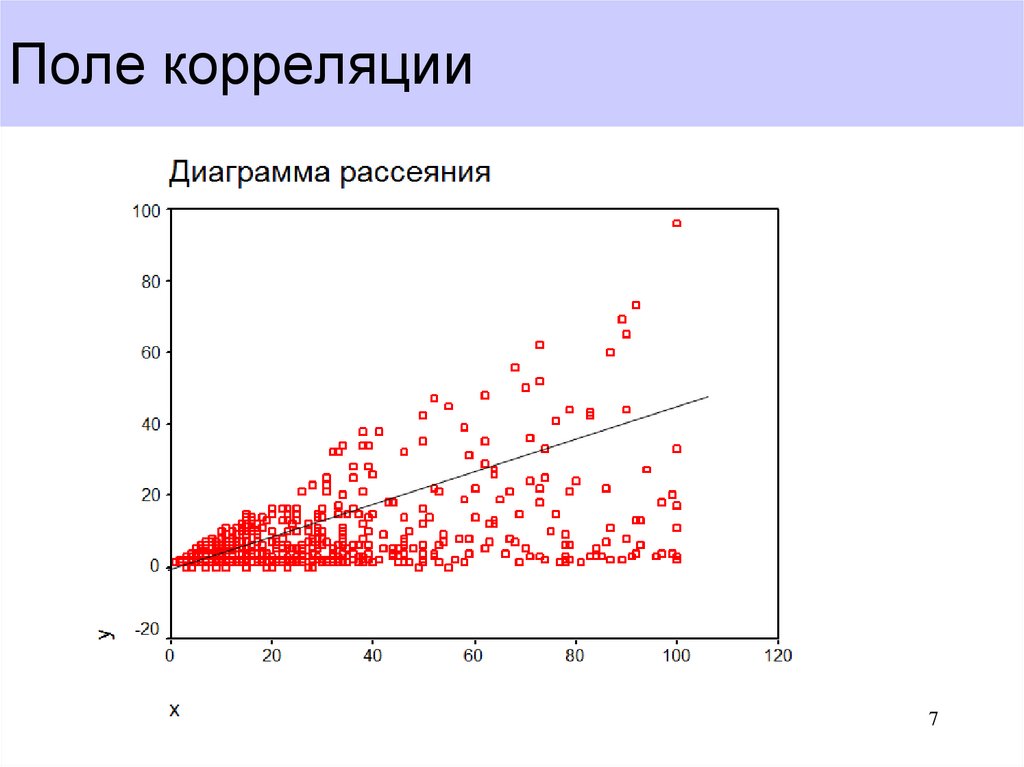
• Поле корреляции – графическое
изображение взаимосвязи двух признаков
6

7. Поле корреляции

7

8. Классификация статистических связей

• Связи между явлениями и их признаками
классифицируются:
По тесноте:
сильная, умеренная, слабая или
отсутствует
По направлению:
прямая или обратная
По аналитическому выражению:
линейная или нелинейная
8

9. Виды корреляционной зависимости

• Парная корреляция – линейная
зависимость между двумя переменными
• Частная корреляция – линейная
зависимость между двумя переменными
при исключении влияния других
• Множественная корреляция - линейная
зависимость между набором переменных
9

10. Этапы статистического изучения связи

1. Качественный анализ на наличие
объективной зависимости
2. Построение модели связи:
Метод приведения параллельных данных
и построение поля корреляции
Корреляционный анализ
Регрессионный анализ
3. Содержательная интерпретация
полученных результатов моделирования
10

11. Характеристика тесноты и направления связи

• Цель состоит в количественном описание
тесноты и направления связи
• В качестве характеристики используется
коэффициент корреляции (r):
11

12. Регрессионный анализ

• Регрессионный анализ заключается в
аналитическом выражении связи:
Нахождение функциональной зависимости
среднего (математического ожидания)
признака (y) от значений независимой
переменной (x):
___
y x f x ,
ε случайный остаток
12

13. Определение параметров регрессии

• Определение класса функций для
выражения функциональной зависимости
среднего признака (y) от значений
переменной (x)
• Оценка параметров функции регрессии:
метод наименьших квадратов
n
y
f xk min
2
k
k 1
• Проверка случайности остатков и
адекватности модели связи
13

14. Пример

• Пусть имеются данные по 9 студентам:
Признак (x) – количество пропущенных
студентом занятий по дисциплине
Признак (y) – полученная студентом
оценка на экзамене
14

15. Пример

Исследуем зависимость среднего
значения (y) от признака (x)
1. Ясно, что такая объективная зависимость
может существовать
(хотя и не функциональная)
k
15

16. Пример

2. Построение модели связи
• Метод приведения параллельных данных
16

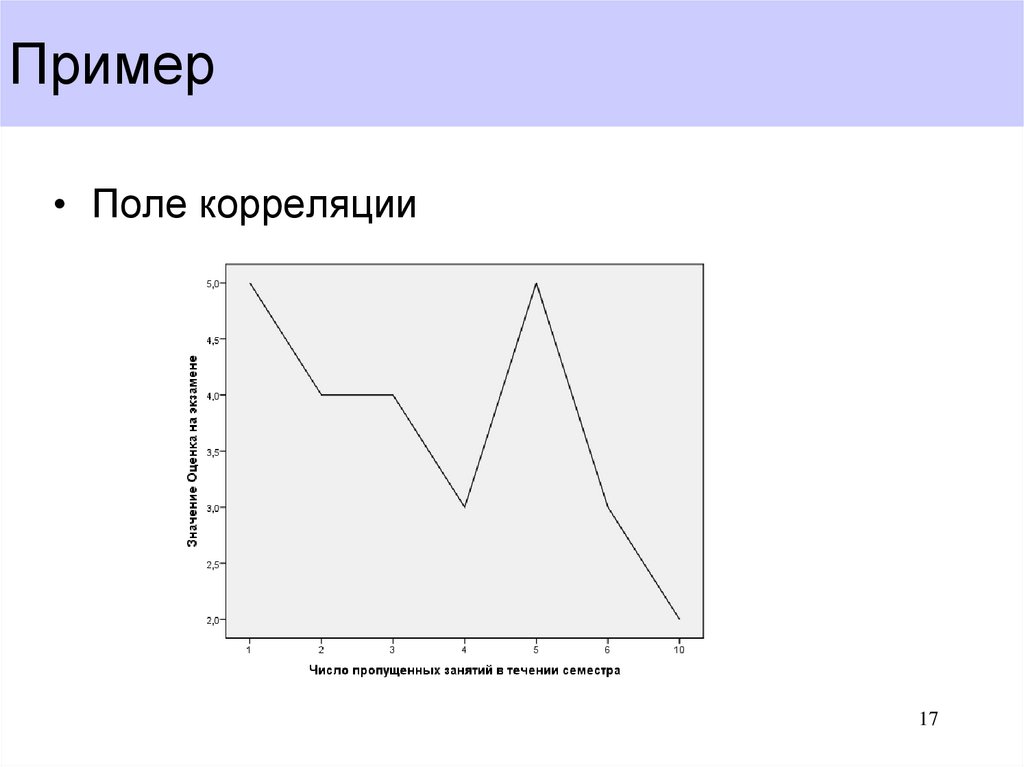
17. Пример

• Поле корреляции
17

18. Пример

• Теснота и направление связи между
количественными переменными
измеряются с помощью коэффициента
корреляции Пирсона:
___
r
cov( x. y )
x y
xy x y
x y
n
1 / n xi yi x y
i 1
n
n
i 1
i 1
1 / n ( xi x ) 2 1 / n ( yi y ) 2
18

19. Пример

19

20. Пример

• Делать выводы о тесноте и направлении
связи пока преждевременно: нужно
проверить значимость коэффициента
корреляции (r)
• Гипотеза H0: истинное значение
коэффициента корреляции (R) равно «0»
• Для проверки значимости коэффициента
корреляции (r) применяется T-критерий
Стьюдента
20

21. Пример

• По выборке рассчитываем значение
статистики:
n 2
9 2
tr r
1 r
2
0.76
1 0.76
tr 3.09 t0.05,7 2.365 : коэфф. корреляции значим
2
3,09
21

22. Вывод

• Корреляционная связь:
Обратная - коэффициент корреляции (r)
отрицательный
Умеренная ( r 0,76 0,8),, но близкая к
сильной
22

23. Регрессионный анализ

• Наблюдается существенная линейная
корреляционная зависимость, поэтому
аналитическое выражение связи будем
искать в линейной форме:
23

24. Регрессионный анализ

• Необходима проверка значимости
полученного уравнения регрессии
- в целом
- каждого коэффициента в отдельности
• Тем не менее, пользуясь полученным
уравнением регрессии, находим, что,
например, при x = 3, оценка ожидается 4:
___
y x (3) 4.86 0.27 3 4.05
24

25. Регрессионный анализ

• Значимость полученного уравнения
регрессии (в целом) проверяется по
F-критерию Фишера:
Гипотеза H0: все коэффициенты регрессии
равны «0»
25

26. Регрессионный анализ

Уравнение регрессии в целом значимо,
если выполняется условие:
R2 (n 2) QR (n 2)
F
F ;1;n 2
2
E
QE
26

27. Регрессионный анализ

• Так как yˆ k y (a0 a1 xk ) (a0 a1 x) a1 ( xk x)
то объясненное регрессией отклонение от
среднего уровня:
n
n
QR ( yˆ k y ) 2 a12 ( xk x ) 2 a12 (n x2 )
k 1
k 1
0,272 9 6.67 4.38
Полное отклонение от среднего уровня:
Q n 9 0,84 7.56
2
y
Отклонение, необъясненное регрессией:
QE Q QR 7.56 4.38 3.18
27

28. Регрессионный анализ

• Значение F-статистики:
QR ( n 2) 4.38 (9 2)
F
9.61
QE
3.18
• Вывод: так как вычисленное значение
F-критерия:
F 9,61 F0,05;1;7 5,59,
то уравнение регрессии значимо
28

29. Регрессионный анализ: коэффициент детерминации

2
Q
R 2 R R2
Q
• В силу правила сложения дисперсий для
R2 имеем 0 R 2 1; 2 R2 E2
• В примере коэффициент детерминации:
4,38
R QR / Q
0,58
7,56
2
• Вывод: предсказанные по регрессии
значения объясняют вариацию
результативного признака (y) на 58%
29