Похожие презентации:
Формальные описания реальных объектов и процессов
1. Формальные описания реальных объектов и процессов
2.
• Ответами к заданиям являются слово,словосочетание, число или
последовательность слов, чисел. Запишите
ответ без пробелов, запятых и других
дополнительных символов.
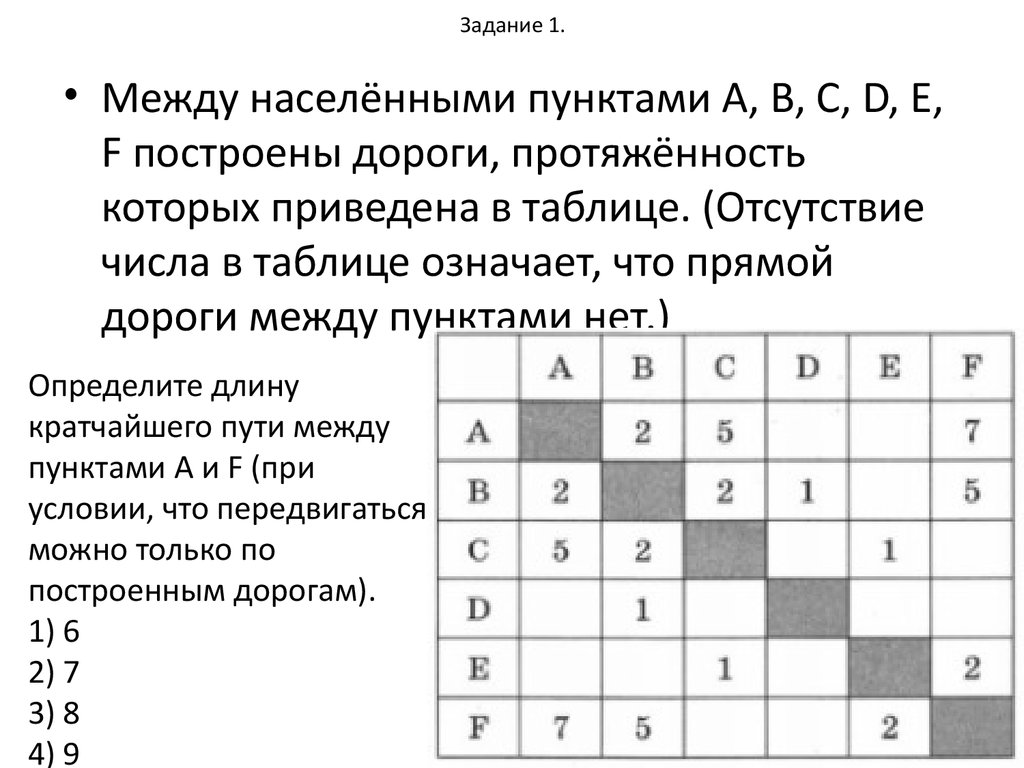
3. Задание 1.
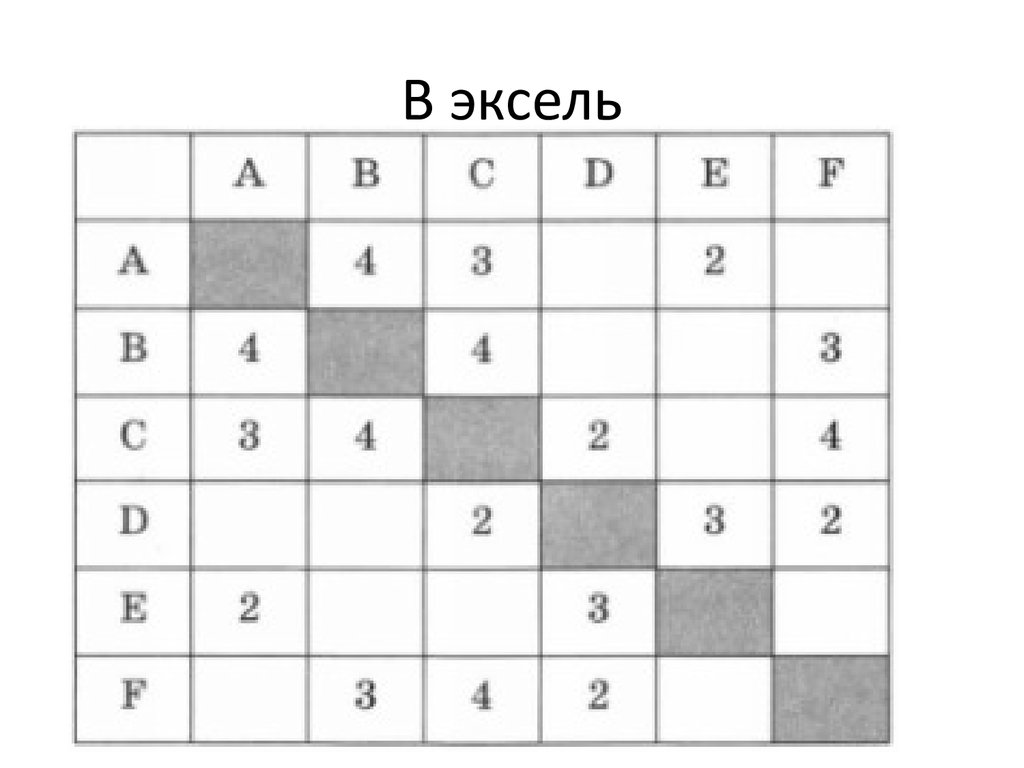
• Между населёнными пунктами А, В, С, D, Е,F построены дороги, протяжённость
которых приведена в таблице. (Отсутствие
числа в таблице означает, что прямой
дороги между пунктами нет.)
Определите длину
кратчайшего пути между
пунктами А и F (при
условии, что передвигаться
можно только по
построенным дорогам).
1) 6
2) 7
3) 8
4) 9
4. Понятия (что это?)
• Таблица• Граф
• Дерево
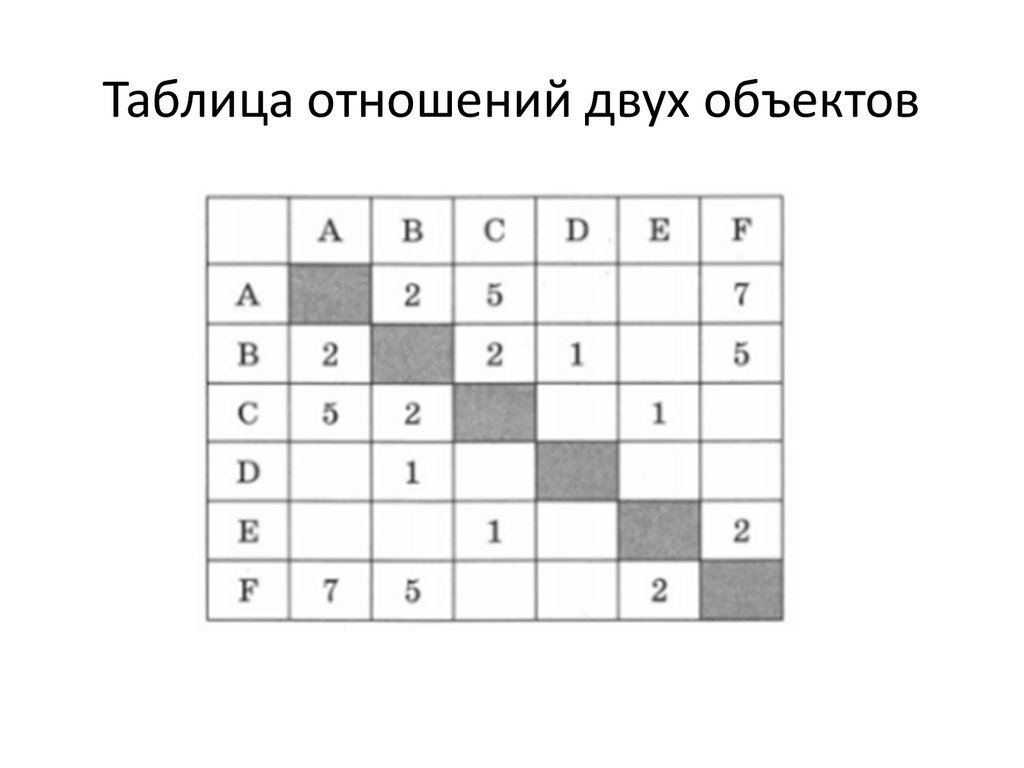
5.
• Это виды представления информации6. Таблица отношений двух объектов
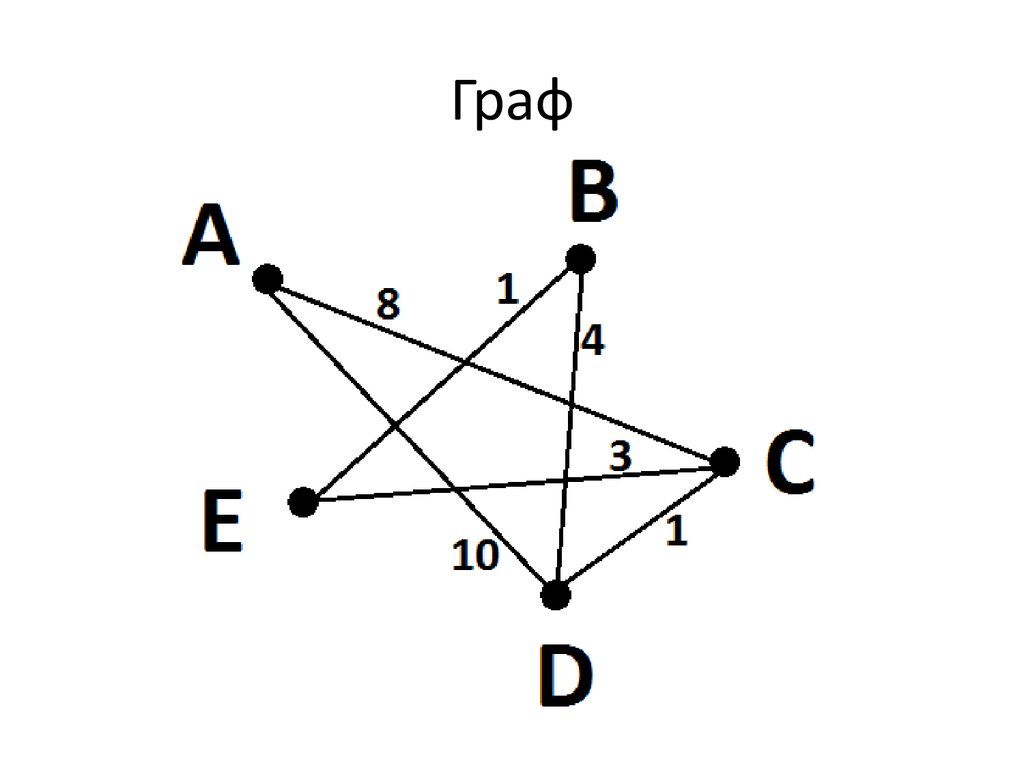
7. Граф
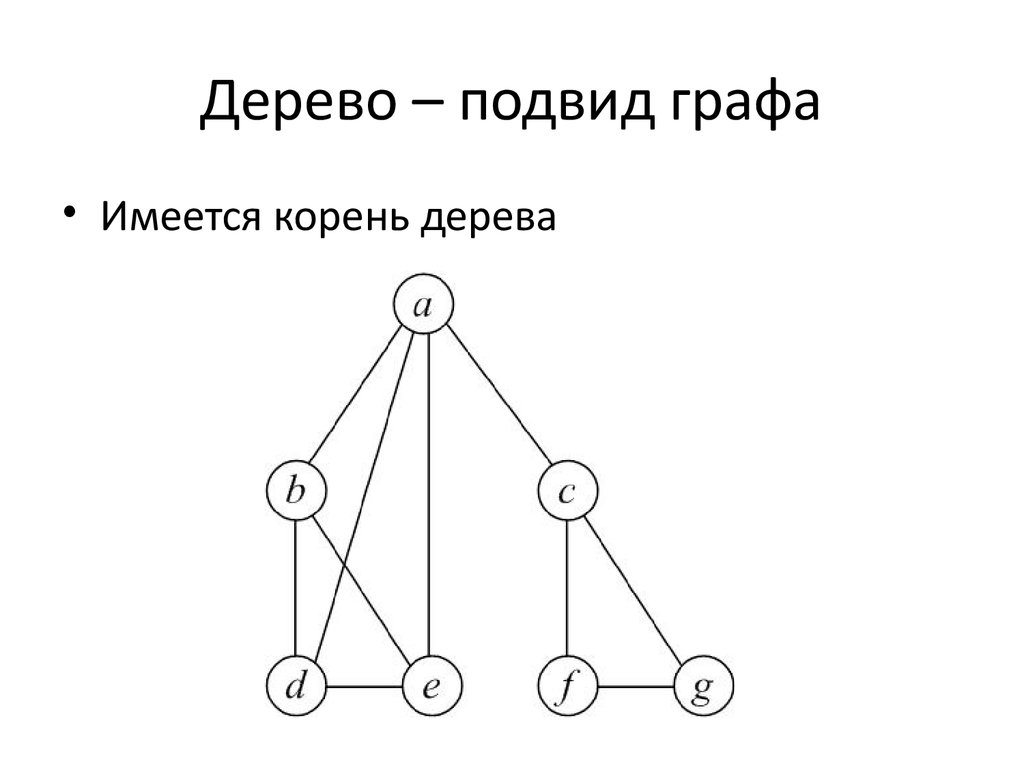
8. Дерево – подвид графа
• Имеется корень дерева9. Для решения
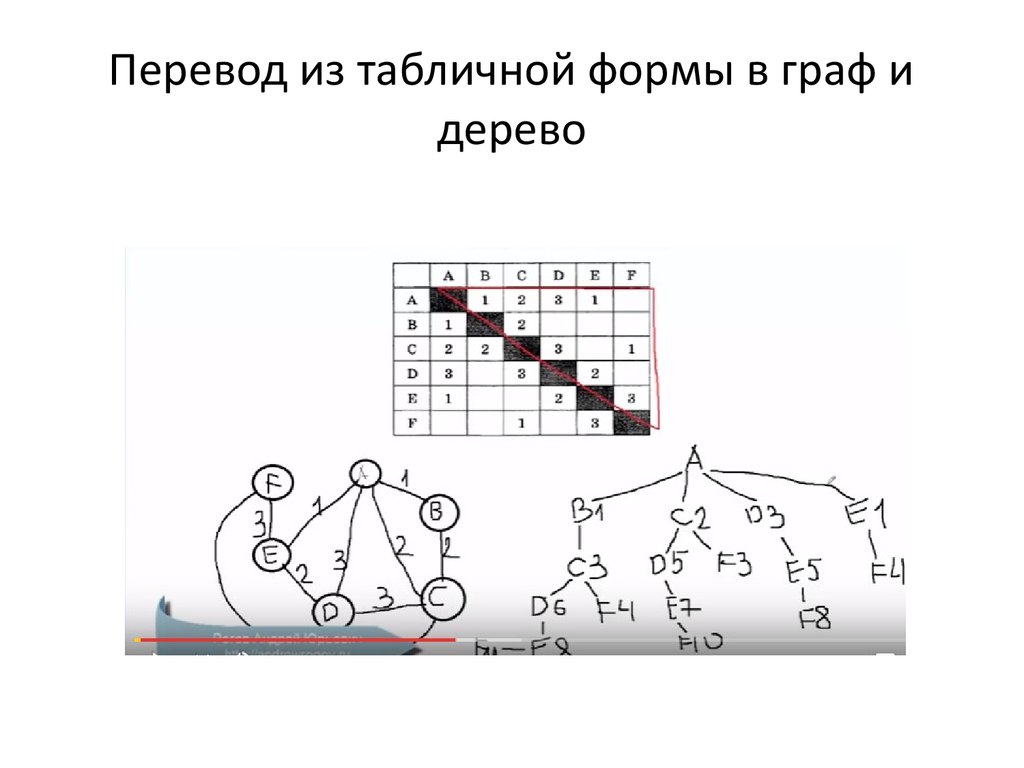
• Необходимо из табличной формыпредставления информации сделать граф
или наоборот.
10. Перевод из табличной формы в граф и дерево
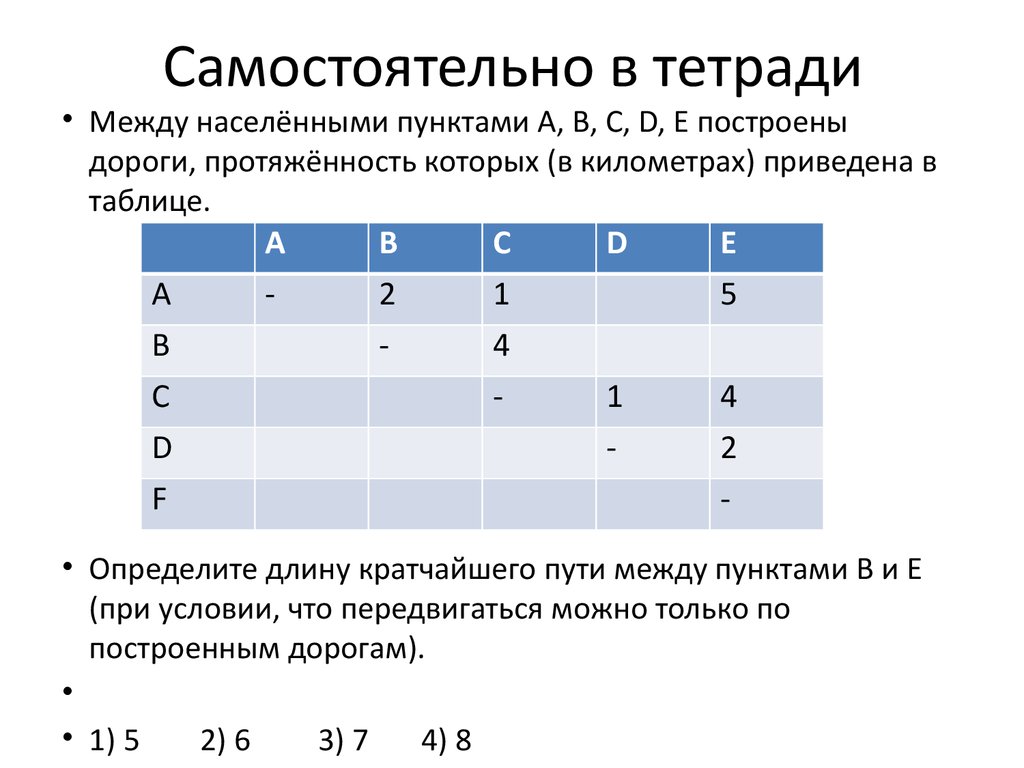
11. Самостоятельно в тетради
• Между населёнными пунктами A, B, C, D, E построеныдороги, протяжённость которых (в километрах) приведена в
таблице.
A
B
C
D
E
A
B
C
D
F
-
2
-
1
4
-
5
1
-
4
2
-
• Определите длину кратчайшего пути между пунктами B и E
(при условии, что передвигаться можно только по
построенным дорогам).
• 1) 5
2) 6
3) 7
4) 8
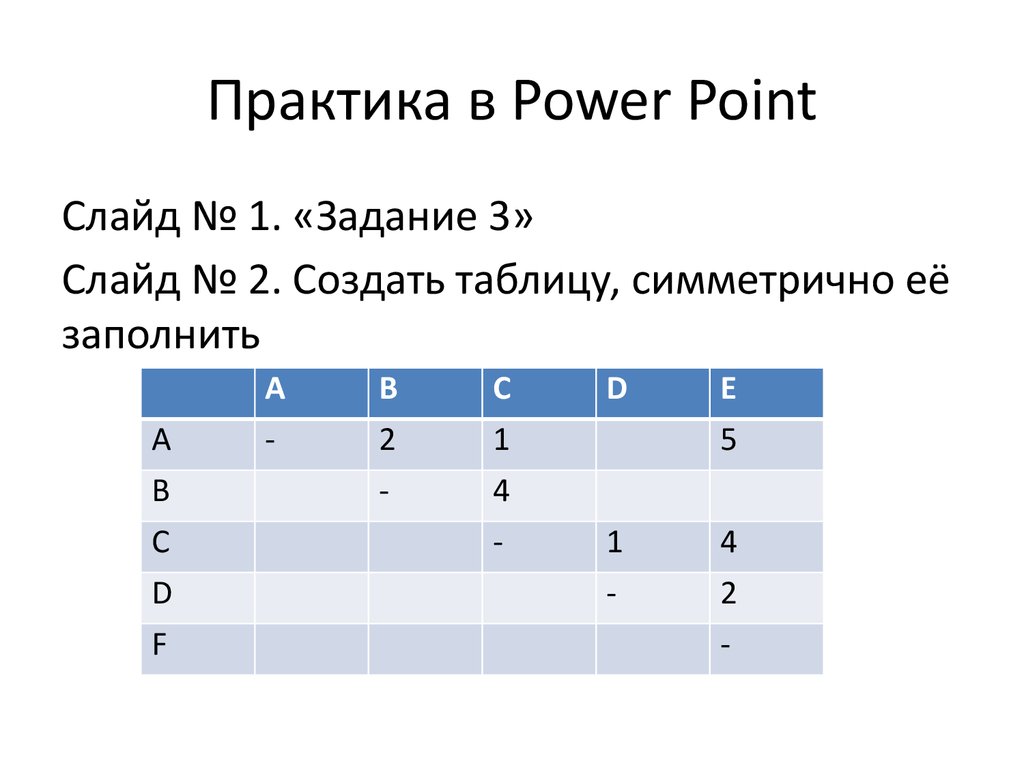
12. Практика в Power Point
Слайд № 1. «Задание 3»Слайд № 2. Создать таблицу, симметрично её
заполнить
A
B
C
D
F
A
-
B
2
-
C
1
4
-
D
E
5
1
-
4
2
-
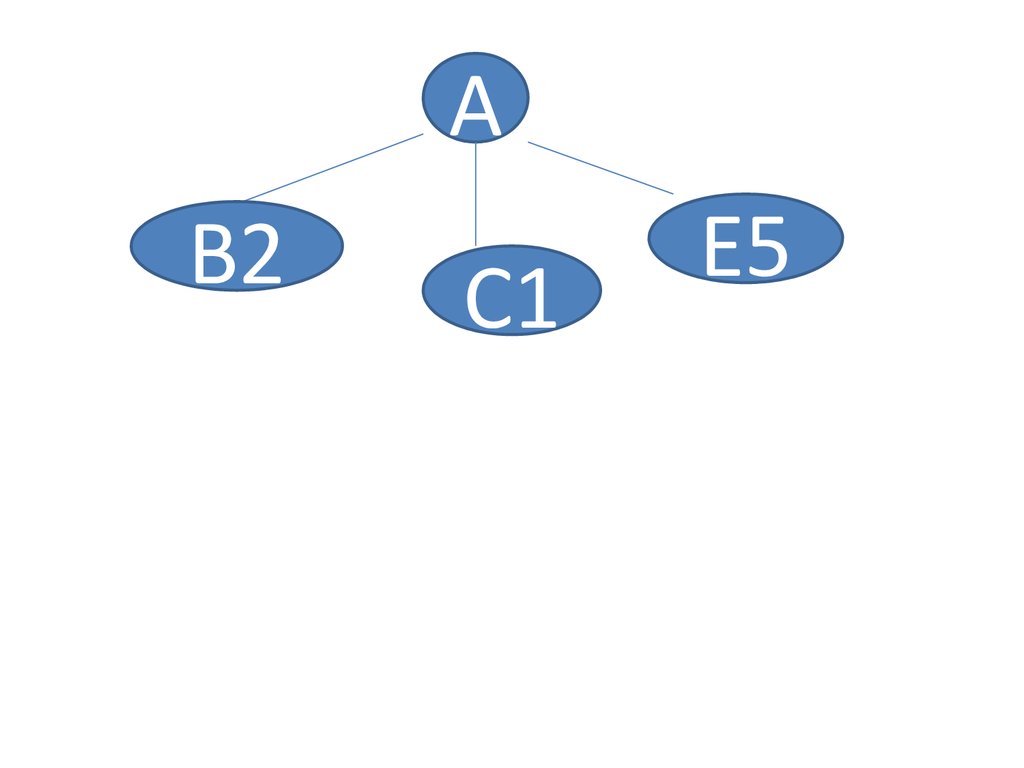
13.
• Слайд 3.• Построить дерево по таблице, для каждого
нового элемента создать анимацию
появление
14.
АВ2
С1
Е5
15. Перемена
16.
• Задача 1. Между девятью планетами солнечнойсистемы установлено космическое сообщение.
Рейсовые ракеты летают по следующим маршрутам:
Земля – Меркурий; Плутон – Венера; Земля – Плутон;
Плутон – Меркурий; Меркурий – Вене; Уран – Нептун;
Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и
Марс – Уран. Можно ли долететь на рейсовых ракетах с
Земли до Марса ?
• Решение: Нарисуем схему условия: планеты изобразим
точками, а маршруты ракет – линиями.
17.
• Теперь сразу видно, что долететь с Землидо Марса нельзя.
18.
• Задача 3. В городе Маленьком 8 телефонов.Можно ли их соединить проводами так,
чтобы каждый телефон был соединен
ровно с пятью другими ?
19.
• нет20.
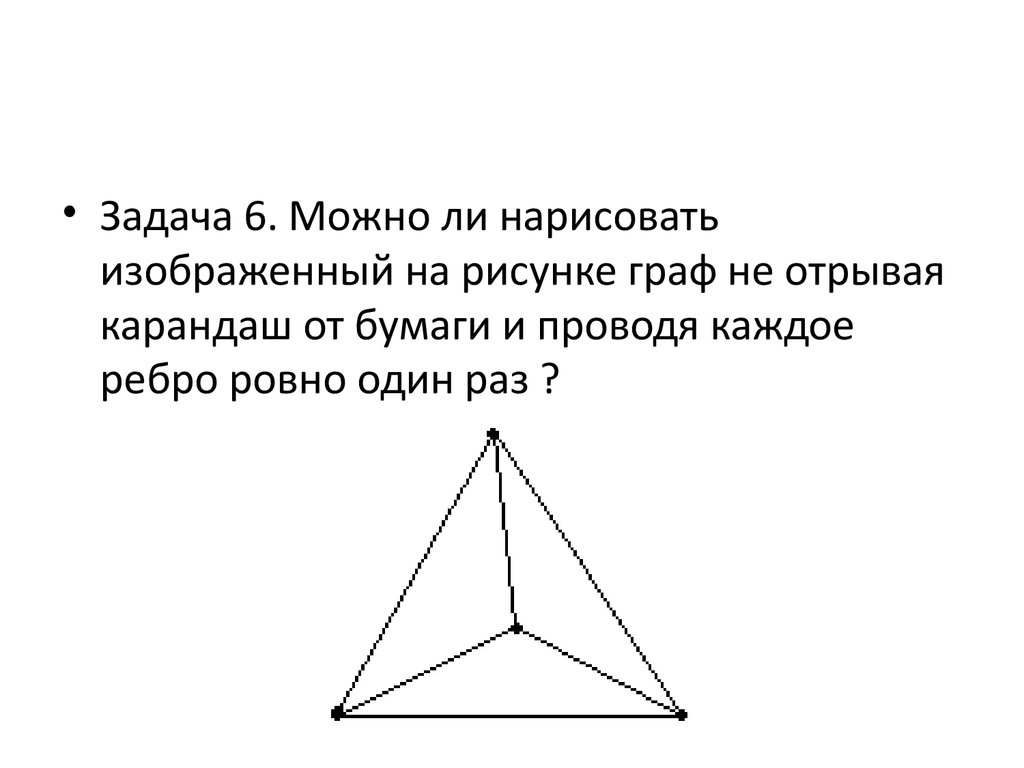
• Задача 6. Можно ли нарисоватьизображенный на рисунке граф не отрывая
карандаш от бумаги и проводя каждое
ребро ровно один раз ?
21.
• 7 Имеется группа островов, соединенных мостамитак, что от каждого острова можно добраться до
любого другого. Турист обошел все острова, пройдя
по каждому мосту розно 1 раз. На острове
Троекратном он побывал трижды. Сколько мостов
ведет с Троекратного, если турист
• а) не с него начал и не на нем закончил?
• б) с него начал, но не на нем закончил?
• в) с него начал и на нем закончил?
22.
• Задача8: Алия решила маме на деньрождения подарить букет цветов (розы,
тюльпаны или гвоздики) и поставить из или
в вазу или в кувшин.
• Сколькими способами это можно сделать.
23.
• Решение. Отметим точками цветы (РТГВК) (вершиныграфа)
• А связи между ними -линиями между точками (рёбра
графа)
• По рисунку видно, что таких сопопбов - 6
• * розы * тюльпан *гвоздики
• * ваза *кувшин
24.
• Задача9. Ранним утром Миша Маша, Асемобменялись приветствиями каждый с
каждым. Сколько всего было приветствий.
Решите задачу с помощью графа.
25.
• Задача10. Шесть футбольных команддолжны сыграть матчи, каждая с каждой.
Уже сыграли матчи.
• А с В, Г,Е Г с А,Д,Е
• Б с В,Д,Е Д с Б,Г,Е
• В с А,Б Е с А,Б,Г,Д
• Сколько матчей сыграно и сколько осталось
сыграть.
26.
• Задача5. В квартирах №1,2,3 жили тридруга: Айдар, Тима и Саша. Известно, что в
квартирах №1 и 2 жил не Айдар. Тима жил
не в квартире №1. В какой квартире жил
каждый из друзей.
27.
• Ответ:Айдар
Тима
Саша
№1
+
№2
+
№3
+
-
28.
• Задача11. Арман, Мадии, Тимур, Сергейзаняли на математической олимпиаде
четыре первых места. Когда их спросили о
распределений мест, они дали три ответа:
Сергей – первый, Мади– второй, Сергей
-второй, Арман – третий, Тимур – второй,
Арман – четвертый. Известно, что в каждом
ответе только одно утверждение верно. Как
распределились места?
29.
• Ответ: С-1 Т-2 А -3 М-4.30.
• Задача7. Григорий играли в шахматы.Каждый сыграл с каждым по одной партии.
Сколько партий было сыграно?
31.
• Решение: Решим задачу с помощью полногографа с четырьмя вершинами А, Б, В, Г,
обозначенными по первым буквам имен
каждого из мальчиков. В полном графе
проводятся всевозможные ребра.
• В данном случае отрезки-ребра обозначают
сыгранные шахматные партии. Из рисунка
видно, что граф имеет 6 ребер, значит, и
партий было сыграно 6.
32.
• Задача8.Из города А в город Б ведут дведороги, из города Б в городок В -тоже две
дороги и из города А в город В – тоже две
дороги. Нарисуй схему и сосчитай все
возможные пути из города А в город В.
33.
• Ответ: 6 партий .34.
• Задача9. Андрей, Борис, Виктор и Григорийпосле возвращения из спортивного лагеря
подарили на память друг другу свои
фотографии. Причем каждый мальчик
подарил каждому из своих друзей
• по одной фотографии. Сколько всего
фотографий было подарено?
35.
• Решение. I способ. С помощью стрелок на ребрахполного графа с вершинами А, Б, В и Г показан
процесс обмена фотографиями. Очевидно,
стрелок в 2 раза больше, чем ребер, т.е. 6*2 = 12.
Столько же было подарено и фотографий.
• II способ. Каждый из четверых мальчиков
подарил друзьям 3 фотографии, следовательно,
всего было роздано 3 • 4 = 12 фотографий.
• О т в е т: 12 фотографий.
36. В эксель
37.
• Выехало три автомобиля из разных городови проехало по разным маршрутам.
Вычислить длину каждого маршрута.
















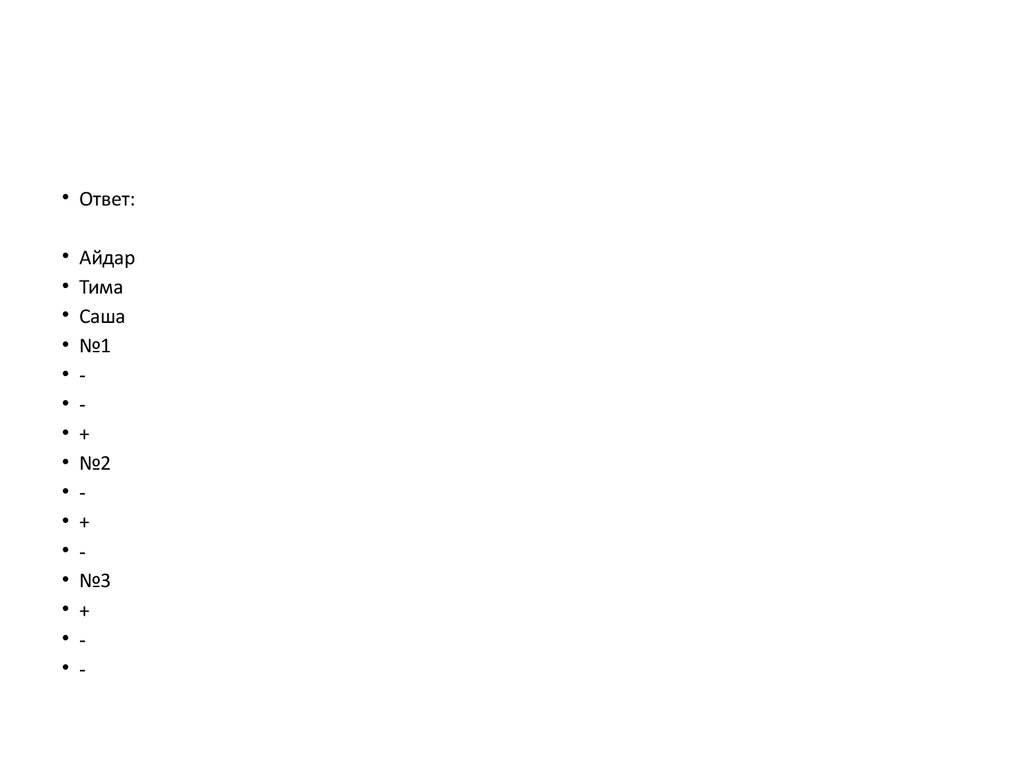









 Информатика
Информатика








