Похожие презентации:
Вращательное движение твердого тела. Уравнение вращательного движения. Угловая скорость и угловое ускорение тела
1. Вращательное движение твердого тела Уравнение вращательного движения
Угловая скорость и угловоеускорение тела
2. Вращательным движением твердого тела называется такое его движение, при котором все точки, принадлежащие некоторой прямой, неизменно связ
Вращательнымдвижением
твердого тела называется такое
его движение, при котором все
точки,
принадлежащие
некоторой прямой, неизменно
связанной с телом, остаются
неподвижными.
Эта прямая называется осью
вращения тела.
3.
Всеостальные
точки
тела
движутся
в
плоскостях,
перпендикулярных оси вращения,
и описывают окружности, центры
которых лежат на этой оси.
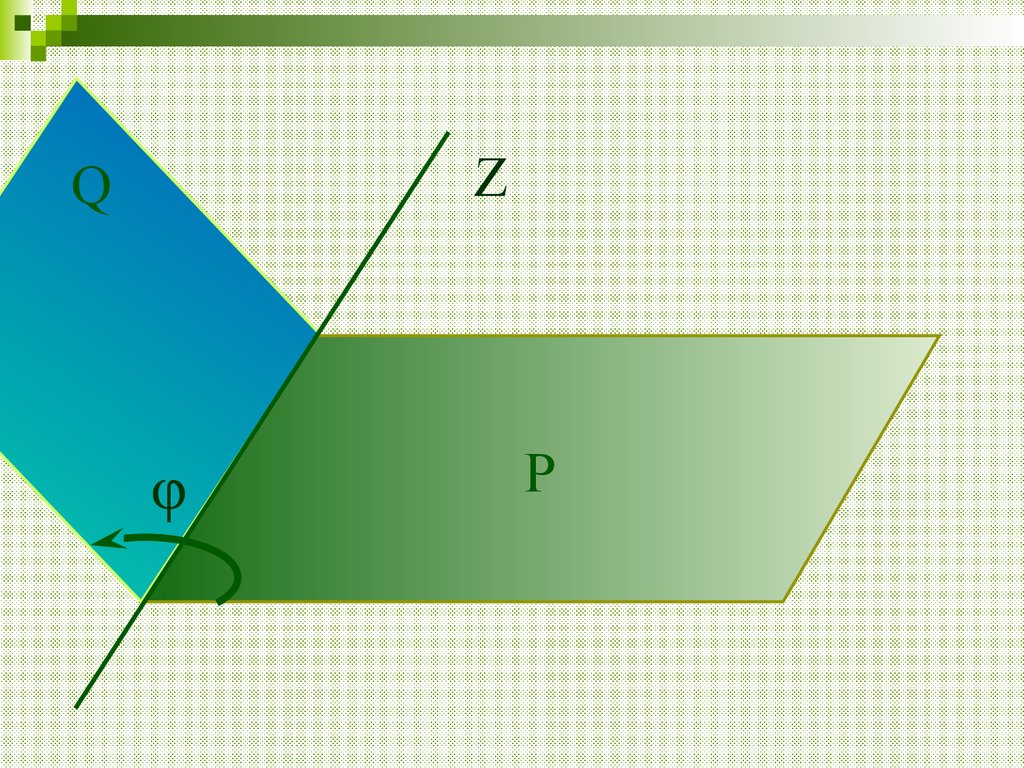
4. Зададим направление оси вращения z. Проведем через эту ось две полуплоскости: неподвижную полуплоскость P и подвижную полуплоскость Q, связ
Зададим направление осивращения z. Проведем через эту
ось две полуплоскости:
неподвижную полуплоскость P и
подвижную полуплоскость Q,
связанную с твердым телом и
вращающуюся вместе с ним.
5.
Двугранный угол между этимиполуплоскостями, отчитываемый
от неподвижной полуплоскости P
к подвижной полуплоскости Q,
называется углом поворота
тела.
6.
ZQ
φ
P
7. При вращении тела угол поворота изменяется в зависимости от времени, т.е. является функцией времени t:
f (t )Это уравнение называется уравнением
вращательного движения тела.
Оно полностью определяет положение
тела в любой момент времени.
8. Угловая скорость и угловое ускорение тела
Величина, характеризующаябыстроту изменения угла
поворота с течением времени,
называется угловой скоростью
~
d / dt
тела (1 рад/с).
9.
Числоваявеличина,
характеризующая
быстроту
изменения угловой скорости с
течением времени, называется
угловым ускорением тела
(1 рад/c2).
2
2
~
d / dt
10. Уравнение равномерного вращения тела
Вращение тела с постоянной скоростьюназывается равномерным.
Пусть в начальный момент
времени t0=0 угол поворота
имеет значение 0 , тогда
d / dt const ; d dt.
11.
Проинтегрируем уравнение впределах, соответствующих
начальному моменту t0=0 и
произвольному моменту
времени t:
t
d dt;
0
0
0
t 0 t .
12. Уравнение равнопеременного движения тела
Вращение тела, при которомугловое ускорение постоянно,
называют равнопеременным
вращением.
13.
При этом, если абсолютнаявеличина угловой скорости
увеличивается, то вращение
называют равноускоренным, а
если уменьшается –
равнозамедленным.
0 0t t / 2
2
14.
Из формулынаходим
угловой
скорости
0 / t ,
т.е. при равнопеременном вращении
абсолютное
значение
углового
ускорения тела равно отношению
изменения угловой скорости тела за
некоторый промежуток времени к
числовой
величине
этого
промежутка.
15.
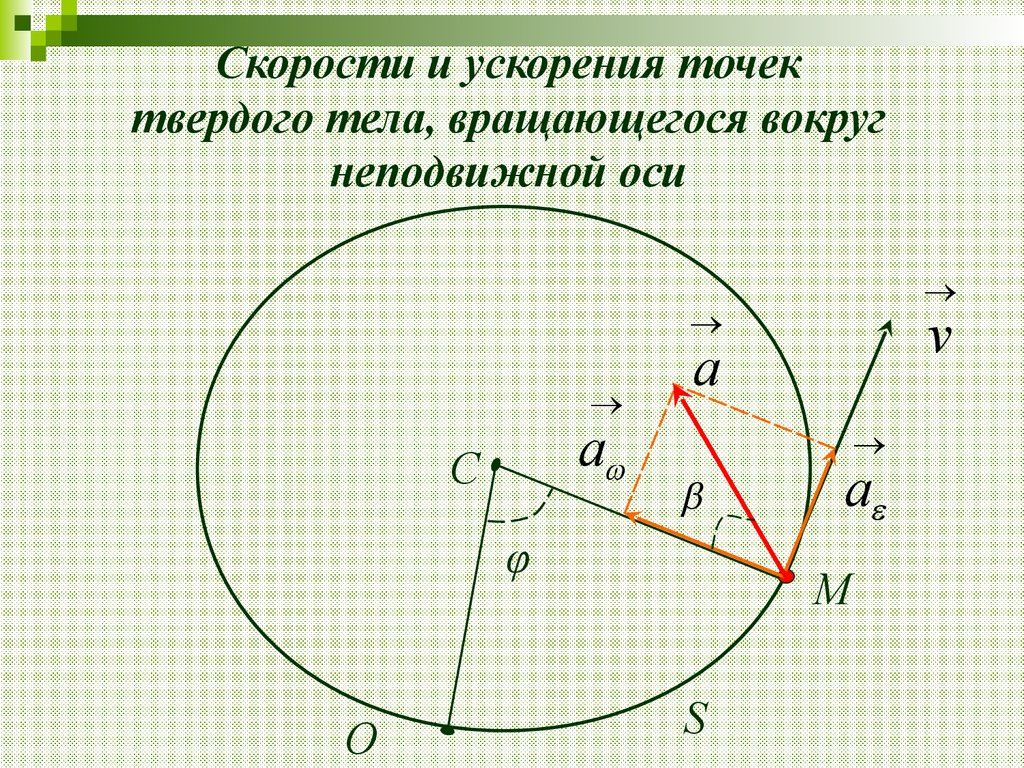
Скорости и ускорения точектвердого тела, вращающегося вокруг
неподвижной оси
a
C
a
φ
O
v
a
M
S
16. Определим модуль скорости точки М, называемой вращательной или окружной скоростью этой точки
v ds / dt R d / dt RМодуль вращательной скорости точки
твердого тела равен произведению расстояния
от точки до оси вращения на угловую скорость
тела.
Модули вращательных скоростей
различных точек вращающегося тела пропорциональны расстояниям от этих точек до оси
вращения.
17. Определим ускорения точек вращающегося тела:
Модуль вращательногоускорения точки твердого тела
равен произведению расстояния
от точки до оси вращения на
~
~
aмодуль
dv / dt ускорения
R d / dt R
углового
a
18.
Модуль центростремительногоускорения точки твердого тела
равен произведению расстояния
от точки до оси вращения на
квадрат угловой скорости точки.
a an v / R R / R R
2
2
2
2
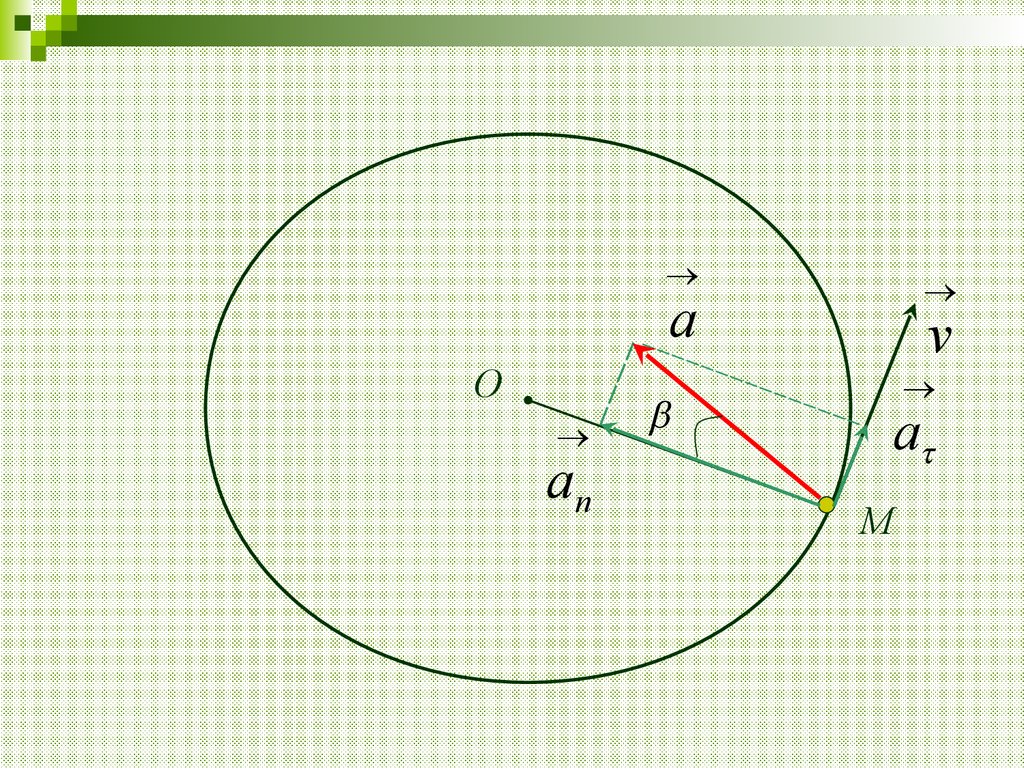
19.
Модуль полного ускорения точкиравен
a a a
2
R
2
2
n
4
20.
Тангенс угла , составленноговектором ускорения a с
радиусом окружности СМ:
tg a / a n R /( R ) /
2
2
21. Пример решения задачи
22. Пример 1
Вращение маховика в периодпуска машины определяется
уравнением
3
(1 / 3)t ,
где t – в секундах, – в радианах.
23.
Определить модуль инаправление ускорения точки,
отстоящей от оси вращения на
расстоянии 50 см, в тот момент,
когда ее скорость равна 8 м/с.
24.
aO
an
v
a
M
25. Решение: По уравнению вращения маховика находим его угловые скорость и ускорение: 1. 2.
Решение:d / dt вращения
t
По
уравнению
маховика 2находим
2 его угловые
d
/
dt
2
t
скорость и ускорение:
1.
2
26.
Используя формулу v R ,находим момент времени t1, когда
скорость точки М равна 8 м/с:
1 v1 / R 8 / 0,5 16 рад / с.
Из (1) находим t1:
t1
1 16 4c.
27. Далее вычисляем:
1 2 4 8 рад / с;1
a R 1 0,5 8 4 м / с ;
2
a R 0,5 16 128 м / с ;
n
1
2
1
2
1
2
a1 (a ) (a )
2
n 2
1
4 128 128,6 м / с .
2
2
2
28.
Направление ускорения точкиопределяется углом :
tg 1 1 / 8 / 16
2
1
2
1 / 32 1 1 48 .
0
'
29. Пример 2
Якорь электродвигателя, имеющийчастоту вращения n=50c-1, после
выключения тока, сделав N=500
оборотов, остановился.
Определить угловое ускорение
якоря.
30. Дано:
n=50c-1N=500
ε=?
31. Решение:
Закон движения:где 2 N
Тогда
t
0t
2
2
,
0 2 n
t
2 N 2 nt
2
2
(*)
32.
С другой стороны:0 t
Так как якорь остановился, то
Получаем:
0
0 2 n t
2
n
Тогда t
Подставим в формулу (*)
2
2 n 2 n
2 n
2 N 2 n
2
2
2
33.
Отсюдаn
N
2
15,7c
1





























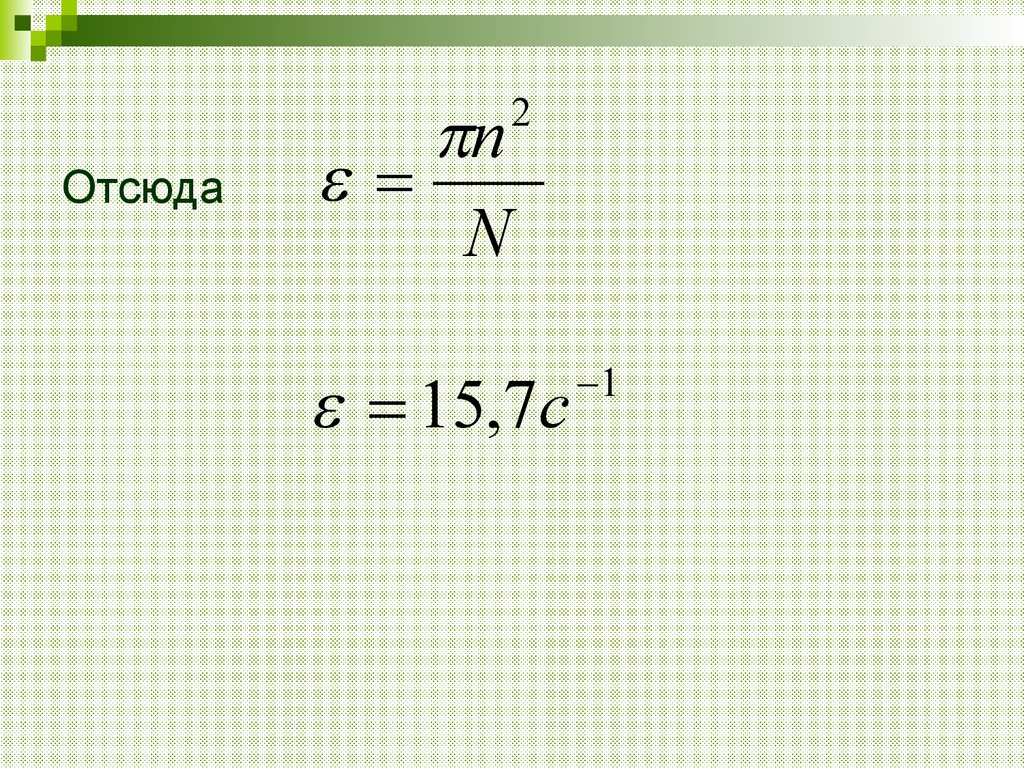
 Физика
Физика








