Вписанная окружность

1. Вписанная окружность

Урок геометрии от 23.04.2020

2. Вписанная окружность

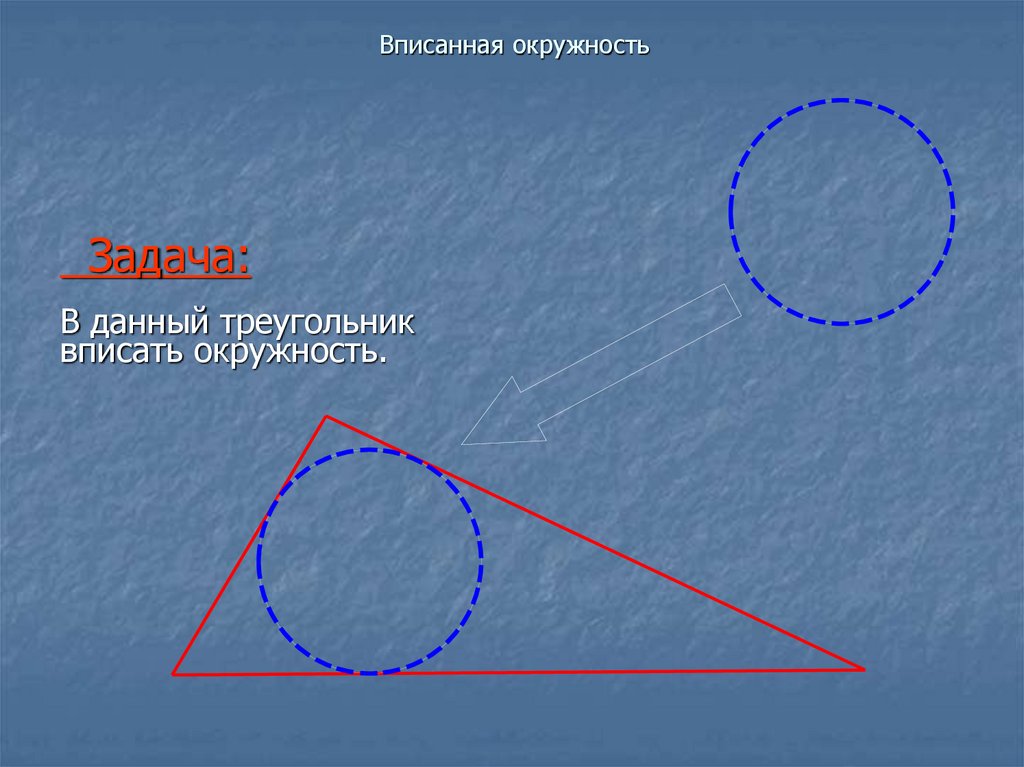
Задача:
В данный треугольник
вписать окружность.

3. Вписанная окружность

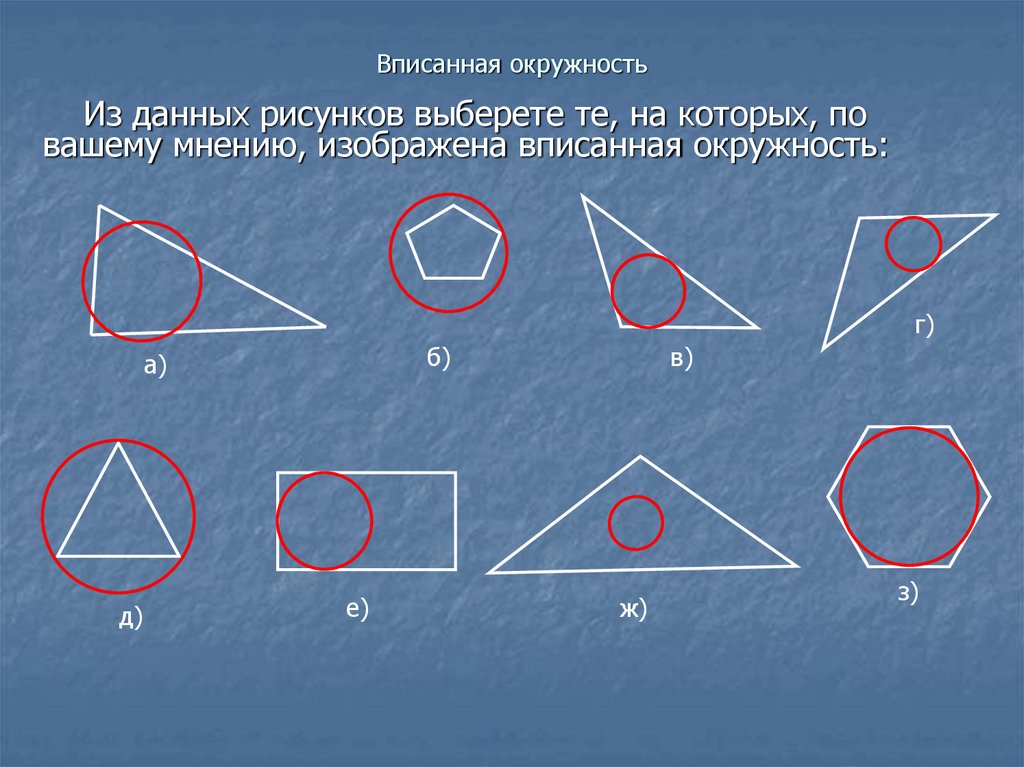
Из данных рисунков выберете те, на которых, по
вашему мнению, изображена вписанная окружность:
г)
б)
а)
д)
е)
в)
ж)
з)

4. Вписанная окружность

Определение:
Окружность называется вписанной в
многоугольник, если она касается всех
его сторон.

5. Вписанная окружность

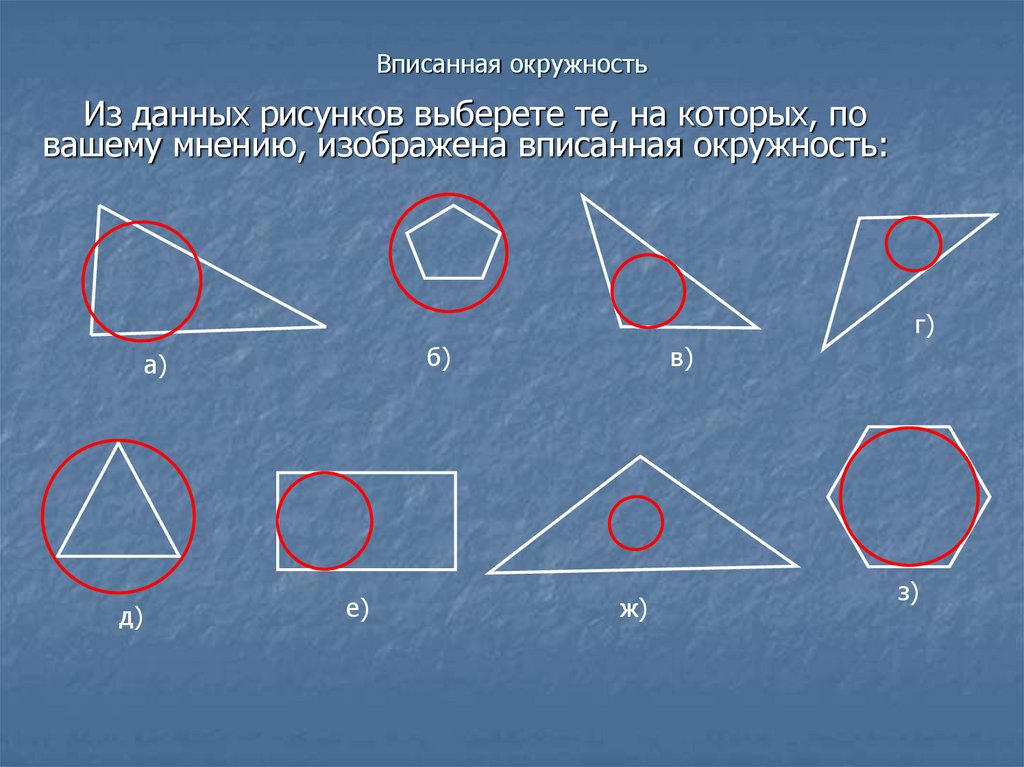
Из данных рисунков выберете те, на которых, по
вашему мнению, изображена вписанная окружность:
г)
б)
а)
д)
е)
в)
ж)
з)

6. Вписанная окружность

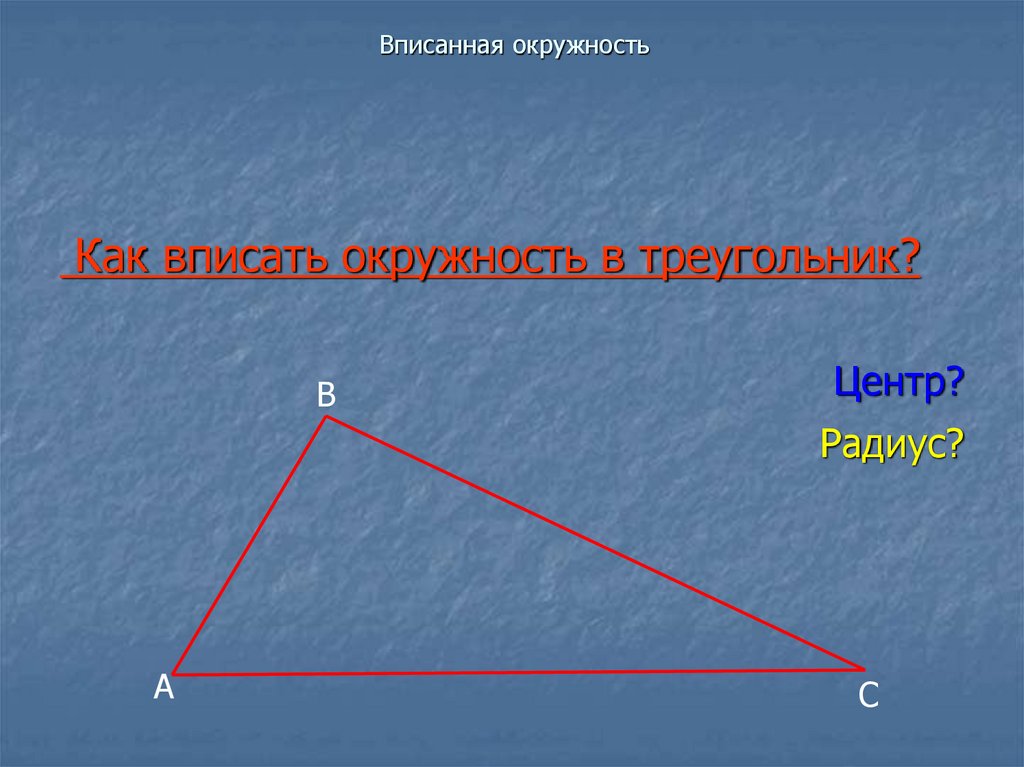
Как вписать окружность в треугольник?
В
Центр?
Радиус?
А
С

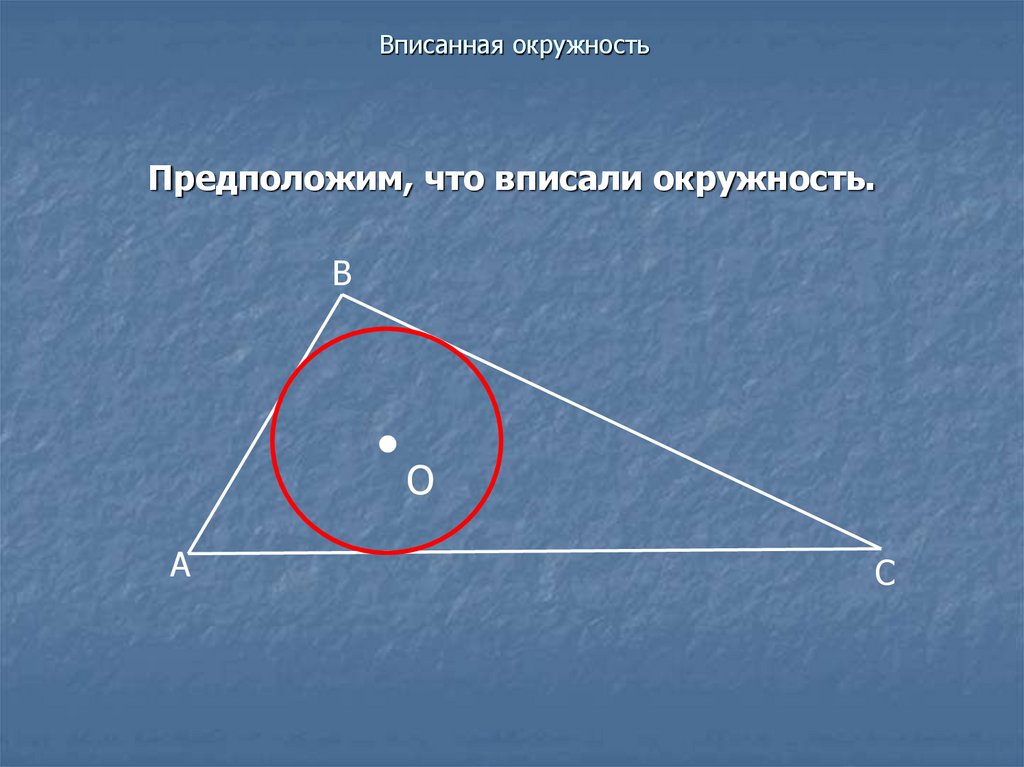
7. Вписанная окружность

Предположим, что вписали окружность.
В
О
А
С

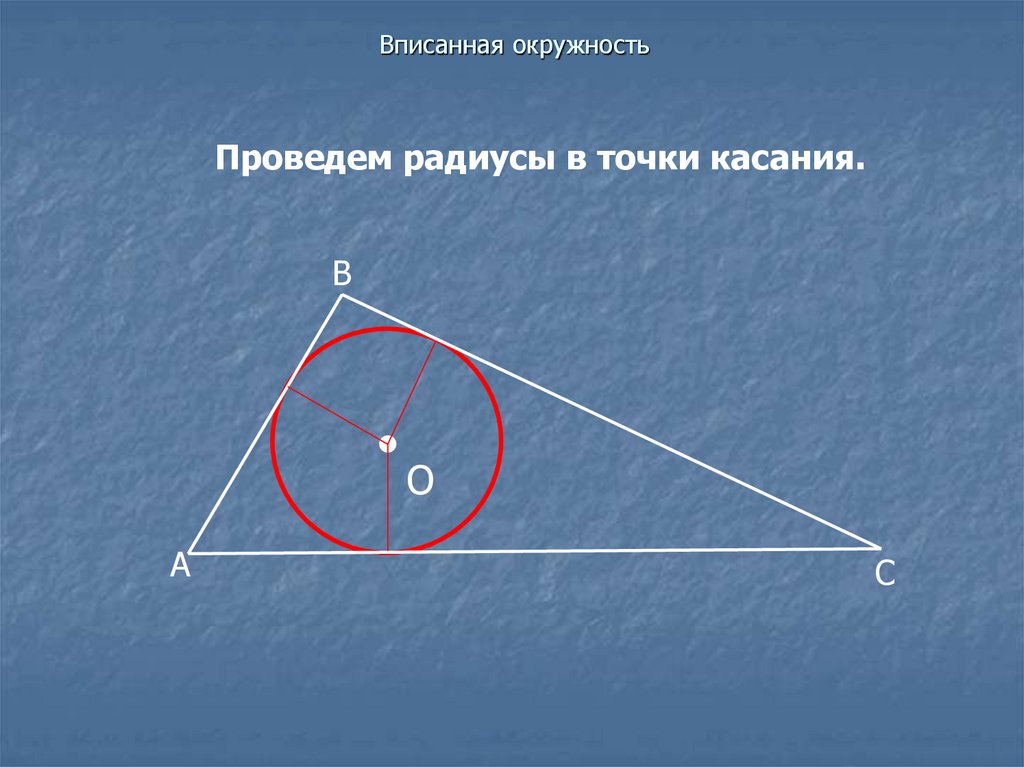
8. Вписанная окружность

Проведем радиусы в точки касания.
В
О
А
С

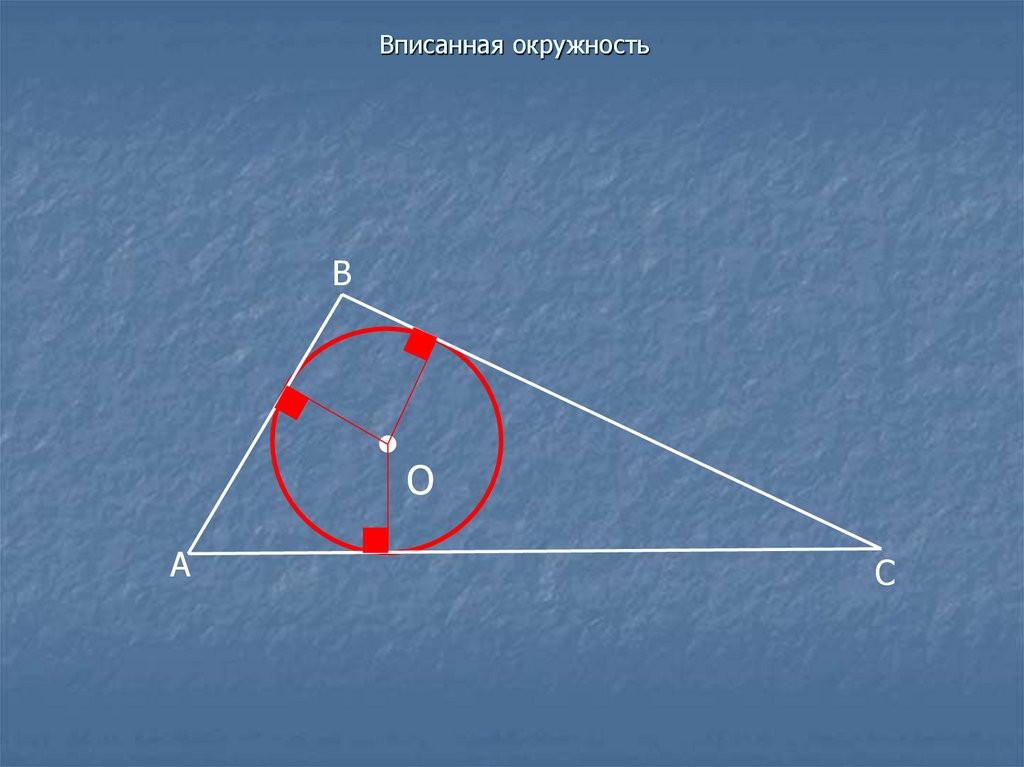
9. Вписанная окружность

В
О
А
С

10. Вписанная окружность

В
О
А
С

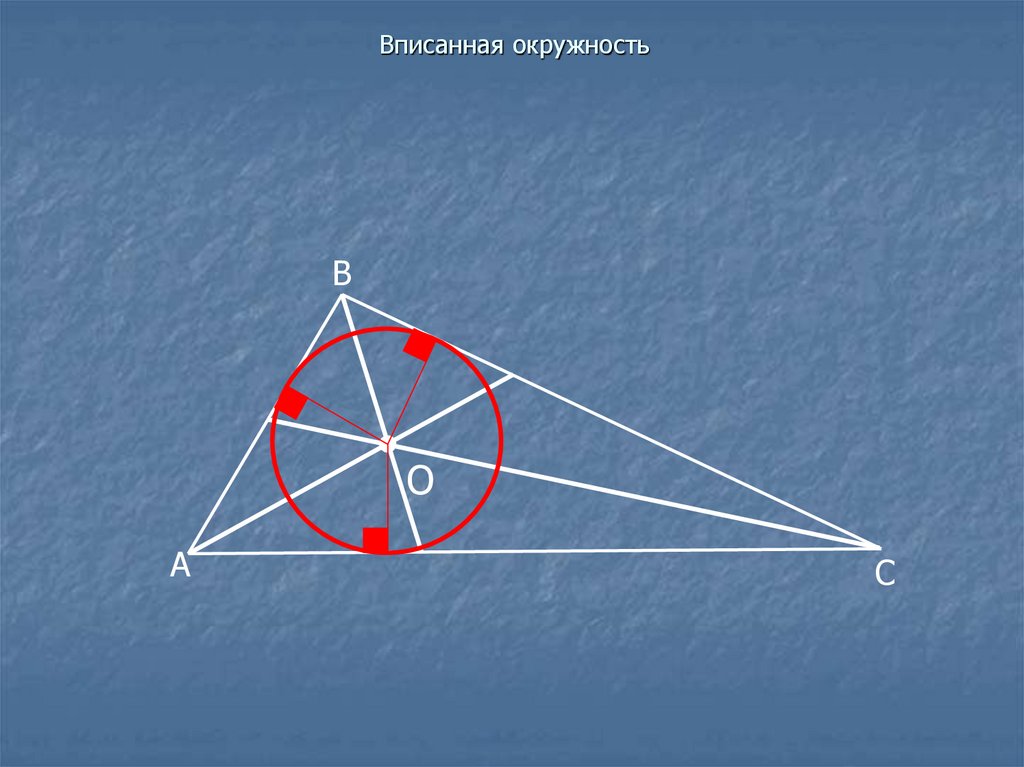
11. Вписанная окружность

В
О
А
С
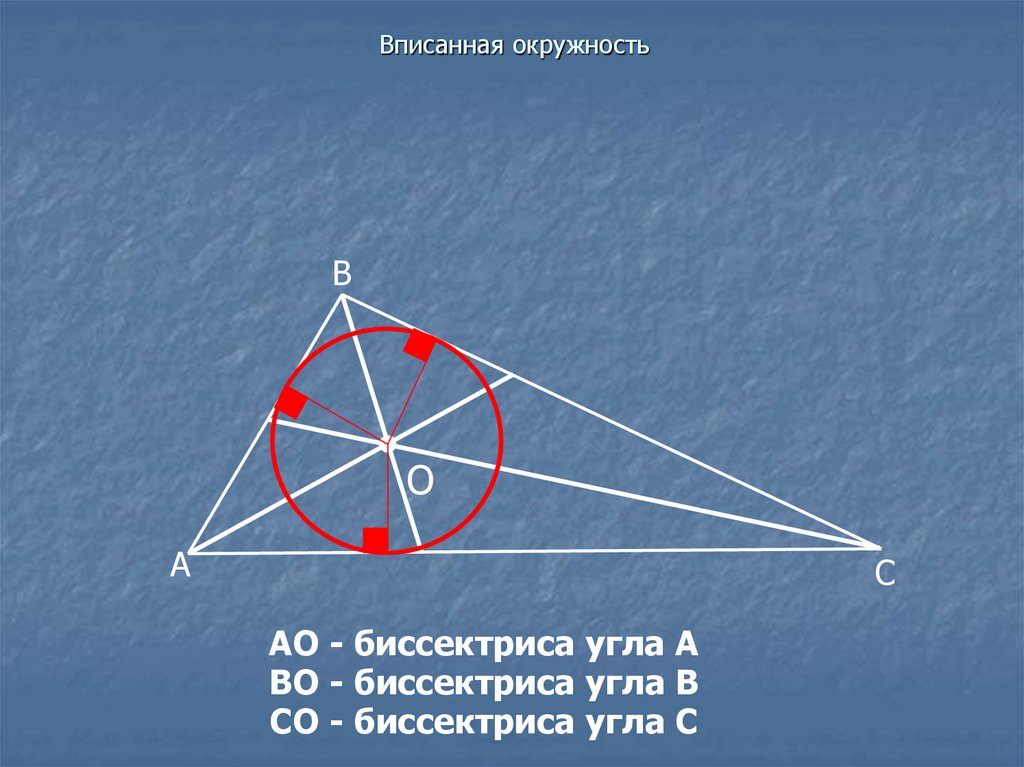
АО - биссектриса угла А
ВО - биссектриса угла В
СО - биссектриса угла С

12. Вписанная окружность

Таким образом,
центр вписанной окружности – это точка
пересечения биссектрис треугольника,
радиус – это расстояние от центра
окружности до сторон треугольника.

13. Вписанная окружность

Для того, чтобы вписать окружность в
треугольник, надо:
1). Найти точку пересечения биссектрис
треугольника (центр окружности);
2). Опустить перпендикуляры из центра
окружности к сторонам треугольника
(радиус окружности);
3). Провести окружность.

14. Вписанная окружность

В
А
С

15. Вписанная окружность

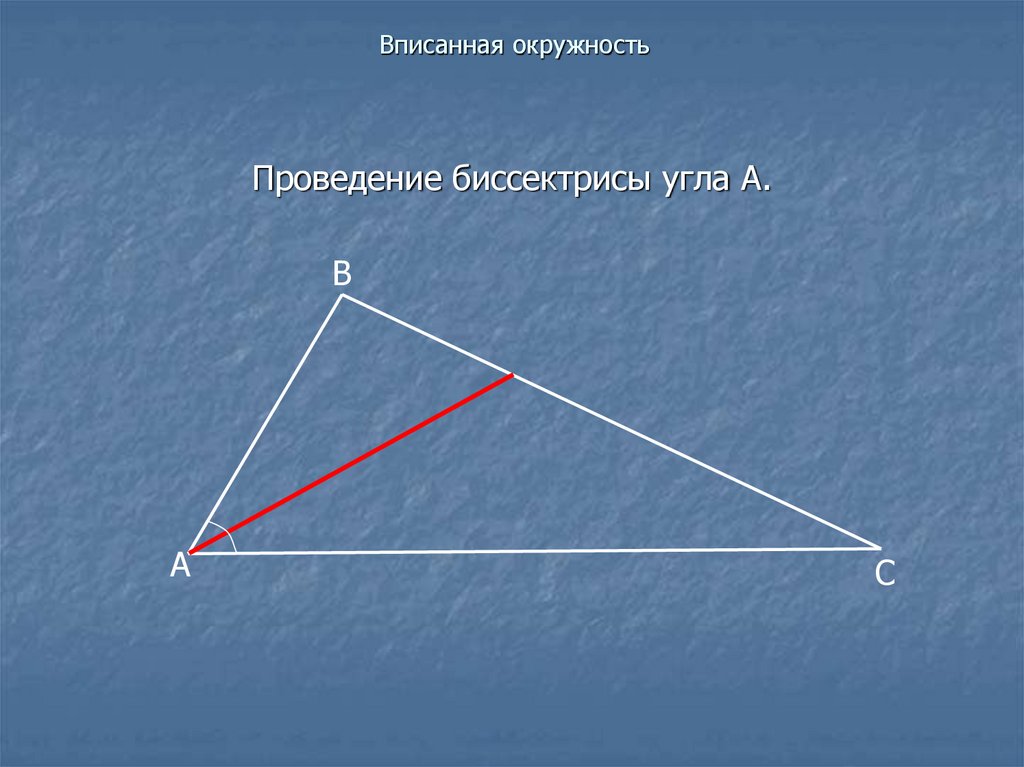
Проведение биссектрисы угла А.
В
А
С

16. Вписанная окружность

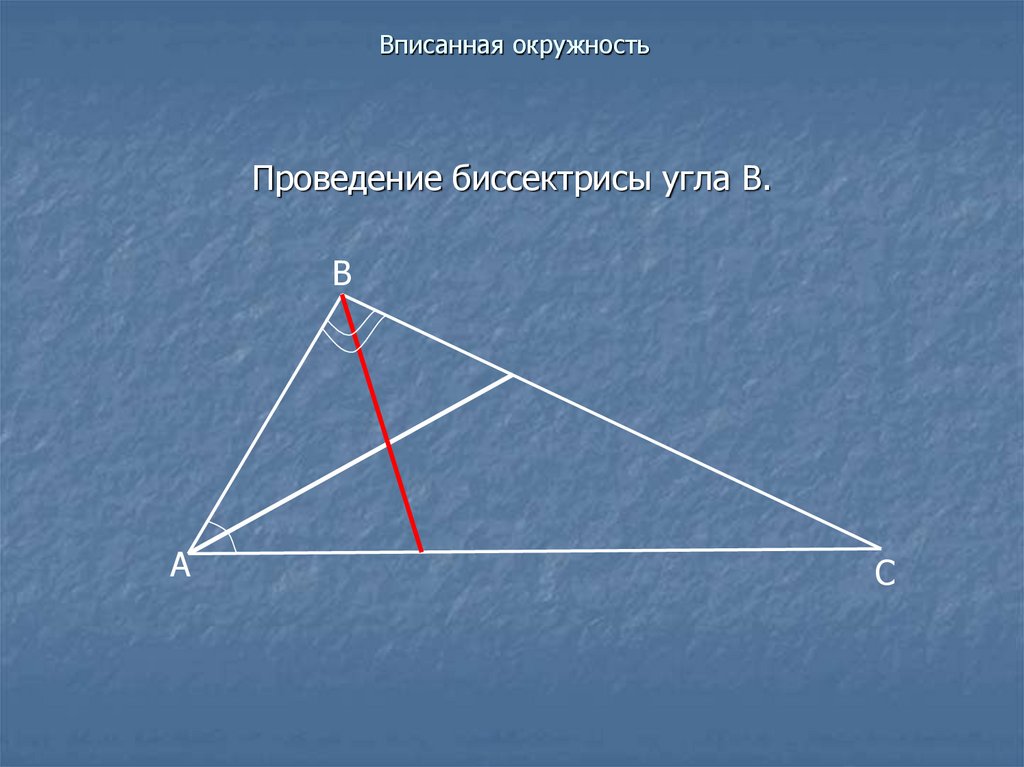
Проведение биссектрисы угла В.
В
А
С

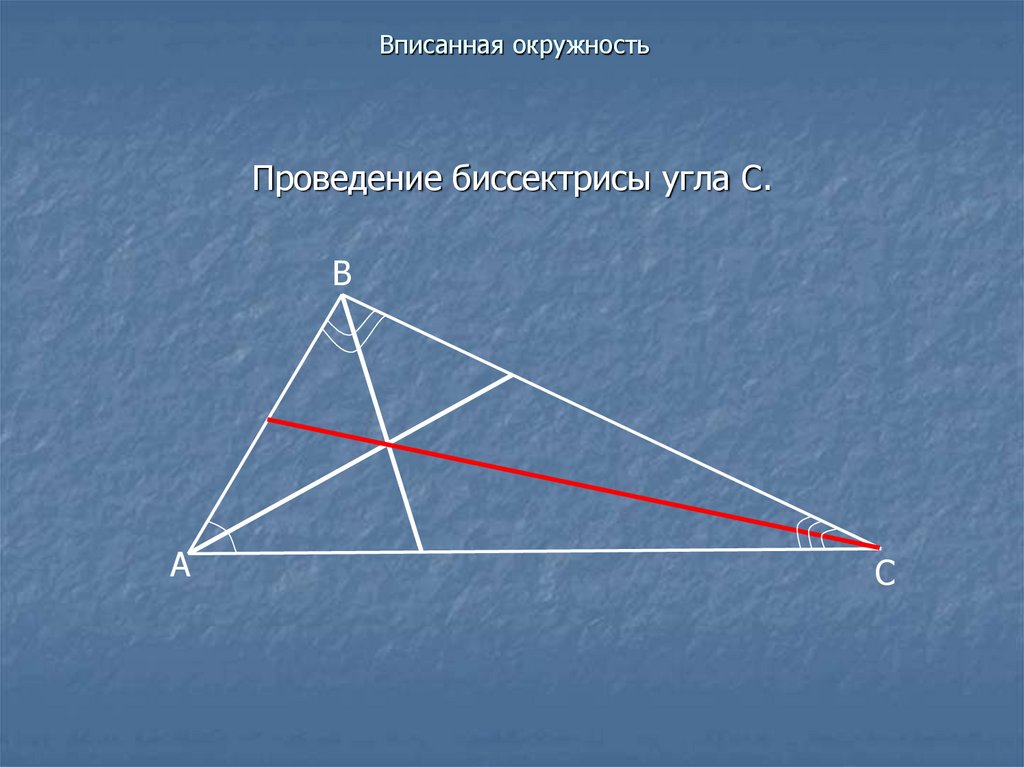
17. Вписанная окружность

Проведение биссектрисы угла С.
В
А
С

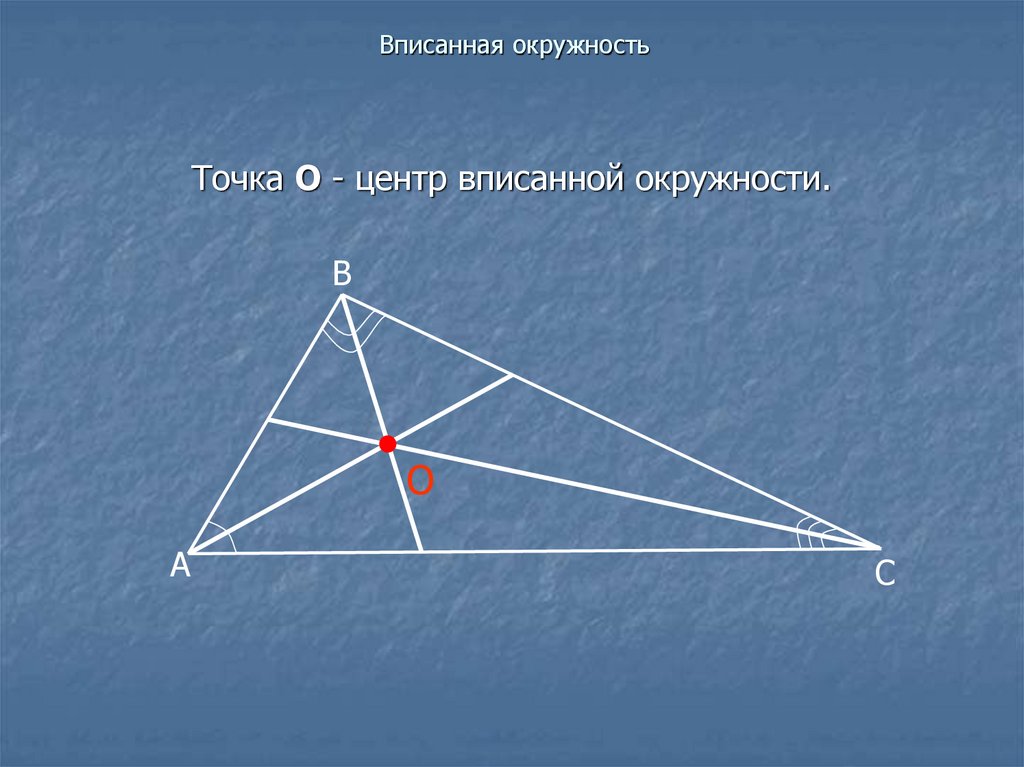
18. Вписанная окружность

Точка О - центр вписанной окружности.
В
О
А
С

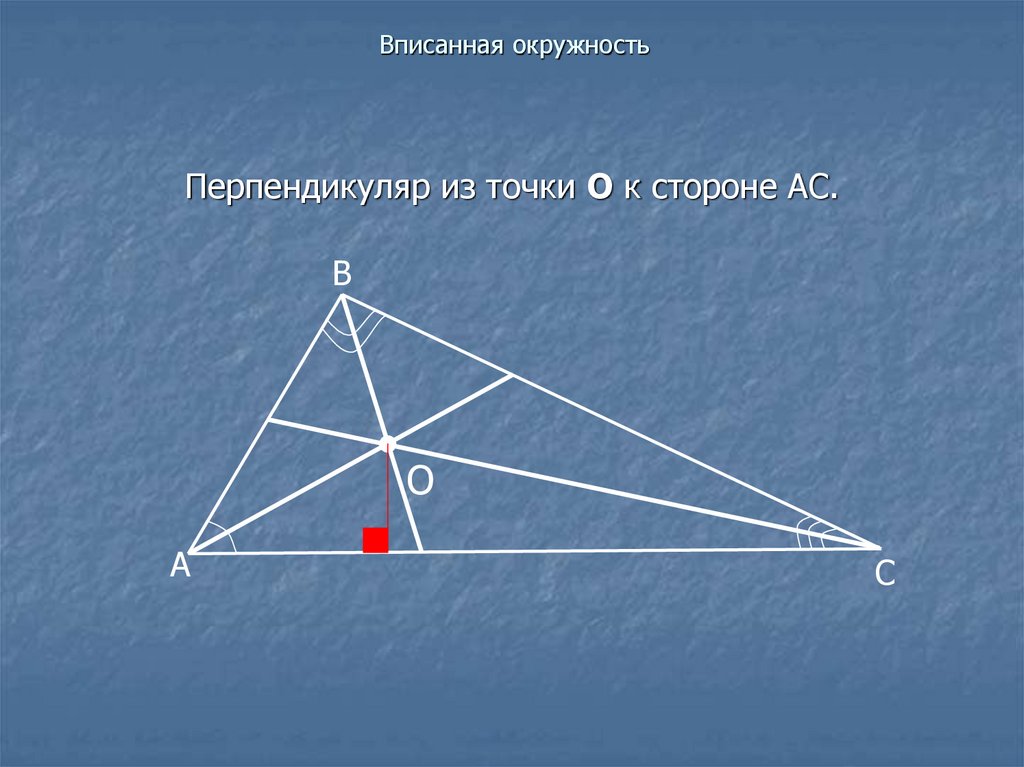
19. Вписанная окружность

Перпендикуляр из точки О к стороне АС.
В
О
А
С

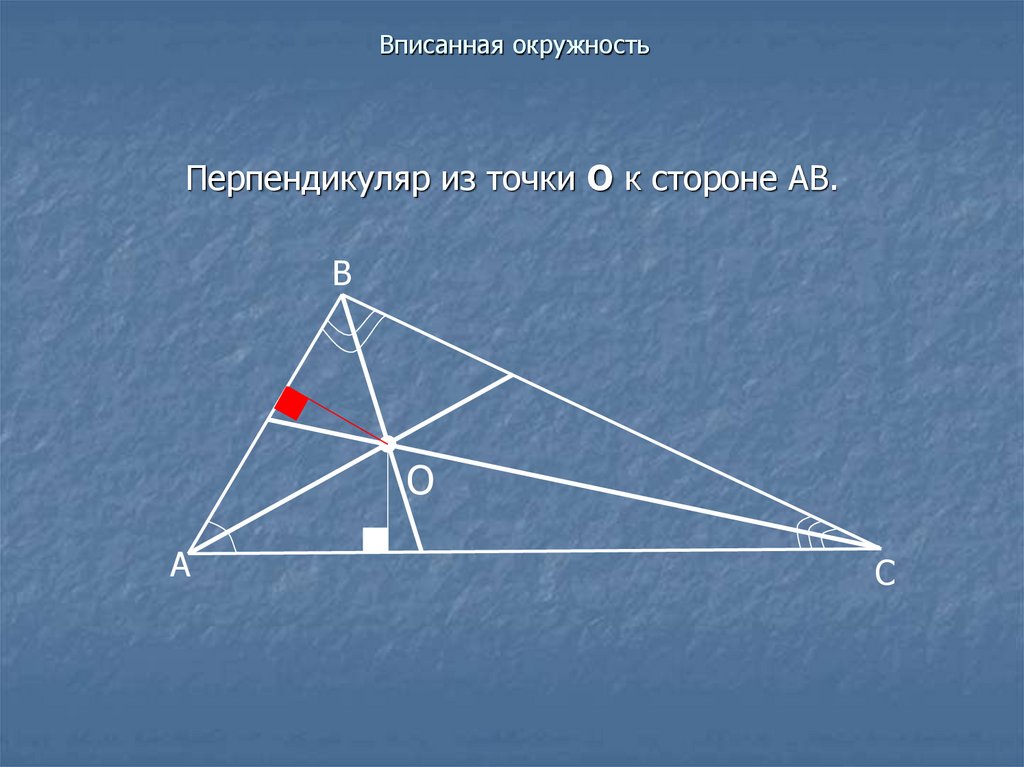
20. Вписанная окружность

Перпендикуляр из точки О к стороне АВ.
В
О
А
С

21. Вписанная окружность

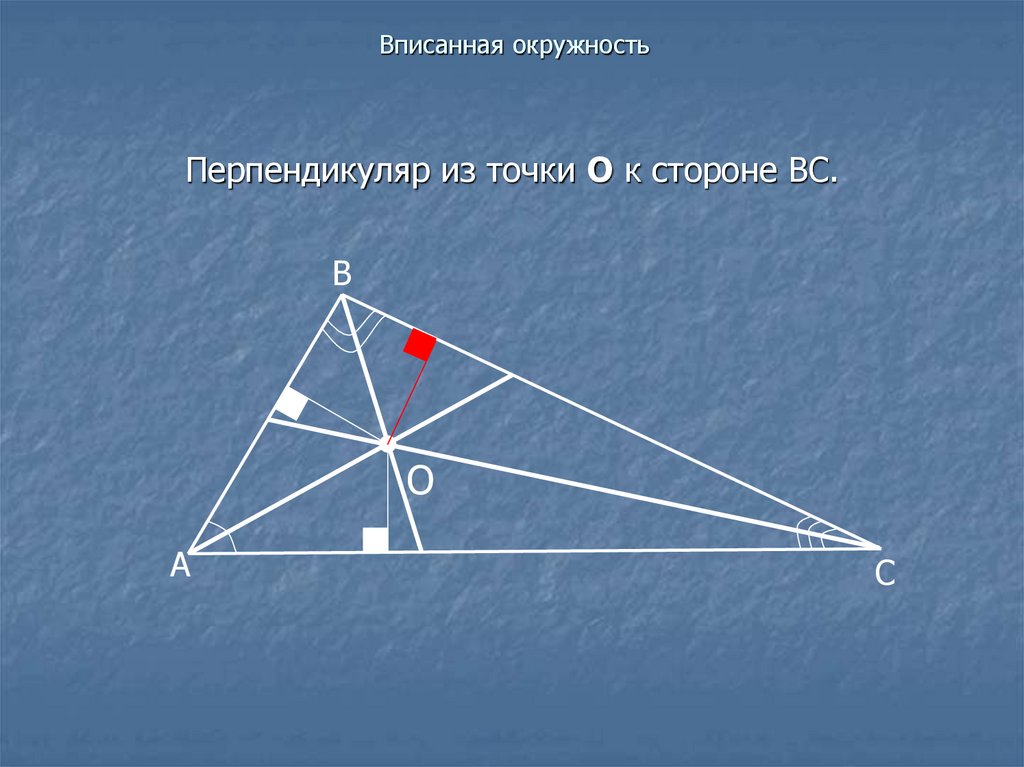
Перпендикуляр из точки О к стороне ВС.
В
О
А
С

22. Вписанная окружность

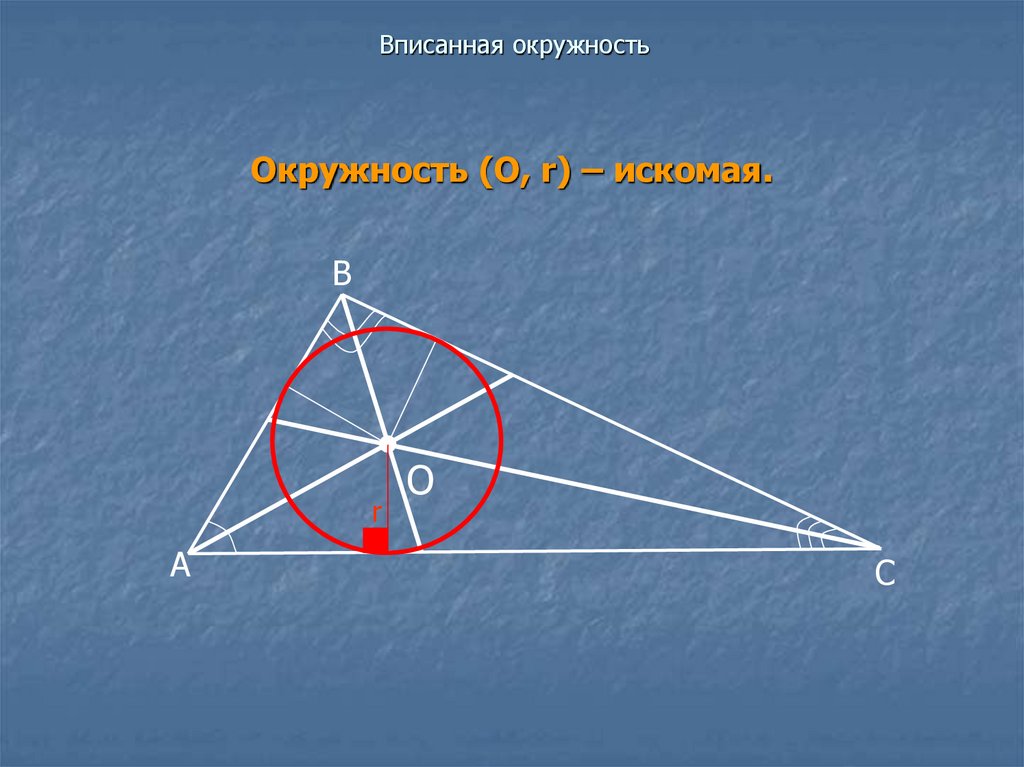
Окружность (О, r) – искомая.
В
r
А
О
С

23. Домашнее задание:

1.
2.
3.
4.
Изучить презентацию или прочитать в
учебнике п.77 на с. 178-180;
Выучить алгоритм построения
вписанной окружности в треугольник +
построить вписанную окружность по
образцу слайдов №14-22 (можно в
д/з);
Решить №689
Д/з прислать к 28.04. до 15.00