Построение таблиц истинности. 9 класс

1.

Построение таблиц
истинности
Информатика
9 класс

2.

• Когда инверсия истинна и когда инверсия
ложна? Если высказывание истинно, то инверсия ложна и, наоборот,
Если высказывание ложно, то инверсия истинна.
• В каком случае дизъюнкция ложна?
Если оба высказывания ложны, то дизъюнкция ложна, в остальных случаях
дизъюнкция будет истинна.
• В каком случае конъюнкция истинна?
Если оба высказывания истинны, то конъюнкция тоже истинна. В остальных
случаях конъюнкция будет ложна.
• В каком случае импликация ложна?
Импликация ложна только в одном случае: если первое высказывание истинно, а
второе ложно. В остальных случаях будет истинна.
• В каком случае эквиваленция истинна и в
каком ложна?
Эквиваленция истинна, если оба высказывания либо истинны, либо ложны. В
остальных случаях ложна.

3.

Понятие таблицы истинности
• Таблица истинности – это таблица, в
которой перечислены все возможные
значения входящих логических переменных
и соответствующие им значения функции.
• Например,
А
В
F(A,B)
0
0
0
0
1
1
1
0
1
0
0
0

4.

Алгоритм построения таблиц
Определить число переменных
Определить число строк в таблице истинности
Записать все возможные значения переменных
Определить количество логических операций и их
порядок
5. Записать логические операции в таблицу
истинности и определить для каждой значение
6. Подчеркнуть значения переменных, для которых
7.
F = 1.
1.
2.
3.
4.

5.

Определение количества строк в
таблице.
q
N= 2
Где N – количество строк в таблице
q – количество логических переменных,
участвующих в данном высказывании.

6.

Порядок выполнения действий
1.
2.
3.
4.
5.
6.
Инверсия (отрицание)
Операции в скобках
Конъюнкция (логическое умножение)
Дизъюнкция (логическое сложение)
Импликация (следование)
Эквиваленция(равенство)

7.

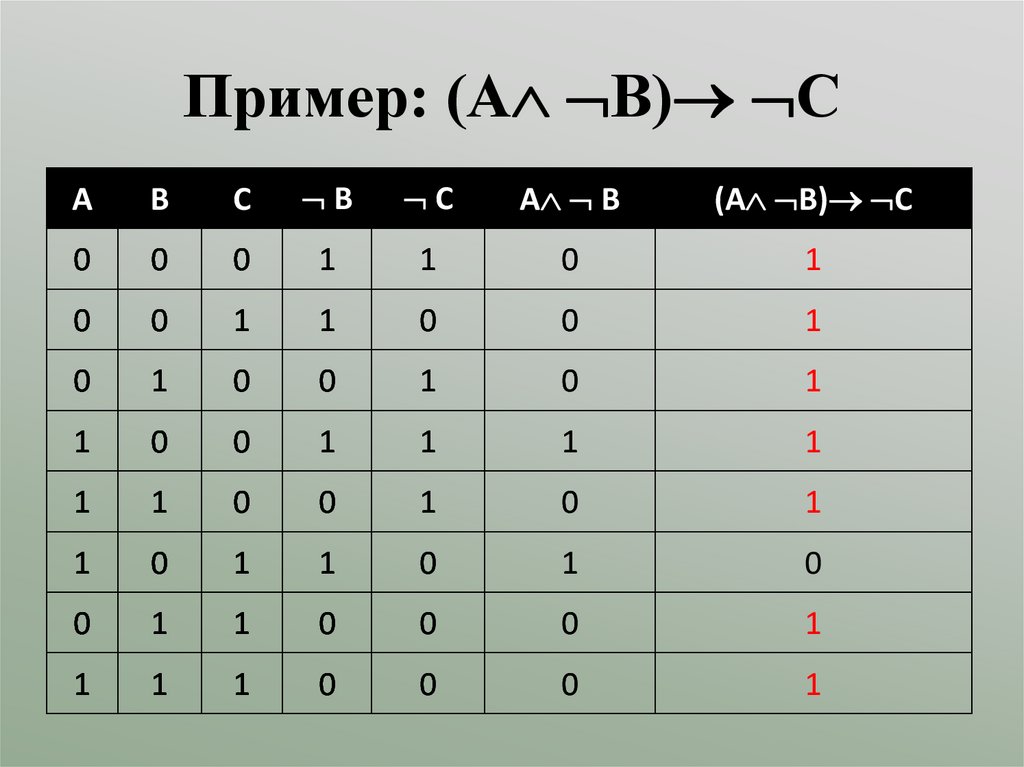
Пример: (А В) С
А
В
С
В
С
А В
(А В) С
0
0
0
1
1
0
1
0
0
1
1
0
0
1
0
1
0
0
1
0
1
1
0
0
1
1
1
1
1
1
0
0
1
0
1
1
0
1
1
0
1
0
0
1
1
0
0
0
1
1
1
1
0
0
0
1

8.

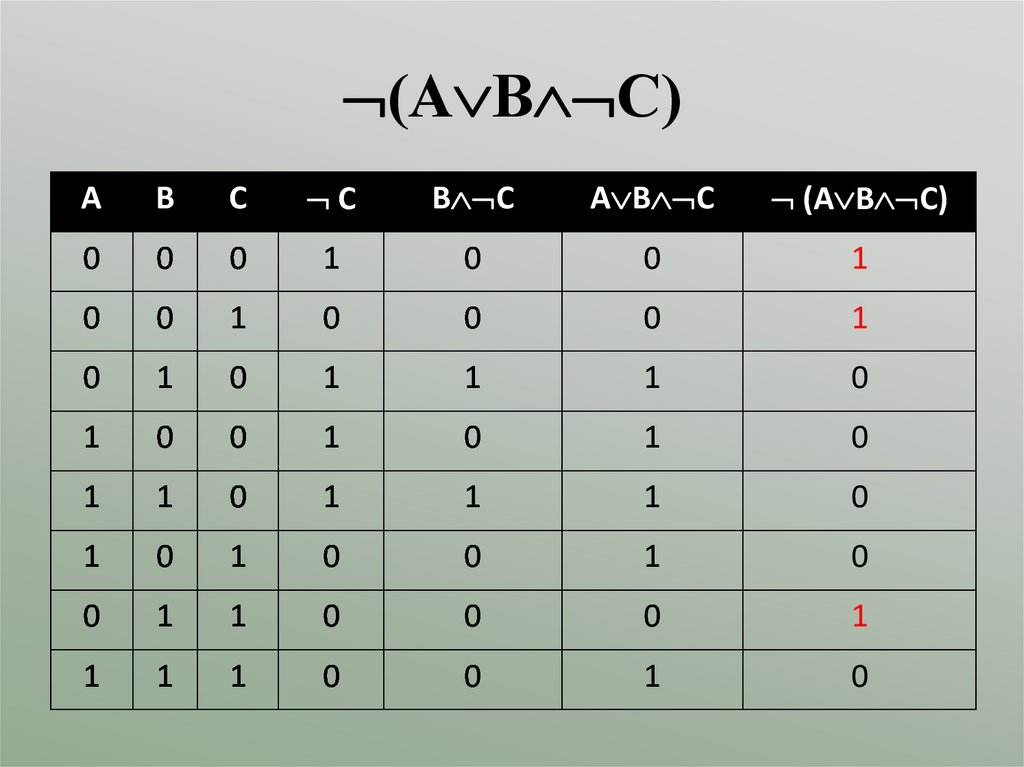
(А В С)
А
В
С
С
В С
А В С
(А В С)
0
0
0
1
0
0
1
0
0
1
0
0
0
1
0
1
0
1
1
1
0
1
0
0
1
0
1
0
1
1
0
1
1
1
0
1
0
1
0
0
1
0
0
1
1
0
0
0
1
1
1
1
0
0
1
0

9.

Самостоятельная работа
Вариант1
1. Расставьте над
символами логических
операций номера в
порядке выполнения
операций при
вычислении выражения.
а) А (В С)
б)А (В С) D
2. Составьте таблицу
истинности
((А В) С)
Вариант2
1. Расставьте над
символами логических
операций номера в
порядке выполнения
операций при
вычислении выражения.
а) А В С)
б) (А В) С
2. Составьте таблицу
истинности А В С

10.

3
4
2
1
2
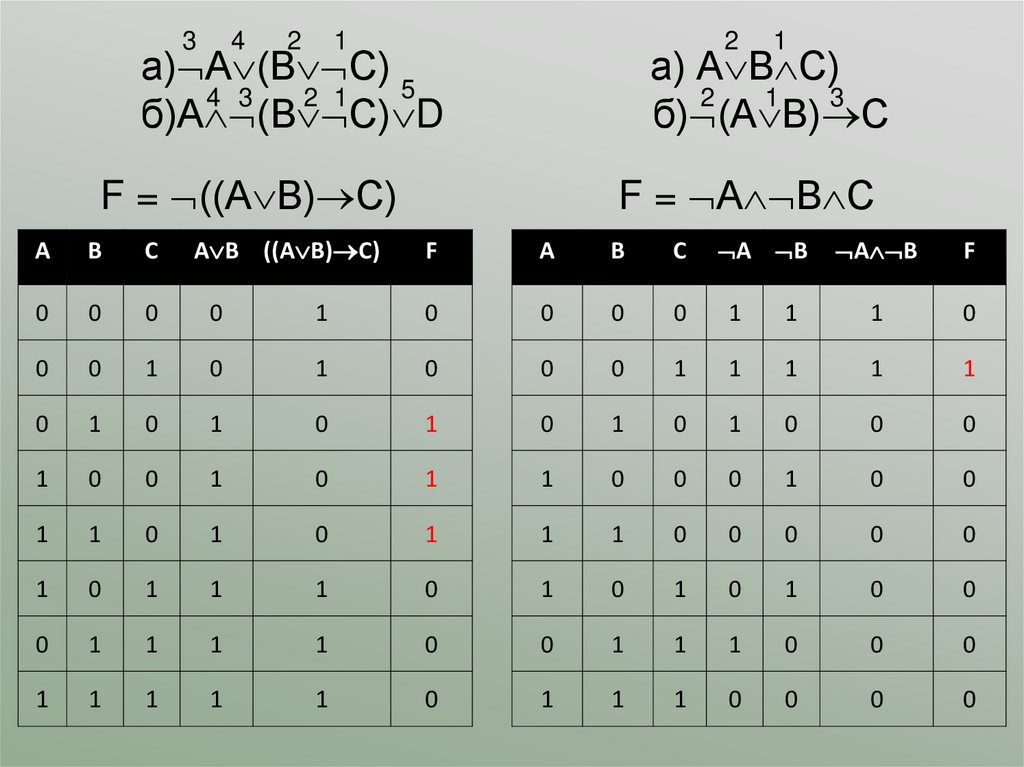
а) А (В С) 5
4 3
2 1
б)А (В С) D
а) А В С)
2
1
3
б) (А В) С
F = ((А В) С)
А
В
С
0
0
0
0
0
0
1
0
1
1
1
F = А В С
А В
F
1
1
0
1
1
1
1
0
1
0
0
0
0
0
0
1
0
0
1
1
0
0
0
0
0
0
1
0
1
0
1
0
0
1
0
0
1
1
1
0
0
0
1
0
1
1
1
0
0
0
0
А В ((А В) С)
A B
F
A
B
C
1
0
0
0
0
1
0
1
0
0
0
1
0
1
0
1
0
1
0
0
1
0
1
1
1
1
0
1
0
1
1
0
1
1
1
0
1
1
1
1
1
1
1

11.

Домашнее задание
Составьте таблицу истинности:
1. (А В) (С В);
2. (А В) ( С А)