Похожие презентации:
Закон распределения дискретной случайной величины (ДСВ)
1. Урок № 81 Тема: Закон распределения дискретной случайной величины (ДСВ)
2.
Цели обучения:10.2.1.5 - знать определение дискретной
и непрерывной случайной величины и
уметь их различать;
10.2.1.6 - составлять таблицу закона
распределения некоторых дискретных
случайных величин
3.
Критерии оценивания:- различает дискретные случайные
величины и непрерывные случайные
величины
- составляет таблицу закона распределения
ДСВ
4. Распределение дискретной случайной величины
Пусть дана случайная величина x имножество значений этой величины {xk}.
Пусть известны вероятности событий
p(xk)-вероятности, что случайная
величина x примет значение xk. Тогда
говорят, что задано дискретное
распределение случайной величины
5.
Важнейшие особенности случайныхвеличин
Распределения случайных величин могут быть
конечными и бесконечными. Примером конечного
распределения может служить распределение
случайной величины x - числа попаданий в цель при
трех выстрелах. Очевидно,что x принимает значения
из множества {0, 1, 2, 3}. Данное распределение
конечное. Примером бесконечного распределения
может служить распределение случайной величины x
- числа выбрасывания двух кубиков до тех пор, пока
не выпадет 12 очков. Очевидно, что теоретически
величина x может принимать сколь угодно большие
значения. Данное распределение бесконечное.
6. Конечное распределение
Если мы имеем конечное распределениеслучайной величины x, принимающей n
значений, то:
n
p( x
k 1
k
) 1
7. Бесконечное распределение
nlim
n
p( x ) p( x ) 1
k 1
k
k 1
k
8.
9. Пример
В урне находится 6 белых и 4 черныхшара. Из нее без возвращения
вынимают 3 шара. Случайная величина
x – число белых шаров среди
вытащенных.
10.
Очевидно, что x может принимать значения 0,1, 2 и 3, т.е. мы имеем дело с конечным
распределением.
Найдем вероятности p(x).
11. P(x):
p( Хp( Х
p( Х
p( Х
4 3 2 1
0)
10 9 8 30
6 4 3 9
1) 3
10 9 8 30
6 5 4 15
2) 3
10 9 8 30
6 5 4 5
3)
10 9 8 30
12. Запишем полученные результаты в таблицу:
X0
1
2
3
p(x)
1/30
9/30
15/30
5/30
Мы получили ряд распределения
случайной величины x.
13. Распределение случайной величины
Пусть случайная величина принимает числовыезначение xk с вероятностями pk соответственно,
причем Σpk=1. Тогда зависимость pk(xk)
называется законом распределения
случайной величины x.
14.
15.
§ 23, стр. 126-127, изучить;№23.1 решить










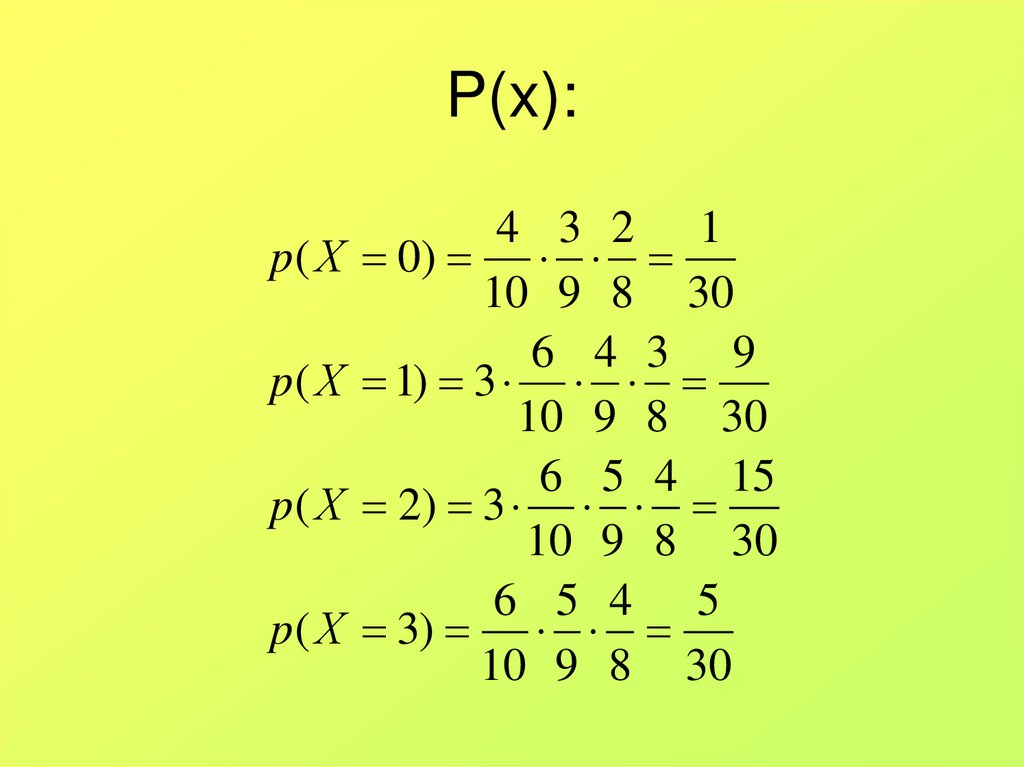




 Математика
Математика








