Вентильные схемы и алгебра логики

1.

ВЕНТИЛЬНЫЕ СХЕМЫ
И
АЛГЕБРА ЛОГИКИ

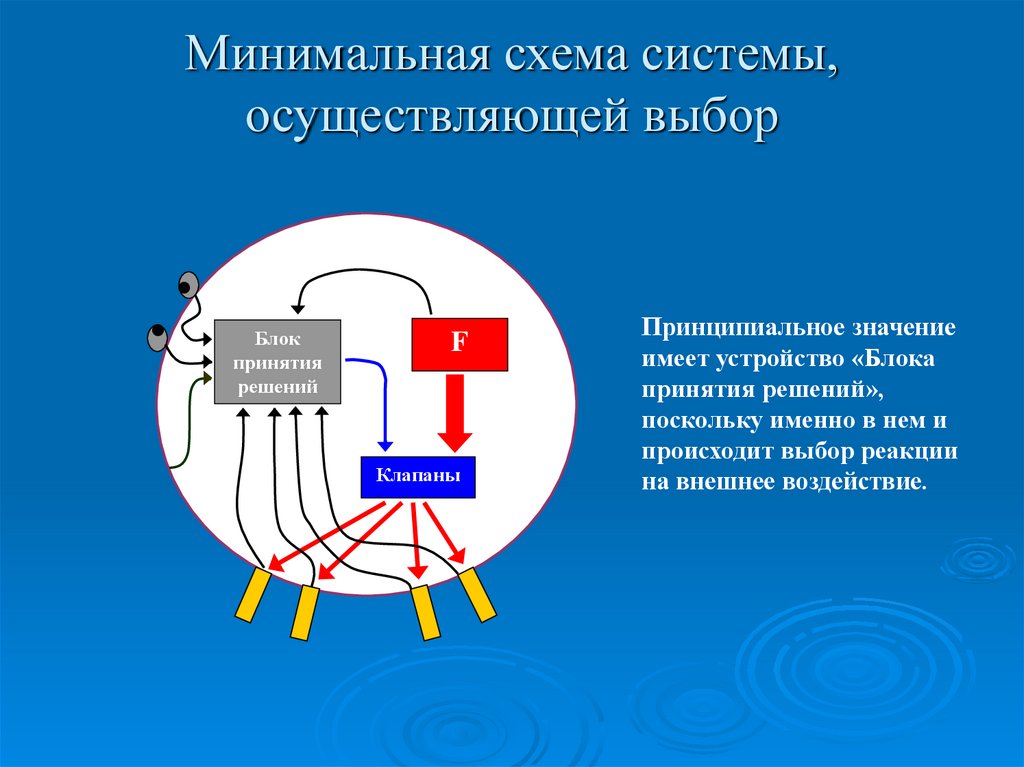
2. Минимальная схема системы, осуществляющей выбор

Блок
принятия
решений
F
Клапаны
Принципиальное значение
имеет устройство «Блока
принятия решений»,
поскольку именно в нем и
происходит выбор реакции
на внешнее воздействие.

3.

ПРЕДСТАВЛЕНИЕ ВХОДНОГО ВОЗДЕЙСТВИЯ И
ОТКЛИКА СИСТЕМЫ В БИНАРНОМ ВИДЕ («ЕСТЬ»/«НЕТ»
ПРЕДСТАВЛЕНИЕ)
Любой вариант поведения и любой выбор конкретного варианта
поведения можно представить в виде комбинации отдельных
бинарных выборов.
Инфузория:
(движется/неподвижна)
(движется: быстро/медленно)
(движется: вперед/назад)
(движется: прямо/поворачивает)
(поворачивает: налево/направо)
Для определенности, наличие сигнала (или отклика системы)
обозначается «1» (истина), а его отсутствие как «0» (ложь).
Это позволяет установить взаимно-однозначное соответствие межу
описанием поведения и исчислением высказываний.

4.

ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
Высказыванием называется всякое утверждение (или всякое
предложение), о котором можно судить, истинно оно или ложно.
“2 > 0” является высказыванием и оно истинно.
“2 < 0” является высказыванием и оно ложно.
“x2 + y2 =z2” высказыванием не является.
Высказывание считается простым, если никакая его часть не
является высказыванием.
Сложные высказывания характеризуются тем, что образованы
из нескольких высказываний с помощью определенных
способов соединения высказываний.
Запись высказываний при помощи символов называют
логической формулой или формулой алгебры высказываний.

5.

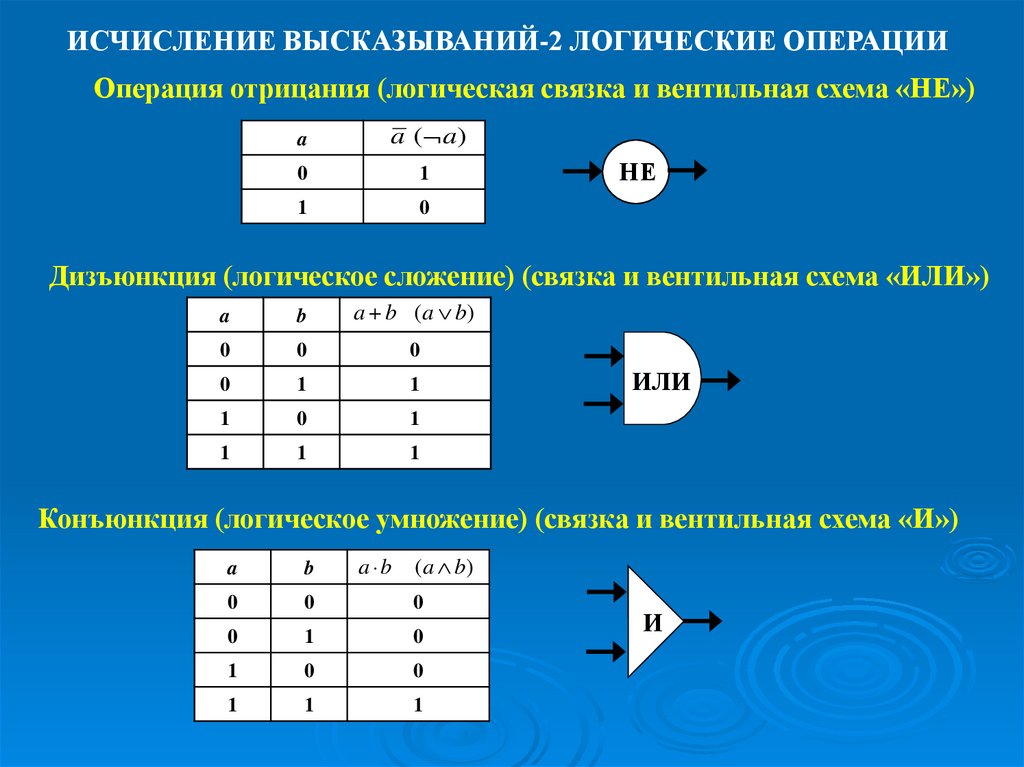
ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ-2 ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Операция отрицания (логическая связка и вентильная схема «НЕ»)
a
a ( a)
0
1
1
0
НЕ
Дизъюнкция (логическое сложение) (связка и вентильная схема «ИЛИ»)
a
b
a b ( a b)
0
0
0
0
1
1
1
0
1
1
1
1
ИЛИ
Конъюнкция (логическое умножение) (связка и вентильная схема «И»)
a b
( a b)
a
b
0
0
0
0
1
0
1
0
0
1
1
1
И

6.

ВАЖНЕЙШИЕ ТАВТОЛОГИИ – ЗАКОНЫ ЛОГИКИ
1. a b b a
11. a 1 1
2. a b b a
3. (a b) c a (b c)
12. a 1 a
4. (a b) c a (b c)
14. a a b a
5. a (b c) a b a c
15. a b b a b
6. a b c (a b) (a c)
16. (a b) b a b
7. a a a
17. ( a b) a b
8. a a a
9. a 0 a
18. a b a b
10. a 0 0
13. a ( a b) a
19. a a 0
20. a a 1
21. a a

7.

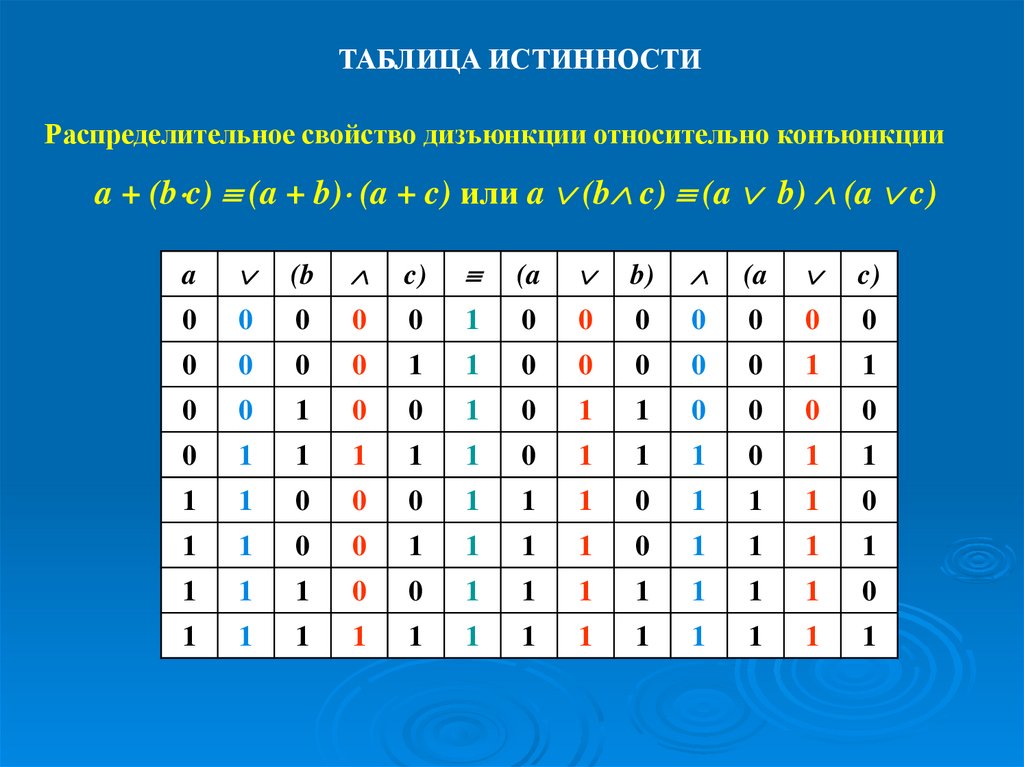
ТАБЛИЦА ИСТИННОСТИ
Распределительное свойство дизъюнкции относительно конъюнкции
a + (b c) (a + b) (a + c) или a (b c) (a b) (a c)
a
(b
c)
(a
b)
(a
c)
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
1
0
0
1
0
0
1
0
1
1
0
0
0
0
0
1
1
1
1
1
0
1
1
1
0
1
1
1
1
0
0
0
1
1
1
0
1
1
1
0
1
1
0
0
1
1
1
1
0
1
1
1
1
1
1
1
0
0
1
1
1
1
1
1
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1

8.

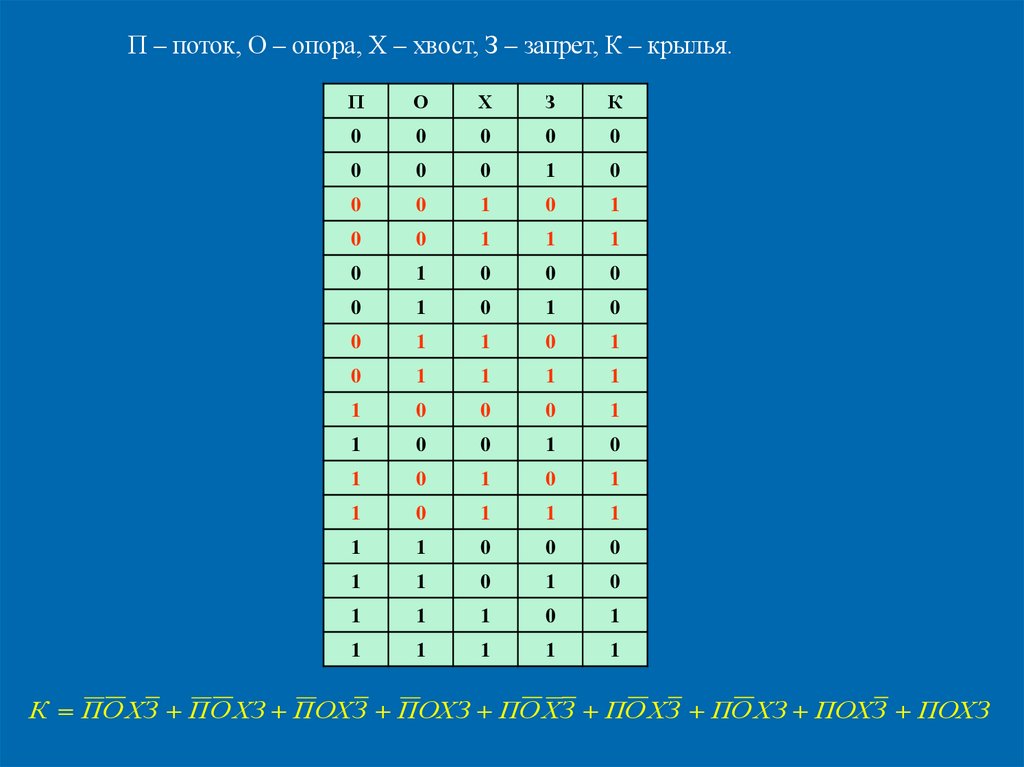
П – поток, О – опора, Х – хвост, З – запрет, К – крылья.
П
О
Х
З
К
0
0
0
0
0
0
0
0
1
0
0
0
1
0
1
0
0
1
1
1
0
1
0
0
0
0
1
0
1
0
0
1
1
0
1
0
1
1
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
1
1
0
1
1
1
1
1
0
0
0
1
1
0
1
0
1
1
1
0
1
1
1
1
1
1
К ПО ХЗ ПО ХЗ ПОХЗ ПОХЗ ПО ХЗ ПО ХЗ ПО ХЗ ПОХЗ ПОХЗ

9.

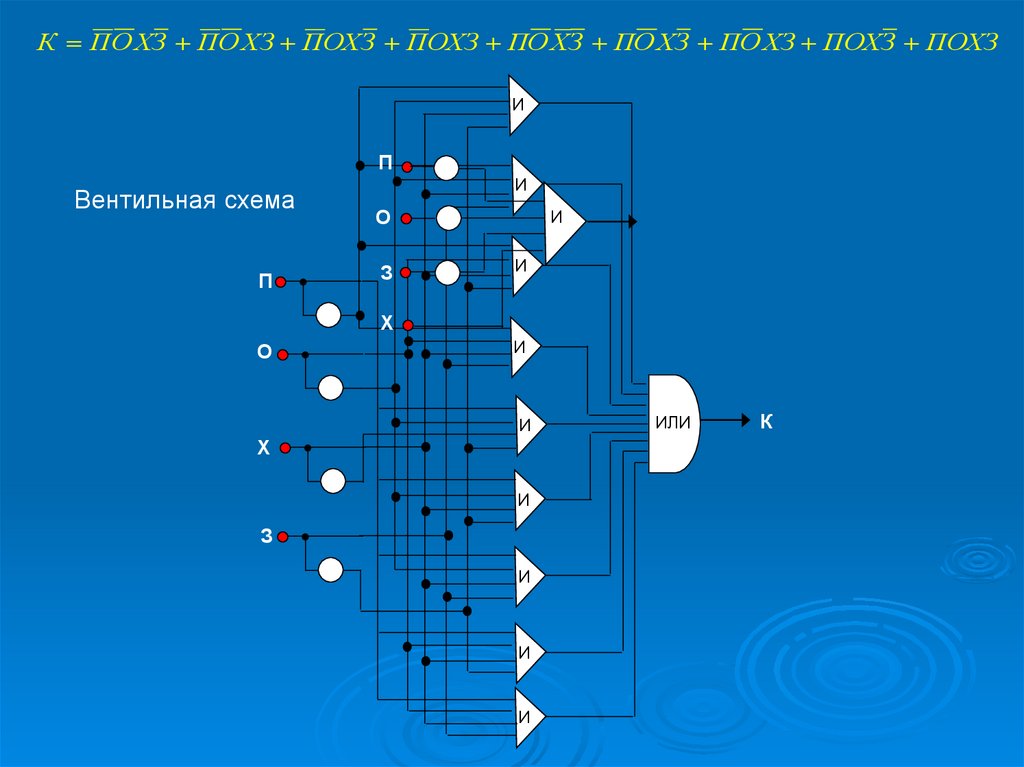
К ПО ХЗ ПО ХЗ ПОХЗ ПОХЗ ПО ХЗ ПО ХЗ ПО ХЗ ПОХЗ ПОХЗ
И
П
Вентильная схема
П
И
О
З
И
И
Х
О
И
И
Х
И
З
И
И
И
ИЛИ
К

10.

1. a (b c) a b a c
К ПО ХЗ ПО ХЗ ПОХЗ ПОХЗ ПО ХЗ ПО ХЗ ПО ХЗ ПОХЗ ПОХЗ
К ( ПО ХЗ ПО ХЗ) ( ПОХЗ ПОХЗ ) ПО ХЗ ( ПО ХЗ ПО ХЗ) ( ПОХЗ ПОХЗ)
К ПО Х (З З ) ПОХ (З З ) ПО ХЗ ПО Х (З З ) ПОХ (З З )
К ПО Х ПОХ ПО ХЗ ПО Х ПОХ
2. a b c ( a b ) ( a c )
3. ( a b ) a b
4. a b a b
5. a ( a b ) a
6. a a b a
7. a b b a b
8. ( a b ) b a b
К ( ПО Х ПОХ ) ПО ХЗ ( ПО Х ПОХ )
К ПХ (О О) ПО ХЗ ПХ (О О)
К ПХ ПО ХЗ ПХ
К ( ПХ ПХ ) ПО ХЗ
9. a b b a
10. a b b a
11. ( a b) c a (b c)
12. ( a b) c a (b c)
13. a a a
14. a a a
15. a a 0
К Х ( П П ) ПО ХЗ
К Х ПО ХЗ
К Х ПО З
16. a a 1
17. a 0 0
18. a 0 a
19. a 1 a
20. a 1 1
21. a a

11.

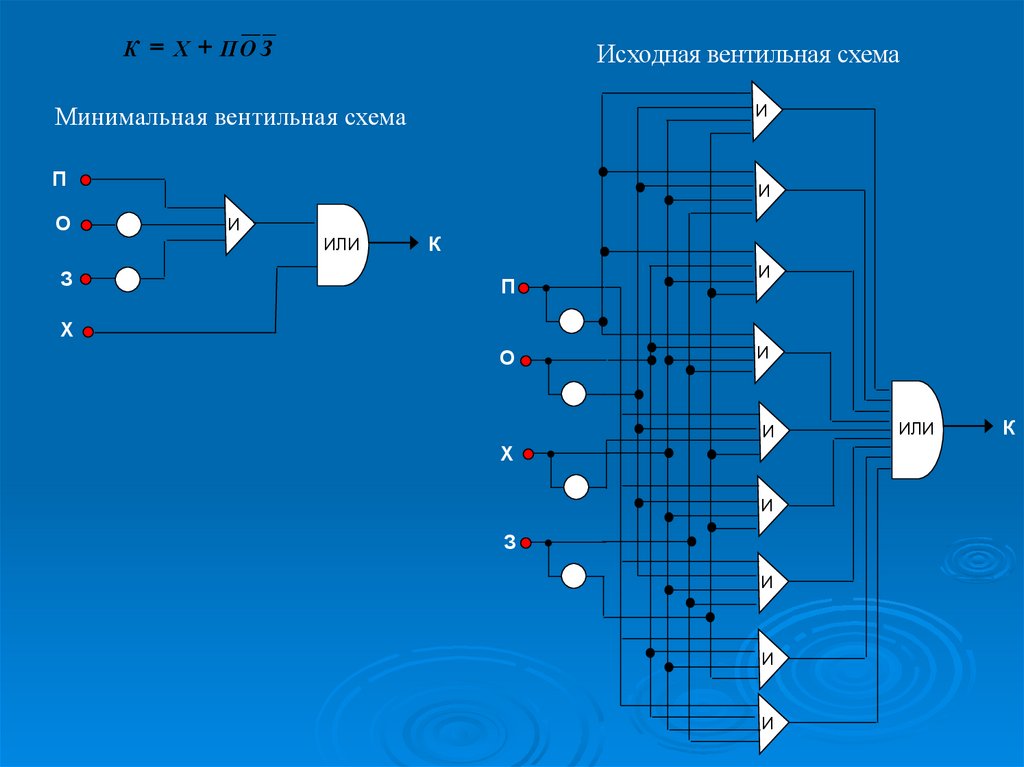
К Х ПО З
Исходная вентильная схема
И
Минимальная вентильная схема
П
О
З
И
И
ИЛИ
К
П
И
Х
О
И
И
Х
И
З
И
И
И
ИЛИ
К

12.

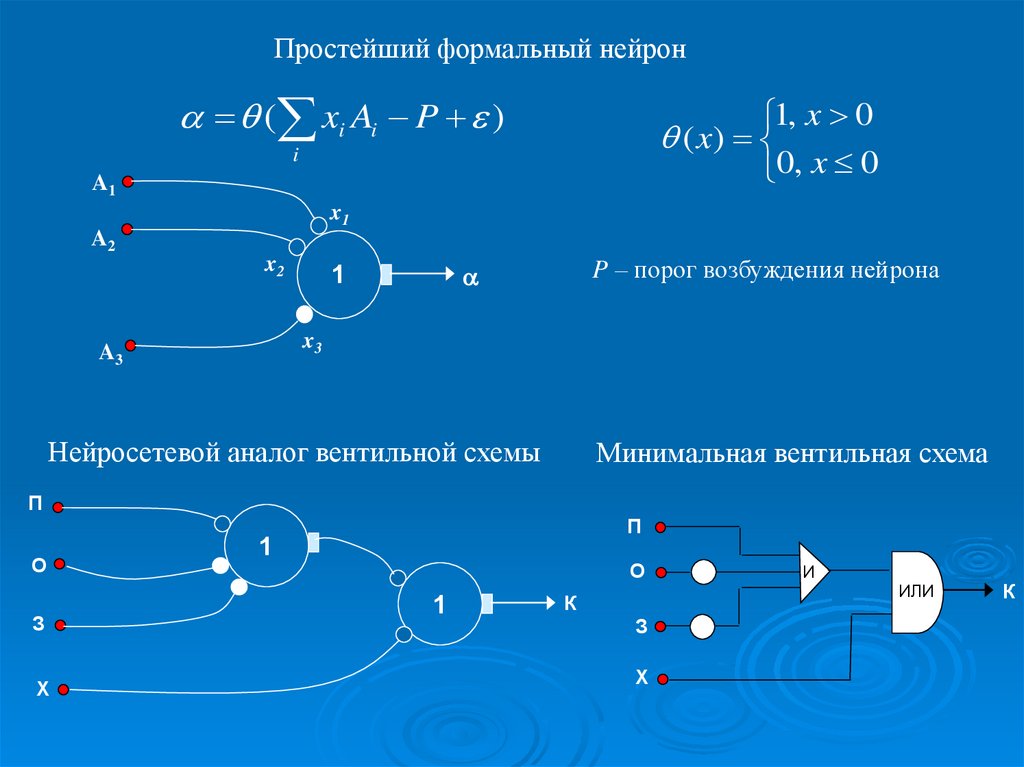
Простейший формальный нейрон
( xi Ai P )
1, x 0
( x)
0, x 0
i
A1
x1
A2
x2
P – порог возбуждения нейрона
1
x3
A3
Нейросетевой аналог вентильной схемы
Минимальная вентильная схема
П
О
З
Х
П
1
О
1
К
З
Х
И
ИЛИ
К

13.

ВХОД: Л – левый "глаз", П – правый "глаз", Г – голод.
ВЫХОД: L – левая "нога", R – правая "нога", B - реверс.
Л
П
Г
L
R
B
0
0
0
1
0
0
0
0
1
1
1
0
0
1
0
0
1
1
0
1
1
1
0
0
1
0
0
1
0
1
1
0
1
0
1
0
1
1
0
1
1
1
1
1
1
1
1
0
Этот вариант получается
сразу, без преобразований.
Как?
L ( ЛПГ ЛПГ )
Варианты, преобразуемые друг в друга. Как? Найти.
L ЛП ПГ ЛГ
L Л (Г П ) Л (Г П)
R ПГ ПГ ПЛ
R ПГ ПГ ЛГ
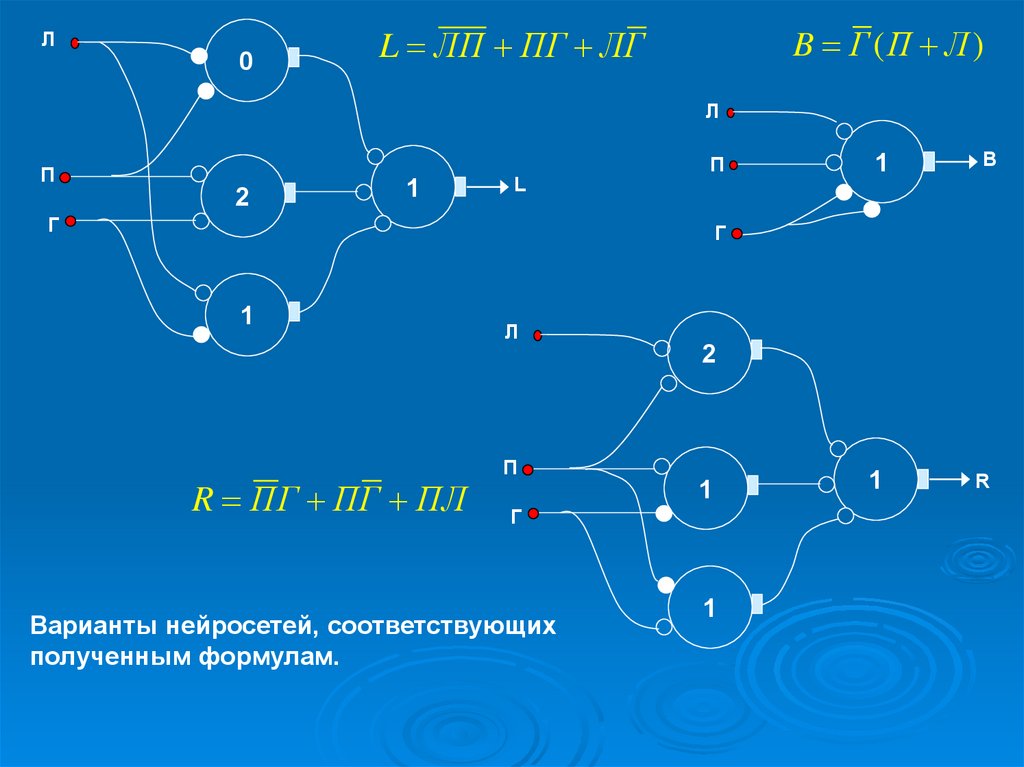
B Г (П Л )

14.

Л
0
B Г (П Л )
L ЛП ПГ ЛГ
Л
П
П
2
1
1
B
L
Г
Г
1
Л
2
R ПГ ПГ ПЛ
П
1
Г
Варианты нейросетей, соответствующих
полученным формулам.
1
1
R

15.

Существуют задачи выживания, решение которых не
может быть обеспечено вентильными схемами.
Например. Мышь, управляемая вентильной схемой
увидела кошку. В естественном ужасе она
поворачивается к ней хвостом чтобы убежать. Но!! Как
только кошка исчезает из поля зрения мышь начинает
спокойно пастись дальше. Чего-то мыши не хватает,
чтобы выжить. Чего?
Правильно! Памяти и умения ее использовать. Это
реализуется в системах называемых конечными
автоматами.

16.

Продолжение следует…