Похожие презентации:
Системы счисления (Лекция 02)
1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ
СИСТЕМЫ СЧИСЛЕНИЯ1
2. КРУГЛЫЕ ЧИСЛА
«Из«Из подъезда
подъезда вышел
вышел человек
человек лет
лет около
около 49,
49, пройдя
пройдя по
по улице
улице
метров
метров 147,
147, он
он зашел
зашел вв магазин,
магазин, купил
купил там
там две
две семерки
семерки яиц
яиц и
и
пошел
пошел дальше…»
дальше…»
(неточная
(неточная цитата
цитата из
из книги
книги С.В.
С.В. Фомина
Фомина «Системы
«Системы счисления»)
счисления»)
Когда
Когда мы
мы оцениваем
оцениваем какую-то
какую-то величину
величину —
— возраст
возраст человека,
человека,
расстояние
расстояние ии т.
т. п.
п. —
— приблизительно,
приблизительно, то
то мы
мы всегда
всегда пользуемся
пользуемся
круглыми
круглыми числами
числами ии говорим
говорим обычно
обычно «метров
«метров 150»,
150», «человек
«человек лет
лет 50»
50»
ии т.
т. п.
п.
Круглыми
Круглыми числами
числами проще
проще оперировать,
оперировать, чем
чем некруглыми,
некруглыми, их
их легче
легче
запомнить,
запомнить, сс ними
ними удобней
удобней производить
производить арифметические
арифметические действия.
действия.
Например,
Например, ни
ни для
для кого
кого не
не составит
составит труда
труда умножить
умножить вв уме
уме 100
100 на
на 200,
200,
если
если же
же нужно
нужно перемножить
перемножить два
два некруглых
некруглых трехзначных
трехзначных числа,
числа,
скажем
скажем 147
147 ии 343,
343, то
то далеко
далеко не
не всякий
всякий сделает
сделает это
это без
без карандаша
карандаша ии
бумаги.
бумаги.
2
3. КРУГЛЫЕ ЧИСЛА
ГоворяГоворя оо круглых
круглых числах,
числах, мы
мы обычно
обычно не
не отдаем
отдаем себе
себе отчета
отчета вв том,
том, что
что
деление
деление чисел
чисел на
на круглые
круглые ии некруглые,
некруглые, по
по существу,
существу, условно
условно ии что
что
одно
одно ии то
то же
же число
число может
может быть
быть круглым
круглым или
или некруглым
некруглым вв
зависимости
зависимости от
от того,
того, какой
какой системой
системой записи
записи чисел
чисел или,
или, как
как обычно
обычно
говорят,
говорят, какой
какой системой
системой счисления
счисления мы
мы пользуемся.
пользуемся.
Чтобы
Чтобы разобраться
разобраться вв этом
этом вопросе,
вопросе, посмотрим
посмотрим прежде
прежде всего,
всего, что
что
представляет
представляет собой
собой наша
наша обычная
обычная десятичная
десятичная система
система счисления,
счисления,
которой
которой мы
мы все
все пользуемся.
пользуемся. В
В этой
этой системе
системе каждое
каждое целое
целое
положительное
положительное число
число представляется
представляется вв виде
виде суммы
суммы единиц,
единиц,
десятков,
десятков, сотен
сотен ии т.
т. д.,
д., т.
т. е.
е. вв виде
виде суммы
суммы различных
различных степеней
степеней числа
числа
10
10 сс коэффициентами,
коэффициентами, которые
которые могут
могут принимать
принимать значения
значения от
от 00 до
до 99
включительно.
включительно.
(2014)
= 2*1033+0*1022+1*1011+4*1000
(2014)10
10 = 2*10 +0*10 +1*10 +4*10
3
4. КРУГЛЫЕ ЧИСЛА
(7)10=(10)77
10
22
(49)10
=(7
)10
=(100)77
10
10
22
(147)10
=(3*7
)10
=(300)77
10
10
(10)10
=(13)77
10
10
10 - круглое число, потому что оно принято за основание
системы
системы счисления!
счисления!
4
5. СИСТЕМЫ СЧИСЛЕНИЯ
СИСТЕМА СЧИСЛЕНИЯ - СОВОКУПНОСТЬСОВОКУПНОСТЬ
ПРИЕМОВ
ПРИЕМОВ ПРЕДСТАВЛЕНИЯ,
ПРЕДСТАВЛЕНИЯ, ОБОЗНАЧЕНИЯ
НАТУРАЛЬНЫХ
НАТУРАЛЬНЫХ ЧИСЕЛ.
ЧИСЕЛ.
5
6.
СИСТЕМЫ СЧИСЛЕНИЯПОЗИЦИОННЫЕ
НЕПОЗИЦИОННЫЕ
6
7. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
ВВ позиционных
позиционных системах
системах счисления вес цифры
(т.
(т. е.
е. ее
ее вклад
вклад вв число)
число) зависит
зависит от
от ее
ее позиции
позиции вв записи
записи числа.
числа.
Арабская
Арабская система
система счисления
счисления -- позиционная:
9999
9999 –– веса
веса цифры
цифры «9»
«9» различны.
различны.
Римская
Римская система
система счисления
счисления -- непозиционная:
непозиционная:
LXXXII
LXXXII -- восемьдесят
восемьдесят два
два
(L
(L в любой позиции пятьдесят,
Х
Х вв любой
любой позиции десять,
десять,
II в любой
любой позиции один).
один).
7
8. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
ОСНОВАНИЕ СИСТЕМЫ СЧИСЛЕНИЯ - количествосимволов (цифр), используемых для записи числа.
Обозначение: q - основание системы счисления.
Если
Если qq =10,
=10, то используются цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
22
11
00
(651)10
=
6*10
+5*10
+1*10
10
(651)77 = (6*722+5*711+1*700)10
=(336)10
10
10
8
9. ИСТОРИЯ
Первоначальный аппарат счета, причина победыдесятичной системы счисления в процессе
исторического развития
9
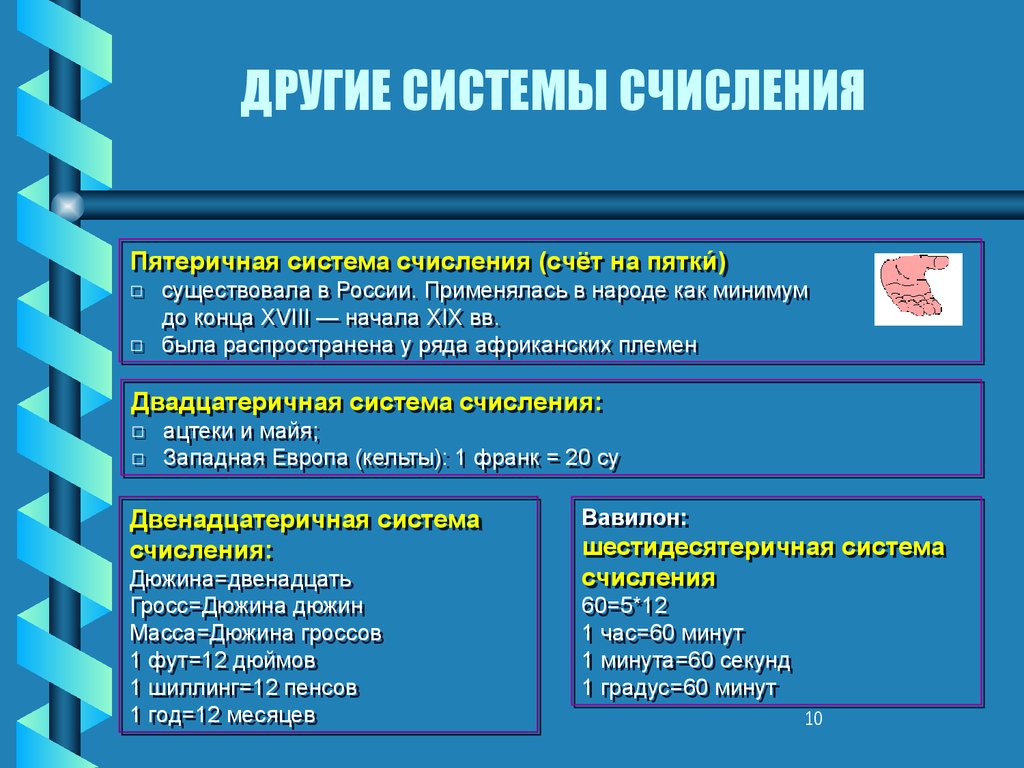
10. ДРУГИЕ СИСТЕМЫ СЧИСЛЕНИЯ
ПятеричнаяПятеричная система
система счисления
счисления (cчёт
(cчёт на
на пятки
пяткии и ))
□□ существовала
существовала вв России.
России. Применялась
Применялась вв народе
народе как
как минимум
минимум
до
до конца
конца XVIII
XVIII —
— начала
начала XIX
XIX вв.
вв.
□□ была
была распространена
распространена уу ряда
ряда африканских
африканских племен
племен
Двадцатеричная
Двадцатеричная система
система счисления:
счисления:
□□ ацтеки
ацтеки ии майя;
майя;
□□ Западная
Западная Европа
Европа (кельты):
(кельты): 11 франк
франк == 20
20 су
су
Двенадцатеричная
Двенадцатеричная система
система
счисления:
счисления:
Дюжина=двенадцать
Дюжина=двенадцать
Гросс=Дюжина
Гросс=Дюжина дюжин
дюжин
Масса=Дюжина
Масса=Дюжина гроссов
гроссов
11 фут=12
фут=12 дюймов
дюймов
11 шиллинг=12
шиллинг=12 пенсов
пенсов
11 год=12
год=12 месяцев
месяцев
Вавилон:
Вавилон:
шестидесятеричная
шестидесятеричная система
система
счисления
счисления
60=5*12
60=5*12
11 час=60
час=60 минут
минут
11 минута=60
минута=60 секунд
секунд
11 градус=60
градус=60 минут
минут
10
11. ПОЧЕМУ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ ИСПОЛЬЗУЕТСЯ ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ?
двоичная система счисления реализуется с помощьютехнических устройств с двумя устойчивыми
состояниями;
представление информации посредством только двух
состояний надежно и помехоустойчиво;
возможно применение булевой алгебры для выполнения
логических преобразований информации;
двоичная арифметика намного проще десятичной.
Недостаток
Недостаток двоичной
двоичной системы
системы счисления:
счисления: длинная
длинная запись
запись
числа
числа
11
12. ПОЧЕМУ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ ИСПОЛЬЗУЮТСЯ ВОСЬМЕРИЧНАЯ И ШЕСТНАДЦАТЕРИЧНАЯ СИСТЕМЫ СЧИСЛЕНИЯ?
От этих систем счисления легко перейти к двоичной иобратно;
Эти системы счисления ближе к десятичной
и поэтому более удобны для человека;
Запись чисел в этих системах короче, чем в двоичной.
12
13. Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему
ПЕРЕВОД ВОСЬМЕРИЧНЫХ И ШЕСТНАДЦАТЕРИЧНЫХЧИСЕЛ В ДВОИЧНУЮ СИСТЕМУ
Так
Так как
как основания
основания восьмеричной
восьмеричной ии шестнадтериной
шестнадтериной систем
систем
счисления
счисления являются
являются степенями
степенями двойки
двойки (16=2
(16=244,, 8=2
8=233),
), то
то
перевод
перевод чисел
чисел из
из этих
этих систем
систем счисления
счисления вв двоичную
двоичную ии
наоборот
наоборот прост
прост ии основан
основан на
на методах
методах триад
триад ии тетрад.
тетрад.
ПЕРЕВОД
ПЕРЕВОД ВОСЬМЕРИЧНЫХ
ВОСЬМЕРИЧНЫХ И
И ШЕСТНАДЦАТЕРИЧНЫХ
ШЕСТНАДЦАТЕРИЧНЫХ ЧИСЕЛ
ЧИСЕЛ
В
В ДВОИЧНУЮ
ДВОИЧНУЮ СИСТЕМУ:
СИСТЕМУ:
каждую
каждую цифру
цифру заменить
заменить эквивалентной
эквивалентной ей
ей двоичной
двоичной триадой
триадой
(тройкой
(тройкой цифр)
цифр) для
для восьмеричных
восьмеричных чисел
чисел или
или тетрадой
тетрадой
(четверкой
(четверкой цифр)
цифр) для
для шестнадцатеричных
шестнадцатеричных чисел.
чисел.
13
14. Перевод из двоичной системы в восьмеричную или шестнадцатеричную
ПЕРЕВОД ИЗ ДВОИЧНОЙ СИСТЕМЫВ ВОСЬМЕРИЧНУЮ ИЛИ ШЕСТНАДЦАТЕРИЧНУЮ
Чтобы
Чтобы перевести
перевести число
число из
из двоичной
двоичной системы
системы вв восьмеричную
восьмеричную
или
или шестнадцатеричную,
шестнадцатеричную, его
его нужно
нужно разбить
разбить влево
влево ии вправо
вправо от
от
запятой
запятой на
на триады
триады (для
(для восьмеричной)
восьмеричной) или
или тетрады
тетрады (для
(для
шестнадцатеричной)
шестнадцатеричной) ии каждую
каждую такую
такую группу
группу заменить
заменить
соответствующей
соответствующей восьмеричной
восьмеричной (шестнадцатеричной)
(шестнадцатеричной)
цифрой.
цифрой.
Если
Если крайние
крайние триады
триады (тетрады)
(тетрады) оказались
оказались неполными,
неполными, они
они
дополняются
дополняются нулями
нулями вв целой
целой части
части числа
числа –– слева,
слева, вв дробной
дробной
части
части (после
(после запятой)
запятой) -- справа.
справа.
14
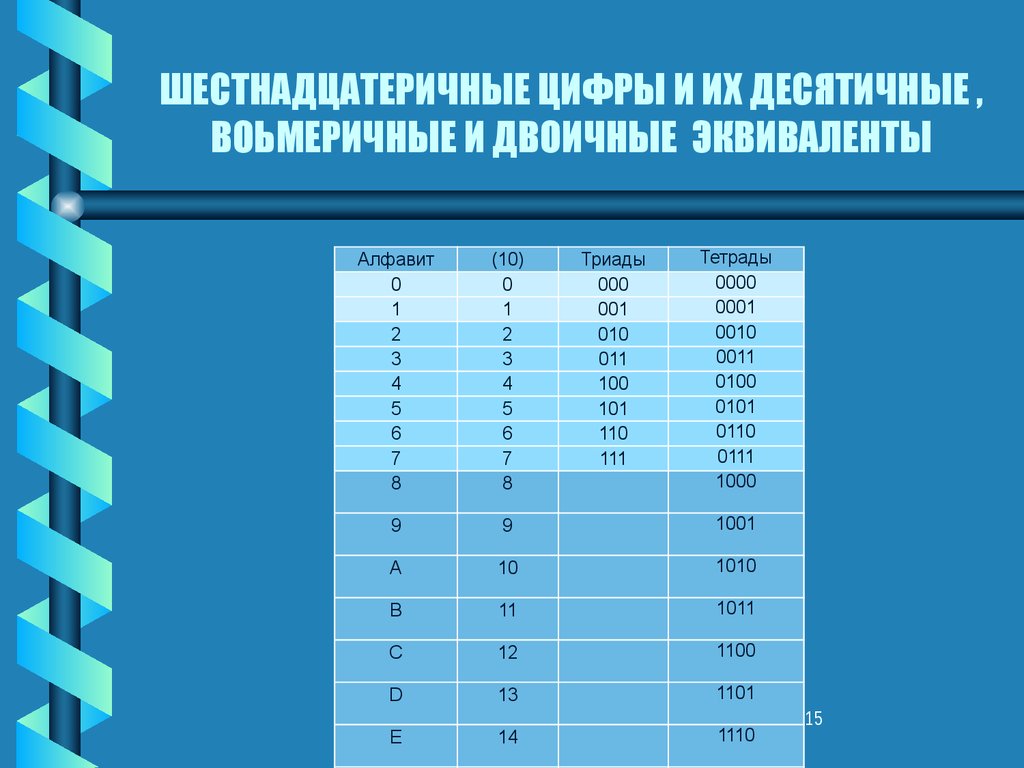
15. ШЕСТНАДЦАТЕРИЧНЫЕ ЦИФРЫ И ИХ ДЕСЯТИЧНЫЕ , ВОЬМЕРИЧНЫЕ И ДВОИЧНЫЕ ЭКВИВАЛЕНТЫ
Триады000
001
010
011
100
101
110
111
Тетрады
0000
0001
0010
0011
0100
0101
0110
0111
1000
Алфавит
0
1
2
3
4
5
6
7
8
(10)
0
1
2
3
4
5
6
7
8
9
9
1001
А
10
1010
В
11
1011
С
12
1100
D
13
1101
E
14
1110
15
16. ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ И ОБРАТНО
ПримерПример 1:
1:
11
0101
11000111
11
0101
11000111(2)
(2)
00110101
11000111
00110101
11000111(тетрады)
(тетрады)
33
55
C
C 77
16
16
11010111000111
1101011100011122 == 35С7
35С716
16
Пример
Пример 2:
2:
11
00
A
A 16
16
0001
0001 0000
0000 1010
1010
11
0000
0000
(тетрады)
(тетрады)
1010
1010
22
10A
= 100001010
10A16
16 = 10000101022
16
17. ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ И ОБРАТНО
ПримерПример 3:
3:
В7,
= 1011 0111,101 (последняя тетрада неполная)
В7, А16
16= 1011 0111,10122 (последняя тетрада неполная)
Пример
Пример 4:
4:
11110,1
11110,122 == 0001 1110,100022=1Е,8
=1Е,816
16
17
18.
ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫСЧИСЛЕНИЯ В ВОСЬМЕРИЧНУЮ И ОБРАТНО
Пример
Пример 5:
5:
10
10 101
101 000
000 111
111
010
010 101
101 000
000 111
111
22 55 00 77
22
(триады)
(триады)
88
1010100011122 == 2507
250788
Пример
Пример 6:
6:
11 00 77
001
001 000
000 111
111
11
000
000 111
111
88
(триады)
(триады)
22
107
10788 == 1000111
100011122
18
19. ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ВОСЬМЕРИЧНУЮ И ОБРАТНО
ПримерПример 7:
7:
4011,25
4011,2588=100
=100 000 001 001,010 101
10122
Пример
Пример 8:
8:
10110,1
10110,122=010
=010 110,10022=26,4
=26,488
19
20. ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ И ОБРАТНО
Упражнение:Упражнение:
Выполнить
Выполнить перевод,
перевод, используя
используя тетрады
тетрады ии триады
триады
1)
1) 1110110,1
1110110,122 == ??88;;
2)
;
2) 101000101
10100010122 == ??16
16;
3)
3) 4011
401188 == ??22;;
4)
= ?22
4) СВ7,9
СВ7,916
16
20
21. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Теорема.Теорема. Пусть
Пусть qq -- натуральное число, qq >1.
>1. Тогда
Тогда любое
любое
натуральное
натуральное число N
N можно
можно представить
представить вв виде:
виде:
n-1
n-1 + ... + a q11 + a q00,
N = annqnn + an-1
q
11
00
n-1
где
где для любого nn ann {0,1,…,q-1};
qq - основание системы счисления;
annan-1
…a11a00 - запись
запись натурального
натурального числа в системе
n-1
счисления
счисления сс основанием
основанием q.
q.
В
В системе
системе счисления
счисления сс основанием
основанием qq для
для записи
записи чисел
требуется
требуется qq цифр,
цифр, одна
одна из
из которых
которых ноль.
21
22. ПЕРЕХОД К СИСТЕМЕ СЧИСЛЕНИЯ С ДРУГИМ ОСНОВАНИЕМ ДЛЯ НАТУРАЛЬНЫХ ЧИСЕЛ q1 q2
ПЕРЕХОД К СИСТЕМЕ СЧИСЛЕНИЯ С ДРУГИМ ОСНОВАНИЕМДЛЯ НАТУРАЛЬНЫХ ЧИСЕЛ
q1 q2
Число
Число делится
делится нацело
нацело на
на qq22 , затем полученное частное
частное на
на qq22 ,,
ии т.
т. д.,
д., пока
пока деление
деление возможно
возможно (частное qq22 ).
).
Последнее
Последнее частное
частное ии остатки, начиная
начиная сс последнего,
последнего,
образуют
образуют запись числа в системе счисления с основанием q22 ..
Деление
Деление выполняется
выполняется в системе с основанием q11..
Пример:
Пример:
20
= 1010022
2010
10
Проверка:
Проверка:
10100
1010022 == 1*2
1*244 ++ 0*2
0*233 + 1*2
1*222 ++ 0*2
0*211 +
0*2
0*200 == 16+4
16+4 == 20
2010
10
22
23.
ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯПример:
Пример:
Переведем
Переведем число
число 75
75 из
из десятичной
десятичной системы
системы вв двоичную,
двоичную,
восьмеричную
восьмеричную ии шестнадцатеричную:
шестнадцатеричную:
Ответ:
== 11 001
Ответ: 75
7510
001 011
01122 == 113
11388 == 4B
4B16
10
16
23
24.
ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯПРЕДСТАВЛЕНИЕ
ПРЕДСТАВЛЕНИЕ ПРАВИЛЬНЫХ
ПРАВИЛЬНЫХ ДРОБЕЙ В СИСТЕМЕ
СЧИСЛЕНИЯ
СЧИСЛЕНИЯ С
С ОСНОВАНИЕМ q:
q:
-m
-m
D= a-1-1 q-1-1 + a-2-2 q-2-2 + ... + a-m
q
-m
==
22
0,2510
2*(1/10)+5*(1/10)
10
Дробь - нормализованная, если a-1-1 0
24
25.
ПЕРЕХОД К СИСТЕМЕ СЧИСЛЕНИЯ С ДРУГИМОСНОВАНИЕМ ДЛЯ ПРАВИЛЬНЫХ ДРОБЕЙ
q1 q2
Умножаем
Умножаем дробь на q22 ,, затем
затем дробную часть
часть произведения
произведения
на
на qq22 ,, ии т.
т. д.,
д., пока
пока не будет достигнуто требуемое число
знаков
знаков или пока дробная часть произведения не станет
равной
равной нулю.
нулю. Умножение
Умножение выполняется
выполняется вв системе
системе счисления
счисления
сс основанием
основанием q11 ..
0,312510
=0,2488
10
25
26.
ЛИТЕРАТУРА1. Фомин С. В. - Системы счисления. М.: Наука.
1987. 48 с.
26























 Информатика
Информатика








