Похожие презентации:
Математические методы в психологии
1.
МАТЕМАТИЧЕСКИЕМЕТОДЫ
В ПСИХОЛОГИИ
.
2.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА• Ермолаев О. Ю. Математическая статистика для психологов:
Учебник. – М.: МПСИ: Флинта, 2004.
• Наследов А. Д. Математические методы психологического
исследования: анализ и интерпретация данных. – СПб.: Речь,
2008.
• Сидоренко Е.В. Методы математической обработки в
психологии. – СПб.: Речь, 2010.
3.
Психолог должен уметь:• организовать исследование так, чтобы
его результаты были доступны
обработке в соответствии с проблемами
исследования;
• правильно выбрать метод обработки;
• содержательно интерпретировать
результаты обработки.
4.
ОСНОВНЫЕ ПОНЯТИЯ• Гипотеза – это научно обоснованное
предположение о свойствах и
закономерностях изучаемого явления.
• Нулевая гипотеза Но – это гипотеза об
отсутствии значимых различий между
какими-либо показателями или о
случайности связи между ними.
• Альтернативная гипотеза Н1 – это
гипотеза о наличии значимых различий
между исследуемыми показателями или о
достоверности связи между ними.
5.
ОСНОВНЫЕ ПОНЯТИЯНаправленные гипотезы:
• Но: Х1 не превышает Х2.
• Н1: Х1 превышает Х2.
Ненаправленные гипотезы:
• Но: Х1 не отличается от Х2.
• Н1: Х1 отличается от Х2.
6.
ОСНОВНЫЕ ПОНЯТИЯ• Генеральная совокупность – это
множество объектов, в отношении
которого формулируется
исследовательская гипотеза.
• Выборка – это ограниченная по
численности группа объектов
(испытуемых, респондентов),
специально отбираемая из
генеральной совокупности для
изучения ее свойств.
7.
ОБЪЕМ ВЫБОРКИ (n)• При разработке диагностической методики
объем выборки должен быть от 200 до 1000
– 2500 человек.
• При сравнении 2-х выборок, их общая
численность должна быть не менее 50
человек.
• При изучении взаимосвязи между какимилибо свойствами объем выборки должен
быть не менее 30 – 35 человек.
• Чем больше изменчивость изучаемого
свойства, тем больше должен быть объем
выборки.
8.
ОСНОВНЫЕ ПОНЯТИЯ• Независимые выборки (несвязанные)
характеризуются тем, что вероятность
отбора любого испытуемого одной
выборки не зависит от отбора любого из
испытуемых другой выборки.
• Зависимые выборки (связанные)
характеризуются тем, что каждому
испытуемому одной выборки поставлен в
соответствие по определенному критерию
испытуемый из другой выборки.
9.
КРИТЕРИИ ОБОСНОВАННОСТИВЫВОДОВ ИССЛЕДОВАНИЯ
• Репрезентативность выборки
• Статистическая достоверность
результатов исследования
10.
СТАТИСТИЧЕСКАЯ ДОСТОВЕРНОСТЬ• Статистическая достоверность
(статистическая значимость,
уровень статистической
значимости, р-уровень) – это
количественно выраженная
вероятность того, что полученные
результаты достоверны.
• р≤0,05 – приемлемая граница
статистической значимости.
11.
Соотношение показателей р-уровня и степенизначимости результатов исследования
р-уровень
р 0,1
Решение
Принимается Но
Сомнения в
0,05 р 0,1 истинности Но,
неопределенность
р 0,05
Значимость,
отклонение Но
р 0,01
Высокая
значимость,
отклонение Но
Возможный статистический вывод
«Статистически достоверные различия
не обнаружены»
«Различия обнаружены на уровне
статистической тенденции»
«Обнаружены статистически
достоверные (значимые) различия»
«Различия обнаружены на высоком
уровне статистической значимости»
12.
СТАТИСТИЧЕСКИЕ КРИТЕРИИ• Статистический критерий – это
решающее правило, обеспечивающее
принятие истинной и отклонение
ложной гипотезы с высокой степенью
надежности (вероятности).
Статистические критерии обозначают и
метод расчета определенного числа и само
это число.
13.
СТАТИСТИЧЕСКИЕ КРИТЕРИИ• Параметрические критерии – это
критерии построенные на основании
параметров данной совокупности и
представляют функции этих
параметров. Они включают в
расчетную формулу параметры
распределения признака (среднее,
дисперсию и др.).
14.
СТАТИСТИЧЕСКИЕ КРИТЕРИИ• Непараметрические критерии
представляют собой функции,
зависящие непосредственно от
вариант данной совокупности с их
частотами. Они основаны на
оперировании частотами и
рангами.
15.
ИЗМЕРИТЕЛЬНЫЕ ШКАЛЫНЕМЕТРИЧЕСКИЕ ШКАЛЫ:
• Номинативная шкала (номинальная,
шкала наименований);
• Порядковая шкала (ранговая шкала).
МЕТРИЧЕСКИЕ ШКАЛЫ:
• Интервальная шкала;
• Абсолютная шкала (шкала
отношений).
16.
ОСНОВНЫЕ ЭТАПЫ СТАТИСТИЧЕСКОЙОБРАБОТКИ ДАННЫХ
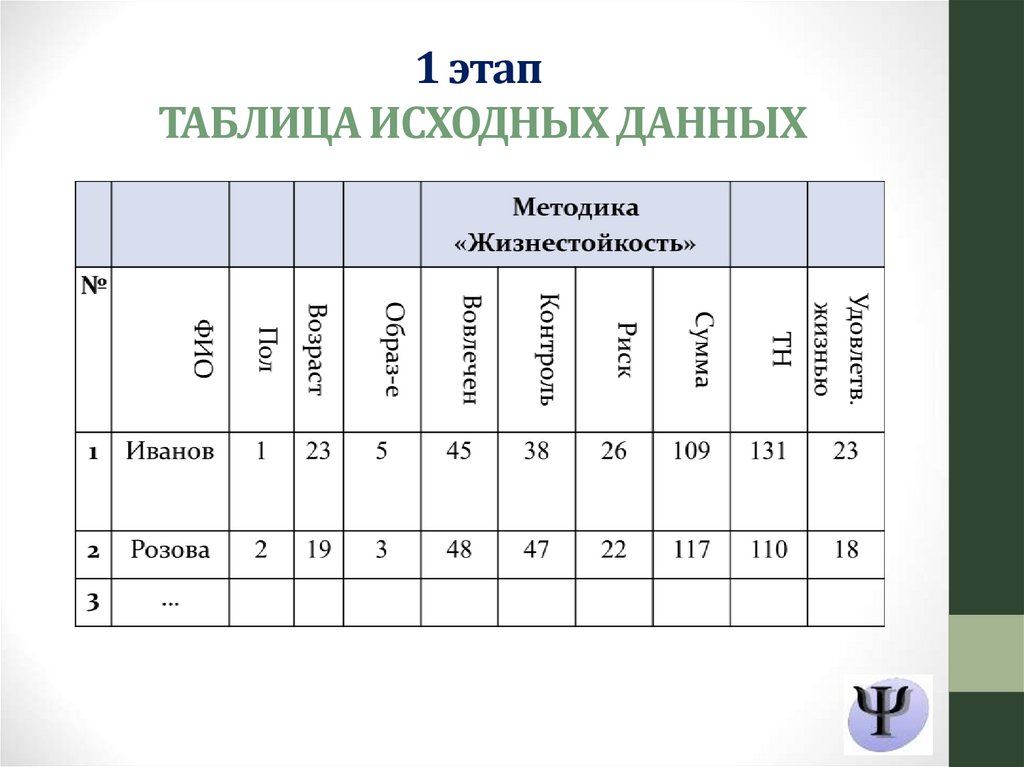
1. Составить таблицу исходных данных.
2. Провести первичный анализ данных (таблиц
и графиков распределения частот,
описательных статистик).
3. Определить характер распределения
признаков.
4. Выбрать статистические методы обработки
данных. Провести статистический анализ.
5. Проинтерпретировать результаты,
сформулировать выводы.
17.
1 этапТАБЛИЦА ИСХОДНЫХ ДАННЫХ
18.
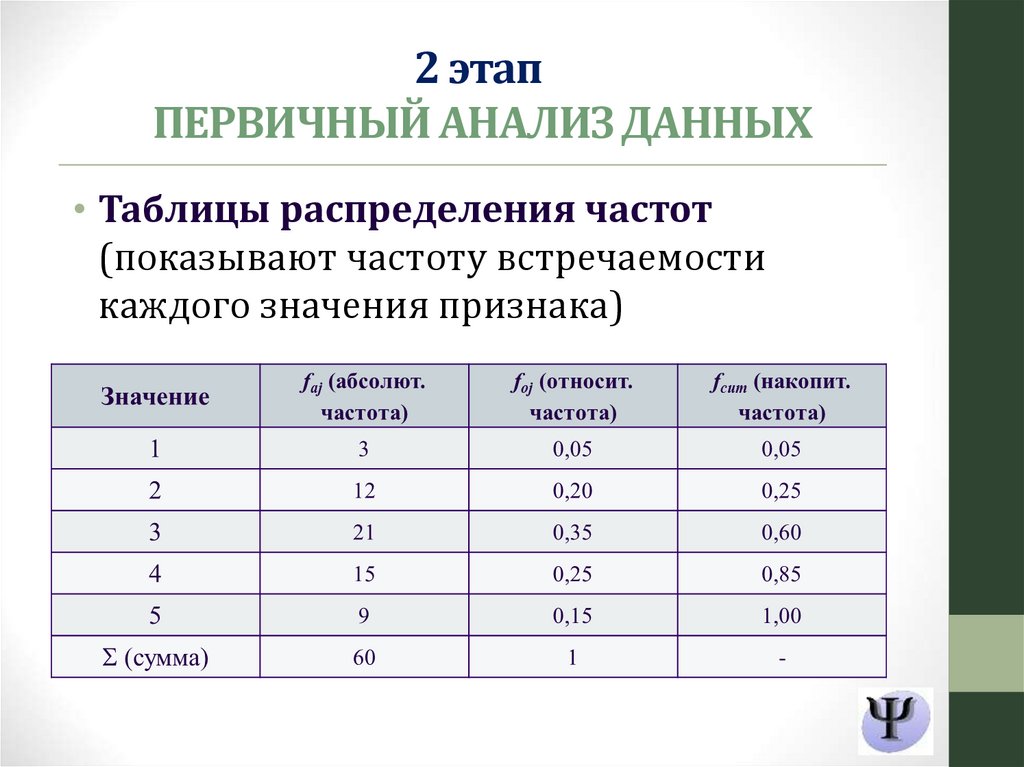
2 этапПЕРВИЧНЫЙ АНАЛИЗ ДАННЫХ
• Таблицы распределения частот
(показывают частоту встречаемости
каждого значения признака)
19.
2 этапПЕРВИЧНЫЙ АНАЛИЗ ДАННЫХ
• Таблицы сопряженности (кросстабуляции) - таблицы совместного
распределения частот двух или более
номинативных признаков, измеренных на
одной группе объектов
20.
2 этапПЕРВИЧНЫЙ АНАЛИЗ ДАННЫХ
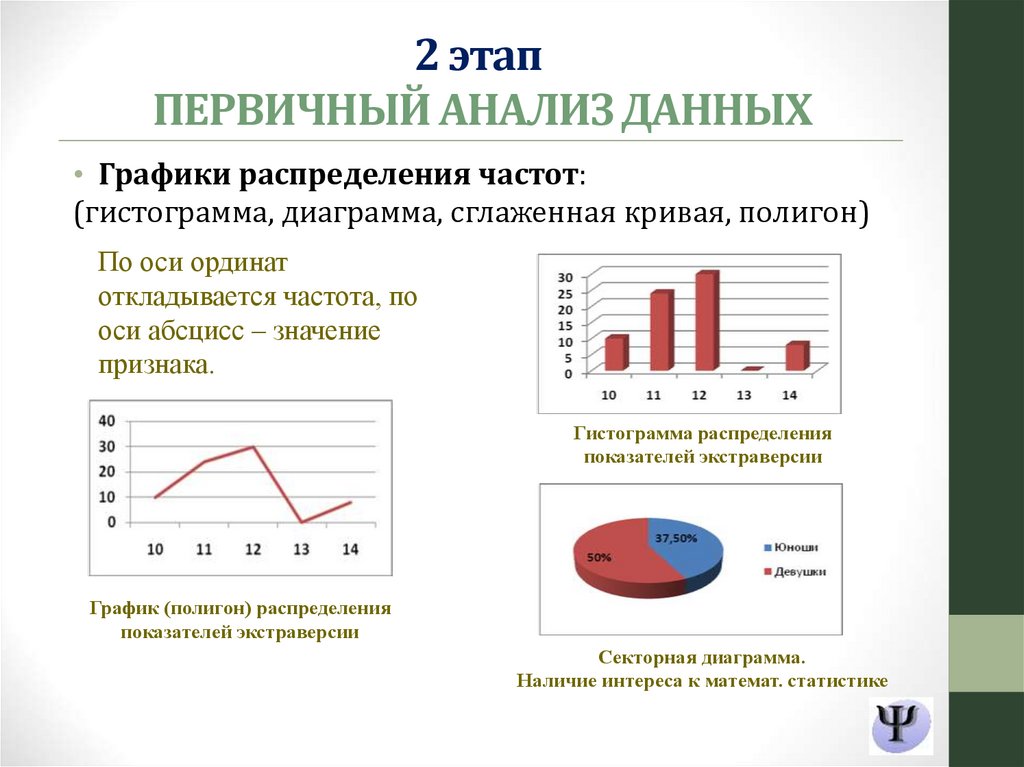
• Графики распределения частот:
(гистограмма, диаграмма, сглаженная кривая, полигон)
По оси ординат
откладывается частота, по
оси абсцисс – значение
признака.
Гистограмма распределения
показателей экстраверсии
График (полигон) распределения
показателей экстраверсии
Секторная диаграмма.
Наличие интереса к математ. статистике
21.
2 этапПЕРВИЧНЫЙ АНАЛИЗ ДАННЫХ
ОПИСАТЕЛЬНЫЕ СТАТИСТИКИ
Меры центральной тенденции:
• Среднее арифметическое (М)
• Медиана (Ме)
• Мода (Мо)
Меры изменчивости признака:
• Размах (R)
• Дисперсия (D)
• Стандартное отклонение (σ)
22.
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕx
М
i
n
xi – сумма наблюдаемых значений признака;
n – количество наблюдений (объем выборки).
23.
ДИСПЕРСИЯ(x M )
D
i
n 1
2
24.
СТАНДАРТНОЕ ОТКЛОНЕНИЕ(x М )
i
n 1
2
25.
СТАТИСТИЧЕСКАЯ ОШИБКА СРЕДНЕГОАРИФМЕТИЧЕСКОГО
m
n
– стандартное отклонение;
п – количество наблюдений (объем выборки).
26.
ПРЕДСТАВЛЕНИЕ ОПИСАТЕЛЬНЫХСТАТИСТИК
• повествовательное изложение
результатов;
• графическое представление результатов;
• представление результатов в виде
таблицы:
№ Психологический
признак
1 Показатель
макиавеллизма
2 …
М±m
σ
73,20±0,78 13,24
min
max
39
106
27.
3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРАРАСПРЕДЕЛЕНИЯ ПРИЗНАКА
ФОРМЫ РАСПРЕДЕЛЕНИЯ ПРИЗНАКА:
• Равномерное распределение.
• Симметричное распределение.
• Асимметричное левостороннее
распределение.
• Асимметричное правостороннее
распределение.
• Нормальное распределение
(симметричное распределение).
28.
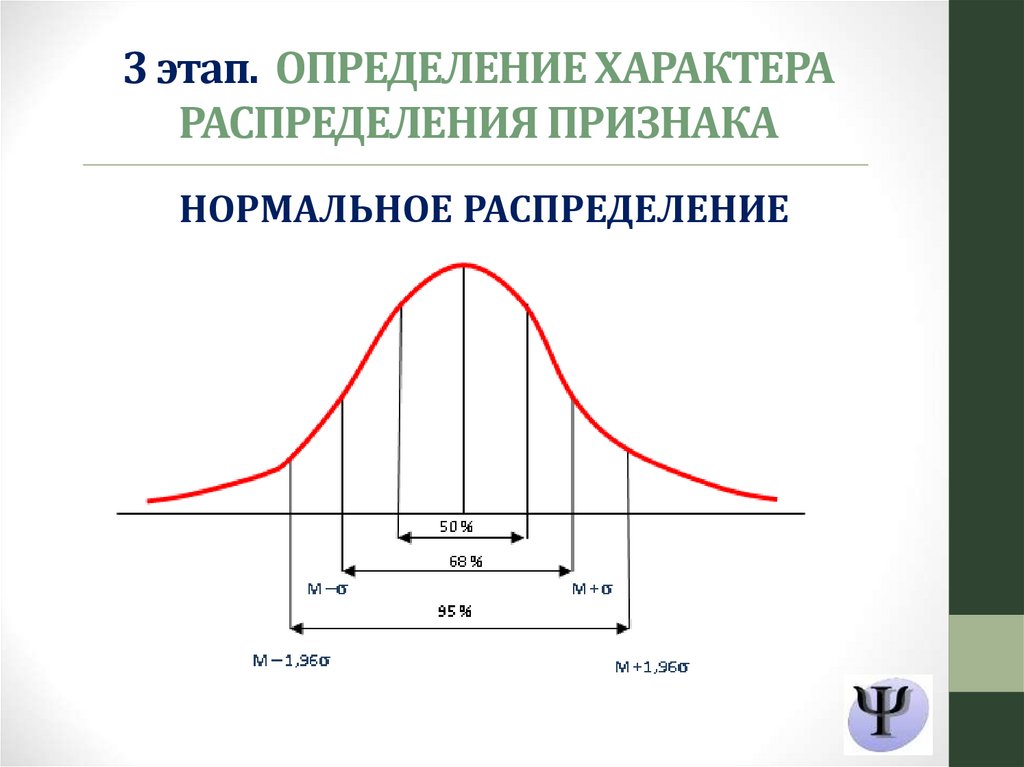
3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРАРАСПРЕДЕЛЕНИЯ ПРИЗНАКА
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
29.
Форма и положение графика нормальногораспределения
Определяется двумя параметрами:
Средним арифметическим ( X )
Стандартным отклонением (s ).
Среднее арифметическое задает положение
кривой на числовой оси, а стандартное
отклонение задает ширину этой кривой.
• критерий проверки соответствия изучаемого
распределения нормальному: если мода,
медиана и среднее арифметическое равны, то
ряд имеет нормальное распределение.
30.
3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРАРАСПРЕДЕЛЕНИЯ ПРИЗНАКА
• Метод оценки мер центральной
тенденции.
• Визуальный (графический) метод.
• Метод оценки показателей асимметрии и
эксцесса.
• Методы, основанные на критериях
согласия распределений.
31.
3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРАРАСПРЕДЕЛЕНИЯ ПРИЗНАКА
Коэффициент асимметрии:
n
As
(x M )
i 1
3
i
n
3
Стандартная ошибка асимметрии:
6
mAs
n
32.
3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРАРАСПРЕДЕЛЕНИЯ ПРИЗНАКА
Показатель эксцесса:
n
Ex
(x M )
i 1
i
n
4
4
3
Стандартная ошибка эксцесса:
6
mEx 2mAs 2 *
n
33.
Задача• Задача. Даны результаты обследования группы
испытуемых (N=36) с помощьютеста Айзенка.
• Показатели экстраверсии: 4, 12, 10, 9, 14, 10, 8, 7, 12,
7,13, 17, 12, 14, 15, 18, 17, 5, 7, 9, 9, 11, 19, 20, 6, 8,
13, 12, 14, 4, 13, 10, 12, 6, 5, 15
• Показатели нейротизма: 10, 11, 19, 14, 9, 20, 7, 20, 20,
19, 9, 7, 12, 11, 4, 13, 13, 6, 12, 23, 11, 15, 16, 8, 21,
17, 18, 13, 15, 12, 14, 10, 16, 21, 14, 23
• Для каждого из показателей (экстраверсии и
нейротизма) следует вычислить выборочную
среднюю, дисперсию, выборочное стандартное
отклонение, медиану и моду.





























 Математика
Математика Психология
Психология








