Похожие презентации:
Учебная дисциплина Физика (третий семестр)
1. Учебная дисциплина Физика (третий семестр)
12.
О программе курсаЧасть 1
Классическая оптика
(волновые свойства света).
Интерференция. Дифракция. Дисперсия.
Поляризация.
Часть 2
Современная физика
(1905 г. Эйнштейн – фотоны).
Квантовая оптика. Квантовая механика.
Физика твердого тела.
2
3. Учебники
• Б.М. Яворский, А.А. Детлаф. Курс физики.И.В. Савельев. Курс общей физики.
И.Е. Иродов. Основные законы физики.
Д.В. Сивухин. Общий курс физики.
В.А. Касьянов. Физика.
Ю.А. Храмов. Физики.
3
4.
45. Классическая оптика
• Оптика – наука о световых явлениях.• С классической точки зрения свет –
электромагнитные волны оптического
диапазона (l=10-8-10-3 м).
5
6.
Электромагнитные волныСуществование
электромагнитных волн
теоретически предсказано
Максвеллом в 1860 г.
(Уравнения Максвелла).
• В 1888 г. Герц экспериментально подтвердил выводы
Максвелла.
• В 1889 г. А.С. Попов повторил опыты Герца и указал
на возможность использования электромагнитных
волн для радиосвязи.
6
7.
МАКСВЕЛЛ Джеймс Клерк(13. VI 1831 —5.XI 1879)
— английский физик
Работы
посвящены
электродинамике,
молекулярной физике, общей статистике,
оптике, механике, теории упругости. В
кинетической теории газов, одним из
основателей которой является, установил в
1859 статистический закон, описывающий
распределение молекул газа по скоростям
(распределение Максвелла).
Самым большим научным достижением
Максвелла является созданная им в 1860 — 65
теория электромагнитного поля, которую он
сформулировал в виде системы нескольких
уравнений
(уравнения
Максвелла),
выражающих все основные закономерности
электромагнитных явлений.
7
8.
ГЕРЦ Генрих Рудольф(22.11 1857-1.1 1894)
— немецкий физик,
Основные работы относятся к
электродинамике, одним из основоположников
которой он является, и механике. В 1888
экспериментально доказал существование
электромагнитных волн, распространяющихся
в свободном пространстве, предсказанных
теорией Максвелла.
В 1887 наблюдал внешний фотоэффект,
заметив, что электрический разряд между
двумя электродами происходит сильнее, если
искровой промежуток (электроды) освещается
светом, богатым ультрафиолетовыми лучами.
Исследования Герца посвящены также
катодным лучам, теории удара упругих тел.
8
9.
ПОПОВ Александр Степанович(16.III 1859—13.1 1906)
— русский физик и электротехник,
изобретатель радио.
Исследования относятся к проблемам
электротехники и радиотехники, в частности
радиосвязи. В 1888 повторил опыты Г. Герца по
получению электромагнитных волн и в 1889
впервые указал на возможность их использования
для передачи сигналов на расстояние.
7 мая 1895 продемонстрировал грозоотметчик
(радиоприемник) на заседании физического
отделения
Российского
физико-химического
общества.
В 1897 впервые обнаружил явление
отражения волн от предметов (в частности,
кораблей),
находящихся
на
пути
их
распространения. Это явление было положено в
основу радиолокации.
День 7 мая стал днем радио.
9
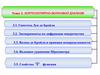
10. Спектр электромагнитных волн и источники их излучения
1011. Уравнения Максвелла
• (имеют такое же значение для физики какзаконы Ньютона и начала термодинамики)
D ds dV
S
V
B ds 0
S
B
E dl t dS
L
S
D
H dl j t dS
L
S
11
12. Уравнения Максвелла в дифференциальной форме
divDdivB 0
B
rotE
t
D
rot H j
t
Материальные уравнения для изотропной линейной среды:
D 0 E
B 0 H
j E
12
13. Уравнения Максвелла в дифференциальной форме для однородной изотропной среды, свободной от токов и зарядов, без гистерезисов и
нелинейностейdivE 0
divH 0
H
rotE 0
t
E
rotH 0
t
(1)
(2)
(3)
(4)
13
14. Вывод волнового уравнения из уравнений Максвелла
• Общий вид волнового уравнения:2
U
1 2U
v 2 t 2
0,
(5)
• U - любое возмущение (звуковое, на
поверхности жидкости, световое);
• v – скорость распространения возмущения в
пространстве (фазовая скорость волны).
14
15.
(3)2
rot (rot E ) grad (divE ) E;
2
rot (rotE ) E;
(1)
H
rot (rotE ) rot ( 0
) 0 (rotH );
t
t
2
E
rot (rot E ) 0 0
;
(4)
t 2
Получаем волновое уравнение для
:E
2
E
2
(6)
E 0 0
0
2
15
t
16.
Аналогично выводится волновое уравнение для(4)
:H
2
rot (rotH ) grad (divH ) H ;
2
rot (rot H ) H ;
(2)
E
rot (rotH ) rot ( 0 ) 0 (rot E );
t
t
2
H
(3) rot ( rot H ) 0 0
;
2
t
2
H
2
(7)
H 0 0
0
2
t
16
17. Свойства электромагнитных волн
(5), (6), (7)1
v
2
0 0
1
v
0 0
Скорость распространения электромагнитной волны в вакууме:
1
c
3 108 м / с
0 0
17
18.
E, H , s- правая тройка ортогональных векторов;
E
H
0
H
E,
0
s
0
E
H,
0
- синфазность;
1
E
B vB .
0 0
18
19. Полученные результаты показывают:
• Электромагнитные волны представляютсобой распространение колебаний векторов
напряженности электрического и магнитного
поля в пространстве.
• Электромагнитные волны в отличие от
звуковых волн распространяются не только в
среде, но и в вакууме.
• Скорость распространения
электромагнитных волн в вакууме является
мировой константой и составляет 3·108 м/с.
19
20.
• Плоская электромагнитная волна –поперечная волна.
• Векторы напряженности электрического и
магнитного поля взаимно ортогональны.
• Векторы напряженности электрического поля,
магнитного поля и скорости распространения
образуют правую тройку ортогональных
векторов.
• Колебания векторов напряженности
электрического и магнитного поля синфазны.
20
21. Энергия и интенсивность электромагнитной волны. Вектор Умова-Пойнтинга.
• Распространение электромагнитных колебаний связано спереносом энергии.
• Объемная плотность энергии электромагнитной волны:
0 E 2 0 H 2
w
;
2
2
0 E 0 H
(8)
w 0 0 EH ;
EH
w
;
v
(9)
(10)
21
22.
• Вектор Умова-Пойнтинга (плотность потока энергии):wv [ EH ].
(11)
• Интенсивность света:
I .
(12)
• Интенсивность плоской монохроматической волны
0
E y A sin( t kx), H z
A sin( t kx).
0
I
0 2 2
A sin ( t kx )
0
1 0 2
I
A . (13)
2 0
22
23. УМОВ Николай Алексеевич (4.II 1846 - 28.I 1915) русский физик
.УМОВ Николай Алексеевич
(4.II 1846 - 28.I 1915)
русский физик
• Работы посвящены теории колебательных
процессов, электричеству, оптике, земному
магнетизму, молекулярной физике.
• Важным результатом его теоретических
исследований было создание учения о
движении энергии. Впервые ввел понятие о
скорости и направлении движения энергии,
о потоке энергии, плотности энергии в
данной точке среды.
• Раскрыл физический смысл многих сложных
формул Гаусса в теории земного магнетизма,
что дало возможность определить вековые
изменения земного магнетизма. Одним из
первых понял и оценил значение теории
относительности.
23
24. ПОЙНТИНГ Джон Генри (9.IX 1852 —30.III 1914) английский физик
• Работы посвящены изучениюэлектрических явлений, переноса
энергии, теории излучения и
давления света, радиации.
• Ввел в 1884 понятие о потоке
электромагнитной энергии (вектор
Умова — Пойнтинга).
• Измерил в 1891 плотность Земли,
в 1893 — гравитационную
постоянную.
• В 1903 высказал идею о
торможении солнечным светом
гелиоцентрического движения
космических тел (эффект
Пойнтинга — Робертсона). Этим
же эффектом он объяснял
поворот хвостов комет в сторону
от Солнца.
24
25.
• Примечание 1. Под интенсивностью света вфизической оптике часто понимают просто квадрат
амплитуды напряженности электрического поля
световой волны (I=A2).
• Примечание 2. Вектор напряженности электрического
поля световой волны называют световым вектором,
так как действие электрического поля световой волны
на оптические электроны атомов вещества
значительно сильнее действия магнитного поля.
Fэл Ee, Fм Bev , B E c
Fэл c
1.
Fм v
25
26. Количественная оценка эффекта
• Солнечная постоянная:4
2
I 1,35 10 Вт / м ;
p 10 5 Па (10 9 Н / см 2 )
• Трудно обнаружить экспериментально.
26
27. Качественное объяснение давления света с точки зрения электромагнитной теории Максвелла
Fм e[v e B].27
28. Излучение электрического диполя
• Электромагнитные волны излучаютсядвижущимися с ускорением зарядами.
• Электрический диполь, момент которого pe
периодически меняется с течением времени,
называют осциллятором.
pe l q,
(1)
l плечо диполя.
q
l
-q
• Осциллятор является примером излучающей
системы – аналогом излучающего атома.
28
29.
2930. Полярная диаграмма излучения линейного гармонического осциллятора
I ( ) const2
sin
r
2
30
31. Волновой цуг
E p (t ) Ap exp[ (t t p )] cos[ (t t p )];Примечание: с точки зрения квантовой теории излучения характерная
длительность цуга равна среднему времени жизни атома в возбужденном
состоянии.
31
32. Интерференция света
• Явление усиления или ослабления интенсивностисвета в данной точке пространства в результате
наложения световых волн.
• Интерференция двух волн:
I I1 I 2
N
• Интерференция многих волн:
I Ii
i 1
• Явление интерференции не противоречит закону
сохранения энергии. При интерференции энергия
волн перераспределяется в пространстве.
32
33.
• Физика явления интерференцииопределяется тем, что для интенсивности не
действует принцип суперпозиции. Покажем
это на примере интерференции двух волн.
• Принцип суперпозиции действует для
напряженности :
E E1 E2.
(1)
2
2
I E E1 E2 .
(2)
E1 A1 sin( t 1), E2 A2 sin( t 2 ).
(3)
33
34.
22
2
2
I A1 sin ( t 1) A2 sin ( t 2 )
2 A1 A2 sin( t 1) sin( t 2 ) .
1
sin ( t 1) sin ( t 2 ) ;
2
2
2
(4)
(5)
sin( t 1) sin( t 2 )
1
cos( 2 1) cos(2 t 1 2 ) ;
2
cos(2 t 1 2 ) 0.
(6)
(7)
34
35.
1 2 1 2I A1 A2 A1A2 cos( 2 1) .
2
2
(8)
1 2
1 2
A1 I1;
A2 I 2 ; 2 1 ;
2
2
A1 A2 A1 A2 A1 A2 2 I1I 2 .
I I1 I 2 2 I1I 2 cos .
(9)
Волны называются когерентными, если
2 1 const .
(10)
35
36. Интерференция когерентных волн
I I1 I 2 2 I1I 2 cos(1)
cos 1 I I max I1 I 2 2 I1I 2 .
(2)
cos 1 I I min I1 I 2 2 I1I 2 .
(3)
Видимость ИК
I max I min
V
I max I min
2 I1I 2
V
I1 I 2
0 V 1
V 1, если I1 I 2
36
37. Разность фаз и разность хода
Примером когерентных волн являются монохроматические волны.S1
l1
l2
M
l0
l ;
n
S2
2
2
k (l2 l1 )
l
lопт
l
l0
разность фаз;
l геометрическая разность хода;
lопт n l оптическая разность хода;
c
n
v
показатель преломления среды.
37
38. Условия максимумов и минимумов
• Интерференционный максимум возникает, есливолны в точку наблюдения приходят в фазе:
cos 1 2 m, l lm,
m 0, 1, 2,....
• Интерференционный минимум возникает, если
волны в точку наблюдения приходят в противофазе:
l
cos 1 (2m 1), l (2m 1),
2
m 0, 1, 2,....
38
39. Интерференция волн от двух точечных источников (ИК – полосы)
XЭ1
I
X
x
l1
h
Y
l2
0
L
Z
L
h << L
39
40.
2h
2
2
l1 L x ;
2
2
h
2
2
l2 L x ;
2
2
2
h
h
l22 l12 L2 x 2 hx L2 x 2 hx 2hx;
4
4
l22 l12 (l2 l1 )(l2 l1 ) 2 L l ;
hx
hxm
2L l 2hx l
lm
;
L
L
mlL
xm
; L xm 1 xm ;
h
lL
L
h
h
L
l
L
40
41.
• Случаи абсолютной когерентности и абсолютнойнекогерентности на практике не реализуются.
• Модель абсоютно когерентного излучения можно использовать
при усовии t<<tког ( l<<lког).
• Модель абсоютно некогерентного излучения можно
использовать при усовии t tког ( l>>lког).
• Ориентировочные численные данные по когерентным
характеристикам различных типов оптических излучений
представлены ниже в виде таблицы.
Тип излучения
n, Гц
tког, с
lког, м
Лазерное
излучение
~ 1-105
~ 10-5-1
~ 103-108
Газовый разряд
(одна линия)
~ 108
~ 10-8
~1
Солнечное
излучение
~ 1014
~ 10-14
~ 10-6
41
42. Соотношения неопределенностей для волновых процессов
• Идеальная плоская монохроматическая волна имеетстрого определенную частоту и строго определенный
волновой вектор, при этом ее длительность
бесконечна и она занимает все пространство.
• Фурье-анализ показывает, что локализация волны во
времени и в пространстве сопровождается
уширением распределений мощности колебаний по
частотам и волновым векторам.
• Таким образом, всем волновым процессам присущи
фундаментальные соотношения:
x k x 1;
y k y 1;
z k z 1;
t 1.
42
43.
МАЙКЕЛЬСОН Альберт Абрахам(19X11 1852 —9.V 1931)
— американский физик,
член Национальной АН (1888), президент в
1923-27.
Основные работы в области оптики и
спектроскопии.
Изобрел
интерферометр
(интерферометр
Майкельсона),
сыгравший
значительную роль в обосновании специальной
теории
относительности
и
в
изучении
спектральных
линий.
За
созданные
прецизионные инструменты и выполненные с их
помощью
спектроскопические
и
метрологические исследования Майкельсону в
1907, была присуждена Нобелевская премия.
В 1890 высказал мысль о возможности
использования
в
астрономии
интерференционных эффектов и сконструировал
для измерения угловых размеров звезд звездный
интерферометр.
Иностранный член АН СССР (1926).
43
44. Способы создания когерентных источников
• Независимые источники всегда взаимнонекогерентны.
• Когерентные волны получаются делением исходной
волны с помощью различных оптических элементов.
• Различают деление волны по амплитуде (пример –
интерферометр Майкельсона) и деление по
волновому фронту (пример – интерференционная
схема Юнга).
44
45.
Зеркало Ллойдаh L,
h
З
l lL
L
.
2h
L
45
46.
Бизеркала Френеля1,
l l(b a)
L
.
2b
b
a
46
47.
Бипризма Френеляl
l(b a)
L
.
2b (n 1)
b
a
47
48.
Билинза Бийеh
L
l lL
L
.
h
48
49. Интерференция в тонких пленках
n2 n1lопт n2 ( AD DC ) (n1 AB l1 2) ;
2d
2d sin r sin i
lопт n2
n1
l1 2 ;
cosr
cosr
49
50.
sin i n2sin r n1
n2
sin i sin r
n1
2d
lопт
(n2 n2 sin 2 r ) l1 2 ;
cosr
lопт 2dn2 cos r l1 2
n1
cosr 1 sin r , sin r sin i
n2
2
lопт 2d
2
n2
2
2
n1 sin i
l1 2
50
51. Полосы равного наклона
• Полосы равного наклона возникают, если падающий пучоксходящийся или расходящийся.
• В отсутствие линзы они локализованы в бесконечности.
• При использовании линзы они локализованы в фокальной
плоскости линзы.
• Явление интерференции в тонких пленках используется для
просветления оптики (просветляющие покрытия).
51
52. Полосы равной толщины
n1=1n2=n
d
0
X
lопт 2dn2 l 2, d d0 x
xm : 2(d0 xm )n l 2 ml,
xm 1 : 2(d0 xm 1)n l 2 (m 1)l,
l
L xm 1 xm
2 n
• Полосы равной толщины локализованы вблизи поверхности
раздела сред.
• Используются для контроля качества поверхностей линз и
других оптических элементов.
52
53. Кольца Ньютона
EO1D, d EF , r ED;r
1, , R d , l;
R
1 2
l 2d l 2, d R R cos R ;
2
r2
l l 2
R
l ml
l
l (2m 1)
2
rmсв
l
R(2m 1)
2
rmтем Rml
53
54. НЬЮТОН Исаак (4.1 1643 - 31.111 1727) выдающийся английский ученый, заложивший основы современного естествознания, создатель
классической физикиСформулировал основные законы классической
механики, открыл закон всемирного тяготения,
дисперсию света, развил корпускулярную
теорию света, разработал дифференциальное
и интегральное исчисление.
Создал огромный труд «Математические
начала натуральной философии» («Начала»),
изданный в 1687. «Начала» содержали
основные понятия и аксиоматику классической
механики, и три закона движения. Тут же дан
его закон всемирного тяготения, исходя из
которого Ньютон объяснил движение небесных
тел (планет, их спутников, комет) и создал
теорию тяготения, что окончательно утвердило
победу учения Коперника.
Велик вклад Ньютона в оптику. В 1666 при
помощи трехгранной стеклянной призмы
разложил белый свет на семь цветов (в спектр).
Предпринял попытку создать компромиссную
корпускулярно-волновую теорию света.
Научное творчество Ньютона сыграло
исключительно важную роль в истории
развития физики. По словам А. Эйнштейна,
«Ньютон был первым, кто попытался
сформулировать элементарные законы,
которые определяют временной ход широкого
класса процессов в природе с высокой
степенью полноты и точности».
54
55. Интерференция многих волн
Метод векторных диаграммA 2 OO1 sin , 2 N 0 ;
2
N 0
sin sin
;
2
2
A1
OO1
;
0
2 sin
2
N 0
sin
2
A A1
sin 0
2
55
56.
N 0sin
2 ,
I I1
2 0
sin
2
2
I1 A12
Условие главных максимумов
0 2 m, m 0, 1, 2,...
Условие минимумов
2 p
0
,
N
p целое число, не кратное N .
Ширина главных максимумов
4
.
N
Интенсивность главных максимумов
I макс I1N 2 .
56
57. Примеры расчетов интерференции многих волн
N=6, I1=1I
0/2
Число минимумов между двумя главными максимумами равно N 1.
N=2, I1=1
I
0/2
57
58. Дифракция света
Совокупность явлений, которые обусловлены
волновой природой света и наблюдаются при его
распространении в среде с резко выраженной
оптической неоднородностью (например, при
прохождении через отверстия в экранах, вблизи
границ непрозрачных тел и т. п.) [1,2].
Отклонение от прямолинейного распространения,
не связанное с отражением, преломлением,
рефракцией и рассеянием (например, в тумане) [4].
Дифракционные явления следуют из уравнений
Максвелла и волновых уравнений.
На практике для наглядности можно пользоваться
упрощенными методами, основанными на
принципе Гюйгенса (1678) и принципе Гюйгенса- 58
Френеля (1816).
59.
ГЮЙГЕНС Христиан (14.1У 1629 - 8.VII 1695)— голландский физик, механик, математик и астроном.
Физические исследования в области механики, оптики,
молекулярной физики. Сконструировал первые маятниковые часы со
спусковым механизмом (1656), разработал их теорию (1673). В
частности, решил задачу об определении центра колебания
физического маятника и его периода колебаний, установил законы,
определяющие центростремительную силу. Исследовал также
столкновение упругих тел и вывел его законы (1669), установил
законы сохранения количества движения..
В 1678 разработал волновую теорию света (опубликована в
«Трактате о свете» в 1690). Объясняя механизм распространения
света, выдвинул известный принцип, названный его именем (принцип
Гюйгенса). Изучал также двойное лучепреломление. Ввел понятие
«ось кристалла». Открыл в 1678 поляризацию света.
Совместно с Р. Гуком установил (1665) постоянные точки
термометра — точку таяния льда и точку кипения воды. С помощью
сконструированного телескопа в 1655 открыл кольцо Сатурна и
первый спутник Сатурна — Титан. Близко подошел к открытию
закона всемирного тяготения. Первый пришел к выводу, что Земля
сжата возле полюсов, и высказал идею об измерении ускорения силы
тяжести с помощью секундного маятника. Значительных результатов
достиг в математике.
59
60. Принцип Гюйгенса
• 1. Каждая точка волнового фронта являетсяисточником вторичных волн,
распространяющихся во все стороны со
скоростью света в данной среде.
• 2. Огибающая вторичных волн определяет
положение нового волнового фронта.
Принцип Гюйгенса позволил объяснить
целый ряд оптических явлений:
60
61. Прямолинейность распространения света в однородной среде
a)б)
• В однородной среде а) плоский волновой фронт остается при
распространении плоским; б) сферический фронт остается
сферическим.
61
62. Проникновение света в область геометрической тени при прохождении через отверстие в непрозрачном экране.
6263. Принцип Гюйгенса-Френеля
• В 1816 Френель вводит представление окогерентности элементарных волн и их
интерференции.
• Метод зон Френеля. Волновой фронт
разбивается на такие зоны, что волны,
приходящие в точку наблюдения от соседних зон
гасят друг друга.
• Если в результате разбиения число зон Френеля
оказывается четным, в точке наблюдения будет
дифракционный минимум.
• Если в результате разбиения число зон Френеля
оказывается нечетным, в точке наблюдения будет
дифракционный максимум.
63
64. Распространение света в однородной среде
A1 A2 A3 ... Ai ...Если
N 1,
1
Ai ( Ai 1 Ai 1);
2
AN A1.
A A1 A2 A3 A4 ... AN
1
1 1
1
1
1
A A1 A1 A2 A3 A3 A4 A5 ... A1
2
2 2
2
2
2
Результирующее действие в точке M полностью открытого фронта
световой волны, возбуждаемой источником S0, равно половине действия
одной только центральной зоны Френеля.
64
65. Расчет радиуса зоны Френеля
hi OC ;ri2 R 2 ( R hi ) 2 ;
l, hi OC R;
ri 2Rhi .
2
l
ri L i L hi 2 ;
2
2 Rhi Lil 2 Lhi ;
2
ilL
hi
;
2( R L)
ilRL
ri
R L
65
66. Дифракция Френеля на круглом отверстии
BC D;D – диаметр отверстия
mlRL
rm
,
R L
2rm D,
D 2 ( R L)
m
.
4lRL
66
67.
1m нечетное максимум : A ( A1 Am ),
2
1
m четное минимум : A ( A1 Am ).
2
При m>>1 Am<<A1, различия между максимумами и минимумами нет,
дифракционная картина не наблюдается.
Следовательно, для наблюдения дифракционных явлений необходимо,
чтобы число зон Френеля было не очень большим.
67
68. Зонные пластинки
D ,D' 2r1,
1
1 2
A A1, I A1 ;
2
4
A' A1, I ' A12 ;
Часть волнового фронта дает освещение
в т. М больше, чем весь волновой фронт.
Амплитудная зонная пластинка (закрываются четные или нечетные зоны):
I ' m 2 2 I .
Фазовая зонная пластинка (фазы четных или нечетных зон сдвигаются на :
I ' m2 I .
Зонные пластинки фокусируют излучение и работают как линзы.
68
69.
• Дифракция Френеля – дифракция в сходящихсялучах.
• Дифракция Фраунгофера – дифракция в
параллельных лучах.
69
70.
ФРЕНЕЛЬ Огюстен Жан(10.V 1788 - 14.VII 1827)
— французский физик,
член Парижской АН (1823).
Работы посвящены физической оптике. Еще в 1811 под
влиянием Э. Малюса стал самостоятельно изучать физику и
вскоре начал экспериментальные исследования по оптике.
Переоткрыл в 1815 принцип интерференции, дополнил
известный принцип Гюйгенса, введя (1816) представление о
когерентности элементарных волн и их интерференции
(принцип Гюйгенса — Френеля). Исходя из этих двух
принципов, разработал в 1818 теорию дифракции света.
Выполнил опыты с бизеркалами (1816) и бипризмами. (1819) по
интерференции света, ставшие классическими. Исследовал
интерференцию поляризованных лучей.
Установил (1823) законы отражения и преломления света
на плоской неподвижной поверхности раздела двух сред
(формулы Френеля).
Исследовал проблему о влиянии движения Земли на
оптические явления, положив (1818) начало оптике
движущихся тел.
Член Лондонского королевского общества (1825). Медаль
Б. Румфорда.
70
71.
ФРАУНГОФЕР Йозеф(6.111 1787 - 7. VI 1826)
— немецкий физик
Работы относятся к физической и практической оптике.
Внес существенный вклад в исследование дисперсии и
создание ахроматических линз. Изготовил достаточно
большие и чистые образцы флинтгласа и кронгласа и
изобрел метод точного определения формы линз, оказавший
значительное влияние на развитие практической оптики,
изобрел машину для шлифования ахроматических линз,
сконструировал спектрометр, ахроматический микроскоп,
окулярный микрометр и гелиометр.
Независимо от У. Волластона наблюдал (1814—15) и
первый исследовал и объяснил темные линии в солнечном
спектре,
названные
в
дальнейшем
его
именем
(фраунгоферовы линии), в частности, используя явление
дифракции, измерил длину их волны. Дифракцию изучал в
параллельных
лучах
(так
называемая
дифракция
Фраунгофера), сначала от одной щели, а затем от многих.
Большой заслугой Фраунгофера является широкое
использование им (с 1821) дифракционных решеток для
исследования спектров (некоторые исследователи даже
считают его изобретателем первой дифракционной решетки).
71
72. Дифракция Фраунгофера на щели
Использование приближенного метода зон ФренеляDC b sin
m
.
l/2
l/2
m четное
дифракционный минимум;
m нечетное
дифракционный максимум;
Условие минимумов:
b sin kl, k 1,2,...
l
sin k k .
b
72
73. Точное решение
Использование метода многолучевой интерференцииРазбиваем волновой фронт на большое число одинаковых участков:
N 0
sin
2 , I A2 ;
I I1
1
1
sin 2 0
2
2
1
N
I I0
2 b
0
sin ;
l N
A1
A0
I
, I1 02 .
N
N
I / I0
sin 2 b sin / l
b sin / l 2
l
sin 1
b
0
-2
-1
0
1
2
b sin / l
73
74. Дифракционная решетка
BC b, BD d ;d – период (постоянная
дифракционной решетки);
N – общее число щелей.
Рассматриваем задачу как
интерференцию многих волн
от всех щелей:
2
0
d sin ;
l
sin( Nd sin / l)
A A
;
sin( d sin / l)
sin( b sin / l)
A A1
;
b sin / l)
74
75.
sin 2 ( b sin / l) sin 2 ( Nd sin / l)I I1
;
2
2
( b sin / l)
sin ( d sin / l)
I1 - интенсивность света в центре экрана, обусловленная действием одной щели;
Главные максимумы:
d sin n nl, n 0, 1, 2,...;
Главные минимумы:
b sin m ml, m 1, 2,...;
Интенсивность в центре главного максимума нулевого порядка:
I 0 N 2 I1
Угловая ширина главных дифракционных максимумов
(в параксиальном приближении):
2l
Nd
75
76. Пример картины дифракции на решетке (N=10, d/b=2,7)
1I / I0
0
3l
4l
d
d
l
b
2l
d
l
d
0
2l
Nd
l
d
3l
d
2l
d
l
b
4l
d
sin
76
77. Дифракция на пространственной решетке
Метод Лауэd1 (cos cos 0 ) n1l,
d 2 (cos cos 0 ) n2l,
d3 (cos cos 0 ) n3l,
cos2 cos2 cos2 1
При заданных углах падения дифракционные максимумы возникают
только для определенных значений длин волн.
При заданной длине волны условия Лауэ можно удовлетворить
только при определенном направлении падающей волны.
При l 2d max (условие оптической однородности среды)
наблюдается только максимум нулевого порядка, нет дифракции.
77
78. ЛАУЭ Макс Феликс Теодор фон (9.Х 1879 —24.IV 1960) немецкий физик-теоретик
• Работы относятся к оптике,кристаллофизике,
сверхпроводимости, теории
относительности, квантовой
теории, атомной физике, физике
твердого тела.
• В 1912 разработал теорию
интерференции рентгеновских
лучей на кристаллах, предложив
использовать кристаллы как
дифракционные решетки для
рентгеновских лучей.
• За открытие дифракции
рентгеновских лучей Лауэ в 1914
удостоен Нобелевской премии.
• Это открытие привело к созданию
мощного способа исследования
структуры вещества —
рентгеноструктурного анализа. 78
79. Метод Вульфа-Брэгга
Дифракция на пространственной решетке рассматривается как результатотражения света от системы параллельных сетчатых плоскостей кристалла,
то есть плоскостей в которых лежат узлы кристаллической решетки:
Условие Вульфа-Брэгга:
2d sin nl
Наблюдение дифракционных максимумов возможно только при определенных
соотношениях между длиной волны и углом
.
79
80. БРЭГГ Генри (2.VII 1862-12.III 1942) английский физик
• Работы посвящены исследованиюрентгеновских лучей, проникающей и
ионизирующей способности быстрых
заряженных частиц, рентгеноструктурному
анализу, рентгеновской спектроскопии.
• Используя явление дифракции рентгеновских
лучей на кристаллах, совместно со своим
сыном Л. Брэггом впервые осуществил (1912)
исследование кристаллических структур, дал
экспериментальное доказательство
периодичности атомной структуры
кристаллов.
• Эксперименты Брэггов по изучению структур
кристаллов положили начало
рентгеноструктурному анализу и
рентгеновской спектроскопии.
• За большой вклад в изучение структуры
кристаллов с помощью рентгеновских лучей
Г. Брэгг (вместе с сыном) удостоен в 1915
Нобелевской премии.
80
81. БРЭГГ Лоуренс (31.111 1890-1.VII 1971) английский физик
Научные исследования относятся к теории
дифракции рентгеновских лучей,
рентгеноструктурному анализу, металлургии,
вопросам полиморфизма и фазовых
переходов в металлах и сплавах, химии белка,
истории физики.
В 1912 независимо от Ю. В. Вульфа нашел
уравнение, связывающее длину волны
рентгеновского излучения с периодом
кристаллической решетки кристалла (формула
Брэгга — Вульфа) и лежащее в основе
спектроскопии рентгеновских лучей.
Усовершенствовал методы
рентгеноструктурного анализа, разработал
методы расшифровки сложных
кристаллических структур. Используя
рентгеновские лучи, получил в 1939
оптическое изображение атомной структуры
кристалла (идея рентгеновского микроскопа).
Рентгеновский микроскоп Брэгга послужил
отправной точкой при разработке идей Д.
Габора по созданию голографии.
81
82. ВУЛЬФ Георгий Викторович (22.VI 1863 — 25. XII 1925) советский кристаллофизик
Основные работы в области
кристаллографии, кристаллофизики,
кристаллооптики, рентгеноструктурного
анализа, минералогии.
Предложил способ вывода всех видов
симметрии кристаллов, разработал
графический метод обработки
результатов измерения кристаллов с
помощью стереографической сетки
(сетка Вульфа).
Обнаружил (1895) влияние силы
тяжести на форму кристалла во время
его роста из раствора, изобрел
вращающий кристаллизатор и
разработал метод получения
кристаллов правильной формы.
Установил закон процесса роста
кристаллов. В 1913 независимо от Л.
Брэгга вывел условия
интерференционного отражения
рентгеновских лучей от кристаллов 82
(формула Брэгга —Вульфа).
83. Рентгеноструктурный анализ (метод Лауэ)
• С помощью дифракции рентгеновского излучения накристаллах можно осуществлять их
рентгеноструктурный анализ, т.е. исследовать
строение кристаллических решеток и определять
межплоскостные расстояния.
• В методе Лауэ используется дифракция узкого пучка
“белого рентгеновского излучения” (с непрерывным
спектром) на неподвижном монокристалле.
• “Изображение” кристалла, получаемое на
фотопластинке в результате дифракции называется
лауэграммой.
83
84. Разрешающая способность оптических приборов
• - способность давать раздельные изображения двухблизких друг к другу точек объекта.
• Любая реальная оптическая система формирования
изображения (линза, зеркало, телескоп, микроскоп)
отображает светящуюся точку в размытое пятнышко.
• Две причины: геометрические аберрации (искажения)
и дифракция света на входной апертуре оптической
системы.
• Геометрические аберрации можно ослабить,
уменьшая входную апертуру и усложняя оптические
элементы системы.
• Дифракционное размытие изображения
принципиально неустранимо, и определяет
предельную разрешающую способность оптической
системы.
84
85. Критерий Релея
• Согласно критерию Рэлея изображения двуходинаковых точечных источников еще можно видеть
раздельно, если центральный максимум
дифракционной картины от одного источника
совпадает с первым минимумом дифракционной
картины от другого.
85
86. Разрешение телескопа
• Согласно критерию Релея две близкиезвезды, наблюдаемые в телескоп в
монохроматическом свете с длиной волны
l видны раздельно, если угловое
расстояние между ними 1,22 l/D, D –
диаметр объектива.
• Величина 0 = 1,22 l/D называется
угловым пределом разрешения
телескопа, а обратная величина 1/ 0 –
разрешающей силой телескопа.
• Условие разрешения для зрительной трубы
и фотоаппарата при рассматривании и
фотографировании удаленных предметов
совпадает с условием разрешения для
телескопа.
86
87. Угловой предел разрешения глаза
• Угловой предел разрешения глазаопределяется дифракцией света на зрачке
(D~2 мм) и зернистой структурой сетчатки
глаза. Он составляет около угловой минуты
1’= 3∙10-3 рад.
• Таким образом, на расстоянии наилучшего
зрения (L ≈ 0.25 м) минимальное
разрешаемое расстояние между точками
составляет 0,1 мм.
• Разрешение 300 dpi (dots per inch – точек на
дюйм = 2.54 см) примерно соответствует
разрешению глаза.
87
88. Спектральная разрешающая способность
• – способность давать раздельныеизображения двух линий спектра с близкими
длинами волн.
• Дифракционная решетка – пример
спектрального прибора. Разрешающая
способность R=l/( l)0.
• Критерий Рэлея дает R=m∙N, m – порядок
спектра, N – общее число штрихов.
• У хороших спектральных оптических
приборов разрешающая способность
составляет 105-106.
88
89. Дисперсия света
• - зависимость фазовой скорости света всреде от его частоты (зависимость
показателя преломления от частоты).
• Сложный немонотонный характер дисперсии.
• Область нормальной дисперсии - показатель
преломления увеличивается с ростом
частоты.
• Область аномальной дисперсии – показатель
преломления уменьшается с ростом частоты.
• Прозрачные среды в оптическом диапазоне
имеют нормальную дисперсию.
• В области аномальной дисперсии
наблюдается сильное поглощение света.
89
90.
Опыт НьютонаЗависимость n(l) для стекла
в видимом диапазоне
sin i
n(n);
sin r
c
n(n)
;
v (n )
c
l ;
n
n n(l).
90
91.
Зависимость n n в широком диапазоне изменения частоты света91
92. Особенности распространения полихроматических волн в диспергирующей среде
It=t1
t=t2
x
• Разложение в интеграл Фурье на гармоники различных частот.
• Каждая гармоника распространяется со своей скоростью.
• Форма светового импульса меняется по мере распространения.
92
93. Фазовая и групповая скорость
• Фазовая скорость синусоидальной волны:S (t , x) A0 sin( t kx );
dx
t kx const ; v ;
dt
v
k
• Понятие групповой скорости. Рассмотрим простой пример.
• Группа волн состоит из двух плоских синусоидальных волн
равной амплитуды A1=A2=A0, но имеющих немного различные
частоты << .
S (t , x) A0 sin( t kx) A0 sin[( d )t (k dk ) x];
sin sin 2 cos
sin
;
2 2
d
dk
t d x dk
S (t , x) 2 A0 cos
sin
t k x ;
2
2
2
t d x dk
A(t , x) 2 A0 cos
- модуляция амплитуды несущего колебания.
93
2
94.
Sx
• Групповая скорость - скорость распространения огибающей
(скорость передачи информации, энергии, сигнала).
• Примечание. Такое определение верно только для
квазимонохроматической волны в недиспергирующей среде.
• Смотрим перемещение точки, в которой амплитуда
постоянна, например, А=0 или А=А0
t d x dk const;
dx
u ;
dt
d
u
dk
94
95. Связь между групповой и фазовой скоростью
v k;2
k ;
l
d d (v k )
dv
v k
;
dk
dk
dk
dl
dk 2 2 ;
l
d
dv
v l ;
dk
dl
dv
u v l
dl
Отсюда видно, что групповая скорость в диспергирующей среде в
случае аномальной дисперсии может оказаться больше фазовой
скорости в данной среде и в принципе даже больше скорости света в
вакууме.
Этот факт не противоречит постулатам теории относительности,
поскольку форма сигнала в диспергирующей среде деформируется и
групповая скорость уже не дает в этом случае скорость
распространения энергии.
Следует также иметь в виду, что в области аномальной дисперсии
95
имеет место сильное поглощение.
96. Классическая электронная теория дисперсии
(1)(2)
(3)
2
n
1
P n0 pe
pe e r
n - показатель преломления; - относительная диэлектрическая проницаемост
(4)
(5)
P
n
e
r
P
E
0 (молекул) среды; pe - наве
восприимчивость среды;0 n0 - концентрация атомов
ная диэлектрическая проницаемость среды;
- диэлектрическая
атома, обусловленный
смещением оптических электронов;
e - элементарный з
атомов (молекул) среды; pe - наведенный полем электрический момент
(поляризованность среды); 0
- электрическая постоянная; E - напряженность
e - элементарный заряд; P - вектор поляризации среды
кая постоянная; E - напряженность электрического поля световой волны.
ких электронов;
96
97.
(6)7)
2
d r
F e E
m
Fa Fb F
2
dt
(9)
(8)
dr
2
Fa k r m 0 r
Fb 2 m
dt
m - масса электрона;
0 - циклическая частота свободных незатухающих
колебаний оптического электрона;
- коэффициент затухания свободных колебаний электрона;
Fa - квазиупругая возвращающая сила;
Fb - сила сопротивления;
F - вынуждающая сила.
97
98.
2d r
(10)
dr
2
2 0 r
2
dt
dt
A
e
E0
m
(11)
e
E
m
E
E0 cos t
(13)
r A cos t 0
(14)
1
2
0 2 2 4 2 2
(12), (13), (4) =>
(12)
P
(15)
2
tan 0
0 2 2
n0 e E0 cos t 0
2
2
2 2
m 0 4
2
0
n0 e E0 cos t
2
(16)
P
(17)
2
m 0
2
2
2
n0 e
2
2
m 0 0
98
99.
22
n
1
n0 e
2
2
m 0 0
(18)
99
100.
• В действительности, как показывают опыты, при прохождениисвета сквозь любое газообразное вещество наблюдается целый
ряд характерных для этого вещества линий поглощения.
• Следовательно, каждое вещество характеризуется
определенным набором различных собственных частот.
• В классической теории дисперсии света вводится
предположение о том, что каждый атом (или молекулу)
вещества можно рассматривать как систему из гармонических
осцилляторов с различными собственными частотами.
• Под действием электрического поля световой волны все эти
осцилляторы совершают вынужденные колебания и вносят свой
вклад в поляризацию вещества, а следовательно, и в
выражение для его показателя преломления.
100
101. Поляризация света
• Плоская электромагнитная волна - поперечная волна(колебания перпендикулярны направлению
распространения).
• В случае поперечных волн возникает понятие
поляризации (состояния поляризации), которое
характеризуется направлением колебаний в плоскости
нормальной направлению распространения, и
характером изменения этого направления.
• Для продольной волны по определению направление
колебаний совпадает с направлением распространения
и такого вопроса не возникает.
101
102.
• Свет называетсянеполяризованным, если
направление колебаний
меняется хаотическим
образом и равновероятно
любое направление под
углом от 0 до 2 к оси Х.
• Свет называется линейно
поляризованным (плоско
поляризованным), если
колебания происходят в
одной плоскости и угол не
меняется с течением
времени.
102
103.
• Когерентная плоская монохроматическая волнавсегда является поляризованной. Но ее поляризация
может быть не только линейной, но и круговой
(правой, левой), когда конец вектора E описывает
окружность, вращаясь с частотой и эллиптической
(правой, левой), когда конец вектора E описывает
эллипс с частотой .
• Под термином “поляризация света” часто
понимают не состояние поляризации, а процесс
выделения линейно поляризованного света из
естественного света.
103
104.
• Поляризатор – устройство, предназначенное дляполяризации света. Действие поляризаторов
основывается на поляризации света при отражении,
преломлении, а также на явлениях двойного
лучепреломления и дихроизма (анизотропия
поглощения).
• Анализатор. Поляризаторы можно использовать в
качестве анализаторов, т.е. для определения
направления и степени поляризации.
• Главная плоскость поляризатора (или
анализатора) - плоскость поляризации света
пропускаемого поляризатором (или анализатором)
называется главной плоскостью поляризатора (или
анализатора).
104
105. Закон Малюса
• Интенсивности линейно поляризованного света, пропущенногоанализатором и падающего на него, связаны законом Малюса:
• - угол между направлением колебаний вектора E падающей
волны pp и главной плоскостью анализатора aa .
A2 Ap cos ,
I 0 A2p ,
I A22 ,
I I 0 cos 2
I( )
I( )
1
• При прохождении естественного света через поляризатор: I 105 I 0
2
106. Закон Брюстера
• Закон Брюстера. Отраженный свет полностью линейнополяризован в плоскости, перпендикулярной плоскости падения
при угле падения, который удовлетворяет условию
tg (iБ ) n21
Полярная диаграмма излучения диполя
• Стопа пластин – при пропускании получаем свет с высокой
степенью поляризации.
106
107. БРЮСТЕР Дэвид (11. XII 1781-10.II 1868) шотландский физик
• Основные работы в области оптики.Исследовал поляризацию света,
установил в 1815 связь между
показателем преломления
диэлектрика и углом падения света,
при котором отраженный от
поверхности диэлектрика свет
полностью поляризован (закон
Брюстера).
• Изучал поглощение света, открыл
двойное лучепреломление в средах с
искусственной анизотропией, круговую
поляризацию (1815), существование
двухосных кристаллов (1818).
• Усовершенствовал стереоскоп (1849),
сконструировал в 1835 линзы для
маяков. В 1826 построил подковообразный электромагнит.
• Автор исследования о жизни И.
Ньютона (1832).
107
108. Формулы Френеля
• p волна (E в плоскости падения);• s волна (E в плоскости, перпендикулярной плоскости
падения).
• Граничные условия: непрерывность тангенциальных
составляющих E и H, непрерывность нормальных
составляющих D и B => формулы Френеля:
отр
0 tg (i r )
E p E p
;
tg (i r )
отр
0 sin( i r )
Es
Es
;
sin( i r )
Rp
Rs
I отр
p
I 0p
I sотр
I s0
tg 2 (i r )
2
tg (i r )
sin 2 (i r )
2
sin (i r )
;
;
108
109.
1) Нормальное падение:sin(i r ) tg (i r ) i r; sin(i r ) tg (i r ) i r;
n21 1
R p Rs
n21 1
i / r n21
tgi Б n21;
2) При падении под углом Брюстера:
i r / 2;
2
R p 0.
tg (i r ) ;
sin 2 ( i r ) (sin i cos r sin r cos i )2
Rs
;
2
2
sin ( i r ) (sin i cos r sin r cos i )
cosr sin i,
cosi sin r.
(sin i sin r )
Rs
(sin 2 i sin 2 r )2
2
2
2
n2 1
Rs 21
n2 1
21
2
109
110. Числовые примеры и графики
n21 1,5; i 0 R p Rs 0,04n21 1,5
n21 1 / 1,5
iБ 56,310
iБ 33,690 , i0 41,810
1
1
0.8
0.8
Rp 0.6
Rp 0.6
Rs
0
Rs
0.4
0.4
0.2
0.2
0
0
0
0
20
40
60
180
80
90
0
0
0
20
40
60
180
80
90
110
111. Степень поляризации
IПP
.
IП IН
Измерение степени поляризации с помощью анализатора:
I max
1
1
I Н I П , I min I Н
2
2
I max I min
P
.
I max I min
111
112. Поляризация плоской монохроматической волны
Ex Ax sin( t kz 1); E y Ay sin( t kz 2 ); 1z const 0; 1 0; 2 1 ;
Ex Ax sin( t ); E y Ay sin( t );
E i Ex j E y ;
2
3
4
Найдем уравнение траектории конца вектора
в координатах (Ex,Ey).
E
112
113.
3 =>Ex
sin( t ) ; E y Ay [sin( t ) cos cos( t ) sin ];
Ax
2
Ex
Ex
cos 1 sin ;
Ay Ax
Ax
Ey
2
Ey
E y Ex
E
x
2
cos sin 2 ;
Ay
Ay Ax
Ax
5
2
Получили уравнение кривой 2-го порядка.
В общем случае это эллипс, гипербола или парабола.
Поскольку Ex и Ey не обращаются в бесконечность,
то это уравнение эллипса.
Поляризация называется эллиптической.
6
113
114. Важные частные случаи
Линейная поляризация:0 Ey
Ay
Ax
Ex ; E y
Ay
Ax
Ex ;
Круговая поляризация:
2
2
2
, Ax Ay A Ex E y A ;
2
114
115. Направление вращения светового вектора
EydEy
Ay
E
Ax
Ax
Ay
dEy
dt
dt
M
Ex
Ay cos( t );
M : Ex Ax ; t ;
2
dEy
Ay cos ;
dt
2
Ay sin ;
sin 0 вращение по часовой стрелке (правая поляризация);
sin 0 вращение против часовой стрелки (левая поляризация).
115
116. Эллипс поляризации при различных j
Эллипс поляризации при различных0
0 /2
/2
/2
Ey
Ex
/2
/2
/2 0
• Движение конца светового вектора по эллипсу совершается от
положительного конца оси опережающего направления к
положительному концу оси запаздывающего направления, если
смотреть навстречу лучу.
116
117. Двойное лучепреломление
Одноосный кристалл:x= y= o;
z= e o;
Oсь Z направлена вдоль
оптической оси MN
• Возникает в оптически
анизотропных средах (одноосных
и двухосных кристаллах).
• В нашем курсе рассматриваем
только одноосные кристаллы
(исландский шпат, кварц,
турмалин, апатит).
• Оптическая ось кристалла –
направление в кристалле, при
распространении вдоль которого
не возникает двойного
лучепреломления.
• Главная плоскость кристалла –
плоскость, образованная
падающим лучом и оптической
осью кристалла.
• Обыкновенный луч:
E оптической оси кристалла.
• Необыкновенный луч: E лежит в
главной плоскости и не
оптической оси кристалла. 117
118.
• Обыкновенный луч подчиняется обычному законупреломления Снеллиуса.
sin i
n0 0 .
sin r
• Необыкновенный луч не подчиняется закону
преломления Снеллиуса.
• Для построения хода лучей в оптически
анизотропных средах используют метод лучевых
поверхностей.
• Лучевая поверхность – г.м.т. концов векторов
фазовой скорости обыкновенной и необыкновенной
волн, проведенных из некоторой точки кристалла по
всем направлениям.
118
119.
• Для обыкновенной волны лучеваяповерхность – сфера.
• Для необыкновенной волны лучевая
поверхность –эллипсоид.
Оптически положительный
кристалл (кварц)
v e v 0 , ne n0
Оптически отрицательный
кристалл (исландский шпат,
турмалин, апатит)
v e v 0 , ne n0
119
120.
Построение обыкновенного и необыкновенноголучей при косом падении методом Гюйгенса
N
A
B
a
Co
Ce
b
M
e
o
MN – главная оптическая ось кристалла;
ab – граница раздела изотропной и анизотропной сред;
о – обыкновенный луч; е – необыкновенный луч.
120
121.
Построение обыкновенного и необыкновенноголучей при нормальном падении методом Гюйгенса
N
N
A
B
a
Co
b
M
M
Ce
o
e
o
MN – главная оптическая ось кристалла;
ab – граница раздела изотропной и анизотропной сред;
о – обыкновенный луч; е – необыкновенный луч.
e
121
122. Фазовые пластинки
• Кристалл вырезается так, что его грань параллельнаоптической оси.
lопт (n0 ne )d ;
d – толщина пластинки;
2
(n0 ne )d ;
l0
lопт l 0 4 ml 0
- пластика l/4 может преобразовать свет
с линейной поляризацией в свет с круговой
поляризацией и наоборот;
lопт l 0 2 ml 0
- пластика l/2 может повернуть плоскость
поляризации на 90.
122
123. Поляризационные призмы
• Призма Николя.• Кристалл исландского шпата (n0=1,66; ne=1,49)
разрезан специальным образом и склеен канадским
бальзамом (n=1,55).
• Используется явление ПВО для обыкновенного луча.
123
124. Тепловое излучение
Излучение любого вида возникает врезультате перехода атомов (молекул) из
возбужденного состояния с большей
энергией в состояние с меньшей энергией.
Тепловое (температурное) излучение
отличается только способом перехода в
возбужденное состояние. Такой переход
осуществляется за счет теплового движения
атомов и молекул.
124
125.
• Тепловое излучение - единственное, которое можетбыть равновесным (равновесие между телом и
излучением, Т=const.). Пример: излучение в
теплоизолированной эвакуированной полости.
• Идеальные отражающие стенки не дадут
равновесного излучения, но достаточно пылинки
(Планк).
• Равновесие связано со вторым началом
термодинамики: не может быть самопроизвольной
передачи тепла от менее нагретого тела к более
нагретому. Отрицательная обратная связь.
125
126.
Энергетическая светимость телаВт
Wизл Rэ ,
2
м
- поток энергии (мощность) с единичной площади поверхности по всем
направлениям в пределах телесного угла 2 стеррадиан.
Спектральная плотность энергетической светимости
dWизл
Вт
rn
,
.
2
dn
м Гц
Спектральный коэффициент поглощения
dWпогл
an
.
dWпад
Равновесие Wизл
Wпогл
Детальное равновесие dWизл dWпогл. в данном dn.
В широком смысле детальное равновесие включает все
характеристики (поляризацию, направление, спектр и проч.)
126
127. Абсолютно черное тело
- такое тело, которое при любой температуреполностью поглощает всю энергию падающих на него
электромагнитных волн независимо от их частоты,
поляризации и направления излучения.
a(n) 1
Физическая модель абсолютно черного тела:
127
128. Закон Кирхгофа
- отношение спектральной плотности энергетической светимоститела к его спектральному коэффициенту поглощения не зависит
от материала тела и равно спектральной плотности
энергетической светимости абсолютно черного тела,
являющейся функцией только температуры и частоты
(универсальная функция Кирхгофа).
rn
0
rn
an
128
129. Доказательство закона Кирхгофа
• Теплоизолированная система состоит из двух бесконечнодлинных пластин.
• Пластина “а” – АЧТ, пластина “b” – имеет характеристики an и rn.
• Тепловое равновесие.
a
b
a
a
b
b
a
b
dWизл
dWпогл
; dWизл
dWпогл
; dWпад
dWпад
.
a
rn0dn dWизл
b
b
dW
dW
rn dn
b
погл
изл
dWпад
;
an
an
an
rn
rn0 .
an
129
130. Понятие серого тела
an constc
an
1.
• Реальные тела бывают серыми только в узком
интервале частот и используется более общее
понятие коэффициента черноты (коэффициента
излучения теплового источника)
0
Rэ Rэ ;
0
a
r
n n dn;
0
.
0
rn dn
0
130
131.
• Поиск универсальной функции Кирхгофа спомощью законов термодинамики позволил
открыть закон Стефана - Больцмана:
0
Rэ
T
4
8
const 5,7 10 Вт /( м K ).
2
4
• Вин показал, что функция Кирхгофа должна
иметь следующий вид (формула Вина):
0
rn
n
n f .
T
3
131
132.
• Результаты экспериментальных исследований сиспользованием модели АЧТ показали, что на малых
частотах
0
2
rn c1n T ;
• на больших частотах (Закон Вина):
rn0
n
c2n exp c3 .
T
3
Эмпирические кривые функции Кирхгофа.
Закон смещения Вина.
nm
b
b1; l m ;
T
T
(b 2,9 10 3 м K )
132
133.
Вывод закона Стефана-Больцмана из формулы Вина:n
Rэ0 с4n3 f dn T 4c4 x3 f x dx T 4 ;
T
0
0
n
x ; c4 x3 f x dx.
T
0
Вывод закона смещения Вина из формулы Вина:
n
d
0
3 f
drn
n n T
3n 2 f
0;
dn
dn
T T
d f x
3 f x x
;
dn
Корень этого уравнения имеет
определенное значение, которое
можно обозначить как b1.
xm
nm
b1;
T
133
134.
• Рэлей и Джинс в 1900 г. рассмотрели равновесное излучение вполости с зеркальными стенками с позиций статистической
физики (совокупность стоячих электромагнитных волн с
собственными частотами).
• Число волн – число степеней свободы. На каждую степень
свободы приходится энергия kT (закон о равном распределении
энергии по степеням свободы).
• Получили следующий результат (формула Рэлея-Джинса):
2
2
n
rn0 2 kT .
c
• Классическая физика дает правильный результат для функции
Кирхгофа только в области малых частот.
• Ультрафиолетовая катастрофа классической физики:
Rэ0
2 n 2
2 kT .
0 c
134
135. Формула Планка для излучения АЧТ
• Планк отталкивался от формулы Рэлея-Джинса, ноотказался от использования классического закона
равного распределения энергии по степеням
свободы равновесной системы и искал решение в
виде
rn0
2 n
2
c
2
wn ,
где <wn> - средняя энергия осциллятора с
собственной частотой n.
135
136.
• Октябрь 1900 г. Планк подбором математическихмоделей находит для <wn> выражение
wn
n
const
,
a1n
exp
1
kT
которое согласуется с данными экспериментов во
всем диапазоне частот, что дает для функции
Кирхгофа
3
a
n
2
rn0
,
a1n
exp
1
kT
где a1,a2 - постоянные коэффициенты.
136
137.
• Декабрь 1900 г. Планк дает физическое обоснование своемурезультату на основе квантовой гипотезы.
• Согласно квантовой гипотезе Планка энергия осцилляторов
(атомов) может меняться только дискретными порциями,
пропорциональными некоторой элементарной порции - кванту
энергии w0
• Рассуждения следующие: согласно классическому
распределению Максвелла-Больцмана вероятность
нахождения осциллятора с энергией nw0 при температуре Т
равна
nw0
Pn c exp
; (1)
kT
1
c
; (3)
nw0
exp
kT
n 0
c Pn 1; (2)
n 0
nw
exp 0
kT
Pn
; (4)
nw0
exp
kT
n 0
137
138.
wnnw0 Pn w0 nPn ;
n 0
(5)
n 0
nw0
n exp kT
;
wn w0 n 0
nw0
exp kT
n 0
(6)
(7)
w0
kT
n exp n
wn w0 n 0
exp n
; (8)
n 0
138
139.
Используем формулу для суммы членов геометрическойпрогрессии со знаменателем
q exp ;
(9)
1
1
exp n 1 q 1 exp ;
n 0
(10)
d
d
1
exp( )
n
exp
n
exp
n
; (11)
2
d n 0
d 1 exp( ) [1 exp( )]
n 0
exp( )
exp( )
w0
[1 exp( )]2
wn w0
w0
; (12)
1
1 exp( ) exp( ) 1
139
1 exp( )
140.
22
n
w0
0
rn 2
;
w0
c
exp 1
kT
(13)
• Сопоставление (13) с формулой Вина дает
w0=const·n.
• Константа получила впоследствии имя Планка и
обозначается h.
• Величина кванта w0=hn .
• Искомое выражение для универсальной функции
Кирхгофа или спектральной плотности энергетической
светимости равновесного излучения абсолютно
черного тела имеет вид:
140
141.
22
n
hn
0
rn 2
hn
c
exp 1
kT
2
2
hc
1
0
rl
5
hc
l
exp
lkT
1
rl0
rn0
T=60000
T=60000
50000
50000
40000
n
40000
l
141
142.
• Формула Планка соответствует всем ранееоткрытым законам теплового излучения.
• Спектральная плотность энергетической светимости
связана со спектральной плотностью объемной
плотности энергии соотношением
0
rn (n,T )
c 0
n (n,T ).
4
• Поэтому формула Планка для спектральной
плотности объемной плотности энергии имеет вид
2
8
n
hn
0
n 3
hn
c
exp 1
kT
142
143. Понятие об оптической пирометрии
• Оптическая пирометрия – совокупность оптическихметодов измерения высоких температур, основанных
на законах теплового излучения.
• Приборы, применяемые для этого называются
пирометрами.
• В радиационных пирометрах регистрируется
интегральное (полное) излучение исследуемого
нагретого тела.
• В оптических пирометрах регистрируется излучение
тела в каком-либо одном или двух узких участках
спектра.
143
144. ПЛАНК Макс Карл Эрнст Людвиг (23.IV 1858 —4.Х 1947) — немецкий физик-теоретик, основоположник квантовой теории
Работы относятся к термодинамике, теории
теплового излучения, теории относительности,
квантовой теории.
В 1900, исходя из чуждого для классической
физики предположения, что атомные осцилляторы
излучают энергию лишь определенными порциями
— квантами, причем энергия кванта
пропорциональна частоте колебания (гипотеза
квантов), вывел закон распределения энергии в
спектре абсолютно черного тела.
Ввел фундаментальную постоянную или квант
действия (постоянная Планка).
Закон излучения Планка показал, что, кроме
атомистической структуры материи, существует
атомистическая структура энергии, управляемая
универсальной постоянной, введенной Планком.
Это открытие стало основой для всех исследований
в физике XX в. и с того времени почти полностью
обусловило ее развитие.
Нобелевская премия 1918 г. за открытие кванта
действия.
144
145. КИРХГОФ Густав Роберт (12.III 1824 - 17.Х 1887) — немецкий физик
КИРХГОФ Густав Роберт(12.III 1824 17.Х 1887) —
немецкий физик
Работы посвящены электричеству, механике,
оптике, математической физике, теории упругости,
гидродинамике.
В 1845 открыл закономерности в протекании
электрического тока в разветвленных
электрических цепях (правила Кирхгофа), в 1857
построил общую теорию движения тока в
проводниках.
Установил (1859) один из основных законов
теплового излучения, согласно которому
отношение испускательной способности тела к
поглощательной не зависит от природы
излучающего тела (закон Кирхгофа), предложил
(1862) концепцию черного тела и дал его модель.
Развил (1882) строгую теорию дифракции.
Усовершенствовал теорию магнетизма Пуассона.
Исследовал также упругость твердых тел,
колебания пластин и дисков, форму свободной
струи жидкости, движение тела в жидкой среде.
145
146. ВИН Вильгельм (13.I 1864 - 30.YIII 1928) немецкий физик
ВИН Вильгельм(13.I 1864 30.YIII 1928)
немецкий физик
• Работы относятся к теории теплового
излучения, оптике, термодинамике,
гидродинамике, изучению электрических
разрядов в газах.
• В 1893 распространил понятия температуры
и энтропии на тепловое излучение, показал,
что максимум излучения в спектре
абсолютно черного тела с увеличением
температуры смещается в сторону
коротких волн (закон смещения Вина).
• В 1895 совместно с О. Люммером развил
идеи Г. Кирхгофа об абсолютно черном
теле, показал, что его можно осуществить в
виде полости с внутренними зеркальными
стенками и узким отверстием.
• Исследования Вина сыграли значительную
роль в развитии квантовой теории
• Нобелевская премия 1911 за открытие
146
законов теплового излучения.
147. РЭЛЕЙ Джон Уильям (12.XI 1842 —30.VI 1919) английский физик
Работы посвящены теории колебаний, акустике,
теории теплового излучения, молекулярной
физике, гидродинамике, электромагнетизму,
оптике.
Изучал дифракцию, рассеяние и поглощение
волн.
Заложил основы теории молекулярного
рассеяния света, в частности ввел понятие о так
называемом рэлеевском рассеянии света,
объяснил голубой цвет неба.
В 1894 вместе с У. Рамзаем открыл новый
химический элемент — аргон и определил его
свойства и место в периодической системе
элементов (Нобелевская премия, 1904).
В 1900 вывел закон распределения энергии
излучения в спектре абсолютно черного тела
(закон Рэлея — Джинса).
Yстановил разрешающую силу призменных и
дифракционных приборов.
147
148. ДЖИНС Джеймс Хопвуд (11.IX 1877 —16.1Х 1946) английский физик и астрофизик
• Основные физические исследованияпосвящены кинетической теории газов
и теории теплового излучения
(формула Рэлея — Джинса).
• Работы Джинса посвящены также
квантовой теории, математической
теории электричества и магнетизма,
теоретической механике, теории
относительности.
• Астрофизические исследования
Джинса относились к фигурам
равновесия вращающихся жидких тел,
строению и эволюции звезд и их
систем, происхождению Солнечной
системы.
• Джинс был одним из лидеров
кембриджской школы современного
физического идеализма. Написал
много научно-популярных книг.
148
149. Внешний фотоэлектрический эффект
• Внешний фотоэлектрический эффект (внешнийфотоэффект) – явление вырывания электронов из
твердых и жидких веществ под действием света.
• Существует аналогичное явление в газах (ионизация
атомов и молекул газа под действием света), которое
называется фотоионизацией.
• Фотоэффект у металлов впервые был подробно
исследован русским физиком А.Г. Столетовым в
1888-1890 гг.
149
150. СТОЛЕТОВ Александр Григорьевич 29.VII 1839-14.V 1896 русский физик.
Научные работы посвящены
электромагнетизму, оптике,
молекулярной физике, философским
вопросам науки.
Впервые снял кривую магнитной
проницаемости ферромагнетика (кривая
Столетова). Предложил два важных
метода магнитных измерений веществ —
метод тороида с замкнутой магнитной
цепью и баллистическое измерение
намагниченности.
В 1888 — 90 выполнил цикл работ по
исследованию явления внешнего
фотоэффекта, обнаруженного Г. Герцем
в 1887.
Рассмотрел вопрос об инерционности
фототока и оценил его запаздывание по
отношению к освещению в 0,001 с.
Открыл законы внешнего фотоэффекта).
Изучал несамостоятельный газовый
разряд. Исследовал критическое
состояние вещества.
150
151. Опыт Столетова
• S – источник света;• C – медная сетка;
• D – цинковая
пластинка;
• Б – аккумуляторная
батарея;
• G – гальванометр;
• V – вольтметр.
151
152. Усовершенствованная установка
• Используется вакуумная трубка, монохроматическоеизлучение; напряжение регулируется потенциометром.
152
153. Вольтамперные характеристики фотоэффекта
• E – освещенность фотокатода;• Iн – ток насыщения;
• U0 – задерживающее напряжение.
153
154. Законы фотоэффекта
• 1. Максимальная начальная скоростьфотоэлектронов определяется частотой света и не
зависит от его интенсивности.
• 2. Для каждого вещества существует красная
граница фотоэффекта, т.е. минимальная частота n0
света, при которой еще возможен внешний
фотоэффект (n0 зависит от химической природы
вещества фотокатода и состояния его поверхности).
• 3. Фототок насыщения пропорционален
освещенности фотокатода.
• 4. Фотоэффект практически безынерционен.
154
155. Формула Эйнштейна для фотоэффекта
• Законы 1,2,4 не имеют классического объяснения.• Объяснение законам фотоэффекта дал Эйнштейн в
1905 г, использовав квантовую гипотезу Планка.
hn A
2
mv max
2
• h=6,62 ·10-34 Дж·с – постоянная Планка;
• А – работа выхода;
• m – масса электрона.
155
156. ЭЙНШТЕЙН Альберт (14.III 1879 - 18.IY 1955) выдающийся физик-теоретик
ЭЙНШТЕЙН Альберт(14.III 1879 18.IY 1955)
выдающийся физик-теоретик
Создатель специальной и общей теорий
относительности, коренным образом
изменивших представления о пространстве,
времени и материи.
Oткрыл закон взаимосвязи массы и энергии.
Это соотношение Эйнштейна лежит в основе
всей ядерной физики.
В 1905 создал фотонную теорию света.
Нобелевская премия, 1921, за открытие
законов фотоэлектрического эффекта.
Предсказал в 1916 явление
индуцированного излучения, ввел
вероятности спонтанного и вынужденного
излучений (коэффициенты Эйнштейна).
В статистической физике развил в 1905
молекулярно-статистическую теорию
броуновского движения, в 1924 — 25 создал
квантовую статистику частиц с целым
спином (статистика Бозе — Эйнштейна).
156
157. Экспериментальное определение постоянной Планка
2mv max
eU 0
2
A
n0
h
n0
eU 0 h(n n 0 )
A
h
h tg
157
158. Многофотонный фотоэффект
• При большой интенсивности света (например отлазера) становится существенной вероятность того,
что на электрон одновременно упадут два или
несколько одинаковых фотона.
• В этом случае фотоэффект приобретает
классические черты.
• Нарушается закон красной границы фотоэффекта.
• Максимальная начальная скорость фотоэлектронов
возрастает с увеличением интенсивности света.
• Такие многофотонные процессы взаимодействия
света высокой интенсивности с веществом
изучаются в нелинейной оптике.
158
159. Масса и импульс фотона
• Помимо энергии фотон обладает также массой иимпульсом.
• Формула для массы фотона может быть
непосредственно выведена из формулы,
выражающей взаимосвязь массы и энергии в теории
относительности.
W mc2 ; Wф hn; mфc hn;
2
hn
mф 2 ;
c
• Масса фотона существенно отличается от массы
микроскопических тел и масс других «элементарных»
частиц. Это отличие состоит в том, что фотон не
обладает массой покоя. Покоящихся фотонов не
159
существует.
160.
mm0
v
1
c
2
• Фотон всегда в любом веществе движется со
скоростью с. Этот вывод не противоречит тому, что
фазовая и групповая скорости света в веществе
отличны от с. Распространение света в среде
сопровождается процессами «переизлучения» —
фотоны поглощаются и вновь испускаются частицами
среды.
• Из сказанного видно, что современные квантовые
представления о свойствах света существенно
отличаются от ньютоновской корпускулярной теории
света.
160
161.
W c p2 m02c2 mc2 ;pф mфc
2 n
k
; (3)
c
h
;
2
hn h
pф mфc
k ;
c l c
(1)
(2)
(4)
(6)
n ;
2
pф k
(5)
(7)
• Фотон обладает всеми тремя характеристиками любой
движущейся частицы: массой, импульсом, энергией, которые
связаны с волновой характеристикой n.
161
162. Давление света
• Давление света успешно объясняется какволновой, так и квантовой теорией.
• С квантовой точки зрения давление света на
поверхность какого-либо тела обусловлено
тем, что при соударении с этой поверхностью
каждый фотон передает ей свой импульс.
162
163. Изотропное излучение
• Рассматриваем замкнутую полость с идеальноотражающими стенками.
• Фотоны движутся подобно молекулам идеального
газа.
h
n
i
1
2
m
;
i
pV miv i ;
2
c
3
2
m
v
i i hni W ;
v i c;
W – полная энергия всех фотонов в полости;
W w
p
3V 3
w – объемная плотность энергии излучения;
163
164. Поток монохроматического излучения, падающий нормально на поверхность.
• Пусть n – число фотонов, падающих на единицуплощади поверхности в единицу времени.
• R – коэффициент отражения;
• Давление равно импульсу, переданному этими n
фотонами поверхности.
2hn
hn
nhn
p
Rn (1 R)n
(1 R);
c
c
c
I
p (1 R) w(1 R)
c
I=nhn – интенсивность излучения;
w=I/c – объемная плотность энергии падающего излучения.
164
165. Эффект Комптона
• При рассеянии монохроматического рентгеновскогоизлучения легкими веществами (графитом,
парафином и др.) возникает изменение длины волны
излучения.
• Длина волны l’ рассеянного излучения оказывается
больше длины волны l падающего излучения.
• Разность l l’ l зависит только от угла рассеяния:
l l l 2l к sin 2 ( / 2),
lк – комптоновская длина волны.
• Эффект Комптона не имеет классического
объяснения и является прямым доказательством
существования фотонов.
165
166.
• С квантовой точки зрения рассеяние света, как ифотоэффект, является результатом взаимодействия
фотонов падающего на вещество излучения с
электронами этого вещества.
• В отличие от фотоэффекта в эффекте Комптона
электроны “легких” веществ являются почти
свободными. Для них энергия связи с системой, в
которой они находятся, пренебрежимо мала. При
этом поглощение фотона электроном невозможно.
166
167.
Предположим, что такое поглощение возможно. Тогда:(m m0 )c 2 hn, mv hn / c.
2
m0c
1 hn,
2
2
1 v / c
m0v
hn
.
c
1 v 2 / c2
1
• Можно показать, что последние два равенства не могут
выполняться одновременно при произвольных частотах,
отличных от нуля и бесконечности.
• Таким образом фотоэлектрическое поглощение света
свободными электронами невозможно, так как это противоречит
законам сохранения энергии и импульса.
167
168.
• Фотоэффект может происходить только на“связанных” электронах. В этом случае уравнения
законов сохранения принимают вид
2
hn m0c
1 W ,
2
2
1
v
/
c
m0v
k
p.
1 v 2 / c2
W
p
1
- энергия связи электрона с системой.
- импульс, передаваемый этой системе при фотоэффекте.
При v<<c первое уравнение
совпадает с уравнением
Эйнштейна для фотоэффекта:
m0v 2
hn
W,
2
168
169.
Схема опыта КомптонаРИ
D1 D2
ЛВ
РС
РИ – рентгеновский источник;
D1,D2 – диафрагмы с отверстиями;
ЛВ – легкое рассеивающее вещество;
РС – рентгеновский спектрограф.
169
170. КОМПТОН Артур Холли (10.IХ 1892—15.III1962) американский физик
• Работы посвящены атомной иядерной физике, физике космических
лучей.
• Открыл в 1922 явление изменения
длины волны рентгеновского
излучения вследствие рассеяния его
электронами вещества (эффект
Комптона) и независимо от П. Дебая
построил его теорию (Нобелевская
премия, 1927).
• Тем самым было получено прямое
доказательство существования
фотона.
• Наблюдал явление полного
внутреннего отражения рентгеновских
лучей и разработал метод измерения
длины волны рентгеновского
излучения.
170
• В 1921 пришел к идее спина.
171. Теория эффекта Комптона
Закон сохранения импульсаpф pe pф
2
pe
2
pф
2
2 pф pф cos pф ;
Закон сохранения энергии
W0 Wф W Wф
m0c cpф c
2
2
pe
2 2
m0 c
;
cpф
(2)
171
(1)
172.
(1),(2) =>m0c
pф
pф
;
m0c pф (1 cos )
h
pф ;
l
h
pф ;
l
1
l
1
h
l
(1 cos )
m0c
l l
(3)
;
h
(1 cos );
m0c
172
173.
l l l 2l к sin 2 ( / 2),h
lк
2,42621 10 12 м
m0c
Кинетическая энергия электрона отдачи:
WK W W0 Wф Wф h(n n );
(3) =>
m0c 2
n n
;
2
m0c hn(1 cos )
2 sin 2 ( / 2)
WK hn
,
2
1 2 sin ( / 2)
hn
.
2
m0c
173
174. Корпускулярно-волновая двойственность свойств света
• 1.
Фотоэффект и эффект Комптона демонстрируют
корпускулярные свойства света.
Интерференция и дифракция указывают на то, что
свет – это волны.
Встал вопрос о том, как примирить в единой теории
непрерывность волн и дискретность корпускул.
Вопрос был разрешен диалектически. Свет
одновременно обладает свойствами непрерывных
электромагнитных волн и свойствами дискретных
фотонов. Свет представляет собой диалектическое
единство этих противоположных свойств.
174
175.
• 2.
В проявлении этих противоположных свойств света
имеется вполне определенная закономерность.
С уменьшением длины волны (увеличением частоты)
все более отчетливо сказываются квантовые
свойства света.
Наоборот, у длинноволнового излучения квантовые
свойства видны в малой степени и основную роль
играют его волновые свойства.
Таким образом, если «перемещаться» по шкале
электромагнитных волн слева направо, от длинных
волн в сторону более коротких, то волновые
свойства электромагнитного излучения будут
постепенно уступать место квантовым свойствам.
175
176.
• 3.
Взаимосвязь между двойственными корпускулярноволновыми свойствами света находит простое
истолкование при статистическом подходе.
Интенсивность света (квадрат амплитуды световой
волны) в какой-либо точке пространства является
мерой вероятности попадания фотонов в эту точку.
Корпускулярные свойства обусловлены тем, что
энергия, импульс и масса излучения локализованы в
дискретных «частицах» — фотонах.
Волновые свойства обусловлены статистическими
закономерностями распределения фотонов в
пространстве, т. е. закономерностями,
определяющими вероятности нахождения фотонов в
различных точках пространства.
176
177.
• 4.• Вероятностный, недетерминированный характер
поведения присущ отдельным фотонам.
• Фотоны отличны от корпускул, которые движутся по
законам механики Ньютона, начальные условия не
определяют движения фотонов.
• Создание квантовой теории излучения – не возврат к
механической корпускулярной теории Ньютона, а
качественный скачок в более глубоком понимании
свойств излучения.
177
178. Корпускулярно-волновая двойственность свойств вещества
• В 1923 г. французский физик Луи де Бройльвысказал гипотезу, согласно которой корпускулярноволновая двойственность является универсальным
свойством любых материальных объектов, а не
только света.
• Частица массой m, движущаяся со скоростью v,
характеризуется не только координатами, импульсом
p и энергией E, но и подобно фотону частотой n и
длиной волны lБ:
E hn
h
p
lБ
178
179. Длина волны де Бройля
• Любой частице, обладающей импульсомp, соответствует длина волны де Бройля:
h
lБ
p
179
180. БРОЙЛЬ Луи де(р. 15.УП 1892) французский физик-теоретик, один из создателей квантовой механики
Работы в области классической и квантовой
механики, теории поля, квантовой
электродинамики, истории и методологии
физики.
В 1923 распространил идею А. Эйнштейна о
двойственной природе света на вещество,
предположив, что поток материальных
частиц должен обладать и волновыми
свойствами, однозначно связанными с
массой и энергией.
Это сопоставление вскоре (1927) получило
блестящее подтверждение в экспериментах
по дифракции электронов в кристаллах.
Идею о всеобщности корпускулярноволнового дуализма Э. Шредингер
использовал при создании своей волновой
механики.
За открытие волновой природы электрона
де Бройль в 1929 удостоен Нобелевской
премии.
180
181. Численные оценки
• Пуля массой 10 г, летящая со скоростью 660м/c.
l Б 1,0 10
34
м
• Электрон, движущийся в атоме со скоростью
2·106 м/с.
l Б 3,6 10
10
м
181
182. Дифракция электронов
• Формула де Бройля экспериментально подтвердилась в опытахДэвиссона и Джермера в 1927 году, наблюдавших рассеяние
электронов монокристаллом никеля.
182
183.
hh
;
lБ
p mv
v c;
(1)
2
p
W
;
2m
(2) =>
p 2mW ;
W eU уск ;
(4)
h
lБ
;
2meU уск
(3)
(6)
(5)
2d sin nl Б ;
(7)
183
184.
(6), (7) =>U уск
nD,
(8)
h
D
.
2me 2d sin
(9)
Результат опыта Дэвиссона и Джермера
184
185. ДЭВИССОН Клинтон Джозеф (22.Х 1881 — 1.11 1958) американский физик
• Работы относятся ктермоэлектронной и термоионной
эмиссии, электронной
микроскопии, тепловому
излучению, физике кристаллов,
квантовой теории.
• Вместе со своим сотрудником Л.
Джермером открыл в 1927
явление дифракции электронов
на кристалле никеля (независимо
от Дж. П. Томсона), что было
экспериментальным
подтверждением теории де
Бройля о волновых свойствах
материи (Нобелевская премия,
1937).
• Развил метод электронной
фокусировки.
185
186. ДЖЕРМЕР Лестер Халберт 10.Х 1896 — З.Х 1971 американский физик
• Исследования посвященыизучению термоионных
явлений, физике кристаллов,
атомной физике. В 1927
совместно с К. Дэвиссоном
(независимо от Дж. П.
Томсона) открыл дифракцию
электронов на
монокристалле никеля.
• Усовершенствовал
аппаратуру для получения
дифракционной картины при
помощи электронов низких
энергий.
186
187.
• В том же 1927 г. волновые свойства электронов былиэкспериментально обнаружены П. С. Тартаковским в
Ленинградском и Дж. П. Томсоном в Абердинском
университетах при прохождении пучков электронов сквозь
тонкие поликристаллические пленки золота и меди.
Сопоставление картин дифракции рентгеновских лучей
и электронных пучков на поликристаллических образцах
187
188. ТОМСОН Джордж Паджет З.V 1892—10.IХ 1975 английский физик
• Работы относятся к атомной иядерной физике, квантовой
механике, аэродинамике,
электрическим разрядам в
газах.
• Независимо от К. Дэвиссона и Л.
Джермера открыл в 1927
явление дифракции электронов,
чем была экспериментально
доказана волновая природа
электронов (Нобелевская
премия, 1937).
• Осуществил исследования по
геометрии электронограмм,
теории рассеяния.
188
189.
• Волновые свойства частиц не являютсяих коллективной характеристикой, а
присущи каждой частице в отдельности
(1949 г., опыты В.А. Фабриканта, Л.М.
Бибермана, Н.Г. Сушкина).
189
190. ФАБРИКАНТ Валентин Александрович (1907-1991) советский физик
Работы посвящены физической
электронике и оптике плазмы.
В 1939 показал возможность усиления
света за счет вынужденного испускания
в плазме с инверсией населенностей
на энергетических уровнях.
В 1949 наблюдал совместно с Л. М.
Биберманом и Н. Г. Сушкиным
дифракцию поочередно летящих
электронов.
В 1951 совместно с М. М. Вудынским и
Ф. А. Бутаевой сформулировал
принцип усиления электромагнитного
излучения при прохождении сред с
инверсной населенностью (идея
квантового усилителя).
За разработку люминесцентных ламп
совместно с другими удостоен в 1951
Государственной премии СССР.
Золотая медаль С. И. Вавилова (1965).
190
191.
• Кроме формулы де Бройля на частицы можноперенести соотношение
• W=hn=ћ ,
где W – полная энергия.
Наличие волновых свойств у движущихся частиц,
обладающих массой покоя, является универсальным
явлением, не связанным с зарядом и спецификой
структуры.
Вместе с тем, волновые свойства можно наблюдать
только у микрочастиц.
Для макрочастиц длина волны де Бройля настолько
мала, что говорить об экспериментах по их
дифракции бессмысленно.
Поэтому, волновые свойства у макроскопических тел
практически отсутствуют.
191
192. Свойства волн де Бройля
hh
l
;
mv p
(1)
p k ;
(2)
v
- скорость частицы
m
- масса частицы
Фазовая скорость свободной частицы (волны де Бройля):
v фаз
W mc2 c 2 c 2ml
;
k k p mv v
h
(3)
• Выводы.
• Фазовая скорость волны де Бройля всегда больше
скорости света.
• Волна де Бройля обладает сильной дисперсией даже
в вакууме.
192
193.
Групповая скорость волны де Бройляd d ( ) dW
u
;
dk d ( k ) dp
W c p
dW
dp
2
2 2
m0 c ;
(1)
(2)
c p c mv
v;
2
mc
p 2 m02c 2 W
cp
2
2
(3)
Групповая скорость волны де Бройля равна скорости частицы
193
194. Связь между корпускулярными и волновыми свойствами свободных частиц, обладающих скоростью v и массой m
Скоростьv
Длина волны
l=h/(mv)=h/p
m
Частота волны
n=W/h
p
Групповая скорость
u=v
Масса
Импульс
Энергия
W=p2/2m
Фазовая скорость
vфаз=c2/v
194
195. Вероятностный смысл волн де Бройля
• Волны де Бройля имеют специфическую квантовуюфизическую природу, не имеющую аналогии с
волнами в классической физике.
• Волна де Бройля описывается так называемой пси–
функцией или волновой функцией Y(x,y,z,t).
• Статистический подход при анализе дифракционных
экспериментов дает основание определить волновую
функцию Y таким образом, что квадрат ee модуля
|Y|2 в данной точке дает плотность вероятности того,
что частица обнаруживается в этой точке.
• Сама волновая функция Y при этом в общем случае
является комплексной и непосредственного
физического смысла не имеет.
195
196.
• Согласно данному определению2
2
dP Y dV Y dxdydz
• где dP - вероятность того, что частица будет
обнаружена в объеме dV.
• При этом должно выполняться условие нормировки
вероятностей:
Y
2
dxdydz 1.
196
197.
• Волновая функция в квантовой механике являетсяосновной характеристикой состояния микрообъектов
(элементарных частиц, атомов, молекул).
• С ее помощью могут быть вычислены средние
значения физических величин.
• Например, среднее расстояние электрона от ядра
вычисляется по формуле:
r
r Y
2
dxdydz;
• Для вычисления среднего квадрата расстояния
электрона от ядра используется выражение
r
2
r
2
2
Y dxdydz;
r x2 y 2 z 2 .
197
198. Соотношения неопределенностей Гейзенберга
• Всем волновым процессам присущифундаментальные соотношения неопределенностей:
x k x 1 / 2;
y k y 1/ 2;
z k z 1/ 2;
t 1/ 2.
среднеквадратическая неопределенность
соответствующей величины. Например:
x
( x x ) 2 .
198
199.
• Для волн де Бройляp x k x ; k x p x / ;
p y k y ; k y p y / ;
p z k z ; k z p z / ;
W ; W / .
199
200.
• Поэтому в квантовой механике фундаментальныесоотношения неопределенностей можно
представить в виде
x px ;
2
(1)
y p y ;
2
(2)
t W .
2
(4)
z pz ; (3)
2
• Соотношения (1)-(4) называются соотношениями
неопределенностей Гейзенберга.
• Соотношения (1)-(3) показывают, что, чем точнее известна
координата, тем больше неопределенность проекции
импульса и наоборот.
• Соотношение (4) указывает на то, что неопределенность в
энергии обратно пропорциональна временной
неопределенности.
200
201. ГЕИЗЕНБЕРГ Вернер Карл (5.ХИ 1901-1.11 1976) немецкий физик-теоретик
Работы относятся к квантовой механике,
квантовой электродинамике, релятивистской
квантовой теории поля, теории ядра,
магнетизму, физике космических лучей,
теории элементарных частиц, философии
естествознания.
В 1925 разработал матричную механику —
первый вариант квантовой механики
(Нобелевская премия, 1932).
В 1927 сформулировал принцип
неопределенности, ограничивающий
применение к микрообъектам классических
понятий и представлений.
Вслед за Д. Д. Иваненко пришел к протоннонейтронной модели ядра (1932).
В последние годы усилия Гейзенберга были
направлены на создание единой теории поля.
Немало его работ посвящено философским
проблемам физики, в частности теории
познания, где он преимущественно стоит на
позициях идеализма.
201
202. Численные оценки
• Для макротел волновая неопределенностьнесущественна. Например, для пылинки d=10-6 м;
103 / 3
10 34
12
v x
10
м / с.
16
6
md 5 10 10
• Для электрона, локализованного в атоме, понятие
траектории теряет смысл:
10 34
6
v x
10
м / с.
29
10
m x 9,1 10 10
202
203. Уравнение Шредингера
• Исходя из идей де Бройля о волнах материи, австрийский физикЭрвин Шредингер ввел для описания состояния микрообъекта
волновую функцию и разработал теорию движения микрочастиц
— волновую механику, в основу которой положил уравнение,
названное впоследствии его именем.
Y
i
Y UY
t
2m
2
Y Y( x, y, z, t ) волновая функция;
U U ( x, y, z, t ) потенциальная энергия частицыв силовом поле;
2
2
2
Y
Y
Y
оператор Лапласа Y 2 2 2 ;
x
y
z
203
204.
• Уравнение Шредингера играет в атомныхпроцессах такую же фундаментальную роль,
как законы Ньютона в классической
механике.
• Уравнение Шредингера не выводится, а
постулируется.
• Тем не менее можно привести следующие
рассуждения, которые приводят к этому
уравнению.
204
205. “Вывод” уравнения Шредингера
Y a exp[ i( t kx)];p
p k ; k ;
(1)
W
W ; ;
i
Y a exp ( px Wt ) ;
Y
i
1 Y
a WY;
W i
;
t
Y t
Y
p
2 Y;
2
x
2
2
1 Y
p
;
2
Y x
2
2
(2)
(3)
(4)
2
(5)
205
206.
Wполная энергия;
U
потенциальная энергия;
p2
2m
2
p
W
U
2m
кинетическая энергия.
(6)
1 Y
1 Y
i
U;
2
Y t
2m Y x
(7)
Y
i
Y UY;
t
2m
(8)
2
2
2
“Q.E.D.”
206
207. Стационарное уравнение Шредингера
• На практике важное значение имеют стационарныерешения, когда |Y|2 и U не зависят от времени.
Y( x, y, z, t ) ( x, y, z ) (t );
2
i
U
t
2m
(1)
1
;
1
2 1
i
U ;
t
2m
(2)
207
208.
• f1(t)=f2(x,y,z) только в том случае, если f1 и f2 независят от координат и времени =>
1
1
i
U const ( x, y, z, t ) W ;
t
2m
2
• Нетрудно видеть, что W имеет размерность энергии.
Более детальный анализ показывает, что W
является полной энергией частицы.
1
i
W
t
2 1
U W
2m
W
0 exp i t
(3)
2
U W
2m
(4)
208
209. ШРЕДИНГЕР Эрвин (12.УШ 1887-4.1 1961) австрийский физик-теоретик
Основные работы в области статистической
физики, квантовой теории, квантовой
механики, общей теории относительности,
биофизики.
Исходя из идей де Бройля о волнах материи
и принципа Гамильтона, разработал (1926)
теорию движения микрочастиц — волновую
механику, в основу которой положил
уравнение (уравнение Шредингера),
играющее в атомных процессах такую же
фундаментальную роль, как законы
Ньютона в классической механике, и ввел
для описания состояния микрообъекта
волновую функцию.
За создание волновой механики в 1933 (с П.
Дираком) удостоен Нобелевской премии.
Сделал несколько попыток по разработке
единой теории поля. Интересы Шредингера
были чрезвычайно разнообразны: он
занимался лепкой, написал книгу по
греческой философии, исследовал
209
проблемы генетики и т. д.
210. Движение свободной частицы
• Частица движется вдоль оси X со скоростью v вотсутствие потенциального силового поля (U=0).
mv 2 p 2
W
;
2
2m
2
p2
;
2m
2m
p
2mW
k
210
211.
22
k
0;
2
x
l2 k 2 0; l1, 2 ik; Ae l1 x Be l 2 x .
A exp(ikx) B exp( ikx);
2mW
A exp i
2mW
x B exp i
W
2mW
Y A exp i t
x ;
W
2mW
x B exp i t
x ;
211
212.
• С учетом движения частицы вдоль положительногонаправления оси X B=0.
W
2mW
Y A exp i t
x ;
• Таким образом решением является плоская
монохроматическая волна, распространяющаяся вдоль оси Х.
2
Y A2 const .
• Полная неопределенность координаты х местоположения
частицы.
• Полная определенность импульса частицы
p p x mv.
212
213. Электрон в потенциальном ящике
• Одномерный потенциальный ящик (яма, колодец) снепроницаемыми (бесконечно высокими стенками).
• Например, электроны в металле тоже находятся как
бы в потенциальной яме, но трехмерной и конечной
глубины, равной работе выхода.
U
, x 0;
U ( x) 0, 0 x L;
, x L.
X
0
L
213
214.
Y 2m2 [W U ( x)] 0;
2
x
2
Внутри ящика:
2Y
2mW
2
k 0; k
2
x
l2 k 2 0; l1, 2 ik; Ae l1 x Be l 2 x .
2mW
A exp i
2mW
x B exp i
x ;
С учетом граничных условий:
C sin kx ;
sin kL 0;
kn L n ;
214
215.
Получаем квантование энергииn 2 2 2
Wn
2mL2
2mWn
kn L
L n
(2n 1) 2 2
Wn Wn 1
;
2
2mL
Wn (2n 1) 2
;
2
Wn
n
n
(1)
n – квантовое число
n=1,2,…
(2)
U
(3)
0
n=4
W4
n=3
W3
n=2
n=1
W2
W1
L
X
215
216. Волновые функции и плотность вероятности
22
nx
n ( x) dx C sin L dx 1 C
0
L
n ( x)
2
;
L
2 nx
sin
, 0 x L, n 1,2, ...
L L
216
217. Пример 1. Молекула газа в сосуде при комнатной температуре.
Численные оценкиПример 1. Молекула газа в сосуде при
комнатной температуре.
m 10 27 кг , L 0,1м Wn 6,8 10 20 n эВ;
Wn kT 2,6 10 2 эВ.
• Молекула газа практически имеет сплошной
энергетический спектр. Дискретность уровней
несущественна.
217
218. Пример 2. Свободный электрон в металле.
m 0,91 10 30 кг , L 0,01м Wn 6,8 10 15 n эВ;Wn Wn 1 эВ.
• Для свободных электронов в металле расстояние
между уровнями мало по сравнению с их энергией,
но дискретность уровней оказывает существенное
значение на статистику распределения электронов
по энергиям.
218
219. Пример 3. Электрон в ящике атомных размеров.
m 0,91 10 30 кг , L 10 10 м Wn 75n эВ;Wсвязи 10 эВ.
• Для электрона в атоме дискретность энергетического
спектра оказывается весьма существенной.
219
220. Принцип соответствия Бора
• Выводы квантовой механики при больших квантовыхчислах должны соответствовать классическим
результатам.
• При больших n дискретность становится
несущественной. В рассмотренном примере
Wn (2n 1) 2
;
2
Wn
n
n
• В общем виде: любая новая теория должна в
предельных случаях соответствовать старой.
220
221. Туннельный эффект
• Прохождение (проникновение, просачивание) частицы сквозьпотенциальный барьер конечной высоты и конечной ширины в
том случае, если энергия частицы меньше высоты
потенциального барьера.
• Скачок потенциальной энергии аналогичен скачку показателя
преломления в оптике. Есть отражение и преломление
(проникновение).
• Для классической частицы туннельного эффекта нет, она
заперта барьером.
U
II
I
0, x 0;
U ( x) U 0 , 0 x L;
0, x L.
III
U0
W
X
0
L
221
222.
В областях I и III - уравнения волн для свободных частиц.Для области II - уравнение Шредингера имеет вид.
2 2 ( x )
(U 0 W ) ( x) 0;
2
2m x
(1)
2 ( x) 2m(U 0 W )
( x) 0;
2
2
x
(2)
2m(W U 0 )
l
0;
2
2
( x) Ae
l1x
l2 x
Be
;
2m(U 0 W )
l1,2
;
2m(U 0 W )
( x) B exp
x ;
(3)
(4)
222
223. Прозрачность прямоугольного барьера
2 2m(U 0 W )( x) (0) exp
x ;
2
2
D
( L )
2
(0 )
2
;
2L
D D0 exp
2m(U 0 W ) ;
D0 1;
(5)
(6)
(7)
(8)
D0 учитывает потери при прохождении волны вероятности через
границы раздела областей.
223
224.
• Численные оценки показывают, что туннельныйэффект может играть заметную роль только в тех
случаях, когда линейные размеры потенциального
барьера соизмеримы с атомными размерами.
m 0,91 10 30 кг , U 0 W 1 эВ, L 10 10 м
D 0,359.
m 0,91 10 30 кг , U 0 W 1 эВ, L 10 8 м
D 10 45.
224
225. Прозрачность барьера произвольной формы
2 xiD Di exp
2m[U ( xi ) W ]
i
i
2 xi
exp
2m[U ( xi ) W ] ;
i
2 x2
D exp 2m[U ( xi ) W ]dx
x1
(9)
225
226.
• Туннельный эффект позволил объяснитьявление холодной эмиссии электронов из
металла, когда под действием слабых
(недостаточных для вырывания полей)
происходит утончение потенциальных
барьеров и сквозь них начинают
просачиваться электроны.
• Туннельный эффект объясняет альфараспад радиоактивных ядер, наличие
энергетических зон в твердых телах,
контактную разность потенциалов и др.
226
227.
• Туннельный эффект находит широкоеприменение в технических приложениях.
Например, сканирующий туннельный
микроскоп (СТМ) позволяет исследовать
поверхность с молекулярным разрешением и
имеет широкие перспективы в связи с
развитием нанотехнологий.
227
228. Квантовый гармонический осциллятор
• Гармонический осциллятор – система,совершающая гармонические колебания.
• Малые колебания физических систем вблизи
положения устойчивого равновесия с
высокой точностью являются
гармоническими.
• В квантовой механике примером таких
колебаний являются колебания атомов в
твердых телах, молекулах, колебания
электронов в атомах и т.д.
228
229. Классический одномерный (линейный) осциллятор
kx 2 m 02 x 2k
F kx, U ( x)
, 0
.
2
2
m
U
x a;
W
X
-a
2W
a
.
2
m 0
a
229
230. Классическая плотность вероятности w(x) гармонического осциллятора
x a sin( 0t );(1)
dt
2
w( x)dx
; T
; (2)
T /2
0
x
a
dx
t
dt
-a
0
1
w( x)
; (3)
(dx / dt)
T/2
dx
a 0 cos( 0t ) 0 a 2 x 2 ; (4)
dt
230
231.
1, x a;
2
2
w( x) a x
0, x a.
(5)
231
232. Нулевые колебания
• Формула (7) – закон квантования энергиигармонического осциллятора.
• Основные особенности – эквидистантность уровней и
наличие нулевых колебаний с энергией W0=hn0 при
n=0, которые сохраняются у кристаллов при T=0 и
которые нельзя отнять.
• Нулевые колебания играют важную роль:
обусловливают отсутствие кристаллизации жидкого
гелия (квантовая жидкость) при T=0; объясняют
природу сил молекулярных взаимодействий,
особенности сил поверхностного натяжения и других
молекулярных явлений.
• Экспериментально нулевые колебания
обнаруживаются в опытах по рассеянию света
кристаллами при низких температурах.
232
233.
• Значение нулевой энергии осциллятора согласуетсяс требованиями соотношения неопределенностей:
x a0 ;
(8)
p ma0 0 ;
(9)
x p
a02
2W
; (11)
2
m 0
m 0 a02 ;
(10)
0
W
; (12)
2
0 hn
W0
2
2
Q.E.D.
233
234. Сравнение квантового решения с классическим
• При n→∞ квантовая плотность вероятности приближается кклассической, как того и требует принцип соответствия.
234
235. Квантовые свойства атомов
• Атомные системы являются объектами, дляописания которых следует использовать
законы квантовой механики.
• Именно поэтому в рамках классической
физики значительная часть
экспериментальных результатов атомной
физики не поддается объяснению.
• К числу таких результатов в первую очередь
можно отнести то, что излучение атомов
состоит из дискретных спектральных линий.
235
236. Излучение атомов
• Для атома водорода еще в 1885 г. эмпирически была найденаформула, получившая название обобщенной формулы
Бальмера.
1
1
1
R 2 2 ;
l nk
k
n
(1)
1
1
R 2 2 .
k
n
(2)
n nk
• Здесь R’=1,09737·107 м-1, R=R’/c – постоянная Ридберга; n,k –
целые числа.
• Формулы отражают присущую атомам квантовую природу. С
учетом формулы Планка W=hn можно сделать вывод о
дискретности, т.е. о квантовании энергии атома.
236
237. Серии излучения атома водорода
237238. Спектральный анализ
• - метод определения химического состава и другиххарактеристик вещества по его спектру излучения
или поглощения.
238
239. Опыт Франка-Герца (1913 г.)
• - один из простых опытов, убедительно подтверждающихквантовые свойства атомов;
• основной элемент установки – трехэлектродная лампа,
заполненная парами ртути.
239
240. Зависимость анодного тока от ускоряющего напряжения
• Из графиков следует, что первое возбужденное состояние атомартути отделено от основного состояния энергетическим
промежутком в W=4,9 эВ.
• Возбужденные атомы ртути возвращаются в исходное состояние
путем испускания ультрафиолетового излучения:
W hn
hc
hc
l
2,53 10 7 м 253 нм.
l
W
240
241. ФРАНК Джеймс 26.VII 1882 — 21.V 1964 немецкий физик
Работы посвящены атомной и ядерной
физике, молекулярной спектроскопии и ее
применению к химии, фотосинтезу.
Вместе с Густавом Герцем осуществил
(1912—14) ряд экспериментов по
возбуждению и ионизации атомов паров
ртути ударами электронов (опыты Франка
— Герца) и открыл законы столкновений
электронов с атомами, . что послужило
доказательством дискретности уровней
энергии атомов и подтвердило теорию
атома Бора (Нобелевская премия, 1925).
Изучал атомные скачки и уровни энергии в
атомах, передачу энергии в атомных
системах при флюоресценции, развил
спектральный метод исследования
химических сил, исследовал
фотохимические процессы в молекуле
хлорофилла.
Выступал (1945) против применения
атомной бомбы.
241
242. ГЕРЦ Густав Людвиг 22.VII 1887 — ЗО.Х 1975 немецкий физик
Основные исследования в области
спектроскопии.
В 1912—14 совместно с Дж. Франком
выполнил ряд опытов по столкновению
электронов с атомами газа (опыты
Франка — Герца), что привело их к
установлению некоторых
закономерностей этих столкновений
(Нобелевская премия, 1925).
Опытами Франка — Герца впервые
было доказано существование в атомах
дискретных уровней энергии, что
непосредственно подтверждало
квантовую теорию атома Бора.
Изучал рентгеновские спектры
поглощения.
Выполнил ряд исследований по
диффузии, электронной эмиссии,
разрядам в газах, физике плазмы,
ультразвуку и полупроводникам.
Разработал метод разделения изотопов
242
путем диффузии.
243. Опыты Резерфорда, 1911 г.
rя 10 14 10 15 мrя rа 10 9 10 10 м
243
244. РЕЗЕРФОРД Эрнест (ЗО.УШ 1871-19.Х 1937) английский физик
Исследования посвящены радиоактивности,
атомной и ядерной физике. Своими
фундаментальными открытиями в этих
областях заложил основы современного учения
о радиоактивности и теории строения атома.
За исследования по превращению элементов и
химии радиоактивных веществ Резерфорду в
1908 была присуждена Нобелевская премия по
химии.
В 1908 вместе с Г. Гейгером сконструировал
прибор для регистрации отдельных заряженных
частиц (счетчик Гейгера).
Изучая явление прохождения альфачастиц
через вещество, обнаружил в 1906 их
рассеяние, что привело его в 1911 к открытию в
атоме ядра и созданию новой модели атома —
планетарной.
В 1919 осуществил первую искусственную
ядерную реакцию, превратив азот в кислород,
открыл протон. В 1920 предсказал
существование нейтрона и дейтрона. В 1934
осуществил реакцию синтеза дейтронов с
244
образованием трития.
245. Планетарная модель атома
• В действительности атомы устойчивы и в состоянии сминимальной энергией могут существовать
неограниченно долго.
245
246. Теория Бора атома водорода
Первый постулат Бора• В устойчивом атоме электрон может двигаться лишь
по особым, стационарным орбитам, не излучая при
этом электромагнитной энергии.
• Разрешенными стационарными орбитами являются
только те, для которых момент импульса L электрона
равен целому кратному значению постоянной Планка:
L n , n 1, 2, ...
(3)
246
247. Правило квантования орбит Бора
• С точки зрения современныхквантовых представлений
согласно Бору на длине
окружности каждой стационарной
орбиты укладывается целое
число n длин волн де Бройля,
соответствующих движению
электрона.
• n – главное квантовое число.
2 r
n
lБ
nh
mvrn
2
mvrn Ln n
n 1, 2, ...
247
248. Расчет стационарных орбит по Бору
Согласно 2-му закону Ньютонаи закону Кулона:
В соответствии с правилом
квантования орбит Бора:
rn n
2
0h
2
me 2
(4)
mv 2
e2
2
rn
4 0 rn
nh
v
2 mrn
r1 0,53 10 10 м
v1 2,2 10 м
6
248
249. Орбиты электрона в атоме водорода
249250. Расчет энергетических уровней по Бору
mv 2e2
e2
W
2
4 0r
8 0r
Энергетический уровень – энергия, которой обладает атомный
электрон в определенном стационарном состоянии
r rn n
0h
me 2
см. формулу (4)
Основное состояние атома (молекулы)
- состояние с минимальной энергией
4
1 me
Wn 2 2 2
n 8 0 h
2
2
(5)
W1 13,6 эВ
250
251.
• Возбужденные состояния – состояния сn>1.
• Свободные состояния – энергетические
состояния с положительной энергией
электрона. Энергетический спектр свободных
состояний непрерывен.
• Связанные состояния – энергетические
состояния с отрицательной энергией
электрона. Энергетический спектр связанных
состояний дискретен.
• Энергия ионизации – минимальная энергия,
которую нужно затратить для перевода
электрона из основного состояния в
свободное состояние (Еи=|E1|).
251
252. Поглощение и излучение света атомом
Второй постулат Бора• Испускание или поглощение кванта излучения
атомом происходит при переходе атома из одного
стационарного состояния в другое.
Wk
Wk
hn
Wn
Испускание кванта
hn
Wn
Поглощение кванта
252
253. Правило квантования частот
• Энергия излученного фотона равна (k>n):hn nk Wk Wn .
(6)
• Из (5) и (6) следует, что дискретный спектр частот определяется
формулой, которая в точности соответствует обобщенной
формуле Бальмера:
n nk
1
1
R 2 2 ,
k
n
• причем согласно теории Бора постоянная R может быть
рассчитана теоретически по формуле
me4
R 2 3,
8 0 h
• что дает значение R, хорошо согласующееся с экспериментом.253
254. Значение теории Бора
• Будучи первой квантовой теорией атома, теорияБора имела большое значение для развития
правильных физических представлений об атомных
явлениях.
• Однако, теория Бора внутренне противоречива.
Постулаты не имеют обоснования.
• Попытка распространить эту теорию даже на атом
гелия полностью провалилась.
• Только применение последовательной квантовой
(волновой) механики позволило объяснить
многообразие явлений атомного мира и вскрыть
физическое содержание постулатов Бора.
254
255. БОР Нильс Хендрик Давид 7.Х 1885-18.XI 1962 датский физик-теоретик
В 1913, исходя из идеи М. Планка о
квантовании энергии, Бор на основе
модели атома Резерфорда создал
свою теорию водородоподобного
атома, основанную на двух
постулатах, которые прямо
противоречили классическим
представлениям и законам.
Бор объяснил особенности
периодической системы химических
элементов, предложив свой вариант
изображения периодической системы
элементов, и пришел к представлению
об оболочечной структуре атома,
основанной на классификации
электронных орбит по главному и
азимутальному квантовым числам.
За создание квантовой теории
планетарного атома в 1922 удостоен
Нобелевской премии.
Создал большую интернациональную
255
школу физиков.
256. Квантовая теория атома водорода
2m2 (W U ) 0; (1)
e2
U (r )
;
4 0r
(2)
• Решение уравнения Шредингера (1) при условии (2) показывает,
что квантовое состояние электрона в атоме водорода
(квантовое состояние атома) определяется тремя квантовыми
числами:
• главным квантовым числом n, определяющим полную
энергию электрона,
• азимутальным квантовым числом l, определяющим
орбитальный момент импульса электрона,
• магнитным квантовым числом m, определяющим проекцию
орбитального момента импульса электрона.
256
257. Решение уравнения Шредингера для атома водорода в основном состоянии (n=1, l=0)
2m2 (W U ) 0; (1)
Сферическая симметрия решения:
e2
U (r )
; (2)
4 0r
(r ); (3)
Переходим в сферические координаты:
d 2 2 d 2m
e2
2 W1
Y 0; (4)
2
r dr
4 0r
dr
257
258.
Решение ищем в виде:r
C exp ;
a
(5)
d 2 1
2 ;
2
dr
a
(6)
d
1
;
dr
a
1
2
2m
e2
2 1
2 W1
0;
2
ra
4 0r
2m
a
2
(7)
2
e
1
2
W1
2 ;
4 0r 2m a
ra
(8)
258
259.
W1 не зависит от текущего значения r =>2
2
e
0
4 0r mra
2
4
me
W1
2
2ma
32 2 2 02
2
2 4 0
a
me2
(9)
me4
W1 2 2
8 0 h
(10)
w(r )dr (r ) 4 r dr
2
Плотность вероятности w(r) обнаружить электрон на расстоянии r от ядра:
2r
w(r ) C exp 4 r 2
a
2
(11)
259
260. Квантово-механическая трактовка боровских орбит
dw(r )0
dr
2
4 r 2 8 r 0;
a
r a
• Боровские орбиты электрона представляют собой
геометрическое место точек, в которых с наибольшей
вероятностью может быть обнаружен электрон.
260
261. Квантование энергии
• Главное квантовое число принимает значенияn 1, 2, 3, ...
и определяет полную энергию электрона в любом квантовом
состоянии
m0e4 1
13,6
Wn 2 2 2 2 эВ.
8 0 h n
n
(3)
• Эти значения энергии являются собственными значениями
оператора полной энергии (гамильтониана)
Hˆ W ,
2
Hˆ
U.
2m0
261
262.
• В связанном состоянии электрон в атоме водородаимеет дискретный энергетический спектр, лежащий в
области отрицательных значений и имеющий точку
сгущения W=0.
W
0
n→∞
W4 0,85 эВ (n=4)
W3 1,5 эВ (n=3)
W2 3,4 эВ (n=2)
W1 13,6 эВ (n=1)
262
263. Квантование момента импульса
• Азимутальное квантовое число принимает значенияl 0, 1, 2, ..., n 1
и определяет модуль орбитального момент импульса
электрона в любом квантовом состоянии по формуле
Ll l (l 1).
(4)
• Эти значения момента импульса являются
собственными значениями оператора квадрата
момента импульса
Lˆ2 nlm l (l 1) 2 nlm.
263
264.
• Формула квантования момента импульса (4)принципиально отличается от формулы
Бора.
• В квантовой теории в отличие от
классической возможны состояния атома с
нулевым моментом импульса.
• Эксперименты подтверждают выводы
квантовой теории.
264
265.
Обозначения квантовых состоянийЗначение l ......................... 0 1
Символ состояния .......... s
2
3
4
5 ...
p d
f
g
h ...
l n 1
Возможны следующие состояния электрона:
n 1 1s
n 2 2 s, 2 p
n 3 3s, 3 p, 3d
n 4 4 s, 4 p, 4d , 4 f
265
266. Орбитальное гиромагнитное отношение
L m0v r;L
p
v
M
p
M
p - орбитальный магнитный
момент электрона
M
e 2 1
is r erv;
T
2
pM
e
e
L
2m0
(5)
M
p e L
• В квантовой механике
нет орбит. Указать
направление L относительно орбиты нельзя.
Направление указывается относительно внешнего
по отношению к данному электрону магнитному
полю.
266
267. Квантование проекции момента импульса (Пространственное квантование)
• Магнитное квантовое число принимает значенияm 0, 1, 2, ..., l
и определяет проекцию орбитального момента
импульса электрона на направление внешнего
магнитного поля в любом квантовом состоянии по
формуле
Llz m .
(6)
• Эти значения проекции момента импульса являются
собственными значениями оператора проекции
момента импульса
Lˆ z nlm m nlm.
267
268.
p–состояние (l=1)l (l 1) 2
m 1, 0, 1.
l( l 1 ) 6
m 2, 1, 0, 1, 2.
2
0
d–состояние (l=2)
L1
0
L2
2
Возможное число ориентаций составляет
2l 1
268
269. Магнетон Бора
• Магнетоном Бора называется универсальная постоянная,служащая естественной единицей измерения магнитных
моментов атомов:
e
Б e
0,927 10 23 Дж / Тл.
2m0
• Согласно этому определению и формулам (4), (5), (6) магнитный
момент и проекция магнитного момента атома квантуются по
следующим формулам:
p M e L Б l (l 1) ;
p zM e Lz m Б .
269
270. Опыты Штерна и Герлаха (1921 г.)
• Штерн и Герлах проводили измерения магнитных моментоватомов по отклонению атомных пучков в неоднородном
магнитном поле.
M dB
F pz
.
dz
• Опыты подтвердили наличие пространственного квантования, но
для атомов серебра был получен неожиданный результат.
p zM Б ;
У атомов первой группы – один
валентный электрон, находящийся
в s-состоянии (L=0, pM=0).
Моменты электронов замкнутых
оболочек скомпенсированы.
270
271. Спин электрона
• Результаты опытов Штерна и Герлаха можно объяснить, еслиприписать электрону собственный момент импульса (сокращенно
– спин) таким образом, что
1
Lsz ms , ms .
2
• ms – спиновое квантовое число.
Спиновое гиромагнитное отношение
pszM psM
e
s
2 e
Lsz
Ls
m0
M
ps s Ls
• Спин – особое свойство элементарных частиц, подобное массе и
271
заряду.
272. Несостоятельность классической модели спина
• Рассмотрим электрон, как заряженный шарик, вращающийсявокруг своей оси.
• Классический радиус электрона:
e2
m0c 2 ; (1)
4 0r
e2
15
r
2
,
81
10
м;
2
4 0 m0c
• Момент импульса:
2
I m0r 2 ; (3)
5
1
L I ; (4)
2
(2)
2
1
2v
(5)
m0r
; (2)
5
r 2
• Линейная скорость периферийных областей:
v
5
100 c. (6)
4m0r
• Таким образом классические представления о спине
противоречат теории относительности.
272
273.
• Спин – особое свойство элементарныхчастиц, подобное массе и заряду.
• Дирак показал, что существование спина
вытекает из полученного им релятивистского
волнового уравнения.
273
274. Принцип Паули
• Принцип исключения (запрета).• В любом атоме не может быть электронов, находящихся в
одинаковых стационарных состояниях, определенных набором
четырех квантовых чисел: главного n, орбитального l, магнитного
m, спинового ms.
• Максимальное число электронов, описываемых наборами
квантовых чисел:
Z (n, l , m, ms ) 1;
Z (n, l , m) 2;
Z (n, l , ) 2(2l 1);
n 1
Z (n) 2(2l 1) 2n2 .
l 0
274
275. Таблица 1 Число электронов в состояниях (n,l)
оболочка →слой
K
n=1
L
n=2
M
n=3
N
n=4
O
n=5
s
l=0
p
l=1
d
l=2
f
l=3
g
l=4
Z(n)
2
—
—
—
—
2
2
6
—
—
—
8
2
6
10
—
—
18
2
6
10
14
—
32
2
6
10
14
18
50 275
276. Распределение электронов в атомах по состояниям
• а) порядковый номер химического элемента равенобщему числу электронов в атоме данного элемента;
• б) состояние электронов в атоме определяется
набором четырех квантовых чисел;
• в) действует принцип минимума потенциальной
энергии: с возрастанием числа электронов каждый
следующий занимает место с наименьшей энергией;
• г) действует принцип Паули.
Формула электронной конфигурации атома
Пример:
Кислород :
16
8O
1s 2 2s 2 2 p 4
276
277.
• Реальная периодическая система элементовсложнее схемы, представленной в табл. 1.
• В действительности нужно учитывать
взаимодействие электронов.
• Заполнение идет так, что во внутренних оболочках
остаются свободные позиции.
• Возникают группы редкоземельных элементов
(лантаниды, актиниды).
277
278.
278279. Излучение и поглощение света
WnWm
hn Wn-Wm
Wn
hn Wn-Wm
Wm
• Излучение, происходящее в отсутствие внешних
причин, изменяющих энергию атома, называется
спонтанным (т.е. самопроизвольным) излучением.
• Излучение, происходящее в результате воздействия
на атом внешнего электромагнитного поля,
называется вынужденным (стимулированным)
излучением.
• Объяснить физический механизм спонтанного и
вынужденного излучения можно с помощью
квантовой электродинамики.
• Для формального описания законов излучения и
поглощения света Эйнштейн ввел коэффициенты
279
Аnm, Bnm, Bmn.
280.
• Anm - вероятность спонтанного перехода в единицувремени из состояния n в состояние m с испусканием
фотона.
• Bnm (n) – вероятность вынужденного перехода из
состояния n в состояние m с испусканием фотона
( (n) - объемная спектральная плотность внешнего
электромагнитного поля).
• Bmn (n) – вероятность вынужденного перехода из
состояния m в состояние n с поглощением фотона
280
281.
dN n Anm N n dtN n N n0 exp( Anmt )
t – среднее время жизни атома в возбужденном состоянии;
t W
Wnm ;
t
1
n nm
;
2 t
Wnm=h/2 t – естественная ширина энергетического уровня;
nnm=1/2 t – естественная ширина спектральной линии.
281
282. Вывод формулы Планка для излучения АЧТ по Эйнштейну
• Принцип детального равновесия: для двухпроизвольно выбранных уровней в системе,
находящейся в состоянии термодинамического
равновесия, должно быть равенство между
процессами испускания и поглощения света.
Anm Bnm (n) N n Bmn (n) N m ;
(1)
W
W
N n N0 exp n , N m N0 exp m ;
kT
kT
(2)
Wn
Anm exp
kT
(n) (n, T )
;
W
W
Bmn exp m Bnm exp n
kT
kT
(3)
282
283.
Из условия T→∞, (n,T)→∞ следует, что Bnm=Bmn.Учтем также, что Wn Wm=hn =>
Anm Bnm
( n , T )
;
hn
exp 1
kT
Сопоставляя (4) с формулой Вина
rn0
n
n f ,
T
3
n3
( n , T )
, const (n, T );
hn
exp 1
kT
(4)
получим
(5)
283
284.
При малых частотах (hn<<kT) справедлив закон Рэлея-Джинса8 n 2
(n, T ) 3 kT ,
c
а формула (5) при hn<<kT преобразуется к виду
n2kT
(n, T )
.
h
n2kT 8 n 2
3 kT
h
c
8 h Anm 8 h 3
3 ,
3 n . (6)
Bnm c
c
Получаем известную формулу Планка для излучения АЧТ
0n
8 n 2
hn
3
hn
c
exp 1
kT
c
rn0 (n,T ) 0n (n,T )
4
rn0
2 n 2
hn
2
hn
c
exp 1
kT
284
285. Основы физики лазеров
L – light
A – amplification
S – stimulated
E – emission
R – radiation
• Light amplification by stimulated emission of
radiation - усиление света с помощью
вынужденного (стимулированного)
излучения.
• Лазеры – оптические квантовые генераторы
(ОКГ).
285
286. Основные элементы лазера
23
4
1
L
• 1 – активная (усиливающая) среда, способная за счет
механизма вынужденного излучения усиливать
распространяющиеся в ней оптические колебания в некотором
частотном диапазоне.
• 2 – устройство накачки, обеспечивающее инверсную
заселенность энергетических уровней; накачка может быть
оптической, электронной, химической.
• 3,4 – зеркала, образующие оптический резонатор, который
вносит селективную положительную обратную связь за счёт
многократных отражений. Резонаторная система выделяет
набор различных типов оптических колебаний (мод).
286
287. Механизм усиления в среде с отрицательным поглощением
Закон Бугера — Ламберта — ФабрикантаI I 0 exp[ k ( N 2 N1 ) z ].
k>0 – коэффициент пропорциональности;
N1 – число актов поглощения;
N2 – число актов вынужденного излучения.
По мере роста усиления вследствие
конечности числа возбужденных атомов
инверсия среды уменьшается и возникает
насыщение – равновесие между
вынужденным излучением и накачкой.
287
288. Свойства вынужденного излучения
• Вынужденное излучение является когерентным поотношению к тому излучению, которое его вызывает.
• Вынужденное стимулированное излучение имеет ту
же частоту, фазу, состояние поляризации и
направление распространения, что и
стимулирующее.
• Поэтому, в результате действия положительной
обратной связи за счет многократных отражений от
зеркал оптического резонатора выходящий пучок
обладает высокой направленностью, высокой
временной и пространственной когерентностью.
288
289. Условия возникновения генерации
• 1) Усиление за проход больше потерь , связанных споглощением, рассеянием и дифракцией;
• 2) Согласование фаз:
2L
c
c
2 L nl n ; l n
; nn ; nn n
n
ln
2L
c
n n n n n 1
2L
S
K*
Kус
n
n
nп
n
289
290. Рубиновый лазер
• Трехуровневая схема накачки. Кристалл рубина Al2O3с примесью оксида хрома Cr2O3. Активное вещество
– ионы хрома Cr3+. Оптическая накачка интенсивным
зеленым светом мощной импульсной лампы,
наполненной неоном и криптоном.
A
Переходы без
излучения
Cr3+
B
Метастабильные
уровни
692,7 нм
694,3 нм
C
290
291. Гелий-неоновый лазер
• Активное вещество – неон. Накачка электронным ударом. Гелий– буферный газ (увеличивает число столкновений).
• Резонансный переход энергии от гелия к неону. => Скорость
заселения верхних рабочих уровней неона (3s) значительно
выше скорости заселения нижних рабочих уровней (2p).
• Кроме красной линии имеются линии генерации в ИК-области.
W3
He
Ne
W2
3s
632,8 нм
2p
W1
291
292.
• Некоторые области применения лазеров:связь, локация, лазерный термоядерный
синтез, лазерная обработка материалов,
лазеры в медицине (микрохирургия и др.),
измерительная техника (гидродинамика,
химическая технология, энергетика, экология,
биология и др.)…
• С 1968 года на кафедре физики МЭИ открыта
лазерная специальность. Современное
название «Квантовая и оптическая
электроника».
292
293. Вечерняя Москва от 20.10.2010. Этот волшебный луч Автор: Дмитрий БАЙКАЛОВ
Только лазер способен создать настоящее кино 3D…
Я распечатал текст этой статьи на лазерном принтере, поиграл с котом
– он очень смешно гоняется за пятном от лазерной указки, что висит на
моем брелке, – и поехал в редакцию. Перед тем как сесть в машину, я
зашел в магазин купить банку содовой – продавщица считала
лазерным прибором штрихкод с банки и выбила чек. В машине я
вставил CD-диск в лазерный проигрыватель, заиграла хорошая
медленная музыка, и я поехал – стараясь не превышать скорости, ведь
можно нарваться на штраф, если лазерный измеритель скорости из
камеры наблюдения зафиксирует, что я слишком уж тороплюсь. Мне
позвонил приятель, собирающийся делать лазерную коррекцию
зрения, он волновался – я его успокоил, это совсем не страшно…
По дороге я думал, что хотя всего пятьдесят лет назад был миру
представлен первый в истории лазер на искусственном кристалле
рубина, но он уже проник во все сферы нашей жизни. И основную роль
в создании этого удивительного прибора сыграли двое московских
293
ученых – Прохоров и Басов.
294. ФАБРИКАНТ Валентин Александрович (1907-1991) советский физик
Работы посвящены физической
электронике и оптике плазмы.
В 1939 показал возможность усиления
света за счет вынужденного испускания
в плазме с инверсией населенностей
на энергетических уровнях.
В 1949 наблюдал совместно с Л. М.
Биберманом и Н. Г. Сушкиным
дифракцию поочередно летящих
электронов.
В 1951 совместно с М. М. Вудынским и
Ф. А. Бутаевой сформулировал
принцип усиления электромагнитного
излучения при прохождении сред с
инверсной населенностью (идея
квантового усилителя).
За разработку люминесцентных ламп
совместно с другими удостоен в 1951
Государственной премии СССР.
Золотая медаль С. И. Вавилова (1965).
294
295. БАСОВ Николай Геннадиевич (1922-2001) — советский физик
• Работы в различных областях квантовойрадиофизики и ее применений. Открыл
принцип генерации и усиления излучения
квантовыми системами, разработал
физические основы стандартов частоты,
выдвинул ряд идей в области
полупроводниковых квантовых
генераторов.
• Разработал лазерный метод нагрева
плазмы для управляемого термоядерного
синтеза, выполнил значительный цикл
исследований по мощным газовым
квантовым генераторам, химическим
лазерам, выдвинул новые идеи
применения лазеров в оптоэлектронике.
• В 1964 за фундаментальные
исследования в области квантовой
радиофизики, позволившие создать
генераторы и усилители нового типа —
мазеры и лазеры, присуждена
295
Нобелевская премия.
296. ПРОХОРОВ Александр Михайлович (1916-2002) — советский физик
Исследования в области квантовой
электроники и ее применений,
радиофизики, физики ускорителей,
радиоспектроскопии, лазерного
термоядерного синтеза, нелинейной
оптики, физики твердого тела.
В 1955 совместно с Басовым предложил
принципиально новый метод создания
сред с отрицательным поглощением —
так называемый метод трех уровней. В
1958 предложил новый тип резонатора
для субмиллиметровых волн — так
называемый открытый резонатор в виде
двух параллельных зеркальных
поверхностей, получивший широкое
применение в лазерной технике.
В 1959 за разработку нового метода
генерации и усиления электромагнитных
волн вместе с Басовым удостоен
Ленинской премии, а в 1964 им и
американскому физику Таунсу за
фундаментальные работы по квантовой
296
электронике присуждена Нобелевская
премия.
297. ТАУНС Чарльз Хард (р. 1915) - американский физик
Работы относятся к микроволновой
спектроскопии, квантовой электронике,
созданию лазеров и мазеров и их
применению, нелинейной оптике, радио- и
инфракрасной астрономии. Независимо от
Н. Г. Басова и А. М. Прохорова разработал
принципы усиления и генерации
электромагнитного излучения в квантовых
устройствах, создав в 1954 первый
квантовый генератор — молекулярный
генератор на аммиаке.
Открыл вынужденный эффект Бриллюэна—
Мандельштама, ввел понятие критической
мощности пучка (1964), предсказал эффект
самофокусировки светового пучка (1964) и
предложил самофокусирующие волноводы
(1965).
За фундаментальные исследования в
области квантовой радиофизики, приведшие
к созданию генераторов и усилителей
нового типа — мазеров и лазеров, — Таунс
вместе с Басовым и Прохоровым удостоен в
1964 Нобелевской премии.
297
298. Квантовые статистики и некоторые их применения
298299.
• Статистическая физика изучаетсвойства систем, состоящих из
большого числа частиц (молекул,
атомов, электронов, фотонов и др.).
• Исследования показали, что статистика
квантово-механических частиц в общем
случае существенно отлична от
статистики классических частиц.
299
300.
• Истоки статистичности в классическойфизике связаны с невозможностью
абсолютно точного задания начальных
и граничных условий; практической
невозможностью расчета траекторий
огромного числа частиц.
• В квантовой физике необходимость
статистического (вероятностного)
подхода принципиальна и является
следствием корпускулярно-волновой
двойственности свойств частиц
вещества и излучения.
300
301.
• В квантовой механике существуетважный принцип неразличимости
тождественных частиц (электронов,
протонов, нейтронов и т.д.).
• Состояние системы из n тождественных
частиц описывается полной волновой
функцией полн .
301
302.
• Существует два типа полн:симметричная (не меняет знака при
перестановке любых двух частиц) и
антисимметричная (меняет знак при
перестановке любых двух частиц).
• Тип полной волновой функции
(симметричный или антисимметричный)
зависит от проекции Lsz спинов этих
частиц на направление вектора
внешнего магнитного поля.
302
303.
• Электроны и другие частицы, у которыхLsz равно нечетному числу ±ћ/2,
называются фермионами или
частицами с полуцелым спином.
• Частицы, у которых Lsz равно нулю или
четному числу ±ћ/2 называются
бозонами или частицами с целым
спином.
303
304. Характеристики фермионов и бозонов
СпинФермионы
Бозоны
полуцелый
целый
Полная
антисимметричная симметричная
волновая
функция
Принцип подчиняются
не подчиняются
Паули
Примеры электроны,
фотоны,
протоны
фононы
304
305.
• Обобщенный принцип Пауливыражает особенность поведения
тождественных фермионов:
в заданной системе тождественных
фермионов любые два из них не могут
одновременно находиться в одном и
том же состоянии.
305
306.
• Задачи сводятся к нахождению функцийраспределения частиц системы по тем или
другим параметрам – координатам,
импульсам, энергиям.
• Рассмотрение ведется в фазовом 6-мерном
пространстве ( - пространстве) с
координатами: x,y,z,px,py,pz.
306
307.
• Размер ячейки фазового пространствазадается соотношением неопределенностей:
h3 для бозонов ,
x y z p x p y p z h3
для фермионов.
2
307
308.
• Причины различия в распределении классических (различимых)частиц и квантовых (неразличимых) частиц можно
проиллюстрировать простым примером, в котором две частицы
распределяются по трем состояниям.
Классические частицы
1
2
1
1
2
2
Фермионы
1
2
2
2
Бозоны
1
1
Число распределений – 3,
вероятность каждого – 1/3.
12
12
12
Число распределений – 9,
вероятность каждого – 1/9.
Число распределений – 6,
9,
вероятность каждого – 1/6.
1/9.
308
309. Заполнение ячейки фазового пространства для различных частиц
• Сформулированные принципы квантовоймеханики с помощью комбинаторики, теории
вероятностей, вариационного исчисления
дают следующий общий результат в
квазинепрерывном приближении:
1
f
,
W
exp
kT
309
310.
• f - среднее число частиц в ячейке,соответствующей энергии W;
• для классических частиц параметр 0
—
• для фермионов параметр 1
—
• для бозонов параметр 1 Бозе
газ — распределение Бозе-Эйнштейна);
• – химический потенциал системы.
310
311.
• Химический потенциал системыпоказывает изменение энергии системы
в расчете на одну частицу при
изохорном изоэнтропийном процессе
массообмена.
U
.
n V ,S
311
312. ФЕРМИ Энрико (1901-1954) итальянский физик
Работы в области атомной и ядерной
физики, статистической механики,
физики космических лучей, физики
высоких энергий, астрофизики,
технической физики.
В 1925 (декабрь) разработал
(независимо от П. Дирака) статистику
частиц с полуцелым спином (статистика
Ферми — Дирака).
В 1934 открыл искусственную
радиоактивность, обусловленную
нейтронами, обнаружил явление
замедления нейтронов и дал его теорию
(Нобелевская премия, 1938).
Построил первый ядерный реактор и 2
декабря 1942 впервые осуществил его
запуск, получив
самоподдерживающуюся цепную
реакцию.
Положил начало нейтронной оптике и
нейтронной спектроскопии.
312
313. ДИРАК Поль Адриен Морис (1902 - 1984) английский физик-теоретик
Работы относятся к квантовой механике,
квантовой электродинамике, квантовой
теории поля, теории элементарных частиц,
теории гравитации.
Построил в 1928 релятивистскую теорию
движения электрона, предположил
существование положительно заряженного
электрона, или позитрона, который был
открыт в 1932. Построил теорию дырок
(1930), в 1931 предсказал существование
античастиц, рождение и аннигиляцию
электронно-позитронных пар.
В 1931 выдвинул гипотезу о существовании
элементарного магнитного заряда
(монополь Дирака), в 1933 —
антивещества. За создание квантовой
механики вместе с Э. Щредингером в 1933
был удостоен Нобелевской премии.
Независимо от Э. Ферми разработал в 1926
статистику частиц с полуцелым спином
(статистика Ферми — Дирака).
313
314. Температурный критерий вырождения
• Газ называется вырожденным, если его статистические свойстваотличаются от свойств классического идеального газа.
px x ; (1)
p x ,
a
(2)
a – линейный размер области
локализации частицы;
1
p2
2
p p x ; (3) W
;
3
2 (4) a n0 , (5)
2m 2ma
W
2n02 / 3
2m
; (6)
2n02 / 3 3
kTВ ; (7)
2m
2
n0 –
концентрация
частиц;
2 n02 / 3
TВ
3km
(8)
314
315.
Вырожденный(квантовый)
газ
0
Невырожденный
(классический)
газ
Т
ТВ
315
316. Численные оценки температуры вырождения
• Электронный газ вметаллах сильно
вырожден (статистика
Ферми-Дирака):
• Электронный газ в
полупроводниках всегда
не вырожден
(статистика МаксвеллаБольцмана):
n0 10 29 м 3 , TВ 2 10 4 К .
n0 1018 м 3 , TВ 10 4 К .
316
317.
• Фотонный газ всегдавырожден (статистика
Бозе-Эйнштейна):
• Атомные и молекулярные
газы (вырождение было
бы возможным только
при очень низких
температурах, при
которых газ перестает
быть газом):
m0 0, TВ .
n0 1018 м 3 , TВ 1 К .
317
318. Электронный газ в металлах
1f
W
exp
1
kT
T→0
WF= (0) – энергия Ферми
318
319. Энергия Ферми
• WF= (0) – энергия Ферми – максимальная энергия,которую могут иметь электроны в металле при T 0.
pF 2mWF ;
4 3
pFV
n 3
; (2)
1 3
h
2
(1)
3
3
n
3
3
h
pF3
n0
; (3)
V8
8
1/ 3
h 3n0
pF
2
;
(4)
2
pF
2
h 3n0
WF
2m 8m
2/3
(5)
319
320. Численная оценка
h 2 3n0WF
8m
2/3
В металлах концентрация электронов проводимости составляет
n0 10 29 м 3 ;
WF 10 18 Дж 6 эВ;
При н. у. kT 4 10 21 Дж 0,03 эВ;
kT
1
WF
320
321. Распределение по энергии
dnf ;
dg
В квазинепрерывном случае:
(1)
dn dn dg
dg
f
;
dW dg dW
dW
4 p 2 dpV 8 p 2 dpV
dg
;
3
3
h /2
h
W
p2
2m
;
(4)
pdp
dW
; (5)
m
mdW
dp
;
p
(2)
(3)
(6)
321
322.
8 p 2mdW V 8 2mW mdW Vdg
;
3
3
ph
h
dg 8 V
3
dW
h
dn
dW
2m3 W ;
1
8 V
3
W
h
exp
1
kT
2m3 W ;
T→0
322
323. Теплоемкость электронного газа
Внутренняя энергияТеплоемкость
• Малая теплоемкость вырожденного электронного газа
объясняется характером заполнения квантовых состояний.
• В теплоемкости участвуют только электроны на хвосте функции
заполнения ячеек. Внутренние электроны не могут перейти на
занятые более высокие уровни.
323
324. Фотонный газ в замкнутой полости
4 p 2 dpVdg
; (1)
3
h
hn
p ; (2)
c
hdn
dp
; (3)
c
2
hn h
4 dn V
2
4
n
c
c
dg 3
3 Vdn; (4)
h
c
dg 4 n 2
3 V ; (5)
dn
c
dn
dn dg 8 n 2
1
2
3 V
; (6)
dn
dg dn
hn
c
exp 1
kT
(коэффициент 2 учитывает возможность двух состояний поляризации)
324
325.
Объемная плотность спектральной плотности энергииhn dn 8 n 2
( n )
3
Vdn
c
hn
;
hn
exp 1
kT
(7)
Объемная плотность спектральной плотности
энергетической светимости
c
r (n) (n);
4
(8)
Формула Планка для АЧТ
2 n 2
hn
r (n ) 2
c exp hn 1
kT
325
326. Теплоемкость твердых тел
• Теплоемкость кристаллов в классической физике определяетсятепловыми колебаниями частиц, имеющих три колебательные
степени свободы, на каждую из которых приходится средняя
энергия W=kT => UM=3NAkT.
• Правило Дюлонга и Пти:
CM
Q U
3R 25 Дж /( моль К ) 8 кал /( моль К );
T T
• Для металлов должно выполняться то же правило, т.к.
теплоемкость электронного газа относительно мала.
Результаты
экспериментов:
326
327. Квантовая теория теплоемкости Дебая
• Учитывается взаимодействие атомов решетки. Широкий спектрчастот колебаний. Звуковые волны. Звуковые квазичастицы –
фононы.
W hn;
hn
p ;
v
• Квазиимпульс имеет направление распространения волны.
• При столкновении фонона с фононом в кристаллах
квазиимпульс может передаваться дискретными порциями.
• Lsz=0, =0. Фононы являются бозонами => статистика БозеЭйнштейна.
dn
dg
1
;
hn
exp 1
kT
4 p 2 dp V
4 n 2 dn
dg 3
3
V;
3
3
h
v
Коэффициент 3 учитывает наличие продольных и поперечных колебаний.
327
328.
112n 2V
dn
dn;
3
hn
exp 1 v
kT
dn dn dg
;
dn dg dn
Длина звуковой волны снизу ограничивается периодом решетки
lmin ~ d ~ (V/N)1/3, N – число частиц (число узлов кристаллической
решетки в кристалле объемом V. Минимальной длине волны
соответствует максимальная частота nmax=v/lmin.
Точные расчеты дают следующую оценку верхней границы частот
фононов:
1/ 3
n max
n max
3N
v
4 V
12hV
U hndn
3
v
0
n max
0
;
n3
dn;
hn
exp 1
kT
328
329.
При вычислении U вводится характеристическая температура Дебая1/ 3
TD hn max / k
n max
3N
v
4 V
;
а) T>>TD (высокие температуры):
hn
hn
exp 1
,
kT
kT
U 3NkT ;
12 V
U 3 kT
v
n max
0
CM 3R
12 V
n3max
n dn 3 kT
,
3
v
2
- правило Дюлонга и Пти
б) T<<TD (низкие температуры):
12 hV
n3
4
U
d
n
const
T
;
3
hn
v
0 exp
1
kT
CM const T 3
- закон Дебая
329
330. ДЕБАЙ Петер Йозеф Вильгельм (24.111 1884 —2.Х1 1966) физик и химик
Работы посвящены квантовой теории
твердых тел, теории теплопроводности кристаллов, теории строения молекул, квантовой теории атома. В 1912 ввел
представление о твердом теле как
изотропной упругой среде, способной
совершать колебания в конечном диапазоне
частот (модель твердого тела Дебая).
Исходя из вида спектра в области низких
частот, показал, что теплоемкость решетки
при низких температурах должна быть
пропорциональна третьей степени
абсолютной температуры (закон
теплоемкости Дебая).
В рамках своей модели ввел понятие
характеристической температуры
(температура Дебая), которая определяет
для каждого вещества область, где
становятся существенными квантовые
эффекты.
В 1923 объяснил эффект Комптона. Один из
первых начал исследования полимеров.330
Нобелевская премия по химии (1936).
331. Зонная теория твердых тел
Изолированные атомы (L>>d) имеют дискретные энергетические
уровни. Потенциальные барьеры высокие и широкие, их прозрачность
нулевая. Уширение уровня We связано с естественным временем
жизни атома в возбужденном состоянии.
We te ;
10 34 Дж с
26
7
We
10
Дж
10
эВ;
8
te
10 с
We W 1 эВ.
W – разность энергий соседних
уровней.
331
332.
• В кристаллах L d. Потенциальные барьеры понижаются исужаются, их прозрачность становится существенной.
• Расчеты показывают, что при L 10 10 м и U0 W 6 эВ
прозрачность составит D 0,05.
стота просачивания n Dn, n - частота ударов электрона о
стенку.
v
n 1016 c 1; n 5 1014 c 1;
d
t e n 1 2 10 15 c; We 1 эВ.
• Электроны становятся общими. Энергетические уровни
превращаются в зоны.
332
333. Воображаемая картина превращения энергетических уровней в зоны по мере уменьшения расстояния между атомами
333334. Энергетические зоны в кристаллах
- разрешенные зоны- запрещенные зоны
334
335.
• Разрешенные зоны могут перекрываться, образуягибридную зону.
• Зона, заполненная электронами частично или пустая
при T=0K называется зоной проводимости.
• Самая верхняя зона, целиком заполненная
электронами при T=0K называется валентной
зоной.
• У проводников верхняя зона проводимости
заполнена частично.
• У твердых диэлектриков и полупроводников в
зоне проводимости при T=0K нет электронов,
валентная зона отделена от зоны проводимости
запрещенной зоной.
• Условно считают:
Wзапр 2 эВ диэлектрик;
Wзапр 2 эВ полупроводник;
335
336.
Удельное сопротивление (Ом·м)Металлы
10 8—10 6
Диэлектрики
108—1015
Полупроводники
10 5—108
• У металлов удельное сопротивление растет с
ростом температуры (рассеяние электронов на
фононах).
• У полупроводников удельное сопротивление
сильно уменьшается с ростом температуры
(растет концентрация носителей зарядов в зоне
проводимости и валентной зоне).
336
337. Полупроводники
• В периодической системе элементов Д.И. Менделееваполупроводники образуют компактную группу.
• В кружках дана ширина запрещенной зоны в электрон-вольтах.
• Слева и снизу находятся металлы.
• Справа и сверху расположены элементы, которые в твердом
состоянии являются диэлектриками.
337
338.
• Типичным представителем полупроводниковявляется германий.
• На внешней оболочке у германия четыре валентных
электрона.
• В кристалле германия электроны соседних атомов
вступают в ковалентные связи.
338
339. Собственная проводимость полупроводников
• Энергия активации собственной проводимостипримерно равна ширине запрещенной зоны
(например, у кремния 1,1 эВ).
• Возникает свободный электрон (-e) в зоне
проводимости и свободная квазичастица – дырка
(+e) в валентной зоне => электронно-дырочный
характер собственной проводимости.
339
340. Примесная донорная проводимость полупроводников
• Примеси, приводящие кобразованию донорных
уровней это пятивалентные
элементы (фосфор, мышьяк,
сурьма).
• В результате переброски
электронов с донорных
уровней в зону проводимости
в полупроводнике возникает
электронная примесная
проводимость (проводимость
n –типа, электронный
полупроводник n типа).
340
341. Примесная акцепторная проводимость полупроводников
• Примеси, приводящие кобразованию акцепторных
уровней это трехвалентные
элементы (бор, алюминий,
индий).
• В результате переброски
электронов из валентной зоны
на акцепторные уровни в
полупроводнике возникает
дырочная примесная
проводимость (проводимость
p–типа, дырочный
полупроводник p-типа).
341
342. Фрагмент кристаллической решетки примесных полупроводников
а) донорный полупроводник; б) акцепторный полупроводник342
343. Концентрация носителей
n0 n0соб n0пр ;n0соб
W
пр
W0
exp
;
2kT
We , если п типа,
W p , если р типа.
пр
W
;
n0пр exp
2
kT
W пр W0
• При низких температурах основной вклад в концентрацию
носителей тока вносит примесная концентрация.
• При высоких температурах, наоборот, главную роль играет
концентрация носителей собственной проводимости.
343
344. Фотопроводмимость полупроводников Внутренний фотоэффект
• Электрическая проводимость полупроводников, возбужденнаяэлектромагнитным излучением, называется
фотопроводимостью.
а) Собственная фотопроводимость.
б) Примесная донорная фотопроводимость.
в) Примесная акцепторная фотопроводимость.
hn> W – красная граница внутреннего фотоэффекта у
примесных полупроводников в ИК области.
344
345. Фотосопротивление (фоторезистор)
1 – изолирующая подложка;2 – тонкий полупроводниковый слой;
3 – металлические электроды;
4 – защитное покрытие;
• У фотосопротивлений световая чувствительность
выше, чем у вакуумных фотоэлементов, основанных
на внешнем фотоэффекте.
345
346. Контактные явления
Контакт двух металлов1 – уровень энергии свободно покоящегося электрона;
2 – уровень электрохимического потенциала ( уровень Ферми);
Величина e называется электрохимическим потенциалом.
346
347.
• Схема энергетических зон до контакта двухразличных металлов.
• Металлы 1 и 2 отличаются работами выхода и
электрохимическими потенциалами.
• Во втором металле электронами заполнены более высокие
энергетические уровни, чем в первом.
347
348.
При контакте в состоянии равновесияэлектрохимические потенциалы выравниваются
e 1 1 e 2 2
1
2
348
349.
Внутренняя контактная разность потенциалов:1 2 ( 1 2 ) / e
Оценка возможного изменения концентрации
носителей тока в контактном слое двух металлов
q S
;
C 0 S
0
0
;
3 10 10 м; 1 B
0,03 Кл / м ; n 2 1017 м 2 ;
e
2
n n0 3 10 10 10 29 м 2 3 1019 м 2 ;
n
1
n 150
• Следовательно, удельное сопротивление тонкого контактного
слоя двух металлов практически не отличается от удельного
сопротивления самих металлов.
349
350.
• Кроме внутренней контактной разности потенциаловсуществует внешняя контактная разность
потенциалов, обусловленная разностью работ
выхода электронов из металлов.
1 2 ( A1 A2 ) / e
• Эта разность потенциалов для разных пар металлов
колеблется от десятых долей до единиц вольт и
сильно зависит от чистоты и состояния поверхности.
350
351. Контакт электронного и дырочного полупроводников (р-n переход)
• Такие переходы используются для выпрямления,усиления и генерации переменных токов.
351
352.
• Запирающий слой – двойной слой разноименныхэлектрических зарядов, создающий электрическое
поле на p-n-переходе, препятствующее свободному
разделению зарядов.
352
353. Схема энергетических зон до контакта двух различных полупроводников
353354. Формирование контактного запирающего слоя
• Концентрация основных носителей в примесныхполупроводниках составляет ~1018 м3, поэтому уменьшение
концентрации носителей в контактном слое значительно,
сопротивление слоя велико, а его толщина много больше, чем у
контактного слоя металлов.
354
355. Обратное включение
• Высота потенциального барьера увеличивается на e .355
356. Прямое включение
• Высота потенциального барьера уменьшается на e .356
357. Вольтамперная характеристика полупроводникового диода
357358. Список использованных источников
• 1. Савельев И.В. Курс общей физики, Т. 2.- СПб: «Лань», 2007 г.• 2. Савельев И.В. Курс общей физики, Т. 3.- СПб: «Лань», 2007 г.
• 3. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа,
2000 г.
• 4. Борн М, Вольф Э. Основы оптики. М.: «Наука», 1970 г.
• 5. Сивухин Д.В. Общий курс физики. Оптика. М.: «Наука», 1980 г.
• 6. Храмов Ю.А. Физики. Библиографический справочник. – М.:
«Наука», 1983 г.
• 7. Касьянов В.А. Физика. – M.: «ДРОФА», 2001 г.
• 8. Иродов И.Е. Волновые процессы. Основные законы. М.:
Издательство «Лаборатория базовых знаний», 2001 г.
• 9. Иродов И.Е. Квантовая физика, основные законы. – М.:
Издательство «Лаборатория базовых знаний», 2001 г.
358









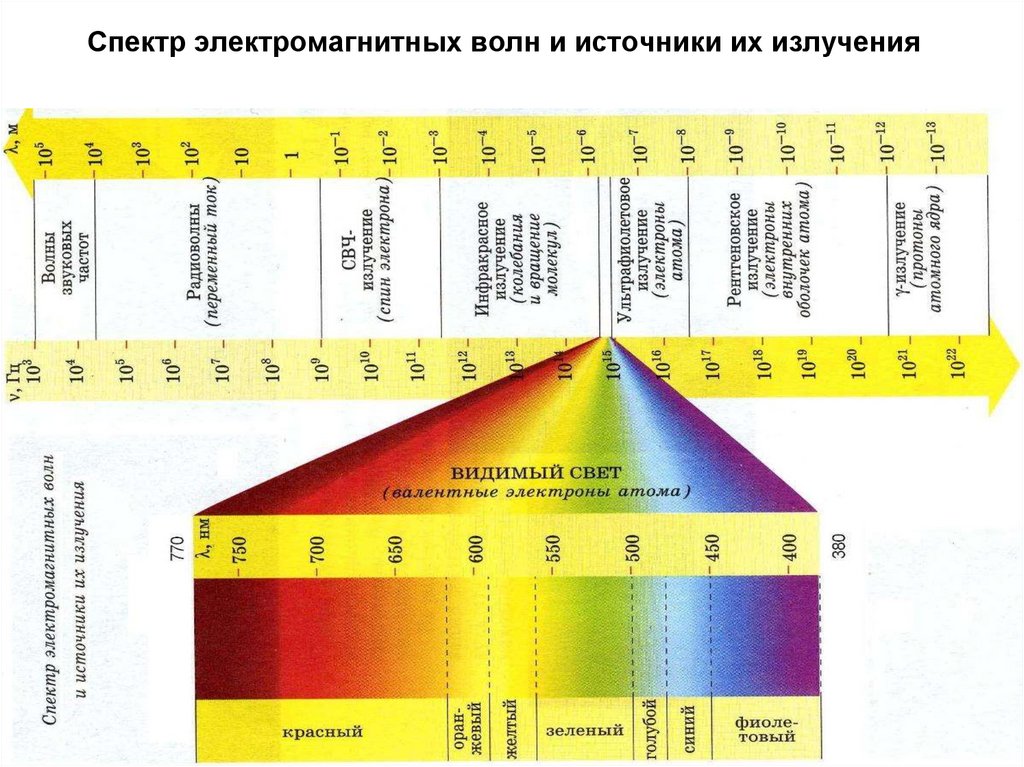







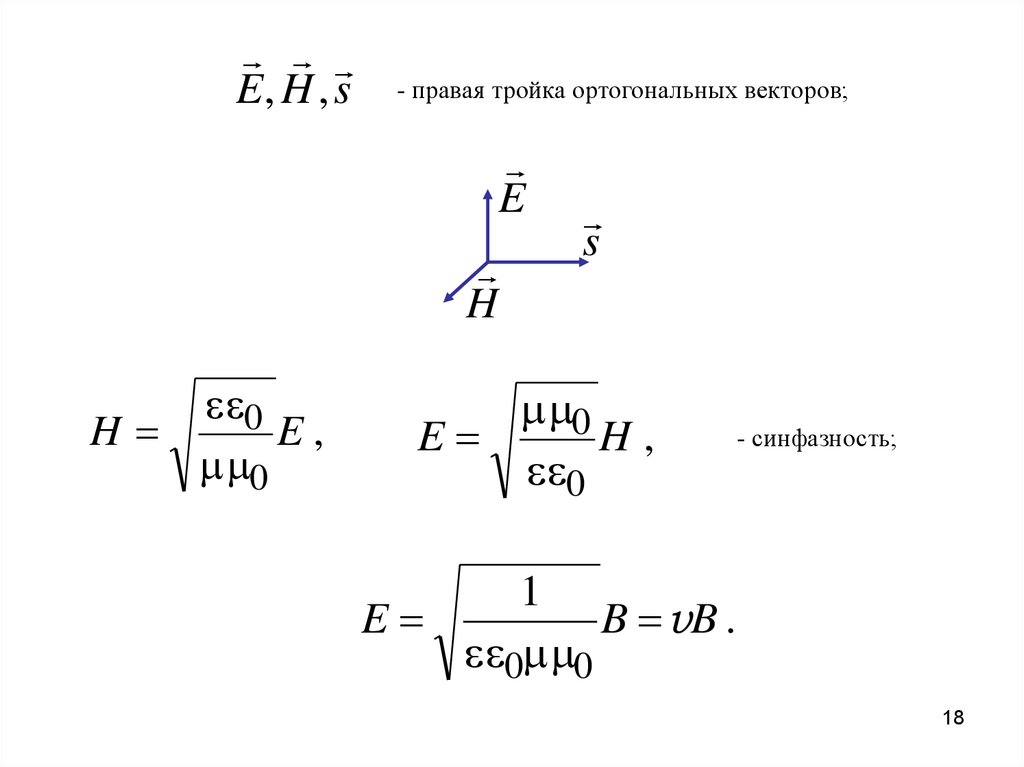








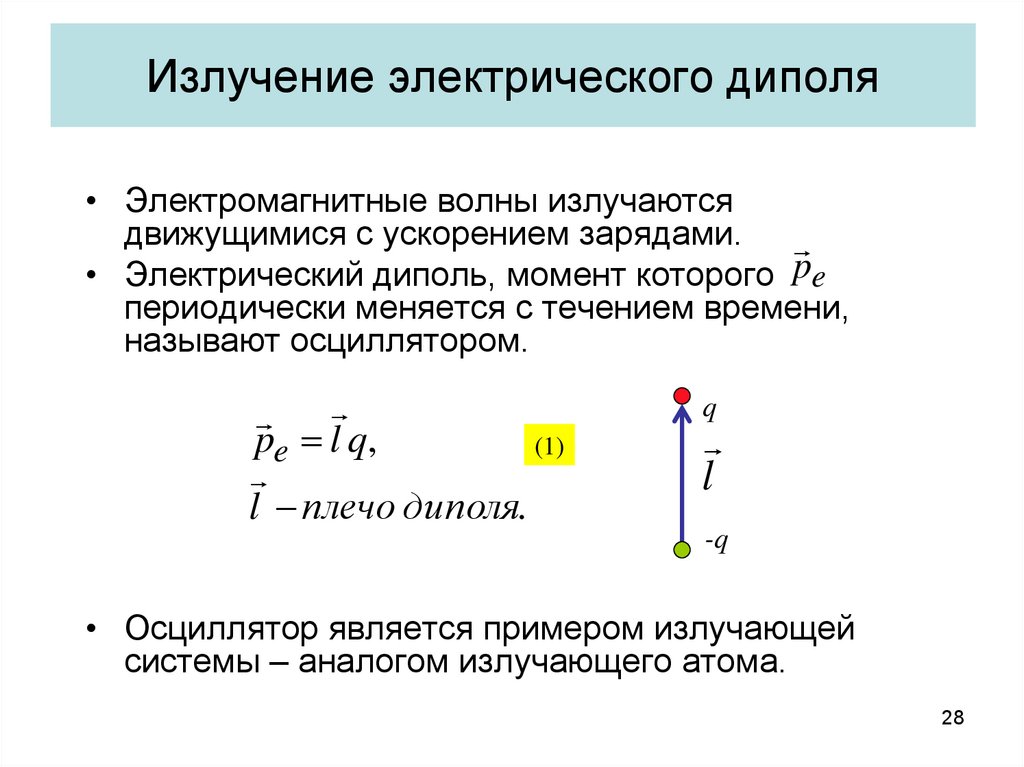
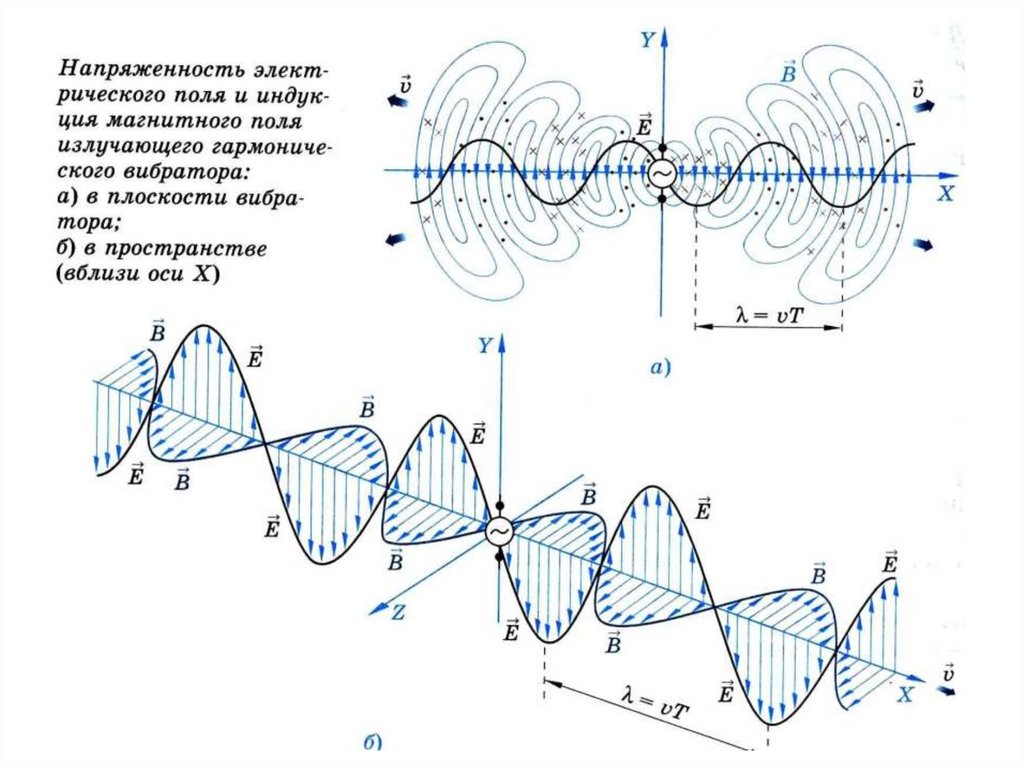
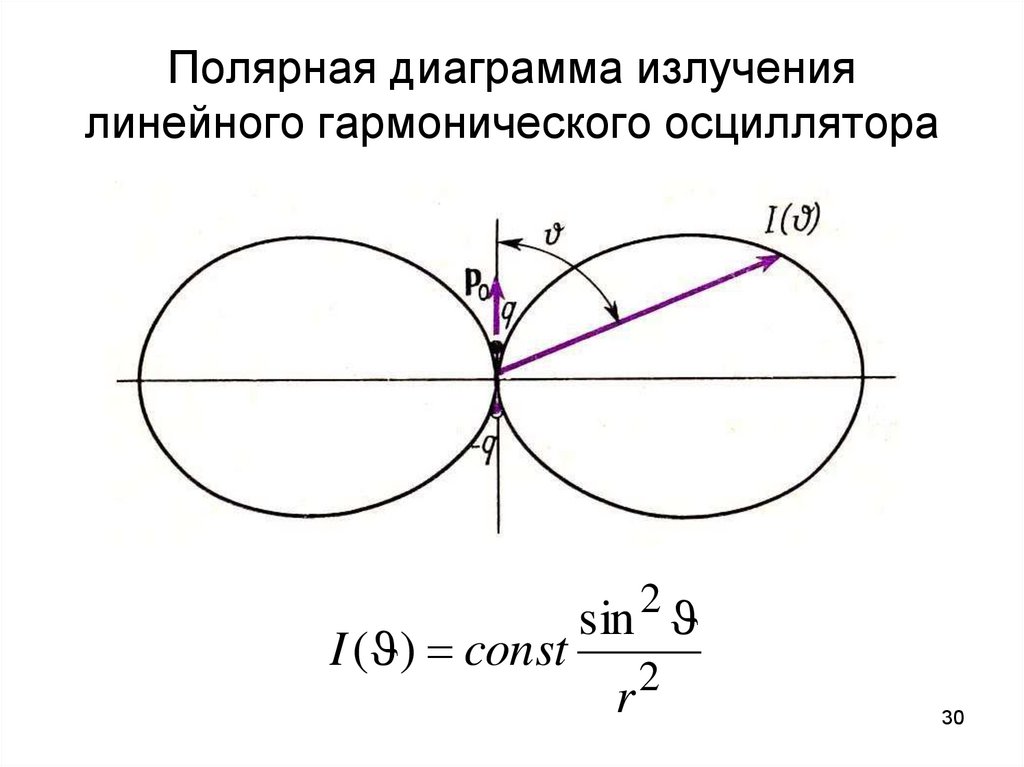
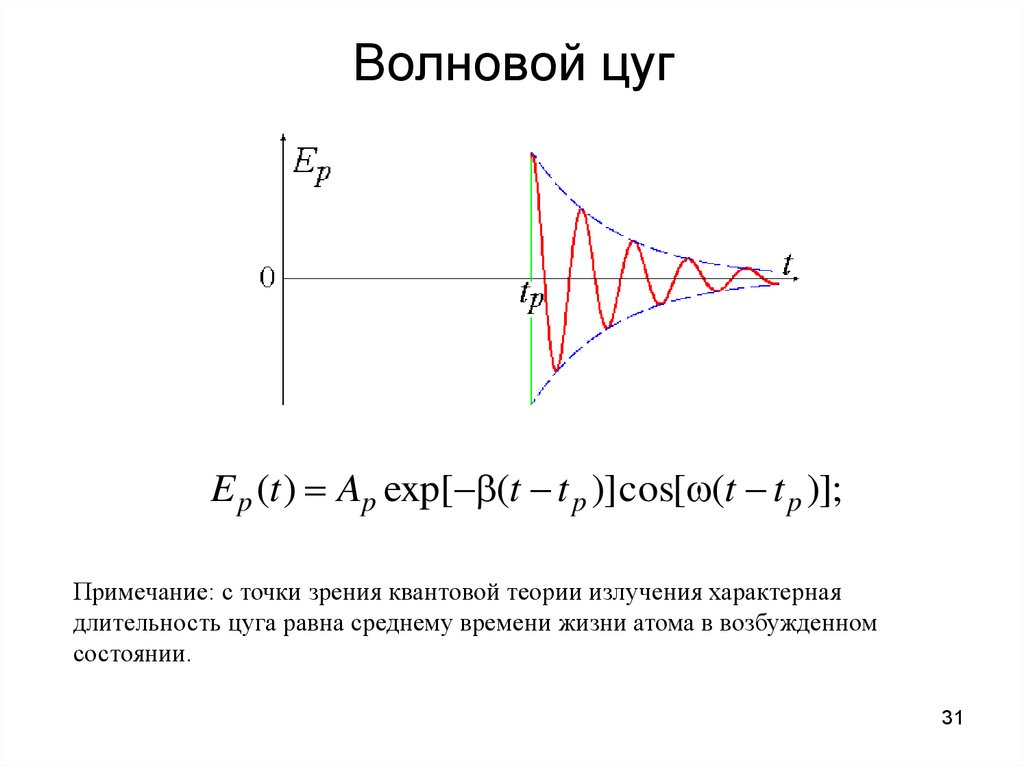


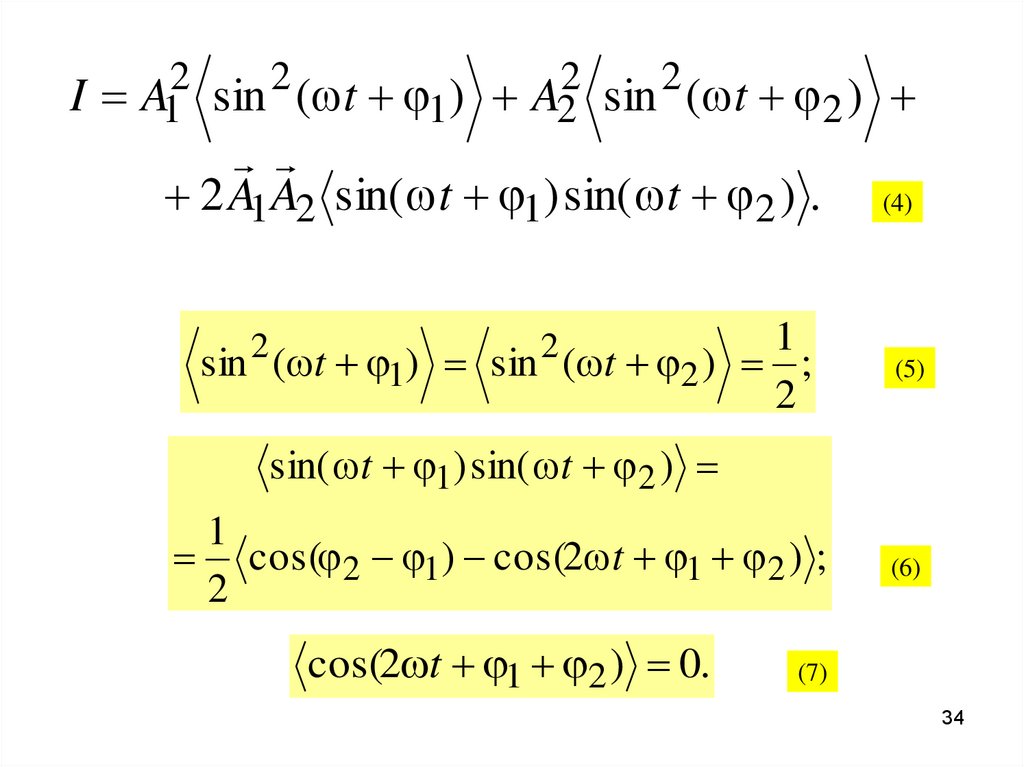


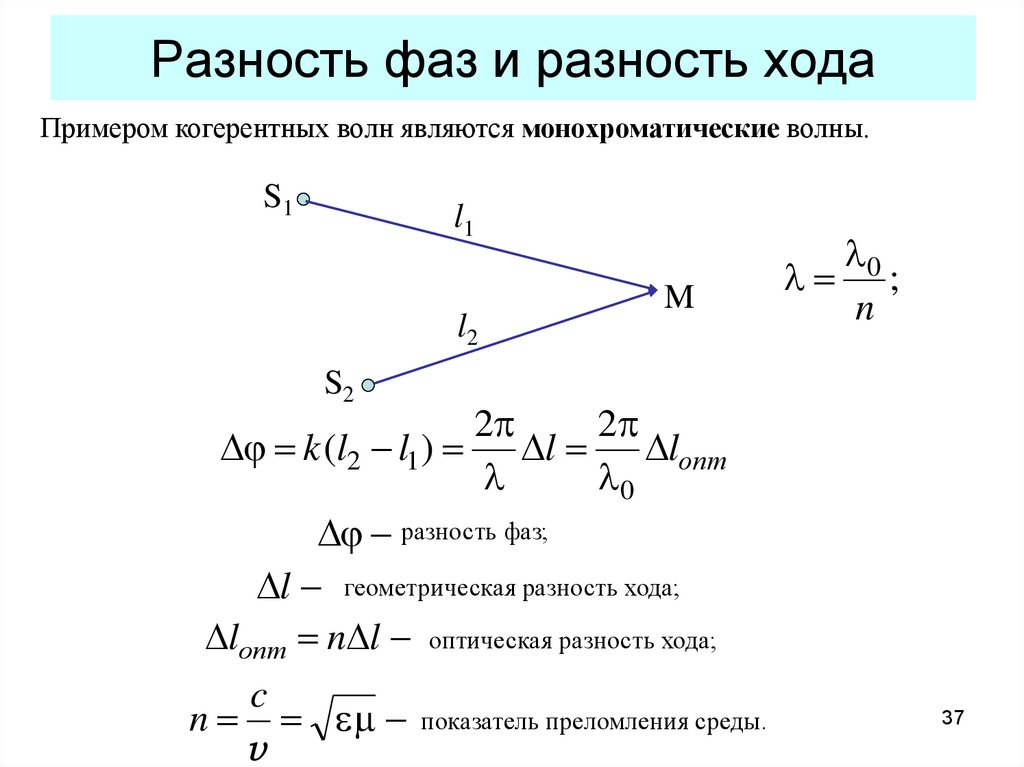

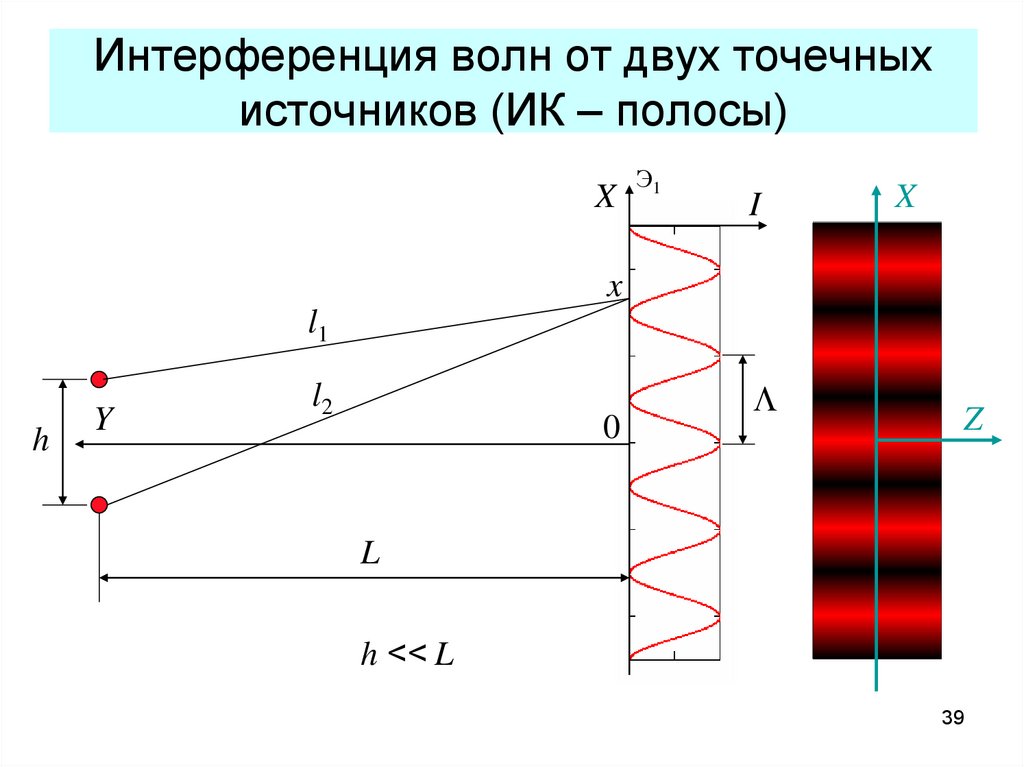

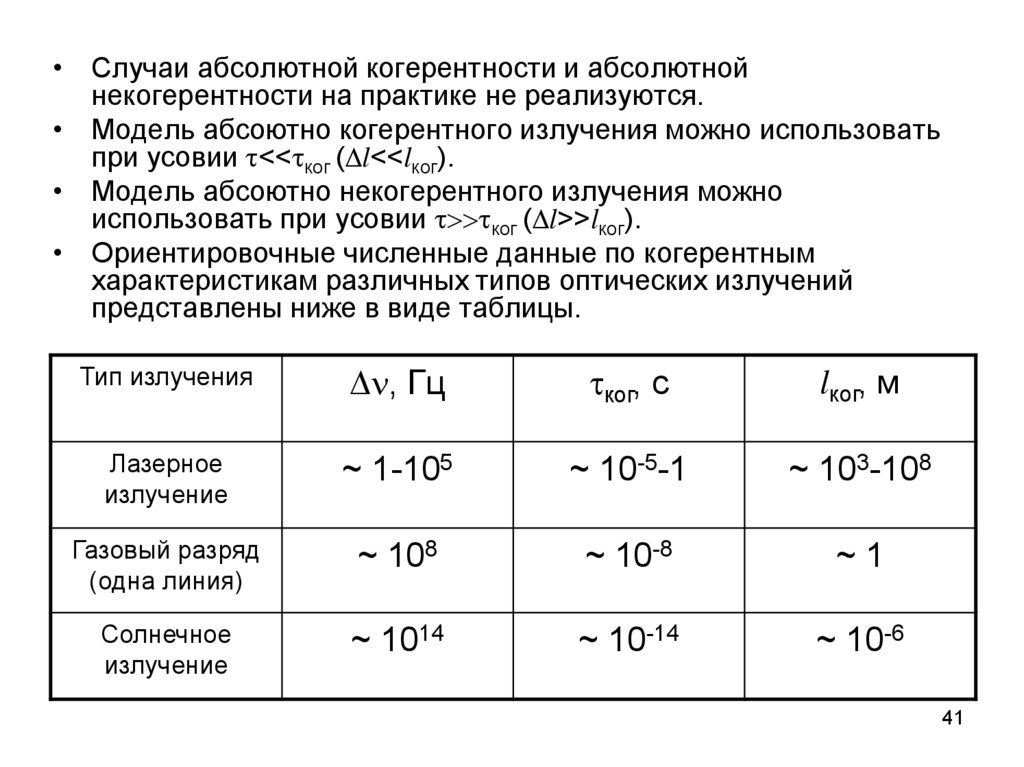


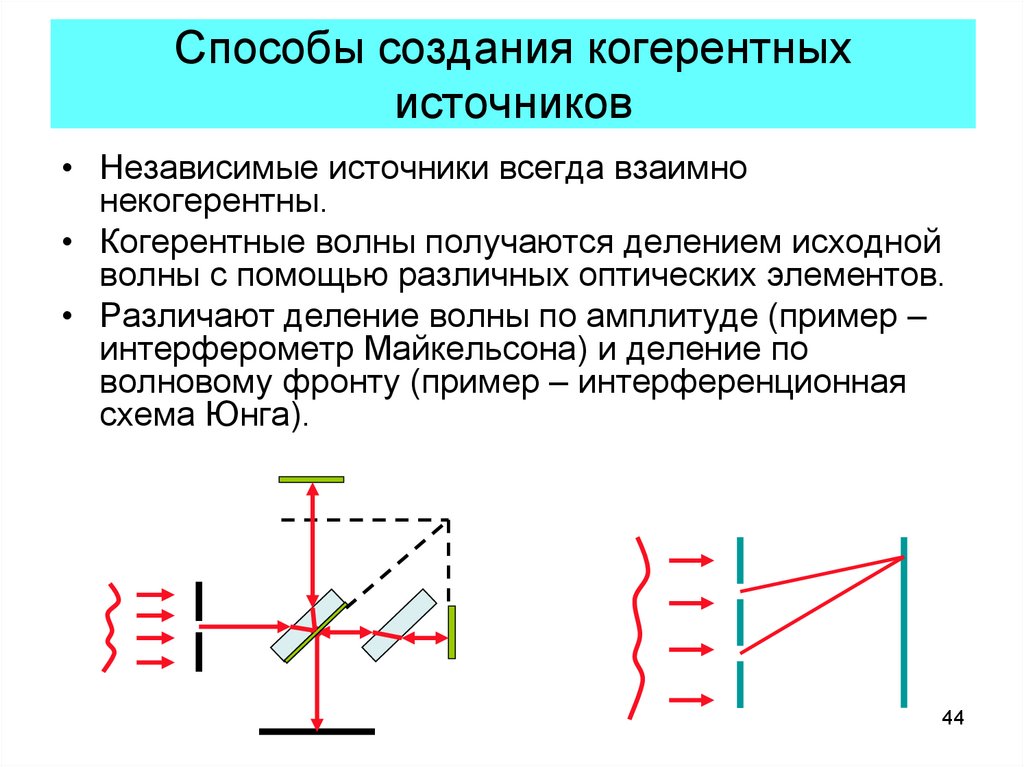
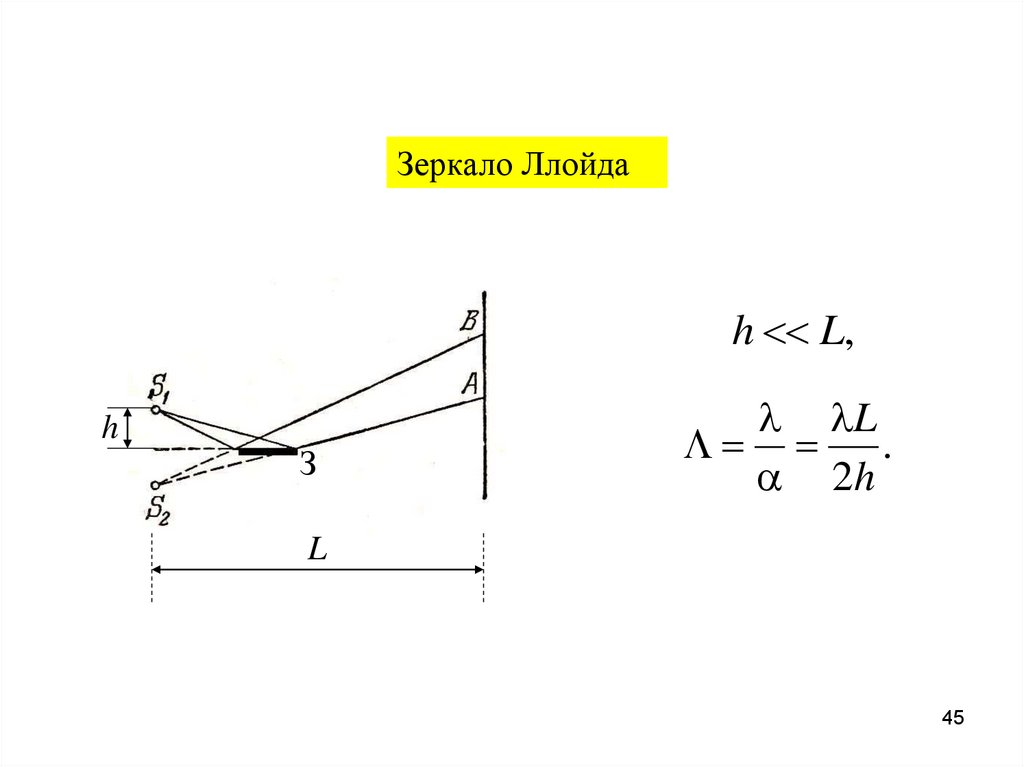
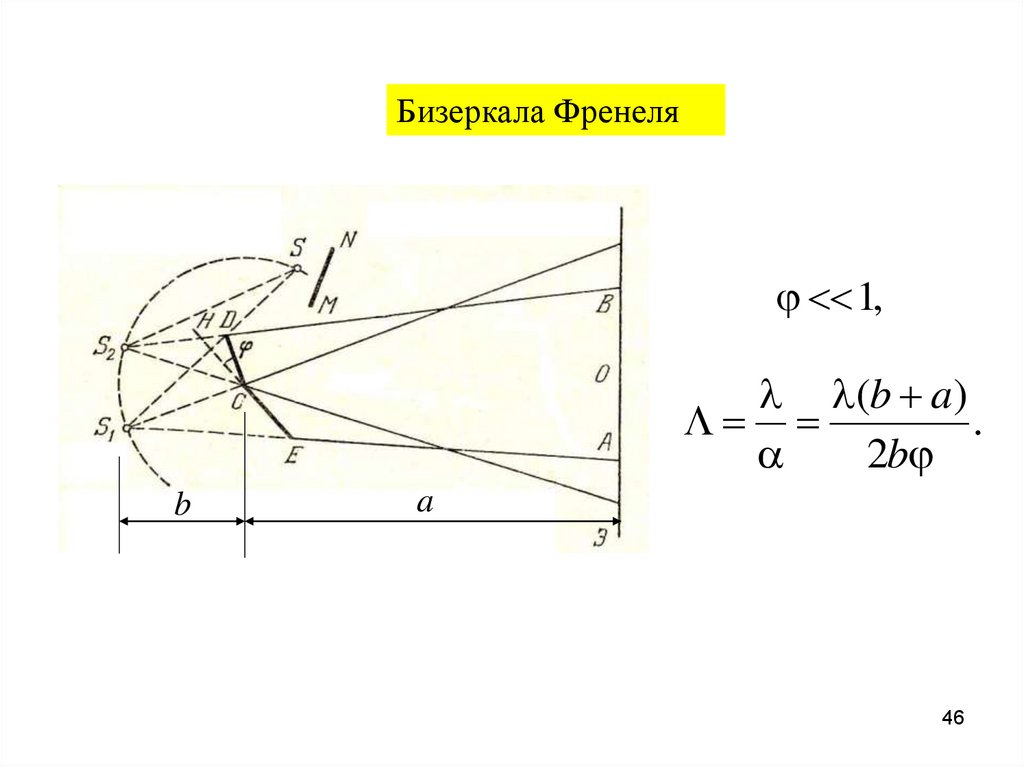
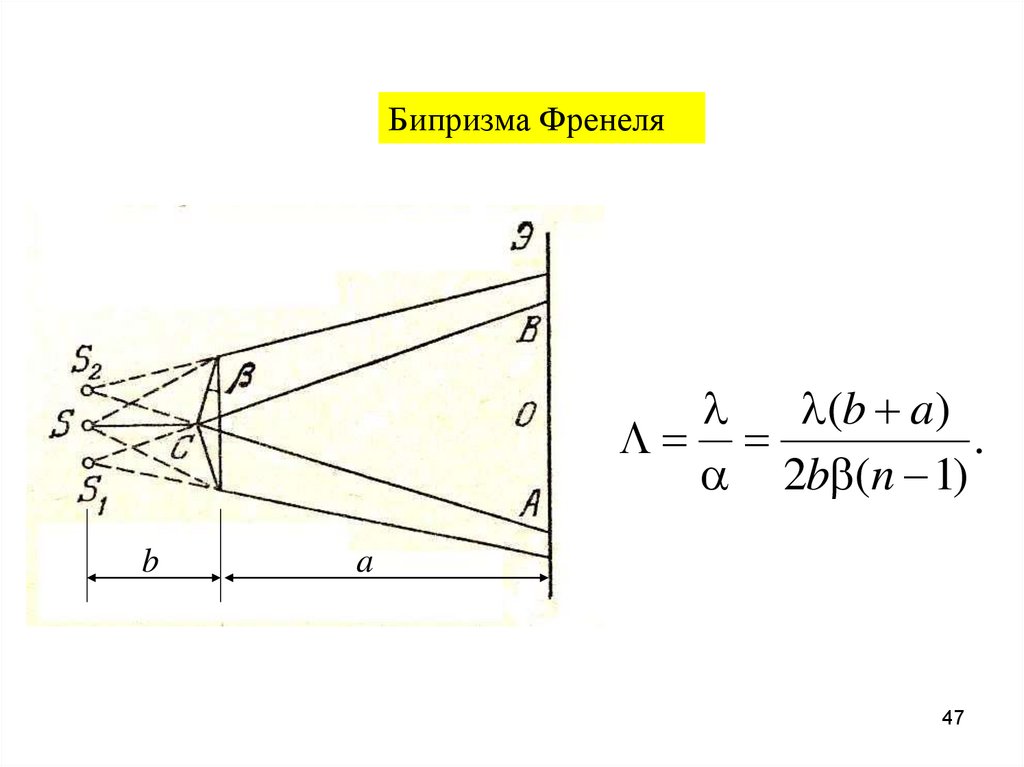
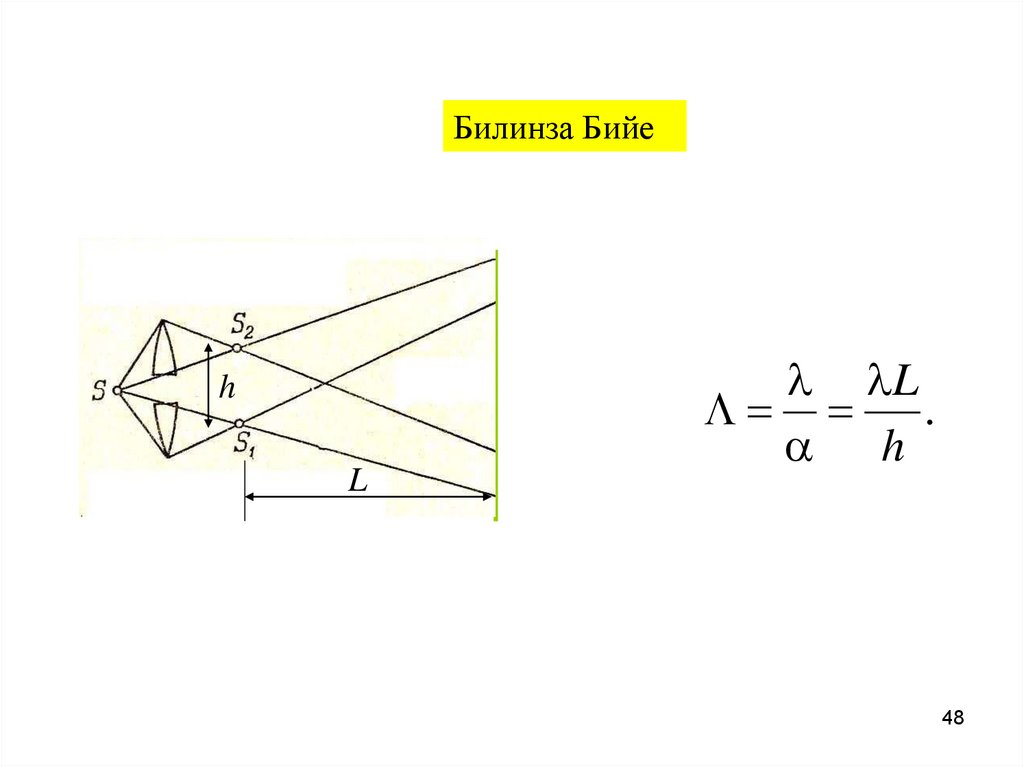
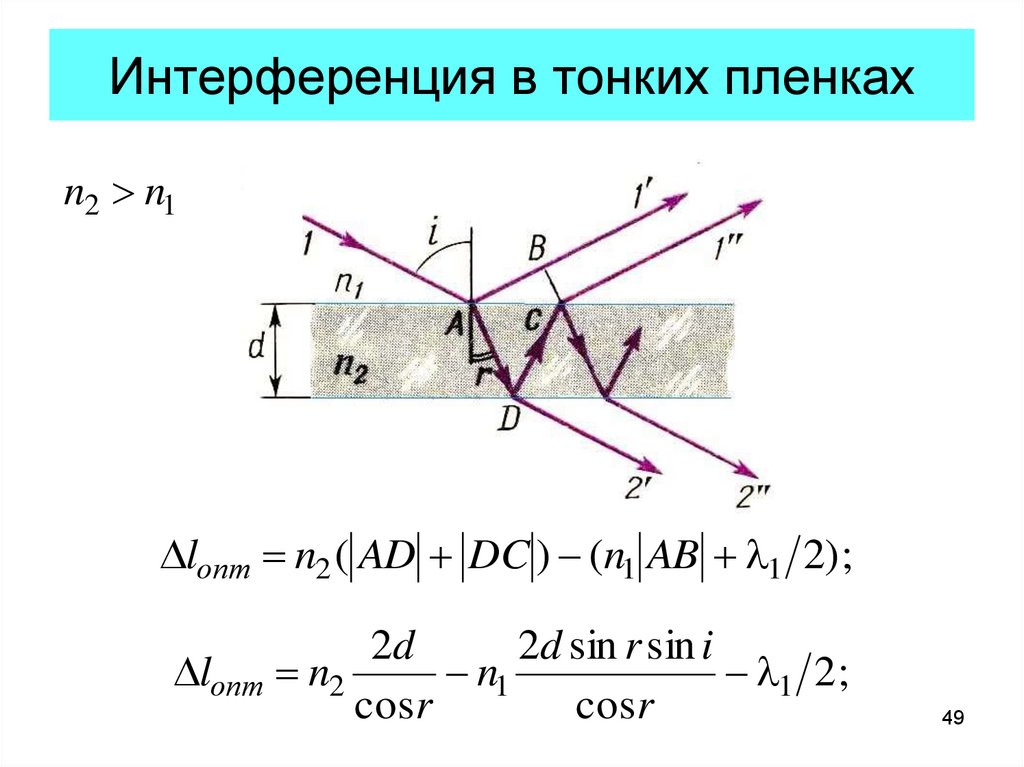

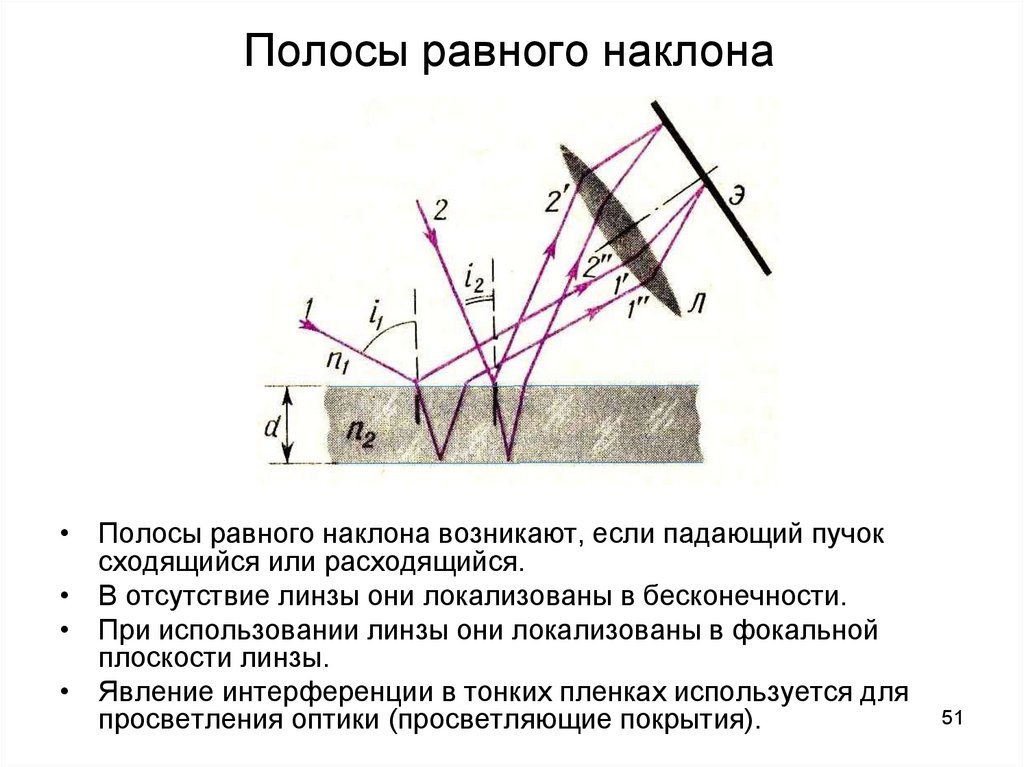
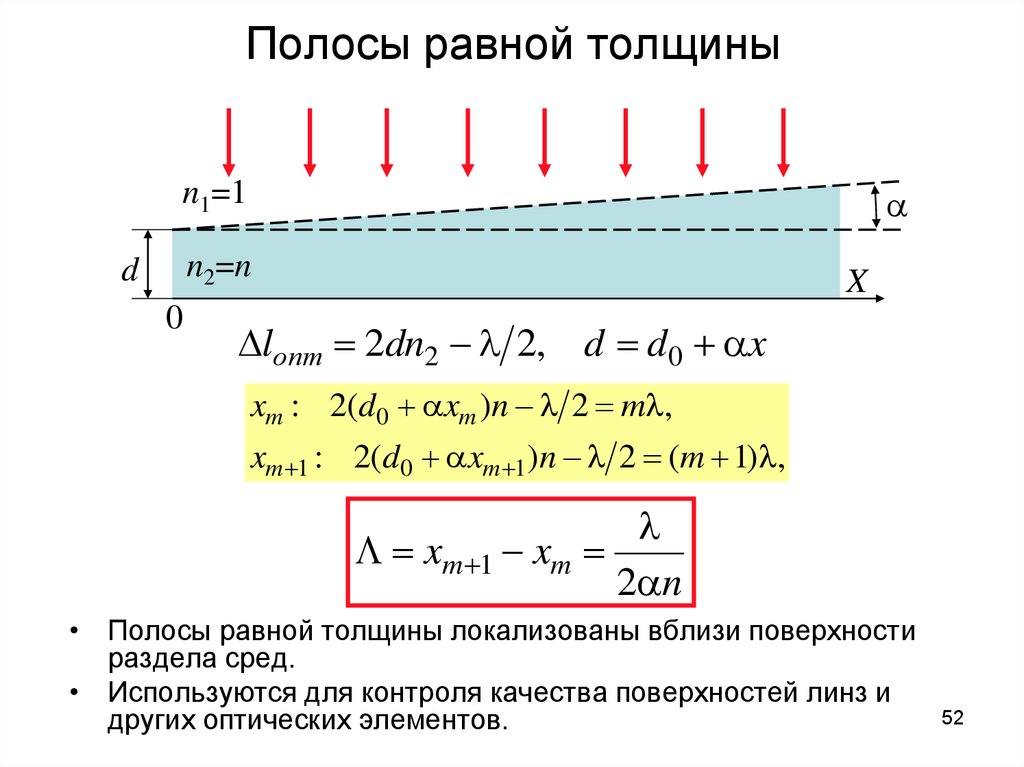
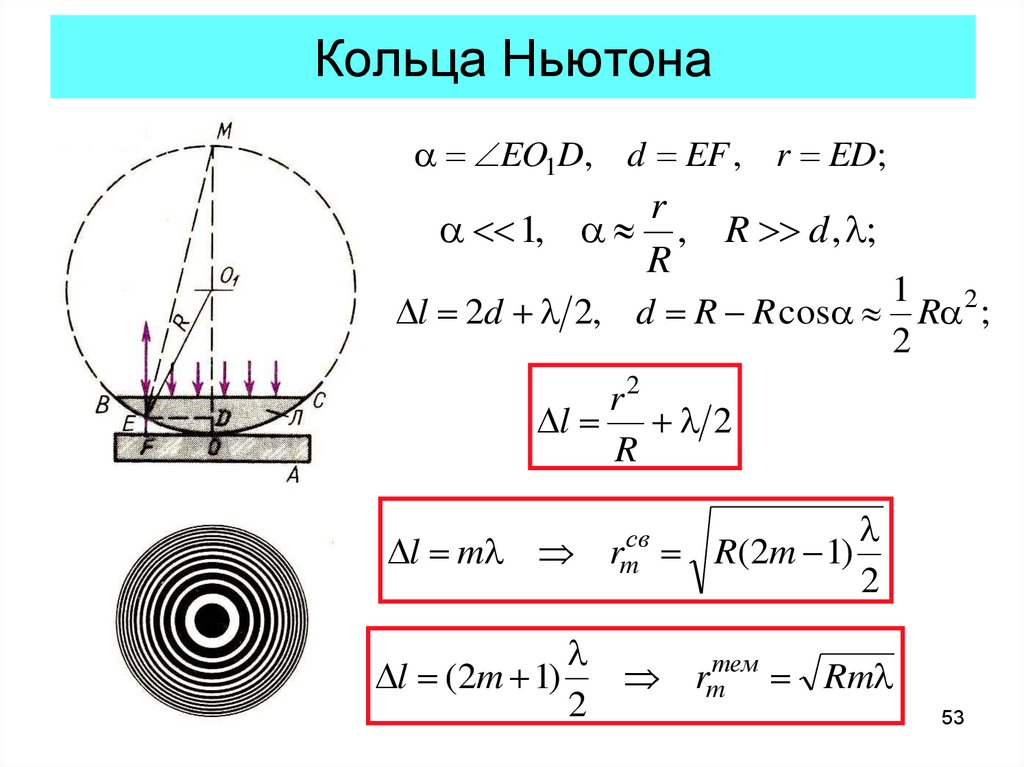

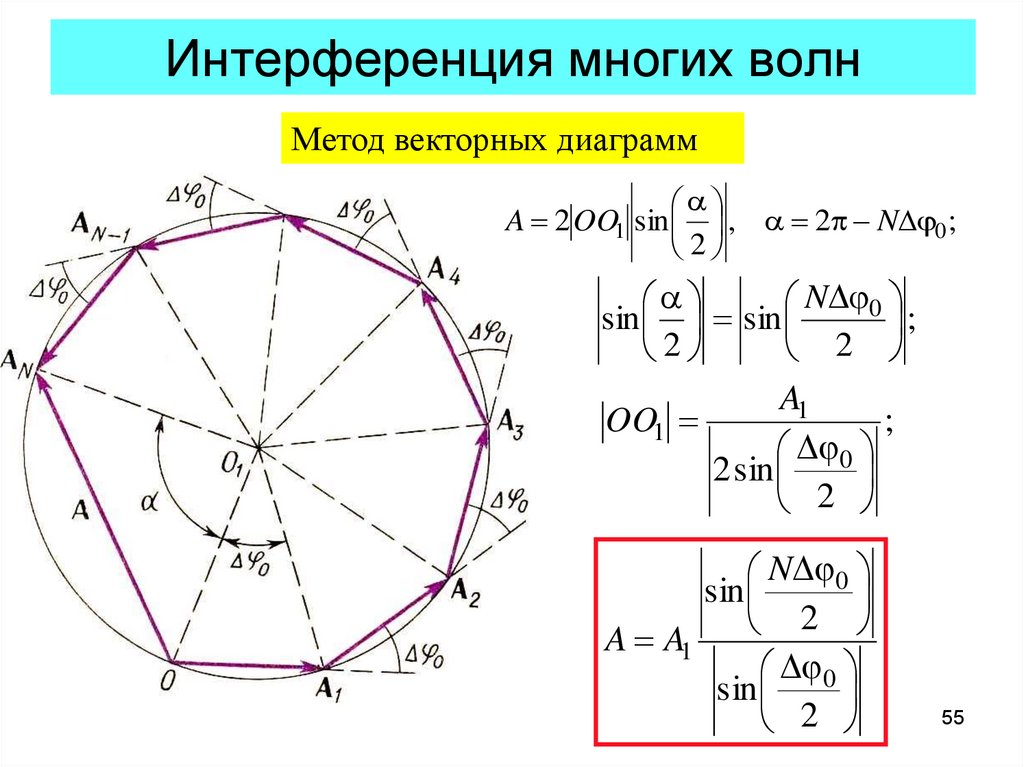
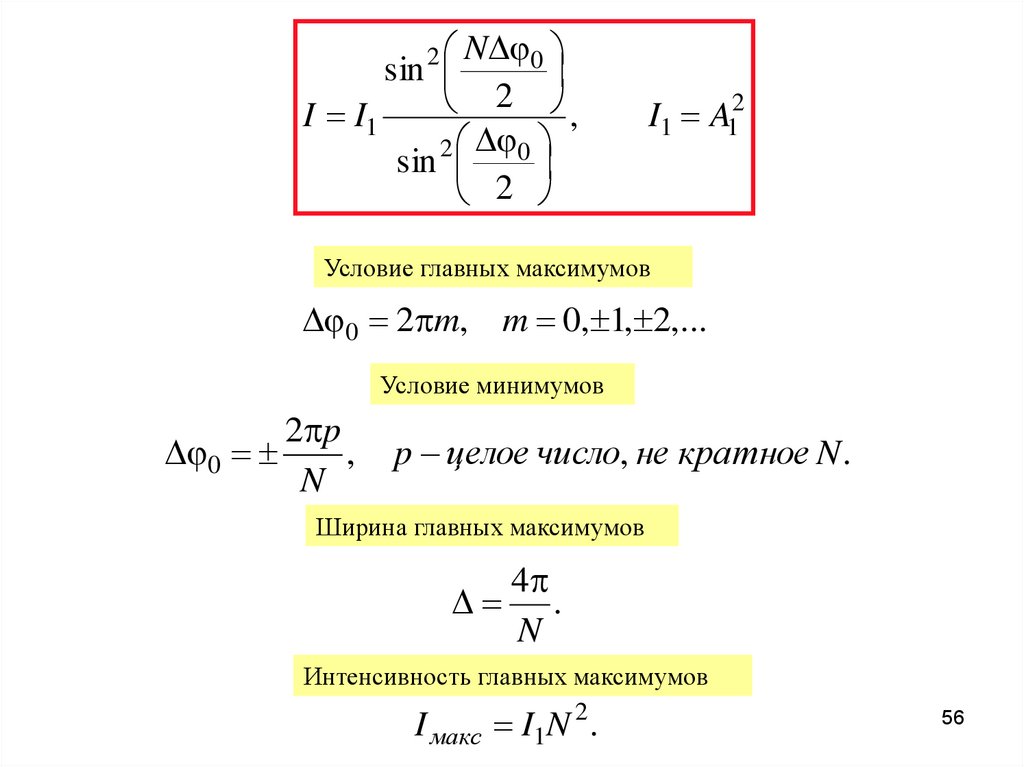
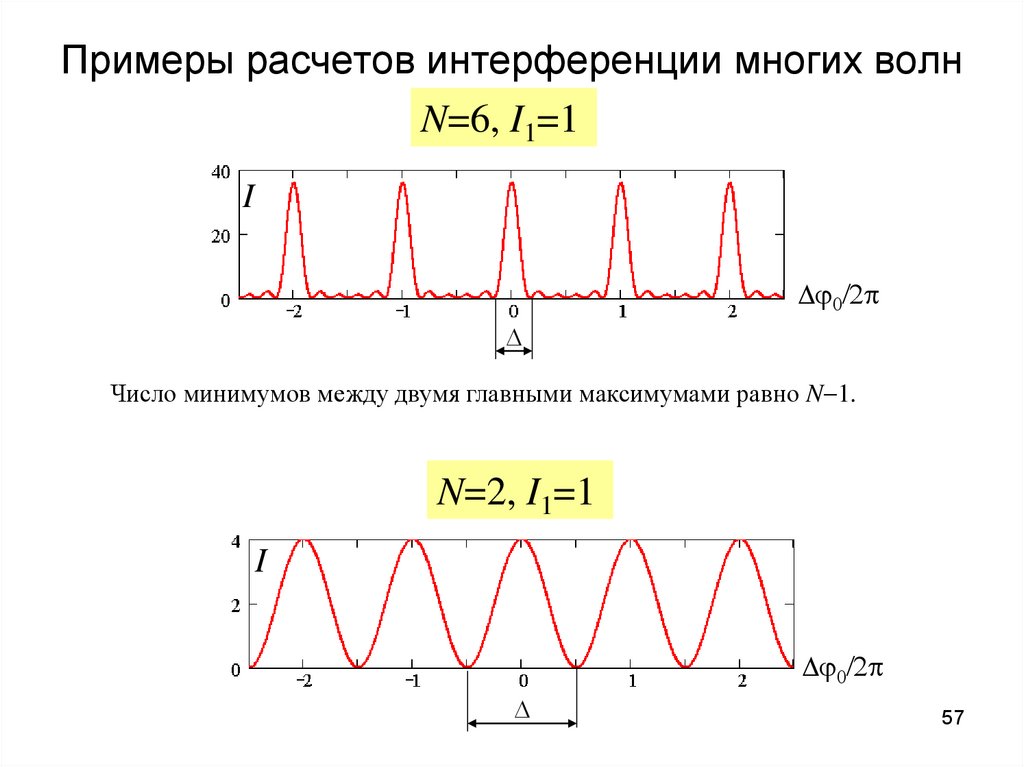



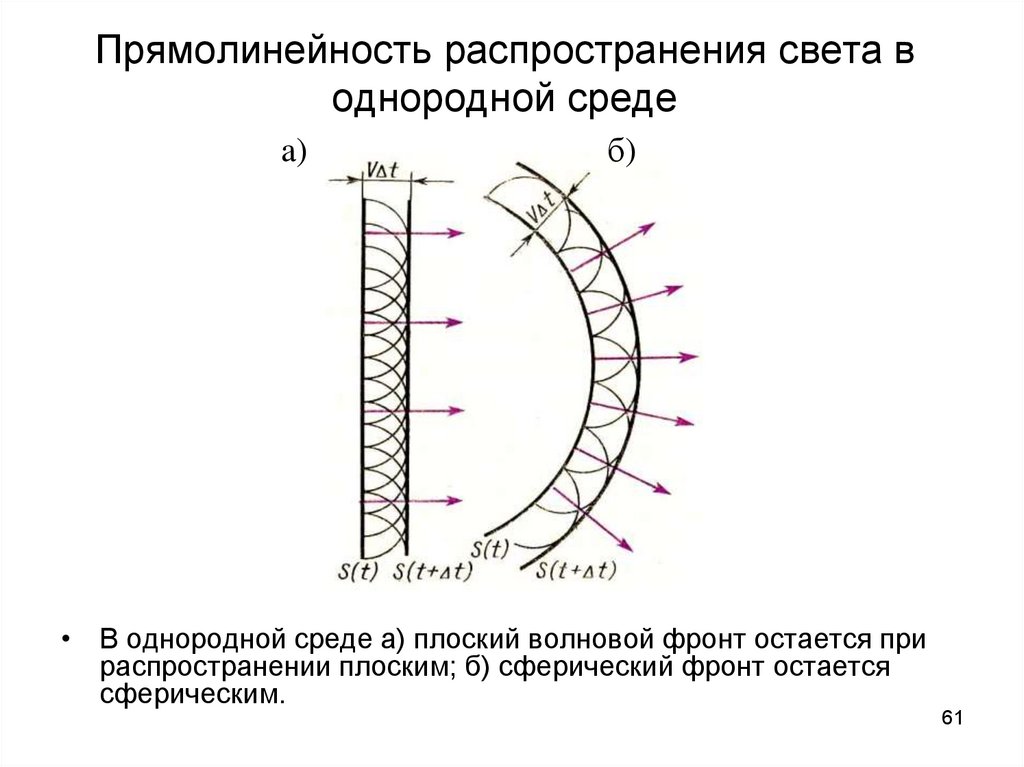
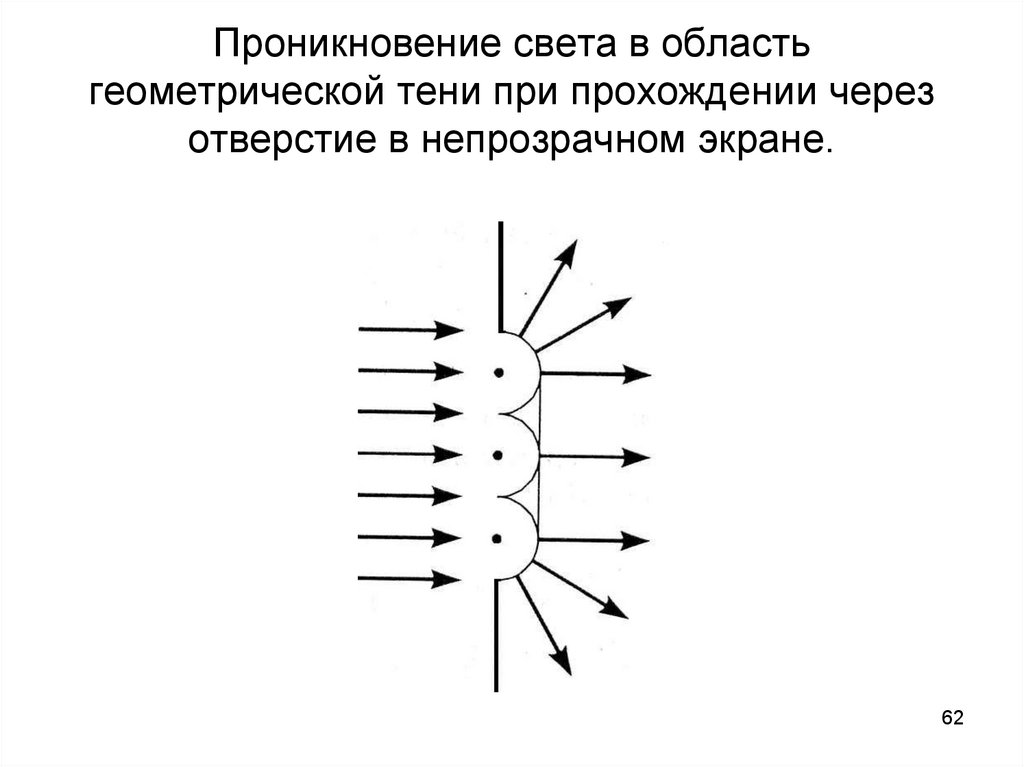

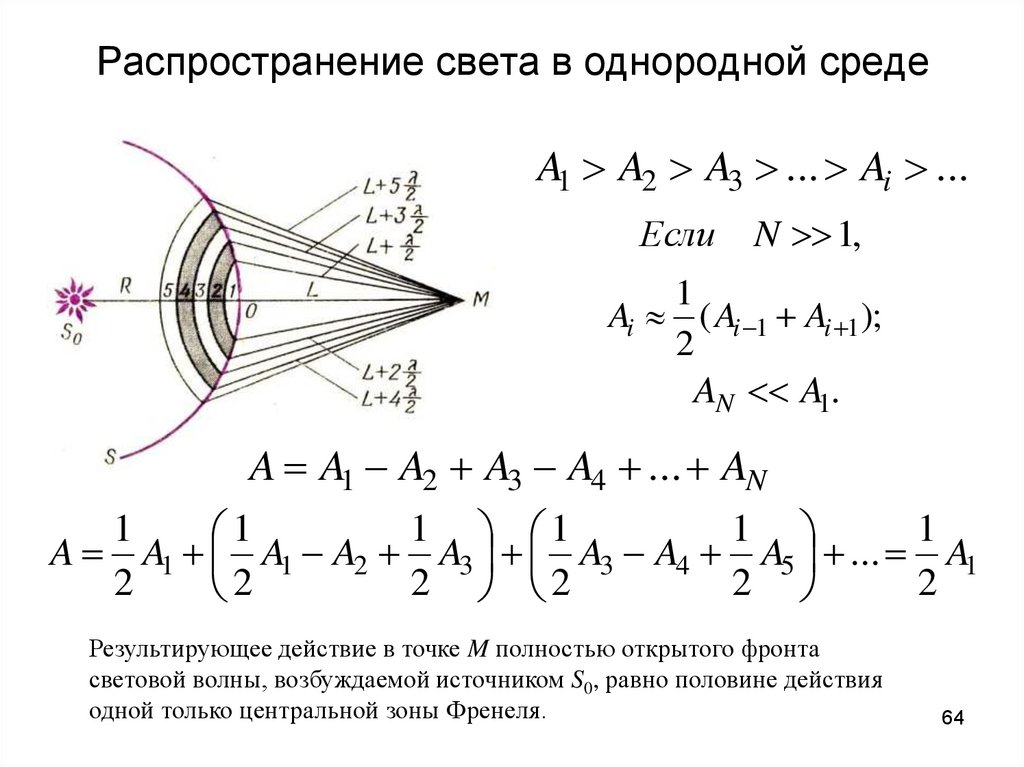
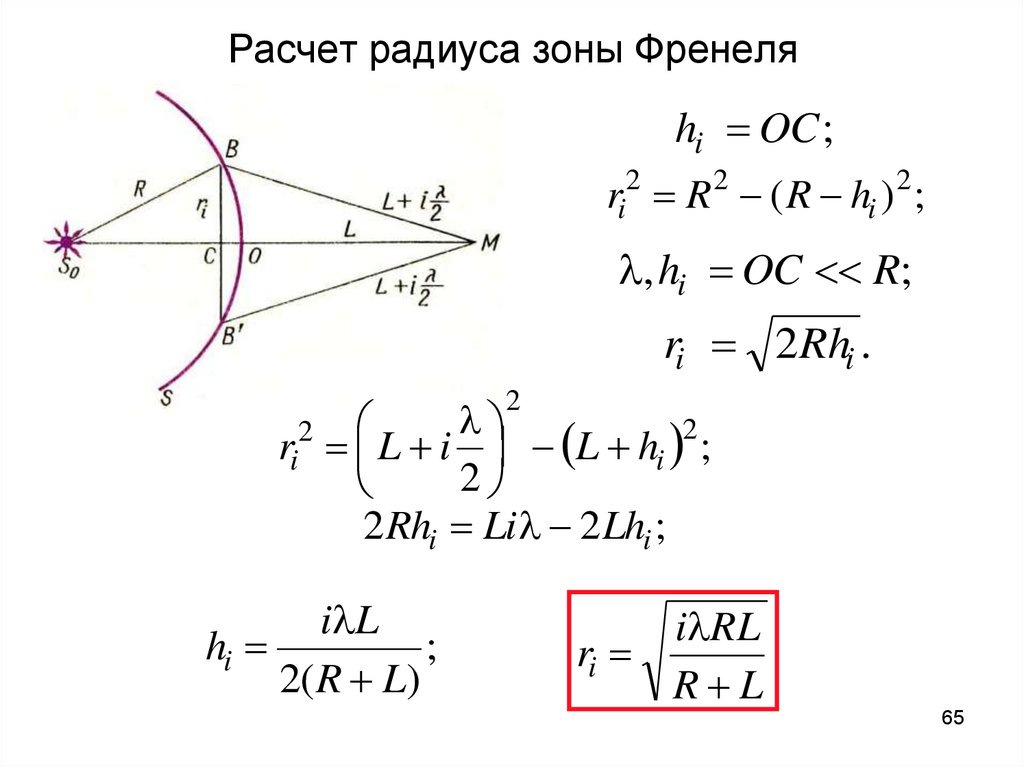


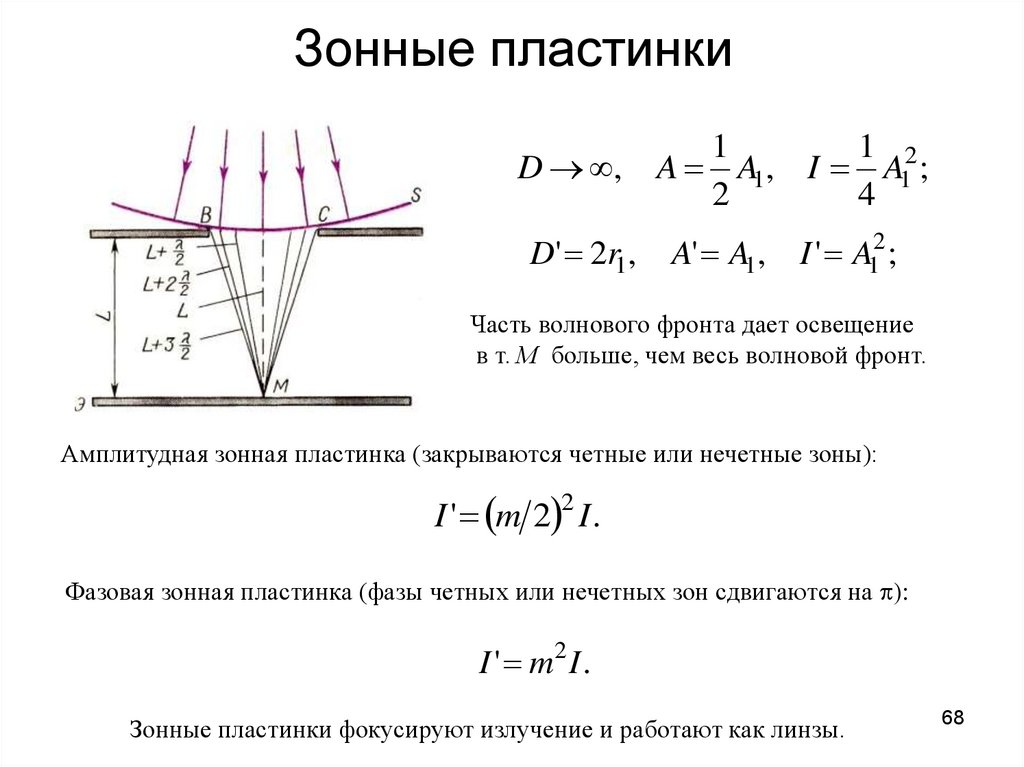
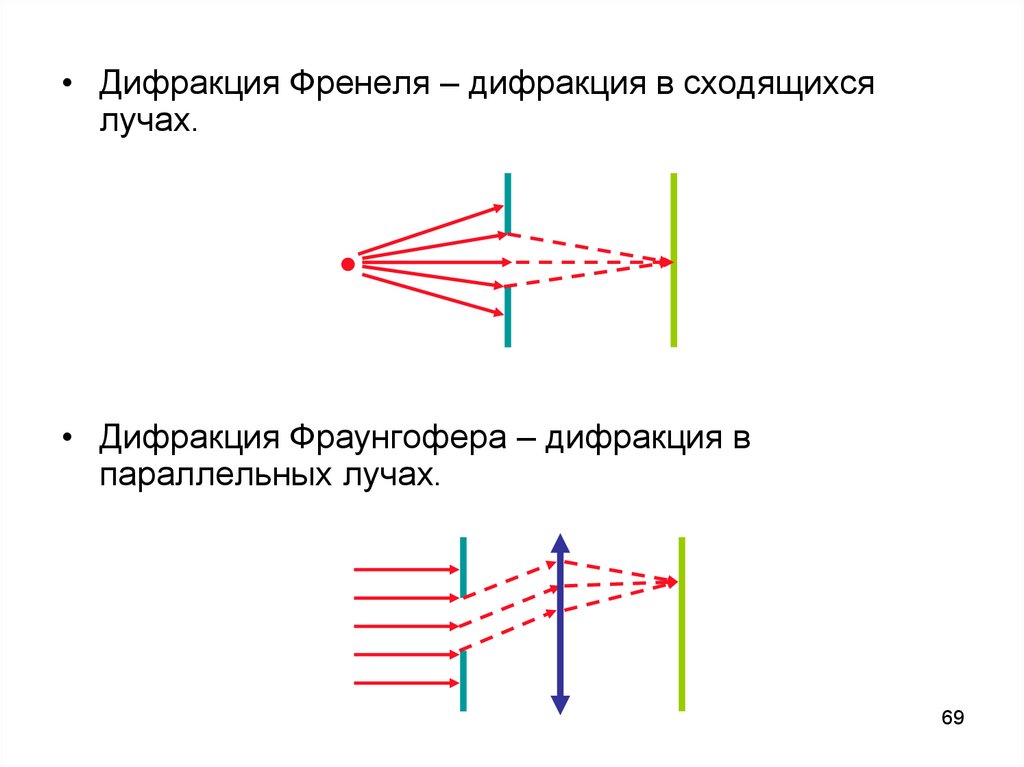



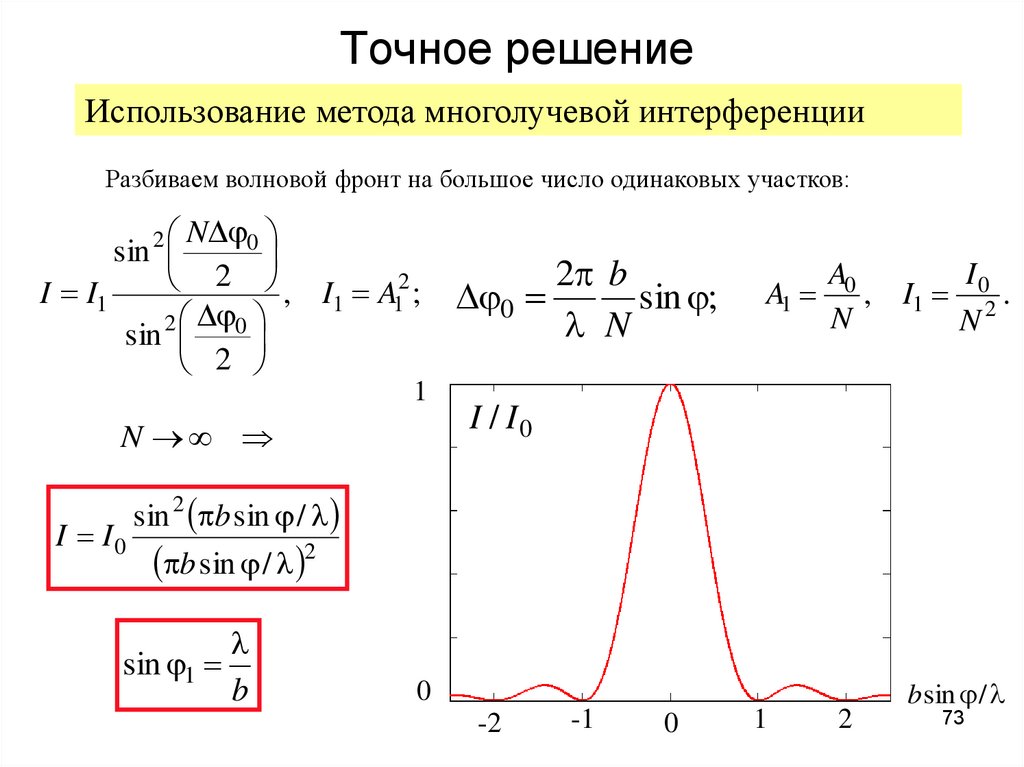
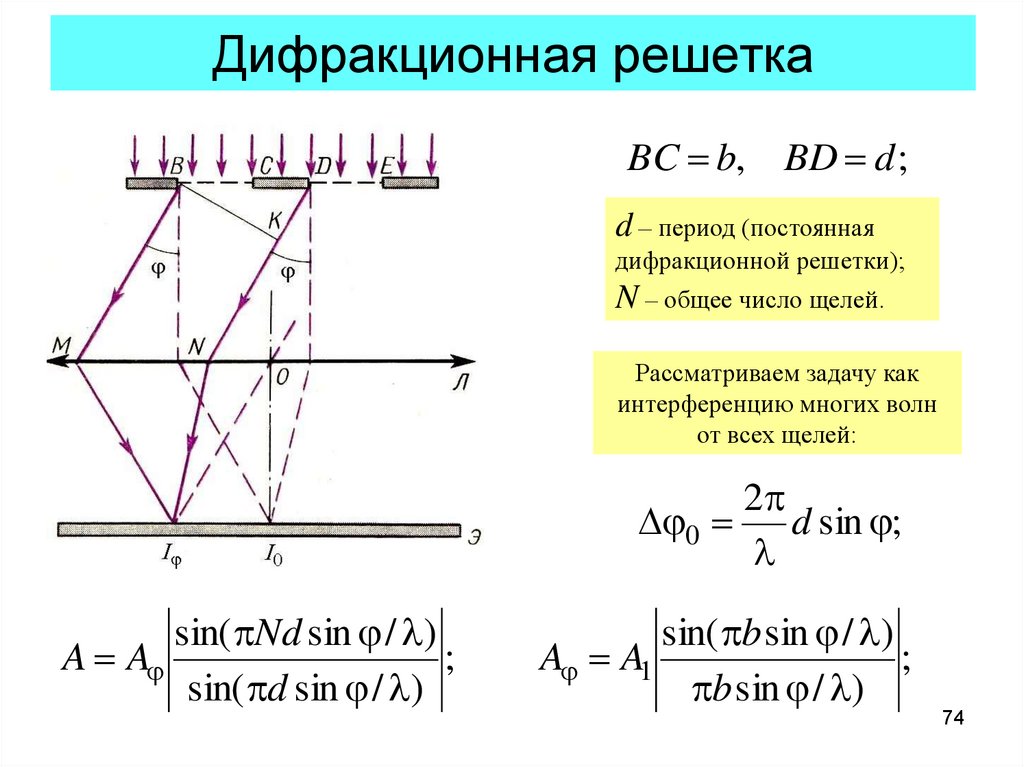

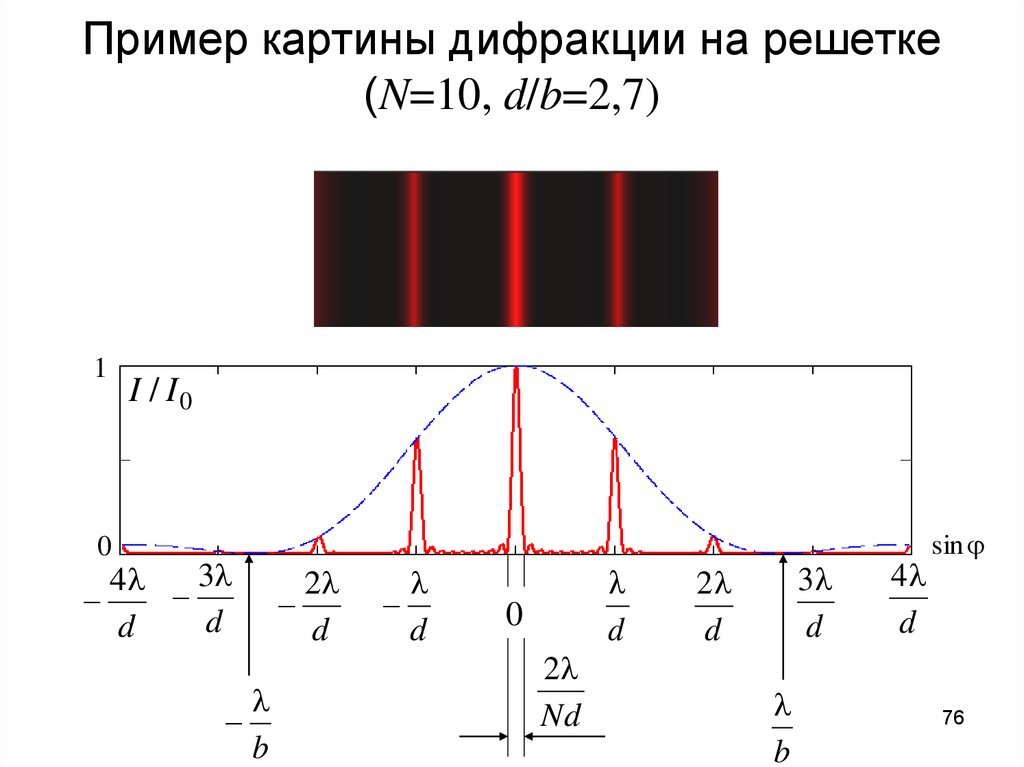
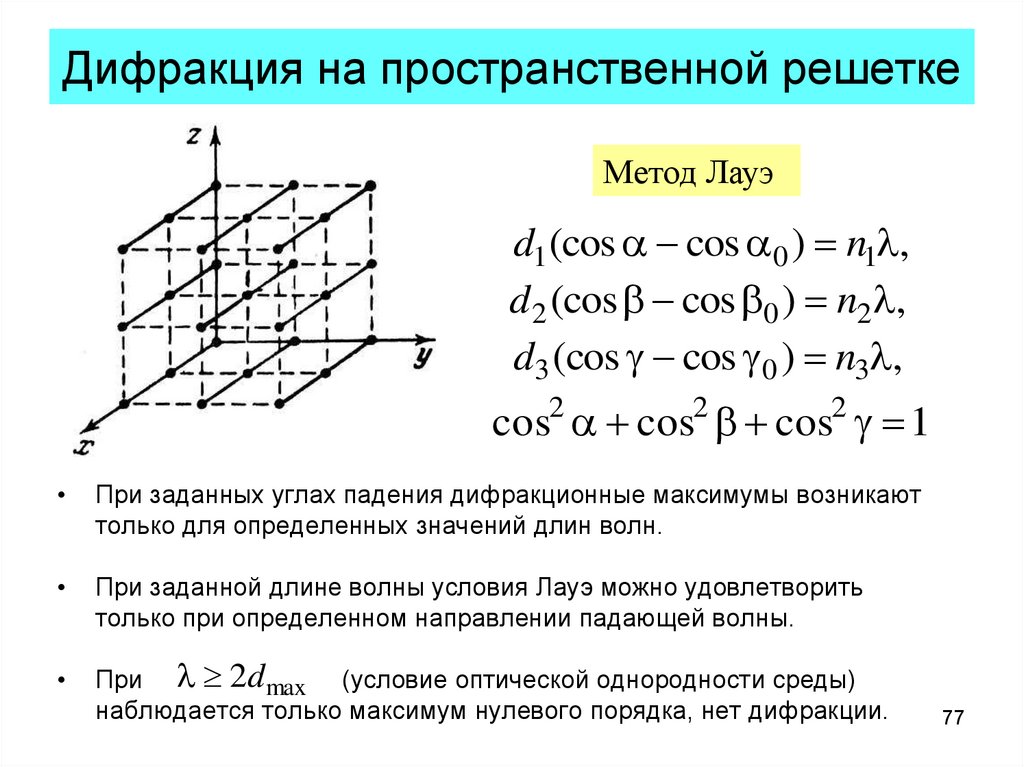







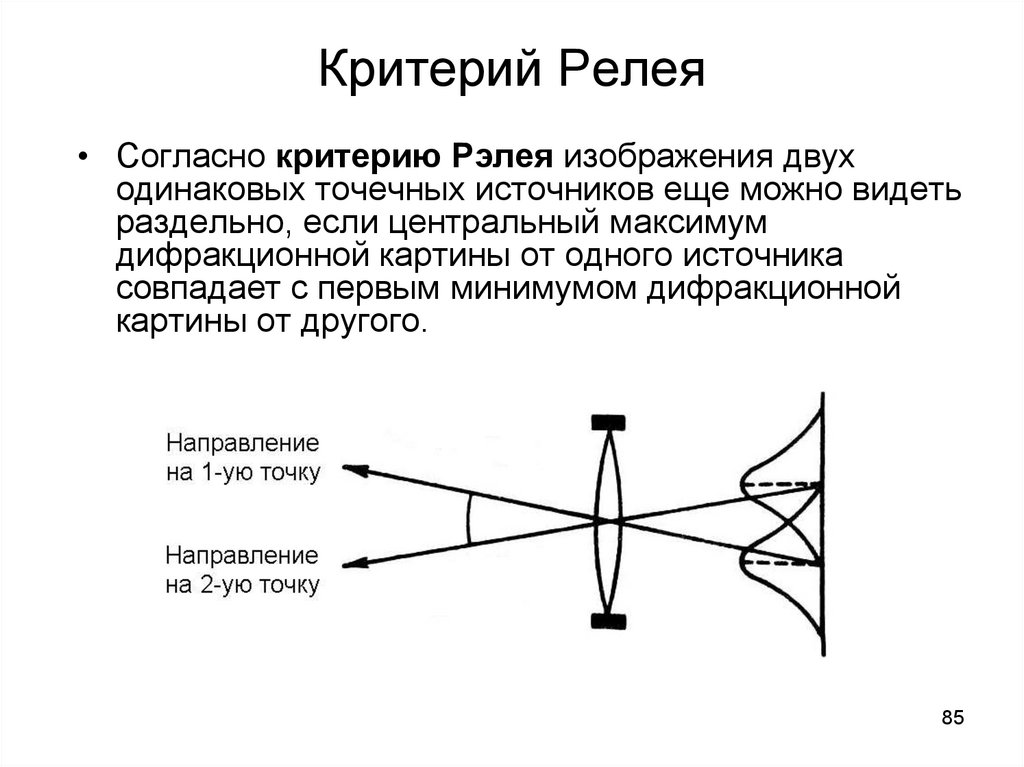
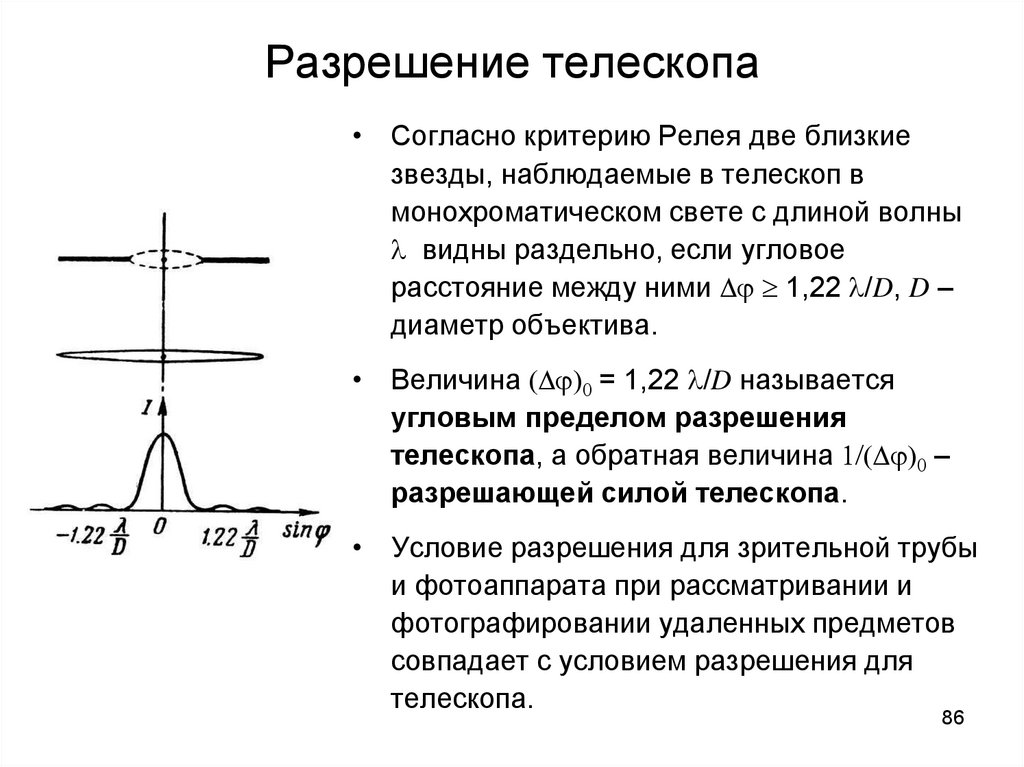



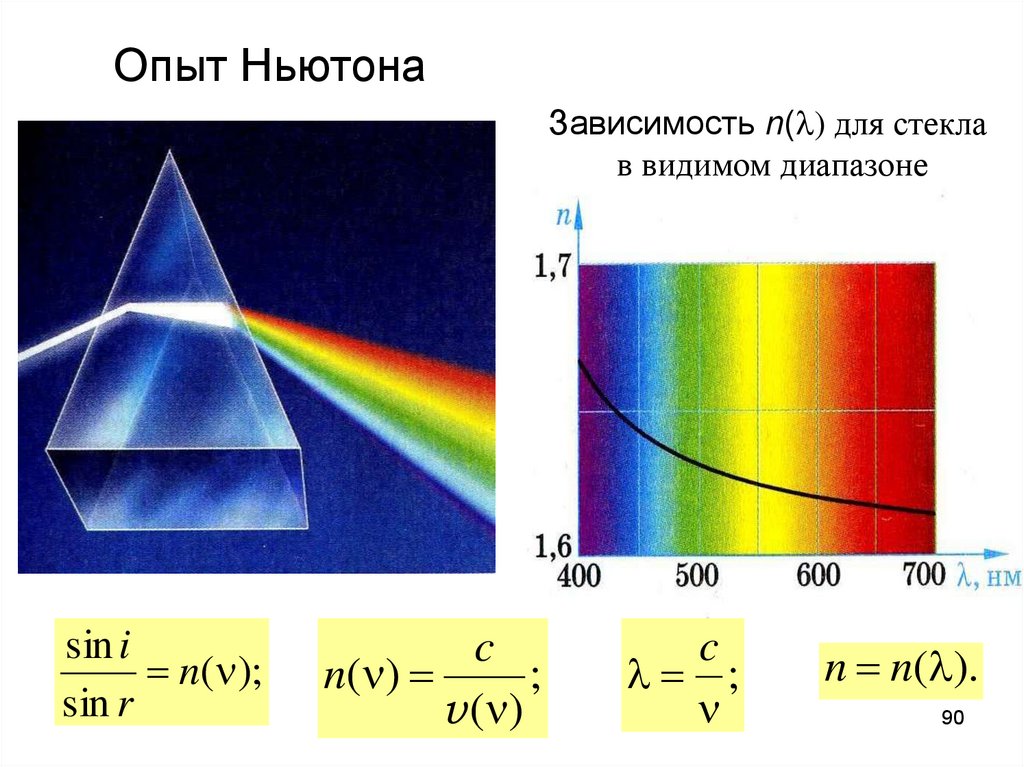
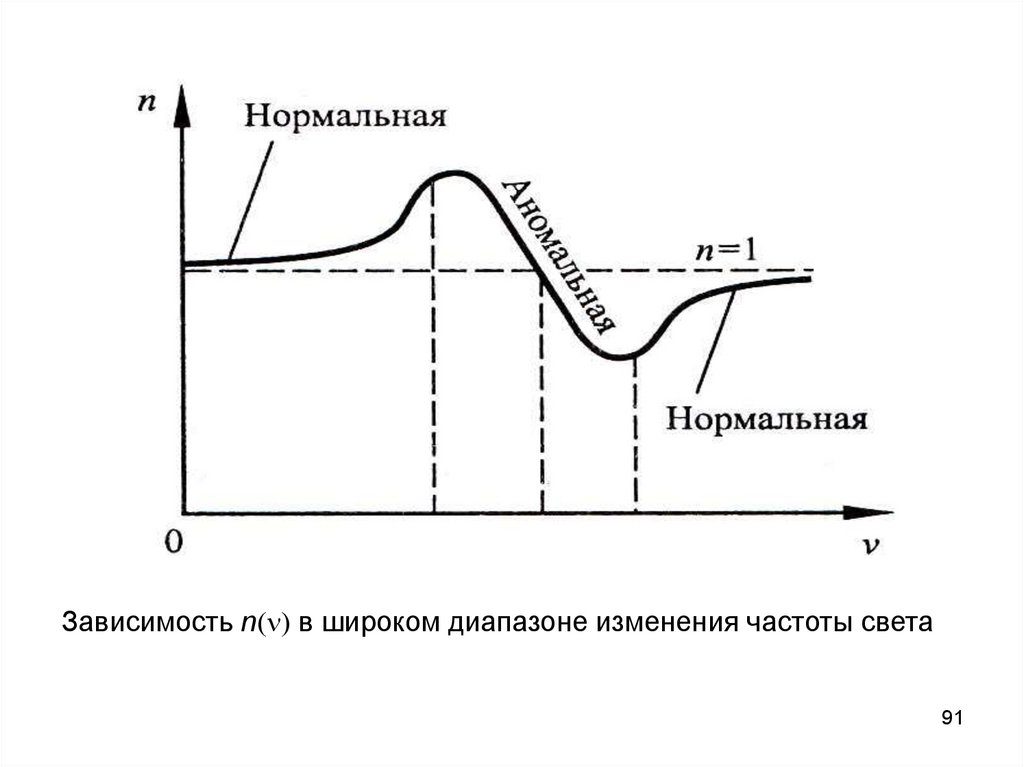
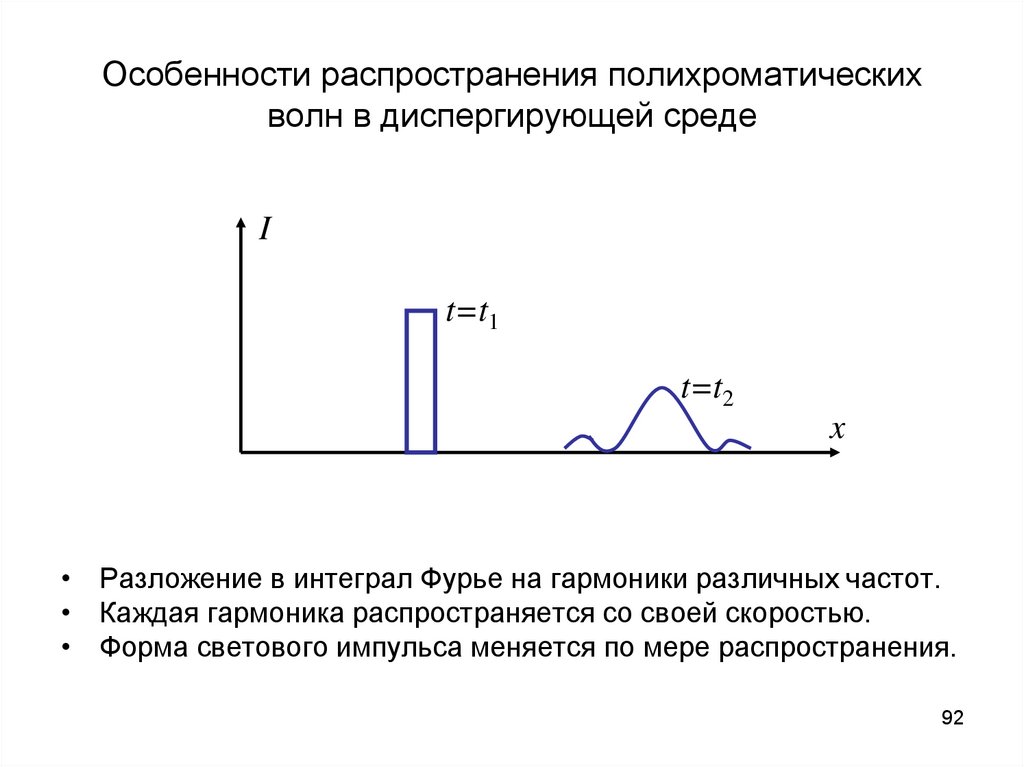

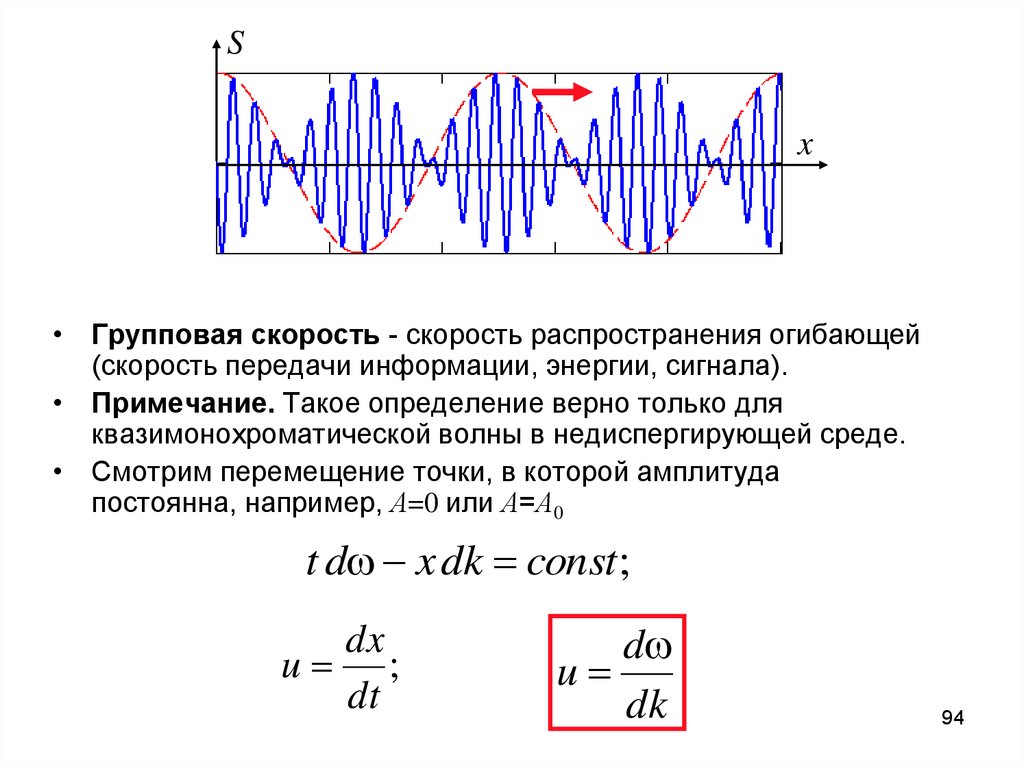




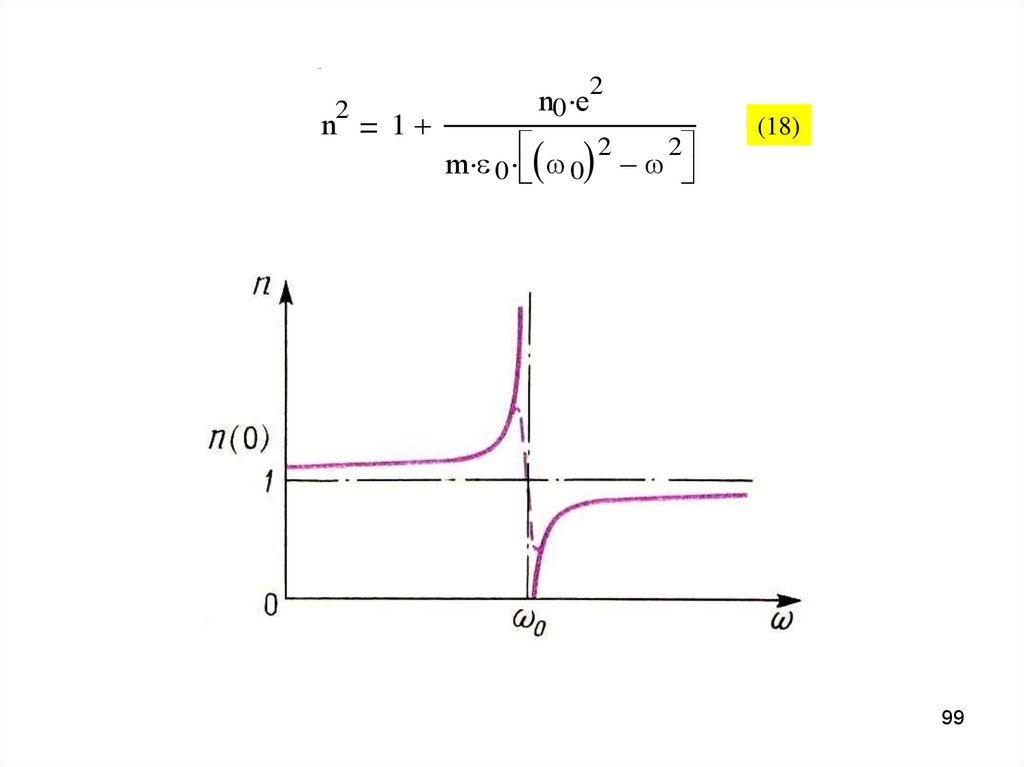
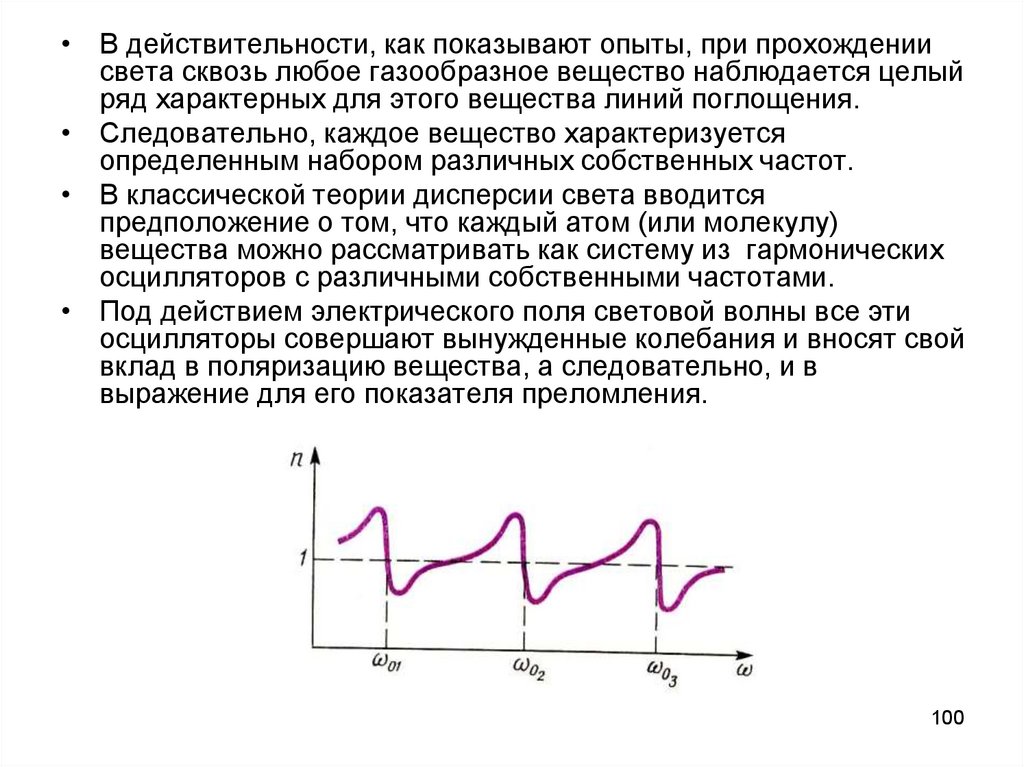
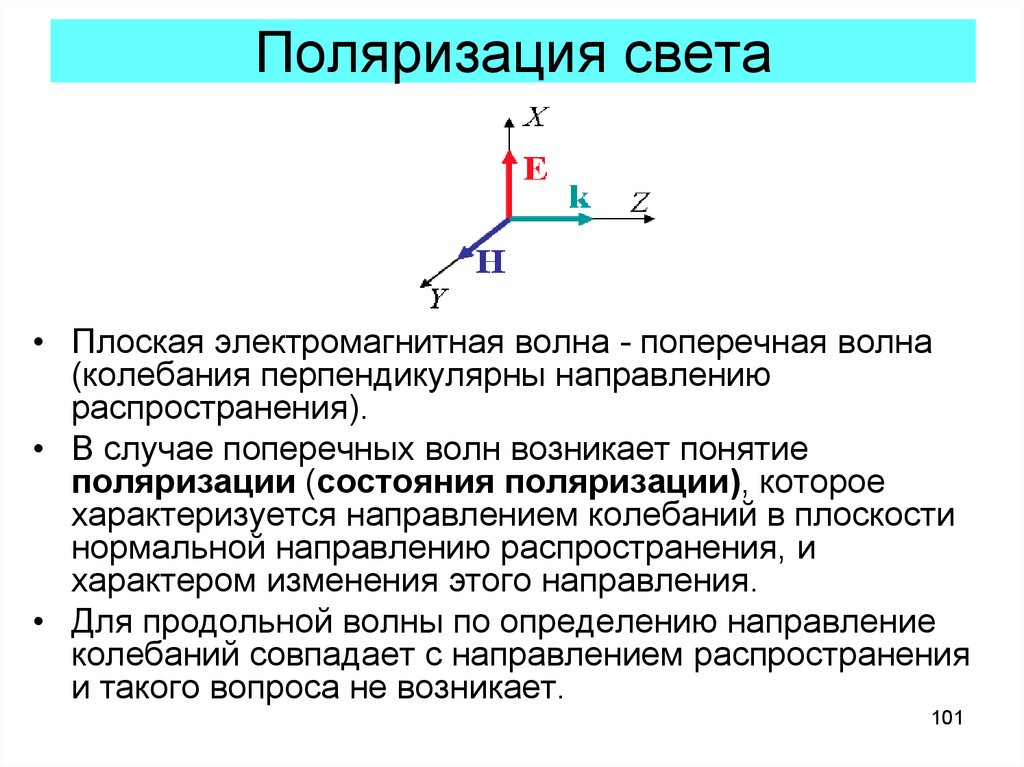
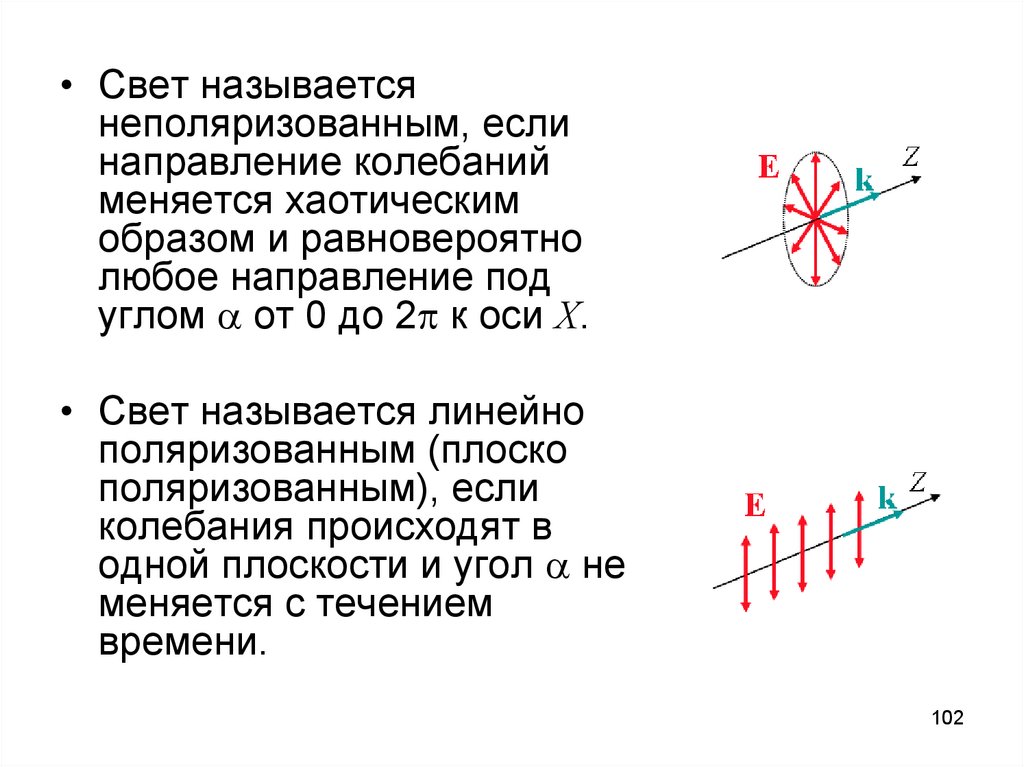


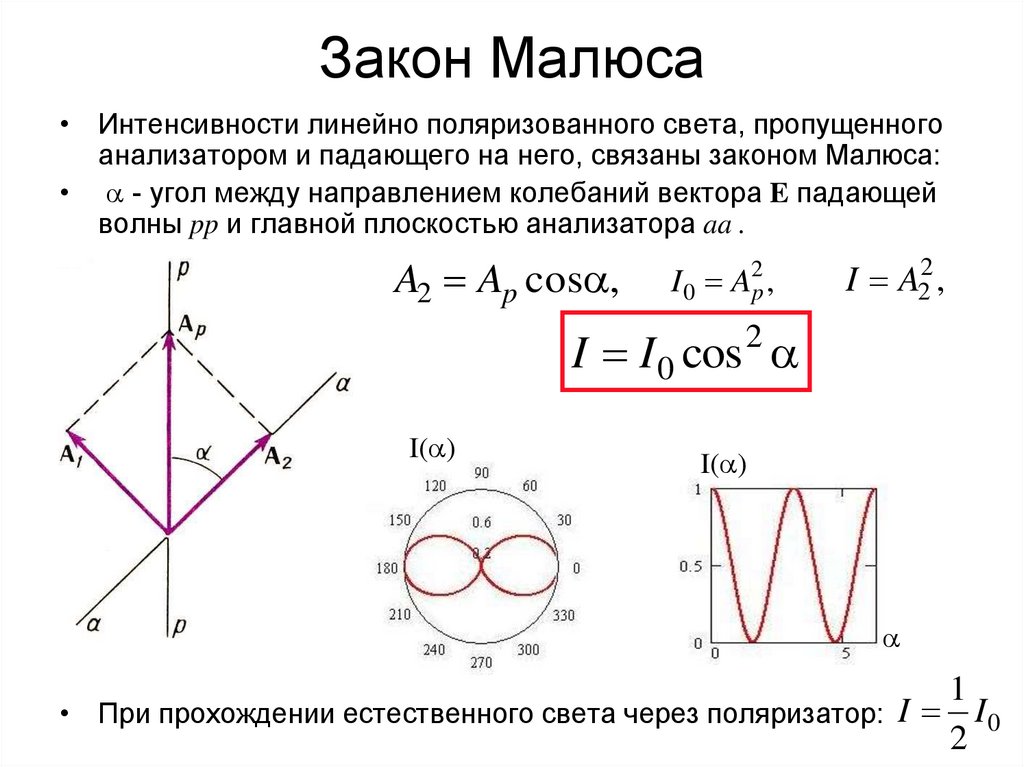
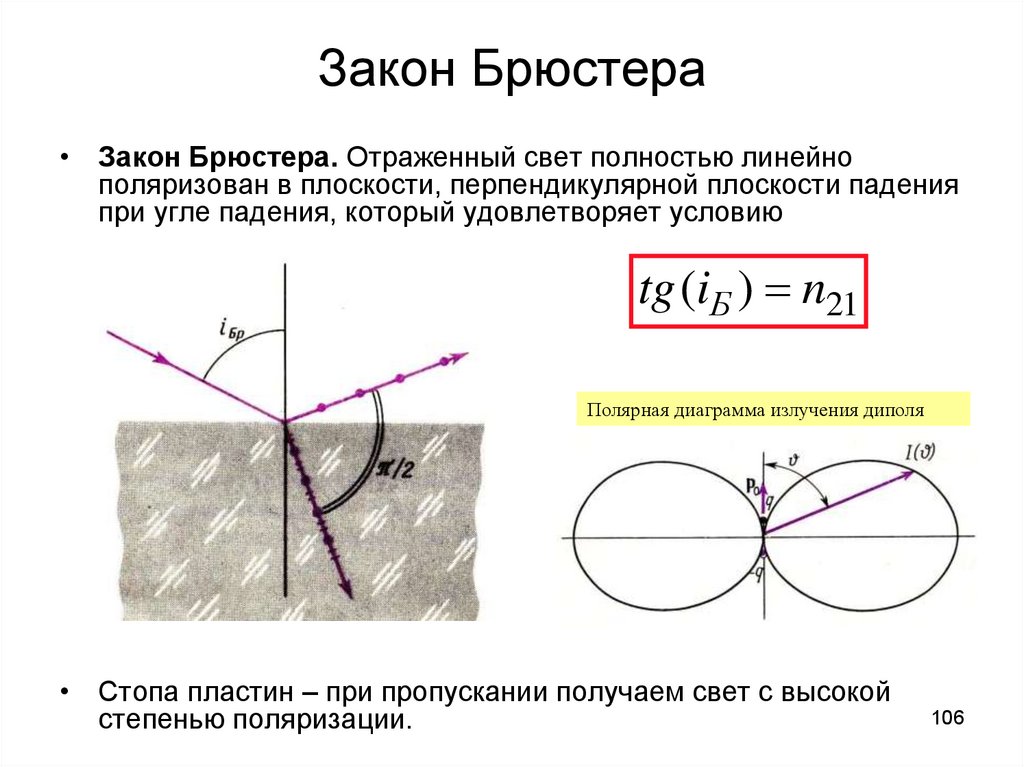



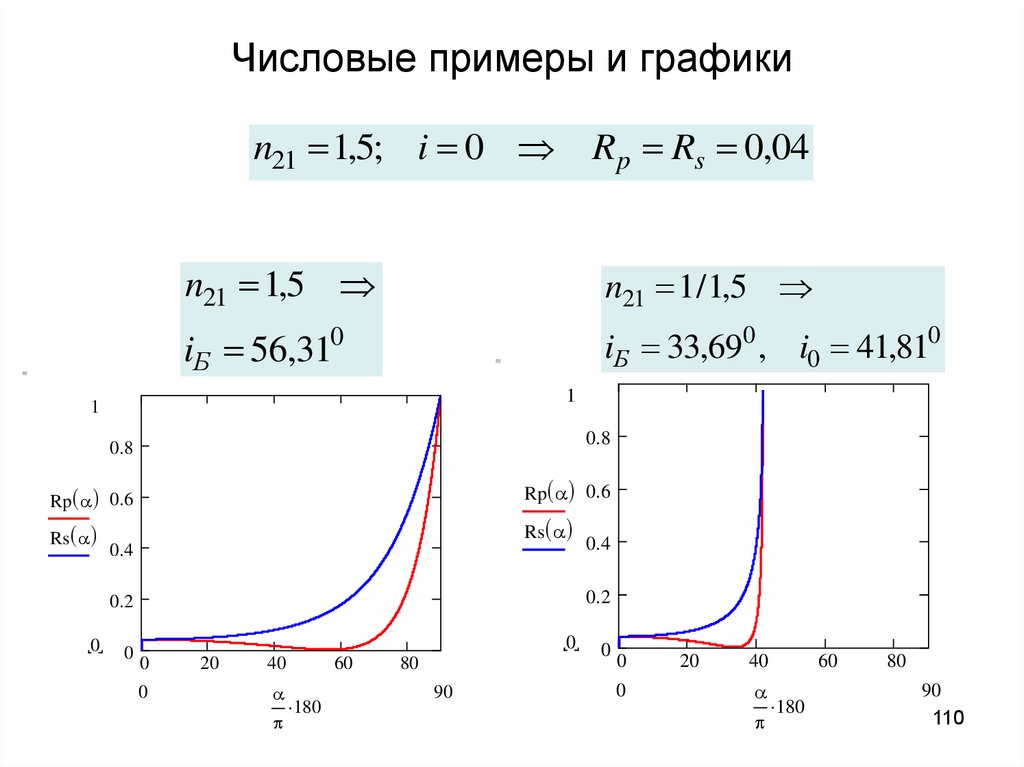





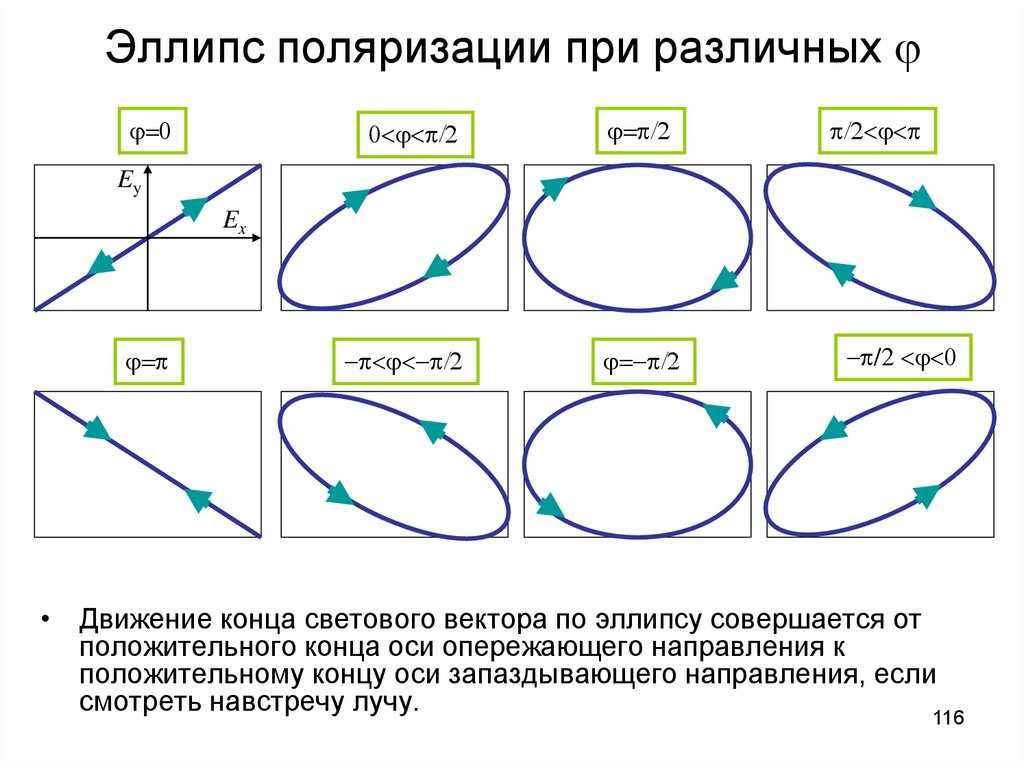
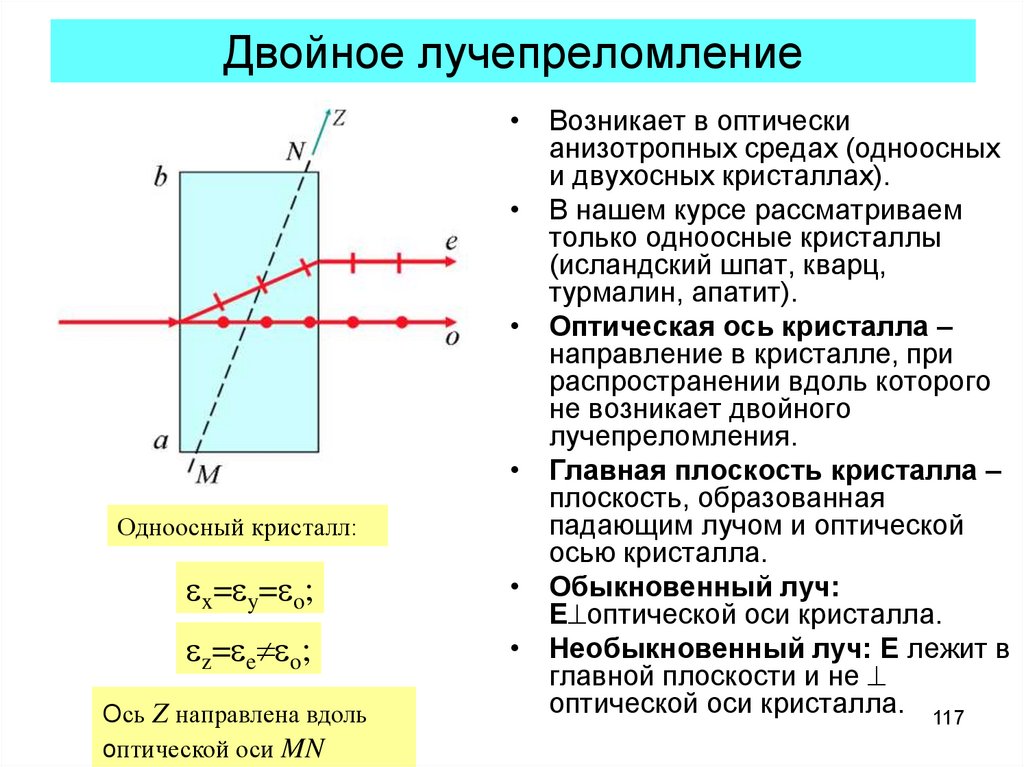

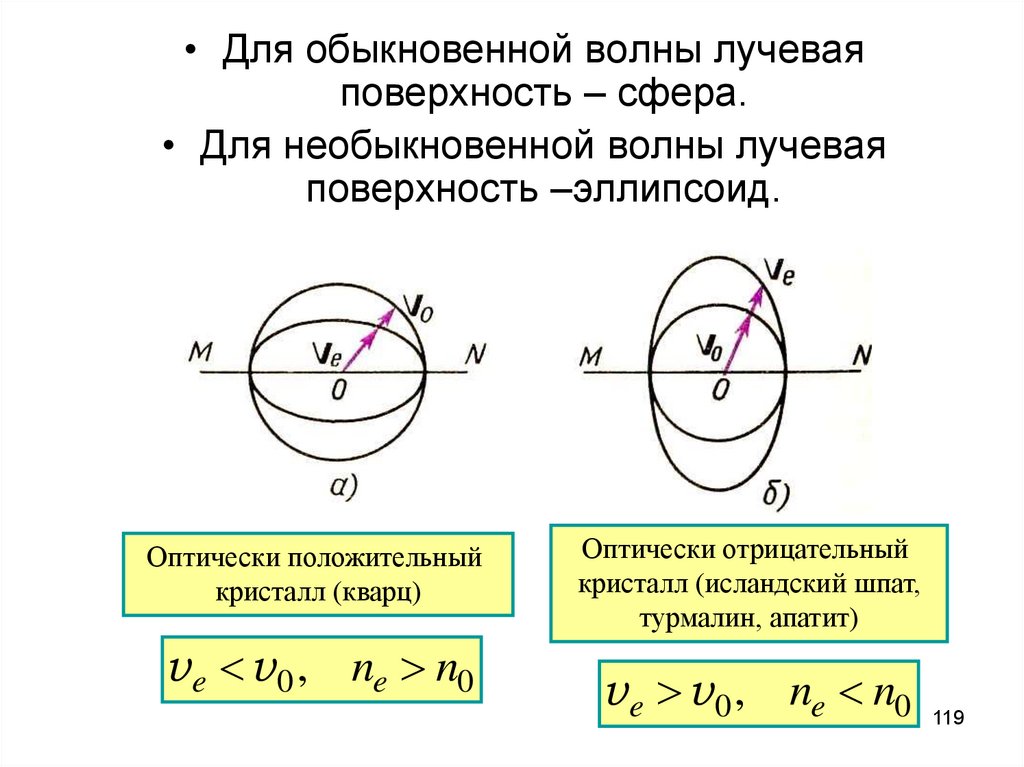
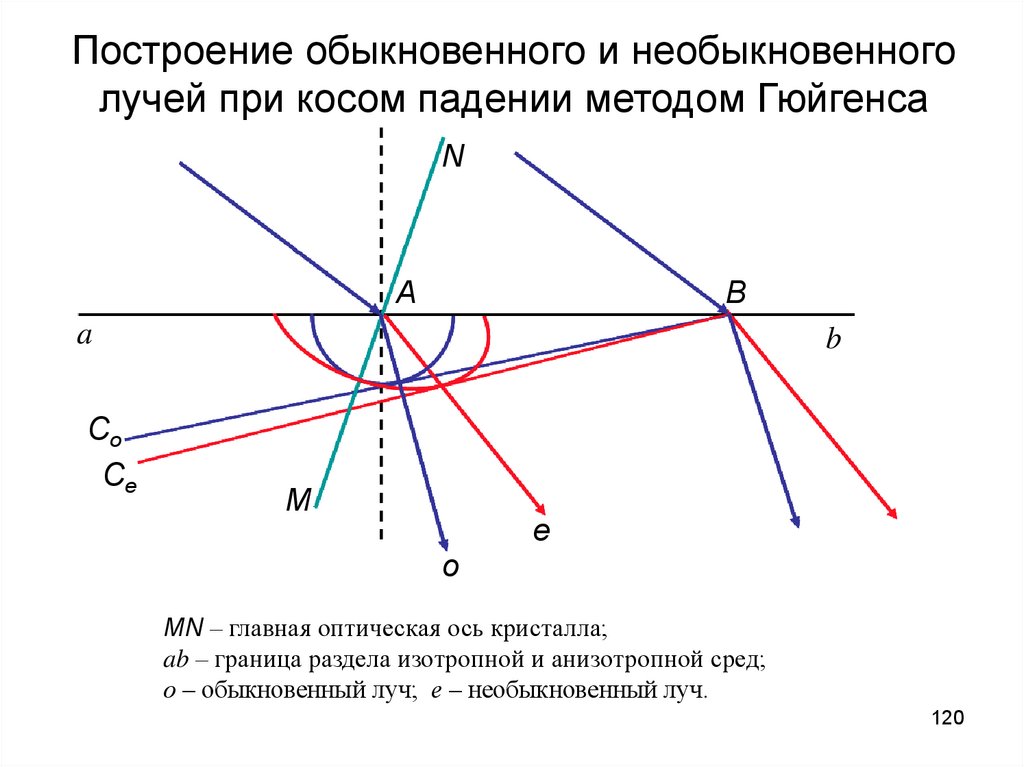
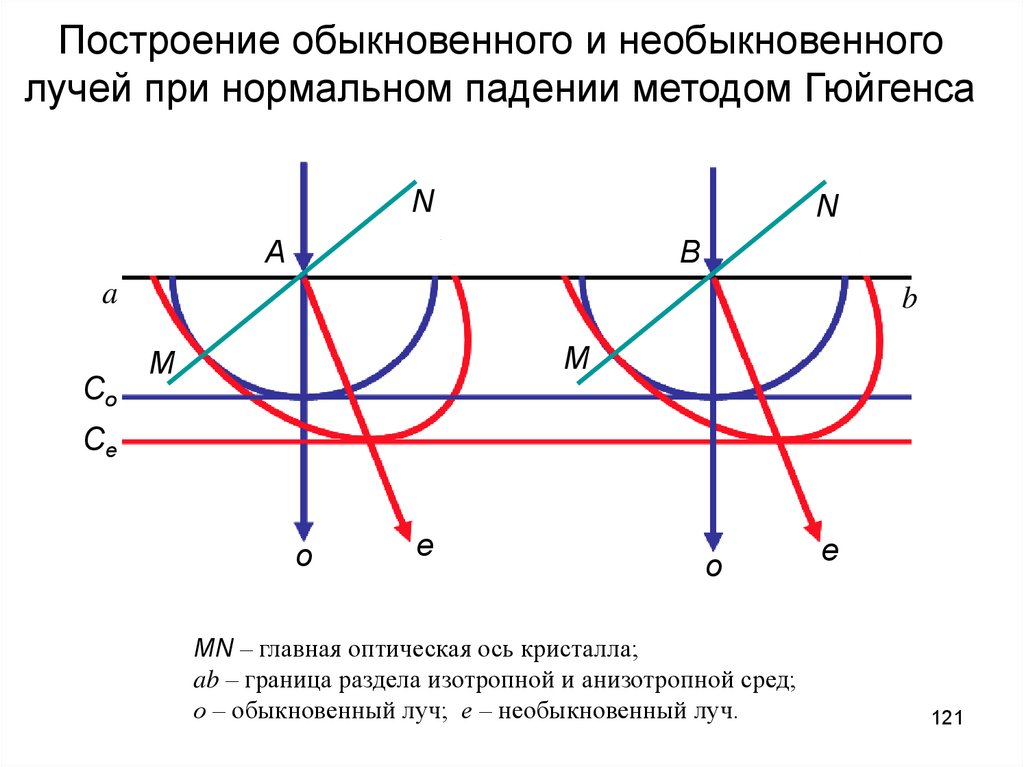
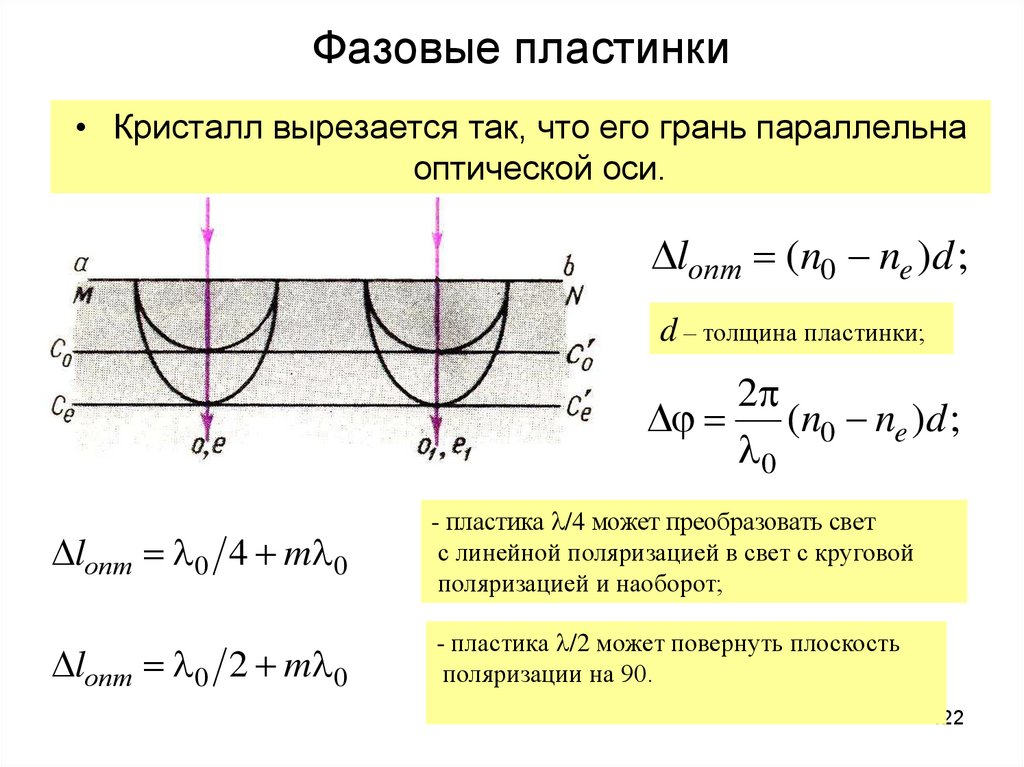
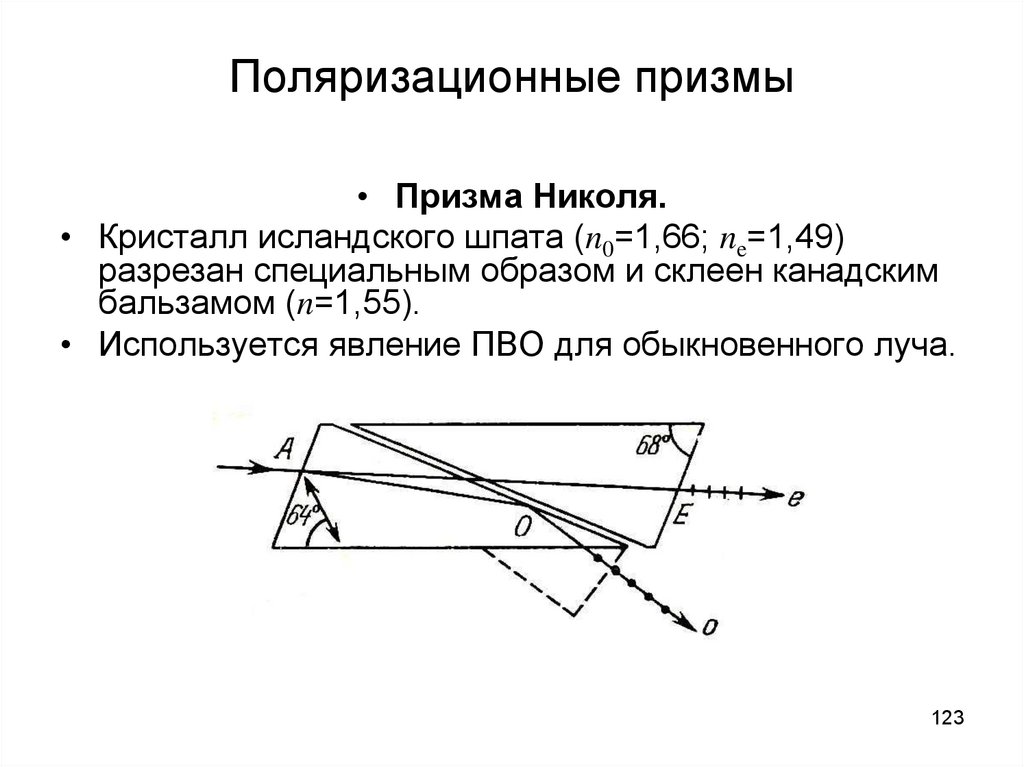








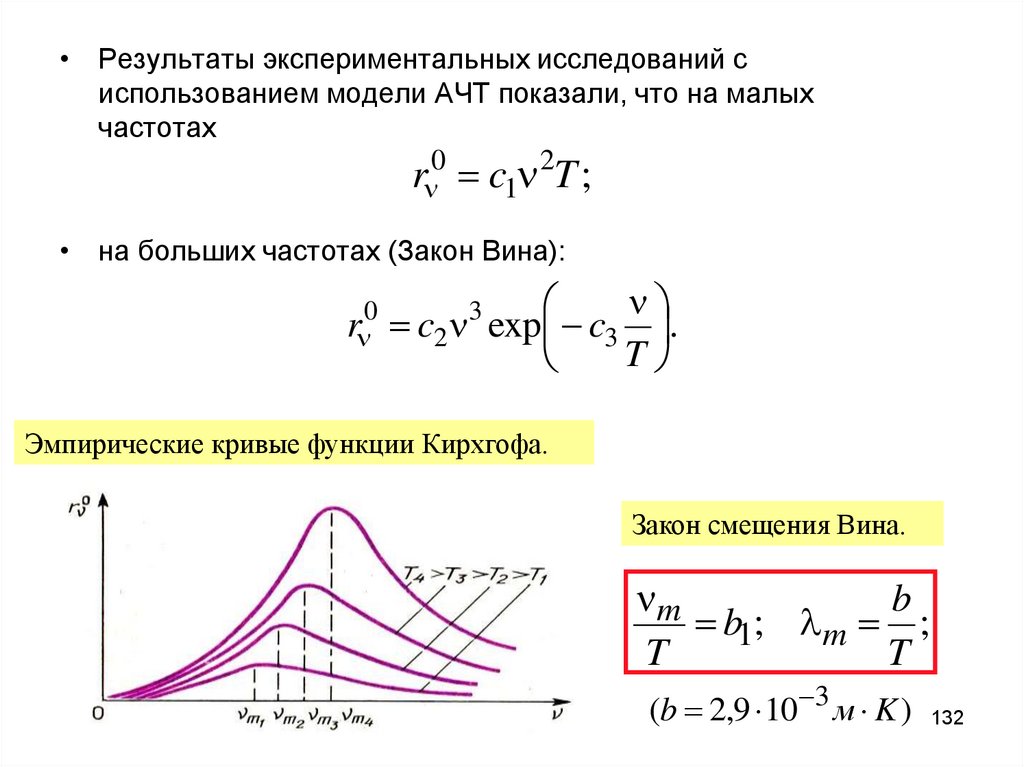








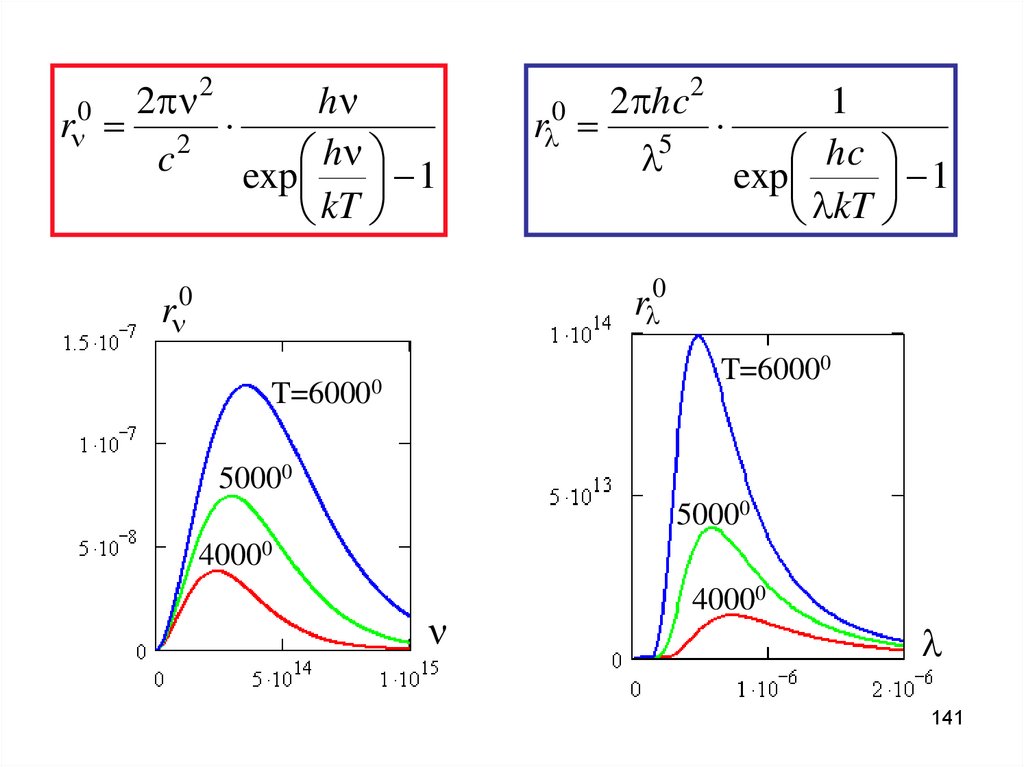









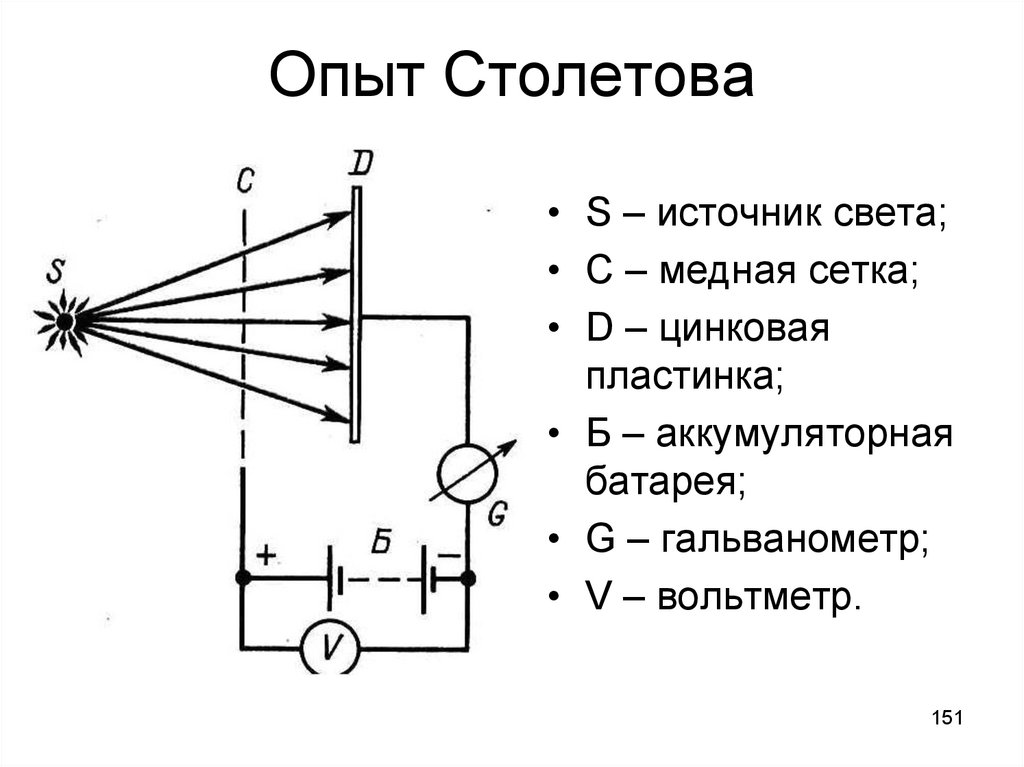
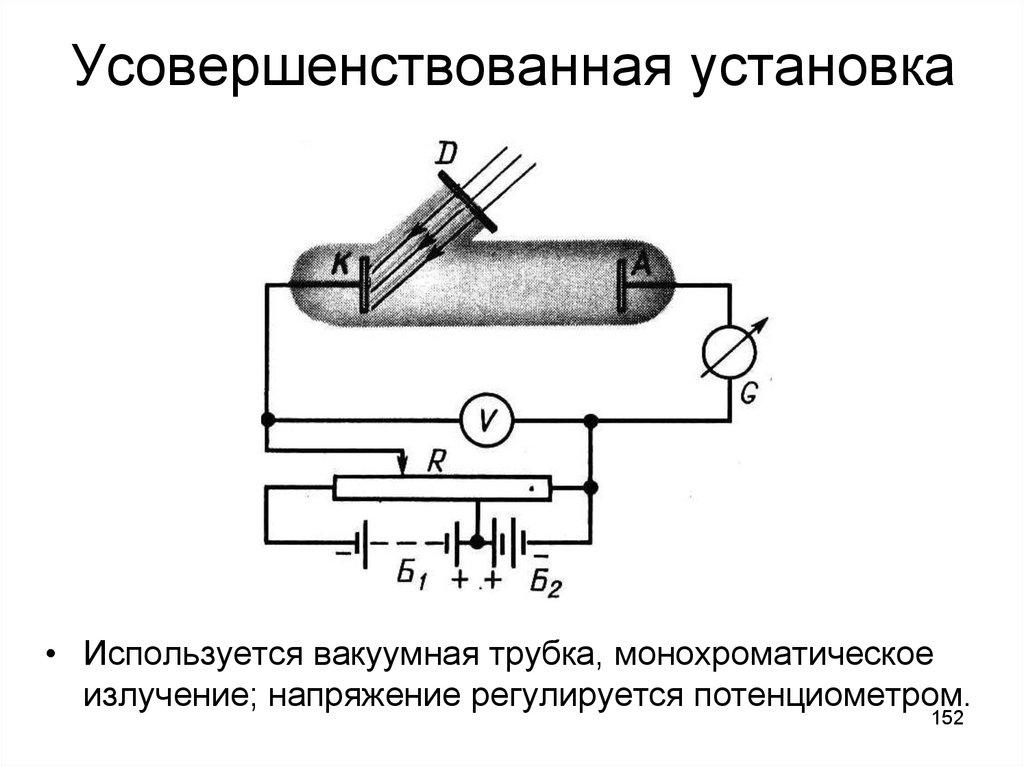




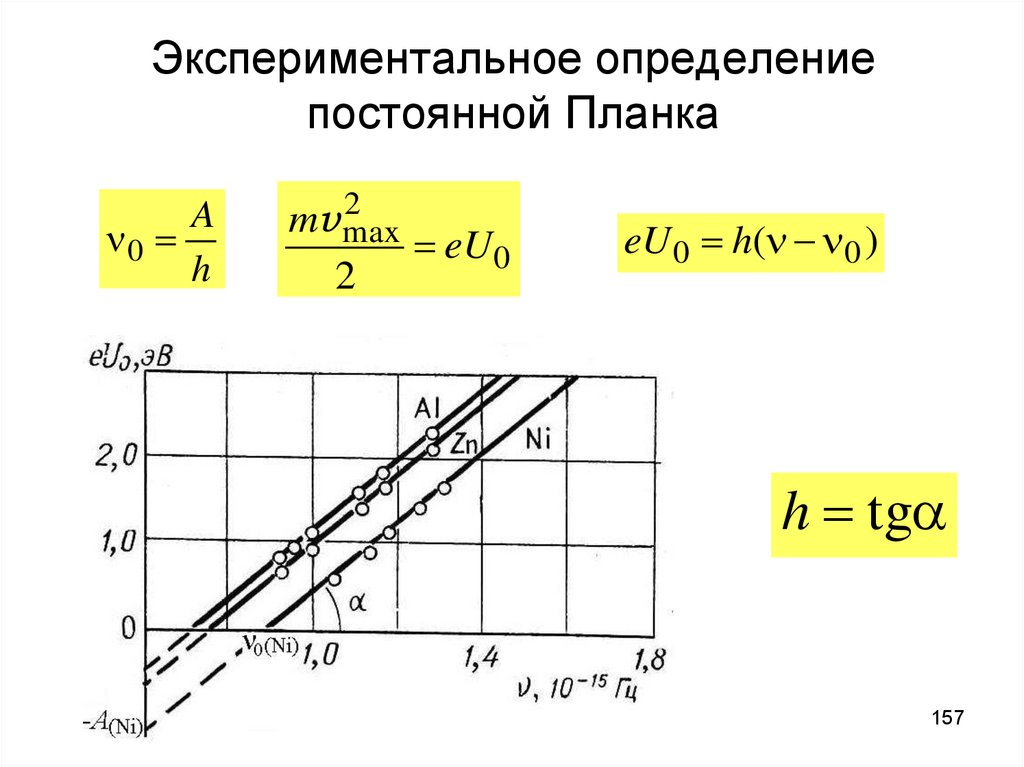











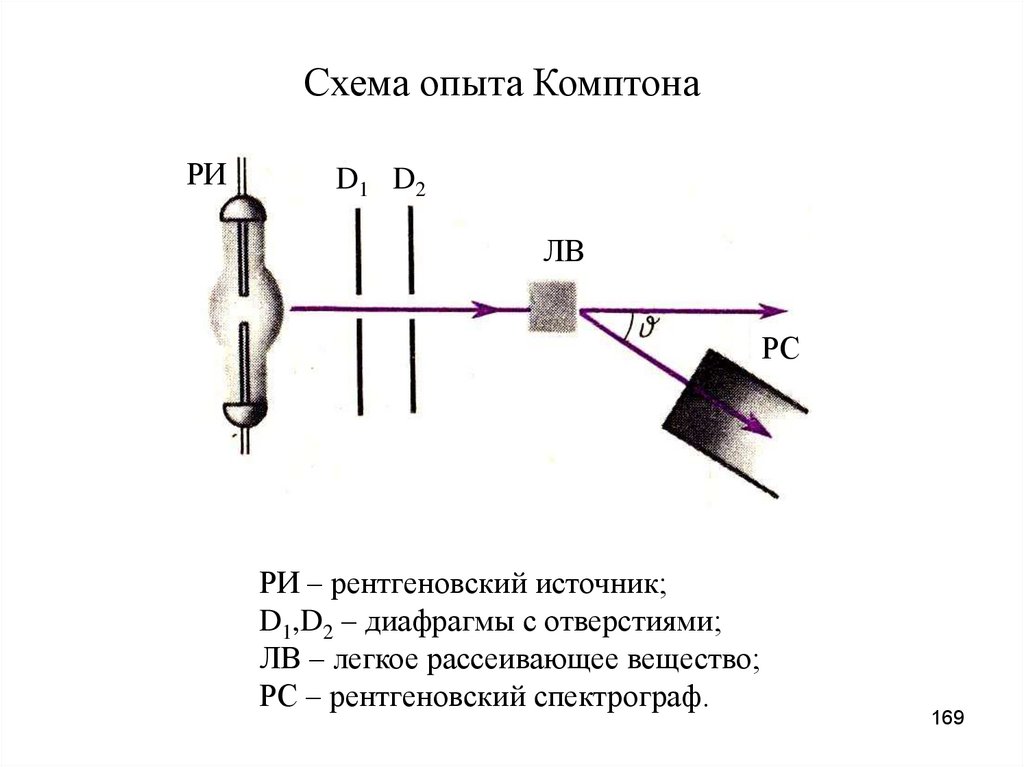

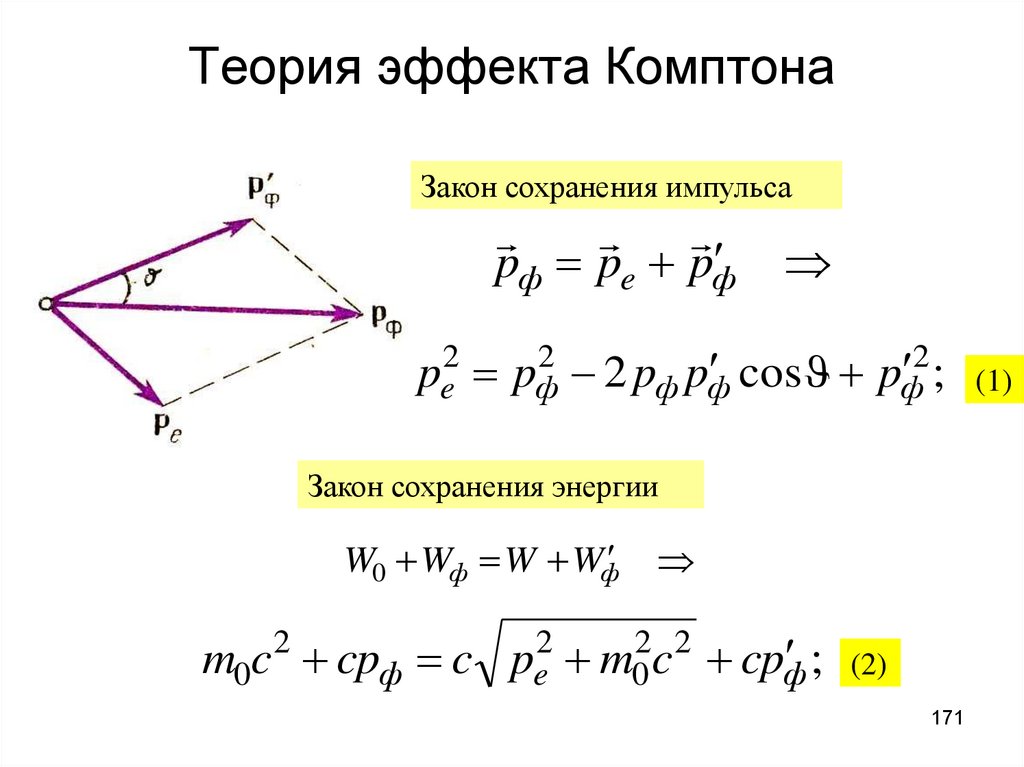










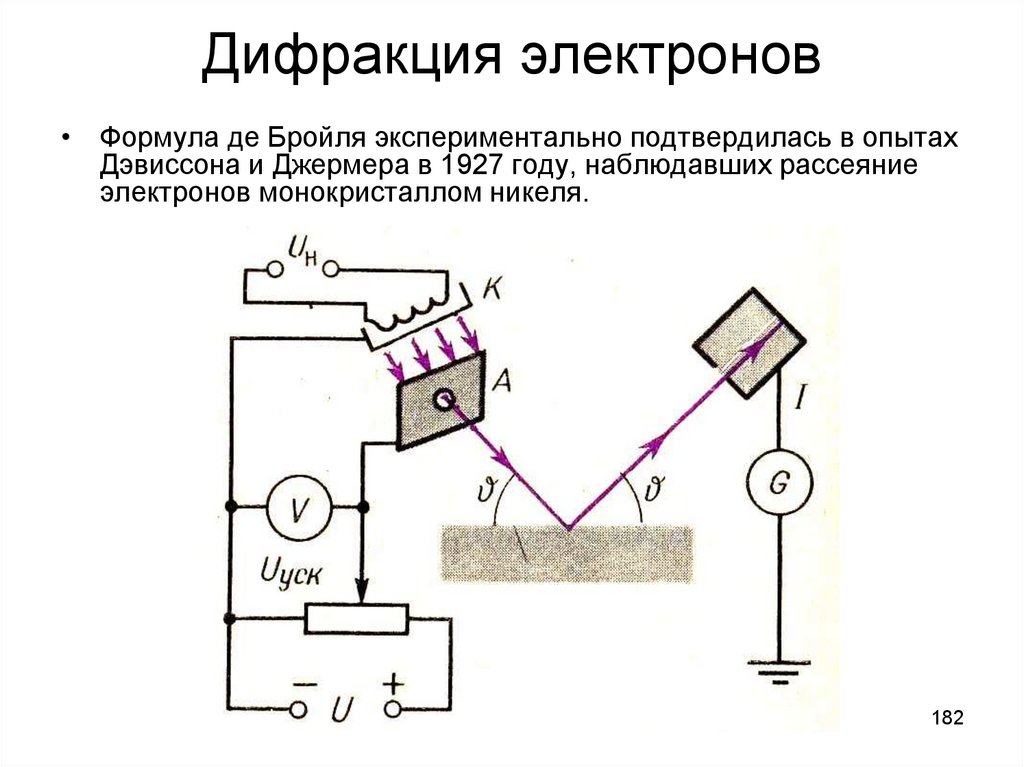

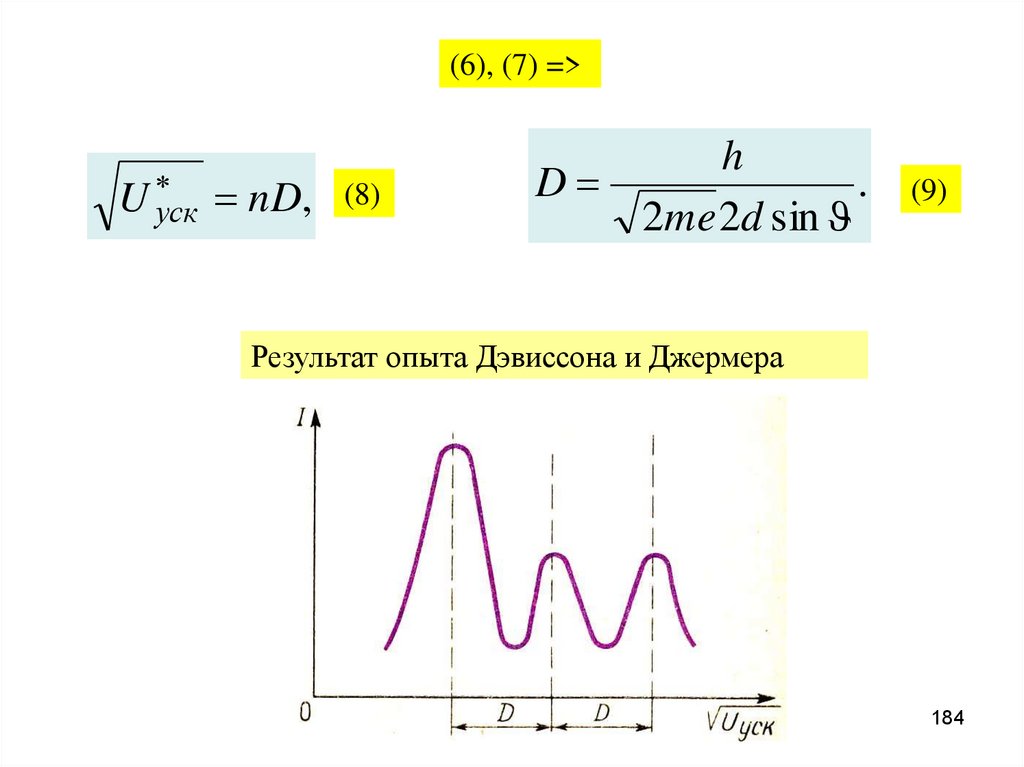


























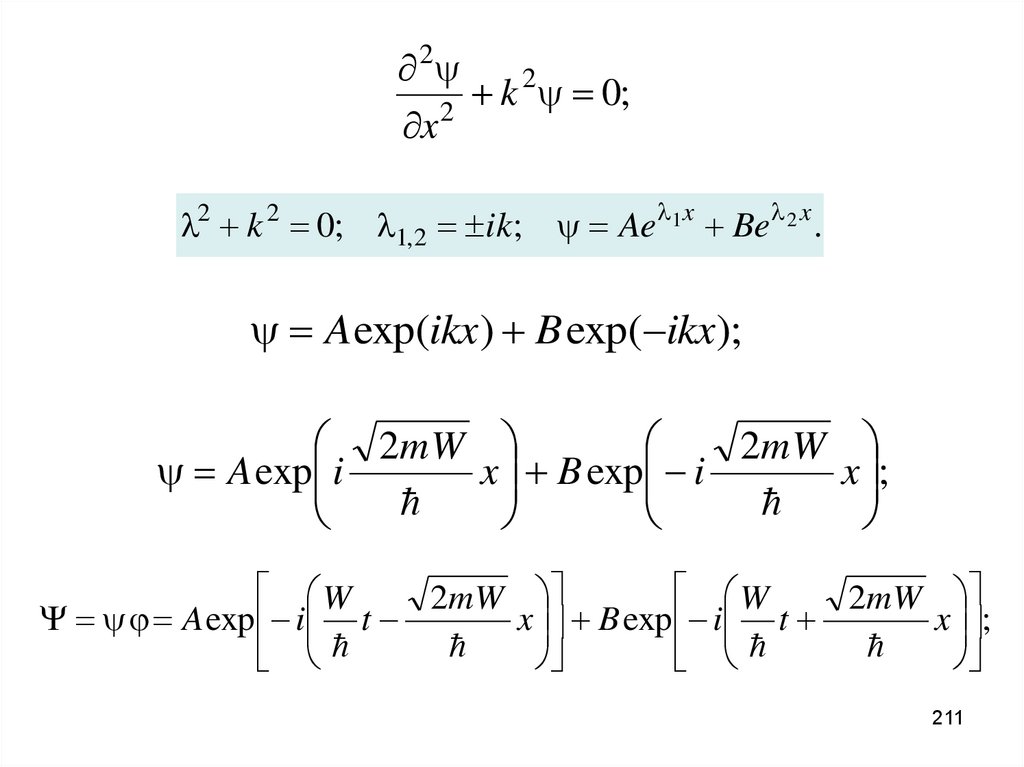

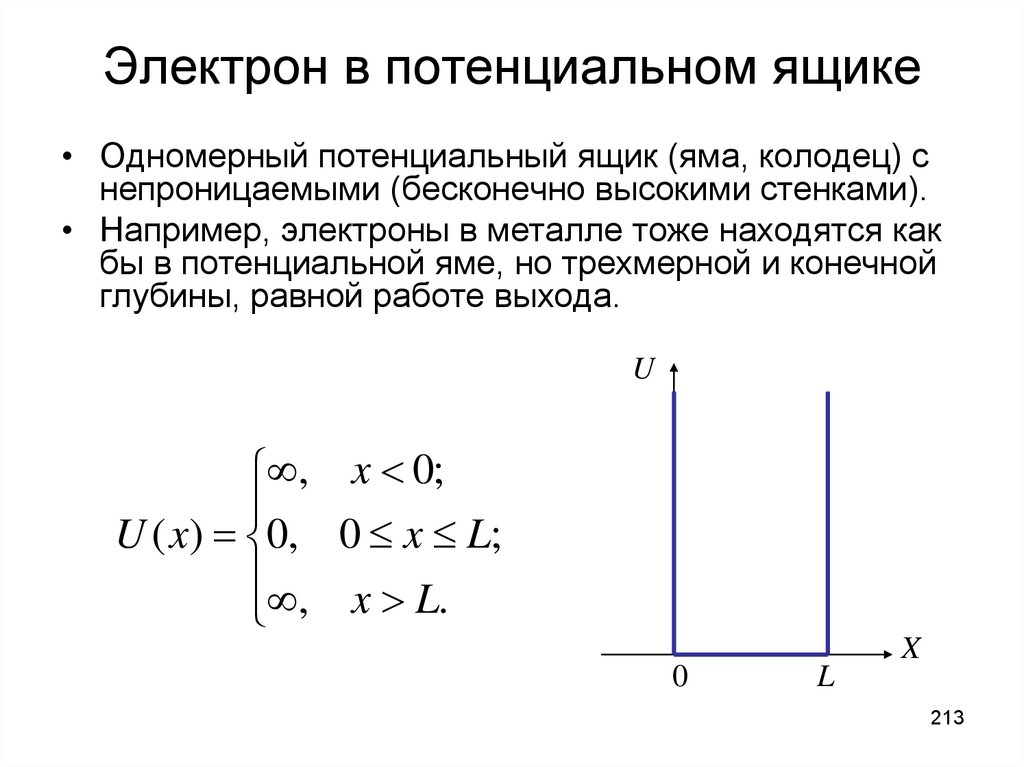

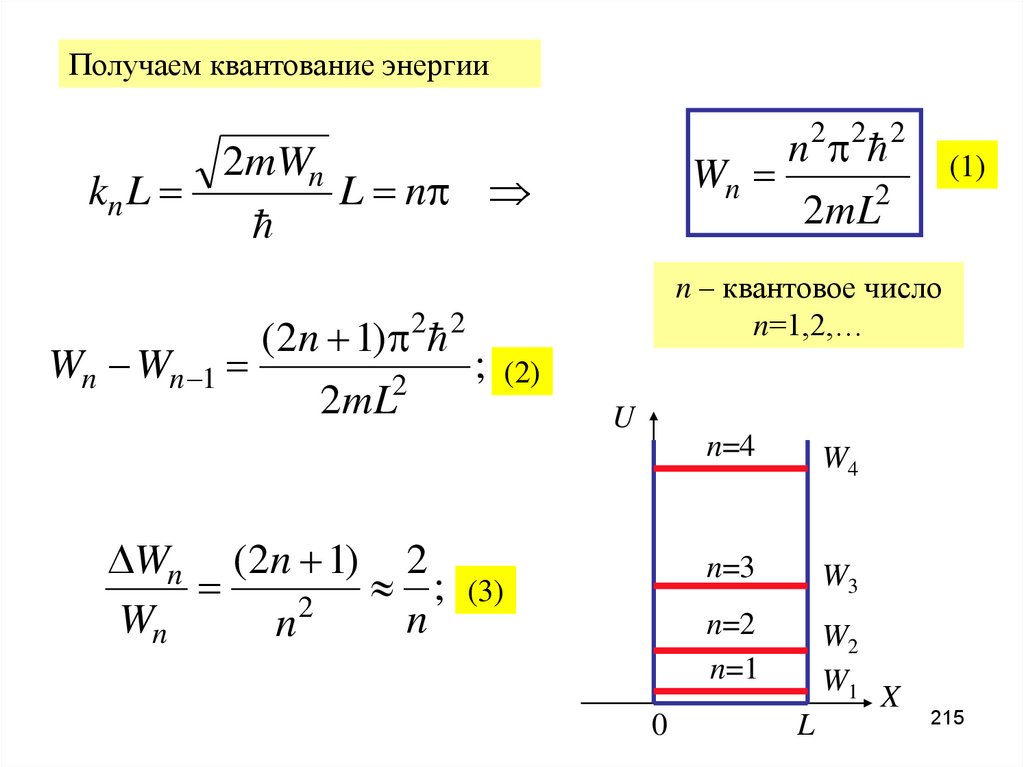
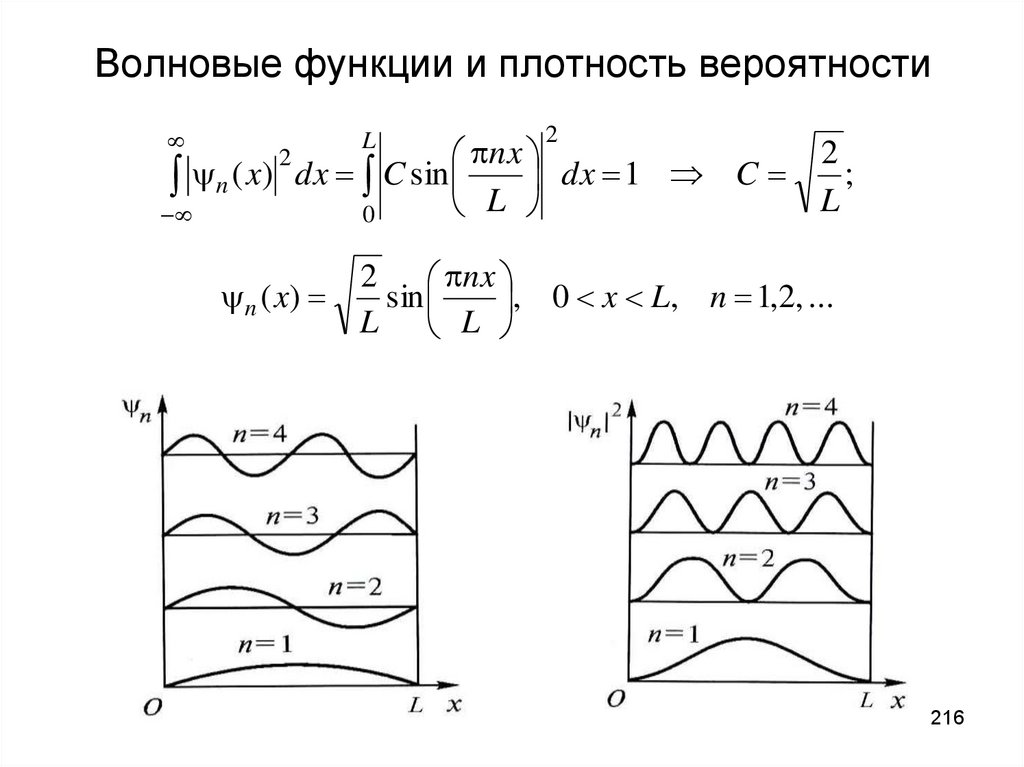












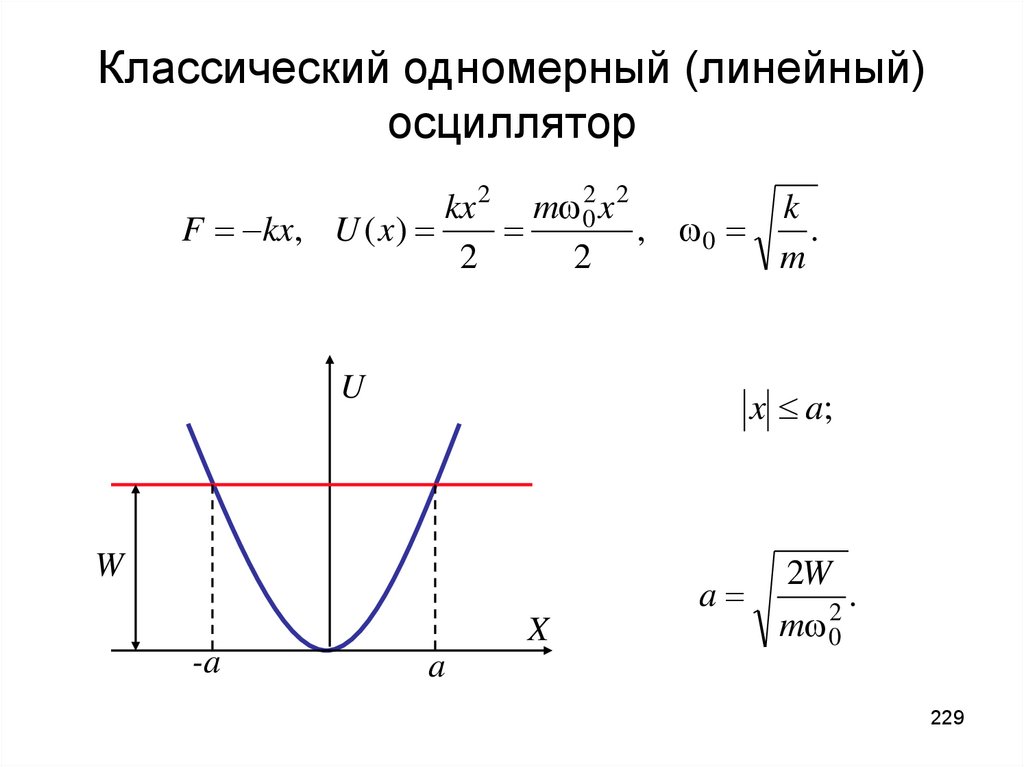

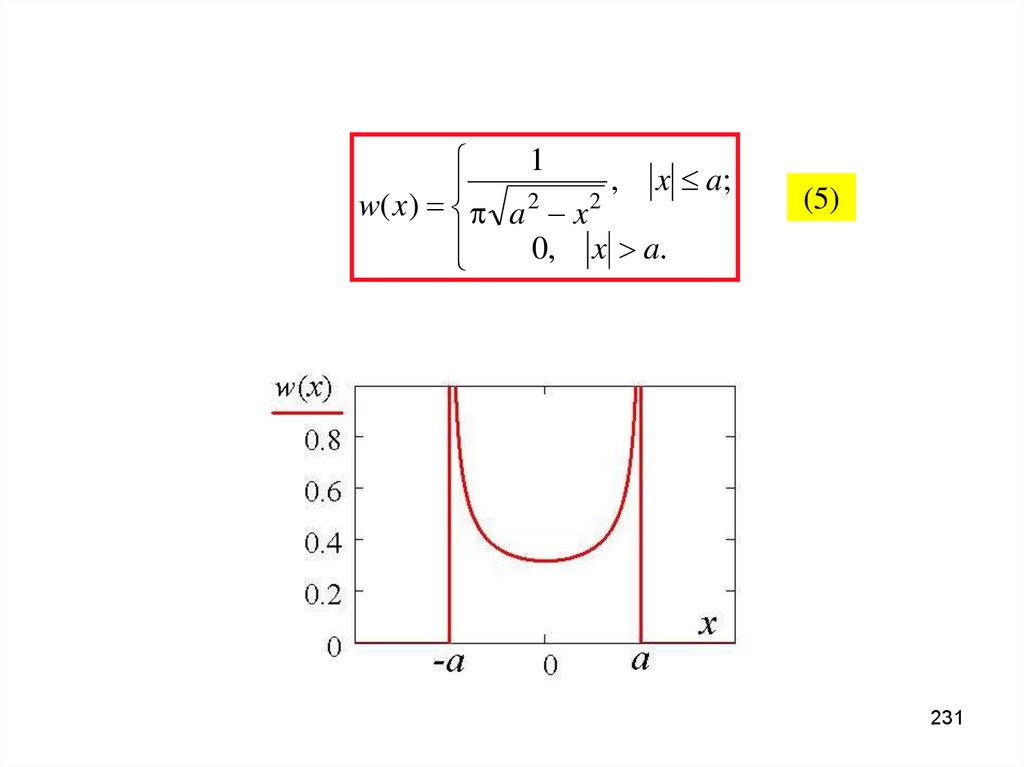


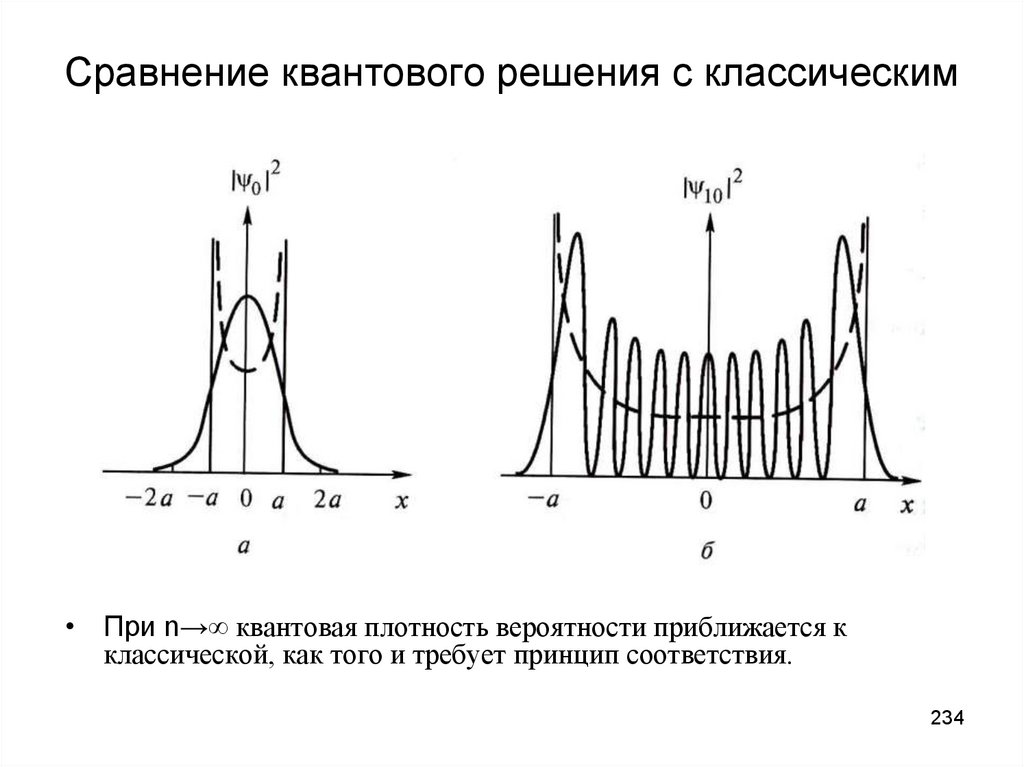


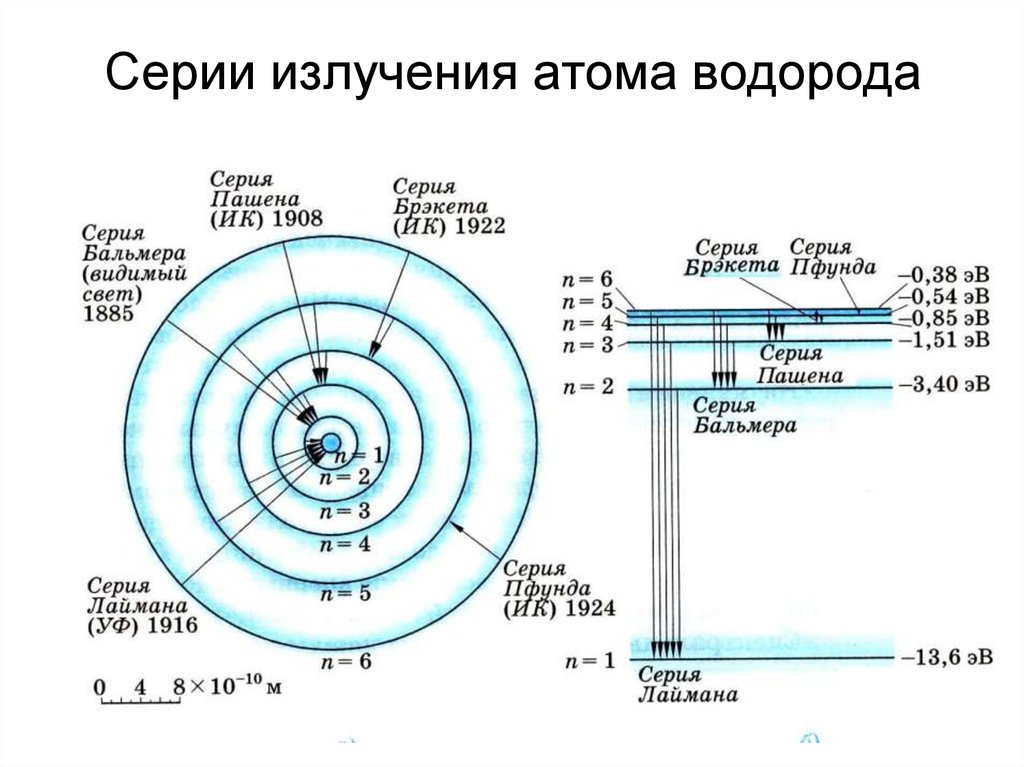
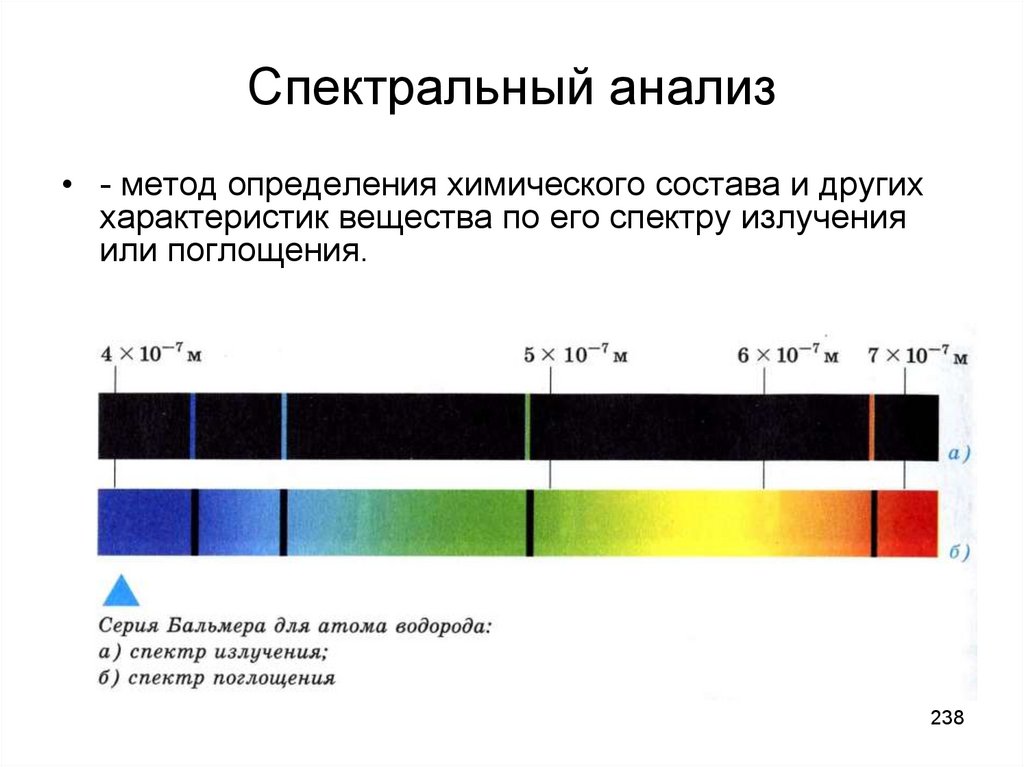
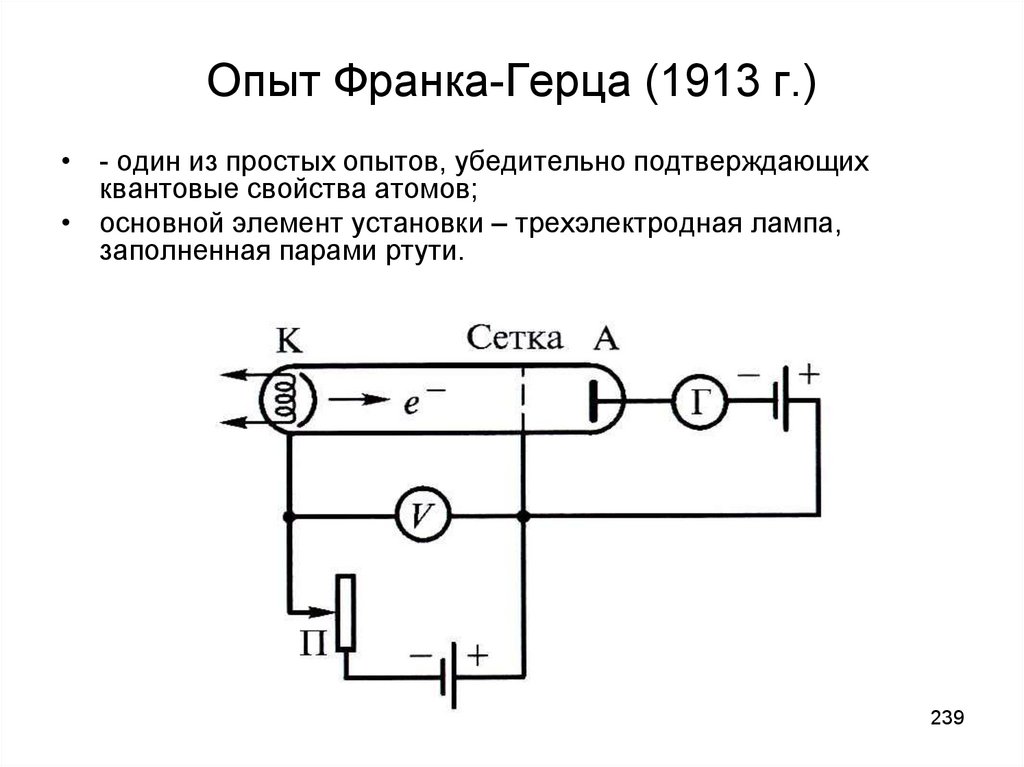
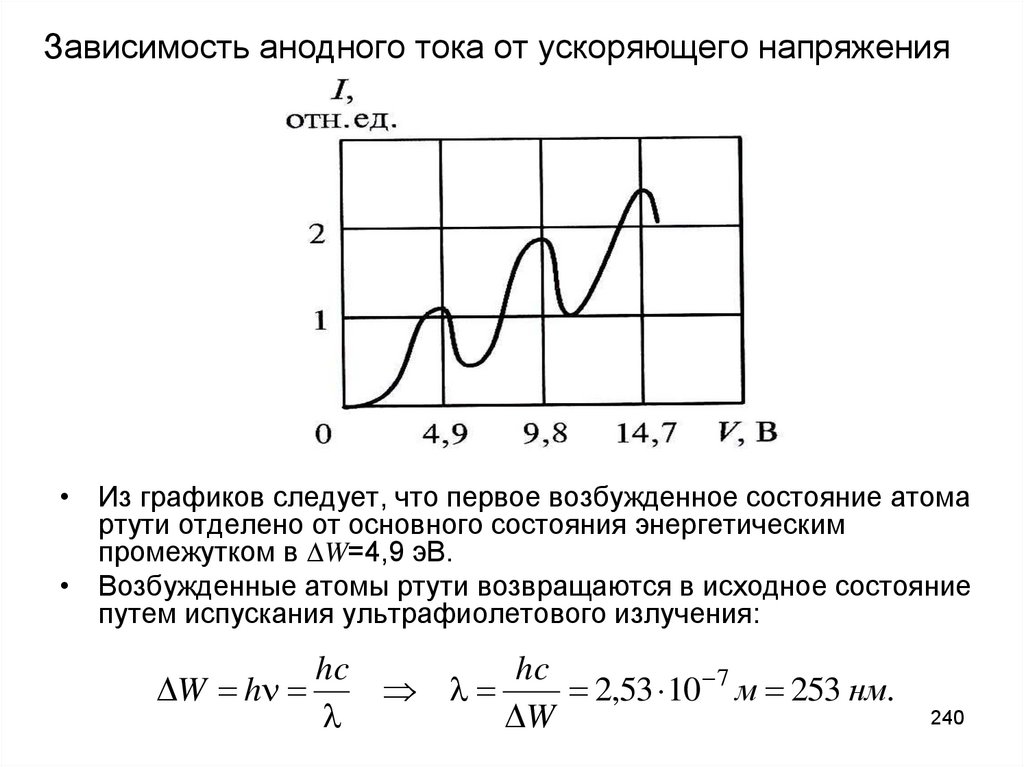


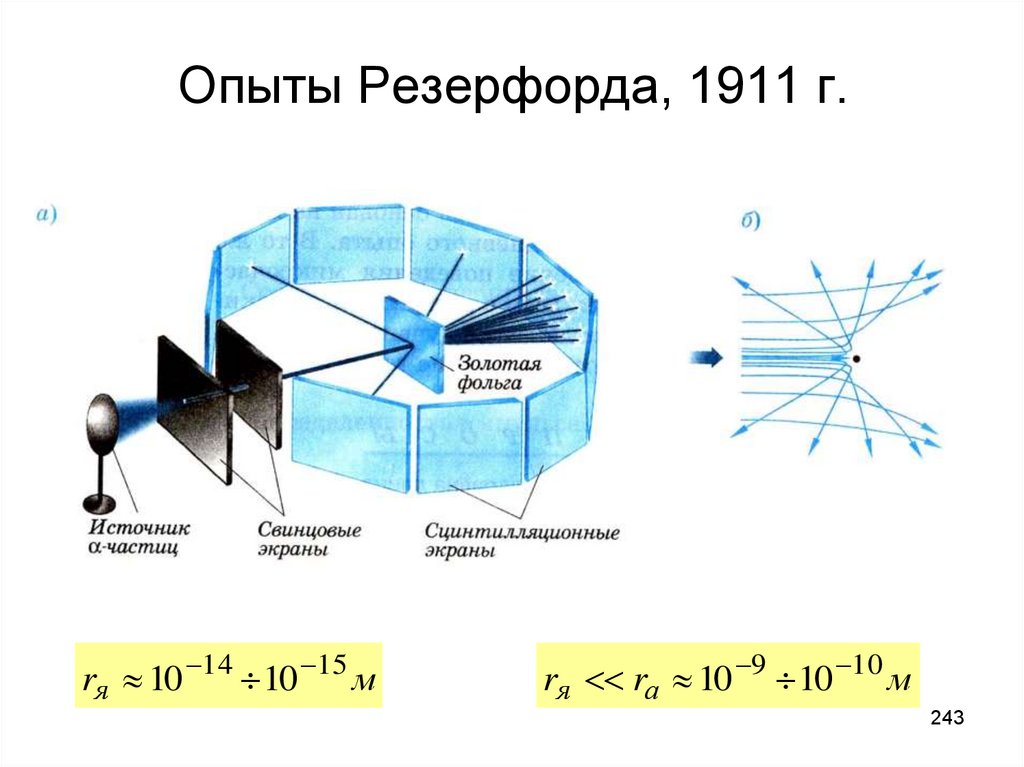

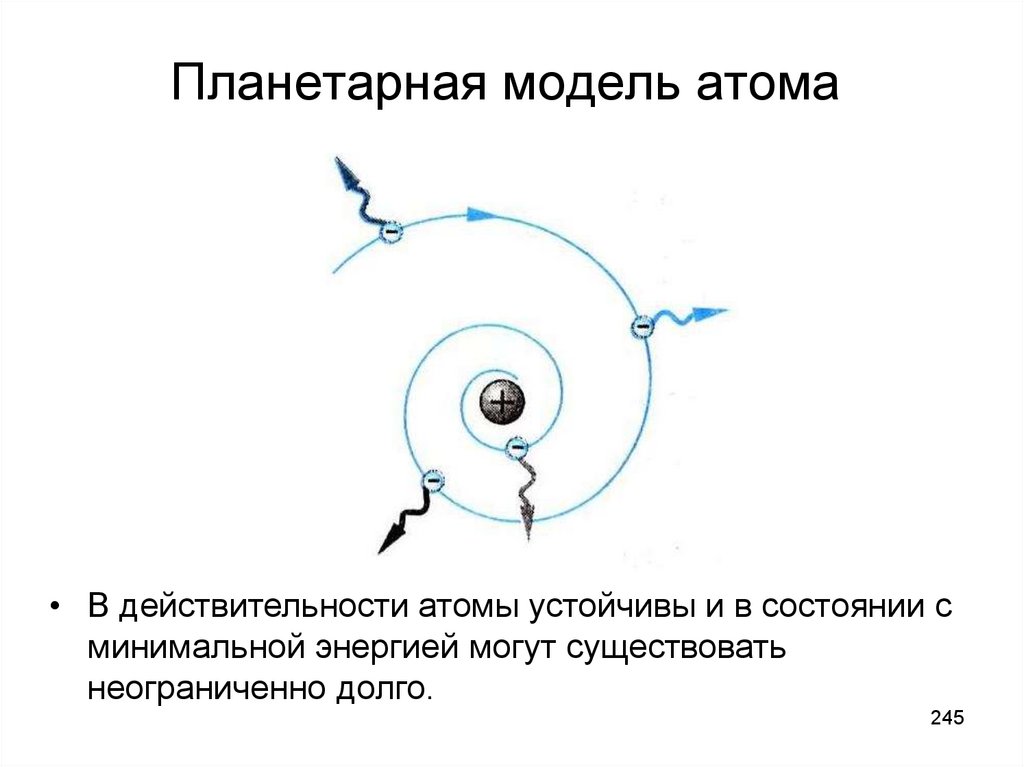






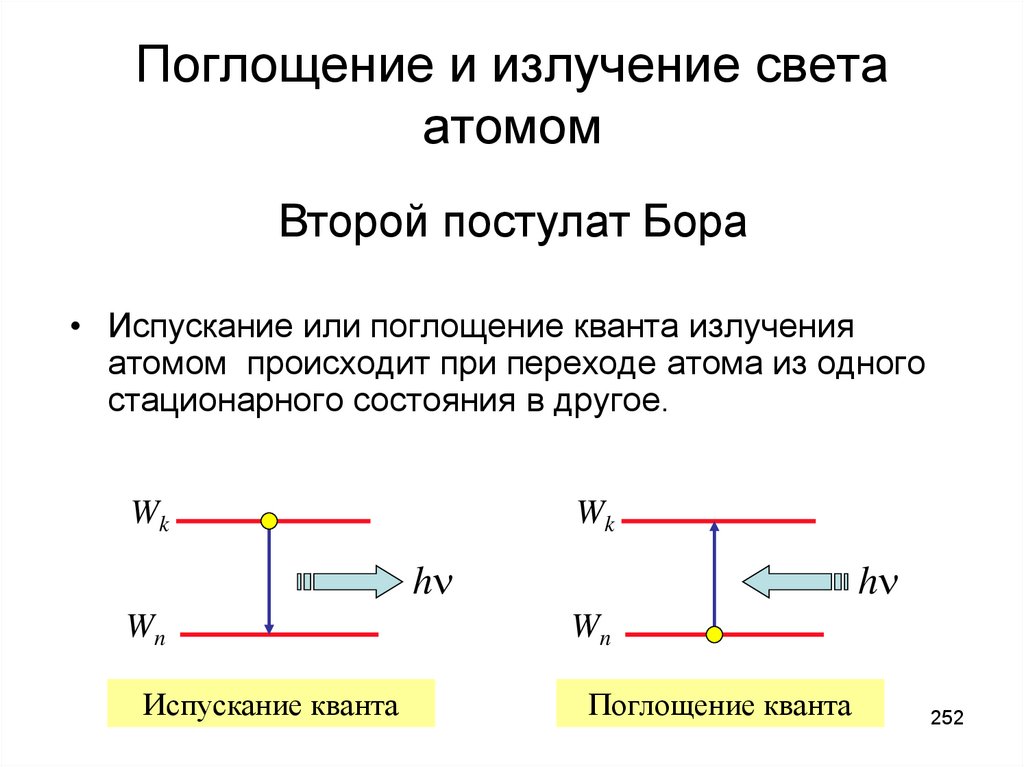



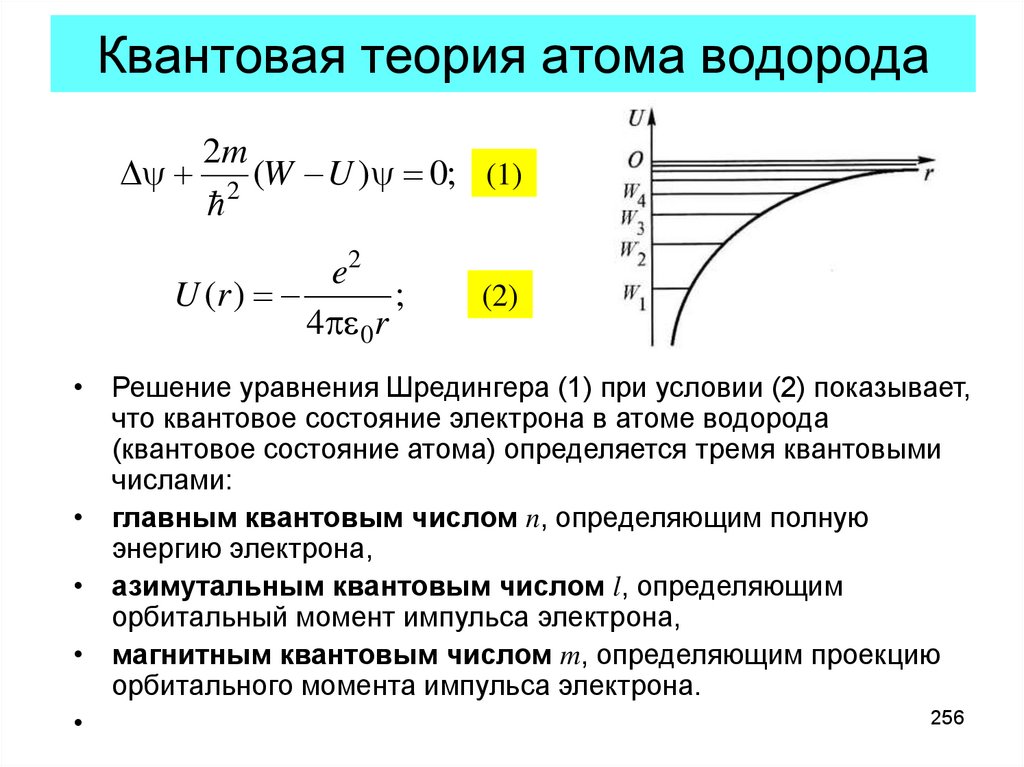



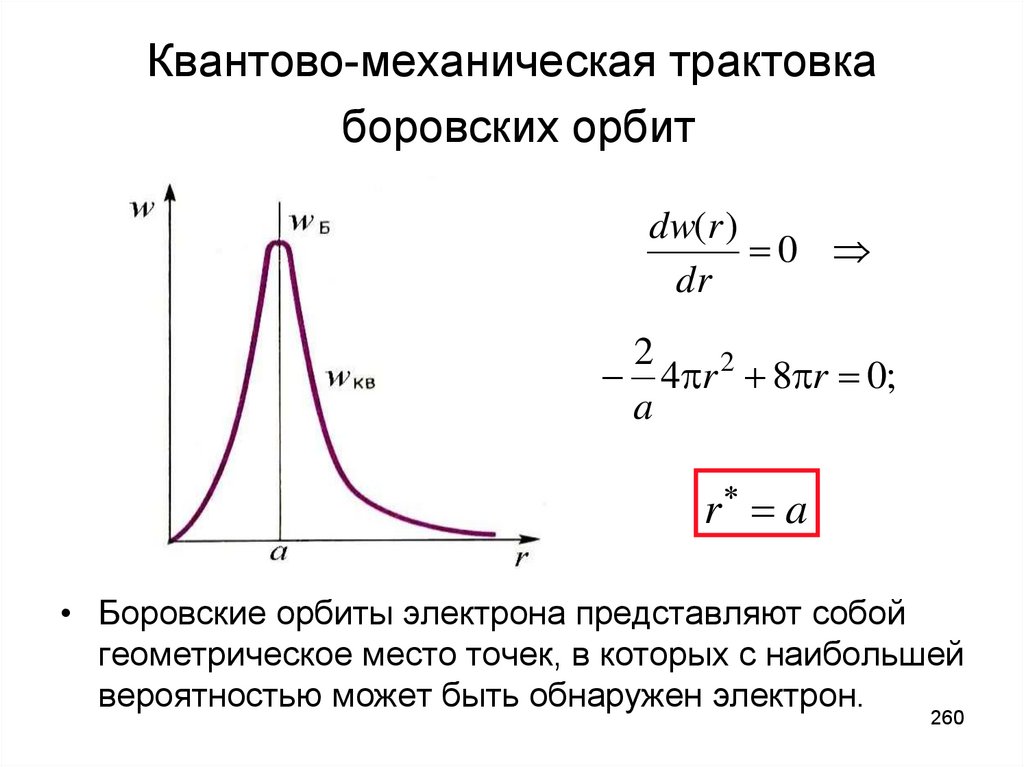

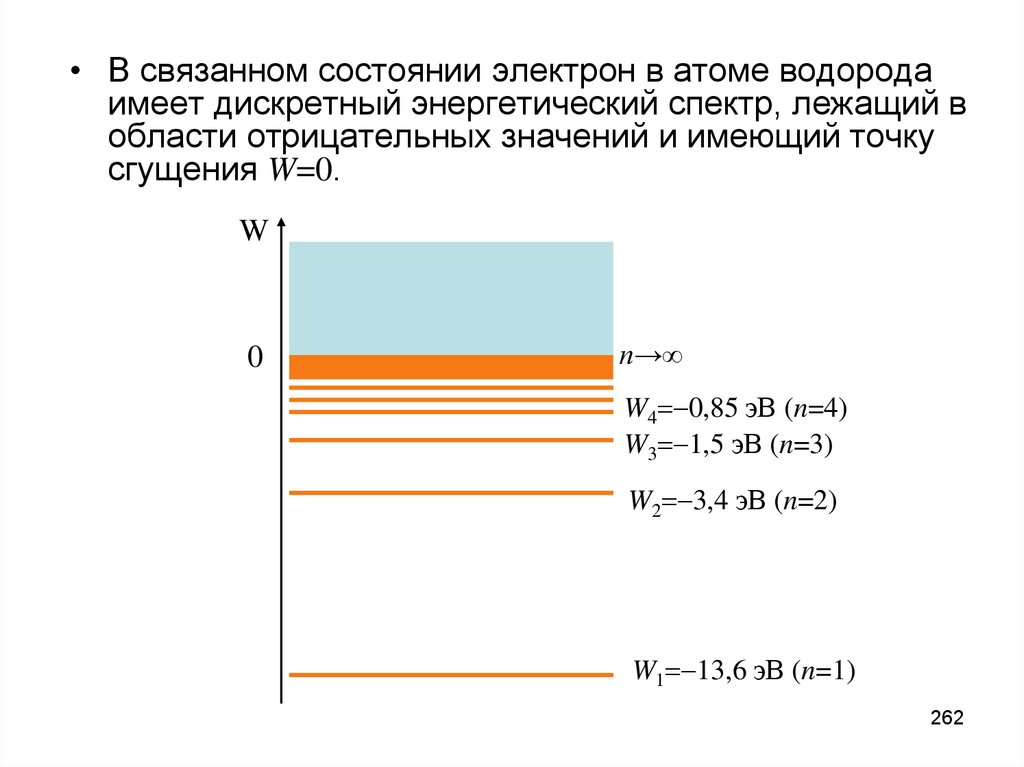












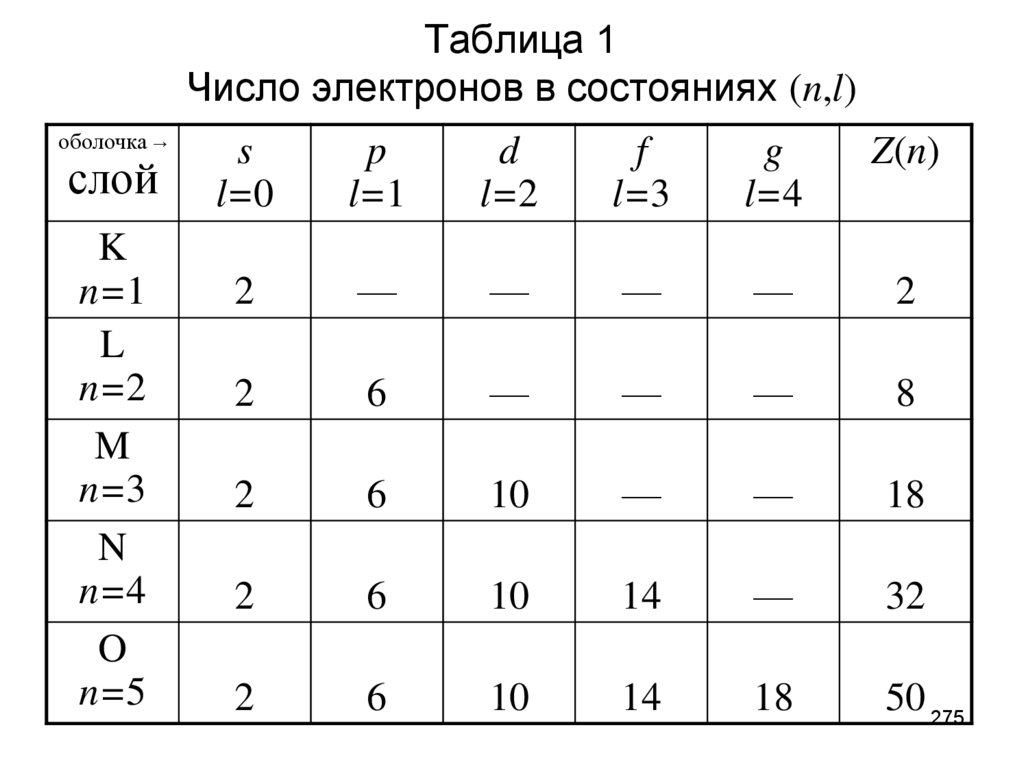


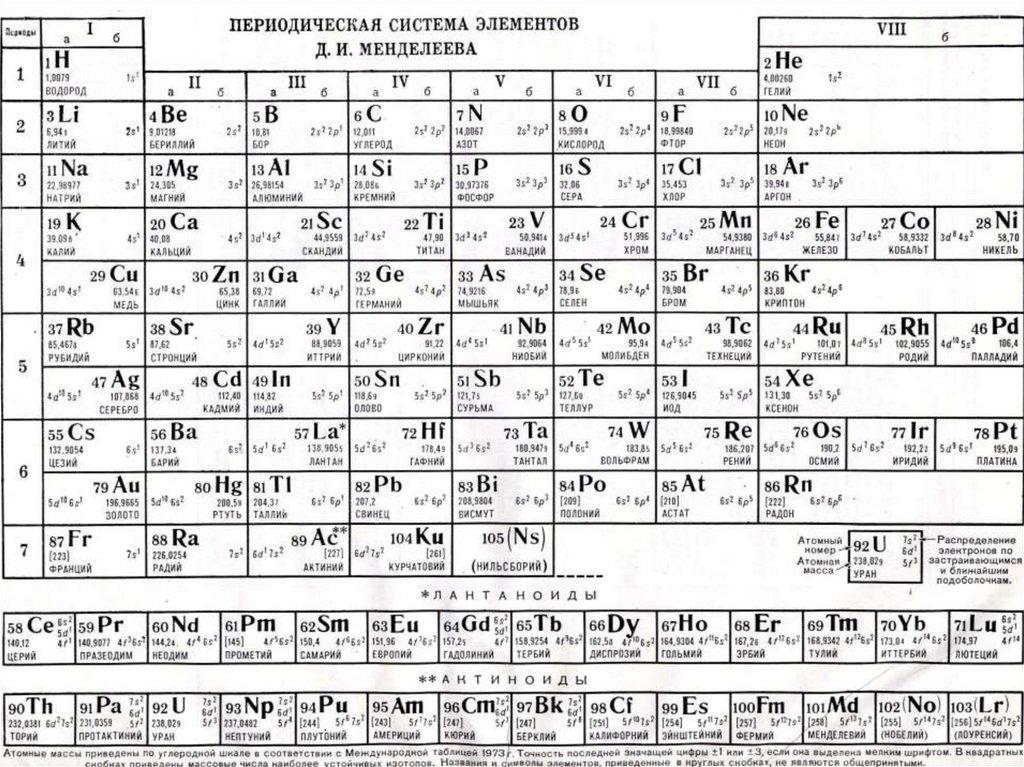
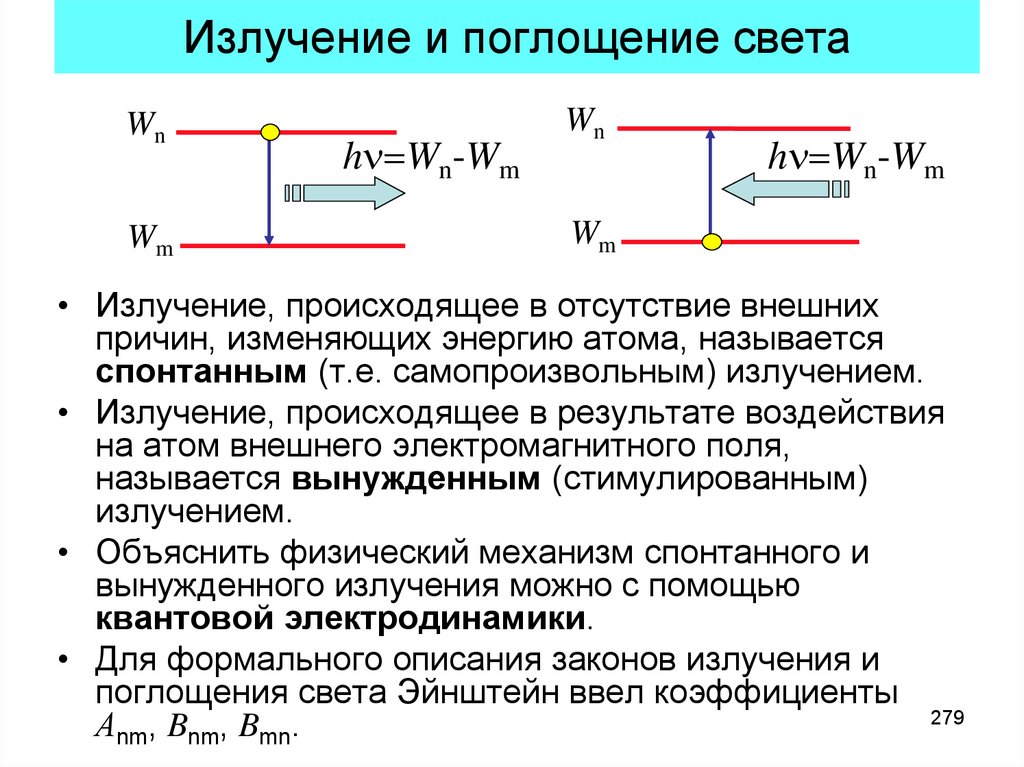






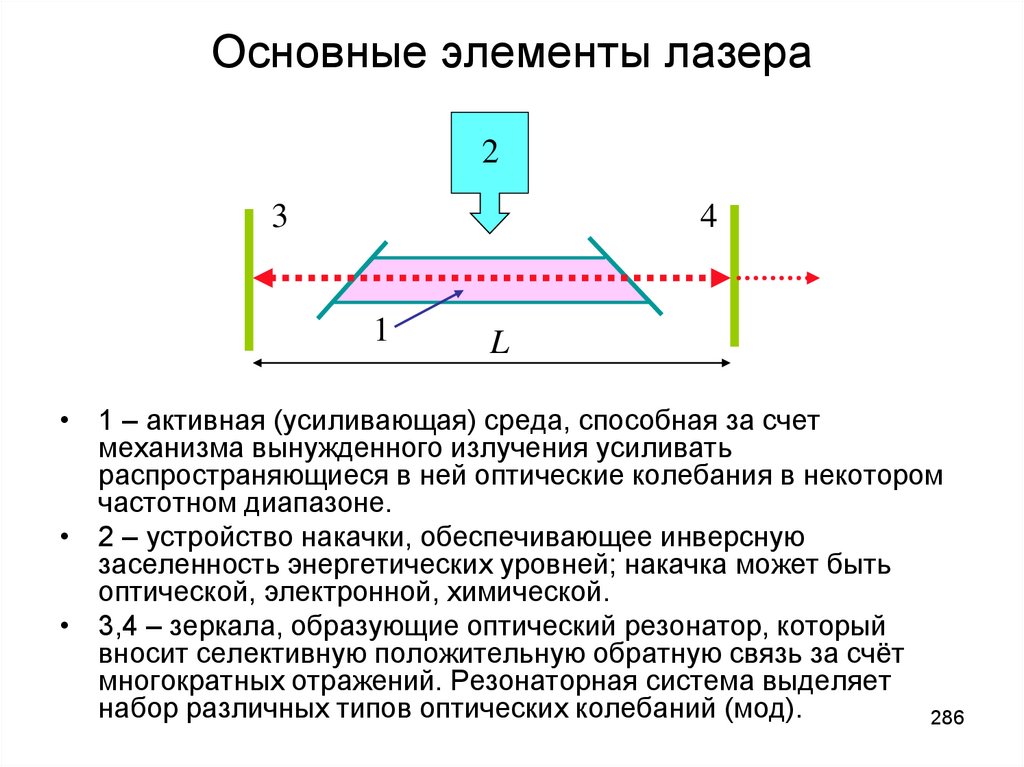
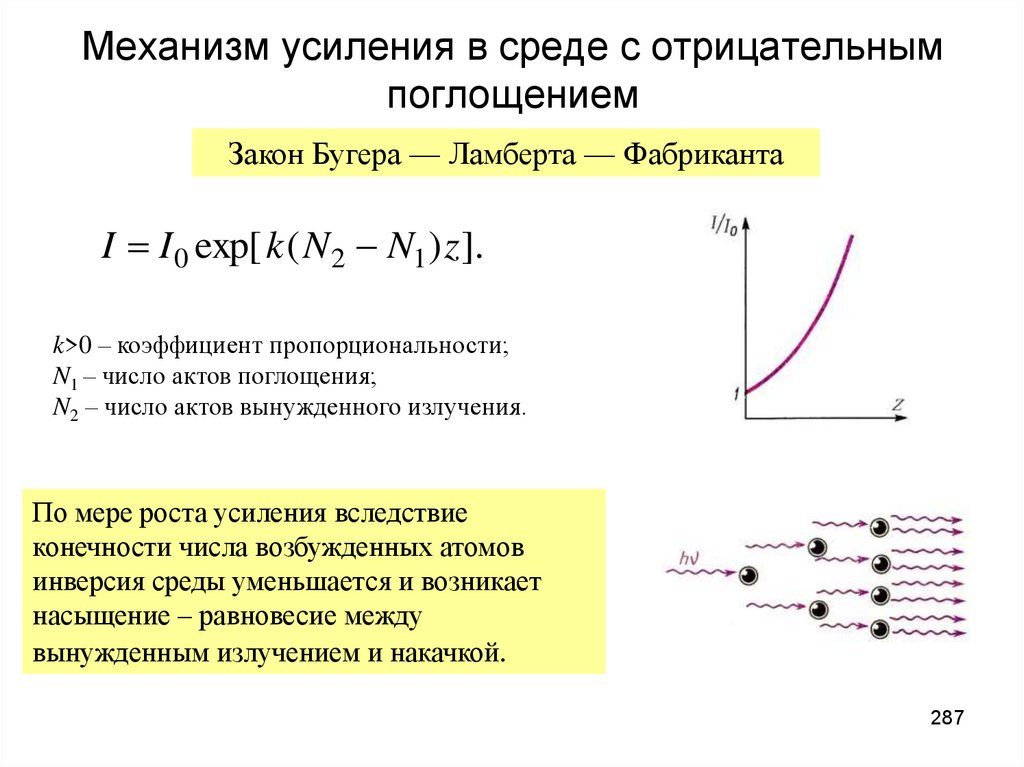

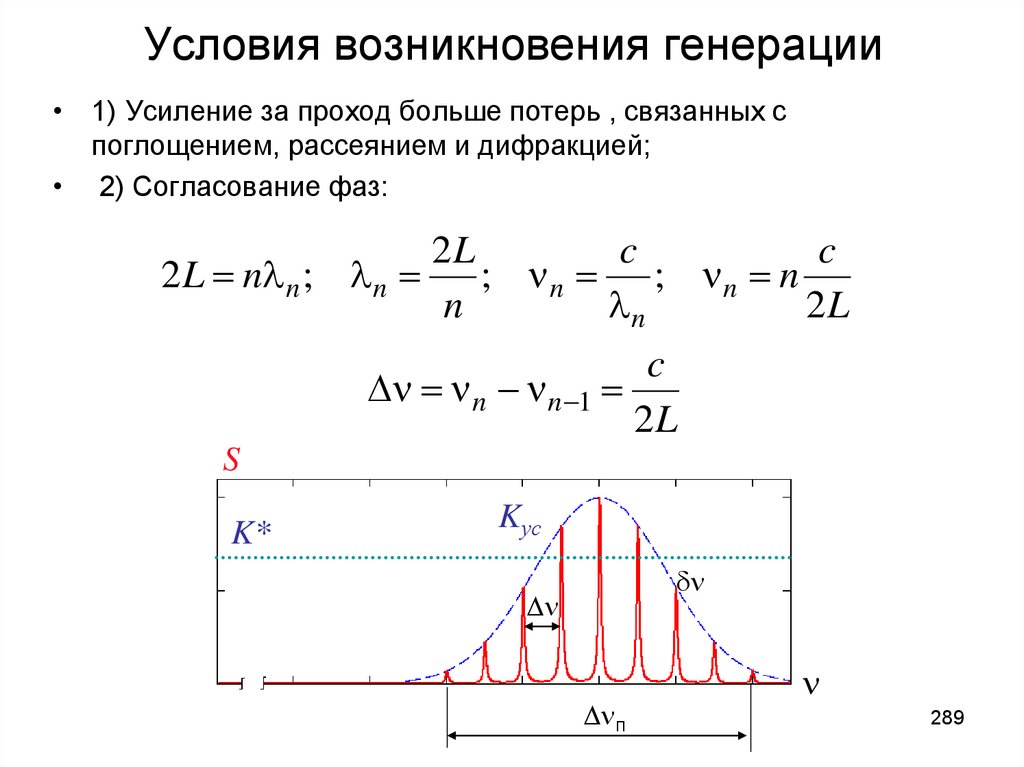
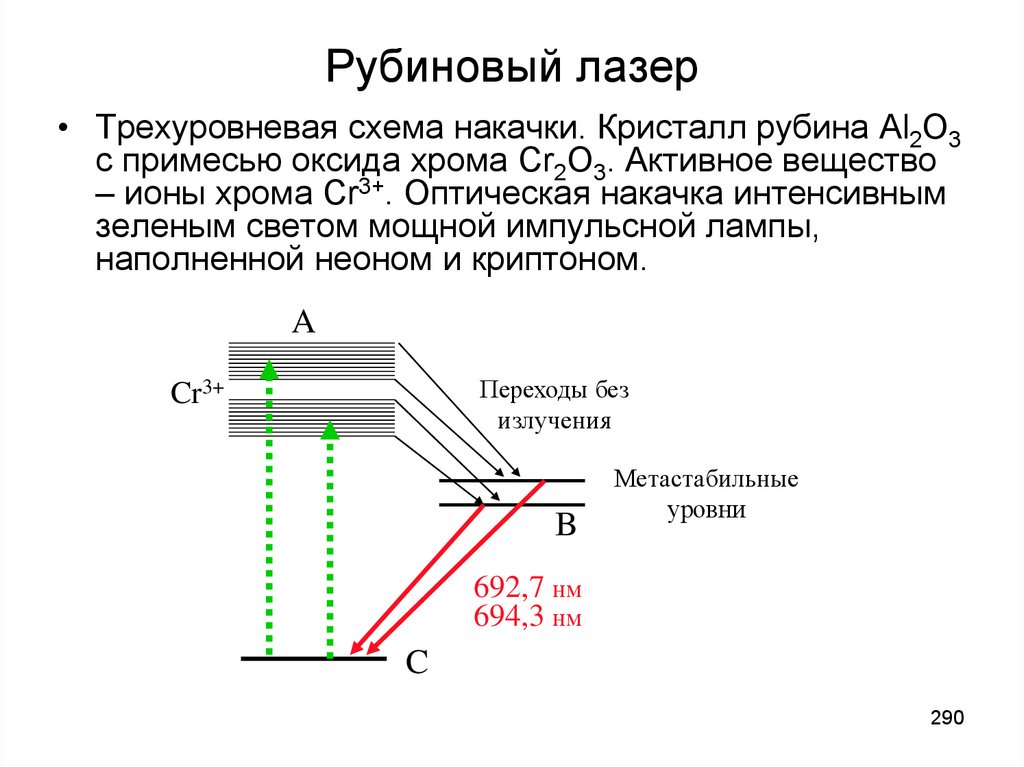
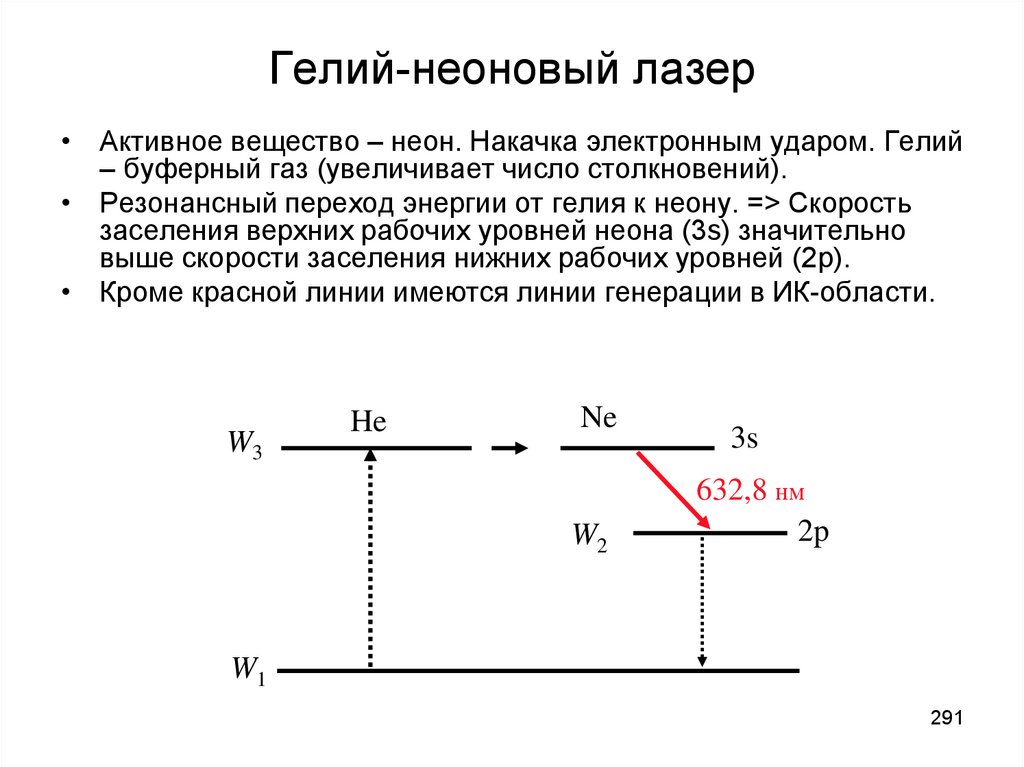












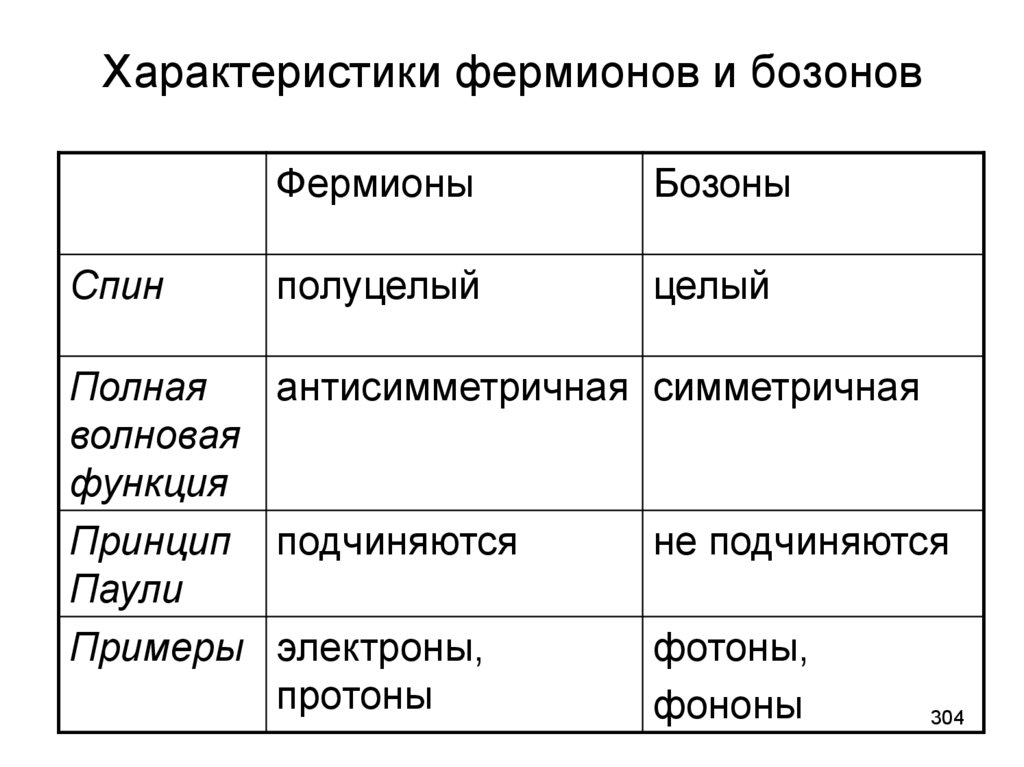



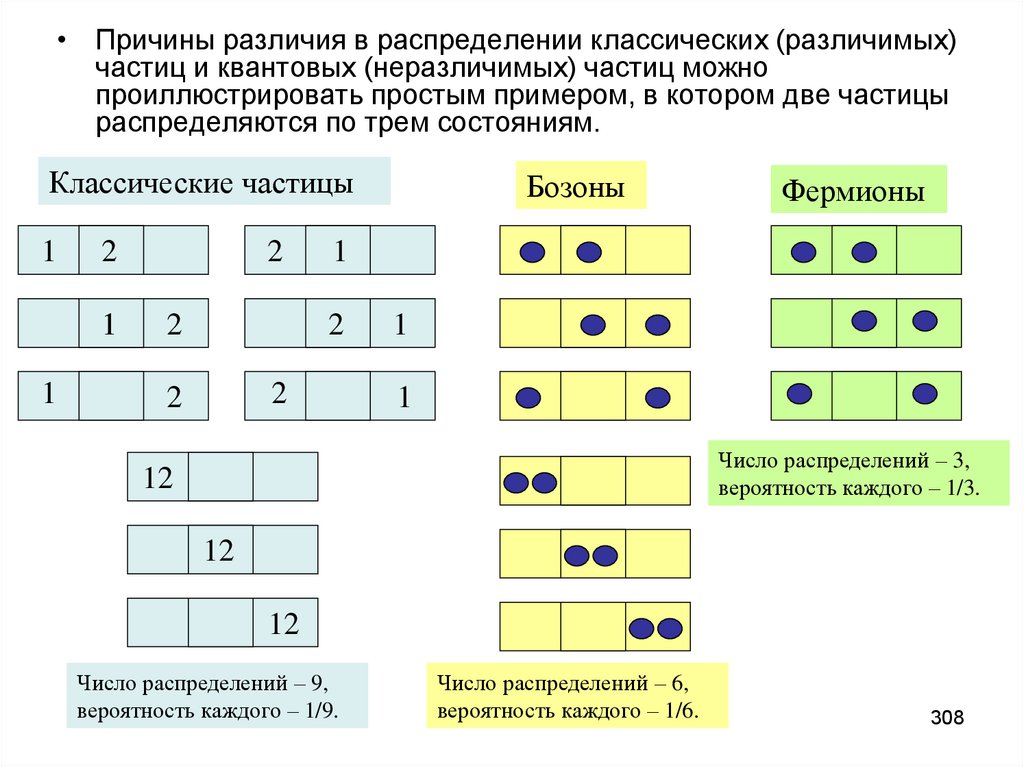





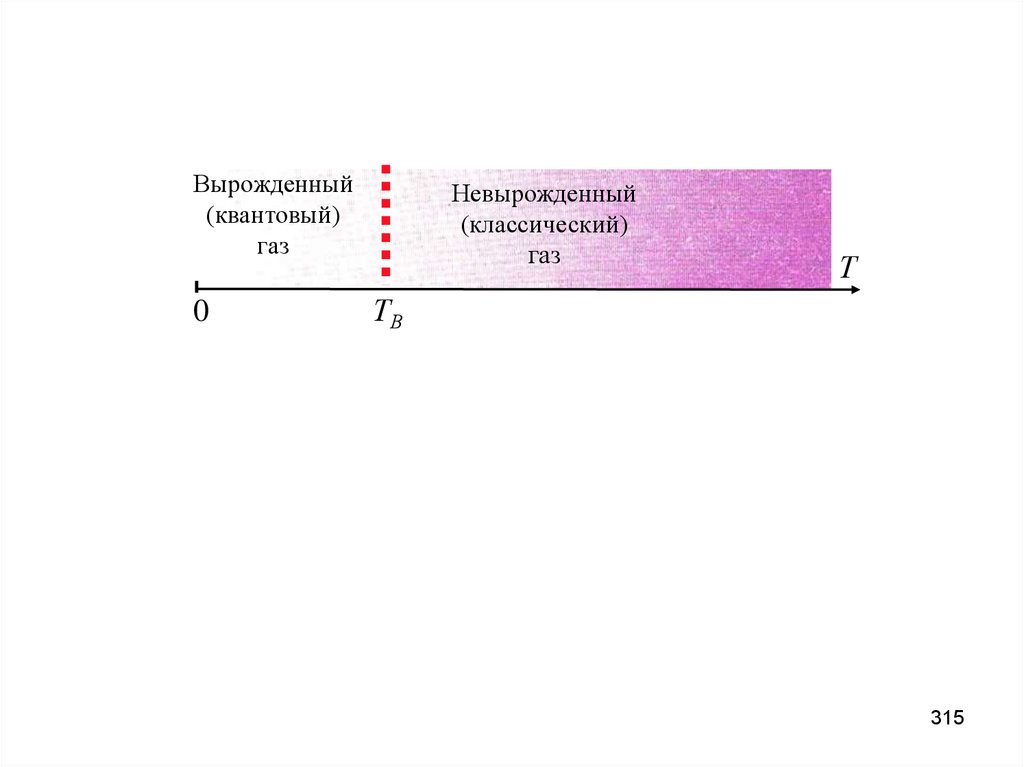


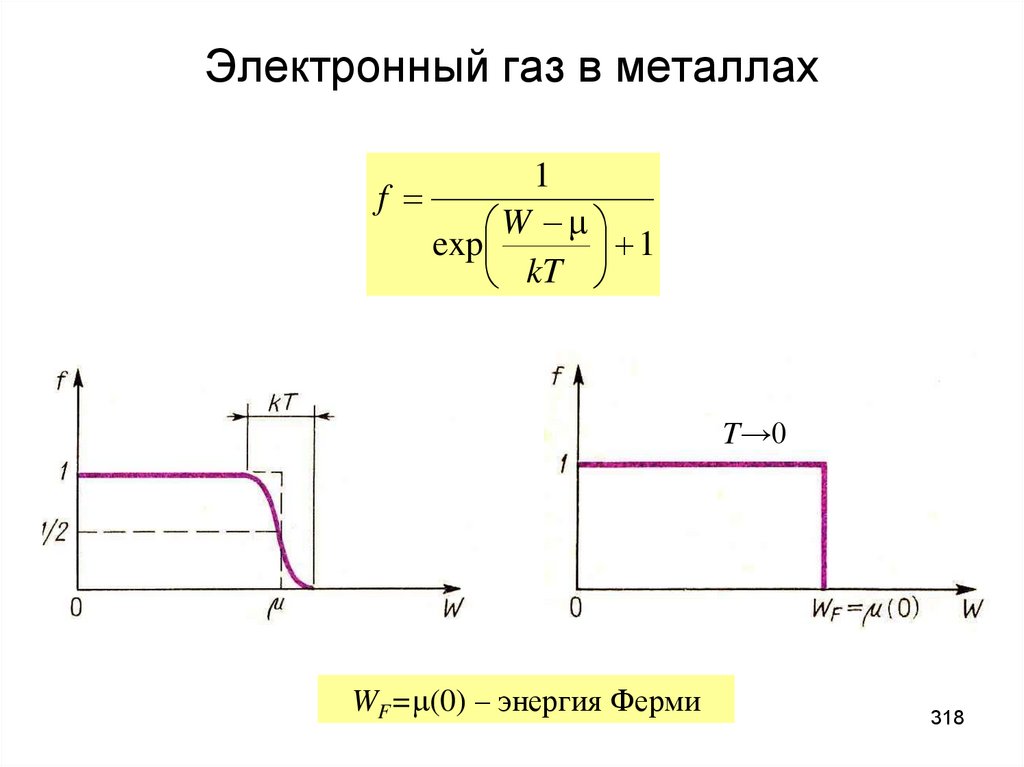


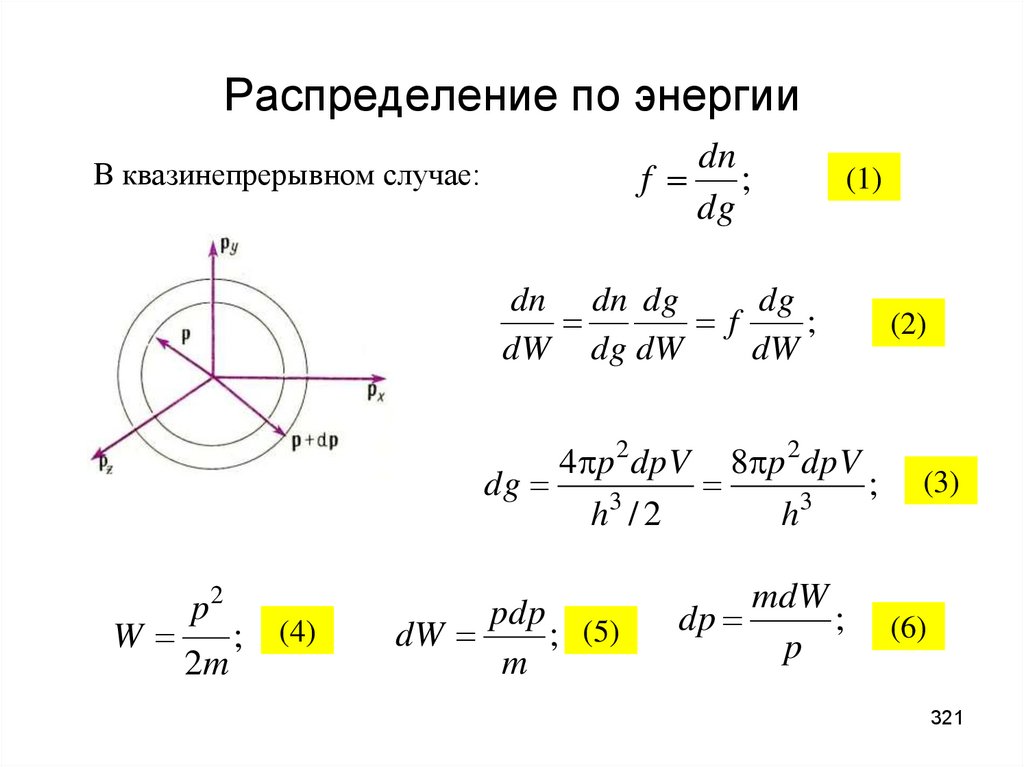
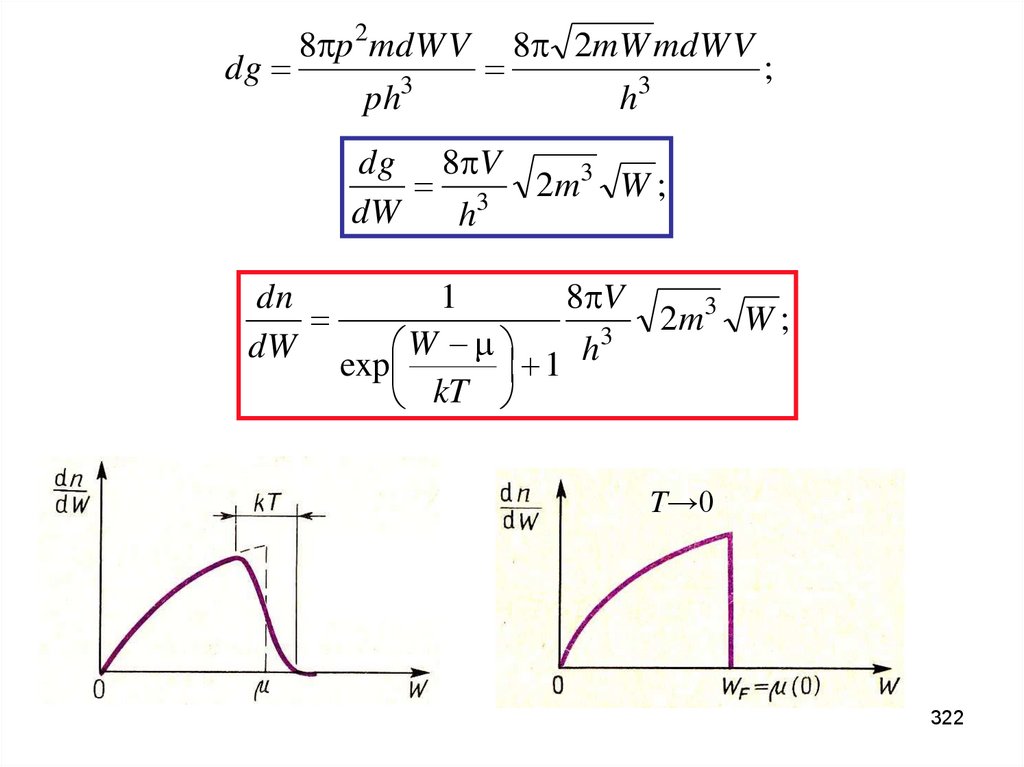
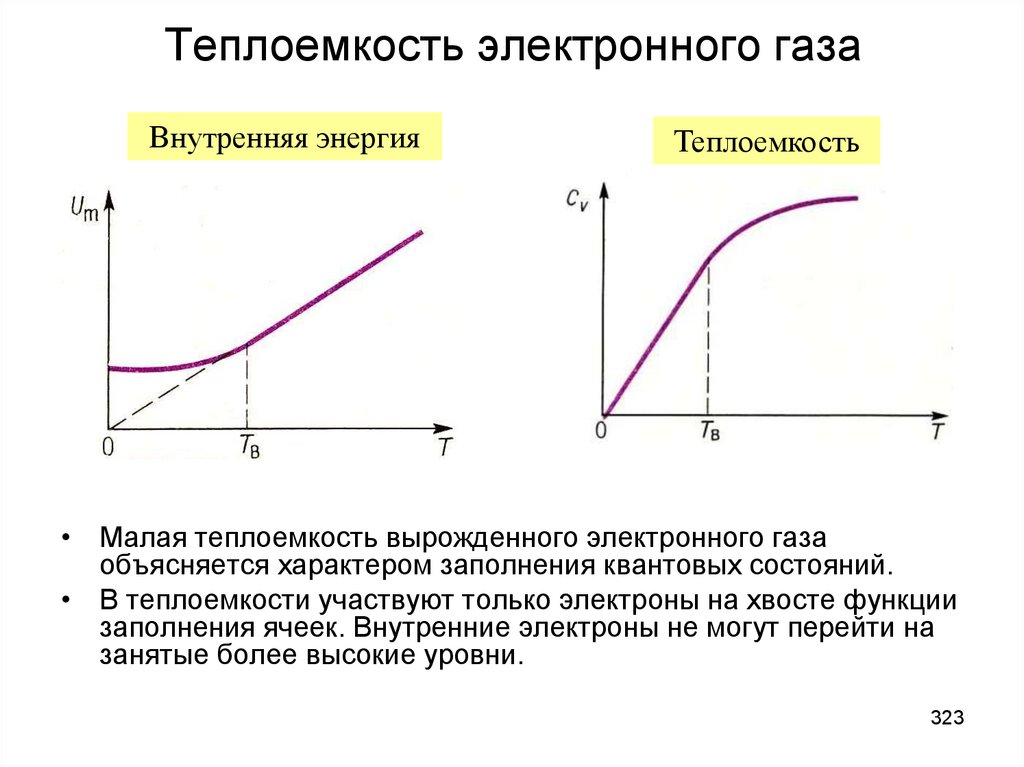


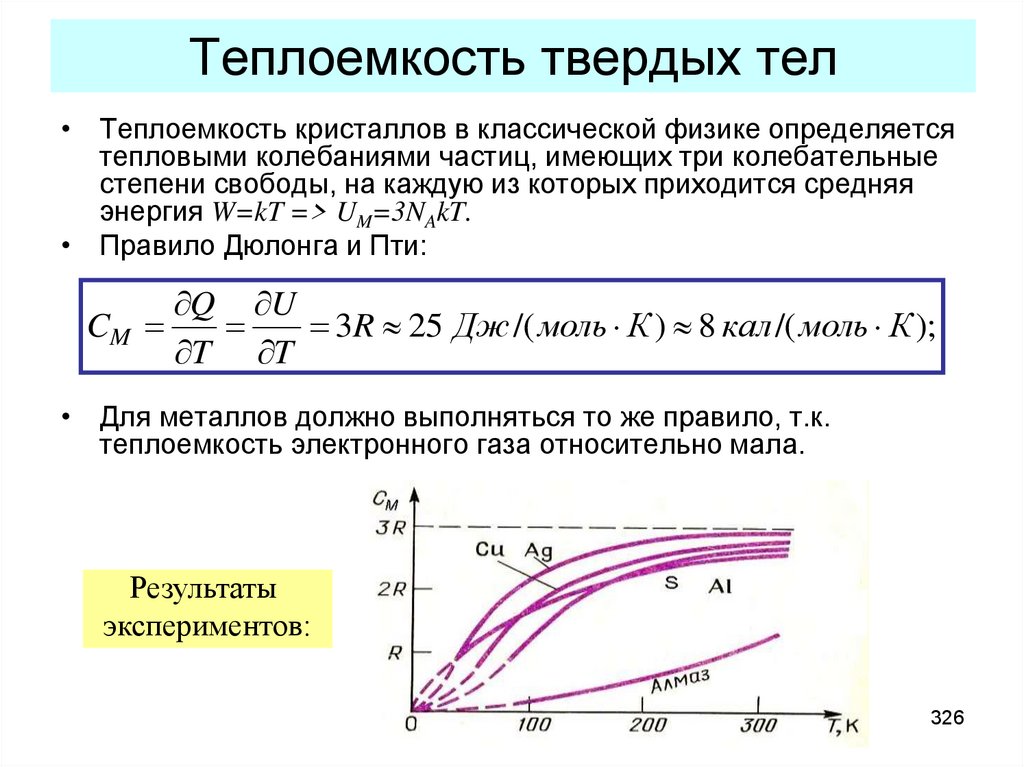






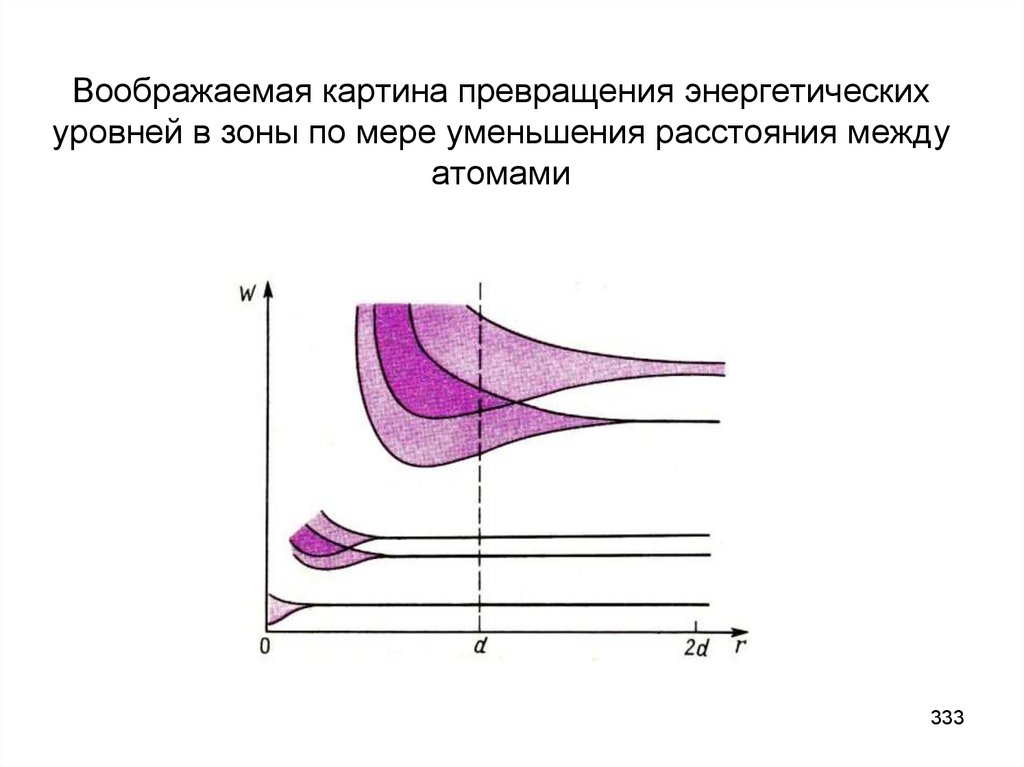



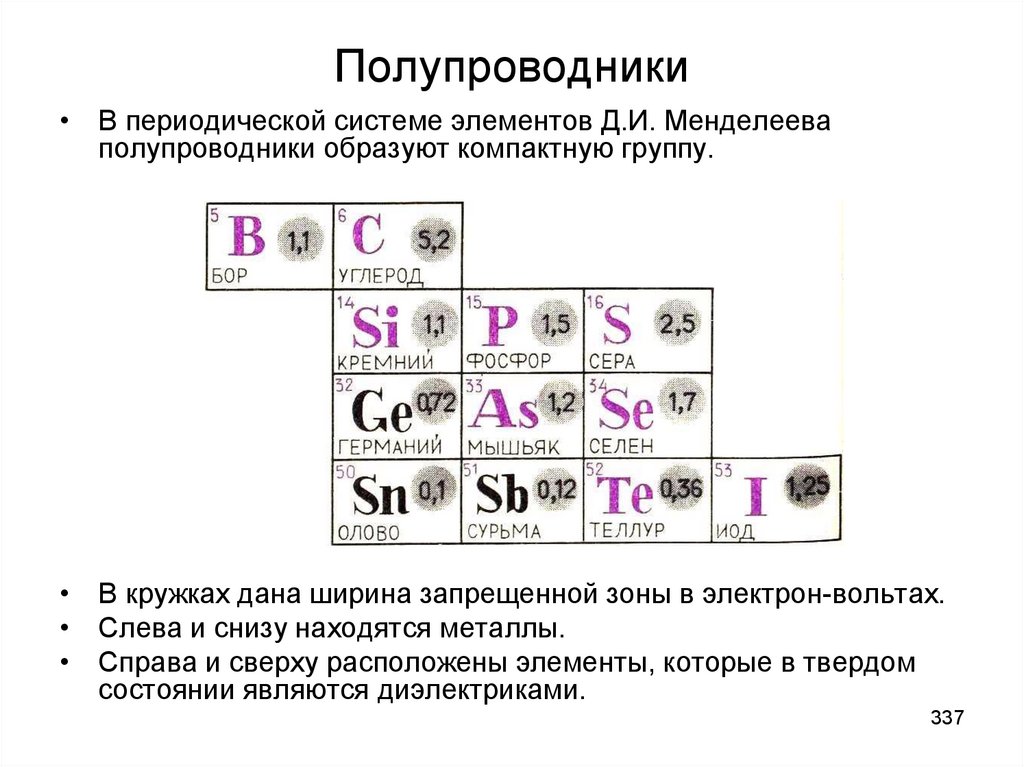
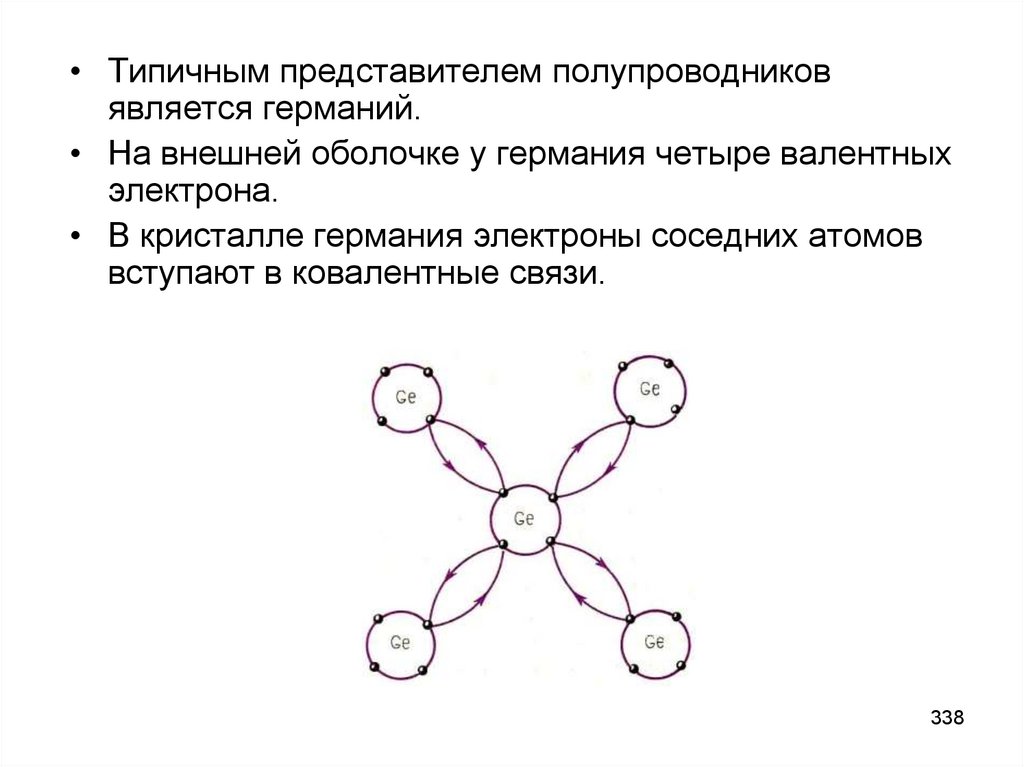
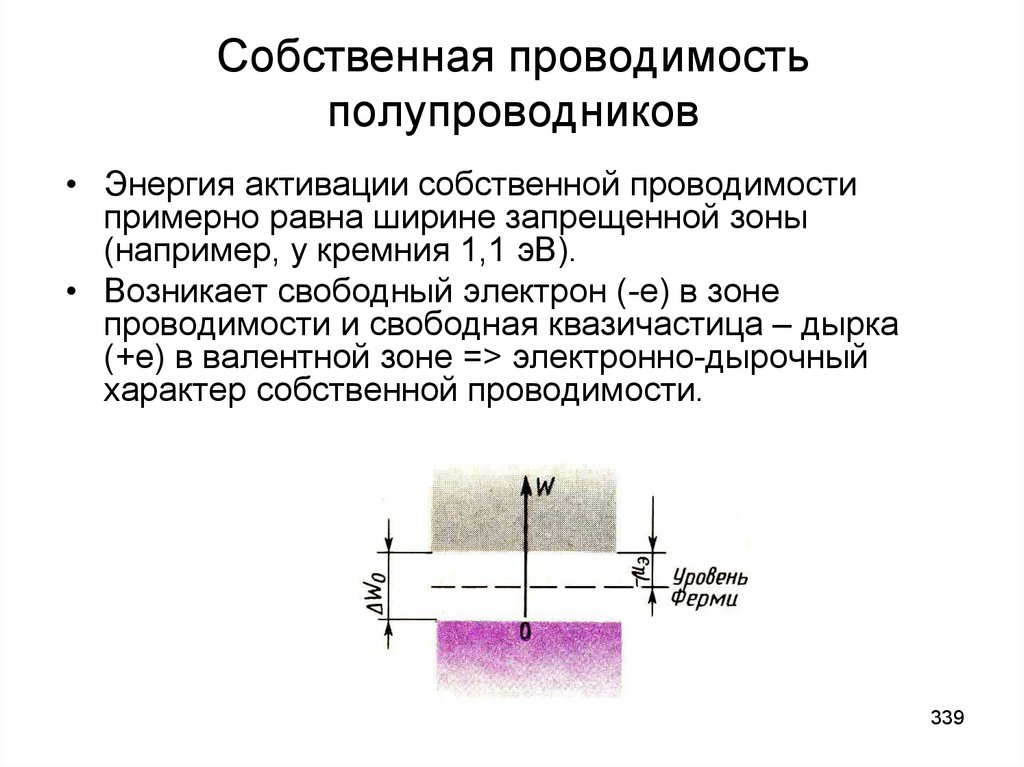

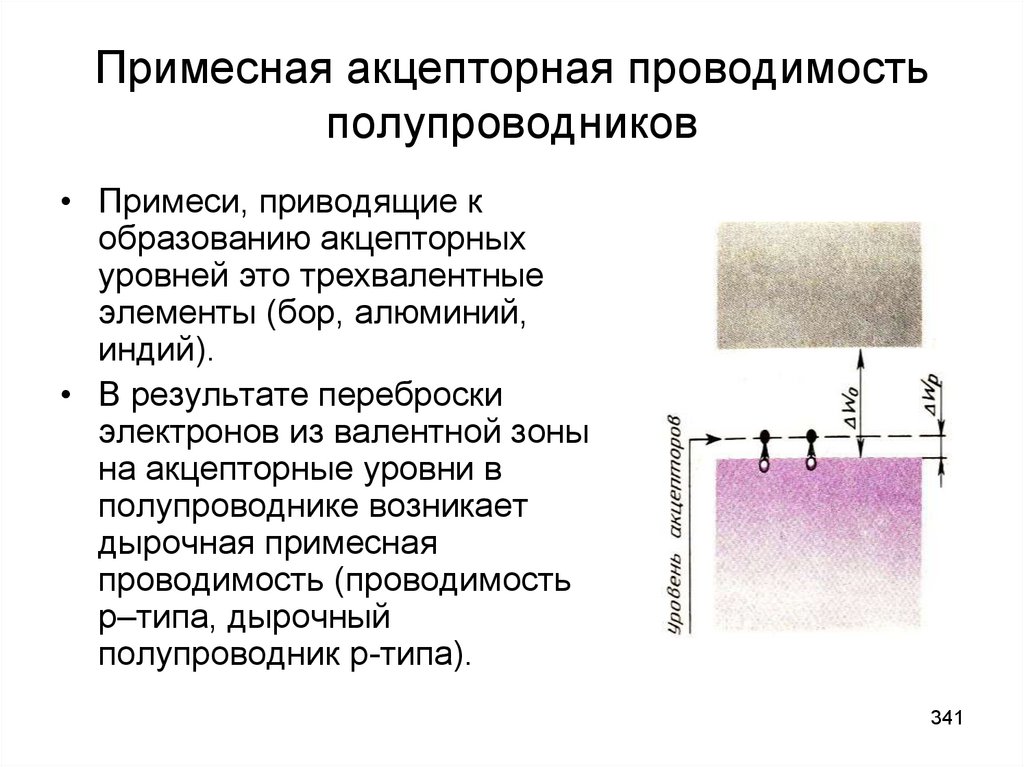
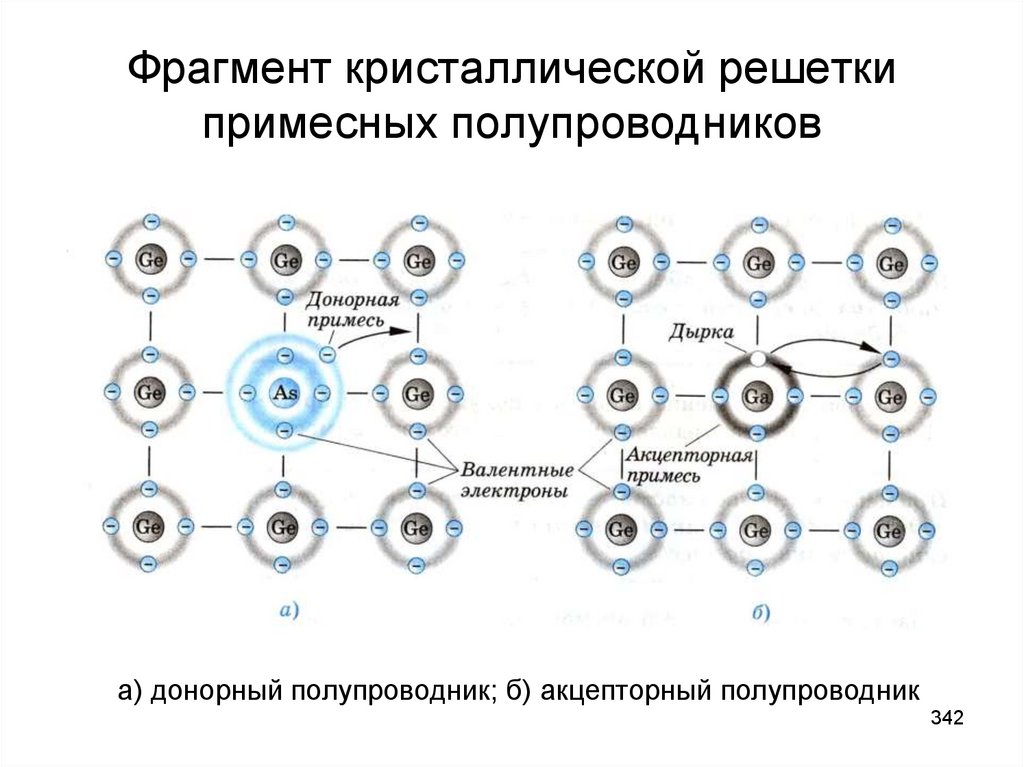

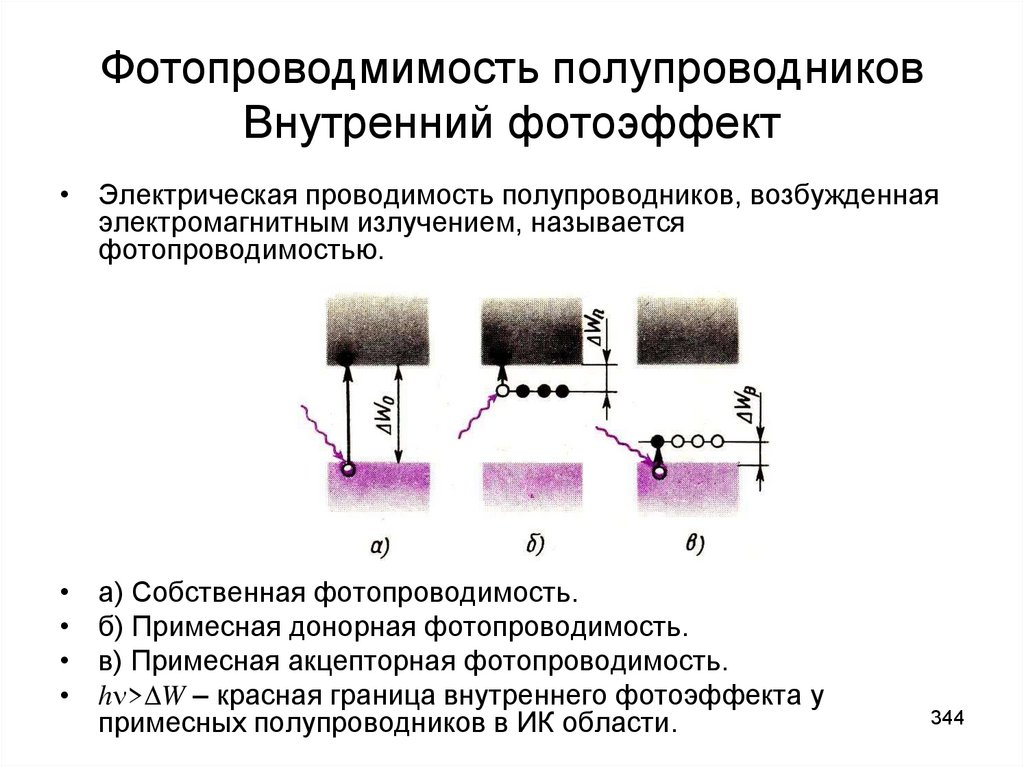
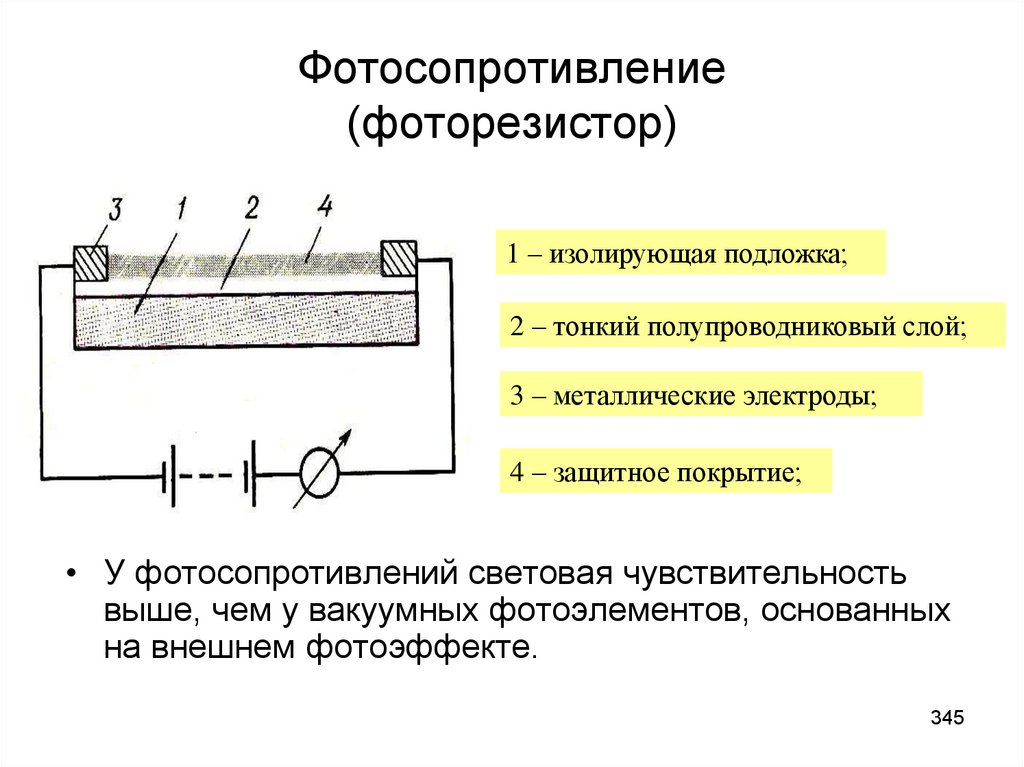

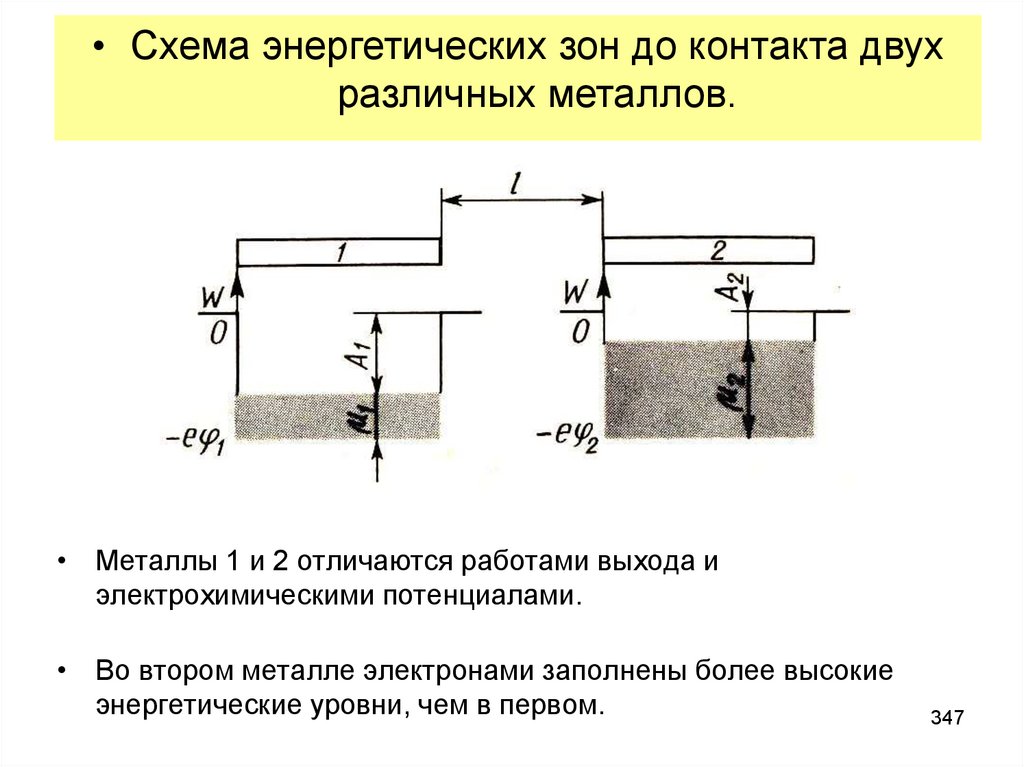
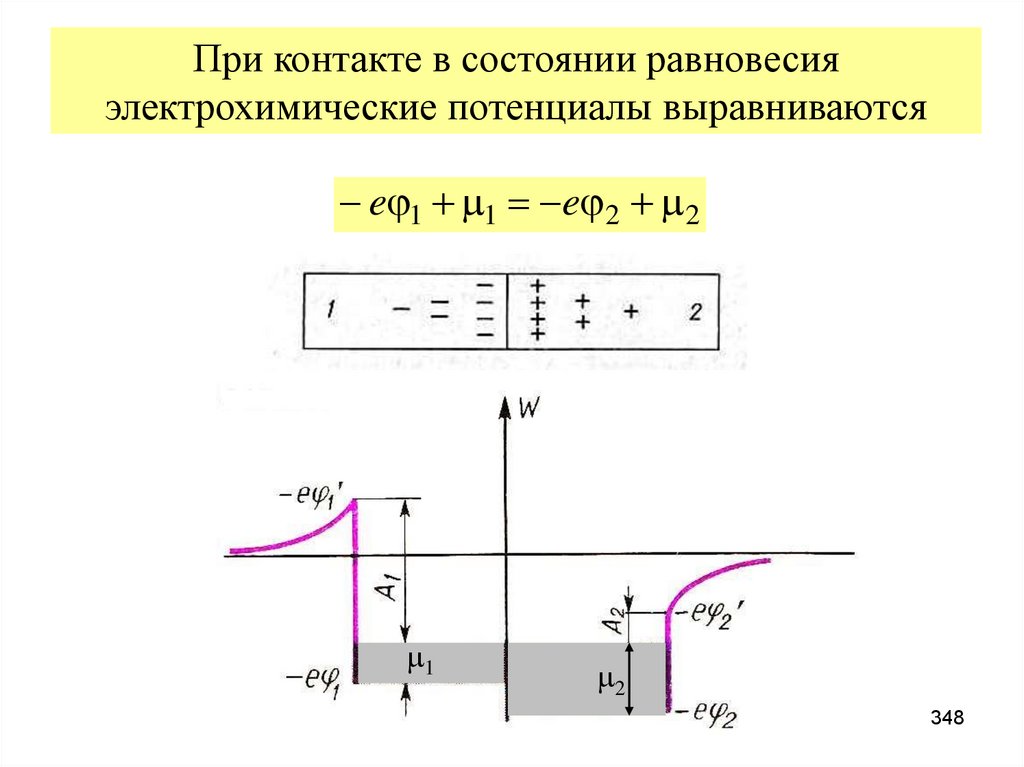



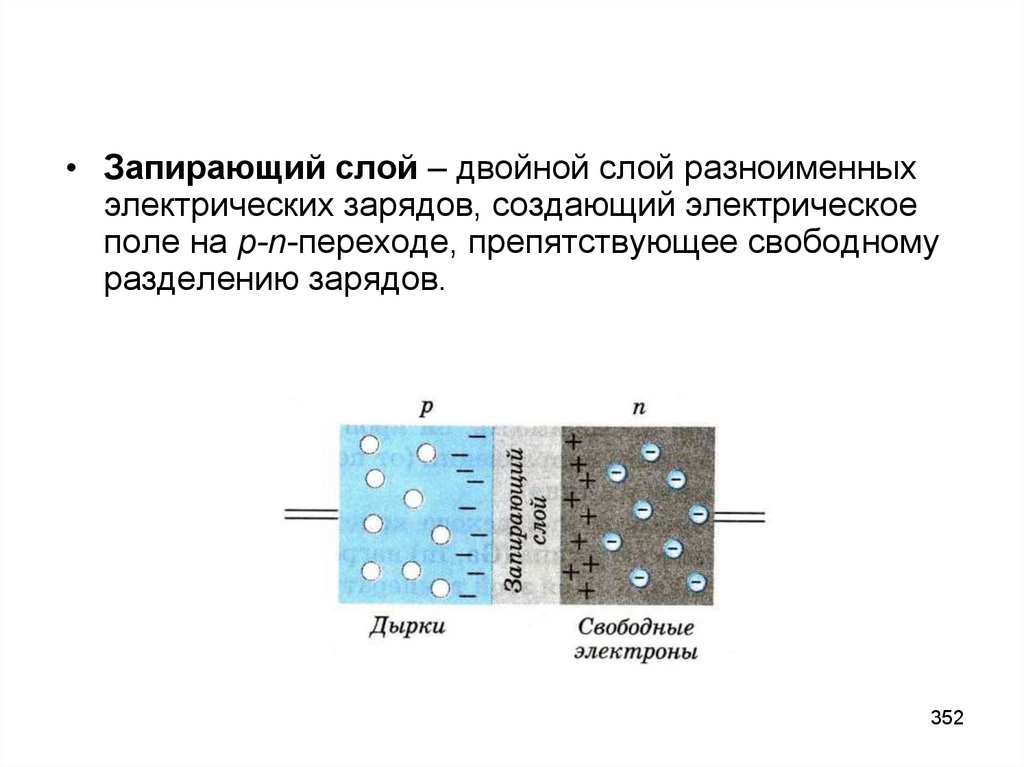
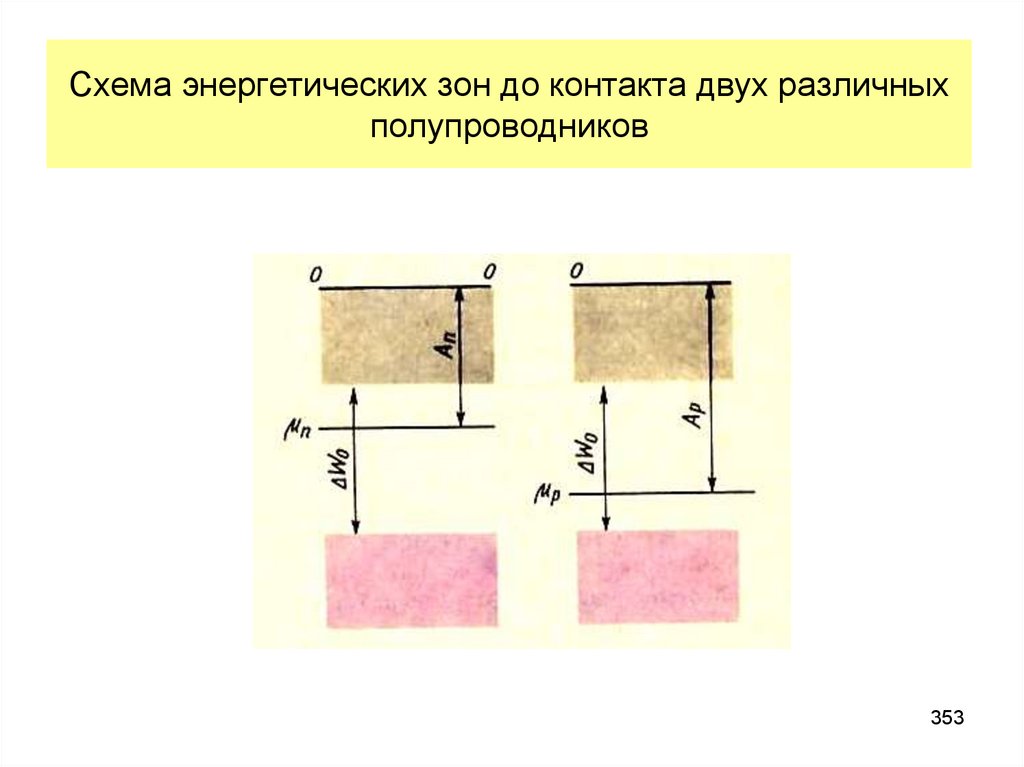
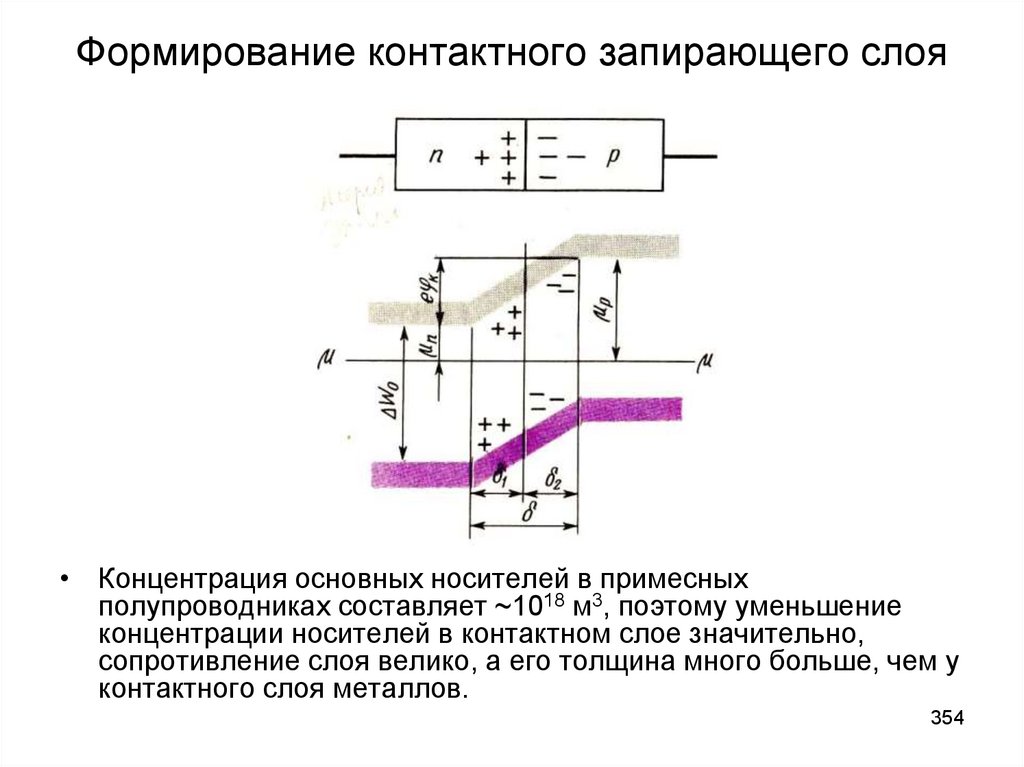
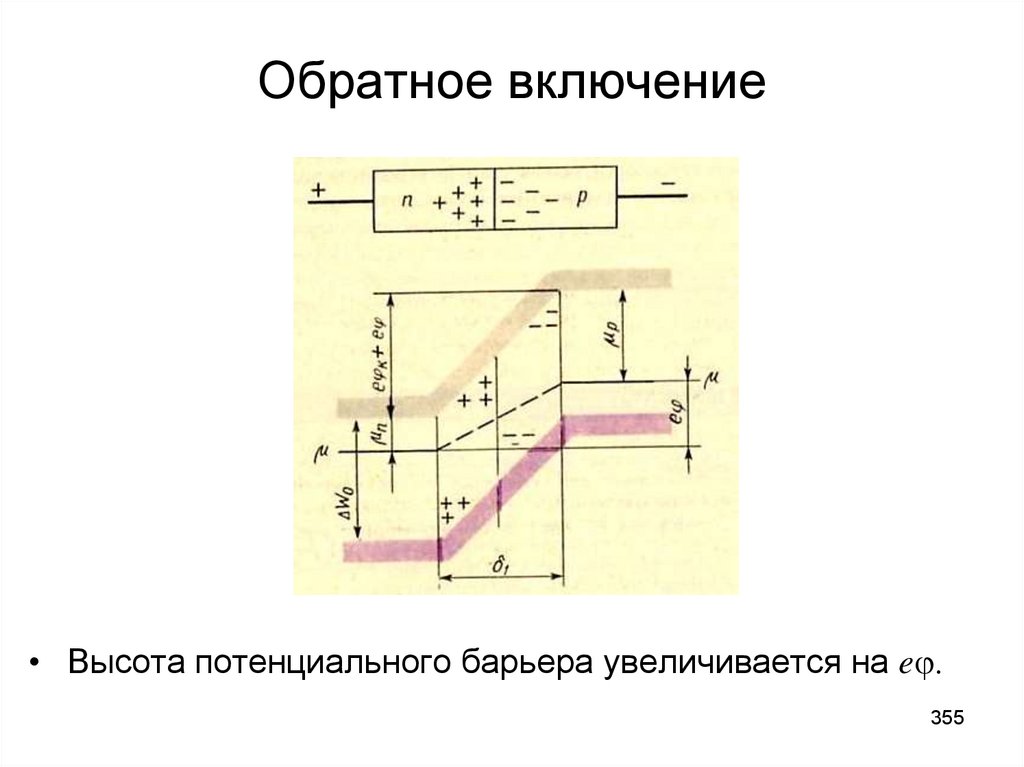
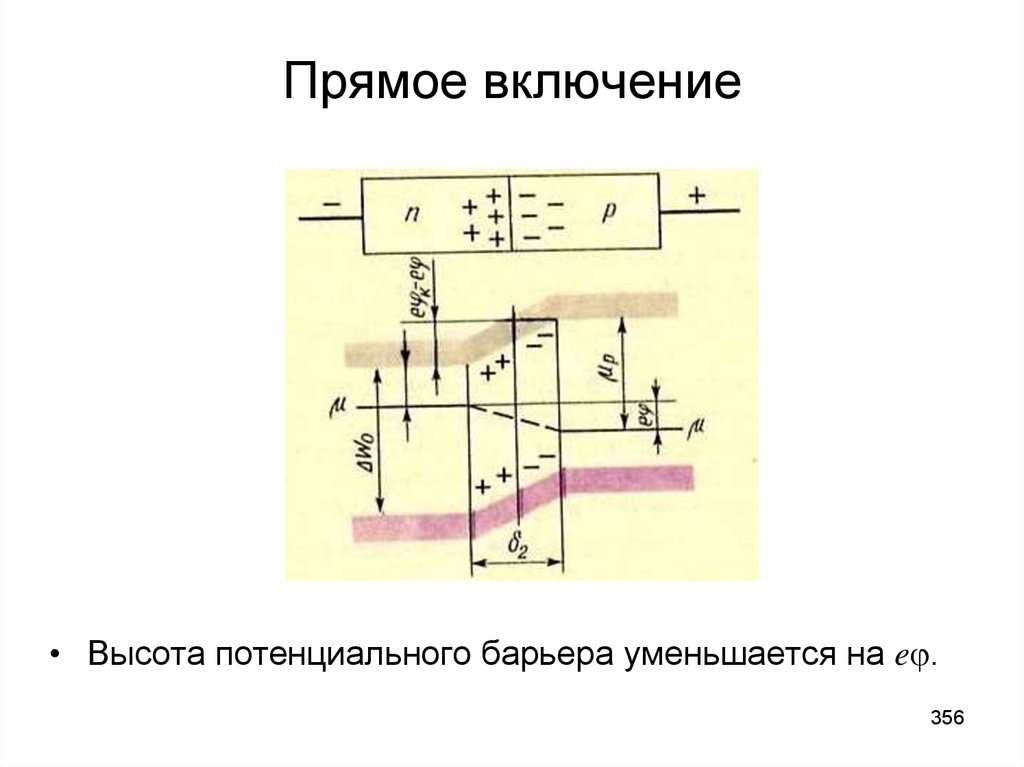
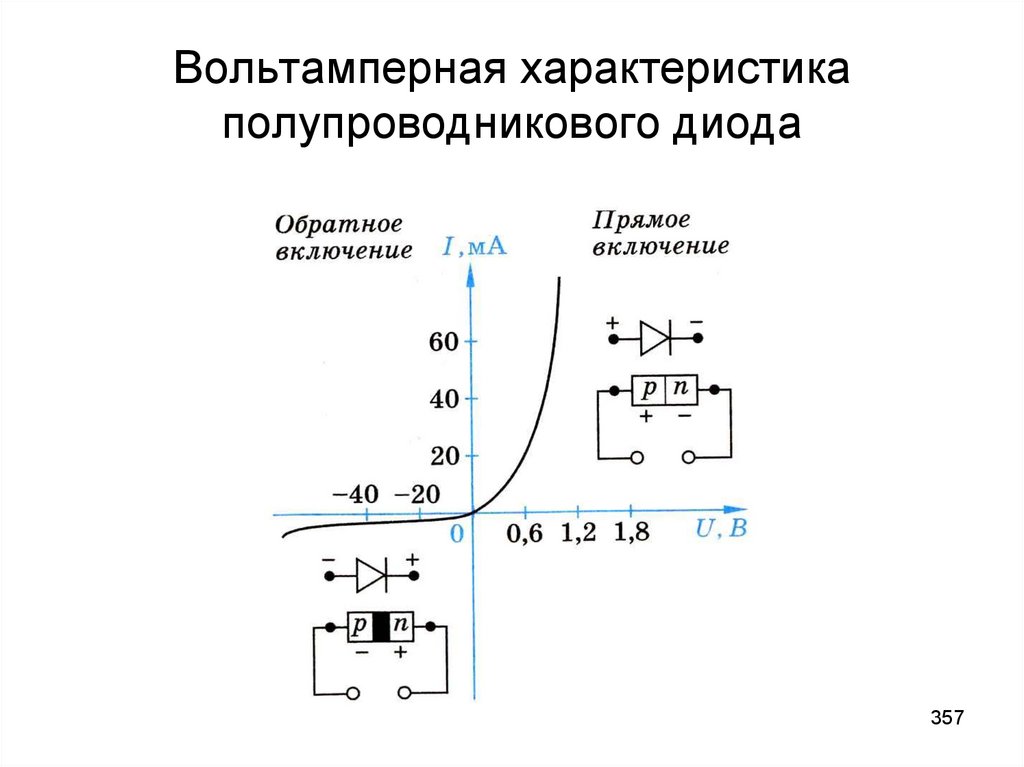

 Физика
Физика