Баскетбольный бросок через призму математики

1.

2.

Цель:
Исследовать баскетбольный бросок одной рукой
сверху с точки зрения математических и физических
представлений,
выявить
условия
эффективности
баскетбольного броска
Задачи:
1. Изучить основы техники баскетбольного броска одной рукой сверху.
2. Изучить элементы вычислительной математики, описывающие
движение баскетбольного мяча.
3. Изучить кинематику баскетбольного броска.
4. Провести и описать эксперимент, подтверждающий или
опровергающий выдвинутую гипотезу.
5. Продемонстрировать вычислительный аппарат математики как
универсальный инструмент описания реальных явлений и процессов.

3.

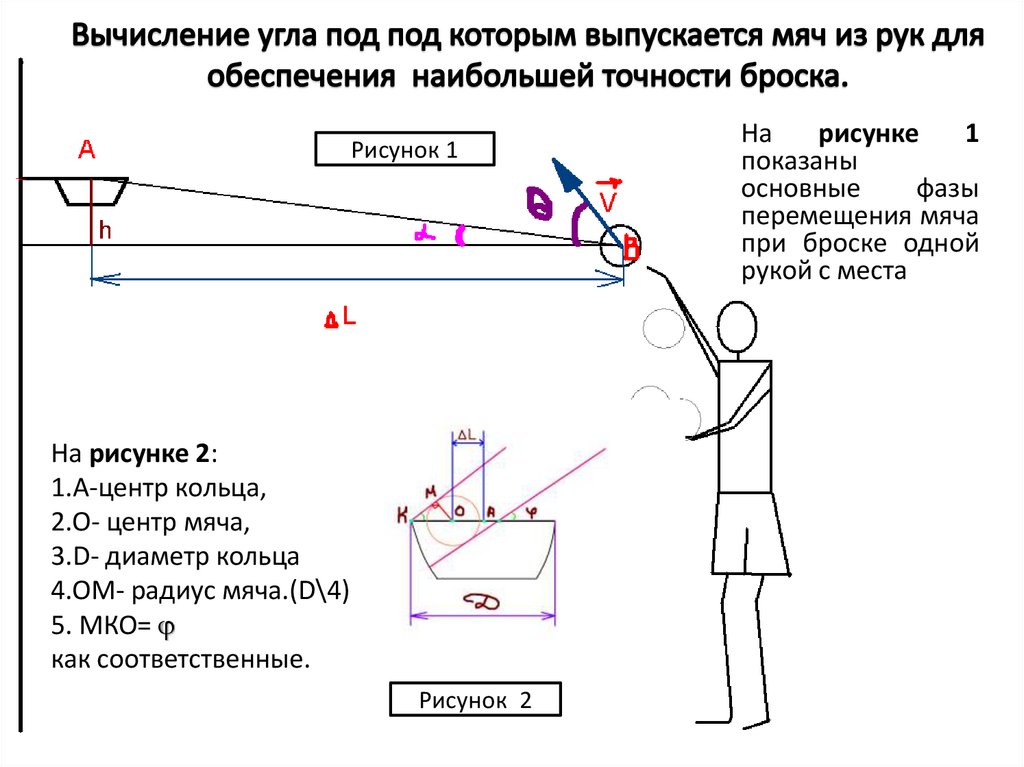
Рисунок 1
На рисунке 2:
1.А-центр кольца,
2.O- центр мяча,
3.D- диаметр кольца
4.OM- радиус мяча.(D\4)
5. МКО=
как соответственные.
Рисунок 2
На
рисунке
1
показаны
основные
фазы
перемещения мяча
при броске одной
рукой с места

4.

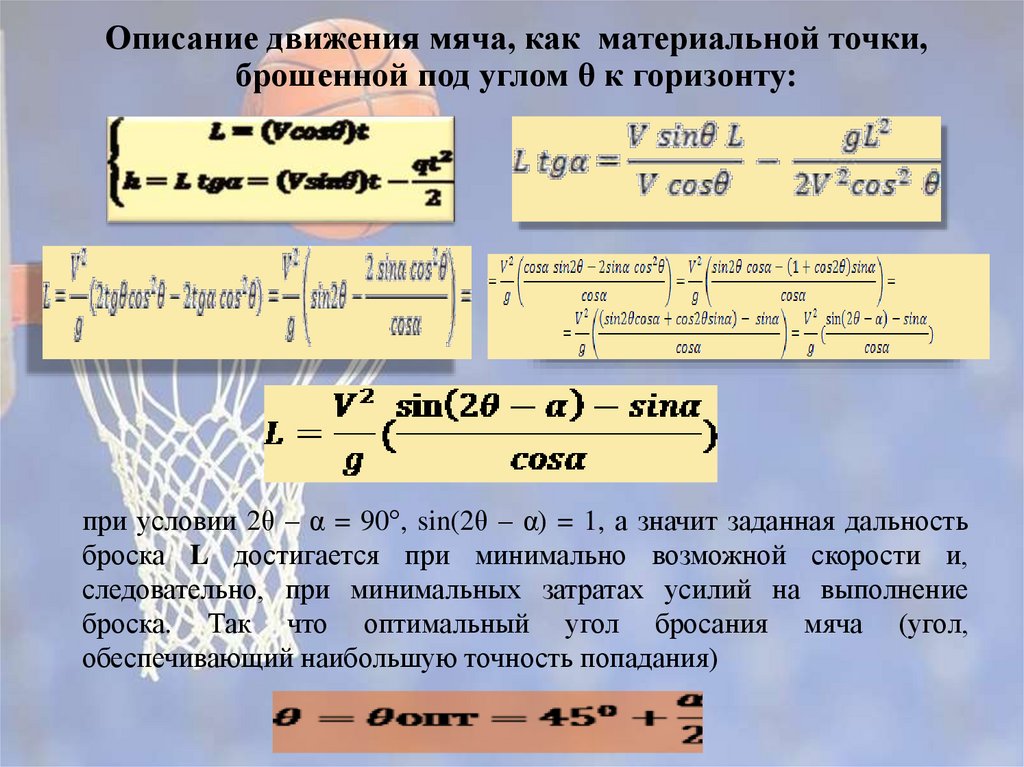
Описание движения мяча, как материальной точки,
брошенной под углом θ к горизонту:
при условии 2θ – α = 90°, sin(2θ – α) = 1, а значит заданная дальность
броска L достигается при минимально возможной скорости и,
следовательно, при минимальных затратах усилий на выполнение
броска. Так что оптимальный угол бросания мяча (угол,
обеспечивающий наибольшую точность попадания)

5.

Vsinθ – gt < 0 при выбранной системе координат,
следовательно Vsinθ – gt = - Vsinθ + gt , следовательно:
= arctg (tgθ – 2tgα) (3)

6.

С помощью тригонометрических преобразований находим:
Таким образом:
Это означает, что при α 30° бросок под углом θопт вообще не
будет точным, поскольку, при < ° мяч не может свободно
пройти сквозь кольцо.

7.

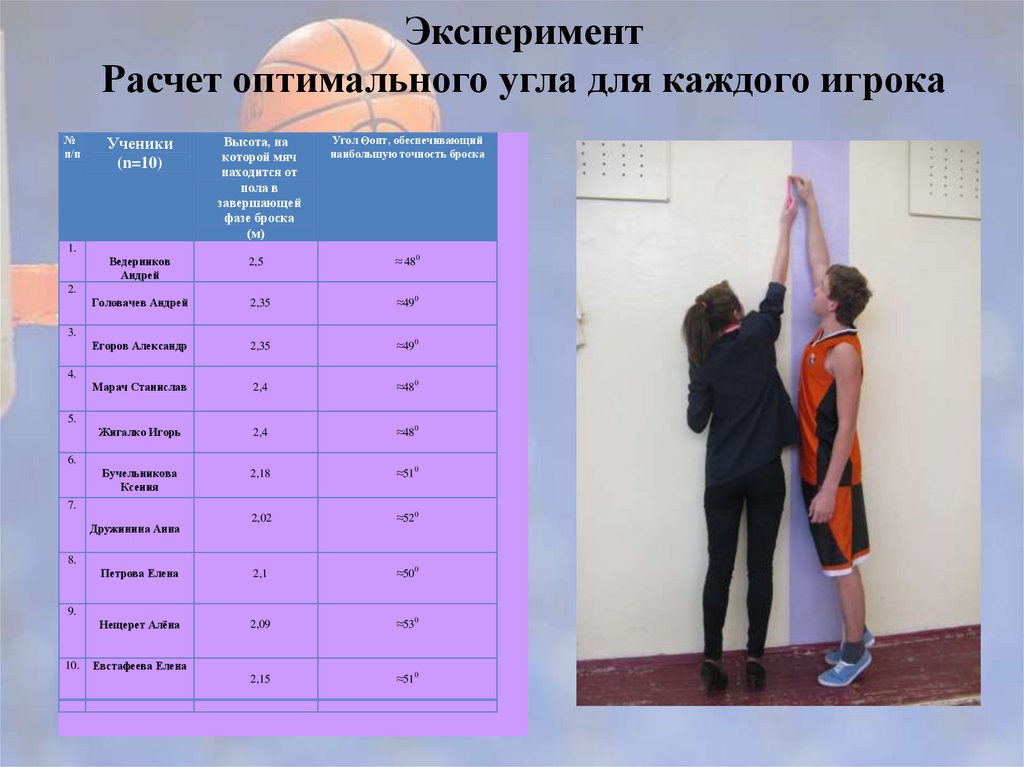
Эксперимент
Расчет оптимального угла для каждого игрока
№
п/п
Ученики
(n=10)
Высота, на
которой мяч
находится от
пола в
завершающей
фазе броска
(м)
Угол опт, обеспечивающий
наибольшую точность броска
Ведерников
Андрей
2,5
≈ 480
Головачев Андрей
2,35
≈490
Егоров Александр
2,35
≈490
Марач Станислав
2,4
≈480
Жигалко Игорь
2,4
≈480
Бучельникова
Ксения
2,18
≈510
2,02
≈520
Петрова Елена
2,1
≈500
Нещерет Алёна
2,09
≈530
2,15
≈510
1.
2.
3.
4.
5.
6.
7.
Дружинина Анна
8.
9.
10.
Евстафеева Елена

8.

Тренажер для повышения результативности броска
мяча в кольцо, созданный авторами проекта

9.

Проверка эффективности
полученных результатов с
помощью t – критерия
Стьюдента
количество результативных бросков
№
п/п
1.
ученики
(n=10)
Ведерников
вспомогательные
расчеты
В начале
эксперимента
(х)
В конце
эксперимента
(у)
d
5
11
6
6
9
3
6
10
4
5
9
4
8
12
4
5
8
3
6
11
5
4
10
6
6
9
3
7
10
3
5,8
8,8
4,1
Андрей
2.
Головачев
Андрей
3.
Егоров
Александр
4.
Марач
Станислав
5.
Жигалко
Игорь
6.
Бучельникова
Ксения
7.
Дружинина
Анна
8.
Петрова
Елена
9.
Нещерет
Алёна
10.
Евстафеева
Елена
Среднее
значение:
Если tэмп
tкрит, то нулевая
гипотеза отклоняется, откуда следует
возможность
принятия
альтернативной гипотезы Н1 о
достоверных
различиях
средних
арифметических т.е. делается вывод
об
эффективности
экспериментального воздействия. В
нашем случае tэмп = 10,8 , а tкрит =
4,780 (табл. Стьюдента), т.е. tэмп
tкрит,
следовательно
нулевая
гипотеза
Н0
отклоняется
и
принимается
альтернативная
гипотеза Н1, т.е. делаем вывод об
эффективности экспериментального
воздействия.