Термодинамические свойства газов

1. Термодинамические свойства газов

Идеальный газ – газ, свойства
уравнением Менделеева-Клапейрона
которого
описываются
pV = nRT
V, p, T – параметры состояния газа. Уравнение, связывающее их – уравнение состояния. Уравнение
Менделеева-Клапейрона не учитывает собственный объем молекул газа и межмолекулярное
взаимодействие. В идеальном газе столкновения молекул между собой и со стенками сосуда абсолютно
упругие.
Реальные газы при высоких давлениях занимают больший объем, чем занимал
бы идеальный газ в аналогичных условиях. Реальные газы описываются
уравнением состояния идеального газа только приближенно, и отклонения от
идеального поведения становятся заметными при высоких давлениях и низких
температурах, особенно когда газ близок к конденсации. Наглядная
характеристика отклонения реальных газов от идеального поведения
оказывается мольный объем газа Vm = V/n

2.

V идеального газа при 101325 Па и 273 K = RT/p =
22.41 л/моль (закон Авогадро)
Газ
Vm, л/моль
Газ
Vm, л/моль
H2
22,43
CO2
22,26
He
22,43
N2O
22,25
Ne
22,42
H2O
22,14
F2
22,42
NH3
22,08
N2
22,40
Cl2
22,02
CO
22,40
SO2
21,89
O2
22,39
C4H10
21,50
CH4
22,36
O3
21,60

3.

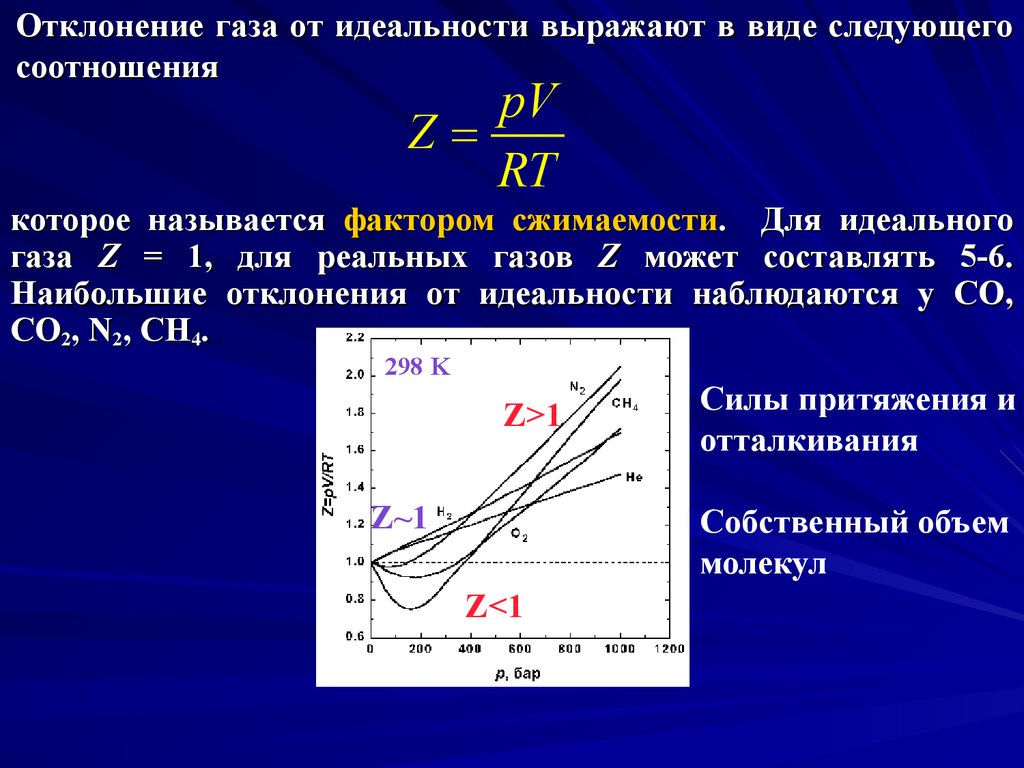
Отклонение газа от идеальности выражают в виде следующего
соотношения
pV
Z=
RT
которое называется фактором сжимаемости. Для идеального
газа Z = 1, для реальных газов Z может составлять 5-6.
Наибольшие отклонения от идеальности наблюдаются у CO,
CO2, N2, CH4.
298 K
Z>1
Z~1
Силы притяжения и
отталкивания
Собственный объем
молекул
Z<1

4.

Неидеальное поведение газа появляется тогда, когда расстояние между
молекулами (I) становится сравнимо с их размерами (Im)

5.

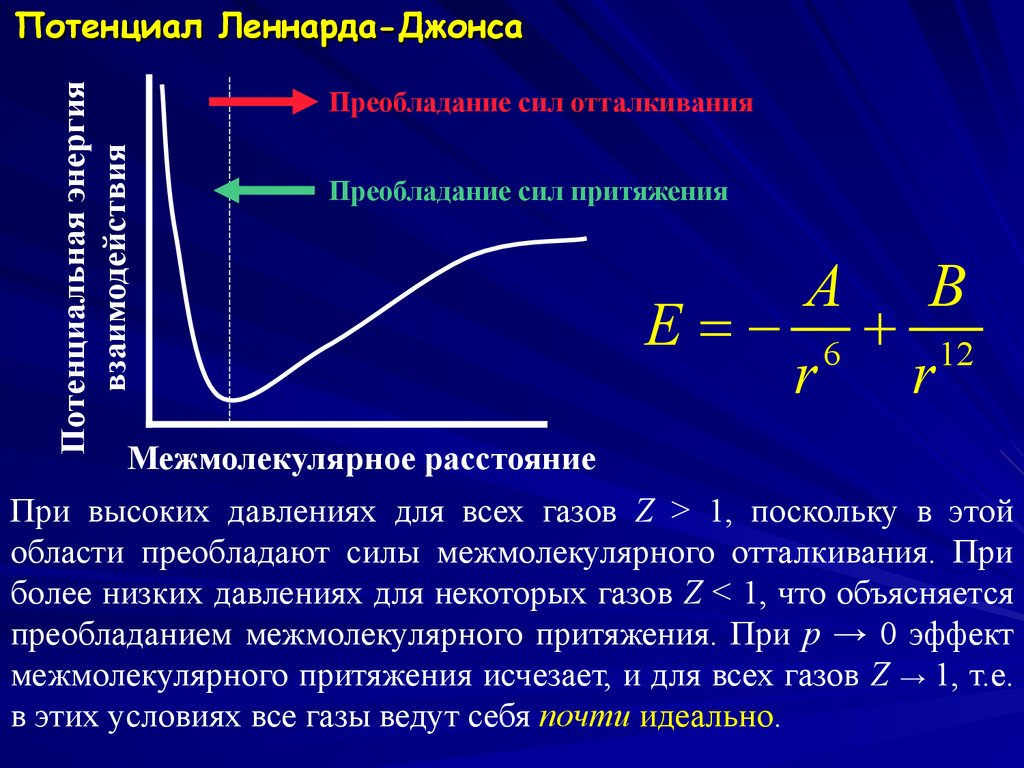
Потенциальная энергия
взаимодействия
Потенциал Леннарда-Джонса
Преобладание сил отталкивания
Преобладание сил притяжения
A B
E = 6 12
r
r
Межмолекулярное расстояние
При высоких давлениях для всех газов Z > 1, поскольку в этой
области преобладают силы межмолекулярного отталкивания. При
более низких давлениях для некоторых газов Z < 1, что объясняется
преобладанием межмолекулярного притяжения. При p → 0 эффект
межмолекулярного притяжения исчезает, и для всех газов Z → 1, т.е.
в этих условиях все газы ведут себя почти идеально.

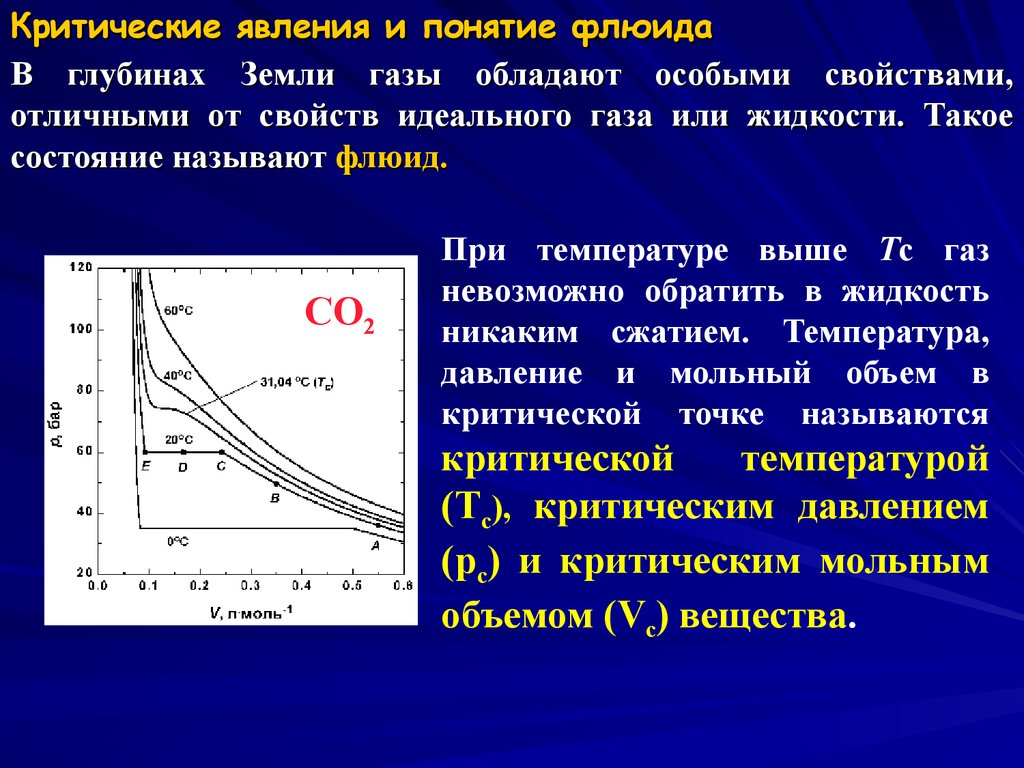
6. Критические явления и понятие флюида

В глубинах Земли газы обладают особыми свойствами,
отличными от свойств идеального газа или жидкости. Такое
состояние называют флюид.
CO2
При температуре выше Tc газ
невозможно обратить в жидкость
никаким сжатием. Температура,
давление и мольный объем в
критической точке называются
критической
температурой
(Tc), критическим давлением
(pc) и критическим мольным
объемом (Vc) вещества.

7.

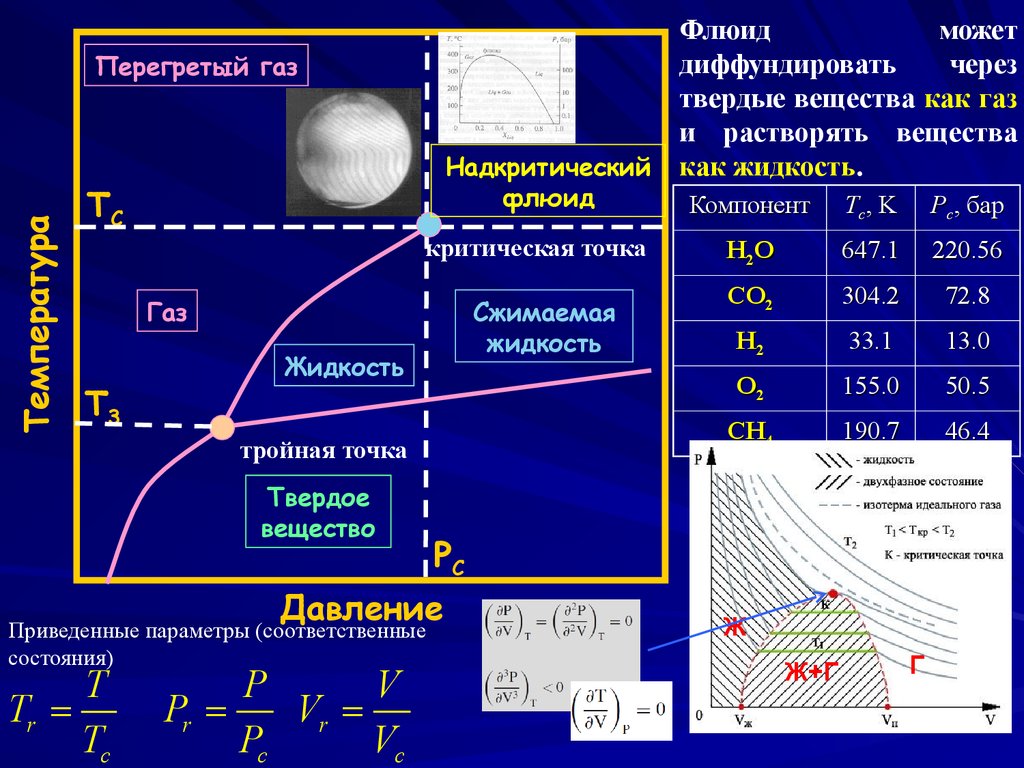
Флюид
может
диффундировать
через
твердые вещества как газ
и растворять вещества
Надкритический как жидкость.
Температура
Перегретый газ
флюид
TC
критическая точка
Газ
T3
Сжимаемая
жидкость
Жидкость
тройная точка
Твердое
вещество
T
Tr =
Tc
P
V
Pr =
Vr =
Pc
Vc
Tc, K
Pc, бар
H2 O
647.1
220.56
CO2
304.2
72.8
H2
33.1
13.0
O2
155.0
50.5
CH4
190.7
46.4
PC
Давление
Приведенные параметры (соответственные
состояния)
Компонент
Ж
Ж+Г
Г

8.

Для расчета молярной свободной энергии Гиббса (или
химического потенциала) чистой фазы i при давлении P
отличном от стандартного (Р0), т.е. Gi(T, P), мы использовали
формулу
P
Gi (T , P ) = Gi (T , P0 ) Vi dp
P0
где Vi – мольный объем компонента, который является
функцией давления и температуры.
Если фаза i – реальный газ, то Vi является сложной функцией
давления и температуры (уравнения состояния газов), и
интегрирование этих функций довольно сложно. Однако для
многих газов составлены справочные таблицы, данные в
которых получены из измерений соотношений T-P-V.

9.

Обычно эти данные включают фугитивность (fi) или
коэффициент фугитивности ( i). Фугитивность представляет
собой эффективное давление, которое заменяет реальное
давление в термодинамических уравнениях. Фугитивность
чистого газа i при давлении P определяется соотношением
P
RT ln f i = RT ln P (Vi V0 )dP
P0
где Vi – мольный объем чистого газа, а V0 – мольный объем
идеального газа при тех же условиях (RT/P).
Если газ идеальный, то fi = p. Если Vi отличается от объема
идеального газа, то необходимо ввести коэффициент
фугитивности
f i = P i

10.

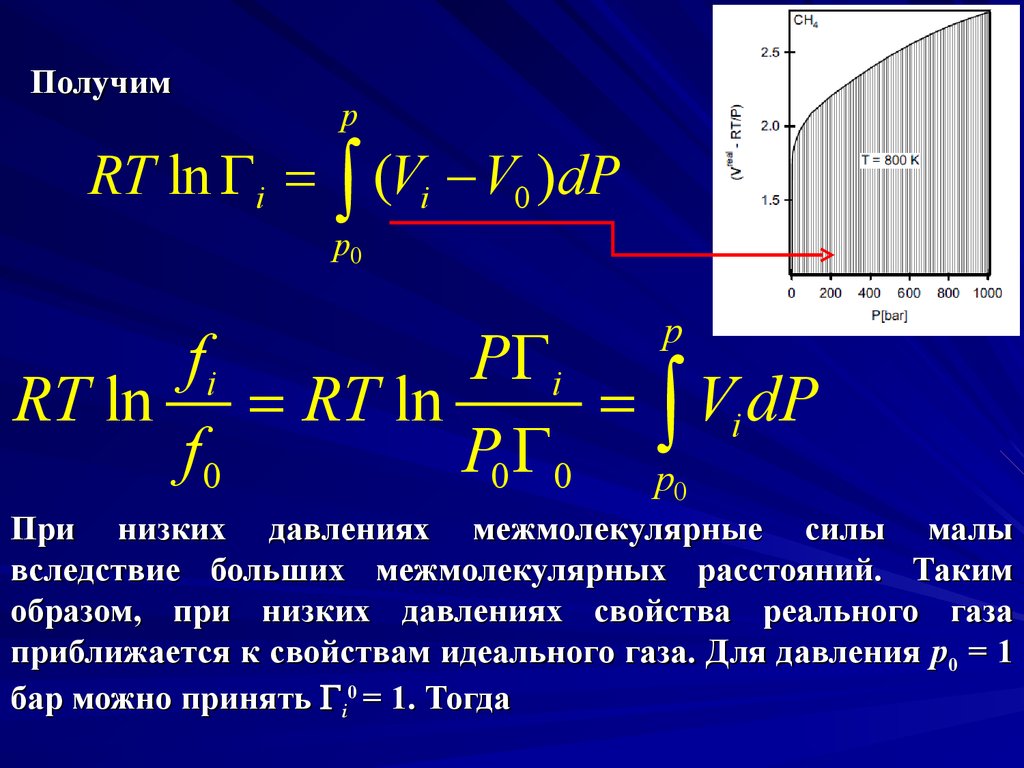
Получим
p
RT ln i = (Vi V0 )dP
p0
p
fi
P i
RT ln = RT ln
= Vi dP
f0
P0 0 p0
При низких давлениях межмолекулярные силы малы
вследствие больших межмолекулярных расстояний. Таким
образом, при низких давлениях свойства реального газа
приближается к свойствам идеального газа. Для давления p0 = 1
бар можно принять i0 = 1. Тогда

11.

p
RT ln f i = RT ln P i = Vi dP
p0
Таким образом, уравнение для свободной энергии Гиббса для
реального газа i можно переписать следующим образом
T
T
Gi = H 0 TS0 C p dT T
T0
T0
Cp
T
dT RT ln P i
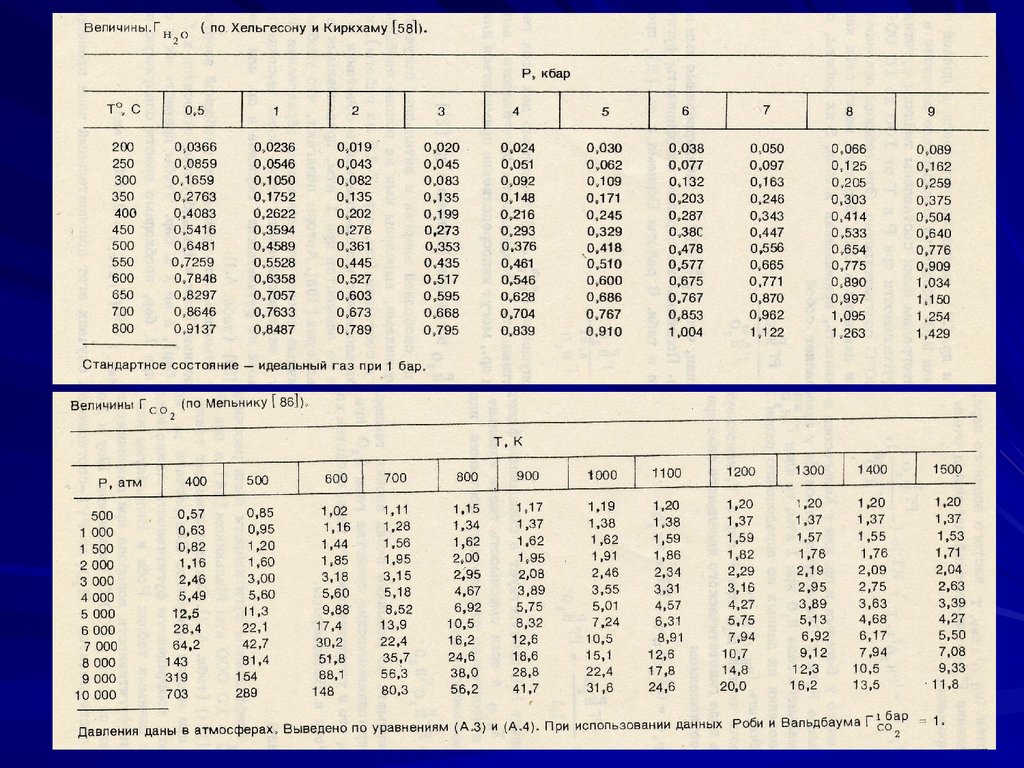
Значения коэффициентов фугитивности меняются в широких
пределах. Намечается следующий ряд коэффициентов
фугитивности для газов (Т = 1000 – 1200 K)
H2O < H2 < NH3 < O2 < H2S < CO2 CO N2 < CH4
Между крайними членами ряда отношение коэффициентов
фугитивности достигает 2-3 порядков. Например при 15 кбар и
1200 K
H2O = 3.101, а CH4 = 67.37

12.

13. Уравнения состояния реальных газов

Уравнение состояния вещества (УС) – это аналитическая
формулировка соотношений между объемом, температурой и
давлением.
f ( P, V , T ) = 0
Наиболее простым УС является уравнение состояния идеального газа (уравнение
Менделеева-Клапейрона), непригодное для описания свойств реальных газов при
повышенных давлениях. Уже при небольших давлениях сказывается влияние
межмолекулярных сил отталкивания и притяжения.
Одним из наиболее ранних является уравнение Ван-дер-Ваальса (1873)
a
( P 2 )(V b) = RT
V
Йоханнес Ван-дер-Ваальс

14.

Константа a в этих уравнениях отражает межмолекулярное взаимодействие, главным
образом способность к взаимному притяжению молекул данного газа. Притяжение
молекул приводит к возникновению дополнительного давления на газ, которое
называется внутренним давлением. Его величина пропорциональная квадрату
молярного объема газа.
Константа b характеризует собственный объем молекул и взаимное отталкивание на
близких расстояниях. Объем b равен учетверенному собственному объему молекул.
Значения констант a и b не зависят от температуры, а зависят только от природы газа.
Константы для уравнения Ван-дер-Ваальса известны для большинства газов. Однако
уже выше 500 бар расчетные значения объема отличаются от экспериментальных.
Газ
a, л2бар/моль2
b, см3/моль
CO2
3.640
42.67
H2 O
5.536
30.49
CH4
2.283
42.78
H
0.2476
26.61

15.

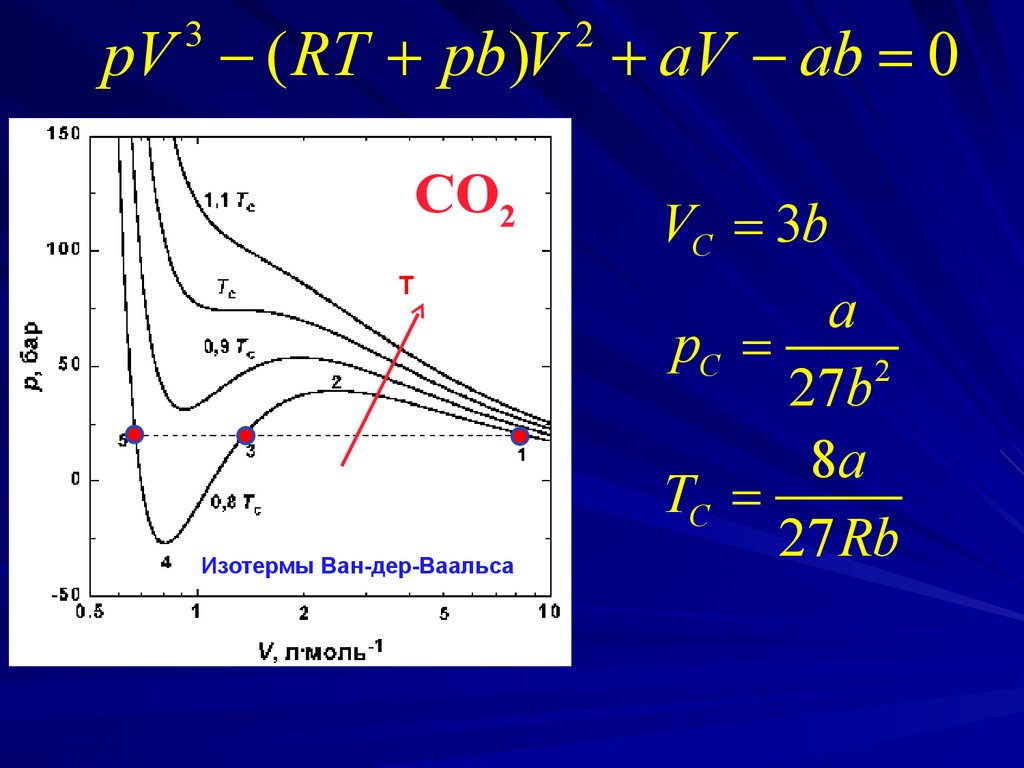
pV ( RT pb)V aV ab = 0
3
2
CO2
T
Изотермы Ван-дер-Ваальса
VC = 3b
a
pC =
2
27b
8a
TC =
27 Rb

16.

RT
b
2a
ln f = ln
V b V b RTV
Принципиальное
значение
уравнения
Ван-дер-Ваальса
определяется следующими обстоятельствами:
1) уравнение было получено из модельных представлений о
свойствах реальных газов и жидкостей;
2) с помощью уравнения Ван-дер-Ваальса впервые удалось описать
явление перехода газа в жидкость и проанализировать критические
явления.
Известны другие уравнения с двумя константами a и b,
например уравнение Редлиха-Квонга
a
( P 0.5
)(V b) = RT
T V (V b)
b
a
RT
a
V
ln f =
ln
ln
1.5
1.5
V b RT (V b)
V b bRT
V b

17.

Вириальные уравнения
PV
2
3
Z=
= 1 B C D ...
RT
где - плотность, B, C, D – вириальные коэффициенты, зависящие от
температуры и природы рассматриваемого газа. B учитывает
взаимодействие между двумя молекулами, С – между тремя и т.д.
PV
Z=
= A BPr CPr2 DPr3 ...
RT
Полиномиальные уравнения (Holland & Powell, 1990)
RT ln f = ( A BT CT )
2
где A, B, C – функции давления.

18.

Закон соответственных состояний (ЗСС)
Поскольку критические константы являются характеристическими
свойствами газов, их можно использовать для создания
соответствующей относительной шкалы, введя безразмерные
приведенные переменные: приведенное давление, приведенный
объем и приведенную температуру.
Vm
Vr =
VC
p
pr =
pC
T
Tr =
TC
CH4
N2

19.

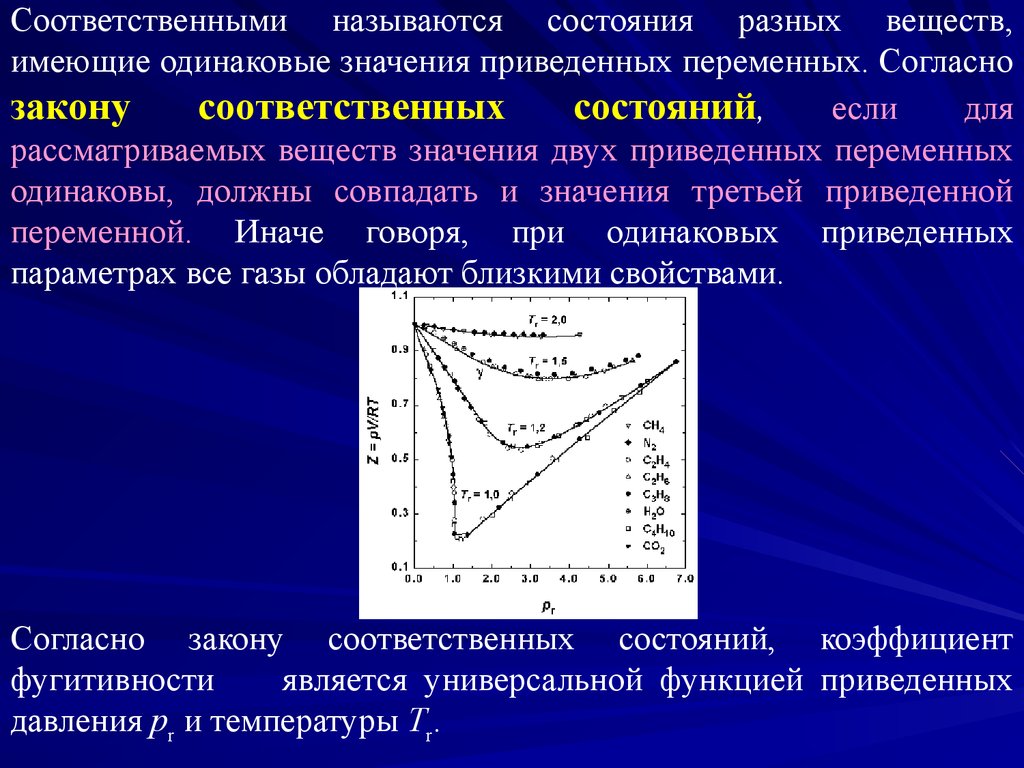
Соответственными называются состояния разных веществ,
имеющие одинаковые значения приведенных переменных. Согласно
закону
соответственных
состояний,
если
для
рассматриваемых веществ значения двух приведенных переменных
одинаковы, должны совпадать и значения третьей приведенной
переменной. Иначе говоря, при одинаковых приведенных
параметрах все газы обладают близкими свойствами.
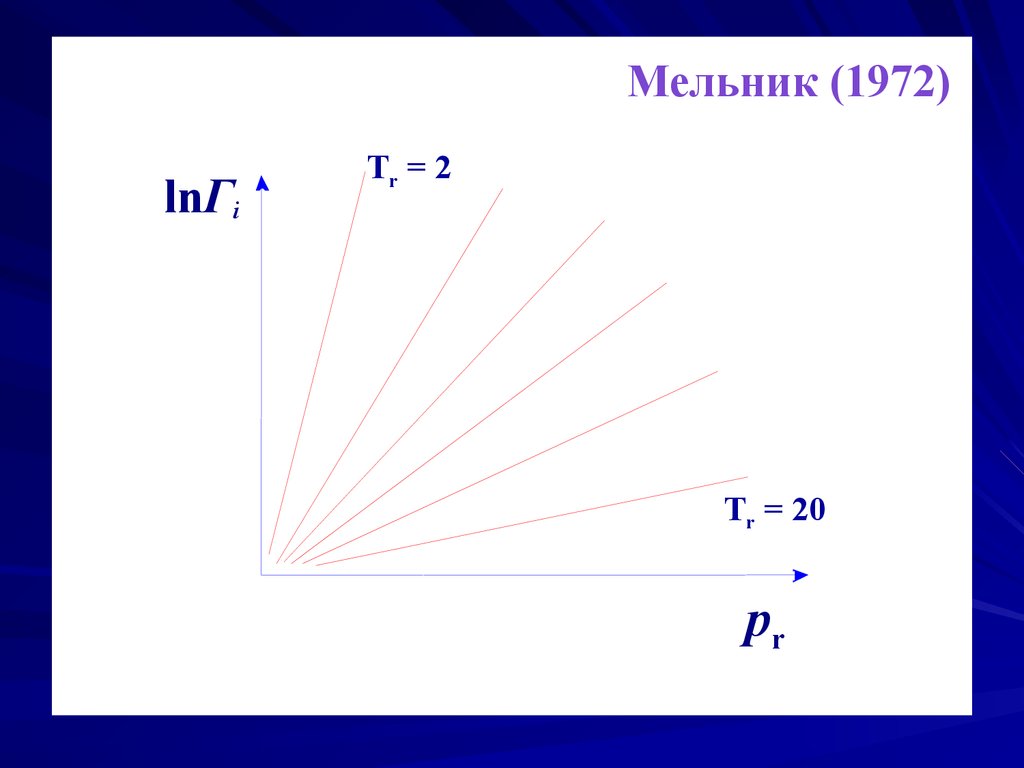
Согласно закону соответственных состояний, коэффициент
фугитивности
является универсальной функцией приведенных
давления pr и температуры Tr.

20.

Мельник (1972)
lnΓi
Tr = 2
=const
Tr = 20
pr

21.

О точности закона можно судить по значению критического
коэффициента
pCVC
ZC =
RTC
Если бы закон соответственных состояний выполнялся абсолютно
точно, то этот коэффициент был бы одинаков для всех веществ.
Однако это не совсем так.
Вещество
pcVc / RTc
Вещество
pcVc / RTc
He
0,300
СО2
0,287
H2
0,304
N2
0,292
Ne
0,296
O2
0,292
Ar
0,291
CH4
0,300
ЗСС не может рассматриваться как всеобщий. Он служит как основа
для классификации веществ по термодинамическим свойствам и
может использоваться для прогнозирования свойств неизученных
веществ.

22.

СО2
линейная молекула O=C=O
отсутствует дипольный момент
Критическая точка: 31.1ОС, 7.36 МПа
Шмонов, Шмулович (1975)
VCO2 = 17.771 25.28856 lg( P 1233) 0.1479286T
3
см
27.40306 lg( P 1447) 0.0354434T lg( P 1447)
Перчук, Карпов (1975)
моль
.

23.

H2О
+
1.515 Å
-
Burnham et al. (1969)
4
85
0.9
Å
нелинейная молекула H=O=H (105OC)
значительный дипольный момент
(способствует растворению ионных
соединений)
Критическая точка: 374.1ОС, 22 МПа

24.

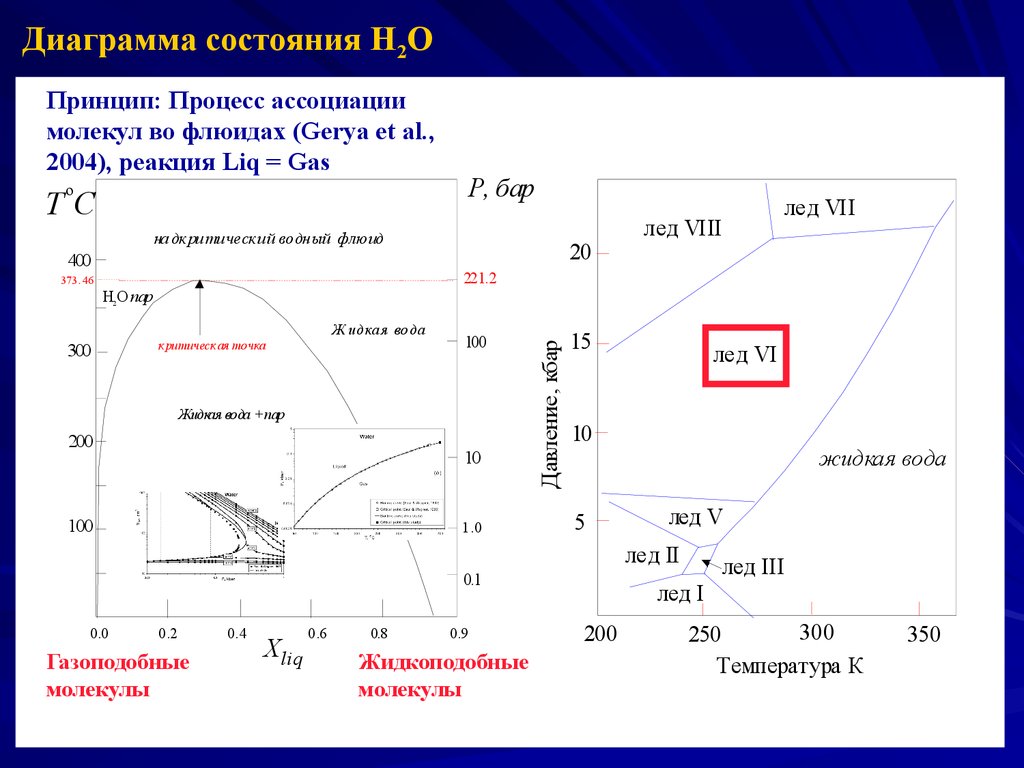
Диаграмма состояния H2O
Принцип: Процесс ассоциации
молекул во флюидах (Gerya et al.,
2004), реакция Liq = Gas
Р, бар
о
ТС
на дк ри тическ ий водный флю ид
400
20
лед VII
лед VIII
221.2
373 . 46
Ж идкая вода
300
к ритическ ая точка
100
Жидкая вода + пар
200
10
100
1.0
Давление, кбар
Н2 О пар
15
лед VI
10
5
жидкая вода
лед V
лед II
0.1
0.0
0.2
Газоподобные
молекулы
0.4
Хliq
0.6
0.8
0.9
Жидкоподобные
молекулы
лед III
лед I
200
300
250
Температура К
350

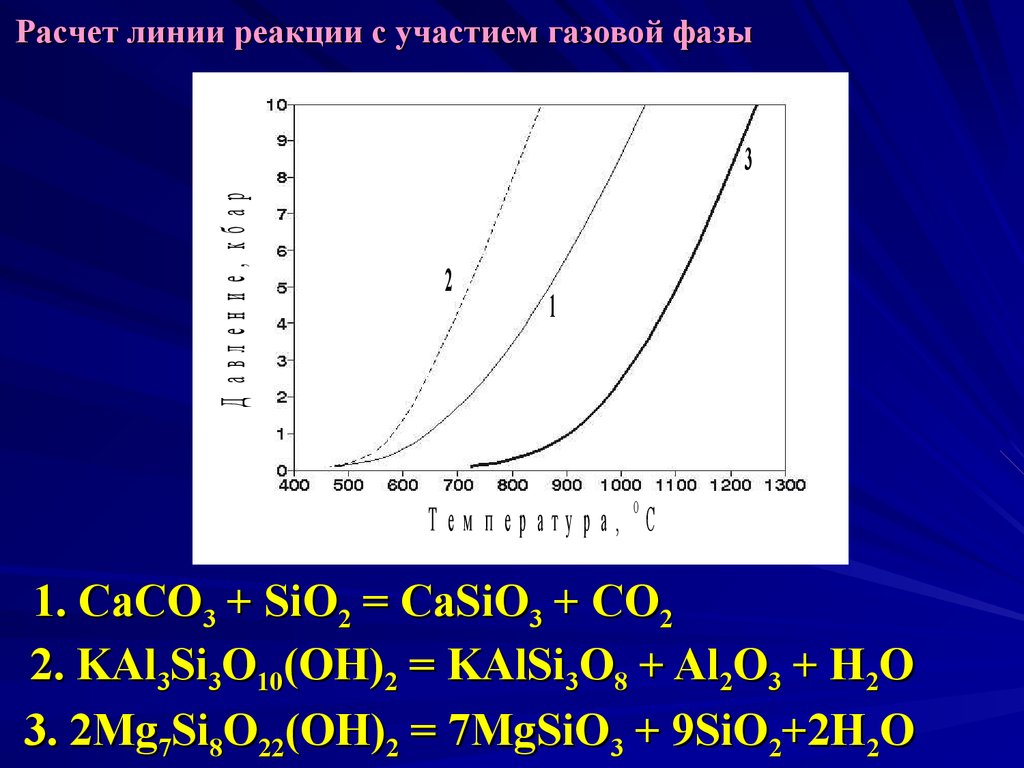
25. Расчет линии реакции с участием газовой фазы

Д авлен ие, кбар
3
2
1
О
Т ем п ер атура, С
1. CaCO3 + SiO2 = CaSiO3 + CO2
2. KAl3Si3O10(OH)2 = KAlSi3O8 + Al2O3 + H2O
3. 2Mg7Si8O22(OH)2 = 7MgSiO3 + 9SiO2+2H2O

26.

Рассмотрим реакцию (1). Условие равновесия этой реакции
запишется следующим образом:
T
T
T0
T0
DG = DH 0 T DS0 DC p dT T
где
DC p
T
p
dT DVdP = 0
p0
DH 0 = D f H 0Wol D f H 0CO2 D f H 0Cal D f H 0Qtz
DS0 = S 0Wol S 0CO2 S 0Cal S 0Qtz
DCP = CPWol CPCO2 CPCal CPQtz
Интеграл по объему можно разбить на две составляющие
p
p
p
DVdP = DV dp V
S
p0
где
p0
CO2
p0
p
p
p0
p0
dP = DVS dP RT ln f CO2 = DVS dP RT ln P CO2
DVS = V 0Wol V 0Cal V 0Qtz
а fCO2 и CO2 – фугитивность и коэффициент фугитивности газа при заданных Т
и Р.

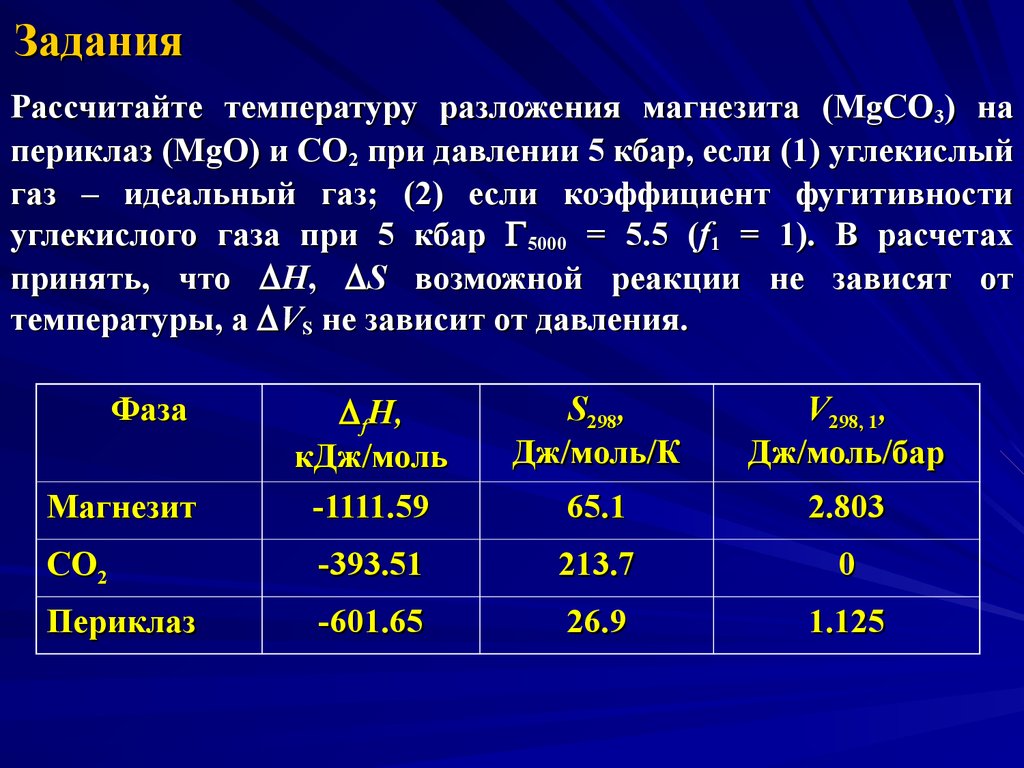
27. Задания

Рассчитайте температуру разложения магнезита (MgCO3) на
периклаз (MgO) и CO2 при давлении 5 кбар, если (1) углекислый
газ – идеальный газ; (2) если коэффициент фугитивности
углекислого газа при 5 кбар 5000 = 5.5 (f1 = 1). В расчетах
принять, что D H, D S возможной реакции не зависят от
температуры, а D VS не зависит от давления.
D fH,
кДж/моль
-1111.59
S298,
Дж/моль/К
V298, 1,
Дж/моль/бар
65.1
2.803
CO2
-393.51
213.7
0
Периклаз
-601.65
26.9
1.125
Фаза
Магнезит

28.

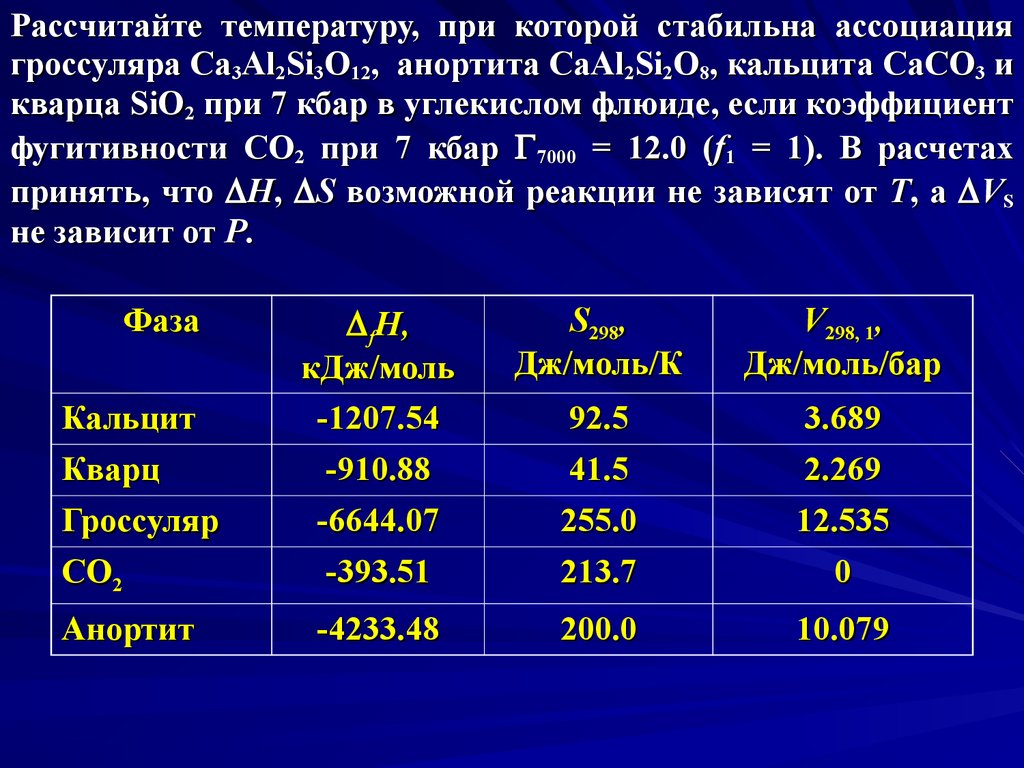
Рассчитайте температуру, при которой стабильна ассоциация
гроссуляра Ca3Al2Si3O12, анортита CaAl2Si2O8, кальцита CaCO3 и
кварца SiO2 при 7 кбар в углекислом флюиде, если коэффициент
фугитивности CO2 при 7 кбар 7000 = 12.0 (f1 = 1). В расчетах
принять, что D H, D S возможной реакции не зависят от T, а D VS
не зависит от P.
Фаза
Кальцит
Кварц
Гроссуляр
CO2
Анортит
D fH,
кДж/моль
-1207.54
-910.88
-6644.07
-393.51
S298,
Дж/моль/К
V298, 1,
Дж/моль/бар
92.5
41.5
3.689
2.269
255.0
213.7
12.535
0
-4233.48
200.0
10.079

29.

30.

Линия реакции дегидратации при высоких давлениях
A B + H2O
Р
dP/dT < 0
dP/dT =
A
B + H2 O
dP/dT > 0
T

31.

Линия реакций декарбонатизации при высоких давлениях
Р, ГПа
11
1
2
3
4
- En + 2Ms = 2Fo + 2CO2
- Dol + 2Cs = Di + 2CO2
- 2Ms + 2Cs = En + 2CO2
- 3Ms + Ky + 2Cs = Prp + 3CO2
4
9
7
3
dP/dT > 0
2
5
3
1000
1
1200
1400
1600
TОС

32. Кислородные буферы

HM (гематит-магнетит)
NNO (Ni-NiO)
QFM (кварц-фаялит-магнетит)
WM (вюстит-магнетит)
IW (железо-вюстит)
2Fe3O4+1/2O2 = 3Fe2O3
Ni+1/2O2 = NiO
3Fe2SiO4+O2 = 2Fe3O4+3SiO2
3FeO+1/2O2 = Fe3O4
Fe+1/2O2 = FeO

33.

Рассмотрим метод расчета fО2 в реакциях окисления металлов (Ме).
m(a 1) n(m a )
nMea 1Om a
O2 = (a 1) MenOm
2
В качестве примера произведем расчет реакции окисления
магнетита (Mag) c образованием гематита (Hem) (буфер HM)
2Fe3O4 + 1/2O2 = 3Fe2O3
при РS = 1 бар
и
Т = 800 К c использованием базы
термодинамических данных (Holland, Powel, 1998):
0
0
DVS0 = 3VHem
2VMag
= 4.026 кал/бар
0
0
0
DG800
= 3GHem
2GMag
0.5GO0 2 = -31040.364 кал
1 RT ln f = DG 0 DV P ,
O2
800
S S
2
откуда
0
DG800
DVS PS
-31040 4.026
lg f O2 =
=
16.96
0.5 × 2.303RT
0.5 × 2.303 ×1.987 × 800
f O2 = 10 16.96 бар

34.

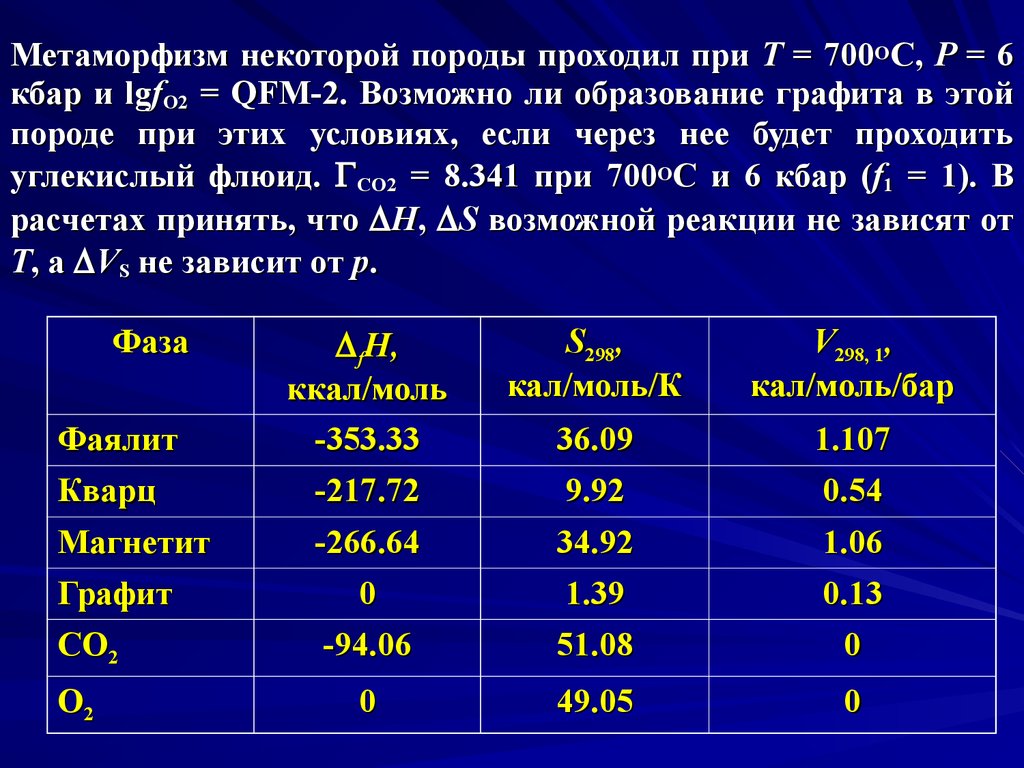
Метаморфизм некоторой породы проходил при Т = 700ОС, Р = 6
кбар и lgfO2 = QFM-2. Возможно ли образование графита в этой
породе при этих условиях, если через нее будет проходить
углекислый флюид. СO2 = 8.341 при 700ОС и 6 кбар (f1 = 1). В
расчетах принять, что D H, D S возможной реакции не зависят от
T, а D VS не зависит от p.
Фаза
Фаялит
Кварц
Магнетит
Графит
CO2
O2
D fH,
ккал/моль
-353.33
-217.72
-266.64
0
-94.06
S298,
кал/моль/К
V298, 1,
кал/моль/бар
36.09
9.92
1.107
0.54
34.92
1.39
51.08
1.06
0.13
0
0
49.05
0