Монополистическая конкуренция с неоднородным трудом

1.

Монополистическая конкуренция
с неоднородным трудом
Филатов А.Ю., Соколовский Ю.М.
(ДВФУ, ИГУ)
[email protected], [email protected],
http://sibscience.org, http://vk.com/baikalreadings,
http://youtube.com/sibscience
Дальневосточный федеральный университет, 3.11.2016
1

2.

Монополистическая
конкуренция
2
Чемберлин’ 1933: реальные рынки существуют между совершенной конкуренцией и монополией
Идеи:
1. Фирмы продают продукты, не являющиеся совершенными заменителями.
2. Фирмы производят единственный вид продукта с возрастающей отдачей
от масштаба и в состоянии назначать цену выше предельных издержек.
3. Число фирм в отрасли достаточно большое, чтобы каждая фирма занимала небольшой объем рынка.
4. На рынке существует свободный вход и выход, прибыль фирм – нулевая.
Диксит-Стиглиц’ 1977:
1. Любовь потребителей к разнообразию (моделируется через CES-функцию
полезности).
2. Возрастающая отдача от масштаба (моделируется через функцию издержек
TC = F + cq).
Недостаток: предположение об однородных фирмах модель Мелица’ 2003.

3.

Модель Диксита-Стиглица
1.
2.
3.
4.
5.
6.
7.
8.
9.
3
Экономика состоит из двух секторов: сельскохозяйственного (традиционного) и промышленного (современного).
В сельском хозяйстве однородный продукт A производится с постоянной
отдачей от масштаба и продается на совершенно конкурентном рынке.
В промышленном секторе производится n разновидностей горизонтально
дифференцированного продукта M с возрастающей отдачей от масштаба.
L потребителей (они же рабочие), чьи предпочтения идентичны и задаются
на верхнем уровне функцией полезности Кобба-Дугласа u M A1 .
Функция полезности нижнего уровня имеет постоянную эластичность
замещения (CES-функция):
Все L рабочих разделяются на αL промышленных и (1–α)L сельскохозяйственных.
Потребности фирмы промышленного сектора в труде: l f cq.
Суммарные издержки на оплату труда (других издержек нет): TC wl.
В сельском хозяйстве f A 0, c A 1, p A 1, wA 1.

4.

Задача потребителя
1
4
1
n
n 1
,
CES-функция полезности: M qi qi
i 1
i 1
0; 1 , 1; , 1 1 , 1 .
Крайние случаи:
= 0, =1 – независимые товары, функция полезности Кобба-Дугласа: M qi
= 1, – совершенные заменители, линейная функция полезности: M qi
Задача потребителя – максимизация полезности от приобретения дифференцированного продукта при условии, что на него тратится доля дохода I:
n
1
q
i 1
i
max,
n
pq
i 1
i i
I .
Функция Лагранжа:
n
q
i 1
i
1
n
I pi qi max,
i 1
qi p j
.
q j pi
1 1
qi pi ,

5.

Задача фирмы
5
Задача фирмы – максимизация прибыли:
i pi qi w f cqi qi pi wc wf max .
pi
Большое число участников рынка цена, установленная j-фирмой,
не влияет на спрос i-фирмы qi const * pi .
i const * pi pi wc wf max ,
1 pi pi 1wc 0,
pi1 pi wc max ,
pi
pi
pi p*
wc.
1
В долгосрочном равновесии прибыль всех фирм равна нулю:
f 1
1 wf , qi q*
.
i qi pi wc wf 0, qi wc
c
1
Размер фирмы (по числу рабочих) и число фирм:
L
li l* f cqi f f 1 f , n*
.
f
Равновесный уровень заработной платы (из баланса предл. и спроса в с/х):
1 L *1 1 Lw 1 L *1 ,
w*
1
.
1

6.

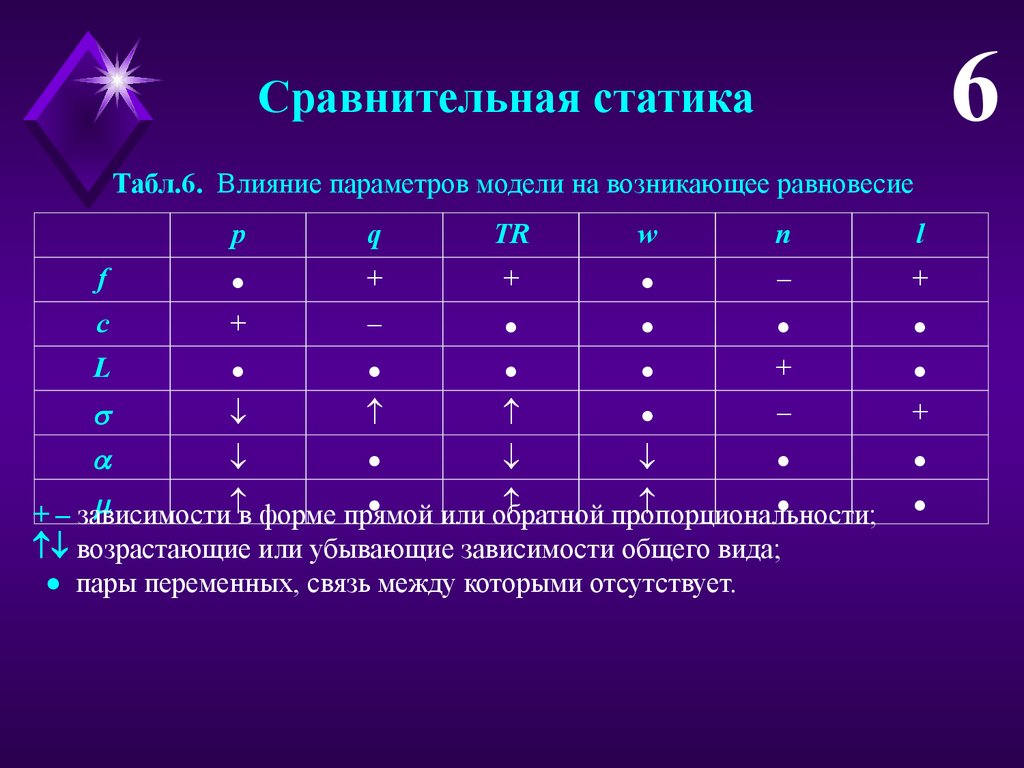
6
Сравнительная статика
Табл.6. Влияние параметров модели на возникающее равновесие
p
q
TR
w
n
l
+
+
–
+
c
+
–
L
+
–
+
f
в форме прямой
+ – зависимости
или обратной
пропорциональности;
возрастающие или убывающие зависимости общего вида;
пары переменных, связь между которыми отсутствует.

7.

Модель с неоднородным трудом
1.
2.
3.
4.
5.
6.
7.
8.
9.
7
Экономика состоит из двух секторов: сельскохозяйственного (традиционного) и промышленного (современного).
В сельском хозяйстве однородный продукт A производится с постоянной
отдачей от масштаба и продается на совершенно конкурентном рынке.
В промышленном секторе производится континуум [0, n] разновидностей
горизонтально дифференцированного продукта M с возрастающей отдачей от масштаба. i – индекс, характеризующий разновидность.
L потребителей (они же рабочие), чьи предпочтения идентичны и задаются
на верхнем уровне функцией полезности Кобба-Дугласа u M A1 .
Функция полезности нижнего уровня – CES-функция.
L рабочих делятся на промышленных различной квалификации c(i) и
однородных сельскохозяйственных. Доли и распределение квалификации
заданы.
Потребности фирмы промышленного сектора в труде: l i f c i q i .
Суммарные издержки на оплату труда (других издержек нет): TC i w i l i .
В сельском хозяйстве f A 0, c A 1, p A 1, wA 1.

8.

1
1
n
n
1
M
q
i
d
q
i
d
i
,
01
0
0
;
,
1
;
,
1
,
1
.
M
q
i
n
n
n0q
0 iq
1
p1 ijd i
ij
a.
m
xI, n0 0p i qd
Im
1
1
ax, qi p i .
Задача потребителя
CES-функция полезности:
Крайние случаи:
0, 1 – независимые товары, функция полезности Кобба-Дугласа:
1, – совершенные заменители, линейная функция полезности:
8
Задача потребителя – максимизация полезности от приобретения дифференцированного продукта при условии, что на него тратится доля дохода I:
Функция Лагранжа:

9.

i j pw ij i cp f 1 c wwwi cqji ic 0 , wi, p qp wif w
j m cp a iix 1 c c ,wij oi n c swt 11* .i 1p f
c 1 ji f
qcppqonii sq t *i
w
i qw
m
., i cqi
p a
w
ifw
ix
m
a
,
p
fix
c
1
.
i
l f cq f 1 f .
Задача фирмы
9
Задача фирмы – максимизация прибыли:
Большое число участников рынка цена, установленная на один товар,
не влияет на спрос на другой товар
В долгосрочном равновесии прибыль всех фирм равна нулю:
Связь заработной платы и производительности труда:
Размер фирмы по числу рабочих:

10.

c
i
c
.
1
,
1
2
pk W
,w
w
c
p
w
c
,
n
L
f
,
n
L
f
1q
1
2
2
1
1
2
2
1
1
2 , w21Lqwk 2 1f1 L, 1 1 2w1L 1k221 , 1Lw 2 1T R 1 1w2C 2 01 L , k 1w1 1 f 12w . ,Tl1R112 L 1 C .2.w,
f11 1 1 L w
Модель с двумя типами
промышленных рабочих
10
L рабочих делятся на
α1 L высококвалифицированных промышленных,
α2 L низкоквалифицированных промышленных,
α3L= (1–α1–α2) сельскохозяйственных.
Полученные параметры равновесия:
Суммарный доход населения:
Равновесный уровень заработной платы (из баланса предл. и спроса в с/х):

11.

11
Сравнительная статика
Табл.1. Влияние параметров модели на возникающее равновесие
p1
p2
q1
q2
TR1
TR2
w1
w2
n1
n2
l
+
+
+
+
+
–
–
+
c
+
–
–
–
+
L
+
–
–
+
1
+
+
2
+ – зависимости
пропорциональности;
в форме
прямой
или
обратной
возрастающие или убывающие зависимости общего вида;
пары переменных, связь между которыми отсутствует.
f

12.

Сравнительная статика
1.
2.
3.
4.
5.
6.
12
Рост постоянных издержек приводит к укрупнению фирм и сокращению их
числа, но не влияет на цены, зарплаты и суммарные продажи.
Увеличение переменных издержек, напротив, повышает цены и сокращает
поставки фирм.
Рост населения пропорционально увеличивает число фирм и разнообразие
продукции, не влияя более ни на что.
Рост различий между секторами приводит к сокращению производства неэффективного сектора, росту цен в обоих секторах и увеличению дифференциации заработных плат.
Усиление взаимозаменяемости модификаций товара обостряет конкуренцию. Фирмы снижают цены и расширяют поставки продукции, увеличивается дифференциация зарплат. При этом обороты фирм неэффективного сектора изменяются немонотонно: сначала (разновидности можно считать независимыми товарами) падают, а затем (по мере приближения к совершенным заменителям) начинают расти.
Расширение одного из промышленных секторов роняет цены и зарплаты во
всей промышленности, рост спроса на мануфактурный товар действует противоположным образом.

13.

Модификация с фиксированным
уровнем заработной платы
13
Институциональные ограничения, не позволяющие разграничивать эффективных и неэффективных рабочих (Echazu, Lugovskyy’ 2007):
1. Централизованно зафиксированный уровень зарплаты (ЕТС).
2. Действия профсоюзов.
3. Отсутствие у фирмы информации о качестве конкретного работника на момент заключения контракта.
Схема стимулирования высококвалифицированных рабочих:
1. Зарплата установлена на едином низком уровне.
2. Прибыль неэффективных фирм равна нулю.
3. Прибыль эффективных фирм положительна.
4. За счет прибыли эффективные фирмы платят премии своим сотрудникам
(при CES-функции полезности схема распределения прибыли неважна).

14.

14
Равновесие в модели
с фиксированной зарплатой
Полученные параметры равновесия:
p1
wc,
p2
wc,
1
1
q1 f 1 1 c , q2 f 1 c ,
l1 f 1 1 1 , l2 f .
1 L
2L
n1
,
n
2
f
f 1 1 1
TR1 p1q1 fw 1 ,
TR2 f w,
1 fw 1 1 ,
2 0.
TC1 fw 1 1 1 , TC2 f w,
Доходы высококвалифицированных рабочих:
1
w 1
I1 w
.
l1 1 1 1
Равновесный уровень заработной платы (из баланса предл. и спроса в с/х):
1
,
1 1 2 L 1 1Lw
Lw
1
L
2
1
2
1
1 1
1
1 1 2
w
.
k2
,
1
1 1k 2 2
1 1

15.

15
Сравнительная статика в модели
с фиксированной зарплатой
Табл.2. Влияние параметров модели с фиксированной зарплатой на равновесие
p1
p2
q1
q2
TR1
TR2
I1
I2
n1
n2
l1
l2
–
–
+
Отличия от базовой модели:
1. Увеличение различий между секторами благоприятно сказывается на эффективном секторе: укрупнение фирм, снижение цен, расширение поставок.
2. Усиление взаимозаменяемости ведет к укрупнению фирм обоих секторов.
3. При усилении взаимозаменяемости уровень зарплат не только падает, но с
некоторого критического значения начинает возрастать.
4. При усилении взаимозаменяемости в эффективном секторе не наблюдается
неограниченного роста доходов.
5. При очень высоких значениях оба сектора выравниваются из-за падения
прибыли.

16.

Сопоставление базовой модели и
модели с фиксированной зарплатой
16
Табл.3. Изменение равновесных значений переменных при фиксации зарплаты
p1
p2
q1
q2
~
TR1 TR2 TC1 TC2
w1
w2
I1
I2
n1
n2
l1
l2
~
~
Последствия фиксации зарплаты:
1. Выравнивание доходов в эффективном и неэффективном секторах, несмотря
на попытки уменьшить эффект с помощью распределения прибыли.
2. Увеличение разрыва в ценах секторов. Товары эффективного сектора благодаря сокращению расходов на зарплату становятся еще более доступными, а
в неэффективном секторе рост зарплат увеличивает его неэффективность.
3. Укрупнение фирм эффективного сектора при одновременном сокращении
разнообразия предоставляемых продуктов, что уменьшает достигаемое значение полезности потребителей.

17.

k 1112 m
2 a x1
12 k12 2 1121 2
k 0 ; 1
21
Модификация «деиндустриализация
неэффективного сектора»
17
Если равновесная зарплата в неэффективном секторе промышленности ниже
зарплаты в сельском хозяйстве, часть неквалифицированных рабочих «уезжает в деревню». Миграция продолжается до выравнивания зарплат.
Поиск доли населения , «переезжающего в деревню»:
– доля в базовой модели.
– доля в модифицированной модели.
Сопоставление моделей:
Деиндустриализация неэффективного сектора при фиксации уровня зарплаты по промышленности будет ниже, чем в базовой модели. Это может
в некоторой степени компенсировать сокращение разнообразия и не вполне справедливое перераспределение доходов в пользу рабочих низкой квалификации.

18.

f 1,cL 120, 2,
3,
0,25
0,25.
1
2
18
Численный пример
Табл.4. Равновесие в примере
= 0,7
= 0,5
= 0,5, деинд.
Базов. Фикс. Базов. Фикс. Базов. Фикс.
Цена продукции
Объем производства
Выручка фирмы
Издержки фирмы
Заработная плата
Доходы рабочих
p1
4,295
3
1,841
1,286
2,381
1,5
p2
5,411
6
2,319
2,571
3
3
q1
2
8
2
8
2
8
q2
1
1
1
1
1
1
TR1
8,589
24
3,681
10,286
4,762
12
TR2
5,411
6
2,319
2,571
3
3
TC1
8,589
18
3,681
7,714
4,762
9
TC2
5,411
6
2,319
2,571
3
3
w1
2,863
2
1,227
0,857
1,587
1
w2
1,804
2
0,773
0,857
1
1
I1
2,863
2,667
1,227
1,143
1,587
1,333
I2
1,804
2
0,773
0,857
1
1

19.

0; 1 . 0;1
Модификация с образованием
и эндогенным определением
долей рабочих по секторам
1.
2.
3.
4.
19
Возможен свободный переток рабочих из сельского хозяйства в неэффективный промышленный сектор и обратно.
Возможен переход с издержками на образование из неэффективного промышленного сектора в эффективный.
Издержки на образование зависят от
– индивидуальной «несклонности к обучению», равномерно распределенной на отрезке.
Издержки получения образования для
TC
наиболее способного ( = 0) – нулевые.
T
Издержки получения образования для
наиболее неспособного ( = 1) равны T.
Образование получает доля α1 наиболее
α1 T
способных рабочих с несклонностью к
обучению
0
α1
1

20.

w123 k 1 11 T .12 , 23 1, 2 1 1 k1 T 1 2 1.k 1 , 2 k1 1 T k1 1 .
Модификация с образованием
и эндогенным определением
долей рабочих по секторам
20
Рабочие переходят из сельского хозяйства в неэффективный промышленный
сектор или обратно до выравнивания зарплат: w2=1.
Повышают квалификацию те рабочие, для которых издержки образования не
превышают разницу зарплат: k1w2 – w2 = α1T, k1 –1 = α1T.
В модели с фиксированным уровнем зарплаты все представленные соотношения сохраняются с заменой коэффициента k1 на k2!

21.

21
Сравнительная статика
Табл.2. Влияние параметров модели на возникающее равновесие
p1
p2
q1
q2
+
+
+
+
c
+
–
–
L
+
–
f
TR1 TR2
w1
n1
n2
l
α1
α2
α3
+
–
–
+
+
+
+
+
T
–
–
Отличия от базовой модели:
1. Увеличение различий между секторами промышленности приводит к росту
зарплат в эффективном секторе и перетоку рабочих из неэффективного сектора в эффективный при неизменности образовательных издержек.
2. Усиление степени независимости товаров приводит к сокращению перехода
рабочих в эффективный сектор из-за падения зарплат и сокращению числа
фирм эффективного сектора.
3. Рост спроса на промышленную продукцию не увеличивает цены и зарплаты.

22.

w1 i n0Ll i w1c, d 1 i nwL 1w; n0 p 1, 1i n 1 1 w i c1L d,, q Li w1 f 1c i 1 1 ., 1 l 1 . fi ,1 ni L 1f .
cW
Обобщение: произвольное число
типов промышленных рабочих
22
Задано распределение квалификации рабочих:
Число рабочих, необходимых для производства единицы продукции на i-фирме:
с – показатель самого квалифицированного рабочего.
Соответствующий уровень зарплат:
w – зарплата самого квалифицированного рабочего.
Простейший случай – линейно возрастающие издержки:
Расчетные формулы:
Суммарная зарплата рабочих промышленного сектора:
Равновесный уровень заработной платы (из баланса предл. и спроса в с/х):

23.

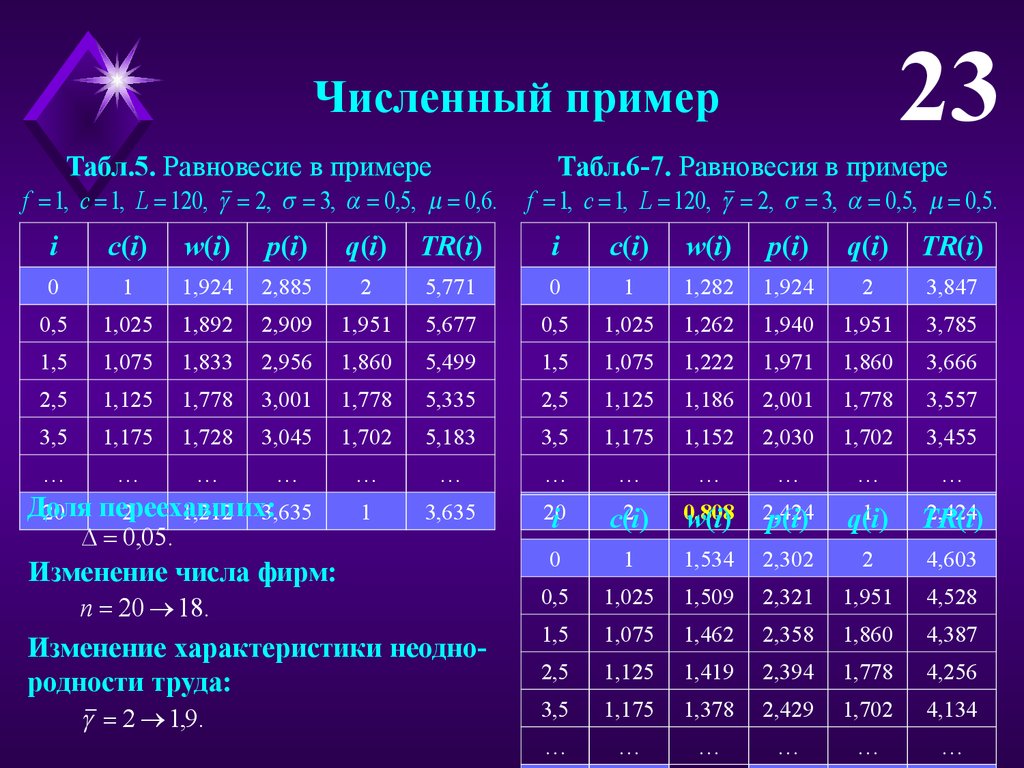
23
Численный пример
Табл.5. Равновесие в примере
f 1, c 1, L 120, 2, 3, 0,5, 0,6.
Табл.6-7. Равновесия в примере
f 1, c 1, L 120, 2, 3, 0,5, 0,5.
i
c(i)
w(i)
p(i)
q(i)
TR(i)
i
c(i)
w(i)
p(i)
q(i)
TR(i)
0
1
1,924
2,885
2
5,771
0
1
1,282
1,924
2
3,847
0,5
1,025
1,892
2,909
1,951
5,677
0,5
1,025
1,262
1,940
1,951
3,785
1,5
1,075
1,833
2,956
1,860
5,499
1,5
1,075
1,222
1,971
1,860
3,666
2,5
1,125
1,778
3,001
1,778
5,335
2,5
1,125
1,186
2,001
1,778
3,557
3,5
1,175
1,728
3,045
1,702
5,183
3,5
1,175
1,152
2,030
1,702
3,455
…
…
…
…
…
…
…
…
…
…
…
…
1
3,635
20
i
2
c(i)
0,808
w(i)
2,424
p(i)
1
q(i)
2,424
TR(i)
0
1
1,534
2,302
2
4,603
0,5
1,025
1,509
2,321
1,951
4,528
1,5
1,075
1,462
2,358
1,860
4,387
2,5
1,125
1,419
2,394
1,778
4,256
3,5
1,175
1,378
2,429
1,702
4,134
…
…
…
…
…
…
Доля
20 переехавших:
2
1,212 3,635
0,05.
Изменение числа фирм:
n 20 18.
Изменение характеристики неоднородности труда:
2 1,9.

24.

с
с01
T
C
x0x 1
f
fx
x
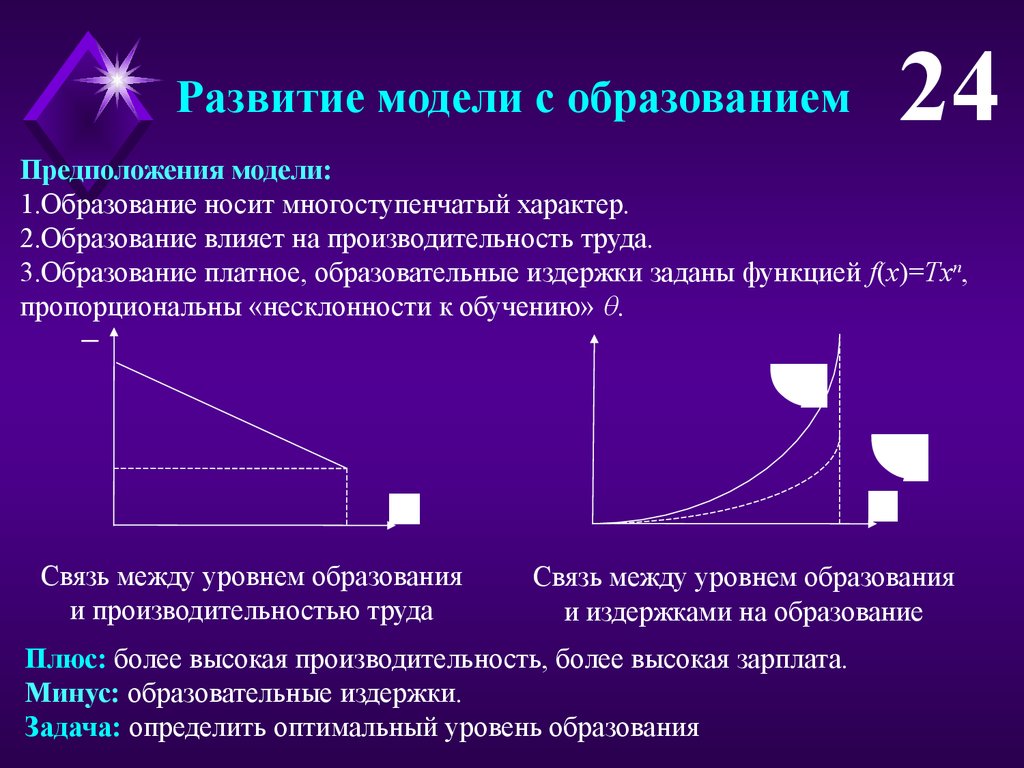
Развитие модели с образованием
24
Предположения модели:
1.Образование носит многоступенчатый характер.
2.Образование влияет на производительность труда.
3.Образование платное, образовательные издержки заданы функцией f(x)=Txn,
пропорциональны «несклонности к обучению» .
Связь между уровнем образования
и производительностью труда
Связь между уровнем образования
и издержками на образование
Плюс: более высокая производительность, более высокая зарплата.
Минус: образовательные издержки.
Задача: определить оптимальный уровень образования

25.

34 , xx**n x * 00, 13..0,2T3и4л1.0, 8.
x
,*1.
0
25
Модель с линейными издержками
0
0
-1
-0.1
-2
-0.2
-3
-0.3
-4
-0.4
-5
-0.5
-6
-0.6
-7
-8
-0.7
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0
0.9
1
-0.8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.4
1.2
-0.2
1
-0.4
0.8
-0.6
0.6
-0.8
0.4
-1
0.2
-1.2
-1.4
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
-0.2

26.

12 ,x x** n 01,0321..1T,x2* и 91л50., 8.
x
0*,1.
26
Модель с квадратичными издержками
0.05
1
0
0
-1
-0.05
-2
-0.1
-3
-0.15
-4
-0.2
-5
-0.25
-6
-0.3
-7
-8
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
1
-0.35
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.4
0.1
0
1.2
-0.1
1
-0.2
-0.3
0.8
-0.4
0.6
-0.5
-0.6
0.4
-0.7
0.2
-0.8
-0.9
0.9
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0

27.

c1 12 1
c
1
L
L
L
1222
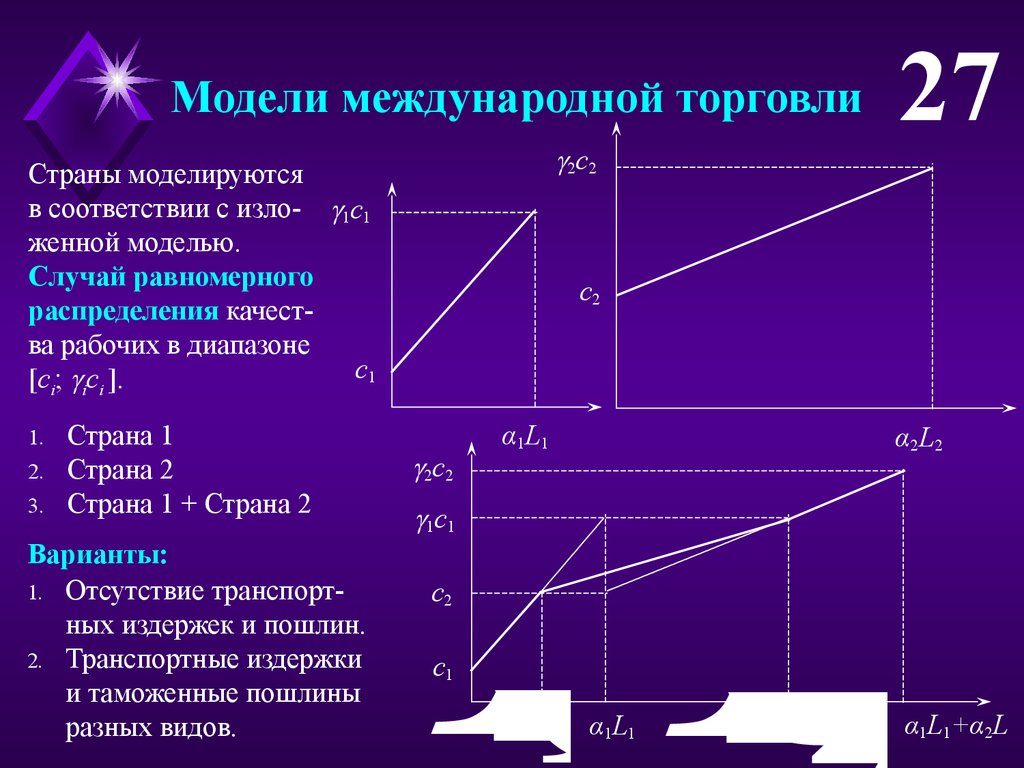
Модели международной торговли
Страны моделируются
в соответствии с изло- 1c1
женной моделью.
Случай равномерного
распределения качества рабочих в диапазоне
c1
[ci; ici ].
1.
2.
3.
Страна 1
Страна 2
Страна 1 + Страна 2
Варианты:
1. Отсутствие транспортных издержек и пошлин.
2. Транспортные издержки
и таможенные пошлины
разных видов.
2c2
27
c2
2c2
α1L1
α2L2
1c1
c2
c1
α 1 L1
α1L1+α2L

28.

L
10,c12 1, 1 22,1
02,6.4f 1,
12
1
2,
23.
28
Эффекты объединения стран
1.
2.
3.
Увеличение разнообразия и рост полезности.
Выравнивание цен в объединенных странах.
Возможная деиндустриализация в стране с неэффективным промышленным
сектором.
Численный пример
Развитая страна:
Развивающаяся страна:
До объединения:
i
c(i)
w(i)
p(i)
q(i)
i
c(i)
w(i)
p(i)
q(i)
0
1
1,609
3,219
1
0
1,2
6,243
14,98
0,833
…
…
…
…
…
…
…
…
…
…
30
2
1,138
4,552
0,5
20
12
1,974
47,38
0,083
i
c(i)
w(i)
p(i)
q(i)
i
c(i)
w(i)
p(i)
q(i)
0
1
2,974
5,948
1
0
1,2
2,715
6,516
0,833
…
…
…
…
…
…
…
…
…
…
30
2
2,103
8,412
0,5
20
12
0,858
20,60
0,083
После объединения:

29.

29
Спасибо
за внимание!
[email protected], [email protected],
http://sibscience.org, http://vk.com/baikalreadings,
http://youtube.com/sibscience