Похожие презентации:
Определение и объявление функций пользователя. Лекция 10 по алгоритмизации и программированию
1. Лекция 10
2.
Определение(описание) и объявление функций пользователяI. Описание функции:
1.
заголовок;
2.
тело функции.
<Описание функции>::=<Заголовок функции> {<Тело функции>}
<Заголовок функции>::=
<Тип результата> <Имя функции> (<Описание параметров>)
<Тип результата>::=void | <Базовые типы> |
<Структурированные типы>
<Имя функции>::=<Идентификатор>
<Список параметров>::=<Тип> <Имя> [, <Список параметров>] | ПУСТО
Если тип результата отличен от void, то в теле функции обязательно
должен присутствовать оператор return <значение>; , где
<значение> – имя переменной, выражение или константа.
Оператор return передает управление вызывающей программе.
<Объявление функции>::=<Заголовок функции>;
3.
• Какая задача реализована в этомфрагменте?
Фрагмент программы:
int a[100];
int j,i,n,r;
for (i=1;i<n;i++) { r=a[i];j=i-1;
while(j>=0&&r<=a[j])
{a[j+1]=a[j];j--;}
a[j+1]=r;
}
4. Сортировка двоичными (бинарными) вставками
• Модификация метода вставок. Пусть элементымассива с А[1] по А[i-1] уже отсортированы. Нужно
вставлять в отсортированную последовательность
элемент А[i]. Для поиска места, куда нужно вставлять
данный элемент сравниваем его со средним
элементом из A[1] …A[i-1], и , если он меньше
среднего элемента, то его место ищем в левой
половине массива А[1]…A[i-1], иначе в правой
половине. Причем дальнейший поиск осуществляем
аналогичным способом: методом деления интервала
пополам.
5.
void sort_bin_insert (int *a, int n) // Сортировка бинарными вставками{ int x,left,right,sred;
for (int i=1; i<n; i++)
{
if (a[i-1]>a[i])
{
x=a[i];
// x – включаемый элемент
left=0;
// левая граница отсортированной части массива
right=i-1;
// правая граница отсортированной части массива
do {
sred = (left+right)/2; // sred – новая "середина" последовательности
if (a[sred]<x ) left= sred+1;
else right=sred-1;
} while (left<=right); // поиск ведется до тех пор, пока левая граница не
окажется правее правой границы
for (int j=i-1; j>=left; j--) a[j+1]= a[j];
a[left]= x;
}
}
}
6. Алгоритм слияния
• Объединить («слить») упорядоченные фрагментымассива A: A[k],...A[m] и A[m+1],..., A[q] в один A[k],...,
A[q], естественно, тоже упорядоченный (k m q).
Основная идея решения состоит в сравнении
очередных элементов каждого фрагмента,
выяснении, какой из элементов меньше, переносе
его во вспомогательный массив D (для простоты) и
продвижении по тому фрагменту массива, из
которого взят элемент. При этом следует не забыть
записать в D оставшуюся часть того фрагмента,
который не успел себя «исчерпать».
7.
#include <iostream>#include <locale.h>
using namespace std;
void Sl(int m[],int k,int q) // или ...int *a
{
// k – нижняя граница упорядоченного фрагмента
// q – верхняя граница фрагмента
int i,j,t,mid,d[20];
i=k;
mid=k+(q-k)/2;
j=mid+1;
t=1;
while (i<=mid && j<=q)
{
if (m[i]<=m[j]) {d[t]=m[i]; i++;}
else { d[t]=m[j]; j++;}
t++;
}
// Один из фрагментов обработан полностью, осталось перенести в D остаток
другого фрагмента
while (i<=mid)
{ d[t]=m[i]; i++; t++;}
while (j<=q)
{ d[t]=m[j]; j++; t++;}
for (i=1;i<=t-1; i++) m[k+i-1]=d[i];
}
8.
// Рекурсивная реализация сортировки слияниемvoid Sort_Sl(int *m, int i,int j)
{
int t;
if (i<j)
// Обрабатываемый фрагмент массива состоит более, чем из
одного элемента
if (j-i==1) {
if (m[j]<m[i])
// Обрабатываемый фрагмент массива состоит из двух элементов*)
{ t=m[i]; m[i]=m[j]; m[j]=t;};}
else {
// Разбиваем заданный фрагмент на два
Sort_Sl(m,i,i+(j-i)/2); // рекурсивные вызовы процедуры Sort_Sl
Sort_Sl(m,i+(j-i)/2+1,j);
Sl(m,i,j);
}
}
9. Двумерные массивы
• Двумерный массив (матрица) –одномерный массив одномерных
массивов.
• <тип элементов> <имя массива>[количество][количество];
• Указывается количество элементов в
одномерном массиве, а потом указывается
количество элементов в одномерных
массивах.
10.
Матрица — это прямоугольная таблица,составленная из элементов одного типа
(чисел, строк и т.д.). Каждый элемент
матрицы имеет два индекса – номера
строки и столбца.
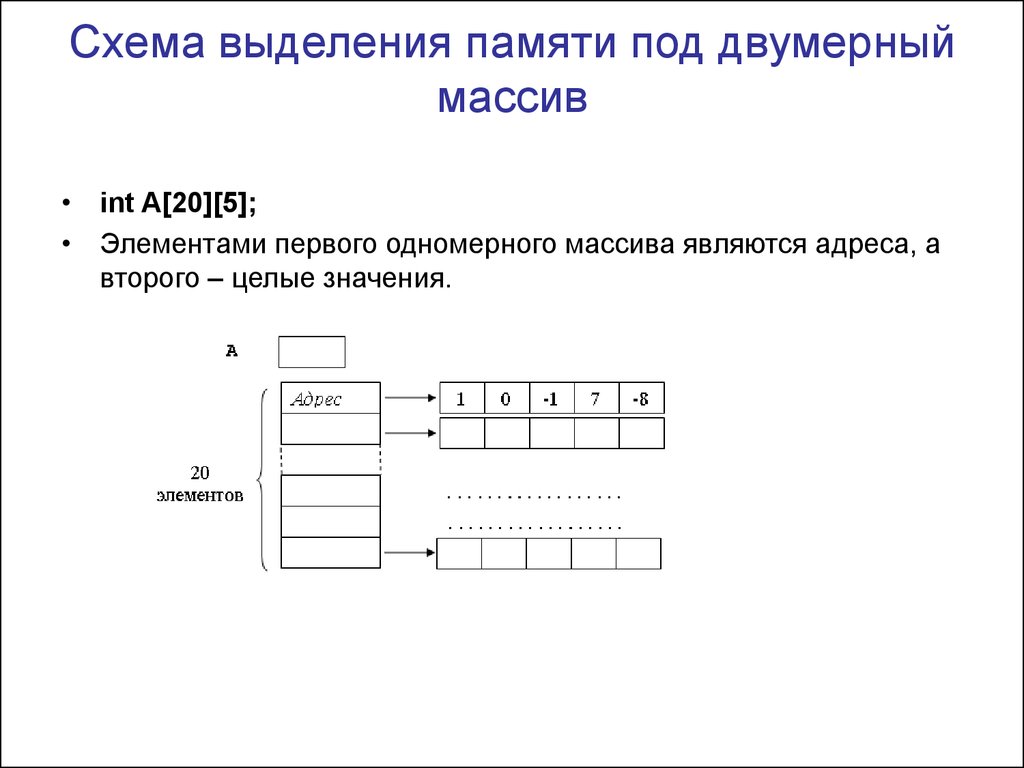
11. Схема выделения памяти под двумерный массив
• int A[20][5];• Элементами первого одномерного массива являются адреса, а
второго – целые значения.
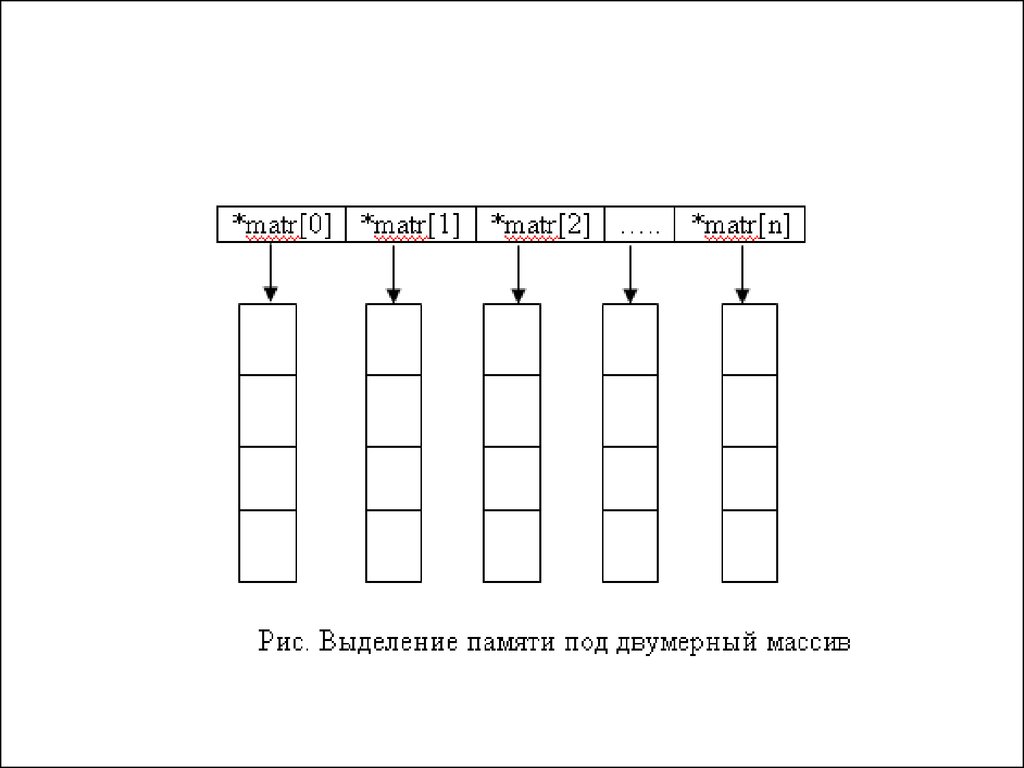
12.
• При формирование матрицы сначала выделяется память длямассива указателей на одномерные массивы, а затем в цикле с
параметром выделяется память под n одномерных массивов.
/*выделение динамической памяти под двумерный динамический
массив*/
int** form_matr(int n,int m)
{
//выделение памяти под массив указателей
int **matr=new int*[n];
for(int i=0;i<n;i++)
//выделение памяти для массива значений
matr[i]=new int [m];
//возвращаем указатель на массив указателей
return matr;
}
13.
14.
• Освобождение памяти из-поддинамического двумерного массива
производится в обратном порядке:
for(int i=0;i<n;i++) delete [] matr[i];
delete [] matr;
15.
• Если двумерный массив являетсяформальным параметром функции, то
его можно описывать двумя способами:
• int **A // ** – указатель, значением
которого будет адрес
• int A[ ][<максимальное количество>]
Например, int A[ ][5]
16. Обращение к элементам двумерного массива
A[i][j]
*(*(A+i)+j)
17.
• Если при описании двумерного массивазадаются значения элементов, то
можно не указывать только количество
строк:
• int b[ ][5]={{1,2,3,,4}, {5,6,7,8,9},
{10,11,12}};
18.
// Заполнение массива по строкамfor ( i = 0; i < N; i++ )
for ( j = 0; j < M; j++ )
{cout << “A[“<<i<<“][“<<j<<“]=“;
cin >>b[i][j];
}
19.
20.
// Печать по строкамfor ( i = 0; i < N; i++ )
{
for ( j = 0; j < M; j++ ) cout << b[i][j]<<“ “;
cout <<endl;
}
// Печать по столбцам
for ( j = 0; j < M; j++ )
{
for ( i = 0; i < N; i++ ) cout << b[i][j]<<“ “;
cout <<endl;
}
21.
// Суммированиеsum = 0;
for ( i = 0; i < N; i++ )
for ( j = 0; j < M; j++ )
sum += A[i][j];
22.
Матрица А:12 14 67 45
32 87 45 63
69 45 14 11
40 12 35 15
Максимальный элемент A[2,2]=87
Минимальный элемент A[3,4]=11
23.
#include <iostream>#include<cstdlib>
using namespace std;
void main()
{
int const N=10;
int const M=15;
int a[N][M];
int i,j, max,k=0;
max=a[0][0];
for(i=0; i<N; i++)
for(j=0; j<M; j++)
{
cout<<"? ";
cin>>a[i][j];
}
max=a[0][0]; k=1;
for(i=0; i<N; i++)
for(j=0; j<M; j++)
if(a[i][j]==max) k++;
else
if(a[i][j]>max) {max=a[i][j]; k=1;}
cout<<"k="<<k<<endl;
}
24.
• Если количество строк и столбцов вдвумерном массиве одинаковое, то такой
массив называется квадратным. Например,
при n=4:
a00 a01 a02 a03
a10 a11 a12 a13
a20 a21 a22 a23
a30 a31 a32 a33
• Диагонали:
• i=j – главная диагональ.Элементы: a[i][i],
a[j][j];
• i+j=n–1 – побочная диагональ. Элементы:
a[i][n-1-i],
• a[n-1-j][j].
25. Перебор элементов матрицы
25Перебор элементов матрицы
Главная диагональ:
for ( i = 0; i < N; i++ ) {
// работаем с A[i][i]
}
Побочная диагональ:
for ( i = 0; i < N; i++ ){
// работаем с A[i][N-1-i]
}
Главная диагональ и под ней:
for ( i = 0; i < N; i++ )
for ( j = 0; j <= i ; j++ )
{
// работаем с A[i][j]
}
26.
#include <iostream>#include<cstdlib>
using namespace std;
void main()
{
int const N=10;
int a[N][N];
int i,j, k;
for(i=0; i<N; i++)
for(j=0; j<N; j++)
{
cout<<"? ";
cin>>a[i][j];
}
for(i=0; i<N; i++)
for(j=0; j<i; j++)
{k=a[i][j]; a[i][j]=a[j][i]; a[j][i]=k;}
for(i=0; i<N; i++)
{for(j=0; j<N; j++) cout<<a[i][j]<<“ “;
cout<<endl;
}
}
27.
#include <iostream>#include<cstdlib>
using namespace std;
void main()
{
int const N=10;
int a[N][N];
Int b[N], c[N];
int i,j;
Int s;
for(i=0; i<N; i++)
for(j=0; j<N; j++)
{
cout<<"? ";
cin>>a[i][j];
}
for(i=0; i<N; i++)
{cout<<"? ";
cin>> b[i];
}
for(i=0; i<N; i++)
{s=0;
for(j=0; j<N; j++)s+=a[i][j]*b[[j];
c[i]=s;
}
for(i=0; i<N; i++) cout<<c[j]<<“ “;
cout<<endl;
}
28.
#include <iostream>#include<cstdlib>
using namespace std;
void main()
{
int const N=10;
int a[N][N],b[N][N],d[N][N];
int i,j, k;
Int s;
for(i=0; i<N; i++)
for(j=0; j<N; j++)
{
cout<<"? ";
cin>>a[i][j];
}
for(i=0; i<N; i++)
for(j=0; j<N; j++)
{
cout<<"? ";
cin>> b[i][j];
}
for(i=0; i<N; i++)
for(j=0; j<N; j++)
{s=0;
for(k=0; k<N; k++)s+=a[i][k]*b[k][j];
c[i][j]=s;
}
for(i=0; i<N; i++)
{ for(j=0; j<N; j++) cout<<c[j][j]<<“ “;
cout<<endl;
}
}


























 Программирование
Программирование








