Конденсационные гигрометры

1.

2.3. Конденсационные гигрометры.
По определению температуры точки росы:
fd
e
1
Ed
e Ed
Зная температуру точки росы td , можно рассчитать Ed и
определить относительную влажность при температуре Т:
f
e Ed
E E
(2.3.1)
Температуру точки росы можно определить по появлению
конденсата на поверхности металлического зеркала. Этот
процесс выполняется автоматически.

2.

2.3. Конденсационные гигрометры.
B
К источнику
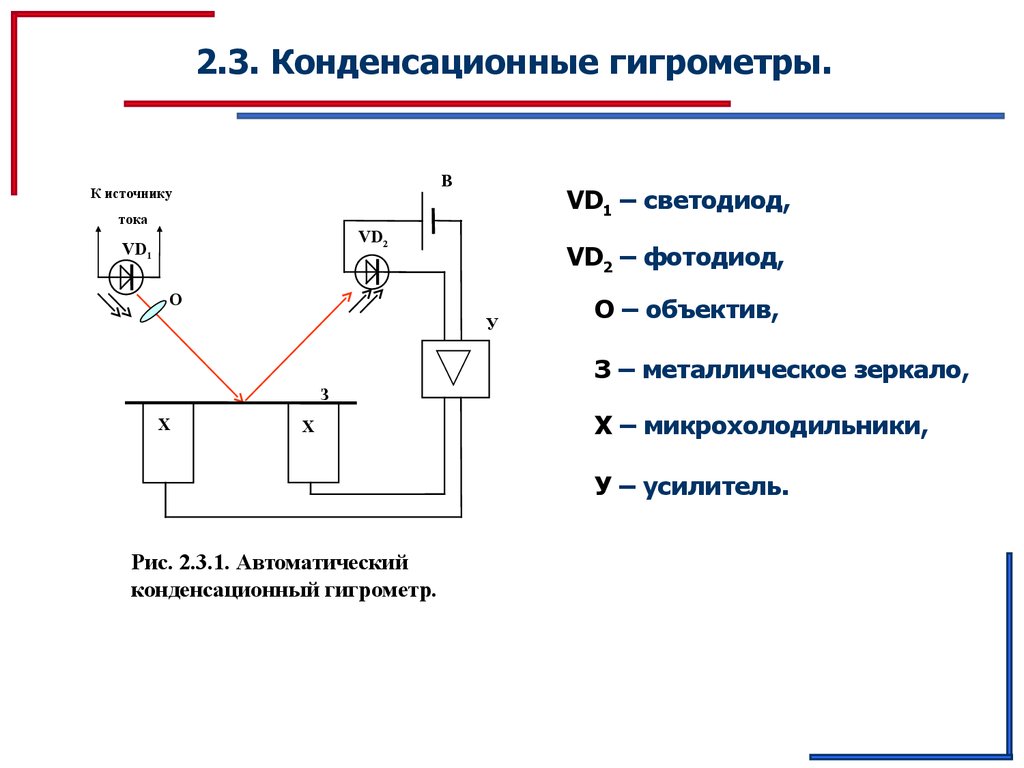
VD1 – светодиод,
тока
VD2
VD1
VD2 – фотодиод,
О
У
О – объектив,
З – металлическое зеркало,
З
Х
Х
Х – микрохолодильники,
У – усилитель.
Рис. 2.3.1. Автоматический
конденсационный гигрометр.

3.

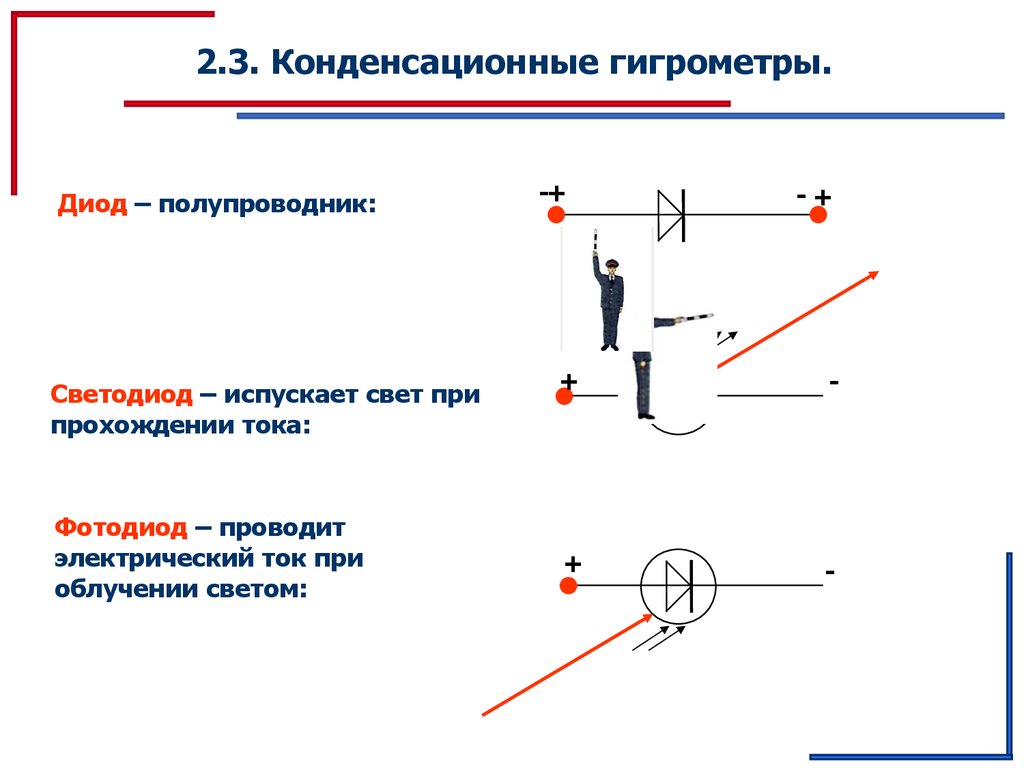
2.3. Конденсационные гигрометры.
Диод – полупроводник:
Светодиод – испускает свет при
прохождении тока:
Фотодиод – проводит
электрический ток при
облучении светом:
-+
-+
+
-
+
-

4.

2.3. Конденсационные гигрометры.
B
К источнику
тока
VD2
VD1
О
У
З
Х
Х
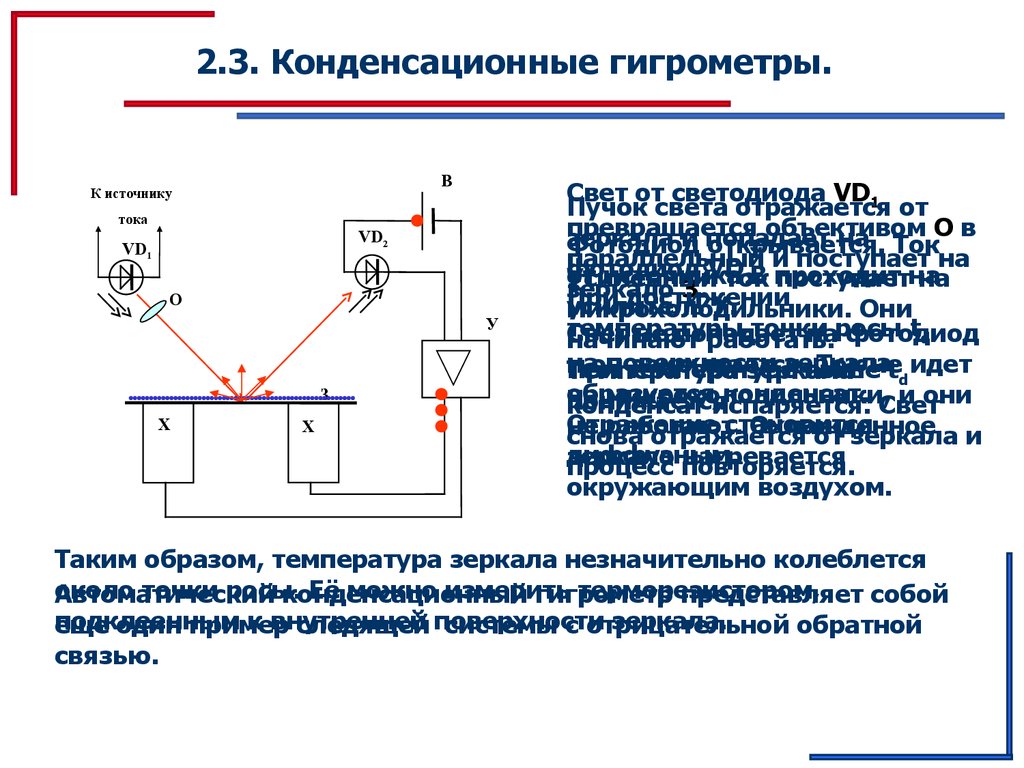
Свет от светодиода VD1
Пучок света отражается от
превращается
объективом
зеркала
и попадает
на ТокО в
Фотодиод
открывается.
параллельный
и поступает на
фотодиод
VD
.
2
от
источника
В
Усиленный
ток проходит
поступаетна
на
зеркало
З.
При
достижении
усилитель У.
микрохолодильники.
Они
температуры
точки
td
Свет не попадает
наросы
фотодиод
начинают
работать.
на
поверхности
зеркала
и он
закрывается.
Ток не
При
температуре
выше
td идет
Температура
зеркала
образуется
конденсат. Свет
на микрохолодильники,
и они
понижается.
конденсат
испаряется.
Отражение
становится
не работают.
Охлажденное
снова
отражается
от зеркала и
диффузным.
зеркало
нагревается
процесс повторяется.
окружающим воздухом.
Таким образом, температура зеркала незначительно колеблется
около точки росы.
Её можно измерить
терморезистором,
Автоматический
конденсационный
гигрометр
представляет собой
подклеенным
к внутренней
зеркала.
еще один пример
следящей поверхности
системы с отрицательной
обратной
связью.

5.

2.3. Конденсационные гигрометры.
Выведем формулу, связывающую температуру точки росы с
относительной влажностью. Для этого воспользуемся
уравнением Клаузеуса-Клапейрона (см.2.1.14):
dE
L
E
Rv
dT
2
T
(2.3.2)
Проинтегрируем его от Ed до E и от Td до T:
E
T
dE
L dT
2
E Td Rv T
ln
E
L 1 1
( )
Ed
Rv T Td
Ed
(2.3.3)

6.

2.3. Конденсационные гигрометры.
С учетом (2.3.1) имеем:
L 1 1
ln f
( )
Rv T Td
Отсюда выразим Td:
R ln f
1
1
v
L
T Td
1
Td
1 Rv
ln f
T L
(2.3.3)

7.

2.3. Конденсационные гигрометры.
1
Td
1 Rv
ln f
T L
Теперь найдем чувствительность конденсационного
гигрометра:
Rv
dTd
1
Rv 1
S
( )
1 R
R
1
df
L
f
L ( v ln f ) 2 f
( v ln f ) 2
T L
T L

8.

2.3. Конденсационные гигрометры.
Rv
S
1 R
L ( v ln f ) 2 f
T L
S, K/%
f=0,2
0,8
0,6
f=0,4
0,4
f=0,8
0,2
-30
-20
-10
0
10
20
30
tC
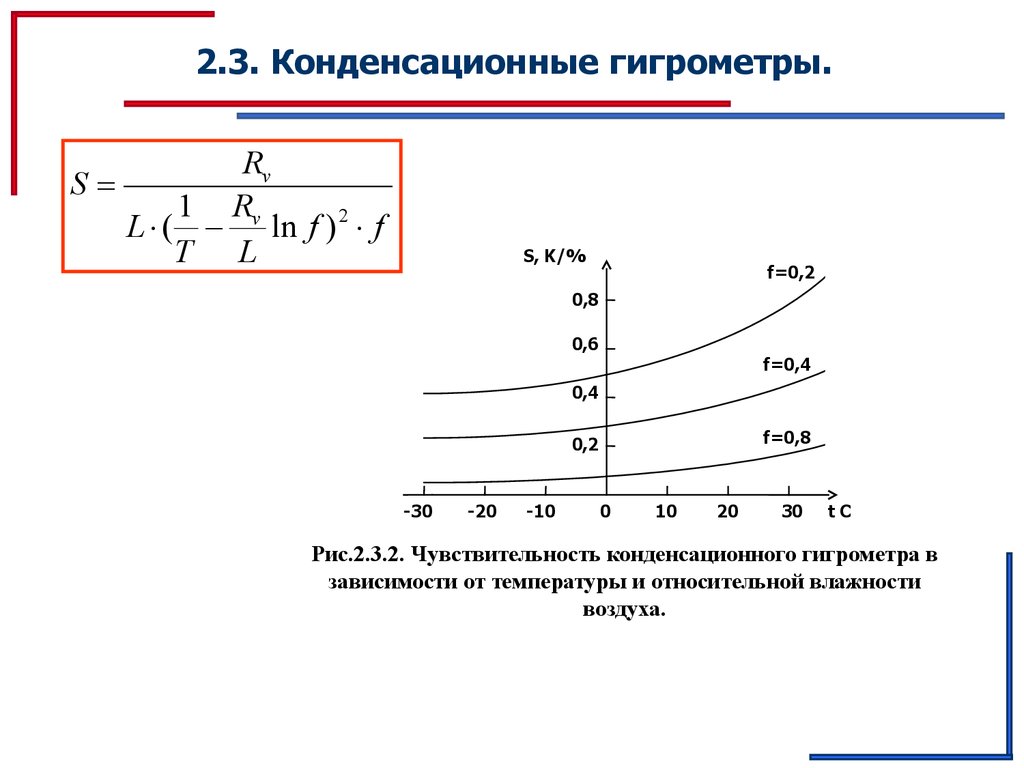
Рис.2.3.2. Чувствительность конденсационного гигрометра в
зависимости от температуры и относительной влажности
воздуха.

9.

2.3. Конденсационные гигрометры.
Чувствительность конденсационного гигрометра в несколько
раз выше чувствительности психрометра!
За точность измерения необходимо платить
временем, затраченным на измерение!
Конденсационные гигрометры являются одними из самых
точных приборов для измерения влажности воздуха. Однако,
в метеорологических измерениях их употребляют редко изза их инерционности.