Разрывной максвеллиан со смещением. Аппроксимация функции распределения. Плотность потока массы
1.
Аппроксимация функции распределенияимеет вид:
2
2
2
(ξ
u
)
ξ
+ξ
n1
x
1
y
z
exp
f1
3/2
2 RT1
2πRT1
f
2
2
2
(ξ
u
)
+ξ
+ξ
n2
x
2
y
z
exp
3/2
f2
2 RT2
2πRT2
при ξ x >0
при ξ x <0
Ищем плотность потока массы
ξ
x
f dξ ξ x ( f1 f 2 )dξ
0
ξ
f dξ x dξ y dξ z
x 2
ξ
0
f dξ x dξ y dξ z
x 1
2.
0ξ
f dξ x dξ y dξ z
x 2
ξ
f dξ x dξ y dξ z
x 1
0
(ξ x u2 ) 2 +ξ 2y +ξ 2z
exp
ξ x dξ x dξ y dξ z
3/2
2 RT2
2πRT2
n2
0
(ξ x u1 )2 ξ 2y +ξ 2z
exp
ξ x dξ x dξ y dξ z
3/2
2 RT1
2πRT1 0
n1
0
ξ 2z ξ 2y
(ξ x u2 ) 2
exp
dξ y exp
dξ z exp
ξ x dξ x
3/2
2πRT2 2 RT2 2 RT2 2RT2
n2
ξ 2z ξ 2y (ξ x u1 ) 2
exp
dξ y exp
dξ z exp
ξ x dξ x
3/2
2πRT1 2 RT2 2 RT2 0 2RT1
n1
3.
0(ξ x u2 )2
(ξ x u2 ) 2
exp 2RT2 ξ x dξ x exp 2RT2 (ξ x u2 ) u2 dξ x
0
0
(ξ x u2 ) 2
(ξ x u2 ) 2
exp
(ξ x u2 )d (ξ x u2 ) u2 exp
d (ξ x u2 )
2 RT2
2 RT2
0
u2
u
2
y2
y2
exp
ydy u2 exp
dy
2 RT2
2 RT2
u2
u2
1
exp 2 y 2 dy 2 u2 exp 2 y 2 dy
2
1
2 2
1
2 2
u2
exp 2 y 2 d ( 2 y 2 ) u2
2 u 2 2
u2
e dz u2
z
u2
e
2 y 2
dy
exp 2 y 2 dy
4.
12 2
u2
u2
e
2 u2 2
2 y
1 2 u2 2
e dz
e
2 2
z
0
2
dy u2 e
2 y
0
2
dy u2
e
2 y
2
u2
1
dy u2
u2
2 2
u2 u2
u
erf (u2 2 ) 2
1 erf (u2 2 )
2 2 2 2
2 2
u2
e
2 y 2
0
e
2 y 2
dy
0
1
dy
erf (u2 2 )
2 2
(ξ x u2 )
1
exp
ξ
d
ξ
2RT2 x x 2 2
0
u2
2
2 u 2 2
e dz u2
z
u2
e
2 y 2
1 2 u 2 2 u 2
e
1 erf (u2 2 )
2 2
2 2
u2
u2 2 u2
RT2 exp
2 RT2 1 erf
2 RT
2 RT2 2
2
dy
5.
(ξ x u2 ) 2 +ξ 2y +ξ 2zexp
ξ x dξ x dξ y dξ z
3/2
2 RT2
2πRT2
0
n2
0
ξ 2y
ξ 2z
(ξ x u2 ) 2
exp
dξ y exp
dξ z exp
ξ x dξ x
3/2
2πRT2 2 RT2 2 RT2 2 RT2
n2
2πRT2
(ξ x u2 ) 2
2πRT2 2πRT2 exp
ξ x dξ x
2 RT2
0
n2
3/2
u2
u2 2 u2
RT2 exp
2 RT2 1 erf
1/2
2 RT
2πRT2
2 RT2 2
2
n2
u2
u2 2 n2u2
exp
1 erf
1/2
2 RT
2
2πRT2
2 RT2
2
n2 RT2
n2
u2
u2 2 n2u2
RT2
exp
1 erf
2π
2
2 RT2
2RT2
6.
(ξ x u1 ) 2 +ξ 2y +ξ 2zexp
ξ x dξ x dξ y dξ z
3/2
2 RT1
2πRT1 0
n1
n1
e
u1
u12 n1u1
RT1
exp
1 erf
2 RT
2π
2 RT1 2
1
1 y
0
2
dy
u1
e
1 y
2
dy
u1
e
1 y
2
dy
0
u1
0
e
1 y 2
dy
1
2 1
1
1
1
erf (u2 1 )
1 erf (u1 1 )
2 1
2 1 2 1
jx / m
ξ
x
f dξ x dξ y dξ z
n1
u12
u2 2
RT1
RT2
exp
exp
n2
2π
2π
2 RT1
2 RT2
u1
n1u1
1 erf
2 RT
2
1
n2u2
u2
1 erf
2 RT
2
2
7.
u2 0u1
u12
RT1
RT2 n1u1
jx / m n1
exp
1 erf
n2
2 RT
2π
2π
2
2 RT1
1


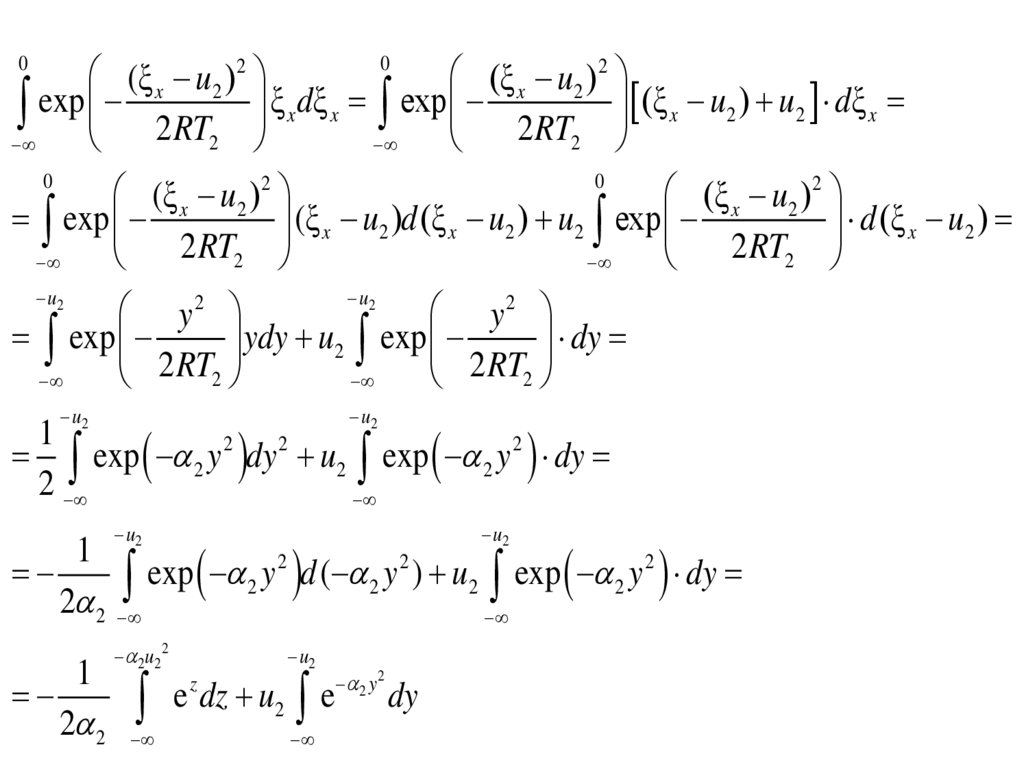
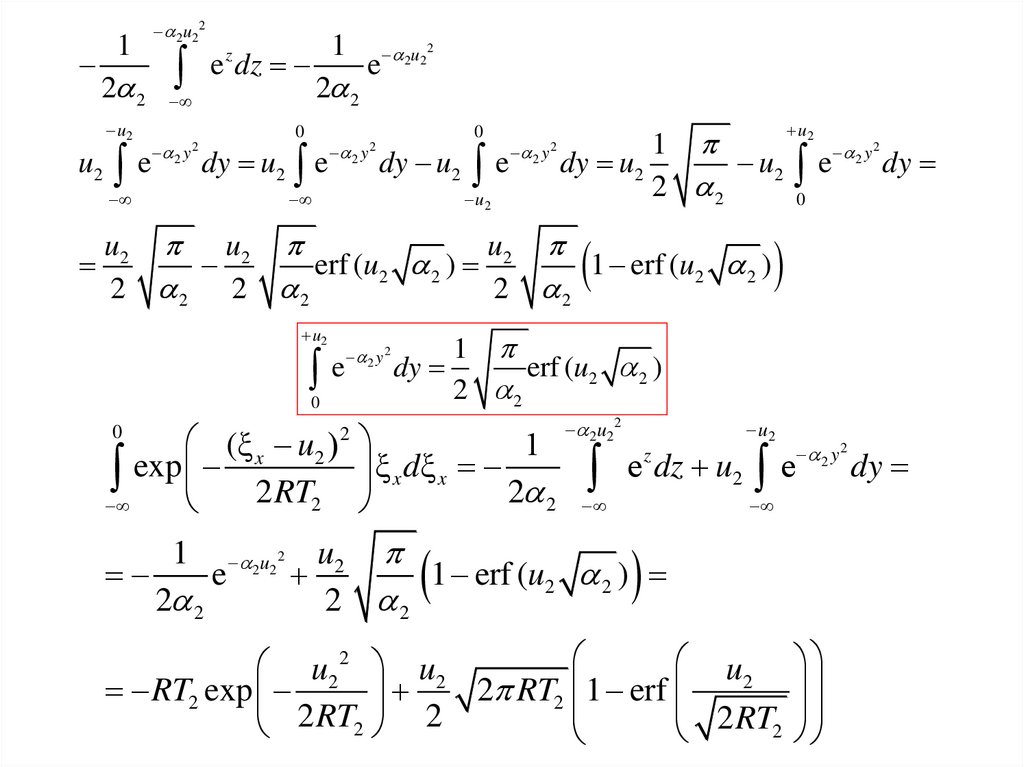
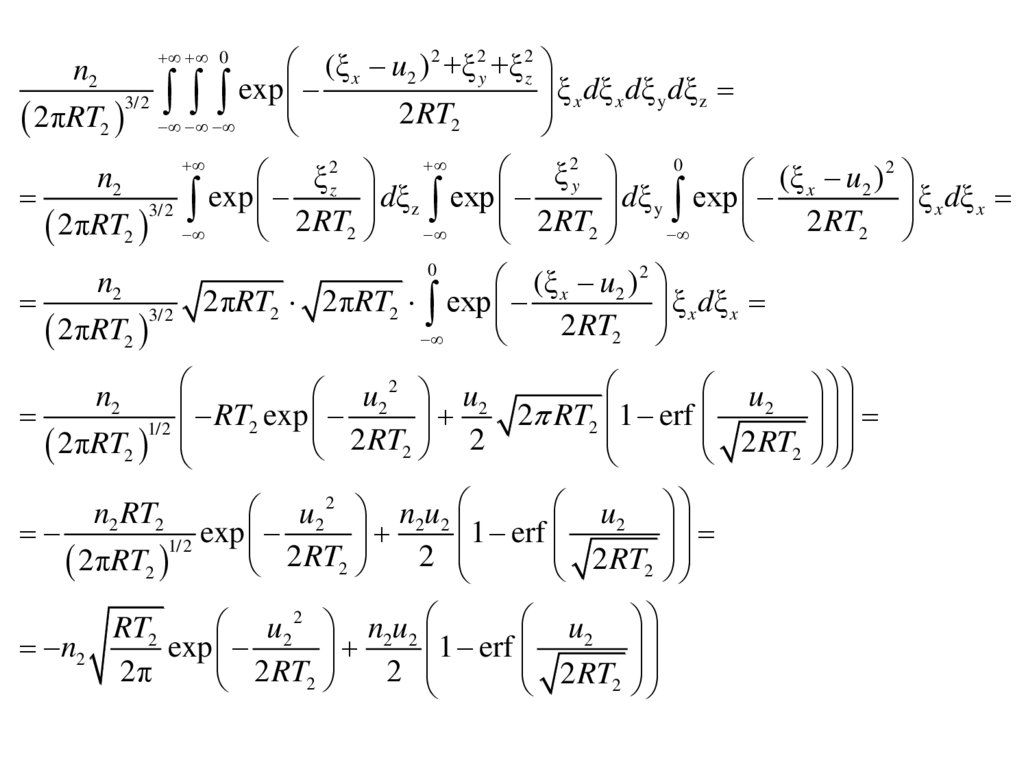
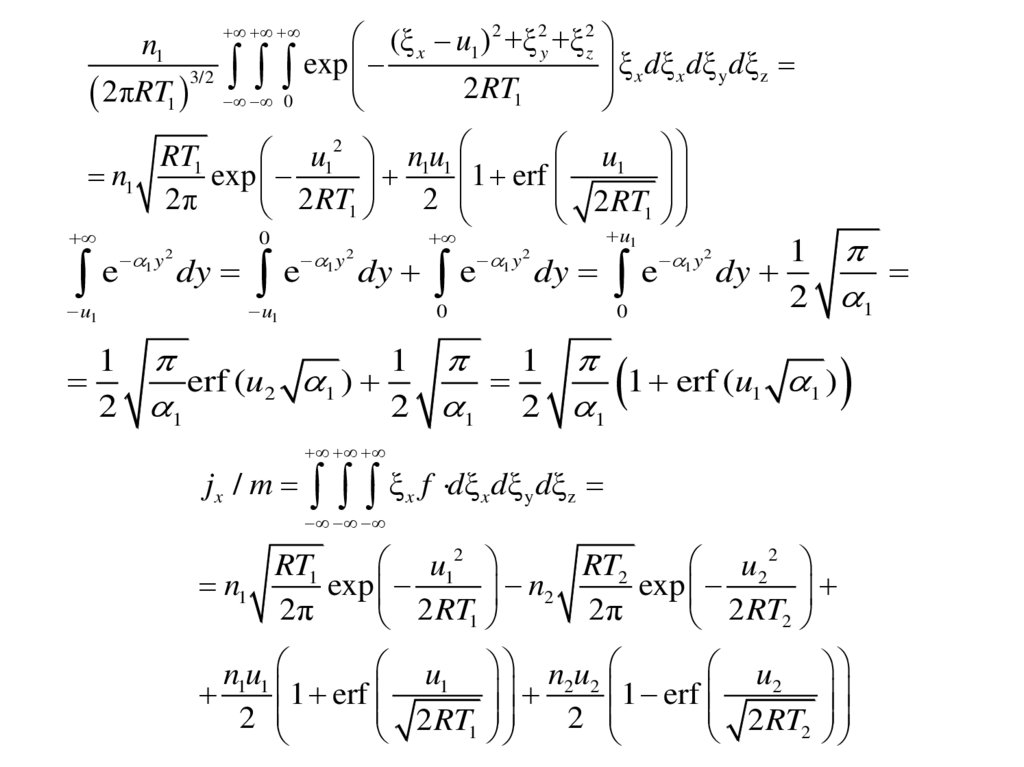







 Физика
Физика