Похожие презентации:
Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума
1. Тема: Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума.
Урок № 39Тема: Промежутки возрастания и убывания,
наибольшее и наименьшее значения, точки
экстремума.
Задание:
1. Составить конспект по презентации, ( на проверку
присылать не нужно)
2. Просмотреть видеоурок, записать решение примера в
рабочую тетрадь).
2. Параметры исследования:
Область определенияМножество значений
Нули функции
Интервалы знакопостоянства
Промежутки монотонности
Точки экстремума
Набольшее и наименьшее значения
функции
3.
Область определения функцииВсе допустимые значения
аргумента x функции y(х).
назад
4.
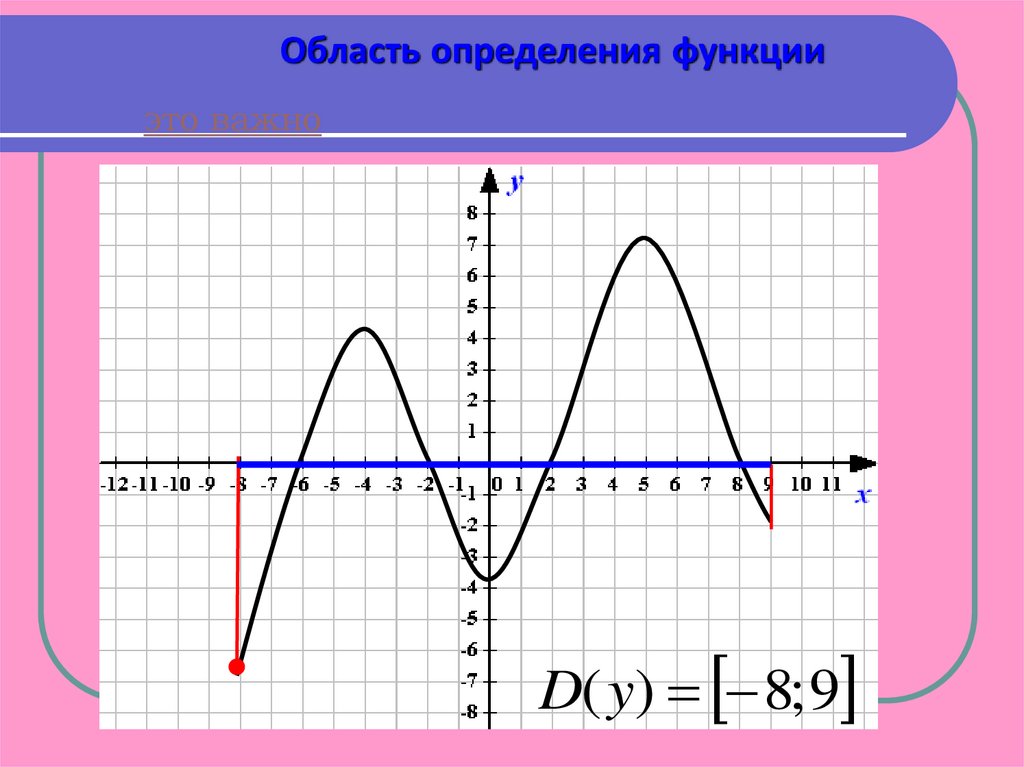
Область определения функцииэто важно
D( y) 8; 9
5.
Область значения функцииМножество, состоящее из всех
чисел y(x), таких, что x
принадлежит области
определения функции y(х).
назад
6.
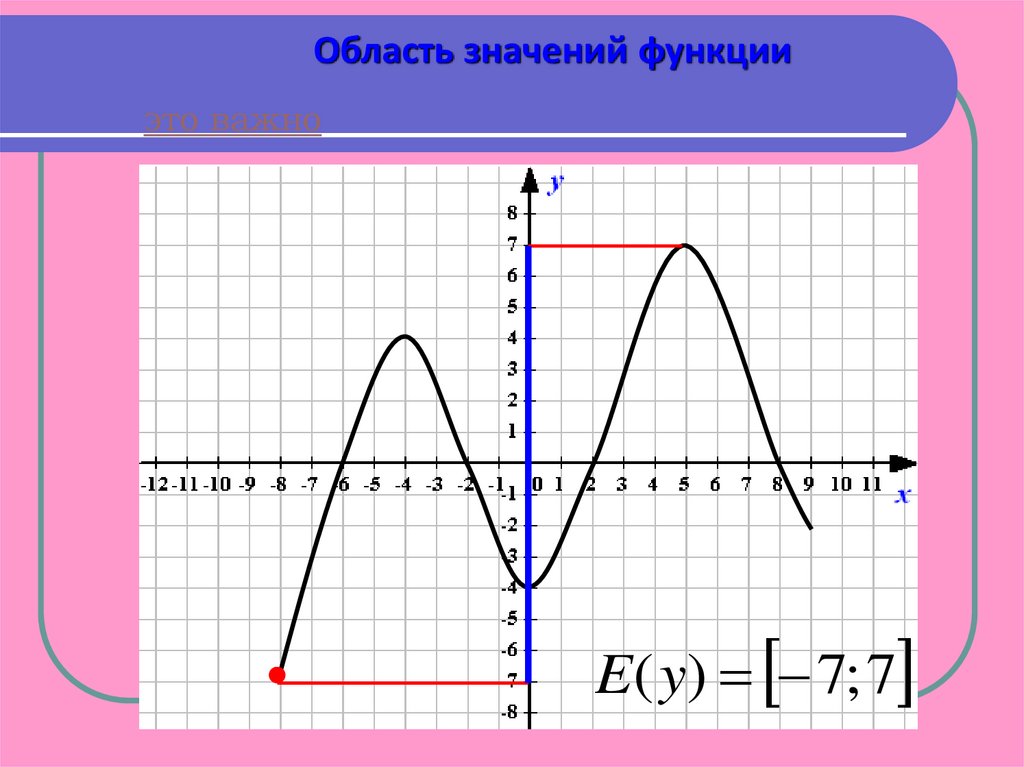
Область значений функцииэто важно
E( y) 7; 7
7.
Нули функцииЭто значения аргумента х, при
которых значение функции у(х)
равно нулю.
назад
8.
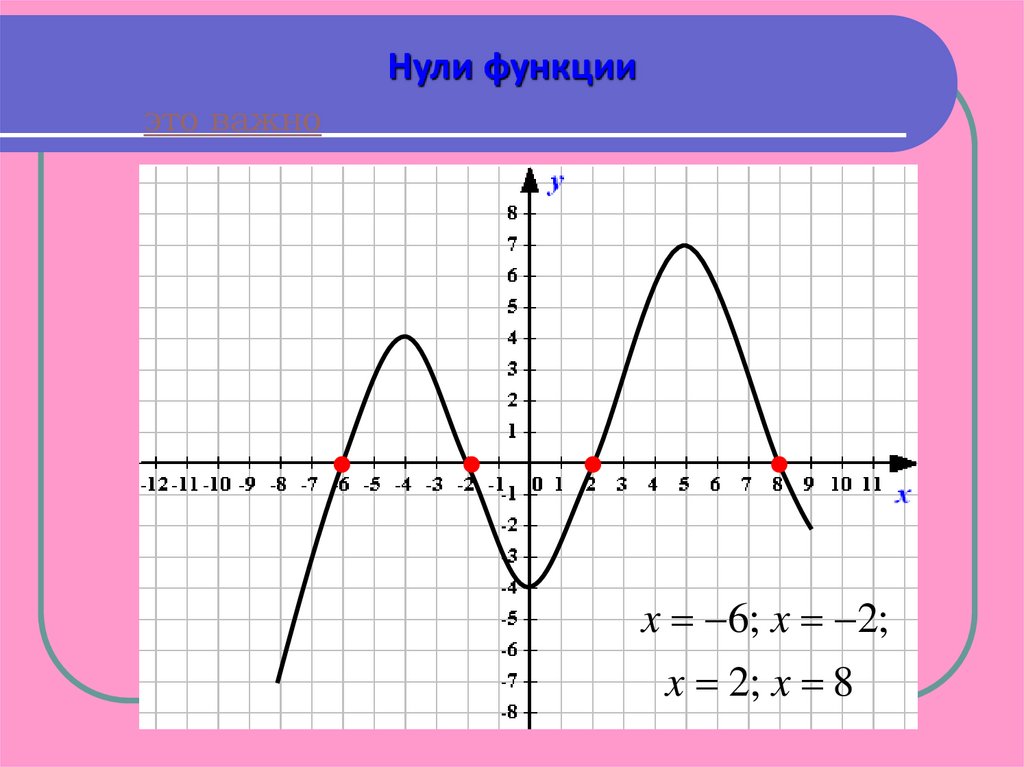
Нули функцииэто важно
x 6; x 2;
x 2; x 8
9.
Интервалы знакопостоянствафункции
Это промежутки, на которых функция
y(х) принимает положительные
(отрицательные) значения.
назад
10.
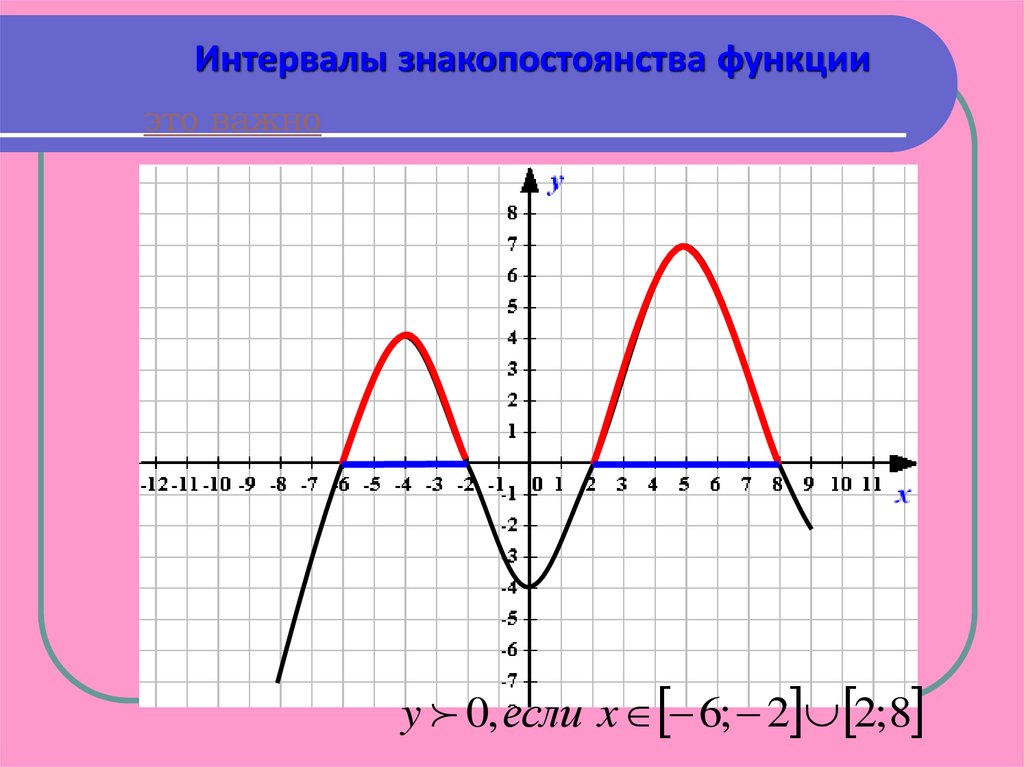
Интервалы знакопостоянства функцииэто важно
y 0, если x 6; 2 2; 8
11.
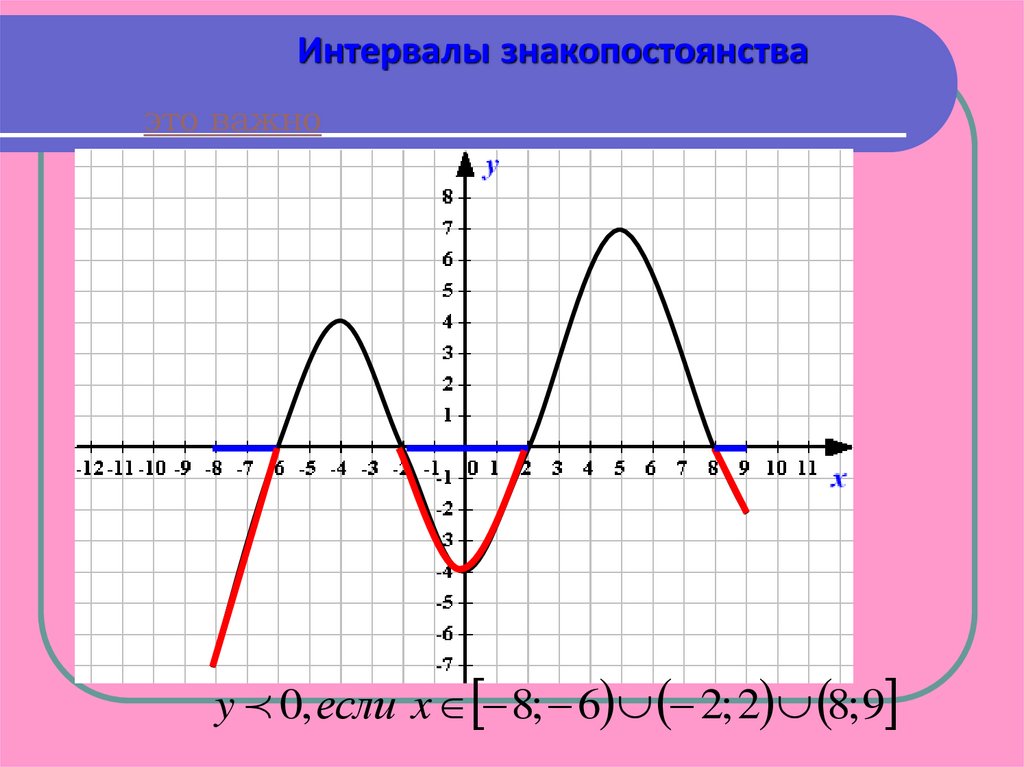
Интервалы знакопостоянстваэто важно
y 0, если x 8; 6 2; 2 8; 9
12.
Монотонность функцииФункция y(х) убывает на множестве P,
если для любых x1 и x2 из множества P
(x1 < x2), выполнено неравенство
y (x2) < y (x1)
назад
Функция y(х) возрастает на множестве P,
если для любых x1 и x2 из множества P
(x1 < x2), выполнено неравенство
y (x2) > y (x1)
назад
13.
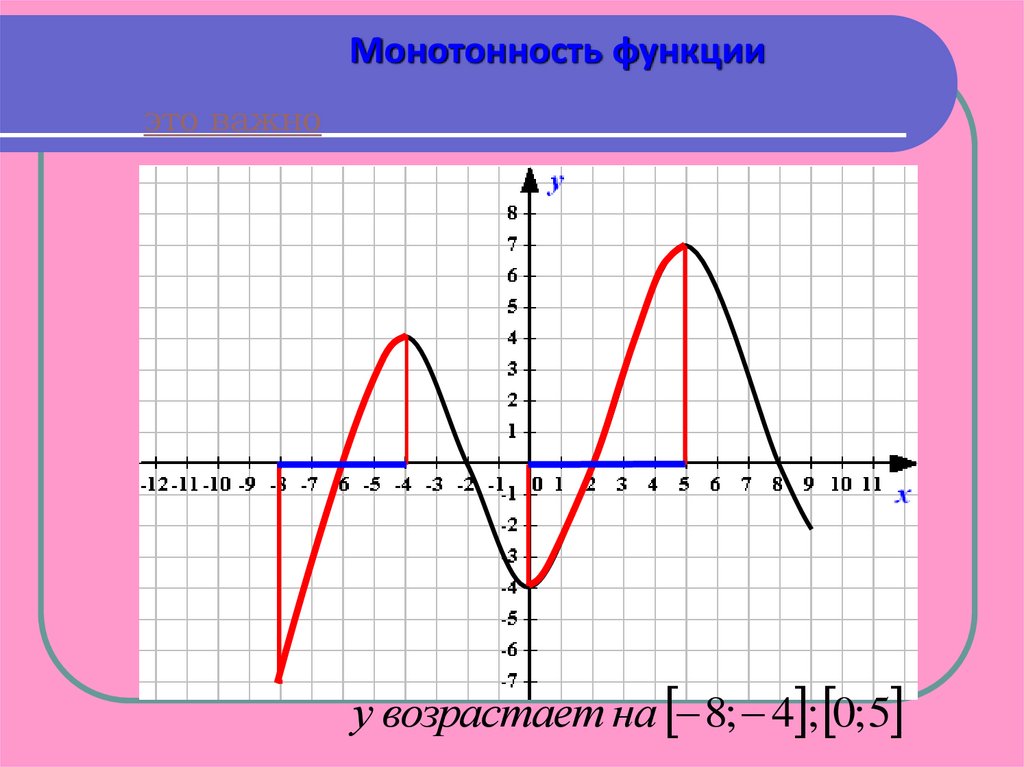
Монотонность функцииэто важно
у возрастает на 8; 4 ; 0; 5
14.
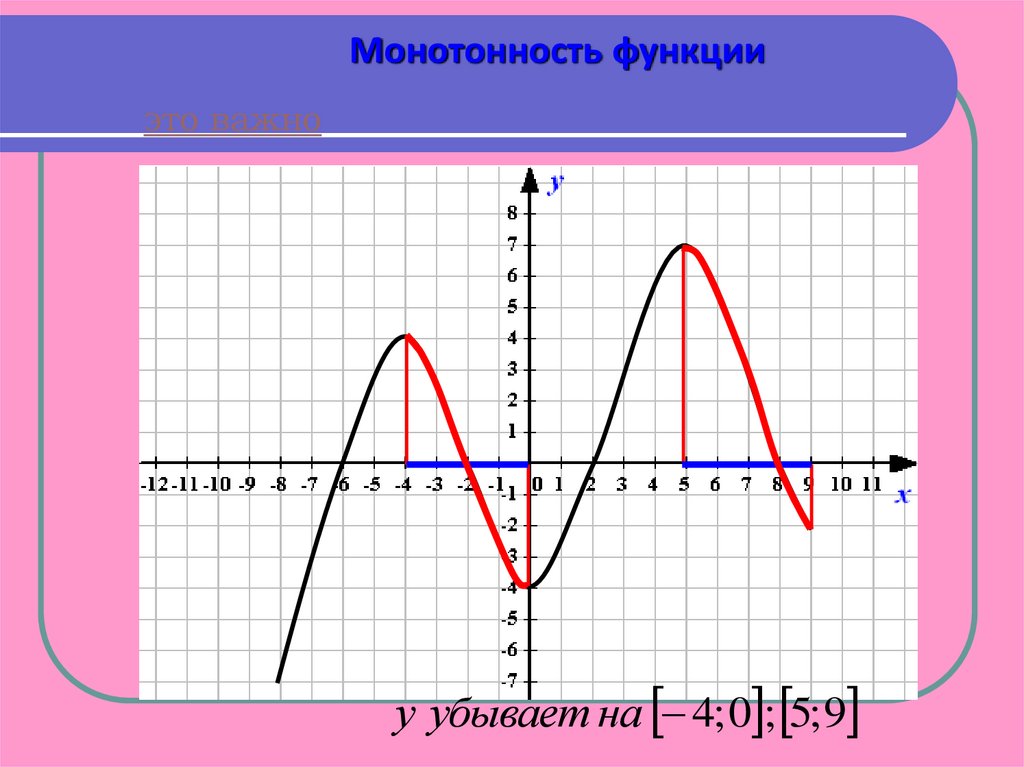
Монотонность функцииэто важно
у убывает на 4; 0 ; 5; 9
15.
Точки экстремума функцииТочка x0 называется точкой минимума функции
y(х), если для всех x из некоторой окрестности
x0 выполнено неравенство
y ( x) y ( x0 )
Точка x0 называется точкой максимума функции
y(х), если для всех x из некоторой окрестности
x0 выполнено неравенство
y ( x) y ( x0 )
назад
16.
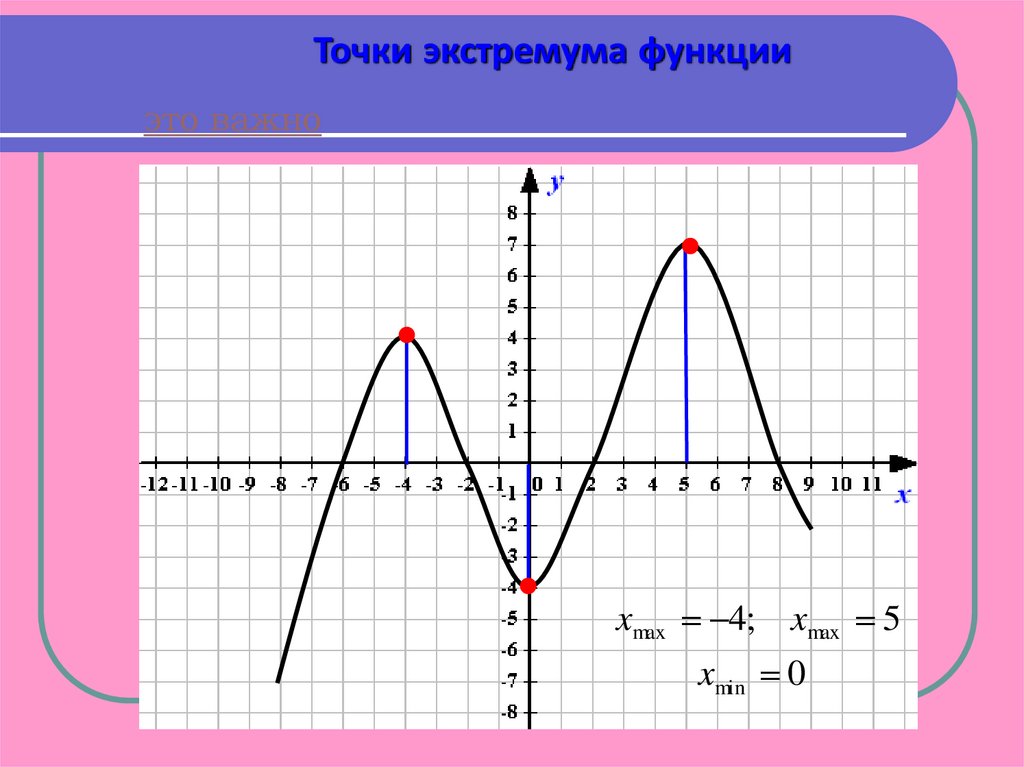
Точки экстремума функцииэто важно
xmax 4; xmax 5
xmin 0
17.
Экстремумы функцииЗначение функции в точках
максимума называют максимумом
функции.
Значение функции в точках
минимума называют минимумом
функции.
Общее название – экстремумы
функции.
назад
18.
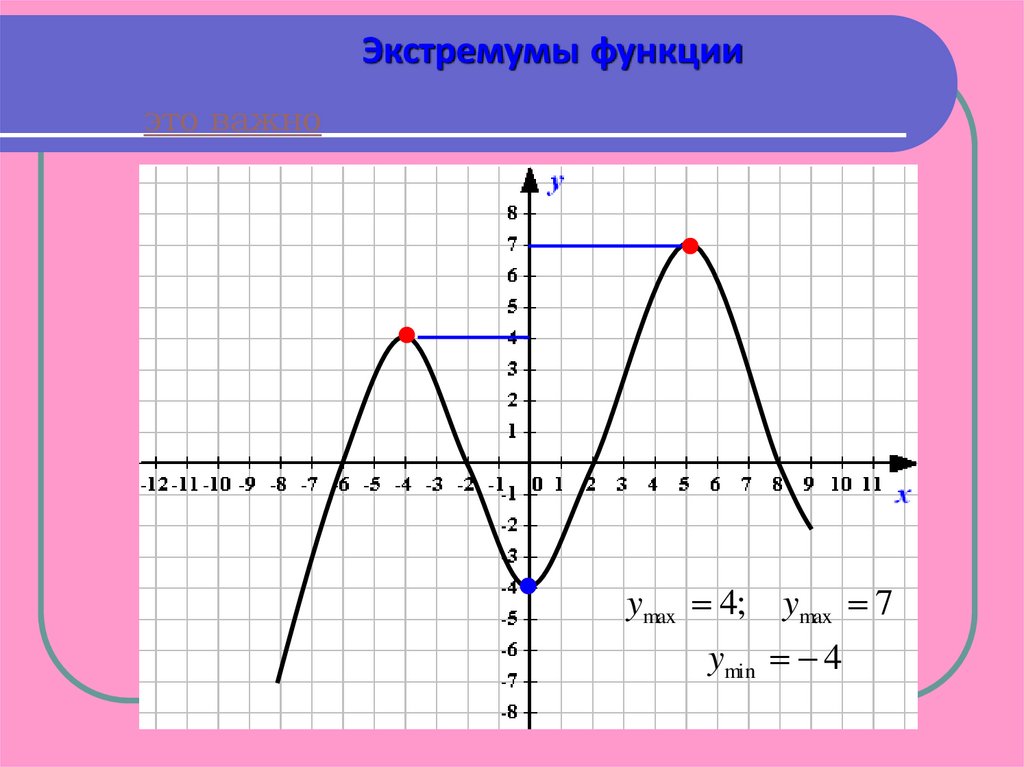
Экстремумы функцииэто важно
ymax 4;
ymax 7
ymin 4
19.
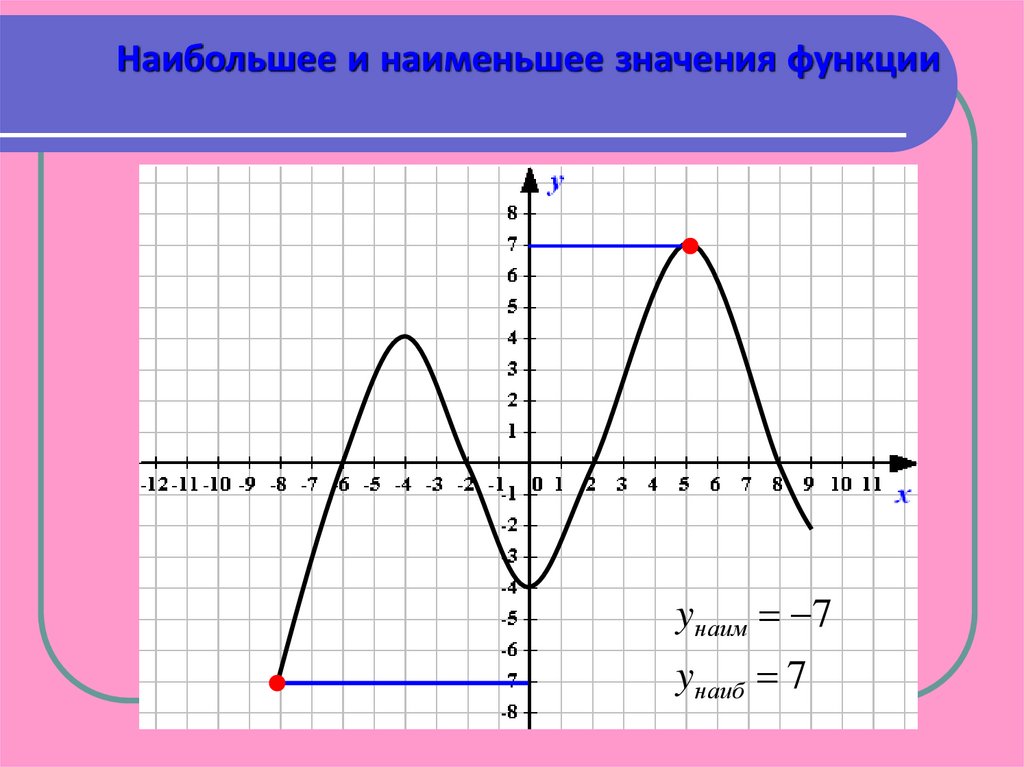
Наибольшее и наименьшее значения функцииyнаим 7
yнаиб 7
20.
!!!!Следует различать понятия точек экстремумаи экстремумов функции
Точки экстремума – точки максимума и минимума
функции , это значения на оси ОХ
Значения функции, которые соответствуют точкам
экстремума называют экстремумами функции, это
значения на оси ОУ
назад










 Математика
Математика








