Векторы в пространстве

1. Векторы в пространстве

вход

2. Вычитание векторов

Вычитание
Сложение с противоположным

3. Вычитание

Разностью векторов и a называется
такой
b
вектор, сумма которого с вектором равна
b
вектору .
a

4. Вычитание

Для вычитания одного вектора из другого необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от этой же точки А отложить вектор AC,
равный b
3. вектор CB называется разностью векторов a и b
B
a
b
Правило трех точек
a
a b
A
b
C

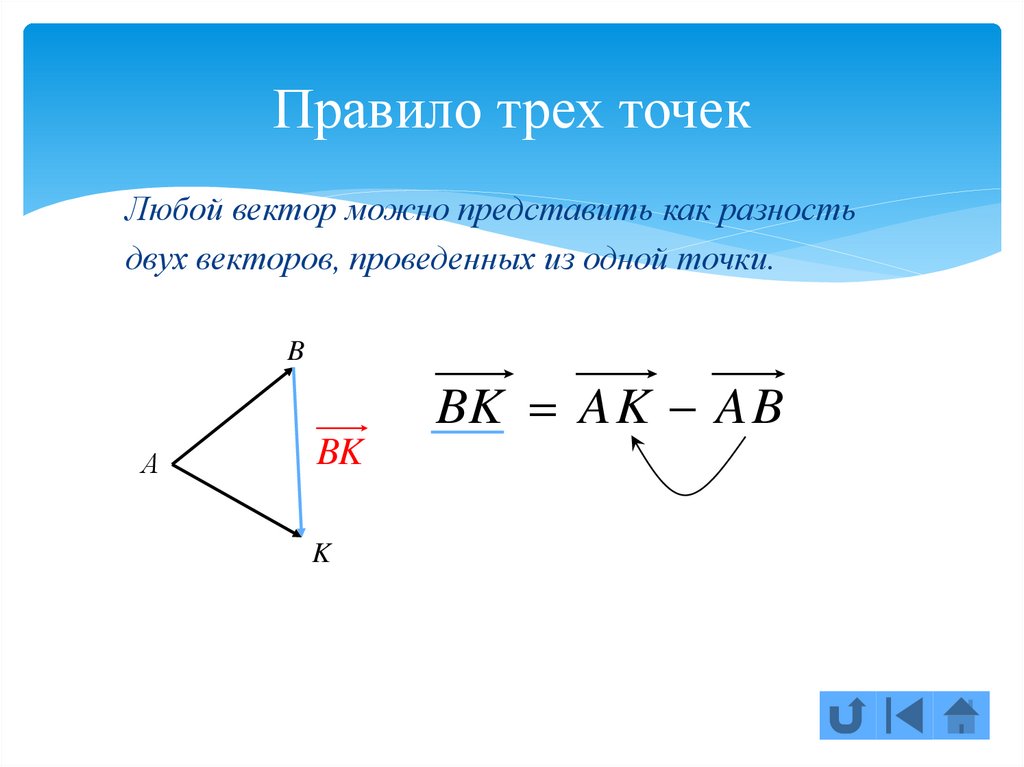
5. Правило трех точек

Любой вектор можно представить как разность
двух векторов, проведенных из одной точки.
B
BK AK AB
А
BK
K

6. Сложение с противоположным

Разность векторов
сумму вектора
вектору
.
a и b можно представить как
иaвектора, противоположного
b
a b a b
a
B
b
a b
b
O
А
a

7. Умножение вектора на число

Произведением ненулевог о вектора a на число k
называется такой вектор b , длина которог о
равна к а , при чем векторы a и b сонаправле ны
при k 0 и противоположно направлены при k 0.
a
2a
b
1
b
3

8. Свойства

Произведением нулевого вектора на любое число
0 n 0
считается нулевой вектор.
Произведение любого вектора на число нуль есть
n 0 0
нулевой вектор.

9. Свойства

Для любыхвект оровa и b и любых
чисел k, l справедливы равенст ва:
(kl)a k(la )
сочет ат ельный закон
k( a b ) k a k b
1 ый распределит ельный
закон
(k l)a k a l a
2 ой распределит ельный
закон

10. Скалярное произведение

Скалярным произведением двух векторов
называется произведение их длин на косинус угла
между ними.
ab a b cos( a ; b )
Справедливые утверждения
Вычисление скалярного произведения в координатах
Свойства скалярного произведения

11. Справедливые утверждения

скалярное произведение ненулевых векторов
равно нулю тогда и только тогда, когда эти
векторы перпендикулярны
a b 0 a 0 b 0 a b
скалярный квадрат вектора (т.е. скалярное
произведение вектора на себя) равен квадрату
его длины
2
a
а
2
а
2

12. Вычисление скалярного произведения в координатах

Скалярное произведен ие векторов a x1 ; y1 ; z1
и b x 2 ; y 2 ; z 2 выражается формулой
a b x 1 x 2 y1 y 2 z 1 z 2
Доказательство

13. Доказательство формулы скалярного произведения

Доказатель ство :
I . при a 0 или b 0, равенство
ab x1 x2 y 1 y2 z1 z 2 справедливо, т.к . 0 0;0;0
II . при a 0, b 0
О произвольн ая точка
B
b
OA a, OB b
если a и b неколлинеа рны, то
α a
AB 2 OA 2 OB 2 2 OA OB cosα ( по т еоремOекосинусов)
A
это равенство верно и в том случае когда векторы
a и b коллинеарн ы
O
B
A
2
2
cosα 1, AB (OA OB)
2
2
OA OB 2OA OB
2
2
OA OB 2OA OBcosα
B
b
O
a
A
2
2
cosα 1, AB (OA OB)
2
2
OA OB 2OA OB
2
2
OA OB 2OA OBcosα

14. Доказательство формулы скалярного произведения

Так как AB b a , OA a , OB b , то
2
2
2
1
ab ( a b b a )
2
a x1 ; y1 ; z1 b x2 ; y2 ; z 2 b a x2 x1 ; y2 y1 ; z 2 z1
2
2
a x y z , b x22 y22 z 22 ,
2
1
2
1
2
1
2
b a (x2 x1 )2 (y 2 y1 )2 (z 2 z1 )2
1
ab (x12 y12 z12 x22 y22 z 22 (x2 x1 )2 (y 2 y1 )2
2
1
(z 2 z1 )2 ) (x12 y12 z12 x22 y22 z 22 x22 2x1 x2
2
x12 y22 2y1 y2 y12 z 22 2z1 z 2 z12 ) x1 x2 y1 y2 z1 z 2

15. Свойства скалярного произведения

Для любых векторов a , b и с и любого
числа k справедливы равенства :
10.
2
a 0 причем a 0 при a 0
20. a b ba (переместительный закон)
(распределительный
0
a
b
c
a
c
b
c
3.
закон)
40. k a b k a b (сочетательный закон)

16. Разложение вектора

По двум неколлинеарным векторам
По трем некомпланарным векторам

17. Разложение вектора по двум неколлинеарным векторам

Теорема.
Любой вектор можно разложить по двум
данным неколлинеарным векторам, причем
коэффициенты разложения определяются
единственным образом.
Доказательство

18. Доказательство теоремы

Дано :
b
a, b неколлинеа рные
векторы
Доказать :
p
a
P
B
p
a
A
p коллинеарен b .
p yb , где y –
1)Пусть
Тогда
некоторое число.
Следовательно,
b
O
p x a yb
Доказатель ство :
A1
p 0 a y b
т.е. p разложен по
векторам a и b .

19. Доказательство теоремы

2) p не коллинеарен ни вектору a , ни вектору b .
Отметим О – произвольную точку.
OA a OB b OP p
PA1 BO PA1 OA A1
p OA1 A1 P(пп правилу треугольника)
но : OA1 и A1 P коллинеарн ы a и b соответственно,
значит OA1 x a , A1 P yb ,
следовательно p x a yb , т.е. p разложен по a и b
ч.т.д.

20. Доказательство теоремы

Докажем, что коэффициенты разложения
определяются единственным образом.
Допустим: p x1 a y1 b
Тогда: p x a y b z c
1
1
-
1
p x a yb z c
0 (x x1 )a (y y1 )b
x x1 0, y y1 0,
если бы x x1 0 то a
y y1
b
x x1
а значит a , и b коллинеарн ы, что
противоречит условию теоремы
значит x x1 0, y y1 0, откуда
x x1 и y y1 .

21. Разложение вектора по трем некомпланарным векторам

Если вектор p представлен в виде
p xa yb z c
где x, y, z – некоторые числа, то говорят, что вектор
разложен по векторам
,
и
.
Числа
a b c разложения.
p x, y, z называются коэффициентами
Теорема
Любой вектор можно разложить по трем данным
некомпланарным векторам, причем коэффициенты
разложения определяются единственным образом.
Доказательство

22. Доказательство теоремы

P
С
pB
с b P2
O
P1
aA
Доказательство :
О произвольн ая точка
Дано :
abc
некомпланр ные
векторы
p x a yb z c
OA a OB b OC c OP p
AP OC AP (AOB) P1 P2 P1 OB
OP OP2 P2 P1 P1 P
OP2 , и OA , PP1 и OB , P1 P , OC коллинеарны
OP2 x OA , P2 P1 y OB , P1 P z OC
OP x OA y OB z OC
p x a yb z c ч.т.д.

23. Доказательство теоремы

Докажем, что коэффициенты разложения определяются единственным образом.
Допустим:
Тогда:
p x1 a y1 b z1 c
p x a yb z c
-
p x1 a y1 b z1 c
0 (x x1 )a (y y1 )b (z z1 )c
x x1 0, y y1 0, z z1 0
x x1
y y1
если бы z z1 0 то с
a
b
z z1
z z1
а значит a , b , и с компланарн ы, что
противоречит условию теоремы
значит x x1 , y y1 , z z1

24. Базисные задачи

Вектор, проведенный в середину отрезка
Вектор, проведенный в точку отрезка
Вектор, соединяющий середины двух отрезков
Вектор, проведенный в центроид треугольника
Вектор, проведенный в точку пересечения
диагоналей параллелограмма
Вектор, лежащий на диагонали параллелепипеда

25. Вектор, проведенный в середину отрезка,

равен полусумме векторов, проведенных из той же
точки в его концы.
С
A
B
O
1
1
1
OC ( OA OB ) OA OB
2
2
2
Доказательство

26. Доказательство

С
A
B
O
Доказательство :
OC OA AC
OC OB BC
Дано :
AB отрезок
AC CB
Доказать :
1
OC ( OA OB )
2
2OC OA AC OB BC OA OB (
AC
BC
)
o
2OC OA OB 2
1
OC ( OA OB ) ч.т.д.
2

27. Вектор, проведенный в точку отрезка

Точка С делит отрезок АВ в отношении т : п.
A
m
Сn
B
O
n
m
OC
OA
OB
m n
m n
Доказательство

28. Доказательство

A
m
Сn
B
Дано :
AB отрезок
AC m
CB n
O
Доказатель ство :
OC OA AC
Доказать :
n
m
OC
OA
OB
m n
m n
m
m
AC
AB
(OB OA)
m n
m n
m
m
OC OA
OB
OA
m n
m n
m
m
OA
OA
OB ч.т.д.
m n
m n

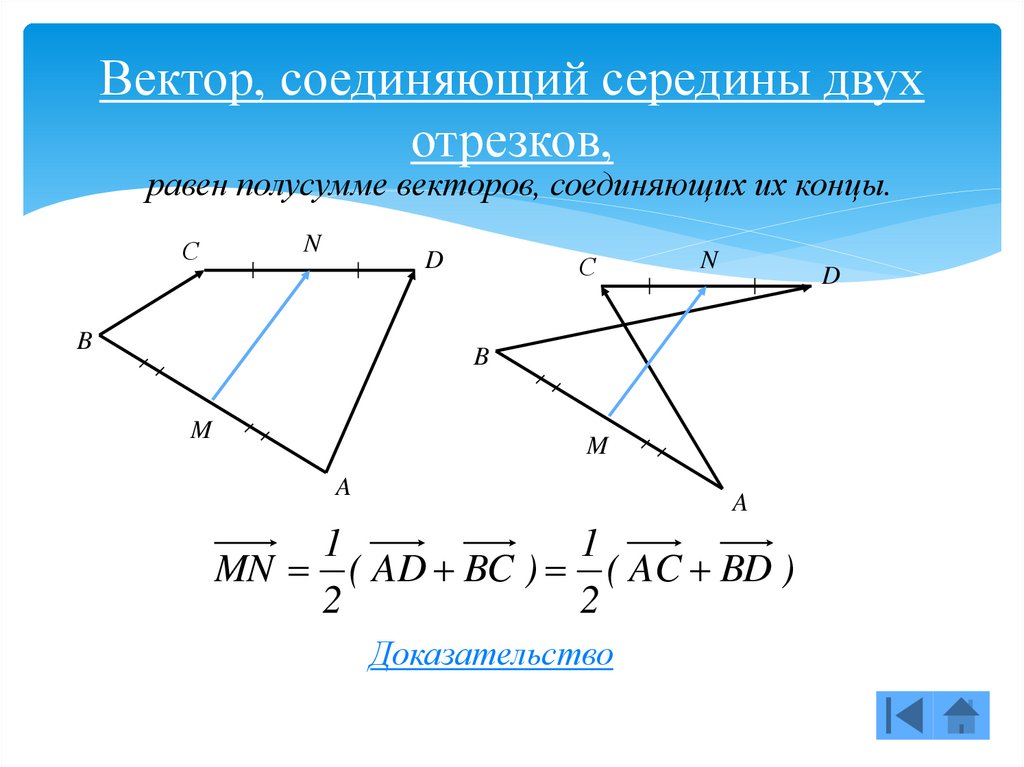
29. Вектор, соединяющий середины двух отрезков,

равен полусумме векторов, соединяющих их концы.
С
N
D
B
С
N
D
B
M
M
A
A
1
1
MN ( AD BC ) ( AC BD )
2
2
Доказательство

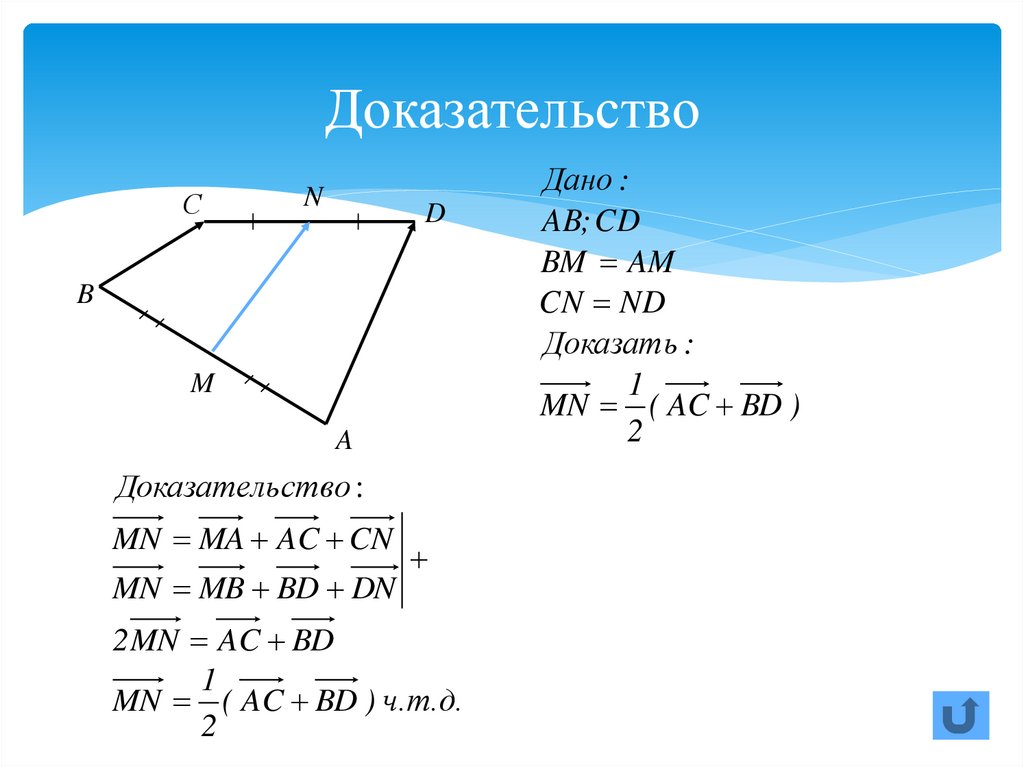
30. Доказательство

С
N
D
B
M
A
Доказатель ство :
MN MA AC CN
MN MB BD DN
2 MN AC BD
1
MN ( AC BD ) ч.т.д.
2
Дано :
AB; CD
BM AM
CN ND
Доказать :
1
MN ( AC BD )
2

31. Вектор, проведенный в центроид треугольника,

равен одной трети суммы векторов, проведенных из
этой точки в вершины треугольника.
Центроид – точка пересечения медиан
треугольника.
O
С
A
M
B
1
OM ( OA OB OC )
3
Доказательство

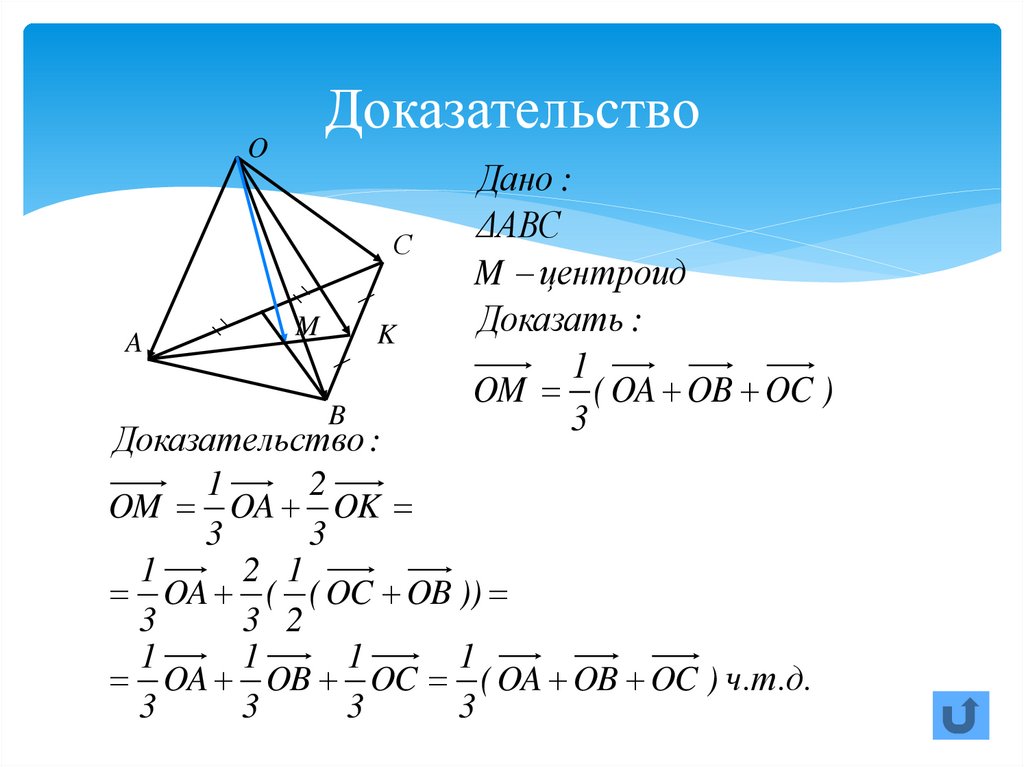
32. Доказательство

O
С
A
M
K
B
Дано :
ΔABC
M центроид
Доказать :
1
OM ( OA OB OC )
3
Доказательство :
1
2
OM OA OK
3
3
1
2 1
OA ( ( OC OB ))
3
3 2
1
1
1
1
OA OB OC ( OA OB OC ) ч.т.д.
3
3
3
3

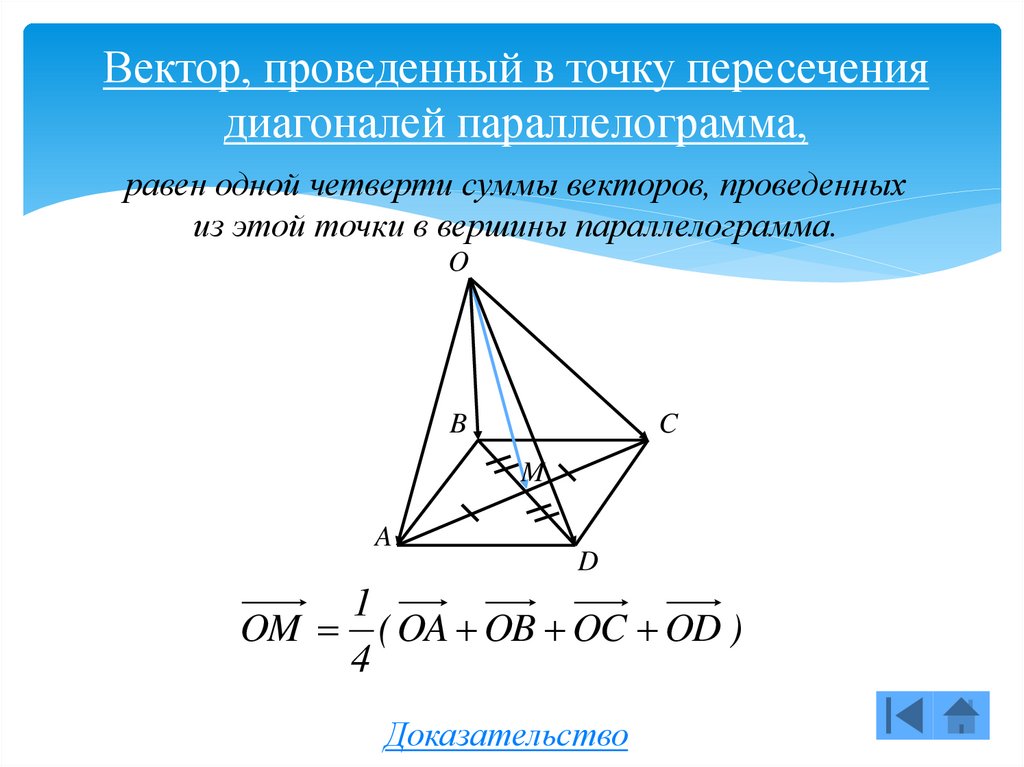
33. Вектор, проведенный в точку пересечения диагоналей параллелограмма,

равен одной четверти суммы векторов, проведенных
из этой точки в вершины параллелограмма.
O
C
B
M
A
D
1
OM ( OA OB OC OD )
4
Доказательство

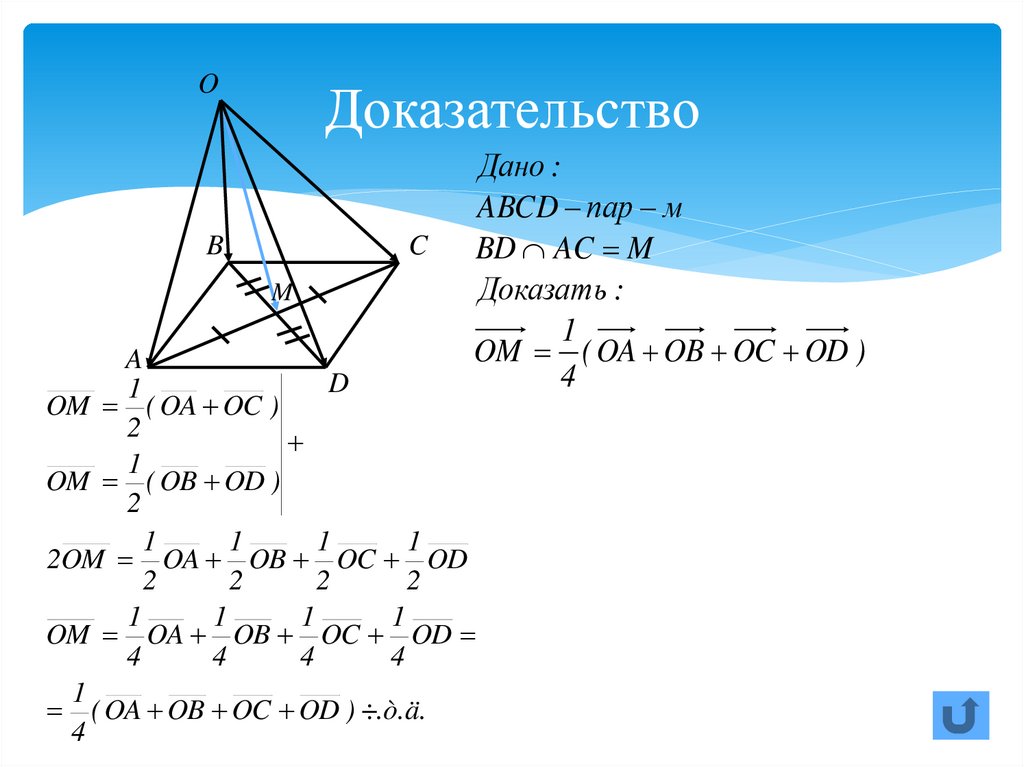
34. Доказательство

O
Доказательство
B
C
M
Дано :
ABCD пар м
BD AC M
Доказать :
1
OM ( OA OB OC OD )
4
A
D
1
OM ( OA OC )
2
1
OM ( OB OD )
2
1
1
1
1
2OM OA OB OC OD
2
2
2
2
1
1
1
1
OM OA OB OC OD
4
4
4
4
1
( OA OB OC OD ) ÷.ò.ä.
4

35. Вектор, лежащий на диагонали параллелепипеда,

равен сумме векторов, лежащих на трех его ребрах,
исходящих из одной вершины.
B1
C1
A1
a
A
d
D1
B
C
b
с
D
d a b c
Доказательство

36. Доказательство

Дано :
B1
C1
A1
a
A
d
AA1 a
D1
B
C
b
D
с
Доказательство :
AC1 AA1 AB1 BC1
AA1 AB AD
a b c ч.т.д.
ABCDA1B1C1D1 пар м
AB b
AD c
AC1 d
Доказать :
d a b c

37. Ответить на вопросы (ответы записать в тетрадь)

Справедливо ли утверждение:
а) любые два противоположно направленных
вектора коллинеарны?
б) любые два коллинеарных вектора сонаправлены?
в) любые два равных вектора коллинеарны?
г) любые два сонаправленных вектора равны?
д) если a b, b c, то a c ?
е) существуют векторы a , b и c такие, что a
и c не коллинеарны, b и c не коллинеарны, а a
и b коллинеарны?
Ответы

38. Задача 1. Задача на доказательство

B1
A1
M
B M1 2
А
Решение
C1
D1
C
D
Дано :
ABCDA1 B1C1 D1 пар д
М 1 , М 2 точки пересечения
медиан ΔА1 ВD и ΔD1CB1
соответственно
Доказать :
AM 1 M 1 M 2 M 2 C1

39. Решение

B1
A1
M
B M1 2
C1
D1
C
Решение
Дано :
ABCDA1 B1C1 D1 пар д
М 1 , М 2 точки пересечения
медиан ΔА1 ВD и ΔD1CB1
соответственно
Доказать :
AM 1 M 1 M 2 M 2 C1
А
D
Доказательство :
Рассм. тетраэдр AA1 BD
M 1 центроид ΔA1 M 1 B
1
AM 1 ( AA1 AB AD )
3
AC1 AA1 AB AD по правилу пар да
1
AM 1 AC1
3
1
M AC1 AM 1 AC1
3
1
аналогично M 2 AC1 C1 M 2 AC1
3
следовательно AM 1 M 1 M 2 M 2 C1 ч.т.д.

40. Задача 2. Разложение векторов

Разложите вектор по a, b и c :
D
N точка пересечения
медиан ABC
a
A
а)
б) DB
в) CB
г) DC
DN
Решение
b
B
N
c
C

41. Решение

а) DB b a
б) CB b c
в) DC c a
г) DN a 1 AN a 1 ( 1 ( b c ))
3
1
1
a b c
6
6
3 2

42. Задача 3. Сложение и вычитание

Упростите выражения:
а)
б)
в)
г)
д)
е)
CM MK
DM MA
SD ST
PL PK
AC BC PM AP BM
AD MP EK EP MD
Решение

43. Решение

а) CM MK CK
б) DM MA DA
в) SD ST TD
г) PL PK KL
д) AC BC PM AP BM
AC CB MP PA BM
AB MA BM AM MA 0
е) AD MP EK EP MD
AD DM MP PE EK
AK

44. Задача 4. Скалярное произведение

Вычислить скалярное произведение векторов:
C1
B1
A1
D1
a
B
A
а) AD B1C1
б) AC C 1 A1
в)D1 B AC
г)BA1 BC 1
Решение
C
D
Дано :
ABCDA1 B1C1 D1 куб
AB a

45. Задача 4. Скалярное произведение

Вычислить скалярное произведение векторов:
B1
C1
O1
A1
D1
a
B
A
д) A1O1 A1 C1
е)DO1 B1O1
ж)BO1 C1 B
Решение
C
D
Дано :
ABCDA1 B1C1 D1 куб
AB a
A1C1 B1 D1 O1

46. Решение

2
а) AD B1C1 AD AD 2 a 2
б)AC диагональ квадрата
AC A1C1 C1 A1
AC C 1 A1 AC ( A1C1 ) AC A1C1 (a 2 )2 2a 2
в)D1 B диагональ куба
D1 B a 2 (a 2 )2 3a(п( т.Пифагора из ΔDD1 B)
2
a3 3
D1 B AC 3a 2 a 2 cos45 a 3 6
2
г)BA1 , BC 1 диагонали квадратов
ΔA1 BC 1 равносторонний, A1 BC 1 60
1 2a 2
a2
BA1 BC 1 a 2 a 2
2
2

47. Решение

д)A1O1 половина диагонали квадрата
A1C1 диагональ квадрата
O1 A1C1 0
a 2
A1O1 A1 C1
a 2 cos0 a 2
2
е)D1O1 , B1O 1 половины диагонали квадрата
a 2 a 2
a2
D1O1 B1O1 D1O1 ( O1 B1 )
2
2
2

48. Решение

ж)I способ решение по определению :
B1
C1
O1
a 2 2 a 6
A1
BO1 a 2 (
)
D1
2
2
C1 B диагональ квадрата
c
B
1
1
C
b a
O1 BC 1 A1 BC 1 60 30
2
2
A
a 6
3 2 D
BO1 C1 B BO1 ( BC 1 )
a 2 cos30 a
2
2
II способ разложение по базису :
1
1
BO1 a b c
2
2
C1 B b a
2
1
1
BO1 C1 B ( a b c ) ( a b ) ( a ab
2
2
2
1
1
1
1 2
1 2
3
a c bc ab b ) ( a a ) a 2
2
2
2
2
2
2