Похожие презентации:
Предел функции в точке и на бесконечности. Свойства пределов. Замечательные пределы
1. Предел функции в точке и на бесконечности. Свойства пределов. Замечательные пределы.
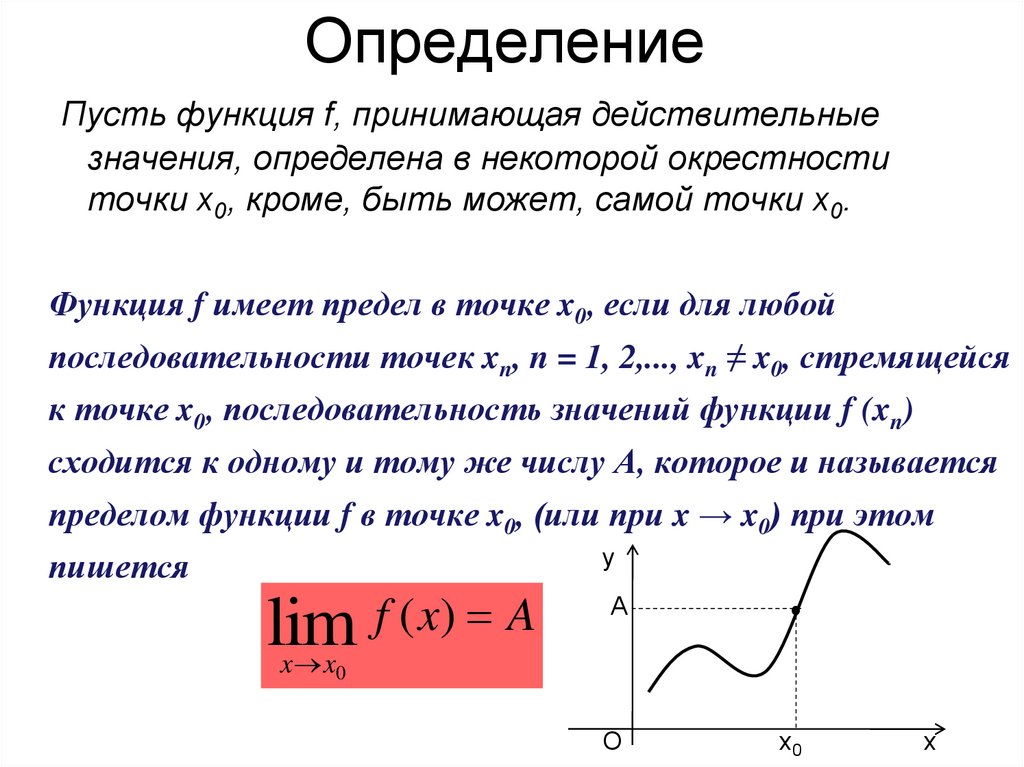
2. Определение
Пусть функция f, принимающая действительныезначения, определена в некоторой окрестности
точки x0, кроме, быть может, самой точки x0.
Функция f имеет предел в точке x0, если для любой
последовательности точек xn, n = 1, 2,..., xn ≠ x0, стремящейся
к точке x0, последовательность значений функции f (xn)
сходится к одному и тому же числу А, которое и называется
пределом функции f в точке x0, (или при x → x0) при этом
у
пишется
lim
f ( x) A
А
x x0
О
х0
х
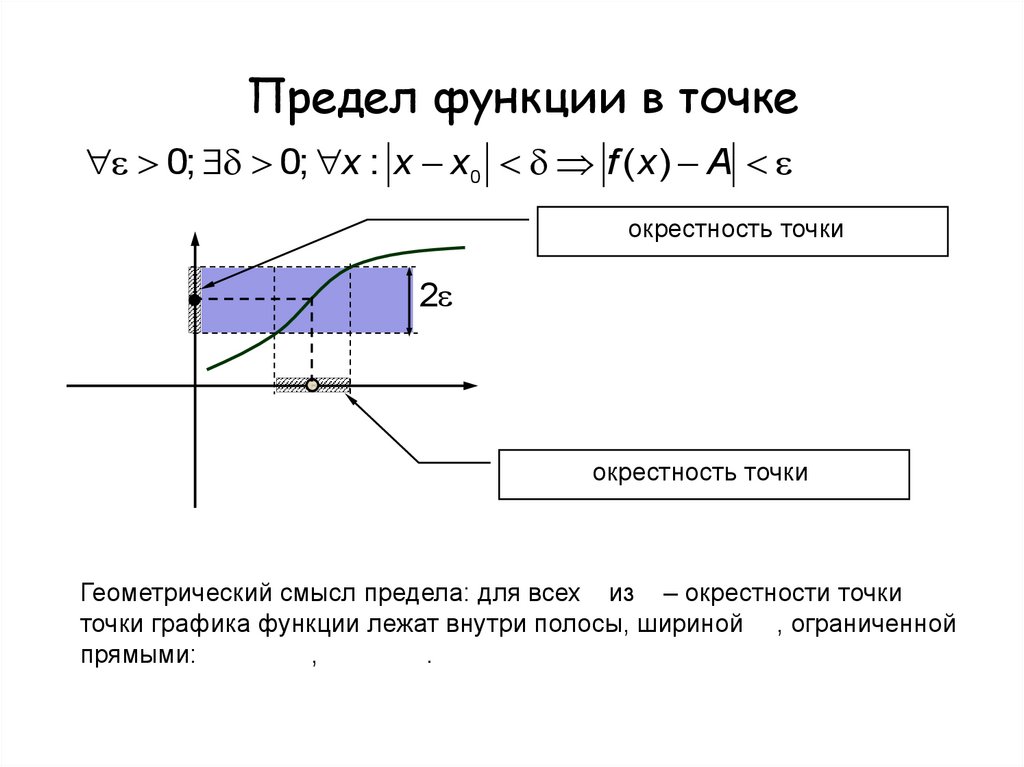
3. Предел функции в точке
0; 0; x : x x0 f ( x ) Aε окрестность точки А
y
2
А
0
х0
х
δ окрестность точки x0
Геометрический смысл предела: для всех х из δ – окрестности точки x0
точки графика функции лежат внутри полосы, шириной 2ε, ограниченной
прямыми: у = А + ε , у = А - ε .
4. Определение
Число А называется пределомфункции f в точке x0, если для любого
числа ε > 0 существует такое число
δ > 0, что для всех точек х ≠ x0,
удовлетворяющих условию
|х — x0| < δ, x ≠ x0, выполняется неравенство
у
|f (x) — A| < ε.
lim f ( x) A
А+ε
А
А-ε
x x0
О
х0
х0-δ
х0+δ
х
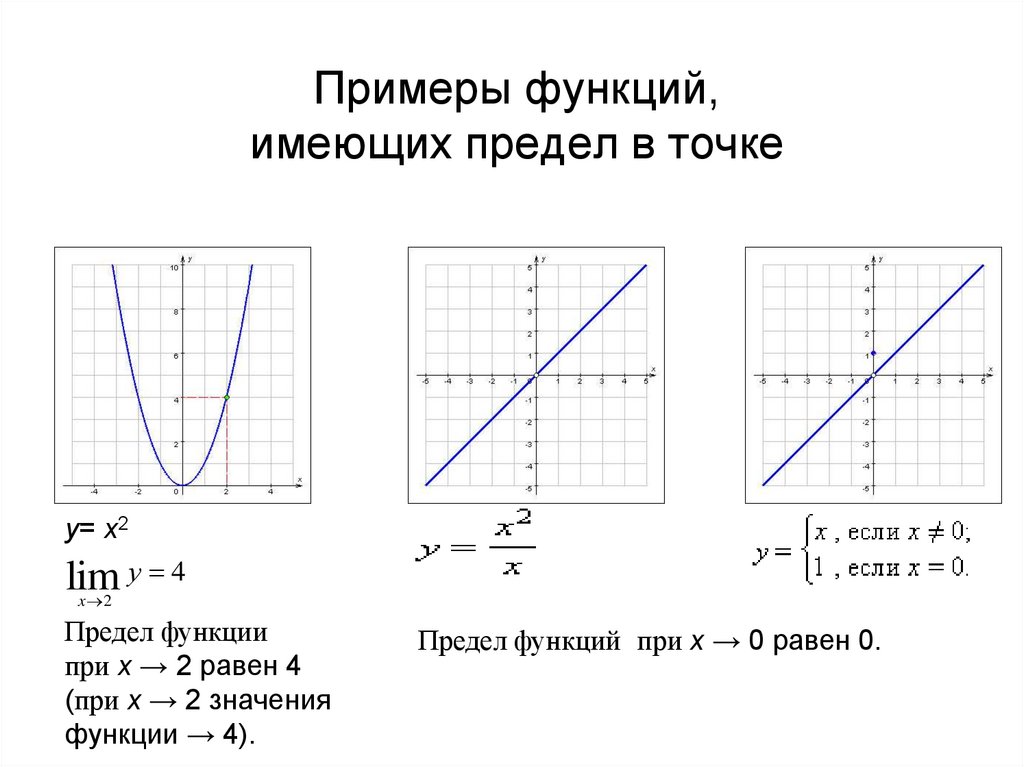
5. Примеры функций, имеющих предел в точке
у= x2lim у 4
x 2
Предел функции
при x → 2 равен 4
(при x → 2 значения
функции → 4).
Предел функций при x → 0 равен 0.
6.
Примеры функций,не имеющих предел в точке
у
у
у
А
1
О
х
-1
О
а
х
О
а
х
7. Основные теоремы о пределах
Рассмотрим теоремы, которые облегчают нахождение пределов функций.Формулировка теорем, когда x
будем пользоваться обозначением:
x0или x аналогичны, поэтому
lim f ( x. )
Предел суммы (разности) двух функций равен сумме (разности)
пределов:
lim f1( x ) f2 ( x ) limf1( x ) limf2 ( x )
Предел произведения двух функций равен произведению пределов:
lim f1( x ) f2 ( x ) lim f1( x ) limf2 ( x )
Постоянный множитель можно выносить за знак предела:
lim C f ( x ) C limf ( x )
8. Основные теоремы о пределах
Предел дроби равен пределу числителя, деленному на пределзнаменателя, если предел знаменателя не равен нулю:
f1( x ) lim f1( x )
lim
f2 ( x ) lim f2 ( x )
lim f ( x ) 0
2
Предел степени с натуральным показателем равен той же степени
предела:
lim f ( x ) lim f ( x )
n
n
Предел показательно – степенной функции:
lim f ( x )
g(x)
lim f ( x )
lim g ( x )
9. Основные теоремы о пределах
Если между соответствующими значениями трех функцийu u( x );
z z( x ); v v ( x )
выполняются неравенства:
u z v, при этом:
lim u( x ) lim v ( x ) A
тогда:
lim z( x ) A
Если функция f(x) монотонна и ограничена при x < x0 или при
x > x0, то существует соответственно ее левый предел:
lim f ( x ) A1
x x0 0
или ее правый предел:
lim f ( x ) A2
x x0 0
10. Вычисление пределов
Вычисление предела:lim f ( x ) A
x x
0
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому числу.
3x 1
3 1 1
lim
2
2
2
x 1
x
1
Если при подстановки предельного
значения x0 в функцию f(x) получаются
выражения вида:
то предел будет равен:
C
0
C
0
11. Вычисление пределов
Часто при подстановке предельного значения x0 в функцию f(x)получаются выражения следующих видов:
0
;
0
; 0 ; 1 ; 0 0 ; 0 ; 0 ;
Эти выражения называются неопределенности, а вычисление пределов
в этом случае называется раскрытие неопределенности.
12. Вычисление предела функции в точке
Сначала просто пытаемся подставить число в функциюlim ( x 2 5x 8) 9 15 8 2
x 3
Найдем
x2 5x 8
lim 2
.
x 3 x x 4
Предел числителя
lim ( x 2 5x 8) 9 15 8 2
x 3
Предел знаменателя
lim ( x 2 x 4) 9 3 4 10
x 3
.
Используя теорему о пределе частного, получим
lim ( x 2 5 x 8)
x 5 x 8 x 3
2 1
lim 2
.
2
x 3 x x 4
lim ( x x 4) 10 5
2
x 3
13.
Найдемx 2 5x 8
lim
.
x 3
x 3
Предел числителя
lim ( x 2 5x 8) 9 15 8 2
x 3
Предел знаменателя равен нулю, поэтому теорему о пределе
частного применять нельзя.
Величина 1/(x-3) является бесконечно большой величиной при
x→3.
Тогда
x 2 5x 8
lim
.
x 3
x 3
14. Раскрытие неопределенностей
Раскрытие неопределенности0
0
x 2 14 x 32
0
x 2 x 16
lim 2
lim
x 2
x 2
x 6x 8
0
x 2 x 4
x 16 18
lim
9
x 2
x 4
2
lim
x 0
Если f(x) – дробно –
рациональная функция,
x 1 1 x 1 1
0 на
x 1 1
необходимо разложить
lim Если f(x) – иррациональная
множители числитель
и x 0 дробь, необходимо умножить
0
x
x x 1 1
знаменатель дроби
числитель и знаменатель дроби
x 1 1
на1выражение,1сопряженное
lim
lim
числителю.
x 0
x 0
x x 1 1
x 1 1 2
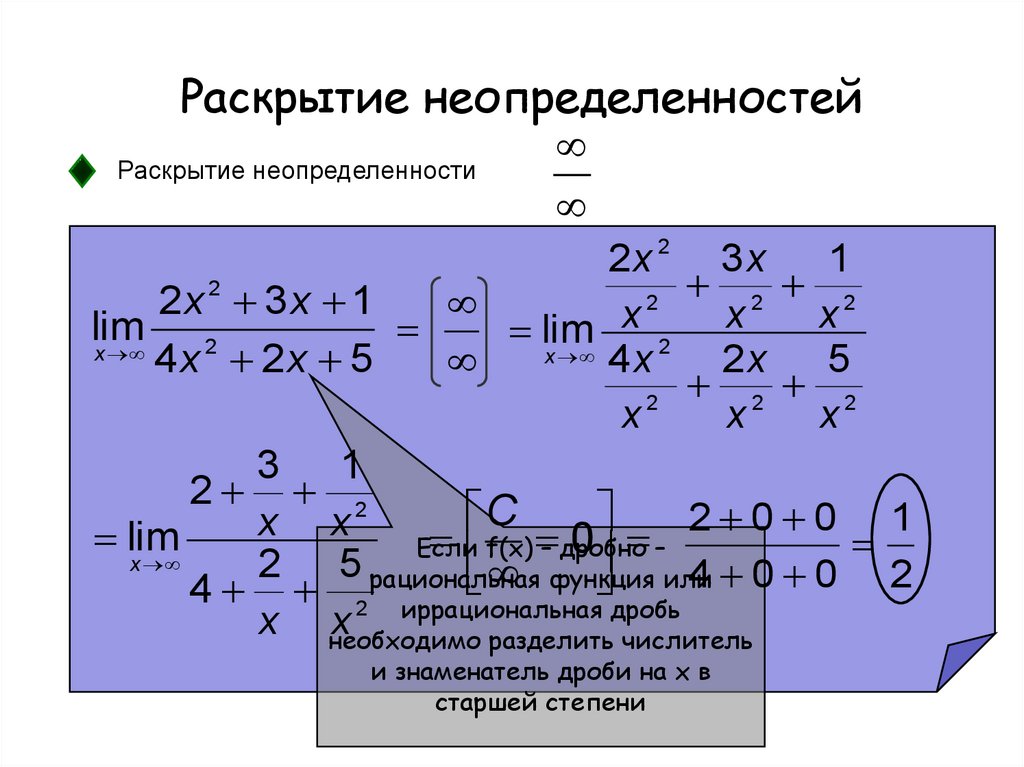
15. Раскрытие неопределенностей
Раскрытие неопределенности2x 2 3 x 1
2 2
2
2x 2 3 x 1
x
x
x
lim 2
lim
x
x 4 x 2
2x 5
4 x 2x 5
2 2
2
x
x
x
3 1
2 2
C
2 0 0 1
x
x
lim
f(x) – дробно
0 –
Если
x
2 5 рациональная
4 0 0 2
функция
или
4 2 иррациональная
дробь
x необходимо
x
разделить числитель
и знаменатель дроби на x в
старшей степени
16. Раскрытие неопределенности
Для того, чтобы раскрыть неопределенность ∞/∞ необходиморазделить числитель и знаменатель на х в старшей степени.
Разделим числитель и знаменатель на х2
17.
Разделим числитель и знаменатель на х418.
Разделим числитель и знаменатель на х2подразумевается не деление на ноль (делить на ноль нельзя), а деление на
бесконечно малое число.
Таким образом, при раскрытии неопределенности
может получиться конечное число, ноль или
бесконечность.
19. Раскрытие неопределенностей
Раскрытие неопределенностиlim x 2 1 x 2 1
x
lim
x
lim
x
x 1 x 1
2
(x
2
2
2
0
2
x2 1 x2 1
Умножим
и разделим функцию
2
1) ( x на
1сопряженное
)
выражение.2
x 1 x 1
2
x 1 x 1
2
2
lim
x
x 1 x 1
2
2

















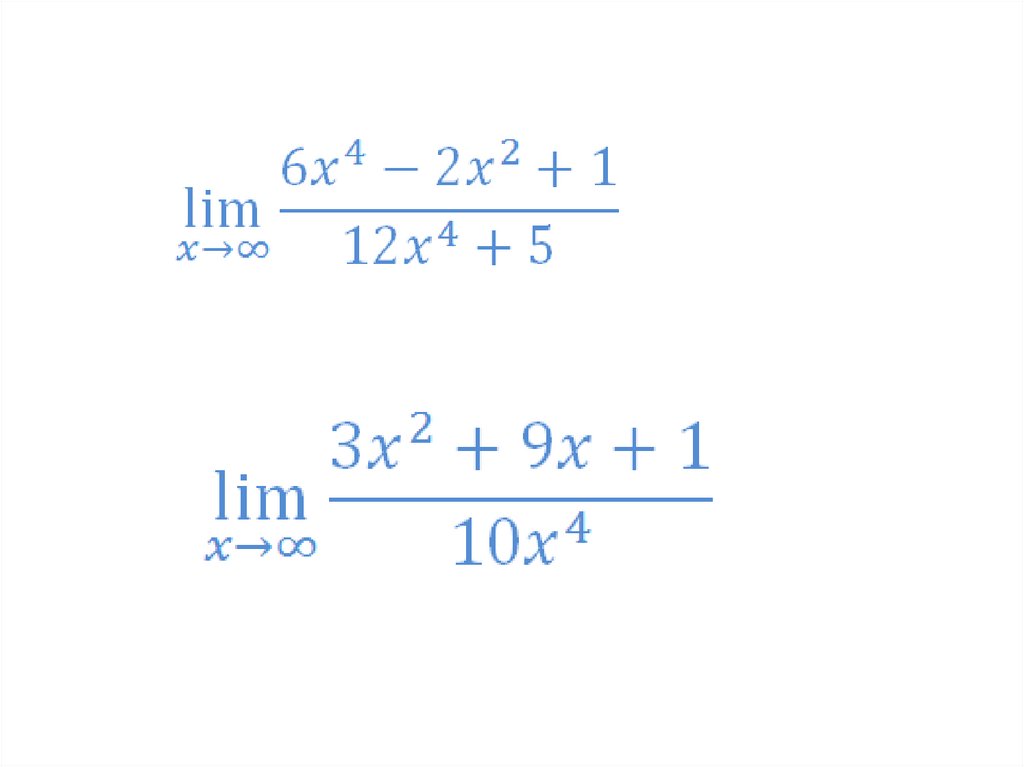
 Математика
Математика








