Похожие презентации:
Вероятное моделирование взаимодействия сооружения с основанием при расчете на землетрясение
1.
2.
2ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ…………………………………………………………………………..
Глава
1.
ОСНОВНЫЕ
ПОДХОДЫ
К
5
ОБЕСПЕЧЕНИЮ
СЕЙСМОСТОЙКОСТИ ЗДАНИЙ И СООРУЖЕНИЙ……………..................
14
1.1. Основные положение теории сейсмостойкости……………………..................
14
1.1.1. Методы теории сейсмостойкости…………………………………………
14
1.1.2. Нелинейные статические методы…………………………………………
19
1.1.3. Нелинейные динамические методы………………………………………
20
1.2. Модели грунтов основания при расчете на землетрясения……………………
23
1.2.1. Модель Мора-Кулона………………………………………………………
24
1.2.2. Модель Друккера-Прагера…………………………………………………
27
1.2.3. Шатровая модель (Cam-Clay)………………………………........................
29
1.2.4.
Модель
с
упрочнением
(Hardening
и
Soil)
ее
модификация……………………………………………………………………….
31
1.2.5. Динамические инерционные модели………………………………………
34
1.2.6. Достоинства и недостатки моделей основания при расчете на
землетрясение……………………………………………………………………….
1.3.
Основные
положения
теории
надежности
и
теории
вероятностей……………………………………………………………………………
1.3.1.
Вероятностный
анализ
метода
предельных
моделирования
сейсмического
состояний……..........................
1.3.2.
Методы
вероятностного
37
38
38
воздействия…………………………………………………………………………...
41
Выводы по главе 1………………………………………………………………………
43
Глава 2. МОДЕЛИРОВАНИЕ СОВМЕСТНОЙ РАБОТЫ СИСТЕМЫ
СООРУЖЕНИЕ ОСНОВАНИЕ
ПРИ
РАСЧЕТЕ
НА
ЗЕМЛЕТРЯСЕНИЕ……………………………………...……………………………
45
2.1. Методика моделирования неотражающих границ………………….....................
45
2.1.1.
Основные
положения
метода
демпфирующего
PML-
слоя………....................................................................................................................
45
3.
32.1.2.
Эффективность
работы
демпфирующего
PML-
слоя……...…………………………………………………………………………….
2.2.
Учет
взаимодействия
сооружения
с
основанием
в
49
корректной
постановке………………………………………………………………........................
53
2.2.1. Используемая методика учета взаимодействия сооружения с основанием
(Soil Structure Interaction - SSI)………………………..............................................
53
2.2.2. Взаимодействие между сооружением и грунтом основания во время
землетрясения………………………………………………………………………..
2.2.3.
Методы
расчета
сооружения
с
учетом
взаимодействия
54
с
основанием…………………………………………………………………………...
56
2.2.4. Численная верификация используемой методики учета взаимодействия
сооружения
с
основанием…………………………………………………………………………..
59
2.2.5. Пример расчета сооружения с учетом взаимодействия сооружения с
основанием по методике SSI…………………………............................................
2.3.
Модифицированная
модель
Мора-Кулона
с
введением
62
критерия
разрушения……………………………………………………………………………..
66
2.3.1. Исследование реакции 15-ти этажного каркасного железобетонного
здания на сейсмическое воздействие………………………………………………
68
2.3.2. Детерминированный расчет 15-ти этажного каркасного железобетонного
здания
с
учетом
повреждений
основания,
возникающих
в процессе
землетрясения………………………………………………………………………..
Выводы по главе 2……………………………………………………………………..
73
76
Глава 3. ОСОБЕННОСТИ ДЕТЕРМИНИРОВАННЫХ РЕШЕНИЙ ПРИ
УЧЕТЕ ВЗАИМОДЕЙСТВИЯ СООРУЖЕНИЯ С ОСНОВАНИЕМ ПРИ
РАСЧЕТЕ НА ЗЕМЛЕТРЯСЕНИЕ…………………………………………………
78
3.1. Учет взаимодействия сооружения с основанием, и трансформация
сейсмического воздействия при землетрясении……………………………………..
78
3.2. Сравнительный анализ реакции 5-ти этажного здания с использованием
модели основания в виде линейно-деформируемого полупространства и модели
Мора-Кулона……………………………………………………………………………
99
3.3. Анализ реакции железобетонного здания повышенной этажности при 102
4.
4различных моделях грунтового основания….………………………………………..
3.4. Методика расчета 9-ти этажного железобетонного здания перекрестностеновой конструктивной схемы при сейсмическом воздействии………………….. 106
Выводы по главе 3………………………………………………………………………
Глава
4.
ВЕРОЯТНОСТНАЯ
ЗАДАЧА
109
ВЗАИМОДЕЙСТВИЯ
СООРУЖЕНИЯ С ОСНОВАНИЕМ………………………………………………..
112
4.1. Вероятностные параметры грунтового основания………………………………. 112
4.2. Надежность системы сооружение–основание при случайном сейсмическом
воздействии, нормированном на интенсивность 8 баллов…………………………..
113
4.3. Надежность системы сооружение–основание при случайном сейсмическом
воздействии, нормированном на интенсивность 9 баллов…………………………...
4.4.
Исследование
землетрясение
при
реакции
9-ти
случайных
этажного
начальных
железобетонного
повреждениях
здания
122
на
грунтового
основания…..
125
Выводы по главе 4………………………………………………………………………
128
ЗАКЛЮЧЕНИЕ…………………………………………………………….................
130
СПИСОК ЛИТЕРАТУРЫ……………………………………………………………
134
ПРИЛОЖЕНИЯ……………………………………………………………………….
145
Приложение А…………………………………………………………………. 145
Приложение Б………………………………………………………………….
151
Приложение В………………………………………………………………….
162
5.
5ВВЕДЕНИЕ
Актуальность темы исследования. Одним из самых разрушительных явлений
природы является землетрясение. В соответствии с картами общего сейсмического
районирования, около 40% территории России являются сейсмически опасными. На Земле
ежегодно происходят более 15 разрушительных катастрофических землетрясений, и около
150 землетрясений средней интенсивности. К мерам предупреждения разрушительных
последствий землетрясений можно отнести: создание достоверных карт сейсмического
районирования, применение адекватных норм сейсмостойкого строительства и новых
методик расчета зданий и сооружений на сейсмические воздействия, учитывающих
нелинейный характер деформирования зданий и сооружений и совместную работу
сооружения с нелинейно деформируемым грунтовым основанием, применение методов
теории надежности строительных конструкций и теории вероятностей.
Лежащая в основе действующих норм проектирования линейно-спектральная теория
не позволяет получить достоверную информацию о реакции сооружения во времени при
землетрясении.
Практика
проектирования
и
анализ
последствий
произошедших
землетрясений свидетельствует о том, что расчетное сейсмическое воздействие должно
назначаться с учетом параметров самой конструкции и являться наихудшим для
сооружения. При проведении расчетов в более строгих постановках необходимо
использовать соответствующие нелинейные методы расчета, которые позволят учитывать
физическую, геометрическую и конструктивную нелинейности в работе надфундаментных
конструкций и грунта основания. Наиболее адекватно расчет может быть произведен
только с применением нелинейных динамических методов расчета, которые позволяют
получить решения во временной области, и которые основываются на прямом
интегрировании уравнений движения.
Особые требования необходимо предъявлять и к самому расчетному воздействию.
Так как сейсмическое воздействие является ярко выраженным нестационарным случайным
процессом, то при расчете необходимо использовать методы теории надежности и теории
случайных процессов. При этом одним из возможных подходов может быть использование
представительного набора акселерограмм, который содержит записи ускорений различной
интенсивности, спектрального состава и продолжительности, а также использование
методов непосредственного моделирования случайного сейсмического воздействия.
6.
6Для обеспечения требуемой сейсмостойкости необходимо использовать методики,
позволяющие корректно учитывать взаимодействие сооружения с основанием и оценивать
надежность всей системы. В этом случае расчеты следует производить в вероятностной
постановке, принимая параметры грунта случайными, а сейсмическое воздействие
представлять в виде нестационарного случайного процесса.
Учет вышеперечисленных особенностей возможен только при использовании
современных
расчетных
комплексов,
а
также
мощных
и
производительных
вычислительных систем, в том числе позволяющих производить параллельные вычисления.
Степень разработанности темы диссертации. Проблемами сейсмостойкого
строительства, развитием динамических методов расчета, а также проблемами учета
взаимодействия конструкции с грунтом основания занималось большое количество
отечественных и зарубежных ученых. Проблему учета взаимодействия конструкции с
грунтом основания изучали Д.Д. Баркан, Н. Бируля, Б.К. Карапетян, А.З. Кац, И.Т.
Мирсаяпов, А.Г. Назаров, Ш.Г. Напетвиридзе, А.Л. Невзоров, А.Е. Саргсян, Н.К. Снитко,
З.Г. Тер-Мартиросян, А.Г. Тяпин, М.Т. Уразбаев, Дж. Хаузнер, Э.Е. Хачиян и другие [7, 29,
28, 31, 38, 39, 59, 61, 62, 63, 71, 84, 85, 86, 87, 88, 89, 105, 106].
Исследования по учету влияния протяженности сооружения на его сейсмостойкость
провели Г.П. Кобидзе, И.Л. Корчинский, Ш.Г. Напетваридзе, А.П. Синицын, Дж. Хаузнер и
другие [34, 35, 61, 73, 105, 106].
Пространственную работу строительных конструкций изучали А.Г. Берая, В.К.
Егупов, Т.А. Командрина, М.А. Марджанишвили, Ю.П. Назаров, Н.А. Николаенко, А.П.
Сапожников [11, 25, 32, 37, 60, 64].
Различные вопросы теории сейсмостойкости специальных сооружений нашли свое
отражение в работах И.И. Гольденблата, Г.А. Джинчвелашвили, Г.Н. Карцивадзе, Б.Г.
Коренева, Ш.Г. Напетваридзе, Н.А. Николаенко, Т.Р. Радишидова, Т.Г. Сагдиева, А Е
Саргсяна, М.Т. Уразбаева, Г.Э. Шаблинского и других авторов [20, 21, 30, 33, 56, 61, 64, 71,
90].
Проблемы
применения
методов
теории
вероятностей
к
оценке
эффекта
сейсмического воздействия на сооружения исследовали Р.О. Амасян, Я.М. Айзенберг, М.Ф.
Барштейн, В.А. Багдавадзе, В.В. Болотин, И.И. Гольденблат, С.С. Дарбинян, А.М. Жаров,
В.Л. Мондрус, О.В. Мкртычев, А.Г. Назаров, Н.А. Николаенко, Э.Ф. Пак, Ю.И. Романов, В.
И. Смирнов, А.Г. Тамразян, С.В. Ульянов и другие [1, 2, 3, 8, 9, 13, 14, 15, 20, 21, 23, 24, 26,
27, 57, 58, 64, 69, 70, 74, 83].
7.
7Вопросы оценки надежности системы сооружение основание при случайном
сейсмическом воздействии и случайных свойствах грунта основания требуют дальнейшего
развития. Без разработки специальных методик невозможно проектировать здания и
сооружения с требуемым уровнем сейсмостойкости при заданной обеспеченности.
Целью диссертационной работы является исследование надежности зданий,
расположенных на грунтовом основании, при сильных землетрясениях с использованием
прямых динамических методов с учетом нелинейного характера деформирования
конструкций и грунтов основания.
Для достижения указанной цели потребовалось решить следующие задачи:
проанализировать существующие в настоящее время нелинейные модели
грунтов;
проанализировать и обобщить используемые методы детерминированного
расчета зданий и сооружений на землетрясения;
провести апробацию и верификацию расчетных моделей в применяемом
программном комплексе;
проанализировать устойчивость работы нелинейных моделей грунтов при
решении динамических задач с помощью численных методов с использованием прямого
интегрирования уравнений движения;
разработать методику корректного учета совместной работы системы
надфундаментная конструкция фундамент грунт основания при расчете на сейсмическое
воздействие;
решить комплекс задач о расчете систем и зданий различных конструктивных
схем на акселерограммы землетрясений с различным спектральным составом и
интенсивностью;
разработать
методику
детерминированного
расчета
системы
сооружение основание, основанную на модифицированной модели Мора - Кулона с
введением критерия разрушения;
произвести вероятностное моделирование грунтового массива со случайными
параметрами и сейсмического воздействия, как нестационарного случайного процесса;
выполнить
оценку
надежности
системы
сооружение основание
при
случайном сейсмическом воздействии с учетом различного спектрального состава
акселерограмм землетрясений, при случайных параметрах грунта, а также при случайном
положении повреждений основания, возникающих в процессе землетрясения.
8.
8Объектом исследования являются железобетонные здания и системы различных
конструктивных схем, расположенные на грунтовых основаниях при интенсивных
сейсмических воздействиях.
Предметом
исследования
являются:
напряженно-деформируемое
состояние
основания при землетрясении (интенсивность деформаций и напряжений), напряженнодеформируемое состояние железобетонных зданий, распложѐнных на грунтах с разными
характеристиками, при интенсивных сейсмических воздействиях; надежность системы
надфундаментная конструкция фундамент грунт основания при случайном сейсмическом
воздействии и случайных свойствах грунтов основания, а также случайном положении
повреждений основания, возникающих в процессе землетрясения.
Новизна научной работы:
разработана методика корректного учета взаимодействия сооружения с основанием
при расчете на землетрясения;
предложена модифицированная модель грунтового основания Мора – Кулона с
введением критерия разрушения;
проведены численные исследования систем грунт конструкция на землетрясения с
учетом возможной потери прочности грунта основания;
проведены численные исследования совместной работы грунта основания с
железобетонными конструкциями, материал которых был задан с помощью нелинейной
модели, в которой учитывалось фактическое армирование;
проведен
сравнительный
анализ
реакции
зданий
различной
этажности,
расположенных на грунтах, с использованием линейных и нелинейных моделей, на
интенсивное сейсмическое воздействие;
проведен расчет 9-ти этажного жилого железобетонного здания на интенсивное
землетрясение в соответствии с методиками, разработанными в диссертационной работе;
выполнен анализ результатов исследования системы сооружение основание на
сейсмическое воздействие различного спектрального состава и интенсивности;
решена вероятностная задача моделирования взаимодействия сооружения с
основанием при случайных параметрах грунтов, при различной доминантной частоте
случайного сейсмического воздействия, а также при случайном положении повреждений
основания в процессе землетрясения;
9.
9выполнена оценка надежности железобетонного здания при учете совместной работы
с грунтом основания при случайных параметрах сейсмического воздействия и случайных
свойствах грунтов.
Теоретическая значимость работы состоит в развитии методов теории надежности
строительных конструкций, основанных на прямых нелинейных динамических методах
расчета конструкций, в которых используется непосредственное интегрирование уравнений
движения по явным схемам, что позволило получить решения во временной области с
учетом физической, геометрической и конструктивной нелинейностей. Разработанные
методики позволяют учесть совместную работу сооружения с основанием в корректной
постановке (Soil Structure Interaction SSI). В исследованиях применяется теория
демпфирующих слоев (PML - perfectly matched layer), которая позволяет уменьшить
размеры используемого в расчетах массива основания и применить неотражающие
границы. Все это позволило разработать методику оценки надежности рассматриваемых
систем, позволяющую проектировать здания и сооружения с требуемым уровнем
сейсмостойкости при заданной обеспеченности.
Практическая значимость работы заключается в:
использовании результатов проведенных исследований при проектировании
зданий и сооружений в сейсмических районах проектными и исследовательскими
организациями;
возможности применения представленных методик и предложенных подходов
к актуализации документов в области сейсмостойкого строительства;
возможности на стадии проектирования учитывать вероятностную природу
сейсмического воздействия, случайные параметры грунтов основания;
возможности использования разработанной методики при выполнении
нормативных расчетов на землетрясения уровня проектного землетрясения (ПЗ) и уровня
максимально расчетного землетрясения (МРЗ).
Методология
и
методы
исследования.
Методологической
основы
диссертационного исследования являлись труды отечественных и зарубежных авторов в
области сейсмостойкости и надежности строительных конструкций. В диссертационной
работе применялись следующие методы.
Моделирование. Проводилось численное моделирование различных систем
сооружение основание, которые затем рассчитывались на сейсмические воздействия с
помощью прямого нелинейного динамического метода интегрирования уравнений
10.
10движения по явным схемам. Осуществлялось моделирование случайного сейсмического
воздействия с помощью метода канонических разложений.
Сравнение. В процессе проведения исследований сравнивался уровень
надежности железобетонных зданий различных конструктивных схем, расположенных на
линейном и нелинейном грунтовом основании.
Анализ. Все полученные результаты численных расчетов подвергались
подробному анализу, на основании которого делались выводы о работе рассматриваемых
конструкций в процессе землетрясения.
Личный вклад автора диссертации заключается в следующем:
разработана методика корректного учета взаимодействия сооружения с основанием
при расчете на землетрясения;
предложена модифицированная модель грунтового основания Мора – Кулона с
введением критерия разрушения;
проведены численные исследования систем грунт конструкция на землетрясения с
учетом возможной потери прочности грунта основания;
проведены численные исследования совместной работы грунта основания с
железобетонными надфундаментными конструкциями, материал бетона для которых был
задан с помощью нелинейной модели Continuous Surface Cap Model (CSCM), в которой
учитывалось фактическое армирование, при этом материал арматуры задавался с помощью
идеально-упруго пластической модели Прандтля с ограничением предельных пластических
деформаций;
проведен
сравнительный
анализ
реакции
зданий
различной
этажности,
расположенных на грунтах, заданных по различным моделям, на интенсивное сейсмическое
воздействие;
проведен расчет 9-ти этажного жилого железобетонного здания на интенсивное
землетрясение с использованием разработанной методики;
выполнено вероятностное моделирование взаимодействия сооружения с основанием
при случайных параметрах грунтов, при различном спектральном составе сейсмического
воздействия, а также при случайном положении повреждений основания, возникающих в
процессе землетрясения;
выполнена оценка надежности 9-ти этажного железобетонного здания при учете
совместной работы с грунтом основания при случайных параметрах сейсмического
воздействия и случайных свойствах грунтов.
11.
11Представленные в диссертационной работе исследования, включающие численное
моделирование конструкций, грунтов основания, проведение расчетов, сравнение, анализ и
апробация полученных результатов, были выполнены лично автором.
Достоверность результатов достигается:
использованием при постановке задач гипотез, принятых в механике
деформируемого твердого тела, в механике грунтов, в теории сейсмостойкости, теории
надежности строительных конструкций, теории вероятностей и теории случайных
процессов;
сравнением полученных результатов с экспериментальными данными и
аналитическими решениями, полученными другими авторами по ряду исследуемых в
работе вопросов;
применением при расчете современных апробированных численных методов
расчета строительных конструкций и оснований, а также расчетных программных
комплексов.
Апробация работы. Основные положения диссертационной работы были доложены
на:
III Всероссийской (II Международной) конференции по бетону и железобетону
«Бетон и железобетон взгляд в будущее», Москва, РАН, 2014 г.
III
Международной
научно-практической
конференции
21
век:
фундаментальная наука и технологии, Москва, 2014 г.
XI Всероссийской научно-практической и учебно-методической конференции
«Фундаментальные науки в современном строительстве», Москва, МГСУ, 2014 г.
VI Международной научно-практической конференции «Научно-техническое
творчество молодежи – путь к обществу, основанному на знаниях», Москва, 2014 г.
XXIII, XXIV, XXV, XXVI R-S-P Seminar «Theoretical Foundation of Civil
Engineering», Вроцлав, Самара, Жилина, Варшава, 2014, 2015, 2016, 2017 гг.
XIII
Всероссийской
научно-практической
конференции
«Современная
строительная наука и образование», Москва, НИУ МГСУ, 2016 г.
V International conference «Integration, partnership and innovation in construction
science and education», Москва, НИУ МГСУ, 2016 г.
г.
7th International Conference on Mechatronics, Control and Materials, Китай, 2016
12.
12международной
XX
межвузовской
научно-практической
конференции
студентов, магистров, аспирантов и молодых ученых «Строительство – формирование
среды жизнедеятельности», Москва, НИУ МГСУ, 2017 г.
В полном объеме диссертационная работа докладывалась на объединенном
заседании кафедр «Сопротивление материалов» и «Механика грунтов и геотехника»
ФГБОУ
ВО
«Национальный
исследовательский
Московский
государственный
строительный университет» (г. Москва, 2018 г.).
Публикации. Научные результаты достаточно полно изложены в 20 научных
публикациях, из которых 4 работы опубликованы в журналах, включенных в Перечень
рецензируемых научных изданий, в которых должны быть опубликованы основные
научные результаты диссертаций на соискание ученой степени кандидата наук, на
соискание ученой степени доктора наук. А также представлены в одном объекте
интеллектуальной
собственности:
базе
данных
«Библиотека
методов
расчета
многоэлементных систем на сейсмическое воздействие с учетом взаимодействия с грунтом
основания в корректной постановке».
На защиту выносятся:
методика детерминированного расчета систем сооружение основание в
корректной постановке;
результаты исследований систем грунт конструкция на землетрясения с
учетом возможной потери прочности грунта основания;
результаты
исследований
совместной
работы
грунта
основания
с
железобетонными конструкциями, материал которых был задан с помощью нелинейной
модели, в которой учитывалось фактическое армирование;
результаты сравнительного анализа работы зданий различной этажности,
расположенных на грунтах, заданных по различным моделям, на интенсивное сейсмическое
воздействие;
результаты
детерминированного
расчета
9-ти
этажного
жилого
железобетонного здания на интенсивное землетрясение;
результаты анализа реакций системы сооружение основание на сейсмическое
воздействие с различным спектральным составом и интенсивностью;
результаты решения вероятностной задачи моделирования взаимодействия
сооружения с основанием при случайных параметрах грунтов, при различных доминантных
13.
13частотах
случайного сейсмического
воздействия, а
также случайном
положении
повреждений грунта основания, возникающих в процессе землетрясения;
результаты выполненной оценки надежности железобетонного здания при
учете совместной работы с грунтом основания при его случайных параметрах и случайном
сейсмическом воздействии, заданном в виде нестационарного случайного процесса.
Структура и объем диссертации. Диссертационная работа состоит из введения,
четырех глав, заключения, списка литературы (127 наименований). Общий объем
диссертации составляет 144 страницы (в том числе приложение 33 страницы), включая 5
таблиц, 168 рисунков.
Соответствие диссертации Паспорту научной специальности. Содержание
диссертации соответствует пунктам 4 и 6 Паспорта специальности 05.23.02 – Основания и
фундаменты, подземные сооружения.
14.
14Глава
1.
ОСНОВНЫЕ
ПОДХОДЫ
К
ОБЕСПЕЧЕНИЮ
СЕЙСМОСТОЙКОСТИ ЗДАНИЙ И СООРУЖЕНИЙ
1.1. Основные положения теории сейсмостойкости
1.1.1. Методы теории сейсмостойкости
Согласно
статической
теории
сейсмостойкости
Ф.
Омори,
сооружение
рассматривается как абсолютно жесткое тело, жестко заделанное в грунт [120]. При
горизонтальных перемещениях основания в движение вовлекаются одновременно все
части сооружения с ускорением, равным ускорению основания.
Развивая теорию сейсмостойкости, в 1920 г. японский ученый Н. Мононобе
рассмотрел установившиеся вынужденные колебания сооружения при движении
основания по гармоническому закону [118].
Первые акселерограммы землетрясений, появившиеся в 30-х годах выявили
сложный характер движения грунта при землетрясениях, не поддающийся точной
математической
американский
интерпретации.
исследователь
Для
М.А.
Био
преодоления
предложил
вскрывшихся
трудностей
экспериментальным
путем
определить динамический эффект, вызываемый землетрясениями, на упрощенной
модели сооружения в зависимости от периода его собственных колебаний [94, 95].
Построив спектры ускорений по акселерограммам, он положил начало спектральному
методу расчета. Экспериментальные исследования землетрясений, проведенные в США,
легли в основу стандартной спектральной кривой, используемой при практических
расчетах.
На основе приближенного подхода к обработке сейсмограмм И.Л. Корчинский
разработал достаточно простую динамическую теорию расчета сооружений на
сейсмические воздействия. Им был получен коэффициент
β-
характеризующий
динамический эффект движения сооружения на основании. Эти работы имели большое
значение
для
внедрения
спектрального
метода
в
практику
проектирования.
Спектральный метод расчета с 1957 года принят в нормах [75].
В теории сейсмостойкости при проведении расчетов строительных конструкций
на землетрясения, так же, как и при решении другого ряда задач с механическими
системами, в основном используются расчетные модели с распределенными либо
дискретными параметрами, в частности массами. Наиболее универсальной, хотя и
15.
15приближенной, является схема с дискретными параметрами. Именно такие модели
обычно используются при выполнении практических расчетов, так как они позволяют
получить решения для схем любой сложности.
При разработке динамических расчетных моделей, заданных как системы с
конечным числом степеней свободы, реальная масса, распределенная по элементам
рассматриваемой конструкции, собирается в определенные места в виде так называемых
материальных точек. Таким образом, фактически при проведении расчетов мы будем
иметь некоторую невесомую систему, которая будет нести заданное количество
сосредоточенных
масс.
Геометрические
параметры,
однозначно
определяющие
положение этих масс в рассматриваемый момент времени, будут определять число
степеней свободы системы.
В областях, в которых сконцентрированы значительные нагрузки, целесообразно
сосредоточить массы исследуемой модели. Адекватность и корректность результатов
расчета напрямую зависят от точного задания расчетной схемы, а также от ее
соответствия реальному поведению конструкции во время землетрясения.
Рассмотрим схему с конечным числом степеней свободы, представленной на
рисунке 1.1.1.
Рисунок. 1.1.1. Расчетная динамическая модель здания, работающего на сдвиг
Пусть на данную систему действуют сейсмические инерционные силы. Используя
метод разложения по формам собственных колебаний, получим уравнение движения
системы:
M U C U K U M Iug (t ).
(1.1.1)
Условия ортогональности собственных форм колебаний будут справедливы для
всех форм колебаний θ m и θ n (m≠n).
16.
16T
θm
m n
n, m n
0,
M θn M
0, m n
T
θm K θn
Kn , m n
(1.1.2)
(1.1.3)
Применив линейное преобразование:
U Φ Y,
(1.1.4)
и подставив уравнение (1.1.2) в уравнение (1.1.1), получим
M Φ Y C Φ Y K Φ Y M Iug (t ).
(1.1.5)
T
При умножении выражения (1.1.5) слева на матрицу Φ , получим
ΦT M Φ Y ΦT C Φ Y ΦT K Φ Y ΦT M Iu (t ).
(1.1.6)
g
Матричное уравнение (1.1.4) представляет собой систему несвязанных уравнений
относительно обобщенной координаты Yn. Используя условия ортогональности (1.1.2) и
(1.1.3), получим:
M jY j C jY j K jY j ΦT M Iu g (t )
2
Y j 2ξ j ω jY j ω j Y j Γ j u g (t ),
или
при Γ j
θj
θj
T
T
M 1
M θ j
(1.1.7)
(1.1.8)
, где j=1,2,…,n фактор влияния форм колебаний.
Общие решения для систем со многими степенями свободы представляются в
виде суперпозиции собственных форм колебаний. Это возможно, потому что движения,
которые описываются координатами
Y , представляют собой гармонические колебания.
Чтобы определить динамическую реакцию воспользуемся линейно-спектральной
теорией (ЛСТ). Пусть спектр ускорений основания будет задан по графику,
изображенному на рисунке 1.1.2, для случая ξ=0,05.
Рисунок. 1.1.2. Спектр ускорения
17.
17Максимальные горизонтальные перемещения по каждому этажу каркаса для
каждой формы колебаний могут быть определены следующим образом:
T
S (ξ j , T j )
θ j M
U max j
θj
.
2
T
ωj
θ j M θ j
(1.1.9)
Эти же перемещения каркаса, но при учете влияния всех форм колебаний будут
иметь вид:
U max j
n
U max
2
.
(1.1.10)
j 1
Тогда инерционные сейсмические силы в уровне каждого этажа могут быть
определены по формуле:
F j M θ j Γ j S (ξ, T j ).
(1.1.11)
Результирующий вектор усилий по этажам:
k
F
.
j 1
n
k 2
Fj
(1.1.12)
На основании вышеизложенного можно сделать вывод, что описанный метод
разложения по собственным формам колебаний, который используется совместно со
спектральной теорией сейсмостойкости для решения динамических задач, имеет
большое прикладное значение.
В основу нормативного варианта линейно-спектральной методики положена
формула (1.1.13), по которой определяются инерционные сейсмические нагрузки,
необходимые для дальнейшего проведения расчетов. Все параметры из этой формулы
получены на основании эмпирических данных уже прошедших землетрясений [41].
Согласно
действующему
СП
[77]
инерционная
сейсмическая
нагрузка,
приложенная к узловой точке k расчетной динамической модели и соответствующая i-й
форме собственных колебаний конструкции, имеет вид
j
j
Sik K0 K1S0ik ,
где
K0
-
коэффициент, который
(1.1.13)
учитывает назначение
сооружения и его
ответственность, K1 - коэффициент, который учитывает допускаемые повреждения
j
конструкции, S0ik - сейсмическая нагрузка для i-й формы собственных колебаний
сооружения, получаемая из предположения об упругой работе конструкции:
18.
18J
S0jik mkj Aβi Kψηik
,
(1.1.14)
j
где mk - масса здания или момент инерции соответствующей массы здания, отнесенные
к точке k по обобщенной координате j, А – значение ускорения в уровне основания, βi коэффициент динамичности, который соответствует i-й форме собственных колебаний
конструкции, K ψ - коэффициент, зависящий от диссипативных свойств конструкций и
J
оснований, ηik - коэффициент, зависящий от формы деформации сооружения при его
собственных колебаниях по i-й форме.
Если говорить о нормативном расчете [77], то в теории сейсмостойкости он
анализируется с двух сторон. Во-первых, предполагается расчет на уровень проектного
землетрясения (слабого и частого). В этом случае расчетные модели зданий и
сооружений следует принимать соответствующими упругой области деформирования.
Расчет проводиться линейно-упругими методами, а предельно допустимые усилия в
элементах конструкции увеличиваются при помощи коэффициента K1 , при этом
предполагается, что при землетрясениях данного уровня здание будет нормально
эксплуатироваться [77]. Во-вторых, для некоторых видов зданий и сооружений
предполагается
проведение
расчетов
на
уровень
максимального
расчетного
землетрясения (сильного и редкого). В этом случае уже необходимо учитывать
конструктивную, физическую и геометрическую нелинейности конструкции, и к таким
расчетам нельзя применять линейно-спектральную теорию, приведенную в СП и
описанную выше. Методы, которые целесообразно применять для проведения расчетов
на уровень максимального расчетного землетрясения, будут разобраны в следующей
главе.
19.
191.1.2. Нелинейные статические методы
Для того чтобы при проведении расчетов на сейсмическое воздействие зданий и
сооружений учитывать различные виды нелинейностей, необходимо применять
нелинейные методы, а именно нелинейно-статические и нелинейно-динамические. Суть
этих методов состоит в проектировании зданий с заданными свойствами. Это один из
важных шагов к корректному проектированию зданий и сооружений разной этажности и
сложности в сейсмических районах. Наиболее часто применяется упругопластический
динамический анализ работы конструкции, который должен проводиться на стадии
проектирования. Данный подход позволяет выполнить оценку колебаний при
землетрясении, однако его реализация достаточно сложна. Более упрощенным методом
является нелинейный статический метод или метод Push over.
Данный метод условно можно условна разделить на 2 этапа. На 1-ом этапе для
рассматриваемой конструкции строится диаграмма нагрузка – перемещение (рисунок
1.1.3), а на 2-ом этапе производится определение сейсмостойкости конструкции в целом
(рисунок 1.1.4).
а)
б)
Рисунок 1.1.3. Диаграмма характеристик
конструкции
Рисунок 1.1.4. Определение характерной
точки свойств конструкции
Нелинейный статический метод позволяет выявлять те недочеты, которые могут
быть сделаны в процессе проектирования. Имея информацию об этих недочетах на
стадии проектирования, появляется возможность на этом же этапе их исправить и уже
на стадии эксплуатации иметь сейсмостойкую конструкцию.
Метод Push over анализа определенно является движением вперед по сравнению с
линейно-спектральным методом, однако он имеет ряд недостатков: рассматривается
однократное нагружение конструкции, силы, по которым строятся кривые несущей
20.
20способности, прикладываются только по первым формам. Перечисленные минусы при
расчете на землетрясения могут существенно влиять на результаты и давать
погрешности.
1.1.3. Нелинейные динамические методы
Используемый в теории сейсмостойкости нелинейный динамический метод
лишен недостатков, указанных для линейно-статического метода.
В основе реализации данного метода лежит дифференциальное уравнение
движения системы (1.1.15). Данное уравнение в матричной форме записано для системы
с конечным числом степеней свободы:
Mu Cu Ku Fa ,
(1.1.15)
здесь u является вектором узловых перемещений, u v – вектором узловых
скоростей, u a – вектором узловых ускорений. В (1.1.15) M является матрицей масс
системы, C – матрицей демпфирования, K – матрицей жесткости, а F
a
– это вектор
нагрузок, которые действуют на систему.
Как уже отмечалось, использование данного метода позволяет решать задачу в
нелинейной
постановке,
то
есть
учитывать
физическую,
геометрическую
и
конструктивную нелинейности. На основании этого стоит отметить, что элементы
матрицы жесткости будут зависеть от напряженно-деформированного состояния
конструкции, а не только от свойств еѐ материала. Иначе говоря, матрица K будет
зависеть
от
некоторого
вектора
перемещений
ut . Таким образом,
решение
дифференциального уравнения (1.1.15) будет сводиться к решению нелинейных
алгебраических уравнений на каждом шаге интегрирования по времени, что заметно
усложнить решение задачи. Для решения системы таких уравнений могут быть
применены два подхода, а именно интегрирование уравнения движения по неявной и по
явной схемам.
В случае применения неявных схем интегрирования, уравнение движение
рассматривается на неизвестном временном слое n 1. На этом же слое производится
дискретизация пространственных производных. Для данного подхода получается, что
все полученные уравнения становятся взаимосвязанными. Тогда решение на новом шаге
n 1 будет иметь вид:
un 1 K1 1Fna 1
(1.1.16)
21.
21Неявные схемы основываются на разных методах, но значительно чаще
применяется метод Ньюмарка, согласно которому на слое n 1 имеют место выражения
для скоростей и перемещений узлов, приведенные ниже.
u n 1 u n 1 u n un 1 t
(1.1.17)
1
u n 1 u n u n t u n u n 1 t 2
2
где , являются параметрами интегрирования Ньюмарка, u n – вектором узловых
перемещений в момент времени tn , u n – вектором узловых скоростей в аналогичный
момент времени, u n – вектором узловых ускорений в тот же момент времени, u n 1 –
вектором узловых перемещений в момент времени tn 1 , u n 1 – вектором узловых
скоростей в тот же момент времени, u n 1 – вектором узловых ускорений при том же
значении времени, а t tn 1 tn .
Введем следующие обозначения. Пусть
a0
1
t 2
, a1
1
1
1, a4 1 , a5 t 2 ,
, a2
, a3
t
2
t
2
a6 t 1 , a7 t .
Тогда выражения (1.1.17) преобразуются к виду:
un 1 a0 un 1 un a2un a3un ,
un 1 un a6un a7un 1 .
(1.1.18)
(1.1.19)
А уравнение примет вид:
a0M a1C K un 1 Fna 1 M a0un a2un a3un C a1un a4un a5un . (1.1.20)
Из (1.1.20) можно определить
un 1 , а из выражений (1.1.18) и (1.1.19) вычислить
скорости и ускорения, перемещения же определяются из (1.1.17).
Однако описанный выше метод может устойчиво работать только при следующих
условиях:
2
1 1
1 1
, , 0.
4 2
2 2
При этом параметры Ньюмарка зависят от некоторого параметра , который
называется численным демпфированием.
22.
221
1
1 2 , .
4
2
При проведении практических расчетов численное демпфирование принимается
малым 0,005 .
В случае решения именно нелинейной задачи уравнение (1.1.20) решается другим
методом: методом Ньютона-Рафсона.
a0M a1C Kin 1 uin 11 Fna 1 Fnnr 1,i M a0 un uin 1 a2un a3un
C a1 un uin 1 a4un a5un ,
(1.1.21)
здесь K in – матрица Якоби в момент времени
tn на итерации i ,
Fna – вектор
приложенных сил в тот же момент времени, Fnnr ,i – вектор восстановленных сил в
момент времени tn на итерации i .
В случае применения к решению явных схем интегрирования, значения
перемещений, скоростей и ускорений на неизвестном временном слое n 1 могут быть
получены на более ранних временных слоях, в частности на слое
n . При этом решение
будет сводиться к системе уже линейных уравнений, для которых составляется
диагональная матрица. Элементы этой матрицы содержат величины, определяемые на
новом n 1 слое, и данная матрица явно может быть разрешена. Перемещения,
скорости и ускорения на рассматриваемом шаге можно определить через их значения на
предыдущих шагах с помощью метода центральных разностей.
Ускорения, которые вычисляются на n-ом слое, определяются по выражению
an M 1 Fnext Fnint ,
(1.1.22)
где Fnext – вектор приложенных внешних и объемных сил; Fnint – вектор внутренних
сил.
Векторы перемещений и скоростей будут определять в соответствии с:
v t t / 2 v t t / 2 at tt
(1.1.23)
u t t u t v t t / 2
(1.1.24)
tt tt t
2
Для определения перемещений на n 1-ом слое используется следующее
выражение:
un 1 un vn 1/2 tn 1/2 ,
(1.1.25)
23.
23здесь vn 1/2 vn 1/2 an tn является вектором скоростей, который может быть
вычислен на некотором промежуточном временном слое n 0,5 : tn 0,5 0,5 tn tn 1 .
1.2. Модели грунтов основания при расчете на землетрясения
В процессе проектирования оснований фундаментов конструкций по несущей
способности, то есть по первой группе предельных состояний, используются
прочностные
характеристики
грунтов.
Для
определения
несущей
способности
грунтового основания могут быть применены две группы методов расчета. Инженерные
и аналитические методы относят к первой группе таких расчетов [42, 78, 79, 80]. Ко
второй же группе относятся методы, которые основаны на численной реализации задачи
с применением известных моделей грунтов [101, 110, 121].
При задании грунтового основания, а именно при его численном моделировании,
необходимо определить свойства и характеристики грунта той территории, на которой
происходит строительство зданий и сооружений. Для того чтобы задать эти свойства
необходимо определить оптимальную модель сплошного грунтового основания. Такие
различные расчетные модели были предложены исследователями в разное время. К
этим моделям относятся: модель Винклера, а также ее модификация, модель упругого
полупространства, модель линейно-деформируемого слоя конечной толщины и
нелинейные модели.
Так как при интенсивном сейсмическом воздействии работа грунта имеет
выраженный нелинейный характер, то при расчете на землетрясения должны
использоваться нелинейные модели грунтового основания. К этим моделям относятся:
модель Мора-Кулона;
модель Друккера-Прагера;
шатровая модель (Cam-Clay);
модель с упрочнением (Hardening Soil) и ее модификация (Hardening Soil
Small-strain);
динамические инерционные модели.
24.
241.2.1. Модель Мора-Кулона
Идеально-упругопластическая модель Мора-Кулона – это модель линейно
деформируемого
пространства,
в
которой
описываются
поля
деформаций
и
используются условие прочности Кулона для предельного состояния.
Условия прочности Кулона или Мора-Кулона применяются в большинстве
случаев решения задач как аналитически, так и численно. В первом условии прочности,
которое имеет различный вид для разных условий испытания образцов грунта,
прослеживается зависимость между прочностью самого грунта и нормальным
давлением, которое будем обозначать ζ (1.2.1-1.2.5):
консолидированно-дренированный сдвиг
η ζ ν tgθ c ;
(1.2.1)
консолидированно-недренированный сдвиг
η (ζ ν u) tgθ c;
(1.2.2)
неконсолидированно-недренированный сдвиг (для водонасыщенных грунтов)
η сu ;
(1.2.3)
консолидированно-недренированный сдвиг, малоподвижные грунты
η (ua u) tgθb (ζ ν u) tgθ c ;
(1.2.4)
η ζ ν tgθ r cr .
(1.2.5)
в случае больших деформаций сдвига
В приведенных выше формулах введены следующие обозначения:
η касательное напряжение, при достижении которого будет происходить разрушение
грунта,
ζ ν эффективное нормальное напряжение, θ эффективный угол
внутреннего
трения,
θ
дреннированный
угол
внутреннего
трения,
c
дреннированные силы удельного сцепления, c эффективные силы удельного
сцепления, ua давление порового воздуха, u давление поровой воды, θ
b
угол
внутреннего трения, зависящий от величины матричного всасывания, θ r остаточный
угол внутреннего трения, c r
остаточные силы удельного сцепления,
cu
недренированная прочность.
Во втором условии прочности определяется зависимость между прочностью
грунта и минимальным ζ3 , а также максимальным ζ1 главными напряжениями (1.2.61.2.7):
для гравелистых, песчаных и крупнообломочных грунтов
25.
25ζ ζ3
(1.2.6)
sin θ 1
;
ζ1 ζ3
для глинистых грунтов
ζ1 ζ3
(1.2.7)
sin θ.
(ζ1 ζ3 2c ctg θ)
Уравнение (1.2.7) при трехмерном напряженно-деформируемом основание
пример вид:
ζ1 ζ 2 2c ctg θ ζ1 ζ 2 sin θ;
ζ 2 ζ3 2c ctg θ ζ 2 ζ3 sin θ;
ζ3 ζ1 2c ctg θ ζ3 ζ1 sin θ
(1.2.8)
Согласно (1.2.8) поверхность текучести Мора-Кулона в пространстве главных
напряжений имеет вид шестигранной пирамиды с вершиной в точке с координатами
c ctgθ; c ctgθ; c ctgθ (рисунок 1.2.1).
Рисунок 1.2.1. Поверхность текучести по критерию Мора-Кулона
На рисунке 1.2.2 приведены предельные огибающие Мора-Кулона, которые могут
быть получены по результатам трехосных испытаний образцов грунта.
а)
б)
26.
26в)
Рисунок 1.2.2. Предельные огибающие Мора-Кулона
а) секущий угол внутреннего трения, б) касательный угол внутреннего трения, в) угол
внутреннего трения, который зависит от угла наклона предельной огибающей
Вид огибающей, представленный на рисунке 1.2.2 а, соответствует такому виду
грунта, для которого характерно определение прочности только трением. Такой грунт
является фрикционным материалом (например, песок). В этом случае условие
прочности для каждого напряженного состояния будет иметь вид:
η ζ tgθs ,
(1.2.9)
здесь θ s секущий угол внутреннего трения, ζ эффективное нормальное
напряжение.
Условие прочности (1.2.1) соответствует изображению, приведенному на рисунке
1.2.2 б. В данном случае предельная прямая получается как наилучшая касательная к
кругам Мора. Однако в общем случае провести такую касательную к кругам
затруднительно, так как зависимость между нормальным давлением и пределом
прочности является существенно нелинейной. Тогда на отдельных участках предельная
кривая аппроксимируется прямой, а на остальных она заменяется огибающей к кругам
Мора.
Модель Мора-Кулона имеет ряд преимуществ и ряд недостатков. Первым и
основным преимуществом является то, что данные различных теоретических и
экспериментальных исследований показали достаточно точные результаты, полученные
для сложных напряженно-деформируемых состояний реальных грунтов. Во-вторых,
набор параметров, которые должны быть известны на момент решения задачи,
достаточно невелик и их значения можно легко найти, как в нормативных документах,
так и в отчетах по инженерно-геологическим изысканиям.
Первый недостаток применения условия прочности Мора-Кулона заключается в
том, что по приведенным выше уравнениям (1.2.6-1.2.8) должна выполняться
27.
27шестикратная проверка на каждом этапе итерационного процесса. Во-вторых, для
данной
модели
характерны
дополнительные
трудности
численной
реализации
алгоритмов теории пластического течения. Это происходит из-за того, что вид
поверхности текучести Мора-Кулона кусочно-линейный. Наличие огромного числа
нерегулярных точек и вызывает эту трудность [44]. В-третьих, деформации, которые
находятся внутри предельной поверхности, являются упругими и обратимыми, поэтому
модель ограничивает уровень напряжений сдвига и ненамного дополняет линейную
модель.
1.2.2. Модель Друккера-Прагера
Основные недостатки модели Мора-Кулона были исключены в модели ДруккераПрагера. Для этой модели характерная форма поверхности текучести определяется
уравнением (1.2.10) и имеет вид, представленный на рисунке 1.2.3 [66]:
J2
где
J2
2
sin θ
2 3c cosθ
I1
0,
(3 sin θ)
3 (3 sin θ)
(1.2.10)
– второй инвариант девиатора тензора напряжений;
тензора напряжений;
с – удельное сцепление;
I1
– первый инвариант
θ – угол внутреннего трения.
Рисунок 1.2.3. Поверхность текучести по критерию Друккера-Прагера
Как видно из рисунка 1.2.3 данная поверхность текучести является прямым
k k k
; ; . Критерий
3α 3α 3α
круговым конусом с вершиной в точке с координатами
Друккера-Прагера представляет аппроксимацию критерия Мора-Кулона гладкой
28.
28функцией, что достигается при помощи инвариантов
характеристик материала грунта
си
J2
и I1 , и при помощи двух
θ . Имеет место два вида таких аппроксимаций:
коническая поверхность вписана в пирамиду;
коническая поверхность описана вокруг пирамиды.
Наряду с описанным выше критерием Друккера-Прагера существуют критерии,
которые были предложены исследователями Ладе-Дунканом и Мацуока-Накаи (рисунок
1.2.4) [96].
Рисунок 1.2.4. Сравнение поверхностей по критериям текучести в девиаторной плоскости
Данные критерии также являются своего рода аппроксимацией модели МораКулона, так как условие прочности в этом случае имеет гладкую поверхность. Стоит
отметить,
что
экспериментальными
данными
опытных
испытаний
грунтов
подтверждается такое, можно сказать, «каплеобразное» очертание поверхности
текучести. Однако и у критериев, предложенных Ладе-Дунканом и Мацуока-Накаи,
имеется один существенный недостаток. Если основание пирамиды аппроксимируется
гладкими кривыми, то вершина пирамиды по-прежнему остается острой. Чтобы
устранить этот недостаток необходимо получить некоторый закон изменения
меридиональной образующей поверхности текучести. Таким законом может быть либо
гиперболическая,
либо
экспоненциальная
зависимости.
гиперболической зависимости представлен на рисунке 1.2.5.
Случай
применения
29.
29Рисунок1.2.5. Изображение гиперболической поверхности текучести
В настоящее время существуют и другие более сложные модели, которые
основываются на той же идее использования «колпачка» в верхушке поверхности
текучести. В следующем пункте этой главы будет описана одна из таких моделей.
1.2.3. Шатровая модель (Cam-Clay)
Обобщенная модель грунта, заданная по модели Cam-Clay, была предложена в
1971 году. Вообще «шатровые» модели (так называют Cam-Clay модели в России) могут
использоваться для моделирования не только грунтов, но и широкого ряда материалов.
Данные модели достаточно хорошо могут быть применены к динамическим задачам, в
том числе к расчету на сейсмическое воздействие. Однако исходные параметры,
которые являются входными при моделировании, определить достаточно сложно, что
является основным недостатком этих моделей.
Так как для «шатровой» модели Cam-Clay характерны разные значения прочности
на растяжение, сжатие и сдвиг, то функция текучести будет иметь более сложный вид:
f (ζ, K0 ,ζ0 ) f ( I1, J 2 , J3 , K0 ,ζ0 ) Γ2 (β,ψ) J 2 fc ( I1, K0 ,ζ0 ) ft ( I1,ζ0 ) f s2 ( I1,ζ0 ) (1.2.11)
где f s ( I1,ζ0 ) ζ0 Ae
(β f I1 )
2
I
α I1, ft ( I1,ζ0 ) 1 H ( I1) f 1
,
R
f
(0,ζ
)
t
s
0
f
2
I K0
fc ( I1, K0 ,ζ0 ) 1 H ( K0 I1) f 1
R f ( K ,ζ ) ,
0
c s
H
–
функция
Хевисайда;
R
–
коэффициент, отвечающий за форму поверхности, в осях I1, J 2 ; K 0 – индикатор
перехода от поверхности шатра к поверхности, отвечающей за сдвиг, I1 – первый
30.
30инвариант тензора напряжений, ζ 0 – постоянная, зависящая от удельного сцепления
f
грунта, A,β ,α
f
– константы материала,
1
1
Γ(β,ψ) 1 sin 2β (1 sin 3β)
2
ψ
3 3J
1
3 ,
где β( J 2 , J 3 ) sin 1
3
2
2J
3
2
(1.2.12)
3 3J 3
1
; ψ – отношение
J 2 , J 3 sin 1
32
3
2
J
2
трехосного растягивающего напряжения к сжимающему.
На рисунке 1.2.6 представлена поверхность текучести.
Рисунок 1.2.6. Поверхность текучести модели Cam-Clay
Модели грунта основываются на так называемой концепции критического
состояния. Согласно этой концепции при постепенно нарастающем формоизменении
грунт переходить в критическое состояние.
Для модели Cam-Clay критическое состояние грунта определяется по следующим
условиям:
удельный объем грунта определяется как функция напряжений ν Γ-λln ζ , а
само течение грунта происходит при неизменном объеме и напряжениях,
постоянных по величине;
девиаторное напряжение пропорционально значению среднего напряжения;
в случае необратимых пластических изменений объема происходит упрочнение.
На рисунке 1.2.7 приведена графическая интерпретация упругопластической
модели Cam-Clay.
31.
31Рисунок 1.2.7. Графическая интерпретация модели Cam-Clay
Данная модель наиболее полно помогает устранить недостатки, связанные с
трудностями при численной реализации, однако некоторые исследователи, например в
[4], считают, что она может быть достаточно эффективна только для искусственных
грунтовых сооружений.
К преимуществам модели Cam-Clay можно отнести простоту разрешающих
уравнений и сравнительно небольшое количество входных параметров. В качестве
основного ее недостатка можно выделить достаточно некорректное описание сдвиговых
деформаций грунта. Также для этой модели характерно то, что численные результаты
плохо согласуются с реальными данными, полученными в ходе испытаний грунтов.
1.2.4. Модель с упрочнением (Hardening Soil) и ее модификация
В последнее время достаточно часто при проведении расчетов грунтовых сред
используется модель грунта с упрочнением или модель Hardening Soil (HS). Данную
модель иногда выделяют вообще в особую группу, для которой характерен независимый
закон поведения грунта при деформации формоизменения. HS более соответствует
реальному поведению грунта, так как использует гиперболическую зависимость
деформаций от девиаторных напряжений.
Модель Hardening Soil была разработана в 1999 году профессором П.А.
Вермейером, впоследствии она была реализована в таких программных комплексах как
PLAXIS и Midas. Эта модель достаточно точно описывает работу грунта при устройстве
подпорных стен, при экскавации грунта, при проходке туннелей. Однако и для нее
свойственны некоторые ограничения в применении. Например, модель грунта с
упрочнением не может быть применима для моделирования динамических процессов, а
32.
32также в ней не могут быть учтены явления ползучести, длительной прочности и явление
анизотропии прочности и жесткости [82, 97, 100, 122, 123].
В модель HS введен модуль деформации разгрузки при снижении напряжений в
элементе.
Для девиаторного нагружения функция текучести задается уравнением:
fs
1
ζ
2 E50 1 ζ
ζa
2ζ
γ p,
Eur
(1.2.13)
m
ref
где E50 E50
c cosθ ζ 3 sin θ
ref
, причем E50 секущий модуль жесткости при
ref
c cosθ p sin θ
половине предельного значения девиатора, который зависит от сцепления
внутреннего трения θ и сдерживающего напряжения ζ 3 ;
m
с,
угла
параметр степени для
зависимости жесткости от уровня напряжений, который для многих видов грунтов
лежит в пределе от 0,4 до 1;
p ref
опорное
всесторонне
ζ
давление;
(с ctgθ +ζ 3 ) 2sin θ
1 sin θ
ζa
, R f 0,75.....1
Rf
-
-
девиаторное
напряжение;
асимптотическое девиаторное
напряжение, которое можно определить по сцеплению и внутреннему трению грунта;
m
ref
Eur Eur
c cosθ ζ 3 sin θ
ref
, причем Eur
ref
c cosθ p sin θ
модуль упругости при разгрузки-
повторном нагружении, который зависит от сцепления с , угла внутреннего трения θ и
p
p
p
p
сдерживающего напряжения ζ 3 ; γ ε1 ε 2 ε3
параметр упрочнения, причем
ε p пластические деформации.
Функция в (1.2.13) описывает пластические сдвиговые деформации и она не
совпадает с потенциальной поверхностью, таким образом, можно сделать вывод, что в
этой модели имеет место неассоциированный закон течения.
В случае изотропного нагружения функция текучести будет определяться
следующим образом:
33.
33c
f
ζ
2
α
2
p 2 p 2p
(1.2.14)
От значений параметра α и преднапряжения консолидации p p зависит форма и
размер поверхности текучести. Параметр α определяет форму эллипса и зависит от
коэффициента бокового давления для нормально-консолидированного грунта, параметр
pp
- размер полуосей эллипса и зависит от опорного модуля жесткости
m
Eoed
ref
Eoed
c cosθ ζ1 sin θ
, который определяется в основном из компрессионных
ref
c
cosθ
p
sin
θ
испытаний при давлении равном p
ref
.
На рисунке 1.2.8 приведена поверхность текучести, которая соответствует модели
Hardening Soil.
Рисунок 1.2.8. Поверхность текучести модели Hardening Soil в пространстве главных
напряжений
Следует
отметить,
что
рассматриваемая
модель
учитывает
некоторые
особенности модели Cam-Clay. Разница состоит в том, что Hardening Soil для описания
деформаций сдвига использует кривые, полученные в ходе лабораторных испытаний
грунтов.
Главным преимуществом применения модели грунта с упрочнением является то,
что она позволяет учитывать наличие пластических деформаций формоизменения на
различных траекториях нагружения. Однако она имеет и ряд недостатков. Во-первых,
это сложность использования модели при практическом ее применении на реальной
задаче, во-вторых, перегруженность модели математическими зависимостями.
34.
34В последнее время относительно часто используется другая модель, которая
носит название Hardening Soil Small-strain (HSS) – модель грунта с упрочнением при
малых
деформациях.
Для
характерно,
HSS
что
при
деформациях
ε1 10 3
устанавливается дополнительная гиперболическая зависимость между напряжениями и
деформациями. Другими словами можно сказать, что в этой модели модуль сдвига
изменяется нелинейно, но только в области малых деформаций.
Ниже приведено уравнение, которое описывает модель HSS:
G
G0
1
1 α
,
γ
(1.2.15)
γ 0,722
m
где G секущий модуль сдвига, G0 G
ref
0
ζ3 c cot θ
ref
начальный модуль сдвига,
p
c
cot
θ
γ угловая деформация, γ 0,722 угловые деформации, при которых секущий модуль
сдвига составляет 72,2% от начального.
На рисунке 1.2.9 приведена графическая интерпретация модели грунта с
упрочнением при малых деформациях.
Рисунок 1.2.9. Графическая интерпретация модели Hardening Soil Small-strain
Основным недостатком модели HSS является то, что невозможно определить
параметры этой модели в лабораторных условиях в стандартных лабораториях.
1.2.5. Динамические инерционные модели
В [71] приводится обоснование модели, которая достаточно часто применяется к
расчету оснований атомных станций [72, 91]. Эта модель получила название
динамической модели линейно деформируемого инерционного основания. В данной
модели не учитывается конечная жесткость фундамента сооружения [36, 44, 45, 46, 47,
65].
35.
35Для прямоугольного в плане фундамента, который находится на поверхности
линейно деформируемого полупространства, заданного с осредненными динамическими
характеристиками, определены квазистатические и мгновенные жесткости основания.
Все значения приведены в таблице 1.2.1.
Таблица 1.2.1.
Мгновенные и квазистатические интегральные жесткости основания для фундамента
прямоугольной формы в плане
Вид движения
Квазистатическая жесткость
Мгновенная жесткость
Горизонтальное
cx 0,576k x R ρ G ,
поступательное по оси
kx 2 1 μ G Lx Ly β x Lx Ly
Lx Ly
х
R
π
Горизонтальное
поступательное по оси
у
Вертикальное
поступательное по оси
z
Вращательное
относительно
горизонтальной оси х
Вращательное
относительно
горизонтальной оси у
k y 2 1 μ G Lx Ly β y Ly Lx
kz
G Lx Ly
kθx
kθy
1 μ
β z Lx Ly
2
x y
GL L
βθx Ly Lx
1 μ
2
y x
GL L
βθy Lx Ly
1 μ
cy 0,576k y R ρ G ,
cz 0,85kz R ρ G ,
cθx
Rθx
cθy
Rθy
0,3kθx Rθx ρ G
,
1 Bθx
4
Lx L3y
3π
0,3kθy Rθy ρ G
,
1 Bθy
4
Ly L3x
3π
3
Вращательное
относительно
вертикальной оси z
16GRθz
kθz
,
3
Rθz Lx Ly L L
4
2
x
2
y
cθz
kθz I z
1 2 I z ρRθ5z
Здесь β x ,β y ,β z ,βθx ,βθy безразмерные коэффициенты, которые зависят от
отношения сторон фундаментной плиты в плане и которые определяются из
соответствующих графиков [71]; Lx , Ly размеры фундаментной плиты в плане по
координатным осям х и у; R, Rθx , Rθy , Rθz приведенные радиусы фундаментной плиты
прямоугольной формы в плане при поступательных и вращательных движениях.
Описываемую модель предполагается использовать при проведении расчетов на
землетрясение, поэтому в качестве входных параметров характеристик грунтового
36.
36основания должны использоваться динамические характеристики, которые могут быть
определены через скорости распространения сейсмических волн [71].
2
s
3δ 2 4
E ρν
,
2
δ 1
(1.2.16)
δ2 2
μ
,
2(δ 2 1)
(1.2.17)
G ρν 2s ,
(1.2.18)
где E динамический модуль деформации, G динамический модуль сдвига, μ
динамический коэффициент Пуассона, δ ν p ν s ,
продольной волны в грунтовом массиве,
ν p скорость распространения
ν s скорость распространения поперечной
волны в грунтовом массиве.
Еще одним подходом к расчету систем сооружение основание является методика,
предложенная А.Г. Тяпиным. Согласно [85, 86] рассматривается три модели основания:
«основание 0» - основание с которым работают изыскатели, «основание 1» - основание,
на котором задано воздействие, «основание 2» - основание, на котором будет работать
сооружение. Следующим шагом, согласно данной методики является пересчет
воздействия с «основания 1» к воздействию на открытой отметки подстилающего
полупространства (решение обратной задачи инженерной сейсмологии). Далее решается
прямая задача инженерной сейсмологии, то есть осуществляется пересчет воздействия
от открытой отметки подстилающего полупространства к свободной поверхности
«основания 2». По итогам работы с введенными моделями формируется горизонтальнослоистая модель основания и пересчитывается сейсмическое воздействие. Затем
выполняется анализ сооружения в отсутствии основания (на защемленном фундаменте).
Поэтапно происходит построение диагональной матрицы динамической инерции. На
следующем
этапе
осуществляется
пересчет
определенного
на
первом
этапе
сейсмического воздействия к сейсмическим нагрузкам на неподвижный фундамент.
После чего фиксируются колебания жесткого фундамента под сооружением, которые
затем предаются на рассматриваемую надфундаментную конструкцию.
37.
371.2.6. Достоинства и недостатки моделей основания при расчете на
землетрясение
Таблица 1.2.2.
Достоинства и недостатки моделей основания при расчете на землетрясение
Название модели
Модель
Кулона
Преимущества
1)
Данные
различных
теоретических
и
экспериментальных
исследований
показали
достаточно точные результаты,
полученные
для
сложных
Моранапряженно-деформируемых
состояний реальных грунтов.
2)
Простота
назначения
параметров, которые можно
найти в любом отчете по
инженерно-геологическим
изысканиям
Недостатки
1)
Должна
выполняться
шестикратная проверка на
каждом этапе итерационного
процесса. 2) Для данной
модели
характерны
дополнительные
трудности
численной
реализации
алгоритмов
теории
пластического течения, что
происходит из-за кусочнолинейного вида поверхности
текучести.
3)
Деформации,
которые
находятся внутри предельной
поверхности,
являются
упругими
и
обратимыми,
поэтому модель ограничивает
уровень напряжений сдвига и
ненамного
дополняет
линейную модель
1) Отсутвие большого числа
1) Наличие нерегулярной точки
Модель Друккера- нерегулярных точек и как
в вершине пирамиды ДруккераПрагера
следствие
гладкий
вид
Прагера
поверхности текучести
1) Некорректное описание
сдвиговых деформаций грунта.
1)
Простые
разрешающие 2) Численные результаты плохо
Шатровая
модель уравнений
и
сравнительно согласуются
с
реальными
(Cam Clay)
небольшое количество входных данными, полученными в ходе
параметров
испытаний грунтов
1) Сложность использования
модели при практическом ее
Модель
с
применении на реальной задаче
упрочнением
1) Позволяет учесть наличие 2) перегруженность модели
(Hardening Soil) и ее пластических
деформаций математическими
модификация
формоизменения на различных зависимостями
(Hardening
Soil траекториях нагружения
3) Невозможно определить
Small-strain)
параметры этой модели в
лабораторных
условиях
в
стандартных лабораториях.
Как показывают проведенные исследования при решении задач с помощью
прямого нелинейного динамического метода с интегрированием уравнений движения по
38.
38явной схеме (см. п. 1.1), целесообразно использовать модель грунтового основания
Мора-Кулона, так как она является наиболее устойчивой и стабильной при решении
задач численными методами.
1.3. Основные положения теории надежности и теории вероятностей
1.3.1. Вероятностный анализ метода предельных состояний
Невозможно точно сказать где, когда, какой интенсивности и с какими
параметрами произойдет землетрясение. Сейсмическое воздействие является ярко
выраженным нестационарным случайным процессом. Одновременно с этим основные
параметры грунта основания (модуль деформации, угол внутреннего трения, удельное
сцепление) также обладают большой изменчивостью. Д.Н. Соболев рассматривал
грунтовое основание упругим, статически-неоднородным (в плане, по высоте), с
коэффициентами
постели,
которые
являлись
случайной
функцией
координат
рассматриваемого массива грунта [43, 76].
Любое состояние системы (элементов конструкции, всей конструкции в целом,
грунтового основания) в процессе эксплуатации характеризуется некоторым известным
числом независимых параметров. Одни параметры определяют прочность материалов,
следующие – нагрузки, которые действуют на эту систему, и в особую группу
параметров выделяют параметры, характеризующие разницу между действительной
работой, например, конструкции, и реакцией на заданную нагрузку принятой расчетной
схемы.
Зная функцию работоспособности g ( x1 , x2 ,..., xn ) можно составить уравнение
границы области допустимых состояний рассматриваемой системы [48, 67, 69]:
g ( x1, x2 ,..., xn ) 0
(1.3.1)
Параметры с обозначением « » будем называть случайными величинами.
Как и при решении обычных задач, в вероятностных задачах присутствуют
параметры, которые относятся только к свойствам грунта или конструкции (системы)
либо которые определяют внешнее воздействие. При таком делении условие
непревышения границы области допустимых состояний для первой группы предельных
состояний может быть записано в виде неравенства:
g ( x1, x2 ,..., xn ) R( x1, x2 ,..., xm ) F ( xm 1, xm 2 ,..., xn ) 0 или g R F 0 (1.3.2)
39.
39В последнем выражении F выраженные через внешнюю нагрузку напряжения или
усилия в исследуемой системе, R либо предел прочности, либо предел текучести, либо
пластический момент (в зависимости от рассматриваемой задачи), g резерв прочности
или резерв несущей способности согласно [68].
В более общей формулировке F и R - случайные функции времени, однако в
нашей постановке они являются случайными величинами, для которых задан
определенный закон распределения.
Исходя из предположения о том, что в случае выполнения неравенства (1.3.2)
можно говорить о безотказной работе конструкции или грунтового основания, тогда
вероятность отказа рассматриваемой системы будет определяться выражением:
0
p
Pf
g
( g )dg ,
(1.3.3)
где pg ( g ) - плотность распределения резерва прочности, которую можно определить по
формуле
pg ( g )
p
R
( g F ) pF ( F )dF .
(1.3.4)
В (1.3.4) pR ( g F ) плотность распределения с аргументами ( g , F ) ; pF ( F )
плотность распределения нагрузочного эффекта.
Подставив (1.3.4) в (1.3.3) получим:
Ps 1
p
F
( F ) PR ( F )dF или Ps
где
p
R
( R) PF ( R)dR
(1.3.5)
PR ( F ), PF ( R) - функции распределения сопротивления и нагрузочного эффекта.
Непревышение максимального перемещения
некоторого заданного значения
w,
полученного из расчетов,
wзад , есть мера надежности в случае проверки по
второй группе предельных состояний. При этом уравнение (1.3.5) записывается в виде:
Ps
wзад .
p( w)dw
(1.3.6)
Для любых законов распределения
F
и
R
будут соответствовать
g R F ; sg sR2 sF2
(1.3.7)
40.
40Обозначение «-» указывает на то, что имеется в виду математическое ожидание каждого
из параметров, s стандартное отклонение (корень квадратный из дисперсии).
Отношение
β
g
R F
sg
sR2 sF2
(1.3.8)
называется «индексом надежности», который показывает, какое число стандартов s g
может поместиться в интервал от
g 0
до
g g [68, 107].
Площадь заштрихованной части графика плотности распределения резерва
несущей способности определяет вероятность отказа (рисунок 1.3.1).
Рисунок 1.3.1. Плотность распределения резерва несущей способности
Вероятность отказа из предположения, что функции F и R распределены по
нормальному закону, может быть выражена в виде
0
1 x g 2
1
Pf P( g 0)
exp 2 sg dx
sg 2π
(1.3.9)
Также (1.3.9) может быть приведено к виду
Pf 1 Φ β
где Φ β
(1.3.10)
β
x2
1
exp
dx интеграл вероятности Гаусса.
2π 0
2
На рисунке 1.3.2 приведен график зависимости безотказной работы от «индекса
надежности».
41.
41Рисунок 1.3.2. Зависимость вероятности безотказной работы от «индекса надежности»
1.3.2.
Методы
вероятностного
моделирования
сейсмического
воздействия
Прогноз силы, времени, а также места землетрясения является одной из основных
задач сейсмологии. На основании этого, как и на основании исторических данных,
составляются карты потенциальной сейсмической опасности, на которых не только
определяют места возможных землетрясений, но и указывают предполагаемую
интенсивность сейсмического воздействия и частоту повторения за некоторый
промежуток времени. Величину предполагаемой интенсивности и закладывают в основу
расчета зданий и сооружений, проектируемых в сейсмически активных районах.
Очевидно, что землетрясение по своей природе является случайным процессом,
поэтому в теории сейсмостойкости целесообразно применять статистические методы
анализа. Одно из таких статистических описаний землетрясения было предложено В.В.
Болотиным [13, 16, 17, 18]. Согласно данному подходу сейсмическое воздействие может
быть
описано
интегральными
признаками
самого
землетрясения,
а
также
нестационарным случайным процессом. Произведение стационарного случайного
процесса y(t) на некоторую детерминированную функцию времени A(t) и есть
представление нестационарного случайного процесса a(t).
a t A t y t
(1.3.11)
В (1.3.11) y(t)– стационарный случайный процесс, A(t) – огибающая, которая
описывается функцией Берлаге:
t
t
A t A0 e t0
t0
где
(1.3.12)
t0 – характеризует продолжительность интенсивной фазы, A0 – характеризует
максимальные ускорения.
42.
42Из анализа существующих инструментальных акселерограмм назначаются
значения параметров из (1.3.12), причем с обязательным выделением стационарных
составляющих. Существуют методы, которые позволяют выделять стационарную
составляющую из записей акселерограмм реальных землетрясений. К таким методам
относятся метод фильтрации, вейвлет-анализ, фрактальный анализ акселерограмм [6, 49,
50, 51, 113]
Для
определения
стационарного
случайного
процесса
y(t)
могут
быть
использованы следующие методы: метод формирующего фильтра, метод канонических
разложений
и
его
модификация,
вейвлет-анализ
[52,
53,
54].
Наиболее
распространенным является метод канонических разложений.
Согласно этому методу, каноническое разложение для стационарных процессов
представляет собой разложение в ряд Фурье:
y(t ) (uk cos
k 0
где
0 t TM , TП TМ , TП
случайные числа,
2π
2π
kt vk sin kt )
TП
TП
(1.3.13)
период случайного процесса, uk , vk
M (uk ) M (vk ) 0 , M (u k vk ) 0 ,
некоррелированные
M (uk ul ) 0 ,
M (vk vl ) 0 при
k l.
Для случайного процесса (1.3.13) существует корреляционная функция, которая
определяется по
K y (t1 , t2 ) M y (t1 ) y (t2 )
2π
2π
2π
2π
M uk cos kt1 vk sin kt1 uk cos kt2 vk sin kt2 (1.3.14)
TП
TП
TП
TП
k 0
k 0
2π 2π
2π 2π
M uk2 cos kt1 cos kt2 M vk2 sin sin kt2 ;
k 0 г
TП TП
TП TП
2
2
где M (uk ) дисперсия uk , M (vk ) дисперсия vk .
Для стационарного процесса в широком понимании необходимо чтобы
M (uk2 ) M vk2 ζ k2
в этом случае
(1.3.15)
43.
432π
2π
2π 2π
K y (t1 , t2 ) ζ 2k cos kt1 cos kt2 sin kt1 sin kt2
k 0
TП
TП
TП TП
(1.3.16)
2π
ζ 2k cos k (t2 t1 ) .
k 0
TП
Обозначив
t2 t1 через η , получим
2π
2
K y (η) ζ k cos
kη
k 0
TП
(1.3.17)
(1.3.17) является разложением заданной функции в ряд Фурье по косинусам,
2
причем дисперсии ζ k есть коэффициенты Фурье:
1
ζ
TП
TП
K
2
0
y
(η)dη
2
ζ
TП
2
k
здесь
(1.3.18)
0
ТП
K
0
y
2π
(η)cos dη
TП
(1.3.19)
TП ηk , η k интервал корреляции случайного процесса. При выполнении этого
неравенства (1.3.18), (1.3.19) примут вид:
ζ 02
1
TП
K y (η)dη
0
S y (0)
2T П
(1.3.20)
2π
Sy
k
TП
2π
2
2
ζk
K y (η)cos
, k 1, 2,3,...
dη
TП 0
T
2
T
П
П
где S y (ω) - спектральная плотность мощности процесса
(1.3.21)
y (t ) .
По заданной спектральной плотности S y (ω) стационарного случайного процесса
2
дисперсии ζ k случайных коэффициентов разложения (1.3.13) могут быть определены с
точностью до постоянных коэффициентов.
Выводы по главе 1
В 1-й главе был проведен обзор литературы, а также о рассмотрены основные
этапы развития теории сейсмостойкости. Описаны принципы, которые применяются
при проведении расчетов систем строительных конструкций на сейсмические
воздействия.
Рассмотрена
линейно-спектральная
теория
расчета
зданий
на
землетрясения. Описаны основные нелинейные методы расчета, которые применяются в
44.
44исследованиях и на которых построены нормативные документы подавляющего
большинства стран с сейсмическими районами.
Сравнительный анализ рассмотренных теорий позволяет сделать вывод, что для
исследования
реальной
работы
системы
сооружение основание
в
условиях
землетрясения необходимо применять нелинейные методы, в частности нелинейный
динамический
метод,
который
предполагает
непосредственное
интегрирование
уравнений движения. Исследования показывают, что наиболее эффективными при
расчетах на интенсивные землетрясения являются явные схемы интегрирования
уравнений движения, которые устойчиво работают при учете взаимодействия
сооружения с основанием.
Выполнен обзор нелинейных моделей грунтового основания, рассмотрены
основные достоинства и недостатки данных моделей. В результате анализа установлено,
что
наиболее
вероятностных
приемлемой
расчетов
моделью
методом
грунтового
основания
статистических
при
испытаний
на
выполнении
случайные
сейсмические воздействия является модель Мора-Кулона.
В главе приводятся положения теории надежности, теории вероятностей и теории
случайных процессов, а также подходы к моделированию сейсмического воздействия
как
нестационарного
случайного
процесса.
Рассмотренные
методы
позволяют
производить исследования работы системы сооружение основание на действие
случайного сейсмического воздействия при учете случайных параметров грунтов
основания.
45.
45Глава 2. МОДЕЛИРОВАНИЕ СОВМЕСТНОЙ РАБОТЫ СИСТЕМЫ
СООРУЖЕНИЕ ОСНОВАНИЕ ПРИ РАСЧЕТЕ НА ЗЕМЛЕТРЯСЕНИЕ
2.1. Методика моделирования неотражающих границ
Моделирование неотражающих границ является важным вопросом для анализа
взаимодействия сооружения с основанием при сейсмическом воздействии [92, 93, 98,
102, 103, 104, 111, 124, 127].
Известно, что волны, распространяющиеся от источника в разных направлениях,
не должны отражаться от границ рассматриваемой области (грунтового массива). В
результате движений волн в прямом и обратном (при их отражении от границ массива)
направлениях имеет место интерференция. Это приводит к искажению реальной
картины волновых процессов и напряженно-деформируемого состояния грунтового
массива во времени.
Также очень важной проблемой является проблема уменьшения размеров
рассматриваемого при моделировании грунтового массива, которая также связана с
введением эффективно работающих неотражающих границ. Что приводит к снижению
времени расчета и повышению эффективности исследований.
Одним из способов задания неотражающих границ является использования
демпфирующих слоев, которые окружают рассматриваемую область. Так же как у
разных видов границ есть некоторые недостатки, так и для демпфирующих слоев
необходимо проводить дополнительные исследования, поскольку главной проблемой
может стать отражение волн от границ между материалами с разными свойствами.
Наиболее эффективным из указанных подходов является метод основанный на
идеально-согласованном слое (PML - perfectly matched layer). Рассмотрим основные
положения, в основе которых лежит метод PML-слоя.
2.1.1. Основные положения метода демпфирующего PML-слоя
Верифицируем
данный
подход
применительно
к
расчету
системы
сооружение основание при расчете на сейсмические воздействия.
Рассмотрим распространение продольной волны в полу-бесконечном стержне
(рисунок 2.1.1).
46.
46Рисунок 2.1.1. Двухслойная модель полу-бесконечного стержня с затуханием
Функция затухания определяется по формуле:
x
f ( x) f 0
L p
m
(2.1.1)
Для стержня конечной длины с защемленным правым концом, который
представлен на рисунке 2.1.2, амплитуда отраженной волны определяется:
R exp 2 F ( L p ) ,
(2.1.2)
где F fdx , L p - размер PML-слоя.
Рисунок 2.1.2. Модель идеально согласованного слоя PML
Параметры
f
,
f0 , L p и m в формулах выше являются эмпирическими и
подпираются опытным путем в зависимости от геометрии области, размера конечного
элемента, а также могут меняться в зависимости от размера самого PML-слоя.
Рассмотрим
задачу
о
распространении
поперечной
волны
в
струне
с
демпфирующим слоем. Колебание струны описываются волновым уравнением:
2u x, t 2 2u x, t
c
t 2
x 2
(2.1.3)
В данной схеме левая граничная точка кратковременно перемещается по
синусоидальному закону, порождая волну, а правая граничная точка жестко закреплена.
Волна, попадая в демпфирующий слой, затухает, а отраженная от правой границы волна
оказывается практически полностью подавленной.
Рассмотрим поперечные перемещения некоторой точки струны (рисунок 2.1.3).
47.
47Рисунок 2.1.3. Колебание рассматриваемой точки
Из рисунка видно, что отраженная от правой границы волна практически
полностью подавляется.
В качестве второго примера рассмотрим поперечные колебания мембраны с
демпфирующим слоем (рисунок 2.1.4 а).
б)
а)
Рисунок 2.1.4. Мембрана с демпфирующим слоем
а) расчетная схема, б) процесс распространения волны в мембране
На рисунке 2.1.4 б изображена картина процесса распространения волны в
мембране в перспективной проекции (показаны изополя вертикальных перемещений).
Анализируя результат, видим, что попавшая в демпфирующий слой волна
подавляется.
Проведенные
исследования
работы
демпфирующего
PML-слоя
показывают его высокую эффективность.
Далее рассмотрим модель грунтового массива (в виде параллелепипеда) с
демпфирующим PML-слоем, который состоит из 8-ми конечных элементов (рисунок
2.1.5 а). Сравним данную модель с аналогичной моделью грунтового массива, в которой
неотражающие границы заданы с помощью демпферов (рисунок 2.1.5 б).
48.
48а)
б)
Рисунок 2.1.5. а) модель с PML-слоем; б) модель с демпферами
На границе грунтового массива приложена равномерно распределенная нагрузка,
изменяющая по закону, представленному на рисунке 2.1.6.
Рисунок 2.1.6. График равномерно распределенной нагрузки
На рисунке 2.1.7 приведены графики, полученных в результате расчета
вертикальных перемещений в центре границы рассматриваемого грунтового массива
(рисунок 2.1.7 а), а также в его углах (рисунок 2.1.7 б). На рисунках видно сравнения для
схем с демпферами и с PML-слоем.
а)
б)
Рисунок 2.1.7. Графики перемещений
а) в центре границы рассматриваемого грунтового массива; б) в углах границы
рассматриваемого грунтового массива
По приведенным выше графикам вертикальных перемещений можно сделать
вывод, что модель PML-слоя дает достаточно точные результаты.
49.
492.1.2. Эффективность работы демпфирующего PML-слоя
Проведем численный анализ работы демпфирующего слоя. В качестве первой
реализации рассмотрим массив грунта, без неотражающих границ (рисунок 2.1.8).
Рисунок 2.1.8. Массив грунта без «неотражающих» границ
Размеры массива в плане 20 м 20 м , глубина 10 м , размер конечного элемента
0,1 м . Грунт был задан в виде линейно-деформируемого основания со следующими
характеристиками: 2000 кг м3 - плотность, Е 50 МПа - модуль деформации,
0,3 - коэффициент Пуассона.
К границе данного массива приложена сила, описываемая функцией Хевисайда
(рисунок 2.1.9).
Рисунок 2.1.9. Закон изменения силы, приложенной к грунтовому массиву
Расчет рассматриваемого грунтового массива был произведен в программном
комплексе LS-DYNA прямым динамическим методом с реализацией явных схем
интегрирования уравнений движения (см. п.1.1).
На рисунках 2.1.10-2.1.12 показано распространение волны в грунтовом массиве
от действия приложенной силы в центре рассматриваемой области. Для наглядного
50.
50отображения распространения волн используется визуализация изополей деформаций.
Для наглядности на рисунке показана половина массива.
Рисунок 2.1.10. Изополя интенсивности деформаций. Начало распространения волны.
Время t=0,03 c.
Рисунок 2.1.11. Изополя интенсивности деформаций. Распространения волны. Время
t=0,07 c.
Рисунок 2.1.12. Изополя интенсивности деформаций. Распространения волны. Время
t=0,15 c
51.
51На рисунке 2.1.13 представлен график результирующей перемещений в точке на
поверхности грунтового массива.
Рисунок 2.1.13. Результирующая перемещений рассматриваемой точки грунта
На рисунках 2.1.10-2.1.11 приведена визуализация распространения волн в
грунтовом массиве без демпфирующего PML-слоя. Представленные результаты
достаточно хорошо позволяют увидеть отражение волн в грунтовом массиве от его
границ. Неучет эффекта отражения волн значительно искажает изменяющееся во
времени
напряженно-деформируемое
состояние
грунтового
массива,
а
также
существенно влияет на точность полученных результатов.
Проведем сравнительный анализ грунтового массива, представленного на рисунке
2.1.14. Рассмотрим два расчѐтных случая: с учетом и без учета PML-слоя.
Рисунок 2.1.14. Массив грунта (красный цвет) с PML-слоем (синий цвет)
Размеры массива в плане 40 м 40 м , глубина 10 м , размер конечного элемента
0,5 м . Материал грунта был задан по аналогии с предыдущим случаем.
В данном случае сила был приложен не в центре массива, а на расстоянии в 10 м
от одной из границ (рисунок 2.1.14). Закон изменения силы приведен в приложении А
на рисунке 1.
52.
52Рассмотрим, как происходит распространение волн в модели с PML-слоем
(рисунки 2.1.15-2.1.17).
Рисунок 2.1.15. Изополя интенсивности деформаций. Начало распространение волн.
Время t=0,03 c
Рисунок 2.1.16. Изополя интенсивности деформаций. Распространение волн. Время t=0,15
c
Рисунок 2.1.17. Изополя интенсивности деформаций. Распространение волн. Время t=0,29
c
На рисунке 2.1.18 приведен график результирующей перемещений для
рассмотренного
случая
грунтового
массива
с
PML-слоем,
а
также
график
53.
53результирующей
перемещений
для
аналогичного
грунтового
массива
без
демпфирующего PML-слоя.
Рисунок 2.1.18. Результирующая перемещений точки грунта с и без PML-слоя
Из рисунка 2.1.18 видно, что колебания, возникающие в грунте с демпфирующим
PML-слоем, достаточно быстро затухают.
Об этом также свидетельствуют изополя интенсивности напряжений в грунте,
приведенные в приложении А на рисунках 2 и 3 для момента времени t=1,178 с.
Анализируя полученные результаты, можно заметить, что картина напряженного
состояния разная. После окончания действия силы в массиве без PML-слоя наблюдается
эффект «ложных» отраженных волн, что вносит существенную погрешность в
результаты расчетов.
Приведенные в данной главе результаты исследований, позволяют сделать вывод
об эффективности задания неотражающих границ, заданных с помощью PML-слоя при
расчете системы надфундаментная конструкция фундамент грунт основания на
сейсмические воздействия.
2.2. Учет взаимодействия сооружения с основанием в корректной постановке
2.2.1. Используемая методика учета взаимодействия сооружения с
основанием (Soil Structure Interaction SSI)
Проблема учета взаимодействия сооружения с основанием связана с тем,
рассматривая ограниченный грунтовый массив, нам необходимо знать закон движения
этого массива грунта. При этом для правильной работы основания во время
землетрясения
мы
должны
организовать неотражающие
границы
по
контуру
рассматриваемого основания. Так как расчетное сейсмическое воздействие задается на
свободной поверхности и существующие расчетные методики не позволяют приложить
кинематическое воздействие и одновременно организовать неотражающие границы, то
54.
54исследование работы эквивалентной системы, в которой грунт закреплен па контору и
по нему заданы неотражающие границы по принципу Д’Аламбера не возможно. Это
связано с тем, что в этом случае необходимо выполнить решение обратной задачи
инженерной сейсмологии, то есть от воздействия на свободной поверхности, которое
всегда известно, перейти к воздействию на границах грунтового массива. С другой
стороны, при совместной работе конструкции с грунтом основания, приложение
воздействия, полученного на свободной поверхности, к массам рассматриваемой
конструкции и просто учет податливости основания без учета трансформации этого
воздействия от пригруза также является некорректным. Погрешность будет тем больше,
чем более массивным будет сооружение и более податливыми будут грунты основания.
2.2.2. Взаимодействие между сооружением и грунтом основания во
время землетрясения
При рассмотрении системы сооружение основание во время землетрясения
можно наблюдать следующую картину. Когда сейсмическая волна Е0 , вызванная
землетрясением, достигает низа фундамента, она разделяется на два типа, как показано
на рисунке 2.2.1.
Рисунок 2.2.1. Распространение волны при взаимодействии сооружения с основанием
Волны, которые передаются конструкции, обозначены как Е1 , те, которые
отражаются обратно в грунт, обозначены как F0 . Волны, возвращающиеся к основанию
конструкции обозначим F1 . Некоторая часть этой волны передается в грунт, а остальная
ее часть возвращается обратно и начинает двигаться вверх по конструкции ( F2 ). Волна,
которая передается в грунт, обозначена R1 .
55.
55Затухание, вызванное волнами излучения, широко известно, как затухание
излучения грунта. Это затухание приводит к увеличению общего демпфирования
системы грунт конструкция по сравнению с затуханием самой конструкции. Кроме
того, под влиянием при взаимодействии сооружения с основанием собственная частота
колебаний системы грунт конструкция будет меньше, чем собственная частота
колебаний грунта [109].
Когда наличие фундамента препятствует колебаниям на свободной поверхности,
мы имеем дело с кинематическим взаимодействием. Когда в фундаменте конструкции
распространяются вертикальные поперечные волны с длиной волны равной глубине
заглубления данного фундамента, тогда кинематическое взаимодействие вызывает в
конструкции вращательные формы колебаний, которые отсутствуют в случае колебаний
на
свободной
поверхности.
Деформации,
вызванные
только
кинематическим
взаимодействием, могут быть вычислены из предположения, что конструкция и
фундамент жесткие, но невесомые как показано на рисунке 2.2.2. Уравнения движения
для этого случая записываются в виде:
M soil uKI K * uKI M soil ub (t )
(2.2.1)
где M soil - матрица массы с предположением, что конструкция и фундамент являются
невесомыми и
жесткости и
uKI
*
- воздействие, приходящее на фундамент, K - матрица
ub (t ) - ускорение границ грунтового массива.
Рисунок 2.2.2. Кинематическое взаимодействие
Эффект взаимодействия сооружения с основанием, связанный с учетом массы
системы
фундамент конструкция,
называется
инерционным
взаимодействием.
Инерционные силы, приложенные к конструкции, приводят к появлению в ее основании
56.
56опрокидывающего момента и сил поперечного сдвига. Деформации, возникающие при
инерционном взаимодействии, могут быть вычислены из следующего уравнения
движения:
M uII K uII M structure uKI (t ) ub (t ) ,
где
M structure
(2.2.2)
- матрица масс при условии, что грунт является невесомым, как
показано на рисунке 2.2.3. Необходимо обратить внимание, что в правой части
уравнения (2.2.2)
стоит инерционная
нагрузка, которая
задается на систему
фундамент конструкция, и которая зависит от колебания грунтового основания и
колебания,
переданного
на
фундамент,
включая
эффект
кинематического
взаимодействия.
Рисунок 2.2.3. Инерционное взаимодействие
2.2.3. Методы расчета сооружения с учетом взаимодействия с
основанием
Существует два основных метода: прямой метод и многоступенчатый метод.
При реализации прямого метода грунт, конструкция и фундамент моделируются
вместе с использованием метода конечных элементов, и анализ осуществляется за один
шаг. Колебания грунтового массива определяются как колебания на свободной
поверхности и прикладываются к границам этого массива. Область грунта с некоторым
характерным ему затуханием ограничивается некоторой фиктивной границей, которая
располагается настолько далеко от конструкции, что волны, возникающие в течение
сейсмического воздействия, не доходят до этих границ. Общие узлы, принадлежащие
системе грунт конструкция, будут обозначаться с индексом f. Узлы, относящиеся к
57.
57конструкции, будем обозначать с индексом st, а узлы, относящиеся к грунту – индексом
s (рисунок 2.2.4).
Рисунок 2.2.4. Конечно элементная модель системы грунт – конструкция для случая
прямого анализа
Силы инерции, действующие на конструкцию, вызывают колебания самой
конструкции, фундамента, грунта в месте расположения общих узлов, и грунта,
расположенного ниже. Уравнения движения для всей системы, показанной на рисунке
2.2.4, можно записать в виде:
Mu Cu Ku M st Iu g ,
(2.2.3)
где M - матрица массы всей конструкции, фундамента и грунта
M st st
M st f
0
st
s
M ;
M M f st M ff M ff
f s
M s f
M ss
0
(2.2.4)
C - матрица затухания для материала конструкции и грунта
Cst st
C C f st
0
Cst f
C stff C sff
Cs f
C f s .
Css
0
(2.2.5)
Здесь матрица демпфирования создается путем построения матрицы демпфирования
грунта и конструкции отдельно от их коэффициента модального демпфирования,
использующего затухание по Релею. Затем они объединяются вместе, и формируется
58.
58окончательная матрица (2.2.5). Имеются общие узлы, принадлежащие как грунтовой
среде, так и конструкции.
K - матрица жесткости всей системы, которая может быть сформирована с
помощью стандартной процедуры сборки
K st st
K st f
0
st
s
K K f st K ff K ff K f s ;
Ks f
K ss
0
(2.2.6)
M st - матрица масс, имеющая ненулевые массы для всех степеней свободы узлов
конструкции
M st st M st f 0
st
M st M f st M ff 0 .
0
0
0
(2.2.7)
I - матрица инерционных сил, u g - вектор ускорений на свободной поверхности, u вектор относительных перемещений.
При реализации прямого метода решать задачу можно не только во временной
области, но и в частотной с использованием преобразования Фурье для колебаний,
полученных на свободной поверхности. Если колебания грунта изменяются во времени,
тогда необходимо в уравнении (2.2.3) изменить коэффициенты в соответствующем
векторе ускорений.
Необходимо учесть, что прямой метод, в котором решение получается во
временной области, хорошо подходит для задач с нелинейными моделями грунта. У
рассмотренного метода имеются следующие недостатки:
достаточно сложное представление матрицы демпфирования;
при пространственном моделировании схемы становятся достаточно
большими и сложными, что значительно увеличивает затраты на
проведение расчетов.
Многоступенчатый или метод суб-конструкции является более эффективным с
вычислительной точки зрения, чем прямой метод, так как он лишен основных
недостатков прямого метода. В этом методе все колебания изначально выражаются
59.
59через колебания, полученные на свободной поверхности. Области грунта либо
фундамента и конструкции рассматриваются, как две независимые модели или субконструкции
[127].
Связь
между
этими
моделями
обеспечивается
силами
взаимодействия равной амплитуды, действующими в противоположных направлениях
от двух суб-конструкций. Общие колебания представляются как сумма колебаний на
свободной поверхности грунта без наличия конструкции и дополнительных колебаний,
возникающих в результате взаимодействия. Как уже было отмечено, применение
данного метода является выгодным, так как он позволяет разделять достаточно сложные
системы грунт конструкция на более простые части, которые могут быть быстрее и
легче рассчитаны. Так как жесткость и демпфирующие свойства грунта не зависят от
частоты, то наиболее удобно проводить анализ реакции на землетрясения в частотной
области, а полученные результаты по известным математическим преобразованиям
перевести затем во временную область.
Хорошо многоступенчатый метод работает для конструкций, расположенных на
жесткой фундаментной плите, которая в свою очередь находится на упругом
полупространстве.
2.2.4.
Численная
верификация
используемой
методики
учета
взаимодействия сооружения с основанием
Рассмотрим простую систему грунтовый массив фундаментная плита (рисунок
2.2.5).
а)
б)
Рисунок 2.2.5. Расчетная схема системы грунтовый массив – фундаментная плита
а) без учета веса плиты, б) с учетом веса плиты и сосредоточенными массами
Чтобы оценить корректность работы рассматриваемой методики проведем
численные исследования двух схем: с учетом и без учета веса фундаментной плиты
(рисунок 2.2.5 а, б) Сейсмическое воздействие (компонента X) прикладывается в
соответствии с акселерограммой, приведенной на рисунке 2.2.6. Взаимодействие между
60.
60фундаментной плитой и грунтом реализовано с помощью прямого метода. В схеме
(рисунок 2.2.15 б) учтем вес фундаментной плиты, а также в узлы фундаментной плиты,
расстояние между которыми 2 м, сосредоточим массы по 20 т каждая.
Рисунок 2.2.6. Компонента X акселерограммы сейсмического воздействия
До 20 с с момента начала расчета выполняется нагружение статической
нагрузкой.
На рисунке 2.2.7 приведены графики ускорений по оси х для системы с невесомой
плитой и исходная расчетная акселерограмма. На рисунке 2.2.8 приведены спектры
данных ускорений.
Рисунок 2.2.7. Сравнение акселерограммы исходного воздействия с ускорением в точке
плиты (невесомая плита)
61.
61Рисунок 2.2.8. Сравнение спектров акселерограммы исходного воздействия с спектром
ускорения в точке плиты (невесомая плита)
Анализ полученных результатов показывает, что для невесомой плиты графики
исходного воздействия, так же, как и спектры, практически полностью совпадают с
ускорениями и спектрами ускорений, полученных на фундаментной плите. Это говорит
о корректной работе методики взаимодействия сооружения с основанием.
Далее выполним расчет системы со сосредоточенными массами в узлах плиты. На
рисунках 2.2.9-2.2.10 приведены результаты расчетов.
Рисунок 2.2.9. Сравнение акселерограммы исходного воздействия с ускорением в точке
плиты (с учетом веса плиты и массами)
62.
62Рисунок 2.2.10. Сравнение спектров акселерограммы исходного воздействия с спектром
ускорения в точке плиты (с учетом веса плиты и массами)
На рисунках видна трансформация исходного воздействия, которая вызвана
взаимодействием фундаментной плиты с грунтом основания.
2.2.5. Пример расчета сооружения с учетом взаимодействия сооружения
с основанием по методике SSI
Проведем численный анализ совместной работы сооружения с грунтовым
основанием при расчете на сейсмическое воздействие с применением прямого метода
(рисунок 2.2.11). Исследования проведены с помощью программном комплексе LSDYNA.
а)
б)
Рисунок 2.2.11. Численная реализация прямого метода: а) система грунт - фундаментная
плита – конструкция, б) общие узлы системы грунт - фундаментная плита – конструкция
Одноэтажное железобетонное здание представлено расчетной схемой, показанной
на рисунке 2.2.12. Несущие элементы здания (колонны, ригели и плита перекрытия)
заданы объемными конечными элементами, а арматура – стержневыми конечными
элементами.
63.
63а)
б)
Рисунок 2.2.12. Расчетная схема
а) система грунт фундаментная плита конструкция слева,
б) арматурный каркас
Основные характеристики конструкции: размер здания в плане 6,8 6,8 м, высота
этажа 3,3 м. Толщина фундаментной плиты - 30 см, сечение балок - 40 40 см, сечение
колонн - 40 40 см, толщина плиты покрытия - 20 см. Бетон класса В25, задавался при
помощи нелинейной модели бетона Continuous Surface Cap Model (CSCM) [119, 126].
Для
рассматриваемого
здания
учитывалось
фактическое
армирование.
Продольная арматура класса А400, поперечная – А240, диаграмма работы материала
арматуры принята идеально-упруго пластической с ограничением пластических
деформаций. Объемные элементы бетона связывались со стрежневыми элементами
арматуры с помощью методики Лагранжево-Эйлерового взаимодействия [10].
Основные характеристики грунта: плотность ρ 2000 кг/м3, модуль деформации
Е 100 МПа, коэффициент Пуассона ν 0,25 .
В
качестве
расчетного
сейсмического
воздействия
принималась
трехкомпонентная акселерограмма, нормированная на 9 баллов (рисунок 2.2.13). При
этом была произведена балансировка акселерограммы в соответствии с [125].
Компонента Х
64.
64Компонента Y
Компонента Z
Рисунок 2.2.13. Расчетное сейсмическое воздействие
Рассмотрим
два
расчетных
случая.
В
первом
расчете
акселерограмма
землетрясения задается на свободной поверхности грунтового массива. Во втором
случае система грунтовый массив фундаментная плита здание рассматривается как
единая система, в которой сейсмическое воздействие на основании принципа
Д’Аламбера прикладывается в виде инерционных сил к сосредоточенным массам
конструкции, представленной системой с конечным числом степеней свободы. Именно
такой подход и реализован в действующем своде правил [77].
Следует отметить, что в обоих случаях заданы неотражающие границы в виде
PML-слоя. На рисунке 2.2.12 данный слой показан синим цветом, а красным цветом сам
грунт. [40, 44, 92, 99, см. п.2.1].
Сравним результаты, которые были получены для двух рассматриваемых случаев.
На рисунке 2.2.14 приведены графики относительного сдвига этажа в горизонтальных
направлениях.
65.
65а)
б)
Рисунок 2.2.14. Относительный сдвиг этажа
а) в направлении Х, б) в направлении Y
На рисунке 2.2.15 представлены графики накопления повреждений в бетонном
элементе балки. В соответствии с принятой моделью бетона 0 на оси ординат на рисунке
соответствует исходному состоянию материала, а 1 полной деградации материала в
результате накопления повреждений.
Рисунок 2.2.15. Накопление повреждений
66.
66На рисунке 2.2.16 показаны изополя развития повреждений в элементах
конструкции, а также виден характер разрушения для разных схем в один и тот же
момент времени.
а)
б)
Рисунок 2.2.16. Изополя развития повреждений. Момент времени t=8,5 с
а) без интерфейса SSI, б) с интерфейсом SSI
На рисунках видна разница в полученных результатах. На основании
вышеизложенного
предложенному
сейсмическое
можно
подходу
сделать
к
воздействие
вывод,
проведению
позволит
что
следование
расчетов
правильно
рассмотренному
железобетонных
оценивать
зданий
и
на
сейсмостойкость
строительных конструкций, проектируемых для сейсмических районов.
2.3. Модифицированная модель Мора-Кулона с введением критерия
разрушения
В работе при проведении расчетов на сейсмические воздействия применяется
идеально-упругопластическая модель Мора-Кулона, так как она наиболее устойчиво
работает при решении задач данного типа. Критерий Мора-Кулона определяет некую
67.
67поверхность текучести. При достижении напряжениями этой поверхности грунт
переходит в пластическую стадию работы. Однако это не означает, что происходит
полная потеря несущей способности грунта.
При этом следует отметить, что при интенсивных землетрясениях в некоторых
случаях наблюдается отказ грунтов с их разрушением и потерей несущей способности.
Расчетные модели должны учитывать данный характер работы грунтового основания.
Для того чтобы учесть потерю несущей способности основания, необходимо
модифицировать модель Мора-Кулона путем введения критерия разрушения. Введем
допущение о том, что превышение деформациями предельных значений будет
свидетельствовать о разрушении, и, как следствие, о потере несущей способности
рассматриваемого грунта.
На рисунке 2.3.1 показаны кривые деформирования, которые получены при
испытаниях на сдвиг [12].
Рисунок 2.3.1. Кривые деформирования при
сдвиге
1 – идеально-пластическое
деформирование, 2 – деформирование с
упрочнением,
3 – деформирование с разупрочнением
Кривая 1 относится к случаю, когда разрушение грунта наступает при постоянном
предельном касательном напряжении
τ max и росте деформаций сдвига. Кривая 2 –
характеризует упрочняющийся грунт. И наконец 3-я кривая соответствует такому
поведению грунта, при котором он упрочняется до
до своего остаточного значения
τ max , а далее прочность уменьшается
τост . Таким образом, за предел прочности для грунтов
принимаются значение деформации сдвига равное 10% и значение линейной
деформации ε1 15% .
Соответствующие ограничения были введены в модель Мора-Кулона, дополнив
ее, таким образом, критерием разрушения. Для апробации этой модели было проведено
некоторое количество расчетов зданий различной этажности, расположенных на
68.
68различных грунтах на сейсмические воздействия с различными доминантными
частотами и шириной спектра. Ниже приведены некоторые результаты расчетов.
2.3.1.
Исследование
реакции
15-ти
этажного
каркасного
железобетонного здания на сейсмическое воздействие
Рассмотрим
задачу
расчета
15-ти
этажного
железобетонного
здания,
расположенного на грунтовом основании, заданном по модифицированной модели
Мора-Кулона. Корректный учет взаимодействия данного здания с основанием
обеспечивается за счет применения методики, изложенной в пп. 2.1, 2.2 (рисунок 2.3.2).
Рисунок 2.3.2. Расчетная схема 15-ти этажного железобетонного здания, расположенного
на грунтовом основании (синий цвет – грунт, зеленый цвет – демпфирующий PML-слой)
В задачах, в которых корректный учет совместной работы конструкции и
основания обеспечивается с помощью указанной методики, расчет осуществляется в два
этапа. На первом этапе проводится только статический расчет со статическими
параметрами грунта: статический модуль деформации Eст 11 МПа ; статический
коэффициент Пуассона νст 0,375 ; статический модуль сдвига Gст 4 МПа ;
статическое удельное сцепление сст 37 кПа ; угол внутреннего трения θ 18 .
Затем решается динамическая задача, в которой учитывается напряженнодеформируемое состояние полученное в статическом расчете и используются
динамические параметры грунта: динамический модуль деформации Eдин 276 МПа ;
динамический коэффициент Пуассона νдин 0, 4 ; динамический модуль сдвига
Gдин 162 МПа ; динамическое удельное сцепление сдин 59 кПа ; угол внутреннего
трения θ 18 [108].
69.
69Расчет производился прямым динамическим методом с интегрированием
уравнений движения по явной схеме. В качестве детерминированного сейсмического
воздействия использовалась акселерограмма землетрясения с доминантной частотой 0,5
Гц и нормированная на 9 баллов (приложение А рисунок 4).
Конструктивная схема здания – полный рамный каркас. Сечение колонн
40 см 40 см , сечение ригелей 40 см 40 см , толщина плит перекрытия 20 см ,
толщина фундаментной плиты 80 см . Колонны и балки смоделированы стержневыми
конечными элементами, плиты перекрытий и фундаментная плита – оболочечными,
грунтовый массив – объемными. Было введено допущение об «оптимальном»
армировании. Это допущение основано на том, что в расчетных сечениях разрушение
сжатой зоны бетона и растянутой рабочей арматуры наступает одновременно [55, 114].
В
приложении
А
на
рисунке
5
показана
деформированная
схема
рассматриваемого здания, а на рисунках 2.3.3 и 2.3.4 приведены изополя интенсивности
пластических деформаций фундаментной плиты и грунтового основания соответственно
в момент времени t=5,34 с.
Рисунок 2.3.3. Изополя интенсивности пластических деформаций
плите, t=5,34 с
ε pl в фундаментной
Рисунок 2.3.4. Изополя интенсивности пластических деформаций
t=5,34 с
ε pl в массиве грунта,
70.
70Видно, что в зоне центральных колонн происходит продавливание фундаментной
плиты. Выполненный на стадии проектирования расчет фундаментной плиты на
продавливание в данном случае дает завышенную оценку прочности. По результатам
наших исследований видно, что несущая способность фундаментной плиты на
продавливание не обеспечена.
В результате продавливания колоннами фундаментной плиты происходит потеря
несущей способности некоторыми элементами грунта, то есть при нагружении
достигается поверхность разрушения (приложение А рисунок 6).
На рисунке 2.3.5 приведены графики вертикального перемещения w в точках
грунта под центральными колоннами, где происходит продавливание и потеря несущей
способности элементов основания.
Рисунок 2.3.5. Графики перемещений w точек грунта в месте продавливания
Про графику видно, что разрушение элементов грунта наступает последовательно
для разных зон в области продавливания.
Продавливание фундаментной плиты с потерей несущей способности некоторых
областей основания приводит к прогрессирующему обрушению всей конструкции
(рисунок 2.3.6).
71.
71Рисунок 2.3.6. Картина начала прогрессирующего обрушения здания в момент времени
t=7,76 с
Рассмотрим работу аналогичной конструкции, но с усилением (увеличением
толщины) части фундаментной плиты в зонах под колоннами (рисунок 2.3.7).
Рисунок 2.3.7. Усиление зоны под колоннами
Толщина основной части фундаментной плиты 80 см , толщина в зонах усиления
– 1 м.
В приложении А на рисунках 7-10 приведены изополя интенсивности напряжений
ζ i , интенсивности общих деформаций ε i , интенсивности пластических деформаций
ε pl , а также изгибающих моментов M x и M y в фундаментной плите соответственно.
Аналогично предыдущему рассмотренному случаю с продавливанием на рисунке
2.3.8 приведены графики перемещений точек фундаментной плиты под центральными
колоннами.
72.
72Рисунок 2.3.8. Графики перемещений w точек грунта в зоне под центральными колоннами
Из графика видно, что осадки фундаментной плиты под колоннами являются
равномерными и
продавливания не
происходит.
Следует отметить, что при
продолжающимся сейсмическом воздействии происходит отказ колонн нижних ярусов
(потеря их несущей способности) с последующим обрушением всего здания (рисунок
2.3.9).
Рисунок 2.3.9. Картина начала прогрессирующего обрушения здания с усилением
фундаментной плиты в момент времени t=8,7 с
73.
732.3.2.
Детерминированный
расчет
15-ти
этажного
каркасного
железобетонного здания с учетом повреждений основания, возникающих в
процессе землетрясения
В [5] отмечается, что не только параметры грунтов могут изменяться под
действием сейсмических колебаний, но и изменившийся под действием этих колебаний
грунт определенным образом влияет на работу конструкции здания. То есть
сейсмическая интенсивность определяется остаточными деформациями, появлением
разломов и трещин, образовавшихся в результате землетрясения [5]. В работе [5]
отмечается, что даже при относительно небольшом ускорении грунта даже самое
сейсмостойкое здание, оказавшееся в зоне разлома, может полностью разрушится.
Рассмотрим 15-ти этажное каркасное железобетонное здание, расположенное на
грунтовом основании, в котором возможно образование разломов (рисунок 2.3.2).
Предположим, что через некоторое время после начала землетрясения (через 0,5 с) в
грунте под зданием образуется разлом. Рассмотрим разлом в грунте, проходящий
поперек здания (рисунок 2.3.10), и вдоль здания (рисунок 2.3.14). Остальные параметры
приняты такими же, как и в предыдущем примере. Ниже и в приложении А приведены
результаты по рассматриваемым двум расчетным ситуациям (рисунки 2.3.11-2.3.13,
2.3.15-2.3.17, в приложении А рисунки 11-14).
Рисунок 2.3.10. Расчетная схема здания с поперечным разломом в основании
(коричневый цвет)
74.
74Рисунок 2.3.11. Изополя интенсивность пластических деформаций
ε pl в массиве грунта
Рисунок 2.3.12. Разрушение элементов грунта основания (коричневый цвет) в момент
времени t=8,44 с
Рисунок 2.3.13. Картина обрушения здания в момент времени t=8,52 с
75.
75Рисунок 2.3.14. Расчетная схема с разломом вдоль здания (коричневый цвет)
Рисунок 2.3.15. Изополя интенсивности пластических деформаций
ε pl в массиве грунта
Рисунок 2.3.16. Разрушение элементов грунта основания (коричневый цвет) в момент
времени t=9,14 с
Рисунок 2.3.17. Картина обрушения здания в момент времени t=8,46 с
76.
76Анализ результатов расчета показывает, что применение модифицированной
модели Мора-Кулона более адекватно отражает работу конструкции.
Анализ результатов обследований последствий землетрясений показывает, что
разрушение зданий во многих случаях происходит из-за отказа (разрушения) грунтов
основания, связанного с возникновением в нем во время землетрясений повреждений
(трещин, разломов). Данное явление необходимо учитывать при расчетах и
проектировании зданий и сооружений при строительстве в сейсмических районах.
Выводы по главе 2
Во 2-й главе рассмотрена проблема отражения сейсмических волн в замкнутом
массиве грунта, описаны подходы к моделированию демпфирующих слоев, а также
выбрана наиболее подходящая для расчетов на сейсмическое воздействие методика
задания демпфирующих слоев в виде PML-слоя.
Были обобщены некоторые известные теоретические положения о работе PMLслоя и проведен ряд численных исследований эффективности его работы.
Была
проанализирована
и
верифицирована
работа
рассматриваемого
демпфирующего слоя на простых системах: струна и мембрана.
Определены
необходимые
соотношения,
которые
позволяют производить
эффективное моделирования грунтового основания минимального размера.
Представлены результаты численных испытаний массива грунта на действия
статических и динамических (сейсмических) нагрузок. Моделирование и расчеты были
проведены в программном комплексе LS-DYNA, который позволяет получить решение
во временной области с учетом нелинейного характера деформирования элементов
конструкций и грунтов основания.
Рассмотрены современные подходы к учету совместной работы сооружения с
основанием (Soil Structure Interaction), а также предложена методика, позволяющая
корректно учитывать взаимодействие системы грунт конструкция при расчете на
землетрясение. Выполнена численная верификация данной методики.
Предложена модифицированная модель Мора-Кулона. В данную модель, кроме
поверхности текучести, была введена поверхность разрушения путем ограничения
величин главной линейной деформации 15-ю процентами и деформации сдвига - 10-ю
процентами. В результате интенсивного землетрясения возможна потеря грунтом
несущей способности, что может повлечь за собой частичное или полное обрушение
77.
77здания. Учет данного вида отказа позволяет повысить обеспеченность сейсмостойкости
системы сооружение основание.
Проведен ряда расчетов зданий, расположенных на грунтовом основании, в
которых наблюдались значительные повреждения в следствии появления разломов в
грунте в процессе землетрясения. Данное явление необходимо учитывать при расчетах и
проектировании зданий и сооружений, строящихся в сейсмических районах.
78.
78Глава 3. ОСОБЕННОСТИ ДЕТЕРМИНИРОВАННЫХ РЕШЕНИЙ ПРИ
УЧЕТЕ ВЗАИМОДЕЙСТВИЯ СООРУЖЕНИЯ С ОСНОВАНИЕМ ПРИ
РАСЧЕТЕ НА ЗЕМЛЕТРЯСЕНИЕ
3.1. Учет взаимодействия сооружения с основанием, и трансформация
сейсмического воздействия при землетрясении
Расчетная динамическая модель имеет вид консольной схемы с конечным
числом степеней свободы жестко защемленной в основании [77]. В такой постановке
ускорения соответствующие землетрясению прикладываются непосредственно к
сосредоточенным массам расчетной схемы сооружения по принципу Д’Аламбера.
Другими словами, в данном случае никак не учитывается взаимодействие конструкции с
грунтовым массивом, а также скорость распространения воздействия по высоте
рассматриваемой конструкции.
Известно, что адекватно оценить реакцию здания на сейсмическое воздействие
можно только корректно учитывая совместную работу сооружения с основанием.
Поставим задачу количественно оценить эффект взаимодействия сооружения с
основанием. Воспользуемся разработанной методикой, подробно изложенной в главе 2.
Рассмотрим одноэтажную пространственную раму без учета (рисунок 3.1.1а) и с
учетом взаимодействия (рисунок 3.1.1б) с основанием. Массив грунта задан в виде
линейно-деформируемого основания.
а)
б)
Рисунок 3.1.1. Расчетные схемы одноэтажной пространственной рамы
а) без учета взаимодействия с основанием, б) с учетом взаимодействия с основанием
Для
учета
нелинейного
характера
деформирования
надфундаментных
конструкций воспользуемся нелинейной модели бетона Continuous Surface Cap Model
(CSCM) [55, 114, 115, 116, 117]. Достоинством данной модели является возможность
учета непосредственного армирования несущих железобетонных элементов здания
79.
79(рисунок 3.1.2). Объемные элементы бетона связывались со стрежневыми элементами
арматуры с помощью методики Лагранжево-Эйлерового взаимодействия [10].
Рисунок 3.1.2. Расчетная схема
(арматурный каркас)
Расчет выполнялся на трехкомпонентную акселерограмму. В приложении Б на
рисунке
1
приведены
графики
соответствующих
компонент,
которые
были
нормированы на 9 баллов. Данные акселерограммы была сбалансирована в соответствии
с [51, 125].
Ниже приводятся результаты расчета здания без учета взаимодействия с
основанием.
На рисунке 3.1.3 показаны пластических деформаций ε pl , а в приложении Б на
рисунках 2-3 изополя интенсивностей напряжений
ζ i , деформаций ε i , возникающие
соответственно в бетоне и арматуре. На рисунке 3.1.4 приведены графики изменения в
процессе землетрясения интенсивности напряжений в наиболее нагруженных элементах
бетона и арматуры в основании колонны.
а)
Рисунок 3.1.3. Изополя интенсивности пластических деформаций
(а) и арматурного каркаса (б)
б)
ε pl для элементов бетона
80.
80а)
б)
Рисунок 3.1.4. График интенсивности напряжений ζ i для элемента бетона (а) и график
напряжений ζ для элемента арматуры (б)
Далее приведены результаты расчета с учетом взаимодействия сооружения с
основанием. Задача решается в два этапа (статический и динамический). Для грунтового
массива принималась модель линейно-деформируемого основания. На первом этапе
решалась статическая задача со следующими статическими характеристиками грунта
основания: плотность грунта ρ 1800 кг/м ; статический модуль деформации
3
Eст 60 МПа ; статический коэффициент Пуассона νст 0,35 . На втором этапе, учитывая
напряженно-деформируемое состояние, полученное на первом этапе, проводился расчет
на сейсмическое воздействие с динамическими параметрами грунта основания:
3
плотность грунта ρ 1800 кг/м ; динамический модуль деформации Eдин 300 МПа ;
динамический коэффициент Пуассона νдин 0,45 [71].
81.
81На рисунках 3.1.5 показаны изополя интенсивностей пластических деформаций
ε pl , а в приложении Б на рисунках 4-5 изополя интенсивностей напряжений ζ i ,
деформаций
ε i , возникающие соответственно в бетоне и арматуре.
а)
б)
Рисунок 3.1.5. Изополя интенсивности пластических деформаций ε pl для элементов
бетона (а) и арматурного каркаса (б)
Примечание: на рисунках в грунтовом массиве показаны границы PML-слоев с разными
параметрами демпфирования.
На рисунке 3.1.6 приведены изополя интенсивности напряжений
интенсивности общих деформаций
ε i в грунтовом основании.
ζi и
82.
82а)
б)
Рисунок 3.1.6. Изополя интенсивности напряжений ζ i (а) и интенсивности деформаций
в грунтовом основании
εi
(б)
На рисунке 3.1.7 приведены графики изменения в процессе землетрясения
интенсивности напряжений в наиболее нагруженных элементах бетона и арматуры в
основании колонны.
а)
б)
Рисунок 3.1.7. График интенсивности напряжений ζ i для элемента бетона (а) и график
напряжений ζ для элемента арматуры (б)
83.
83На основании полученных результатов можно сделать вывод, что реакция
одноэтажной рамы различна при учете и без учета взаимодействия с грунтовым
основанием. Повреждения, полученные конструкцией при учете совместной работы с
грунтовым основанием, являются более значительными.
Таблица 3.1.1.
Элементы
Элементы
бетона
Элементы
арматуры
Сравнительная таблица интенсивности напряжений ζ i с учетом и без учета
взаимодействия с основанием
С учетом
Без учета взаимодействия с
Расхождение
взаимодействия с
основанием
результатов, %
основанием
10,81 МПа
3,92 МПа
25,5
347,74 МПа
197,46 МПа
43,2
На рисунке 3.1.8 представлены перемещения (u – по направлению оси Х, v – по
направлению оси Y, w – по направлению оси Z) точки в центре фундаментной плиты. На
рисунках 3.1.9, 3.1.10 приведено сравнение ускорений и спектров исходного
сейсмического воздействия с соответствующими ускорениями и спектрами, которые
были получены в середине фундаментной плиты.
а)
б)
84.
84в)
Рисунок 3.1.8. Перемещения в середине фундаментной плиты
Компонента Х
Компонента Y
85.
85Компонента Z
Рисунок 3.1.9. Сравнение ускорений исходного воздействия с ускорениями в точке
фундаментной плиты
Компонента X
Компонента Y
86.
86Компонента Z
Рисунок 3.1.10. Сравнение спектров ускорений исходного воздействия со спектрами
ускорения в середине фундаментной плиты
Анализ результатов показывает (рисунки 3.1.9 и 3.1.10), что наличие конструкции
трансформирует исходное сейсмическое воздействие, которое было задано для
свободной поверхности. При этом доминантная частота сейсмического воздействия
смещается в сторону больших периодов, а максимальные ускорения по Х увеличиваются
в 1,8 раза, по Y в 2,5 раза, по Z в 5 раз.
На рисунке 3.1.11 показаны графики перемещений точки в центре плиты
перекрытия для схем с учетом и без учета взаимодействия с основанием. На рисунке
3.1.12 приведены графики соответствующих ускорений.
а)
87.
87б)
в)
Рисунок 3.1.11. Сравнение перемещений точки в центре плиты перекрытия
Компонента X
Компонента Y
88.
88Компонента Z
Рисунок 3.1.12. Сравнение ускорений точки в центре плиты перекрытия
На рисунке 3.1.13 показаны графики относительного смещения этажа для схем
без учета и с учетом взаимодействия с основанием.
а)
б)
Рисунок 3.1.13. Относительные смещения этажа
При учете взаимодействия с грунтом основания на 14 с землетрясения начинается
обрушение рассматриваемой конструкции (рисунок 3.1.11б, в, рисунок 3.1.13б). В то
время как рама без учета взаимодействия с основанием получает некоторые
повреждения, но обрушения не происходит. Можно сделать вывод о дефиците
сейсмостойкости
рассматриваемой
сооружения с основанием.
конструкции
при
неучете
взаимодействия
89.
89Исследуем вопрос и о степени трансформации исходного сейсмического
воздействия для случая 3-х этажной пространственной рамы при учете взаимодействия
сооружения с основанием. Исходные данные и параметры приняты аналогично
рассмотренному выше примеру. На рисунке 3.1.14 приведены расчетные схемы 3-х
этажной рамы.
а)
б)
Рисунок 3.1.14. Расчетные схемы 3-х этажной пространственной рамы
а) без учета взаимодействия с основанием (общий вид, арматурные каркас), б) с учетом
взаимодействия с основанием
Ниже приведены результаты расчетов. На рисунке 3.1.15 показаны изополя
интенсивностей пластических деформаций ε pl , а в приложении Б на рисунках 6-7
изополя интенсивностей напряжений
ζ i , деформаций ε i , возникающие соответственно
в бетоне и арматуре. На рисунке 3.1.16 приведены графики изменения в процессе
землетрясения интенсивности напряжений в наиболее нагруженных элементах бетона и
арматуры в основании колонны.
90.
90а)
б)
Рисунок 3.1.15. Изополя интенсивности пластических деформаций
бетона (а) и арматурного каркаса (б)
ε pl для элементов
а)
б)
Рисунок 3.1.16. График интенсивности напряжений ζ i для элемента бетона (а) и график
напряжений ζ для элемента арматуры (б)
91.
91Далее приведены результаты расчета трехэтажной пространственной рамы с
учетом взаимодействия сооружения с основанием. На рисунке 3.1.17 приведены изополя
интенсивностей пластических деформаций ε pl , а в приложении Б на рисунках 8-9
изополя интенсивностей напряжений
ζ i , деформаций ε i , возникающие соответственно
в бетоне и арматуре.
а)
б)
Рисунок 3.1.17. Изополя интенсивности пластических деформаций
бетона (а) и арматурного каркаса (б)
ε pl для элементов
Примечание: на рисунках в грунтовом массиве показаны границы PML-слоев с разными
параметрами демпфирования.
92.
92На рисунке 3.1.18 приведены изополя интенсивности напряжений
интенсивности общих деформаций
ζi и
ε i в грунтовом основании.
б)
а)
Рисунок 3.1.18. Изополя интенсивности напряжений ζ i (а) и интенсивности деформаций
в грунтовом основании
εi
(б)
На рисунке 3.1.19 приведены графики изменения в процессе землетрясения
интенсивности напряжений в наиболее нагруженных элементах бетона и арматуры в
основании колонны.
а)
б)
Рисунок 3.1.19. График интенсивности напряжений ζ i для элемента бетона (а) и график
напряжений ζ для элемента арматуры (б)
93.
93В таблице 3.1.2 приведем сравнение интенсивности напряжений для двух
рассматриваемых случаев расчета трехэтажной пространственной рамы.
Таблица 3.1.2.
Сравнительная таблица интенсивности напряжений ζ i с учетом и без учета
взаимодействия с основанием
С учетом
Без учета взаимодействия с
Расхождение
взаимодействия с
основанием
результатов, %
основанием
Элементы
Элементы
бетона
Элементы
арматуры
11,53 МПа
7,43 МПа
35,6
350 МПа
1498,2 МПа
76,6
Далее приведены результаты расчета с учетом взаимодействия сооружения с
основанием.
На
рисунке
3.1.20
представлены
фундаментной плиты.
а)
б)
перемещения
точки
в
центре
94.
94в)
Рисунок 3.1.20. Перемещения точки в центре фундаментной плиты
На рисунках 3.1.21, 3.1.22 приведено сравнение ускорений и спектров исходного
сейсмического воздействия с соответствующими ускорениями и спектрами, которые
были получены в середине фундаментной плиты.
Компонента X
Компонента Y
95.
95Компонента Z
Рисунок 3.1.21. Сравнение ускорений исходного воздействия с ускорениями в центре
фундаментной плиты
Компонента X
Компонента Y
96.
96Компонента Z
Рисунок 3.1.22. Сравнение спектров ускорений исходного воздействия со спектрами
ускорения в центре фундаментной плиты
Наличие трѐхэтажной пространственной рамы на грунтовом основании в большей
степени трансформирует исходное сейсмическое воздействие, чем наличие одноэтажной
рамы. И для этого расчетного случая происходит смещение доминантной частоты
сейсмического воздействия в сторону больших периодов. Максимальные ускорения по
Х увеличились в 6 раз, по Y в 10 раз, по Z в 27 раз.
На рисунке 3.1.23 приведены графики перемещений точки в центре плиты
перекрытия для схем с учетом и без учета взаимодействия с основанием. На рисунке
3.1.24 приведены графики соответствующих ускорений. На рисунке 3.1.25 показаны
относительные горизонтальные перемещения верха здания.
а)
97.
97б)
в)
Рисунок 3.1.23. Сравнение перемещений точки в центре плиты перекрытия 3-го этажа
Компонента X
Компонента Y
98.
98Компонента Z
Рисунок 3.1.24. Сравнение ускорений точки в центре плиты перекрытия 3-го этажа
а)
б)
Рисунок 3.1.25. Относительные горизонтальные перемещения верха здания
Для обеих расчетных ситуаций характерно обрушение конструкции (рисунки
3.1.23в, рисунок 3.1.25а), однако рама без учета взаимодействия с основанием
разрушается позже, чем на грунтовом основании. Таким образом, можно сделать, что
при неучете взаимодействия сооружения с основанием имеет место дефицит
сейсмостойкости рассматриваемой конструкции.
Проведенные исследования простых систем показывают, во-первых, что при
учете совместной работы сооружения с основанием происходит трансформация
расчетного сейсмического воздействия, которое получено на свободной поверхности,
99.
99причем степень трансформации существенно отличается для зданий разной этажности.
Во-вторых, неучет взаимодействия сооружения с грунтом основания при проведении
расчетов на сейсмическое воздействие может привести к дефициту сейсмостойкости
проектируемого здания или сооружения.
3.2. Сравнительный анализ реакции 5-ти этажного здания с использованием
основания в виде линейно-деформируемого полупространства и модели
Мора-Кулона
В п. 2.2 главы 2 были описаны нелинейные модели грунтов основания, и
отмечено, что наиболее устойчивой моделью при проведении численных исследований
при сейсмических воздействиях является модель Мора-Кулона.
Рассмотрим два варианта расчета 5-ти этажного железобетонного здания с
полным рамным каркасом: на линейно-деформируемом основании и на основании,
заданном по модели Мора-Кулона (рисунок 3.2.1).
Рисунок 3.2.1. Расчетная схема 5-ти
этажного железобетонного здания,
расположенного на грунтовом
основании (синий цвет – грунт,
зеленый цвет – демпфирующий
PML-слой)
Корректный учет взаимодействия данного здания с основанием обеспечивается за
счет применения методики, изложенной в главе 2. В расчетной схеме используется
демпфирующий PML-слой (рисунок 3.2.1). Расчет производится в два этапа
(статический и динамический). Приняты следующие параметры для грунта основания:
статические статический модуль деформации Eст 11 МПа ; статический коэффициент
Пуассона νст 0,375 ; статический модуль сдвига Gст 4 МПа ; статическое удельное
сцепление
сст 37 кПа ;
угол внутреннего трения
динамический модуль деформации
θ 18 , динамические:
Eдин 276 МПа ; динамический коэффициент
Пуассона νдин 0,4 ; динамический модуль сдвига Gдин 162 МПа ; динамическое
удельное сцепление сдин 59 кПа ; угол внутреннего трения θ 18 [71, 108].
100.
100В приведенной расчетной схеме колонны и ригели моделировались стержневыми
конечными элементами, а плиты перекрытия – пространственными конечными
элементами оболочки. Введено допущение об «оптимальном» армировании. Это
допущение основано на том, что в расчетных сечениях разрушение сжатой зоны бетона
и растянутой рабочей арматуры наступает одновременно [55, 114].
В качестве расчетного сейсмического воздействия принималась сбалансированная
трехкомпонентная акселерограмма, нормированная на 9 баллов (приложение Б рисунок
10).
Доминантная
частота
горизонтальных
компонент
акселерограммы
3
Гц,
вертикальной компоненты – 4 Гц.
На рисунке 3.2.2 показаны изополя интенсивности пластических деформаций ε pl
, которые возникают в грунте, заданном по модели Мора-Кулона.
Рисунок 3.2.2. Изополя интенсивности пластических деформаций
заданном по модели Мора-Кулона
ε pl в грунтовом массиве,
На рисунках 3.2.3 – 3.2.5 приведены графики относительных горизонтальных
перемещений верха здания, ускорений точки середины плиты перекрытия и поперечных
сил в основании колонн для двух вариантов грунтового основания соответственно.
а)
101.
101б)
Рисунок 3.2.3. Относительные смещения этажей
Компонента X
Компонента Y
Компонента Z
Рисунок 3.2.4. Компоненты ускорений точки плиты перекрытия 5-го этажа
102.
102а)
б)
Рисунок 3.2.5. Поперечная сила в основании колонны
По полученным графикам видно, что результаты для здания линейнодеформируемом основании и на основании, заданном по модели Мора-Кулона, хорошо
сходятся. Можно сделать вывод, что расчет на здания небольшой этажности на
землетрясения целесообразно выполнять с использованием более простой линейнодеформируемой модели основания. Однако с увеличением этажности (веса здания и,
соответственно,
давления
под
подошвой
фундамента)
нелинейный
характер
деформирования грунта будет проявляться в большей степени и может существенно
сказываться на поведении конструкции во время сейсмического воздействия.
3.3. Анализ реакции железобетонного здания повышенной этажности при
различных моделях грунтового основания
Рассмотрим 15-ти этажное железобетонное здание с полным рамным каркасом
(рисунок 3.3.1).
103.
103Рисунок 3.3.1. Расчетная схема 15-ти
этажного железобетонного здания,
расположенного на грунтовом основании
(синий цвет – грунт, зеленый цвет –
демпфирующий PML-слой)
При проведении исследований было выбрано наиболее неблагоприятное исходное
сейсмическое воздействие. Доминантная частота всех трех компонент акселерограммы
составляет 0,5 Гц (приложение Б рисунок 11).
Остальные исходные данные аналогичны принятым в п. 2.3.
На рисунке 3.3.2 показаны изополя интенсивности пластических деформаций в
грунтовом основании, заданном по модели Мора-Кулона. Сравнивая распределение
интенсивности пластических деформаций под 5-ти (п.3.2) и 15-ти этажными зданиями
видны значительные различия.
Рисунок 3.3.2. Изополя интенсивности пластических деформаций
заданном по модели Мора-Кулона
ε pl в грунтовом массиве,
Как указывалось выше, значительные пластические деформации в основании 15ти этажного здания при землетрясении вызваны большим весом здания и более
значительным вкладом в НДС основания сейсмического воздействия.
Ниже на рисунках 3.3.3 - 3.3.5 показаны графики относительных горизонтальных
перемещений верха здания, ускорений точки середины плиты перекрытия 15-го этажа и
поперечных сил в основании колонн соответственно.
104.
104а)
б)
Рисунок 3.3.3. Относительные смещения этажей
Компонента X
Компонента Y
105.
105Компонента Z
Рисунок 3.3.4. Компоненты ускорений точки середины плиты перекрытия 15-го этажа
а)
б)
Рисунок 3.3.5. Поперечная сила в основании колонны
Анализируя результаты расчета 15-ти этажного здания можно сделать вывод, что
реакция здания на линейно-деформируемом грунтовом основании и на основании,
заданном по модели Мора-Кулона, имеют определенные различия. При этом следует
отметить, что поперечные силы в основании колонн для двух расчетных случаев
практически совпадают. Однако время начала разрушения элементов конструкции и
характер обрушения зданий значительно разнятся. В приложении Б на рисунке 12
приведены изополя интенсивности напряжений в стержневых элементах конструкции в
момент времени предшествующий началу прогрессирующего обрушения всего здания.
106.
106А на рисунке 3.3.6 показан характер обрушения зданий, расположенных на грунтах
основания, заданных по различным моделям.
а)
б)
Рисунок 3.3.6. Картина начала прогрессирующего обрушения
а) здание на линейно-деформируемом основании; б) здание на основании, заданном по
модели Мора-Кулона
По полученным результатам можно сделать следующий вывод: при интенсивном
сейсмическом воздействии для зданий повышенной этажности необходимо учитывать
нелинейный характер деформирования грунтов основания.
3.4. Методика расчета 9-ти этажного железобетонного здания перекрестностеновой конструктивной схемы при сейсмическом воздействии
Выполним детерминированный расчет жилого 9-ти этажного железобетонного
здания перекрестно стеновой конструктивной схемы, модель которого представлена на
рисунке 3.4.1.
107.
107Рисунок 3.4.1. Расчетная модель жилого 9ти этажного железобетонного здания на
грунтовом основании
Расчет производился в 2 этапа (статический и динамический), при этом
использовался
демпфирующий
PML-слой
в
соответствии
с
разработанной
и
приведенной в главе 2 методикой. Параметры грунтов основания приняты по аналогии с
параграфом 2.3.
Для
определения
параметров
наиболее
неблагоприятного
сейсмического
воздействия был выполнен модальный анализ рассматриваемого здания. Было
установлено, что для данного здания таким воздействием является акселерограмма с
доминантными частотами 1 Гц. На рисунке 3.4.2 приведена компонента X этой
синтезированной акселерограммы, нормированной на интенсивность 9,5 баллов.
Рисунок 3.4.2. Компонента X расчетной акселерограммы
Ниже приведем некоторые результаты расчета.
На рисунке 3.4.3 показан момент начала прогрессирующего обрушения
конструкции (t=10,84 с).
108.
108Рисунок 3.4.3. Начало прогрессирующего обрушения конструкции t=10,84 c
На рисунке 3.4.4 приведены изополя интенсивности пластических деформаций в
элементах конструкций (а), а также в грунтовом основании (б) в данный момент
времени. В приложении Б на рисунке 13 показаны изополя интенсивности напряжений в
тех же элементах расчетной схемы.
б)
а)
Рисунок 3.4.4. Изополя интенсивности пластических деформаций
а) в элементах конструкции, б) в элементах грунтового основания
На рисунке 3.4.5
приведены
графики
перемещений в центре плиты покрытия.
а)
горизонтальных и вертикального
109.
109б)
в)
Рисунок 3.4.5. Графики перемещений точки плиты покрытия конструкции
Таким образом, разработанная методика (глава 2) позволяет выполнять
детерминированный расчет реальных зданий на интенсивное сейсмическое воздействие
прямым динамическим методом с учетом нелинейного характера деформирования
надфундаментных конструкций, фундаментов и грунтов основания в корректной
постановке.
Выводы по главе 3
Произведены исследования работы простых систем с учетом взаимодействия с
основанием при интенсивных землетрясениях. Выполнено сравнение результатов,
полученных при расчете конструкции с учетом и без учета совместной работы с грунтом
основания.
Исследования работы одноэтажной рамы показали, что ее реакция на
землетрясение различна при учете и без учета взаимодействия с грунтовым основанием.
Повреждения, полученные конструкцией при учете совместной работы с грунтовым
основанием, являются более значительными.
110.
110Сравнение графиков интенсивности напряжений в середине плиты перекрытия
показали для расчетного случая, в котором учитывалось взаимодействие с основанием
уменьшение интенсивности напряжений для наиболее нагруженных элементов как
бетона, так и арматуры.
Наличие конструкции трансформирует исходное сейсмическое воздействие,
которое было задано для свободной поверхности. При этом доминантная частота
сейсмического воздействия смещается в сторону больших периодов, а максимальные
ускорения по Х увеличились в 1,8 раза, по Y в 2,5 раза, по Z в 5 раз.
При
значительная
рассмотрении
и
трехэтажной
количественная
и
пространственной
качественная
рамы
трансформация
наблюдается
исходного
сейсмического воздействия, происходит сдвиг спектра в область больших периодов.
Интенсивности напряжений в элементах конструкции уменьшились для случая
взаимодействия с основанием. Максимальные ускорения по Х увеличились в 6 раз, по Y
в 10 раз, по Z в 27 раз.
Проведенные исследования простых систем показывают, во-первых, что при
учете совместной работы сооружения с основанием происходит трансформация
расчетного сейсмического воздействия, которое получено на свободной поверхности,
причем степень трансформации существенно отличается для зданий разной этажности.
Во-вторых, неучет взаимодействия сооружения с грунтом основания при проведении
расчетов на сейсмическое воздействие может привести к дефициту сейсмостойкости
проектируемого здания или сооружения.
Были проведены численные исследования работы 5-ти этажного железобетонного
здания с полным рамным каркасом расположенного, в одном расчетном случае на
линейно-деформируемом основании, в другом – на основании, заданном по модели
Мора-Кулона. Проведение расчетов зданий небольшой этажности на землетрясения
целесообразно выполнять с использованием более простой линейно-деформируемой
модели основания. Однако с увеличением этажности (веса здания и, соответственно,
давления под подошвой фундамента) нелинейный характер деформирования грунта
проявляется в большей степени и существенно сказывается на поведении конструкции
во время сейсмического воздействия.
Проведено исследование 15-ти этажного здания в аналогичной постановке.
Реакция данного здания на линейно-деформируемом грунтовом основании и на
111.
111основании, заданном по модели Мора-Кулона, имеет определенные различия. Время
начала разрушения элементов конструкции и характер обрушения зданий значительно
разнятся. Таким образом, при интенсивном сейсмическом воздействии для зданий
повышенной этажности необходимо учитывать нелинейный характер деформирования
грунтов основания.
Проведен
расчет
жилого
9-ти
этажного
здания
перекрестно-стеновой
конструктивной схемы на интенсивное сейсмическое воздействие по разработанной
методики учета совместной работы сооружения с основанием. Разработанная методика
позволяет выполнять детерминированный расчет реальных зданий на интенсивное
сейсмическое воздействие прямым динамическим методом с учетом нелинейного
характера деформирования надфундаментных конструкций, фундаментов и грунтов
основания в корректной постановке.
112.
112Глава
4.
ВЕРОЯТНОСТНАЯ
ЗАДАЧА
ВЗАИМОДЕЙСТВИЯ
СООРУЖЕНИЯ С ОСНОВАНИЕМ
4.1. Вероятностные параметры грунтового основания
В главе 1 были приведены случайные параметры и методы моделирования
сейсмического воздействия, которое является ярко выраженным случайным процессом.
Следует отметить, что параметры грунтового основания также имеют большую
изменчивость. В общем случае данные параметры являются случайными функциями
координат. Именно поэтому при обработке результатов определений физических и
механических (прочностных и деформационных) характеристик грунтов применяют
методы теории вероятностей и математической статистики [81]. Все это говорит о
необходимости при исследовании и проектировании зданий и сооружений, строящихся
в сейсмических районах, при учете взаимодействия сооружения с основанием
применять методы теории надежности строительных конструкций, теории вероятностей,
теории случайных процессов и случайных функций.
Статистическую обработку результатов испытаний грунтов проводят для оценки
неоднородности и вычисления нормативных и расчетных значений характеристик
грунтов. Неоднородность грунта оценивают с помощью коэффициентов вариации
характеристик грунта. Статистическую обработку проводят для частных значений
характеристик грунтов или фиксируемых в отдельных испытаниях величин, которые
составляют случайную выборку. При наличие закономерного изменения характеристики
в каком-либо направлении (чаще всего с глубиной) статистическую обработку проводят
для
определения
параметров
корреляционной
зависимости
[81].
Значения
доверительной вероятности при вычислении расчетного значения характеристики
грунта принимают в соответствии с рекомендациями норм проектирования различных
видов сооружений. Данные значения должны быть указаны в программе работ на
проведение инженерно-геологических изысканий. Число определений характеристик
грунтов или фиксируемых в опытах значений должно быть не менее 6.
В расчетах будем использовать вероятностные характеристики случайных
параметров грунтов, полученных в результате инженерно-геологических изысканий для
одной из площадок в сейсмическом районе под строительство одного из олимпийских
объектов.
Математическое
ожидание
модуля
деформации
mE 25 МПа ,
113.
113среднеквадратическое отклонение - sE 5 МПа ; математическое ожидание удельного
сцепления mс 34 кПа , среднеквадратическое отклонение - sс 6,8 кПа ; математическое
ожидание угла внутреннего трения m 23 , среднеквадратическое отклонение -
sθ 2,3 .
В проведенных исследованиях будем использовать модель грунтового основания
Мора-Клона со случайными параметрами: модуль деформации Е, удельное сцепление
с и угол внутреннего трения θ .
Будем считать, что все характеристики грунта, принимаемые случайными
подчиняются нормальному закону распределения.
Функция распределения нормального закона:
1
F x
e
sx 2
x
где
x mx 2
2 sx2
dx ,
(4.1.1)
mx математическое ожидание случайной величины x, sx среднеквадратическое
отклонение случайной величины x.
Плотность распределения нормального закона:
f x
Оценка
1
e
s x 2
надежности
x mx 2
2 sx2
системы
.
сооружение основание,
(4.1.2)
выполненная
ниже,
производилась методом статистических испытаний [48, 67, 68, 69]. В приложении В на
рисунках 1 - 3 приведены реализации значений случайных параметров, полученных в
численных испытаниях, а также соответствующие им гистограммы и плотности
распределения.
Рассматриваемые вероятностные параметры грунта основания принимались
полностью корреляционно связанными в плане и по высоте грунтового массива.
4.2. Надежность системы сооружение основание при случайном
сейсмическом воздействии, нормированном на интенсивность 8 баллов
Для оценки надежности 9-ти этажного железобетонного здания с полным рамным
каркасом (рисунок 4.2.1) была выполнена серия численных испытаний.
114.
114Рисунок 4.2.1. Расчетная схема 9-ти
этажного железобетонного здания
Вероятностные параметры грунтового основания были выбраны в соответствии п.
4.1, а вероятностные параметры сейсмического воздействия были приняты в
соответствии с главой 1. Моделирование реализаций нестационарного случайного
процесса сейсмического воздействия производилось с помощью метода канонических
разложений. Доминантная частота сейсмического воздействия была принята равной 0,5
Гц.
Для рассматриваемого 9-ти этажного железобетонного здания построим
гистограммы, плотность и функцию распределения следующих величин: времени
появления пластических деформаций в элементах конструкции, количества колонн, в
которых наблюдается появление пластических деформаций, а также значений
пластических деформаций в грунтовом массиве. В результате проведенных 10
статистических
испытаний
было
зафиксировано
2
обрушения.
Распределение
указанного количества колонн и случайной величины интенсивности пластических
деформаций
выведены
для
сечения
случайного
процесса
t 14,3 c ,
которое
соответствует времени начала обрушения одного из зданий.
На рисунке 4.2.2 приведены гистограмма, плотность и функция распределения
времени появления пластических деформаций в элементах конструкции.
а)
115.
115б)
в)
Рисунок 4.2.2. Гистограмма (а), плотность (б) и функция распределения (в) значений
времени появления пластических деформаций в элементах конструкции при 8-ми бальном
воздействии
На рисунке 4.2.3 приведены гистограмма, плотность и функция распределения
количества колонн, в которых возникают пластические деформации в момент времени
t 14,3 c .
а)
116.
116б)
в)
Рисунок 4.2.3. Гистограмма (а), плотность (б) и функция распределения (в) количества
колонн, в которых возникают пластические деформации в момент времени t 14,3 c при 8ми бальном воздействии
На рисунке 4.2.4 приведены гистограмма, плотность и функция распределения
значений пластических деформаций в грунте в момент времени t 14,3 c .
а)
117.
117б)
в)
Рисунок 4.2.4. Гистограмма (а), плотность (б) и функция распределения (в) значения
пластических деформаций в грунтовом массиве в момент времени t 14,3 c при 8-ми
бальном воздействии
В результате исследований определена частота отказов, которая характеризует
вероятность отказов (при этом за отказ принимаем обрушение здания). В данном случае
вероятность отказа составляет Pf 0,2 . Среднее значение максимальных пластических
деформаций, возникающих в грунте ε pl 0, 0086 . На рисунке 4.2.4в показан график
характеризующий связь между пластической деформации в грунте ε pl и вероятностью ее
возникновения F (ε pl ) . Из графика видно, например, вероятность того, что пластические
деформации в грунте превысят величину ε pl 0,01 составляет F (ε pl ) 0,63 .
Рассмотрим вероятностные характеристики случайной величины интенсивности
напряжений
в
грунте.
Значение
интенсивности
напряжений
для
каждого
рассматриваемого испытания выбиралось как максимальное из семейства кривых для
элементов
грунта.
Аппроксимируем
полученное
эмпирическое
распределение
118.
118напряжений наиболее подходящим теоретическим, используя критерий максимального
правдоподобия Пирсона. Будем рассматривать нормальный закон распределения, закон
Вейбулла и закон Гумбеля.
Определим моменты полученного эмпирического распределения:
n
m
*
x
x
i
i
n
0,2725 МПа
x m
n
*x
i 1
* 2
x
i
n
(4.2.1)
0,0949 МПа
(4.2.2)
*
где mx – математическое ожидание случайной величины, x – среднеквадратическое
*
отклонение случайной величины.
Предположим нормальное распределение интенсивности напряжений (рисунок
4.2.5) [19].
Рисунок 4.2.5. Аппроксимация распределения интенсивности напряжений
нормальным распределением, МПа
ζi
в грунте
С помощью критерия Пирсона проверим корректность применения нормального
закона распределения для аппроксимации эмпирического распределения [19].
t
2
i 1
где
mi npi
npi
2
0, 2193
(4.2.3)
mi – число значений в i-ом разряде, n – общее число испытаний, pi – теоретическая
вероятность попадания случайной величины в i-ый разряд.
119.
119Для определения вероятности распределения интенсивности напряжений
нормальному закону необходимо проинтегрировать плотность распределения
ζ i по
f (ζi ) от
до значения χ 0,2193 . В результате получим, что вероятность распределения
2
интенсивности напряжений по нормальному закону будет равна Pнорм 0,64 .
Далее предположим, что случайная величина интенсивности напряжений в
грунте, распределена по закону Вейбулла [19].
Функция распределения закона Вейбулла:
0, при x 0
F ( x)
,
b
1 exp( x / a) , при x 0
(4.2.4)
где а – параметр масштаба, b – параметр формы кривой.
Плотность распределения закона Вейбулла:
0, при x 0
f ( x)
.
b
b 1
b
b a x exp( x/ a) , при x 0
На рисунке 4.2.6 показана аппроксимация
(4.2.5)
ζ i распределением Вейбулла.
Рисунок 4.2.6. Аппроксимация распределения интенсивности напряжений
распределением Вейбулла, МПа
ζi
в грунте
По критерию Пирсона проверим корректность применения закона распределения
Вейбулла для аппроксимации эмпирического распределения.
t
mi npi
i 1
npi
2
2
0,1719
(4.2.6)
120.
120Для
данной
аппроксимации
вероятность
распределения
интенсивности
эмпирического
распределения
напряжений по закону Вейбулла PВейбулл 0,68 .
На
рисунке
4.2.7
приведена
гистограмма
случайных значений интенсивности напряжений и аппроксимация этого распределения
распределением Гумбеля. Этот закон распределения является актуальным для случаев,
когда анализируются максимальные значения величин.
Функция распределения определяется выражением:
F ( x) exp exp α( x q) ,
где
1 ζx
,
α ζy
1
q mx my ,
α
mx и ζ x
(4.2.7)
математическое
ожидание
и
среднеквадратическое отклонение случайной величины; my и ζ y определяются в
зависимости от длины рассматриваемого ряда.
Плотность распределения закона Гумбеля имеет вид [22]:
f ( x) αexp α( x q) exp α( x q)
Рисунок 4.2.7. Аппроксимация распределения интенсивности напряжений
распределением Гумбеля, МПа
(4.2.8)
ζi
в грунте
С помощью критерия Пирсона проверим корректность применения распределения
по закону Гумбеля для аппроксимации эмпирического распределения.
t
mi npi
i 1
npi
2
2
0,4308
(4.2.9)
121.
121В
результате
получим,
что
вероятность
распределения
интенсивности
напряжений по закону Гумбеля составит РГумбеля 0,51.
На рисунке 4.2.8 для сравнения совместно показаны полученные аппроксимации
эмпирического распределения интенсивности напряжений
ζ i в грунтовом массиве.
Рисунок 4.2.8. Аппроксимация распределения интенсивности напряжений ζ i в грунте,
МПа нормальным распределением (красный график); распределением Вейбулла
(оранжевый график); распределением Гумбеля (зеленый график)
Анализ аппроксимаций эмпирического распределения позволяет сделать вывод,
ζ i с большей вероятностью будут
что значения интенсивности напряжений
распределены по закону Вейбулла (таблица 4.2.1).
Таблица 4.2.1.
Аппроксимация эмпирического распределения интенсивности напряжений
Наименование распределения
Вероятность распределения
χ2
интенсивности напряжений
Нормальное распределение
0,2193
0,64
Распределение по закону
Вейбулла
Распределение по закону
Гумбеля
Построим функцию
используя закон Вейбулла.
0,1719
0,68
0,4308
0,51
распределения
интенсивности
напряжений
в грунте
122.
122Рисунок 4.2.9. Функция распределения значений интенсивности напряжений
грунтовом массиве при 8-ми бальном воздействии
ζi в
Среднее значение максимальной интенсивности напряжений ζi 0,273 МПа . На
рисунке 4.2.9 приведен график, характеризующий связь между интенсивностью
напряжений в грунте ζ i и вероятностью ее возникновения F (ζi ) . Из рисунка видно, что,
например, вероятность того, что интенсивность напряжений превысит значение ζi 0,1
МПа составит F (ζi ) 0,05 .
4.3. Надежность системы сооружение-основание при случайном
сейсмическом воздействии, нормированном на интенсивность 9 баллов
Произведем оценку надежности того же 9-ти этажного железобетонного здания
(рисунок 4.2.1) на случайные реализации сейсмического воздействия, нормированного
на 9 баллов. Вероятностные параметры грунтового основания были выбраны в
соответствии п. 4.1, а вероятностные параметры сейсмического воздействия с
доминантной частотой 0,5 Гц были приняты в соответствии с главой 1.
Для рассматриваемого 9-ти этажного железобетонного здания построим
гистограммы, плотность и функцию распределения следующих характеристик: время
появления пластических деформаций в элементах конструкции, время отказа первого
элемента конструкции, время начала обрушения здания, количество колонн, в которых
появляются пластические деформации на момент начала обрушения, количество
элементов, отказавших (разрушенных) до начала обрушения конструкции, а также
значения пластических деформаций в грунте на момент начала обрушения. В качестве
закона аппроксимации эмпирических распределений будем использовать нормальный
закон.
123.
123В приложении В на рисунках 4-7 приведены гистограммы эмпирического
распределения,
функции
плотности
распределения
и
функции
распределения
следующих значений соответственно: времени появления пластических деформаций в
элементах конструкции, значений времени первого отказа элемента конструкции,
значений времени начала обрушения здания, количества колонн, в которых появляются
пластические деформации.
На рисунке 4.3.1 приведены гистограмма эмпирического распределения, функция
плотности распределения и функция распределения количества конечных элементов,
отказавших (разрушенных) до начала обрушения здания.
а)
б)
124.
124в)
Рисунок 4.3.1. Гистограмма (а), плотность (б) и функция распределения (в) количества
элементов, отказавших до начала обрушения здания
На рисунке 4.3.2 приведены гистограмма эмпирического распределения, функция
плотности распределения и функция распределения значений пластических деформаций
в грунте на момент начала обрушения здания.
а)
б)
125.
125в)
Рисунок 4.3.2. Гистограмма (а), плотность (б) и функция распределения (в) значений
пластических деформаций в грунте на момент начала обрушений
По
графику распределения
количества
отказавших
конечных
элементов
расчетной схемы (рисунок 4.3.1) можно сделать вывод, что среднее количество, которое
приводит к обрушению конструкции составляет nel 170 . При отказе (повреждении)
nel 50 несущих элементов вероятность обрушения конструкции будет равна F (nel ) 0,2
(рисунок 4.3.1в).
Среднее значение максимальных пластических деформаций на момент начала
обрушения ε pl 0, 0233 . Вероятность того, что пластические деформации в грунте
превысят величину ε pl 0,01 составляет F (ε pl ) 0,32 .
4.4. Исследование реакции 9-ти этажного железобетонного здания на
землетрясение
при
случайных
начальных
повреждениях
грунтового
основания
Рассмотрим
9-ти
этажное
железобетонное
здание
перекрестно
стеновой
конструктивной схемы, расчетная схема которого была представлена на рисунке 4.2.1.
Выполним расчет методом статистических испытаний используя случайные
реализации сейсмического воздействия, которое было смоделировано с помощью
метода канонических разложений и нормировано на 8 баллов (доминантная частота 0,5
Гц), параметры грунта основания примем случайными в соответствии с постановкой,
описанной
в
п.4.2.
В
качестве
модели
грунтового
основания
примем
модифицированную модель Мора-Кулона по методике, изложенной в п. 2.3. Положение
126.
126начальных повреждений грунта под фундаментной плитой здания примем случайным и
распределенным по равномерному закону вдоль соответствующих горизонтальных осей.
Рассмотрим следующие расчетные ситуации: поперечные разломы, случайно
реализующиеся вдоль продольной оси и продольные разломы, имеющие случайное
равномерное распределение вдоль поперечной оси. Ниже приведем результаты
расчетов.
На рисунках 4.4.1-4.4.2 показаны изополя интенсивностей напряжений и
пластических деформаций в грунте для обоих расчетных случаев для двух реализаций.
А в приложении В на рисунках 8-21 приведены аналогичные результаты для других
реализаций.
а)
б)
Рисунок 4.4.1. Изополя интенсивности напряжений
ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (1-я реализация поперечного повреждения)
127.
127а)
б)
Рисунок 4.4.2. Изополя интенсивности напряжений
ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (1-я реализация продольного повреждения)
По полученным результатам можно сделать следующие выводы:
несмотря на то, что характер напряженно-деформированного состояния
грунтового массива в значительной степени зависит от положения разлома, ни в одном
из рассматриваемых расчетных случаев не происходит потеря несущей способности
грунтового основания;
появление повреждений грунта в процессе землетрясения существенно не
влияет на реакцию рассматриваемого 9-ти этажного железобетонного здания.
Однако следует отметить, что при расчете высотных зданий и зданий повешенной
этажности, строящихся в сейсмических районах, учет возможности появления разломов
в грунтовом основании под фундаментной конструкцией необходим.
128.
128Выводы к главе 4
Была произведена оценка надежности 9-ти этажного железобетонного здания с
полным рамным каркасом методом статистических испытаний. При проведении
исследований использовалась модель Мора-Кулона для задания грунтового основания
со случайными параметрами: модуль деформации Е, удельное сцепление с и угол
внутреннего трения θ . Реализации сейсмического воздействия как нестационарного
случайного
процесса
были
смоделированы
с
помощью
метода
канонических
разложений.
В результате проведенного вероятностного анализа при случайном сейсмическом
воздействии,
рассматриваемом
как
нестационарный
случайный
процесс,
и
нормированном на 8 баллов, определена частота отказов и вероятность отказа, которая
составляет Pf 0,2 . Получены эмпирические функции распределения различных
параметров реакции системы сооружение основание, в том числе интенсивности
пластических деформаций в грунте.
Была выполнена аппроксимация полученных эмпирических распределений
интенсивности
напряжений
в
грунте
наиболее
подходящим
теоретическим
распределением с помощью критерий максимального правдоподобия Пирсона.
Установлено,
что
значения
интенсивности
напряжений
наилучшим
образом
описываются законом распределения Вейбулла. При этом вероятность того, что
интенсивность напряжений превысит значение ζi 0,1 МПа составит F (ζi ) 0,05 .
Произведена оценка надежности 9-ти этажного железобетонного здания с полным
рамным каркасом методом статистических испытаний при случайном сейсмическом
воздействии, нормированном на 9 баллов. В частности установлено, что при отказе
(повреждении) nel 50 несущих элементов вероятность обрушения конструкции будет
равна F (nel ) 0,2 , а также вероятность того, что пластические деформации в грунте
превысят величину ε pl 0,01 составляет F (ε pl ) 0,32 .
Были произведены исследования реакции 9-ти этажного железобетонного здания,
расположенного на грунтовом основании со случайными параметрами при случайном
сейсмическом воздействии с учетом случайных начальных повреждений грунта (трещин
и разломов). Не смотря на то, что характер напряженно-деформированного состояния
грунтового массива в значительной степени зависит от положения разлома, ни в одном
129.
129из рассматриваемых расчетных случаев не происходит потеря несущей способности
грунтового основания. Появление повреждений грунта в процессе землетрясения
существенно не влияет на реакцию рассматриваемого 9-ти этажного железобетонного
здания. Однако следует отметить, что при расчете высотных зданий и зданий
повешенной этажности, строящихся в сейсмических районах, учет возможности
появления разломов в грунтовом основании под фундаментной конструкцией
необходим.
130.
130ЗАКЛЮЧЕНИЕ
В
рамках
моделирование
диссертационной
взаимодействия
землетрясение,
а
также
работы
было
сооружения
с
произведена
выполнено
основанием
оценка
вероятностное
при
расчете
надежности
на
системы
сооружение основание. Была разработана и апробирована методика корректного учета
взаимодействия конструкции с грунтовым основанием при расчете на случайное
сейсмическое воздействие. Предложен подход к детерминированным расчетам, который
позволяет решать задачу во временной области прямым динамическим методом,
учитывать нелинейный характер работы грунтового основания, возможную потерю
несущей способности грунта. При этом материал надфундаментных конструкций
задается
с
использованием
непосредственное
неотражающие
нелинейных
армирование
границы,
несущих
которые
моделей,
в
элементов.
В
реализованы
при
которых
расчетах
помощи
учитывается
используются
демпфирующего
граничного слоя.
По результатам проведенной работы можно сделать следующие основные
выводы:
1.
Для исследования реальной работы системы сооружение основание в
условиях землетрясения необходимо применять нелинейные методы, в частности
нелинейный
динамический
метод,
который
предполагает
непосредственное
интегрирование уравнений движения. Исследования показывают, что наиболее
эффективными при расчетах на интенсивные землетрясения являются явные схемы
интегрирования уравнений движения, которые устойчиво работают при учете
взаимодействия сооружения с основанием.
2.
В результате анализа результатов исследования установлено, что наиболее
приемлемой моделью грунтового основания при выполнении вероятностных расчетов
методом статистических испытаний на случайные сейсмические воздействия является
модель Мора-Кулона.
3.
Разработана
методика
детерминированного
расчета
системы
сооружение основание в корректной постановке.
4.
Предложена модифицированная модель Мора-Кулона. В данную модель
введен критерий разрушения, который связан с ограничением величин главной
131.
131линейной деформации 15-ю процентами и деформации сдвига 10-ю процентами. В
результате
интенсивного
землетрясения
возможна
потеря
грунтом
несущей
способности, что может повлечь за собой частичное или полное обрушение здания. Учет
данного вида отказа позволяет повысить обеспеченность сейсмостойкости системы
сооружение основание.
5.
Произведены исследования реакции 15-ти этажного железобетонного
здания с полным рамным каркасом, расположенного на грунтовом основании, заданном
по модифицированной модели Мора-Кулона, при детерминированном сейсмическом
воздействии. Расчеты показывают, что в результате интенсивного землетрясения может
произойти потеря грунтом основания несущей способности, что может повлечь за собой
частичное или полное обрушение надфундаментных конструкций.
6.
При проведении расчетов и при проектировании зданий и сооружений в
сейсмических районах необходимо учитывать возможность возникновения в грунтовом
основании во время землетрясения повреждений (трещин и разломов), а также
случайный характер их расположения под фундаментом.
7.
трехэтажной
Выполнен сравнительный анализ работы простых систем (одноэтажной и
пространственных
рам)
при
землетрясении.
Рассматривалось
два
расчетных случая: первый без учета взаимодействия с основанием, второй с учетом
взаимодействия с основанием в корректной постановке по разработанной методике.
Материал бетона элементов конструкций задавался при помощи нелинейной модели
CSCM, которая позволяет учитывать непосредственное армирование. Сравнительный
анализ показывает, что неучет совместной работы с грунтом основания при расчете
многоэтажных зданий и особенно зданий повышенной этажности приводит к
существенной погрешности в результатах расчета, что может привести к дефициту
сейсмостойкости проектируемого здания или сооружения.
8.
При учете совместной работы сооружения с основанием происходит
трансформация расчетного сейсмического воздействия, полученного для свободной
поверхности, причем степень трансформации существенно различается для зданий
разной этажности.
9.
Произведены
численные
исследования
работы
5-ти
этажного
железобетонного здания с полным рамным каркасом расположенного, в одном
расчетном случае на линейно-деформируемом основании, в другом – на основании,
132.
132заданном по модели Мора-Кулона. Результаты исследований позволяют сделать вывод,
что расчеты зданий небольшой этажности на землетрясения целесообразно выполнять с
использованием более простой линейно-деформируемой модели основания.
10.
Выполнен детерминированный расчет на землетрясение 15-ти этажного
здания, расположенного на линейно-деформируемом грунтовом основании и на
основании, заданном по модели Мора-Кулона. Полученные результаты свидетельствуют
о необходимости для зданий повышенной этажности учитывать нелинейный характер
деформирования грунтов основания.
11.
Проведен
детерминированный
расчет
жилого
9-ти
этажного
железобетонного здания перекрестно-стеновой конструктивной схемы на интенсивное
сейсмическое воздействие по разработанной методике учета совместной работы
сооружения
с
основанием.
Разработанная
методика
позволяет
выполнять
детерминированный расчет реальных зданий на интенсивное сейсмическое воздействие
прямым динамическим методом с учетом нелинейного характера деформирования
надфундаментных конструкций, фундаментов и грунтов основания в корректной
постановке.
12.
Произведена оценка надежности 9-ти этажного железобетонного здания с
полным рамным
каркасом
методом
статистических
испытаний. В
результате
проведенного вероятностного анализа при случайном сейсмическом воздействии,
рассматриваемом как нестационарный случайный процесс, и нормированном на 8
баллов, определена частота отказов и вероятность отказа, которая составляет Pf 0,2 .
Получены эмпирические функции распределения различных параметров реакции
системы сооружение основание, в том числе интенсивности пластических деформаций
в грунте.
13.
Выполнена аппроксимация полученных эмпирических распределений
интенсивности
напряжений
в
грунте
наиболее
подходящим
теоретическим
распределением с помощью критерия максимального правдоподобия Пирсона.
Установлено,
что
значения
интенсивности
напряжений
наилучшим
образом
описываются законом распределения Вейбулла.
14.
Произведена оценка надежности 9-ти этажного железобетонного здания с
полным рамным каркасом методом статистических испытаний при случайном
сейсмическом воздействии, нормированном на 9 баллов. В частности установлено, что
133.
133при отказе (повреждении)
nel 50
несущих элементов вероятность обрушения
конструкции будет равна F (nel ) 0,2 . Построены функции распределения различных
параметров, в частности пластических деформаций в грунте. Полученные графики
показывают, что например, вероятность того, что пластические деформации в грунте
превысят величину ε pl 0,01 составляет F (ε pl ) 0,32 .
15.
Произведены исследования реакции 9-ти этажного железобетонного
здания, расположенного на грунтовом основании со случайными параметрами при
случайном сейсмическом воздействии с учетом случайных начальных повреждений
грунта (трещин и разломов). Не смотря на
то, что характер напряженно-
деформированного состояния грунтового массива в значительной степени зависит от
положения разлома, ни в одном из рассматриваемых расчетных случаев не происходит
потеря несущей способности грунтового основания. Появление повреждений грунта в
процессе землетрясения существенно не влияет на реакцию рассматриваемого 9-ти
этажного железобетонного здания. Однако следует отметить, что при расчете высотных
зданий и зданий повышенной этажности, строящихся в сейсмических районах, учет
возможности появления разломов в грунтовом основании под фундаментной
конструкцией необходим.
Рекомендации
использованием
и
перспективы
разработанной
методики
дальнейшей
разработки
темы:
с
выполнить
вероятностный
анализ
и
произвести оценку надежности железобетонных зданий различных конструктивных
схем и различной этажности.
134.
134ЛИТЕРАТУРА
1. Айзенберг, Я.М. Сооружения с выключающими связями для сейсмических районов /
Я.М. Айзенберг. – М.: Стройиздат, 1976. – 229 с.
2. Айзенберг, Я.М. Модели сейсмического риска и методологические проблемы
планирования мероприятий по смягчению сейсмических бедствий / Я.М. Айзенберг //
Сейсмостойкое строительство. Безопасность сооружений. 2004. – № 6. – С. 31-38.
3. Айзенберг, Я.М. Динамические испытания и сейсмостойкость навесных фасадных
систем / Я.М. Айзенберг Я.М., Р.Т. Акбиев, В.И. Смирнов, М.Ж. Чубаков //
Сейсмостойкое строительство. Безопасность сооружений. 2008. – №1. – С. 13-15.
4. Алехин, А.Н. Краткая характеристика моделей грунта / А.Н. Алехин // Академический
вестник. УралНИИПроект РААСН. 2011. №1. С. 75-79.
5. Аптикаев, Ф.Ф. Инструментальная шкала сейсмической интенсивности / Ф.Ф.
Аптикаев. – М.: ООО «Наука и образование», 2012. – 176 с.
6. Бакалов, В.П. Цифровое моделирование случайных процессов / В.П. Бакалов. – М.:
МАИ, 2001. – 81с.
7. Баркан, Д.Д. Современное состояние теории сейсмостойкости и сейсмостойкие
конструкции: (По материалам IV Международной конференции по сейсмостойкому
строительству) / Д.Д. Баркан и др.; под общей редакцией С.В. Полякова. – М.:
Стройиздат, 1973. – 280 с.
8. Барштейн, М. Ф. Приложение вероятностных методов к расчету сооружений на
сейсмические воздействия / М. Ф. Барштейн // Строительная механика и расчет
сооружений. 1960. № 2. С. 6-14.
9. Барштейн, М. Ф. Воздействие сейсмических сил на систему с n степенями свободы /
М. Ф. Барштейн // Снижение стоимости и улучшение качества сейсмостойкого стр-ва.
М.: Госстройиздат. 1961. С. 37-51.
10. Белов, А.А. Геометрически адаптивные сетки для жестких задач Коши / А.А. Белов,
Н.Н. Калиткин, И.П. Пошивайло // Доклады Академии Наук. 2016. Том 466, № 3.
С. 276 – 281.
135.
13511. Берая, А.Г. Вопросы расчета жилых крупнопанельных зданий на сейсмические
воздействия. В сб. "Сейсмостойкость сооружений" / А.Г. Берая. Тблилиси : Изд.
"Мецинереба", 1965. 43 c.
12. Болдырев, Г.Г. Интерпретация результатов лабораторных испытаний с целью
определения прочностных характеристик грунтов / Г.Г. Болдырев, А.С. Колесников,
А.Г. Новичков // Инженерные изыскания. 2014. №5-6. С. 78-85.
13. Болотин, В. В. Применение статистических методов для оценки прочности
конструкций при сейсмических воздействиях / В. В. Болотин // Инженерный сб. /
АН СССР. 1959. Т. 27. С. 58-69.
14. Болотин, В. В. Применение методов теории вероятностей и теории надежности в
расчетах сооружений / В. В. Болотин. М.: Стройиздат, 1971. 255 с.
15. Болотин, В. В. К расчету строительных конструкций на сейсмические воздействия /
В. В. Болотин // Строительная механика и расчет сооружений. 1980. № 1. С. 9-14.
16. Болотин, В.В. Статистическая теория сейсмостойкости сооружений / В.В. Болотин //
Изв. АН СССР, ОТН, Механика и машиностроение. 1959. – № 4. С. 123-129.
17. Болотин, В.В. Статистические методы в строительной механике / В.В. Болотин. – М:
Стройиздат, 1961. – 203 с.
18. Болотин, В.В. Методы теории вероятностей и теории надежности в расчетах
сооружений / В.В. Болотин. – М: Стройиздат, 1982. – 351 с.
19. Вентцель, Е.С. Теория вероятностей. Издание четвертое, стереотипное / Е. С.
Вентцель. М.: Наука, 1969. 576 с.
20. Гольденблат, И. И. О развитии методов расчета сооружений на сейсмостойкость / И.
И. Гольденблат, В. А. Быховский // Методы расчета зданий и сооружений на
сейсмостойкость. М.: Госстройиздат. 1958. С. 5-7.
21. Гольденблат, И. И. Расчет конструкций на действие сейсмических и импульсивных
сил / И. И. Гольденблат, Н. А. Николаенко. М.: Госстройиздат. 1961. 320 c.
22. Гумбель, Э. Статистика экстремальных значений / Э. Гумбель. М.: Мир, 1965.
452 с.
23. Дарбинян, С.С. Сдвиговые колебания систем со многими степенями свободы за
пределами упругости / С.С. Дарбинян. Известия АН Арм. ССР. Серия техн. наук, т.
XIII, № 1, 1960.
136.
13624. Дарбинян, С.С. К вопросу колебаний систем с оной степенью свободы с учетом
упруго-пластических деформаций / С.С. Дарбинян. Известия АН Арм. ССР. Серия
техн. наук, т. XII, № 1, 1959.
25. Егупов, В. К. Пространственные расчеты зданий / В. К. Егупов, Т. А. Командрина, В.
Н. Голобородько. Киев: Будивельник, 1976. 264 c.
26. Жаров, А. М. О некоторых особенностях функции распределения для сейсмического
воздействия / А. М. Жаров // Сейсмостойкость зданий и инженерных сооружений. М.:
Стройиздат. 1972. С. 99-102.
27. Жаров, А. М. Поведение конструкции с малым затуханием при нестационарном
сейсмическом воздействии / А. М. Жаров // Сейсмостойкость зданий и инженерных
сооружений. М. : Стройиздат. 1972. С. 83-85.
28. Карапетян, Б.К. Метод определения приведенных сейсмических ускорений / Б.К.
Карапетян. Известия АН Арм. ССР, т. VIII, № 1, 1955.
29. Карапетян, Б.К. Колебание сооружений, возведенных в Армении / Б.К. Карапетян.
Ереван: Изд. "Айастан", 1967. 172 с.
30. Карцивадзе, Г.Н. Сейсмостойкость дорожных искусственных сооружений / Г.Н.
Карцивадзе. – М.: Транспорт, 1974. – 263 c.
31. Кац, А.З. Динамическое давление на грунт жесткого сооружения, вызываемое
действием последовательности нестационарности сейсмических волн различной
продолжительности / А.З. Кац. Труды института физики Земли АН СССР. № 33
(200), 1963.
32. Командрина, Т.А. О расчете зданий на сейсмические воздействия с учетом
пространственной работы / Т.А. Командрина. Известия АН Арм. ССР. Серия
технонаук. т. XVII, № 4, 1964. 47 c.
33. Коренев, Б. Г. Справочник проектировщика : динамический расчет зданий / Б. Г.
Коренев, И. М. Рабинович. 2-е. изд. М.: Стройиздат, 1984.
34. Корчинский, И.Л. Оценка несущей способности конструкций при сейсмическом
воздействии с энергетических позиций / И.Л. Корчинский. М.: Изд-во литературы по
строительству. В кн.: Сейсмостойкость зданий и инженерных сооружений. – 1967. С.
46-58.
137.
13735. Корчинский, И.Л. Основы проектирования зданий в сейсмических районах / И.Л.
Корчинский, С.В. Поляков, В.А. Быховский, С.Ю. Рузинкевич, B.C. Павлык. – М.:
Госстройиздат, 1961. – 488 с.
36. Курбацкий, Е.Н. Спектры максимальных реакций (откликов) конструкций на
сейсмические и техногенные динамические воздействия / Е.Н. Курбацкий, Л.В. Баев //
Труды IV научно-практического семинара «Надежность и безопасность зданий и
сооружений при сейсмических воздействиях», 2 ноября 2011 г. – 2011. – C. 4-35.
37. Марджанишвили, М.А. Методика учета пространственной работы и протяженности
современных
зданий
при
расчете
их
на
сейсмические
воздействия
/
М.А.
Марджанишвили. – М.: Стройиздат, 1976. – 111 с.
38. Мирсаяпов, И.Т. Влияние процесса упрочнения на прочность глинистого грунта при
режимном трехосном нагружении / И.Т. Мирсаяпов, И.В. Королева // Известия
Казанского госу. архитектурно-строительного ун-та. 2017. №1(39) – с. 145-152.
39. Мирсаяпов, И.Т. Проектирование свайно-плитного фундамента высотного здания с
учетом влияния ветровых воздействий на сейсмостойкость грунтового основания / И.Т.
Мирсаяпов, И.В. Королева // Жилищное строительство. 2015. №5. с. 88-91.
40. Мкртычев, О.В. Моделирование взаимодействия сооружения с основанием при
расчете на землетрясение / О.В. Мкртычев, Г.А. Джинчвелашвили, М.С. Бусалова //
Вестник МГСУ. 2013. №12 – C. 34-40.
41. Мкртычев, О.В. Расчет многоэтажного здания на интенсивное землетрясение с
учетом возможности разжижения грунтов основания / О.В. Мкртычев, М.С. Бусалова //
Вестник МГСУ. 2014. №5 – C. 63-69.
42. МДС 50-1.2007. Проектирование и устройство оснований, фундаментов и подземных
частей многофункциональных высотных зданий и зданий-комплексов. М.: ФГУП «НИЦ
Строительство», 2007. 17 с.
43. Мкртычев, О.В. Задача вероятностного расчета конструкции на линейно и
нелинейно деформируемом основании со случайными параметрами / О.В. Мкртычев,
Г.А. Джинчвелашвили, М.С. Бусалова // Вестник МГСУ. 2014. №12. с. 106-112.
44. Мкртычев, О.В. Безопасность зданий и сооружений при сейсмических и аварийных
воздействиях: монография / О.В. Мкртычев. М.: МГСУ, 2010. – 152 с.
138.
13845.
Мкртычев,
деформируемое
О.В.
Исследование
основание»
на
реакции
системы
вертикальную
«сооружение-нелинейно
компоненту
акселерограммы
землетрясения / О.В. Мкртычев, М.С. Бусалова // Материалы III международной научнопрактической конференции «21 век: фундаментальная наука и технологии». 2014 – с.
127-131.
46.
Мкртычев,
О.В.
Исследование
реакции
системы
здание-фундаментальная
конструкция-грунт основания с учетом и без учета инерционных свойств грунта
основания / О.В. Мкртычев, М.С. Бусалова // XXI Slovak-Polish-Russion Seminar
"Theoretical Foundation of Civil Engineering". 2013. c. 75-81.
47. Мкртычев, О.В. Изменение параметров акселерограммы землетрясения, полученной
для свободной поверхности, при расчете сооружений на сейсмическое воздействие /
О.В. Мкртычев, М.С. Бусалова // Научные труды III Всероссийской (II Международной)
конференции по бетону и железобетону. 2014. Том 2. – с. 110-114.
48. Мкртычев, О.В. Теория надежности в проектировании строительных конструкций:
монография / О.В. Мкртычев, В.Д. Райзер. М.: Изд-во АСВ, 2016. – 908 с.
49. Мкртычев, О.В. Расчет динамической системы на синтезированные акселерограммы
/ О.В. Мкртычев, А.А. Решетов // Вестник МГСУ. – 2010. – №2, С. 100-104.
50. Мкртычев, О.В. Сравнение методов моделирования случайного сейсмического
воздействия / О.В. Мкртычев, А.А. Решетов // Сборник докладов XIII международной
межвузовской научно-практической конференции. 2010 г.
51. Мкртычев, О.В. Синтезирование наиболее неблагоприятных акселерограмм для
линейной системы с конечным числом степеней свободы / О.В. Мкртычев, А.А. Решетов
// International Journal of Computer and Communication System Engineering. 2015.
volume 11, issue 3. P. 101-115.
52. Мкртычев, О.В. Применение вейвлет-преобразований при анализе акселерограмм /
О.В. Мкртычев, А.А. Решетов // International Journal for Computational Civil and Structural
Engineering. – 2011. – Volume 7. С. 118-126.
53. Мкртычев, О.В. Применение вейвлет-анализа для получения характеристик
акселерограмм / О.В. Мкртычев, А.А. Решетов // Вестник МГСУ. – 2013. – №7. С. 5967.
139.
13954. Мкртычев, О.В. Методика моделирования наиболее неблагоприятных акселерограмм
землетрясений / О.В. Мкртычев, А.А. Решетов // Промышленное и гражданское
строительство. – 2013. – № 9. С. 27-29.
55. Мкртычев, О.В. Идентификация расчетных параметров моделей железобетонных
зданий / О.В. Мкртычев, М.С. Дударева // БСТ: Бюллетень строительной техники.
2018. №3(1003). С. 33-35.
56. Мкртычев О.В. Проблемы учета нелинейностей в теории сейсмостойкости (теории и
заблуждения) / О.В. Мкртычев, Г.А. Джинчвелашвили. М.: МГСУ, 20174 192 с.
57. Мондрус В.Л. Оценка надежности большепролетного сооружения с учетом
взаимодействия с грунтом основания / В.Л. Мондрус, О.В. Мкртычев, А.Э. Мкртычев //
Промышленное и гражданское строительство. 2012. №9. С. 14-16.
58. Мондрус В.Л. Исследование большепролетного сооружения на надежность при
случайных сейсмических воздействиях / В.Л. Мондрус, О.В. Мкртычев, А.Э. Мкртычев
// Вестник МГСУ. 2012. №9. С. 56-61.
59. Назаров, А.Г. Метод инженерного анализа сейсмических сил / А.Г. Назаров. Ереван: Из-во АН Арм. ССР, 1959, – 159 с.
60. Назаров, Ю.П. Аналитические основы расчета сооружений на сейсмические
воздействия / Ю.П. Назаров. М.: Наука, 2010. 468 с.
61. Напетваридзе, Ш. Г. Некоторые задачи инженерной сейсмологии / Ш. Г.
Напетваридзе. Тбилиси: Мецниереба. 1973. 162 c.
62. Невзоров, А.Л. Основания и фундаменты / А.Л. Невзоров. – Москва: Изд-во АСВ,
2018. – 154 с.
63. Невзоров, А.Л. Комплексные лабораторные исследования грунтов / А. Л. Невзоров,
И. Ю. Заручевных, В.В. Коптяев и другие. Архангельск: Солти. 2012. 124 c.
64. Николаенко, Н. А. Анализ положений по расчету сооружений в нормах
проектирования для строительства в сейсмических районах / Н. А. Николаенко, Ю.
П. Назаров // Строительная механика и расчет сооружений. 1990. № 2. С. 66-72.
65. Ньюмарк, Н. Основы сейсмостойкого строительства / Н. Ньюмарк, Э. Розенблюэт. –
М.: Стройиздат, 1980. – 312 с.
66. Попов, А.Н. Численное моделирование напряженно-деформируемого состояния
аэродромных покрытий в условиях физической нелинейности грунтового основания
140.
140[Электронный ресурс] / А.Н. Попов, В.В. Волков, А.А. Хатунцев, И.Г. Шашков, А.В.
Кочетков // Науковедение. 2013. №5. Режим доступа: http://publ.naukovedenie.ru
67. Райзер, В.Д. Методы теории надежности в задачах нормирования расчетных
параметров строительных конструкций / В.Д. Райзер. М.: Стройиздат, 1986. 190 с.
68. Райзер, В.Д. Теория надежности в строительном проектировании / В.Д. Райзер. М.:
изд-во АСВ, 1998. 302 с.
69. Ржаницын, А.Р. Теория расчета строительных конструкций на надежность / А.Р.
Ржаницын. М.: Стройиздат, 1978. 239 с.
70.
Романов,
Ю.
И.
Корреляция
высших
форм
свободных
колебаний
при антисейсмических расчетах / Ю. И. Романов // Строительная механика и расчет
сооружений. 1965. № 1. С. 35-39.
71. Саргсян, А.Е. Динамика и сейсмостойкость сооружений атомных станций:
монография / А.Е. Саргсян. Саров: ФГУП «РФЯЦ-ВНИИЭФ», 2013. 550 с.
72. Саргсян, А.Е. Разработка и обоснование механической и математической модели
основания
сооружений
атомных
станций
в
виде
однородного
инерционного
полупространства / А.Е. Саргсян, Е.Г. Гукова, А.С. Гришин // Вестник ЦНИИСК им.
В.А. Кучеренко. Сер. Исследования по теории сооружений. 2009. №1. С. 81-95.
73. Синицын, А.П. Влияние бегущей сейсмической волны на массивные сооружения /
А.П. Синицын. Труды Института физики Земли АН СССР. № 17 (184), 1961.
74.
Смирнов
В.И.
Анализ
надежности
сейсмоизолированных
зданий
при
разрушительных землетрясениях в Японии / В.И. Смирнов // Сейсмостойкое
строительство. Безопасность сооружений. 2009. №5. С. 24-32.
75. СН 8-57 «Нормы и правила строительства в сейсмических районах». М.: Госстрой,
1958. 105 с.
76. Соболев, Д.Н. Статистические модели упругого основания: дис. д-ра техн. наук /
Д.Н. Соболе. - М., 1973. - 242 с.
77. СП 14.13330.2014 «СНиП II-7-81* «Строительство в сейсмических районах». М.:
Аналитик, 2014. 126 с.
78. СП 22.13330.2011 «Основания зданий и сооружений». М.: Минрегион России,
2010. 166 с.
79. СП 24.13330.2011 «Свайные фундаменты». М.: Минрегион России, 2010. 90 с.
141.
14180. Справочник геотехника. Основания, фундаменты и подземные сооружения / под.
ред. В.А. Ильичева, Р.А. Мангушева. М.: АСВ, 2014. 736 с.
81. Стандарты ГОСТ 20522-2012 Грунты. Методы статистической обработки
результатов испытаний. М.: Стандартинформ, 2013. 24 с.
82.
Строкова,
Л.А.
Определение
параметров
деформируемости
грунтов
для
упругопластических моделей / Л.А. Строкова // Вестник Томского государственного
университета. 2013. №367. С. 190-194.
83. Тамразян А.Г. Расчет элементов конструкций при заданной надежности и
нормальном распределении нагрузки и несущей способности / А.Г. Тамразян // Вестник
МГСУ. 2012. №10. С. 109-115.
84. Тер-Мартиросян З.Г. Механика грунтов / З.Г. Тер-Мартиросян Москва: изд-во
МГСУ, 2009. 551 с.
85. Тяпин А.Г. Учет взаимодействия сооружений с основанием при расчетах на
сейсмические воздействия / А.Г. Тяпин. М.: АСВ, 2014. 136 с.
86. Тяпин А.Г. Расчет сооружений
на сейсмические воздействия с
учетом
взаимодействия с грунтовым основанием / А.Г. Тяпин. М.: АСВ, 2013. 400 с.
87. Хачиян, Э.Е. Сейсмические воздействия на высотные здания и сооружения / Э.Е.
Хачиян. Ереван: Айастан, 1973. – 328 с.
88. Хачиян, Э.Е. Динамические модели сооружений в теории сейсмостойкости / Э.Е.
Хачиян, В.А. Амбарцумян. – М.: Наука, 1981. – 204 с.
89. Хачиян, Э.Е. Инженерная сейсмология / Э.Е. Хачиян. Ереван: Айастан, 2006. – 356
с.
90.
Шаблинский
Г.Э.
Сейсмостойкость
строительных
конструкций
атомных
электростанций. Экспериментально-теоретические методы. / Г.Э. Шаблинский, Г.А.
Джинчвелашвили. М.: АСВ, 2017. 352 с.
91. ASCE STANDART 4-98. Seismic Analysis of Safety Related Nuclear Structures.
American Society of Civil Engineers, Aproved September, 1998. 118 p.
92. Basu, U. Perfectly matched layers for transient elastodynamics of unbounded domains / U.
Basu, A. K. Chopra // International Journal for Numerical Methods in Engineering. 2004.
No. 59(8). P. 1039–1074.
142.
14293. Basu, U. Explicit finite element perfectly matched layer for transient three-dimensional
elastic waves / U. Basu // International Journal for Numerical Methods in Engineering. 2009.
No. 77(2). P. 151–176.
94. Biot, М. Mechanical Analysis for the Predication of Earthquake stress / М. Biot. Bull, of
Soc.Seism, of Amer., v.31, №2, 1941.
95. Biot, M. Theory of vibration of buildings during earthquake / M. Biot Zeitschrift fur
Angewandte Mathematik and Mechanik. Band 14 Heft 4, August, 1934.
96. Borja, R.I., Sama K.M., Sanz P.F. On the numerical integration of three-invariant
elastoplastic constitutive models / R.I. Borja, K.M. Sama, P.F. Sanz // . – 2003. – P. 12271258.
97. Brinkgreve, R.B.J. Selection of soil models and parameters for geotechnical engineering
application. Soil Constitutive Models: Evaluation, Selection,
and Calibration / R.B.J Brinkgreve. еd. J.A. Yamamuro, V.N. Kaliakin // American Society of
Civil Engineers. 2005. Vol. 128. Р. 69–98.
98. Clayton, R. Absorbing boundary conditions for acoustic and elastic wave equations / R.
Clayton, B. Engquist // Bull. Seismol. Soc. Am. 1977. Vol. 67 (6). P. 1529–1540.
99. Cun, Hu. Implicit and explicit integration schemes in the anisotropic bounding surface
plasticity model for cyclic behaviours of saturated clay / Hu. Cun, Liu Haixiao // Computers
and Geotechnics. 2014. Vol. 55. P. 27-41.
100. Duncan, J.M., Chang C.-Y. Nonlinear analysis of stress and strain in soils / J.M. Duncan,
C.-Y. Chang // ASCE Journal of the Soil Mechanics and Foundations Division. 1970. №
96 (SM5). Р. 1629–1653.
101. Geo-Slope. Режим доступа: www.geo-slope.com.
102. Givoli, D. Non-reflecting boundary conditions for elastic waves / D. Givoli, J.B. Keller //
Wave Motion. 1990. No. 12 (3). P. 261–279.
103. Givoli, D. Artificial boundary conditions for 2D problems in geophysics / D. Givoli, S.
Vigdergauz // Comput. Methods Appl. Mech. Engrg. 1993. Vol. 110 (1–2). P. 87–101.
104. Higdon, R.L. Absorbing boundary conditions for elastic waves / R.L. Higdon //
Geophysics. 1991. No. 56 (2). P. 231–241.
105. Housner, G. W. Characteristics of Strong-Motion Earthquakes / G. W. Housner // Bull.
Seism. Soc. Am. 1947. N 37(1). P. 19-31.
143.
143106. Housner, G. W. Spectrum Intensities of Strong-Motion Earthquakes / G. W. Housner //
Proc. Symp. Earthq. and Blast Effects Structures / eds. С. M. Duke, M. Feign. Los Angeles:
University of California. 1952. P. 21-36.
107. ISO/TC 98, ST2394 General Principles on Reliability for Structures, 1994. 50 p.
108. Kenji, I. Soil behavior in earthquake geotechnics / I. Kenji. Oxford: Clarendon press,
1996. 385 p.
109. Kramer, S.L. Geotechnical earthquake engineering / S.L. Kramer. NJ: Prentice-Hall,
1996. 653 p.
110. Lewis, B.A. Manual for LS-DYNA Soil Material Model 147. Report No.
FHWA-HRT-04-095 / B.A. Lewis. Federal Highway Administration, 2004. Р. 77.
111. Lysmer, J. Finite dynamic model for infinite media / J. Lysmer, R.L. Kuhlemeyer // J.
Engrg. Mech. Div. 1969. ASCE 95 (EM4). P. 859–877.
112. Manolis, G.D. Boundary Element Methods in Elastodynamics / G.D. Manolis, D.E.
Beskos. London: Unwin Hyman, 1988. 282 p.
113. Mkrtychev, O.V. Modeling Worst-case Earthquake Accelerograms for Buildings and
Structures / O.V. Mkrtychev, A.A. Reshetov // Advances in Engineering Research. 2016.
volume 72. P. 89-94.
114. Mkrtychev, O.V. Verification of the spar model of a reinforced concrete beam / O.V.
Mkrtychev, M.S. Busalova, V.B. Dorozhinskiy // MATEC Web of Conferences. 2017.
117, 00124.
115. Mkrtychev, O.V. Calculation of reinforced concrete structures with a set seismic stability
level on an earthquake / O.V. Mkrtychev, M.S. Busalova // Procedia Engineering. 2016.
vol. 153. P. 475-482.
116. Mkrtychev, O.V. Assessment of seismic resistance of the reinforced concrete building by
nonlinear dynamic method / O.V. Mkrtychev, M.S. Busalova // Advances in Engineering
Research. 2016. vol. 104. P. 160-164.
117. Mkrtychev, O.V. Comparative analysis of results from experimental and numerical
studies on concrete strength / O.V. Mkrtychev, D.S. Sidorov, S.V. Bulushev // MATEC Web
of Conferences. 2017. 117, 00123.
144.
144118. Mononobe, N. Die Eigenschwingungen eingespannter Stabe von veränderlichen
Querschnitt, Zeitschrift für Angewandte Mathematik and Mechanik / N. Mononobe. Band 1,
Heft 6, 1921.
119. Murray, Y.D. Users Manual for LS-DYNA Concrete Material Model 159. McLean.
Report No. FHWA-HRT-05-062. Federal Highway Administration, 2007. 77 p.
120. Omori, F. Seismic Experiments on the Fracturing and Overturning of Columns / F.
Omori. Tokyo: Publ. Earthquake Inter. Comm. in Foreign Languages. No. 4, 1900.
121. Plaxis. Режим доступа: www.plaxis.nl.
122. Schanz, T. Zur Modellierung des mechanischen Verhaltens von Reibungsmaterialien / T.
Schanz. Stuttgart: Mitt. Inst. für Geotechnik 45. Universität Stuttgart, 1998. 152 p.
123. Schanz, T. The Hardening-Soil Model: Formulation and verification / T. Schanz, P.A.
Vermeer, P.G. Bonnier // Beyond 2000 in Computational Geotechnics. 1999. Р. 281–290.
124. Song, C. The scaled boundary finite-element method––alias consistent infinitesimal
finite-element cell method––for elastodynamics / C. Song, J.P. Wolf. Comput. Methods
Appl. Mech. Engrg. 1997. Vol. 147 (3–4). P. 329–355.
125. Trovato, S. An approach for synthesizing tri-component ground motions compatible with
hazard-consistent target spectrum – Italian aseismic code application / S. Trovato, E.
D’Amore, P.D. Spanos, Q.Tue // Soil Dynamics and Earthquake Engineering. 2017. Vol.
93. P. 121 – 134.
126. US Department of Transportation. Federal Highway Administration. Evaluation of LSDYNA Concrete. Material Model 159. McLean. Publication NO. FHWA-HRT-05-063,
2007. 190 p.
127. Wolf, J.P. Dynamic Soil–Structure Interaction / J.P. Wolf. Englewood Cliffs, NJ:
Prentice-Hall, 1985. 481 p.
145.
145ПРИЛОЖЕНИЯ
Приложение А
Рисунок 1. Закон изменения силы, приложенный к грунтовому массиву
Рисунок 2. Изополя интенсивности напряжений в модели без PML-слоя. Время t=1,178 c
146.
146Рисунок 3. Изополя интенсивности напряжений в модели с PML-слоем. Время t=1,178 c
147.
147Рисунок 4. Компоненты расчетного сейсмического воздействия для 15-ти этажного здания
интенсивность – 9 баллов, доминантная частота – 0,5 Гц
Рисунок 5. Деформированная схема конструкций здания
Рисунок 6. Разрушение элементов грунта под колоннами в результате продавливания
фундаментной плиты (коричневый цвет под колоннами)
148.
148Рисунок 7. Изополя интенсивности напряжений
ζi
в фундаментной плите, Па
Рисунок 8. Изополя интенсивности общих деформаций
εi
Рисунок 9. Изополя интенсивности пластических деформаций
а)
в фундаментной плите
ε pl в фундаментной плите
149.
149б)
Рисунок 10. Изополя изгибающих моментов в фундаментной плите
а) момент
M x , Н м , б) момент M y , Н м
Рисунок 11. Изополя интенсивности напряжений ζ i в стержневых элементах
конструкции, Па 15-ти этажного железобетонного здания
Рисунок 12. Изополя интенсивности пластических деформаций ε pl в стержневых
элементах конструкции 15-ти этажного железобетонного здания
150.
150Рисунок 13. Изополя интенсивности напряжений ζ i в стержневых элементах
конструкции, Па 15-ти этажного железобетонного здания
Рисунок 14. Изополя интенсивности пластических деформаций ε pl в стержневых
элементах конструкции 15-ти этажного железобетонного здания
151.
151Приложение Б
а)
б)
в)
Рисунок 1. Компоненты акселерограммы сейсмического воздействия
интенсивность – 9 баллов, доминантная частота горизонтальных компонент – 3 Гц,
вертикальной компоненты – 4 Гц
152.
152а)
б)
Рисунок 2. Изополя интенсивности напряжений ζ i для элементов бетона (а) и
арматурного каркаса (б), МПа
а)
153.
153б)
Рисунок 3. Изополя интенсивности деформаций ε i для элементов бетона (а) и
арматурного каркаса (б)
а)
б)
Рисунок 4. Изополя интенсивности напряжений ζ i для элементов бетона (а) и
арматурного каркаса (б), МПа
154.
154а)
б)
Рисунок 5. Изополя интенсивности деформаций ε i для элементов бетона (а) и
арматурного каркаса (б)
а)
155.
155б)
Рисунок 6. Изополя интенсивности напряжений ζ i для элементов бетона (а) и
арматурного каркаса (б), МПа
а)
б)
Рисунок 7. Изополя интенсивности деформаций ε i для элементов бетона (а) и
арматурного каркаса (б)
156.
156а)
б)
Рисунок 8. Изополя интенсивности напряжений ζ i для элементов бетона (а) и
арматурного каркаса (б), МПа
157.
157а)
б)
Рисунок 9. Изополя интенсивности деформаций ε i для элементов бетона (а) и
арматурного каркаса (б)
158.
158а)
б)
в)
Рисунок 10. Расчетная трехкомпонентная акселерограмма воздействия
интенсивность – 9 баллов, доминантная частота горизонтальных компонент – 3 Гц,
вертикальной компоненты – 4 Гц
159.
159а)
б)
в)
Рисунок 11. Компоненты акселерограммы расчетного сейсмического воздействия для 15ти этажного здания; интенсивность – 9 баллов, доминантная частота – 0,5 Гц
160.
160а)
б)
Рисунок 12. Изополя интенсивности напряжений в момент времени предшествующий
началу прогрессирующего обрушению а) здание на линейно-деформируемом основании;
б) здание на основании, заданном по модели Мора-Кулона
а)
161.
161б)
Рисунок 13. Изополя интенсивности напряжений
а) в элементах конструкции, б) в элементах грунтового основания
162.
162Приложение В
а)
б)
Рисунок 1. Распределение случайного значения модуля деформации грунта Е
а)
163.
163б)
Рисунок 2. Распределение случайного значения удельного сцепления грунта с
а)
164.
164б)
Рисунок 3. Распределение случайного значения угла внутреннего трения грунта θ
а)
165.
165б)
в)
Рисунок 4. Гистограмма (а), плотность (б) и функция распределения (в) значений времени
появления пластических деформаций в элементах конструкции
а)
166.
166б)
в)
Рисунок 5. Гистограмма (а), плотность (б) и функция распределения (в) значений времени
начала отказа элемента конструкции
а)
167.
167б)
в)
Рисунок 6. Гистограмма (а), плотность (б) и функция распределения (в) значений времени
начала обрушения здания
а)
168.
168б)
в)
Рисунок 7. Гистограмма (а), плотность (б) и функция распределения (в) количества колонн,
в которых возникают пластические деформации в момент начала обрушения здания
а)
169.
169б)
Рисунок 8. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (2-я реализация поперечного повреждения)
а)
б)
Рисунок 9. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (3-я реализация поперечного повреждения)
170.
170а)
б)
Рисунок 10. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (4-я реализация поперечного повреждения)
а)
171.
171б)
Рисунок 11. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (5-я реализация поперечного повреждения)
а)
б)
Рисунок 12. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (6-я реализация поперечного повреждения)
172.
172а)
б)
Рисунок 13. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (7-я реализация поперечного повреждения)
а)
173.
173б)
Рисунок 14. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (8-я реализация поперечного повреждения)
а)
б)
Рисунок 15. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (9-я реализация поперечного повреждения)
174.
174а)
б)
Рисунок 16. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (2-я реализация поперечного повреждения)
а)
175.
175б)
Рисунок 17. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (3-я реализация продольного повреждения)
а)
б)
Рисунок 18. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (4-я реализация продольного повреждения)
176.
176а)
б)
Рисунок 19. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (5-я реализация продольного повреждения)
а)
177.
177б)
Рисунок 20. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (6-я реализация продольного повреждения)
а)
б)
Рисунок 21. Изополя интенсивности напряжений ζ i (а) и интенсивности пластических
деформаций ε pl (б) в грунтовом основании (7-я реализация продольного повреждения)




































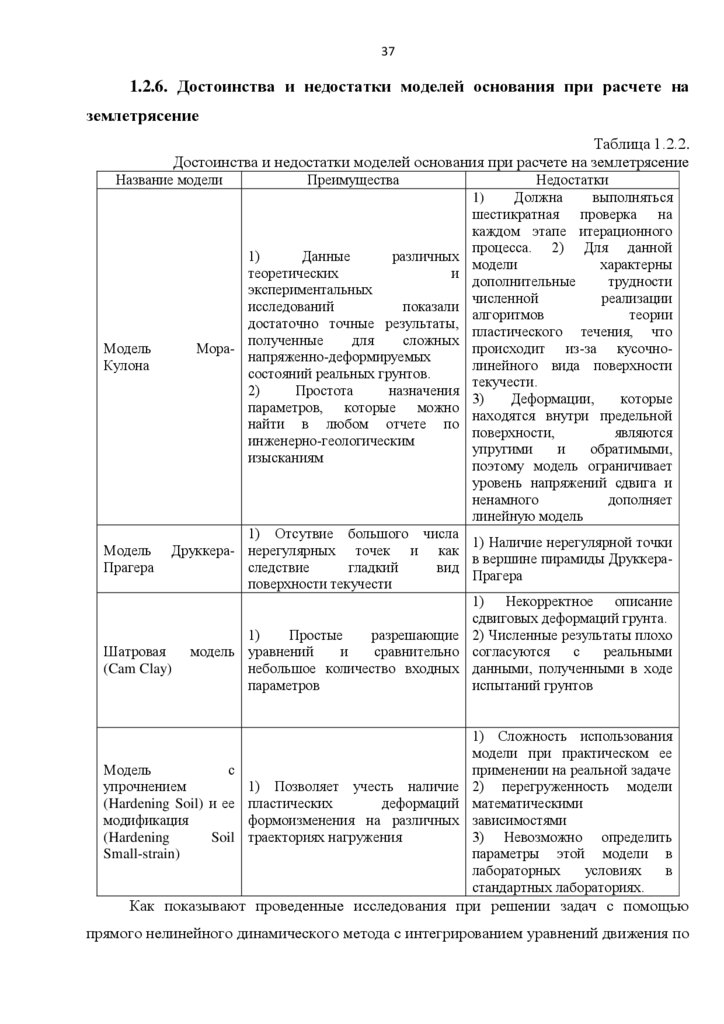


































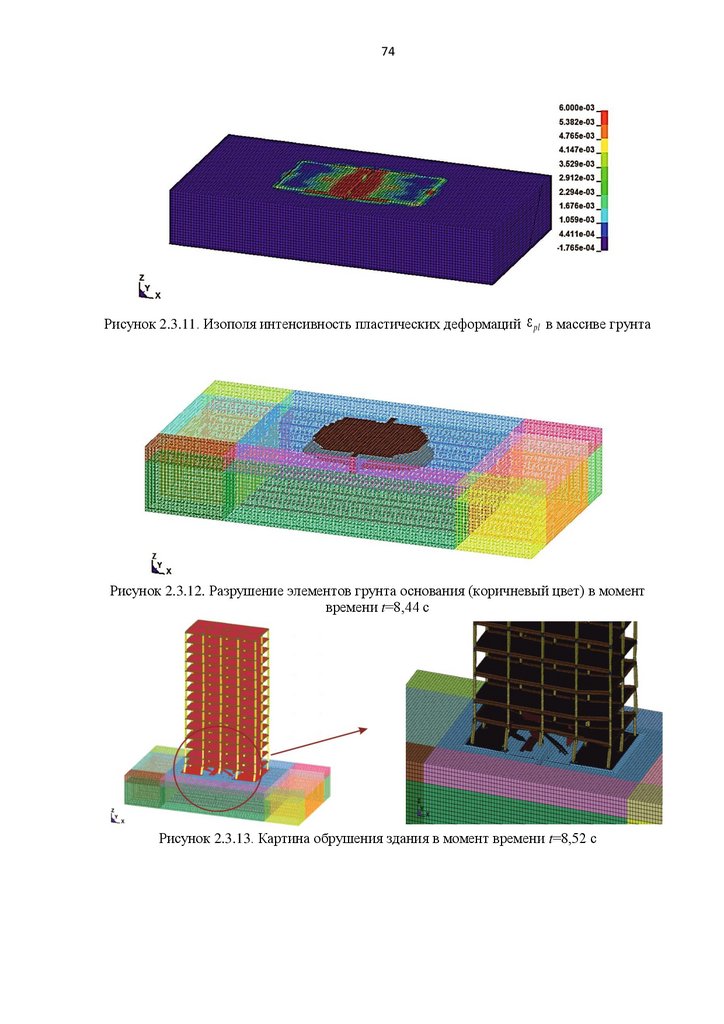







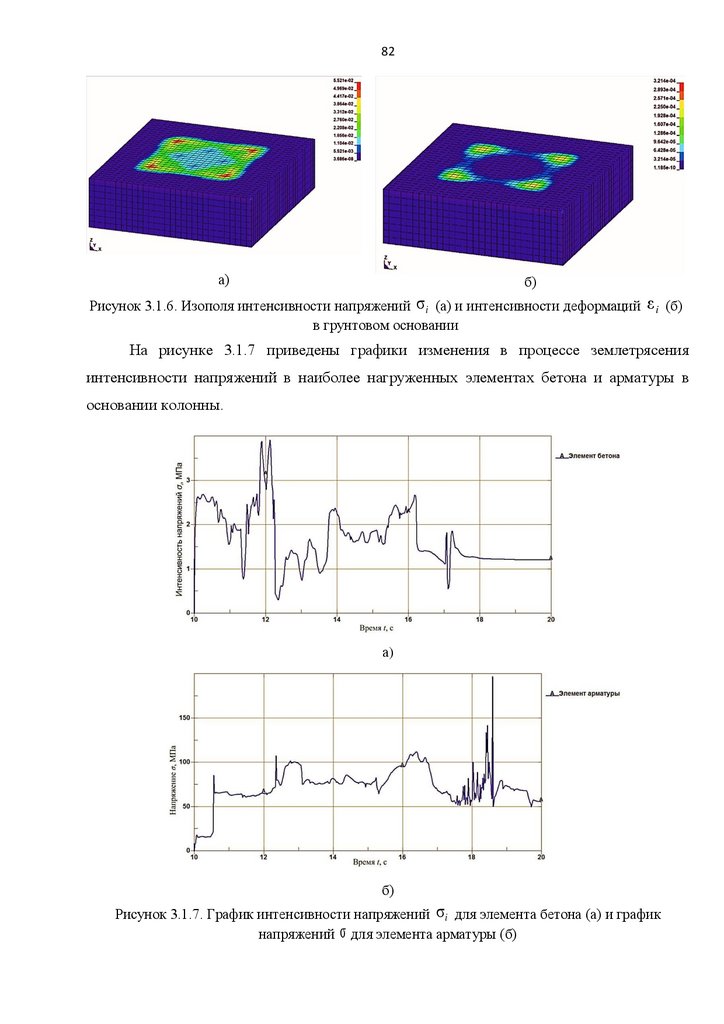


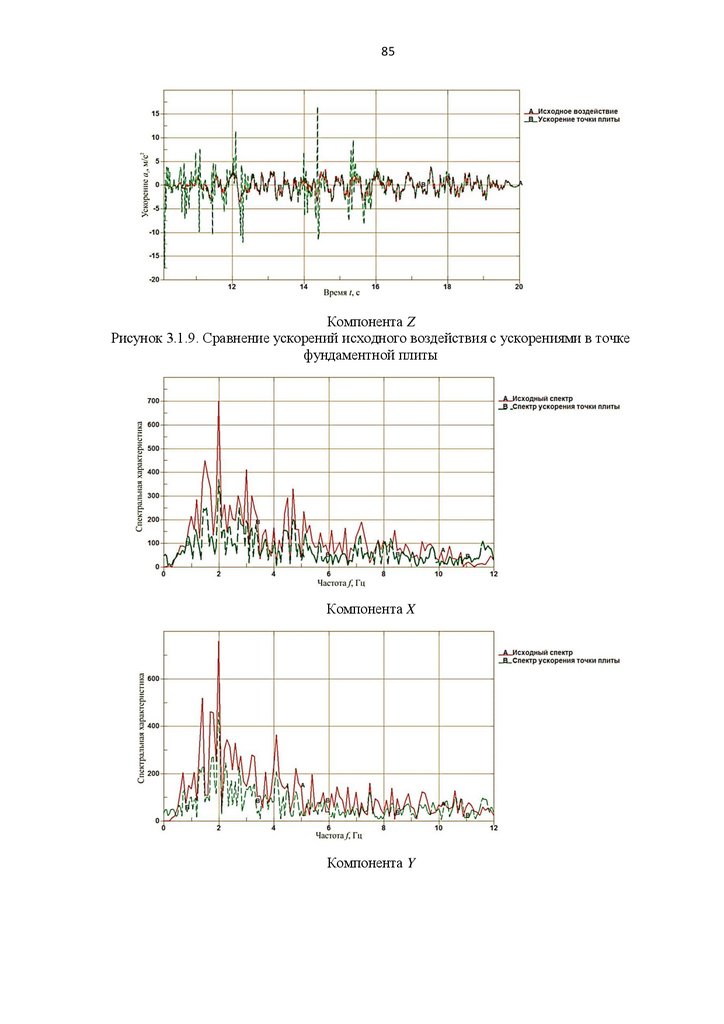
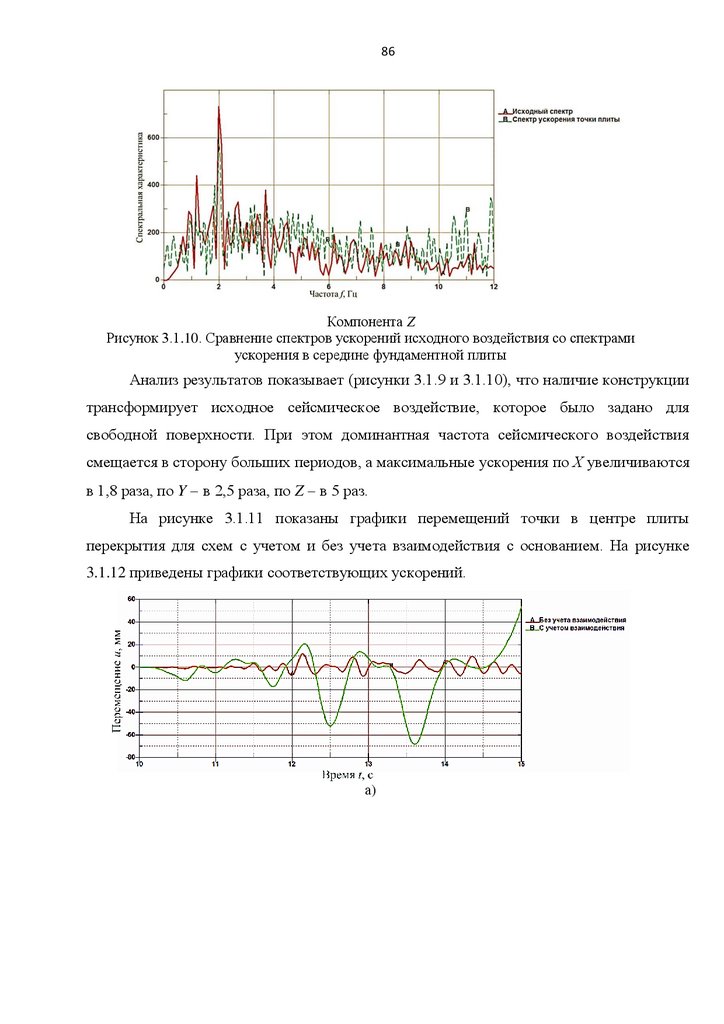

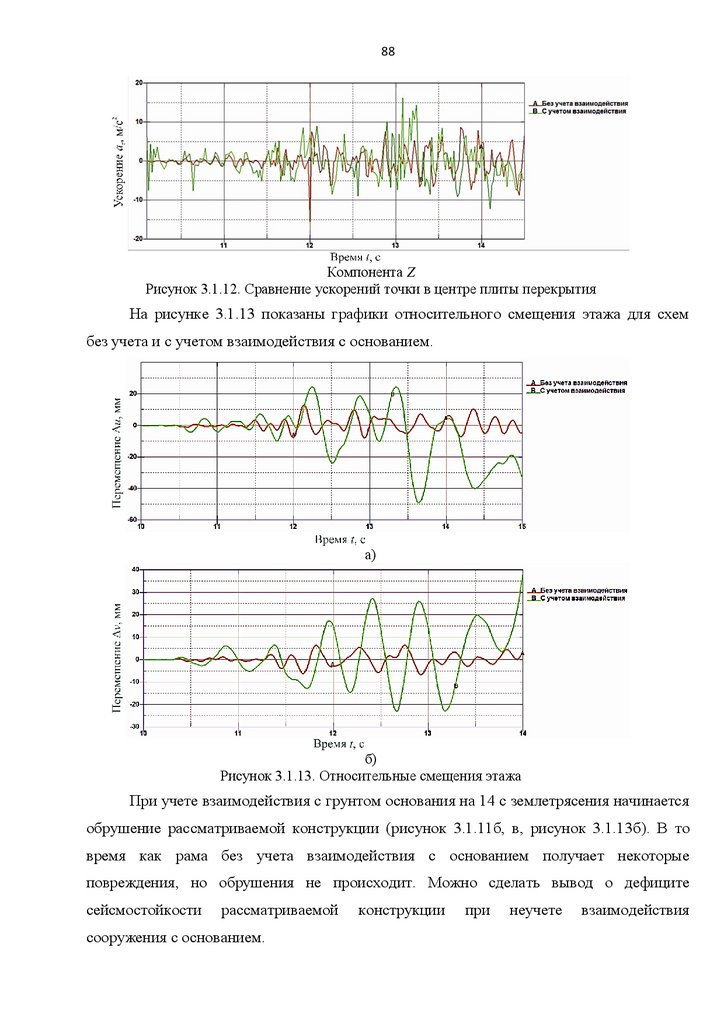

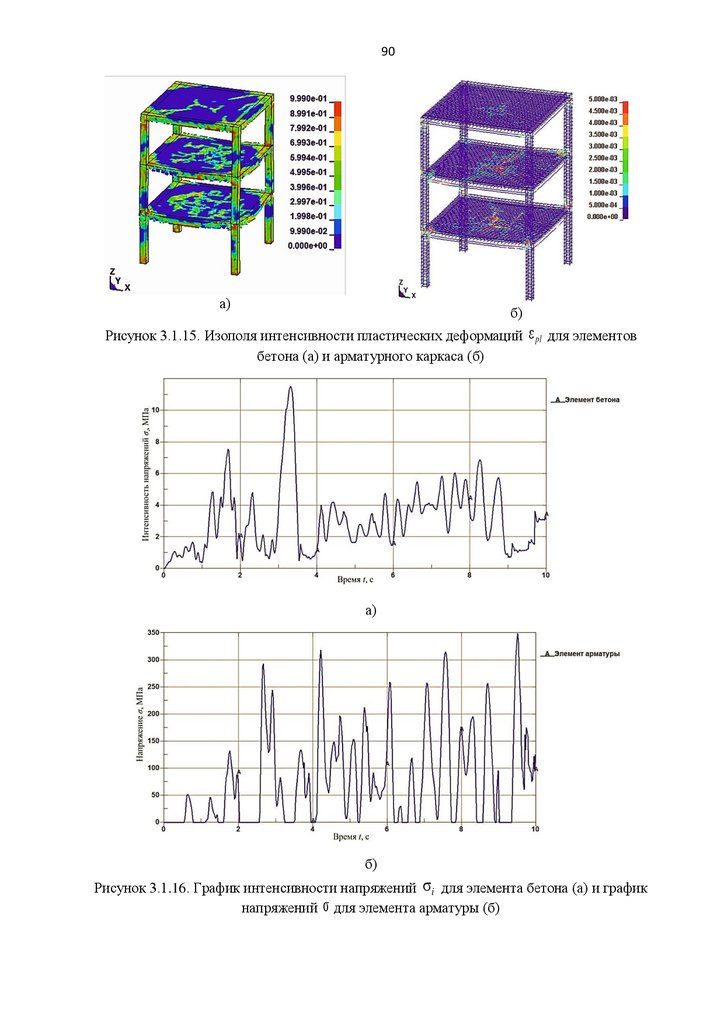
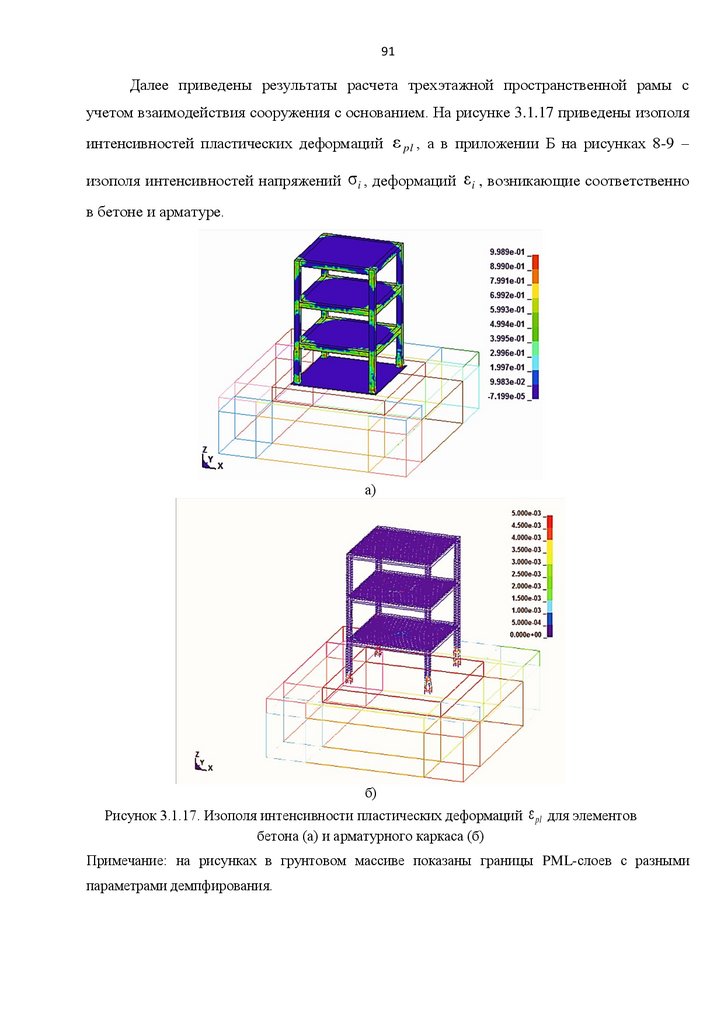





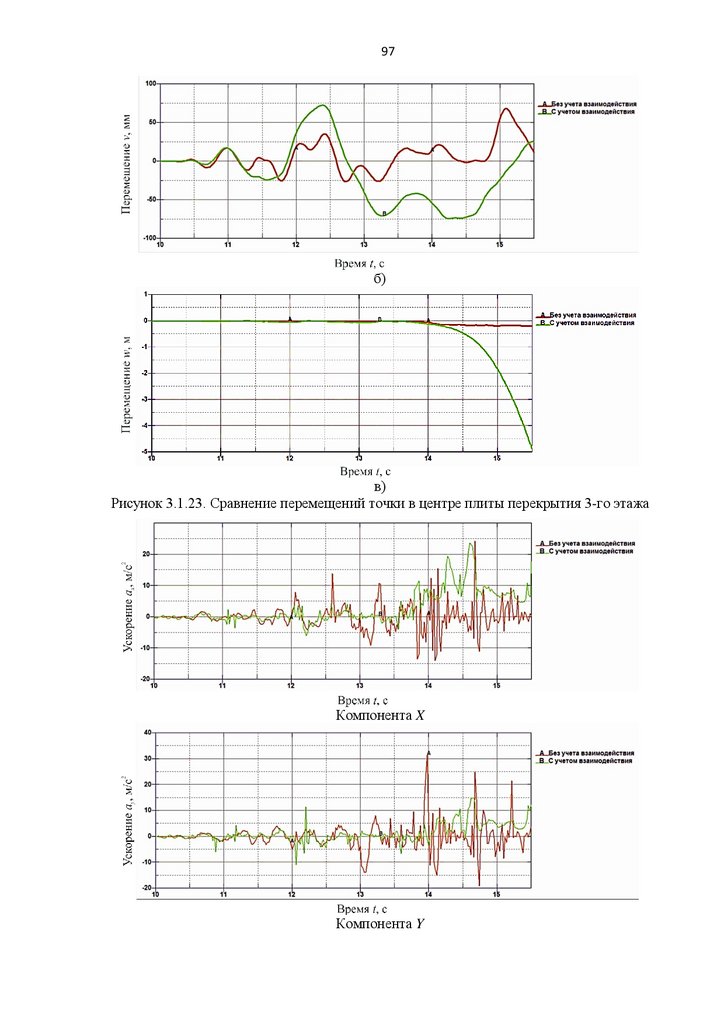


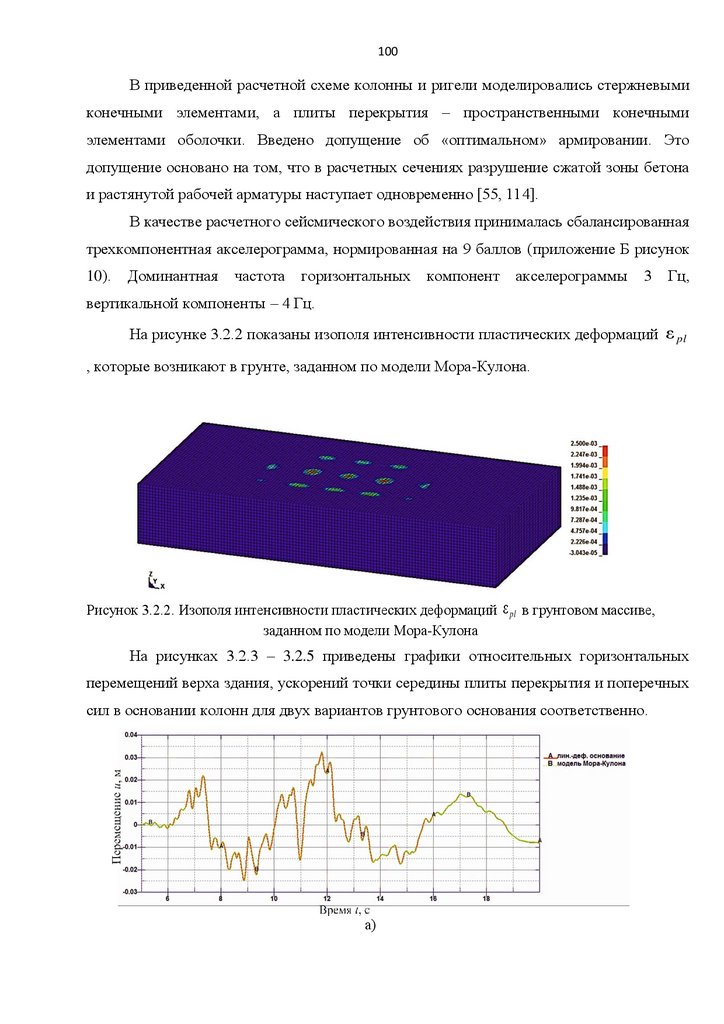














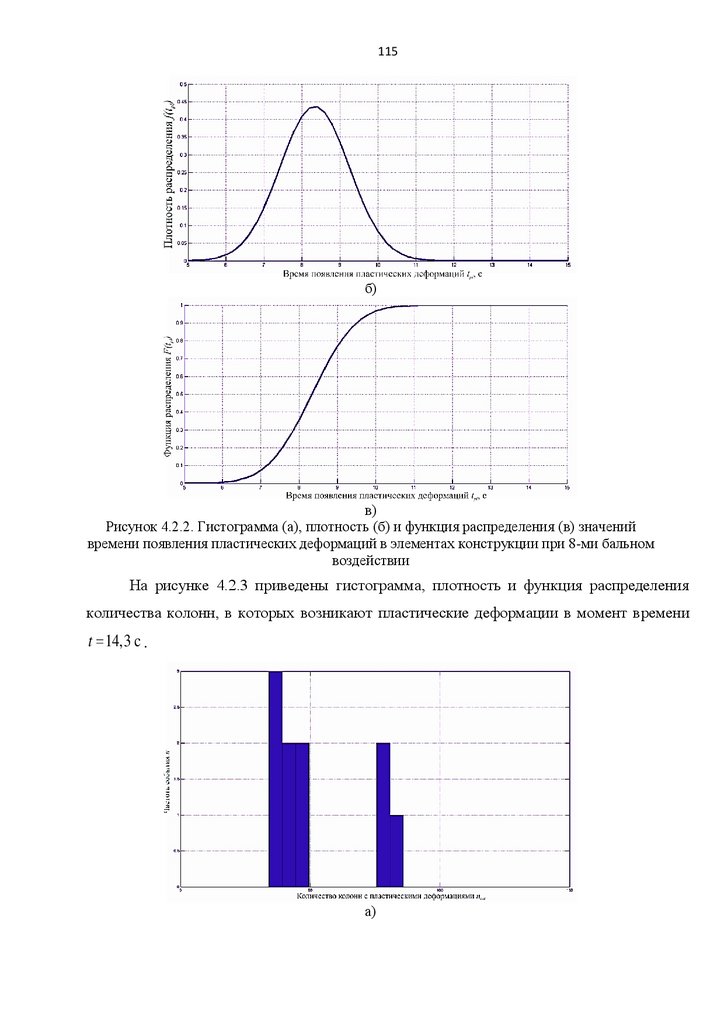



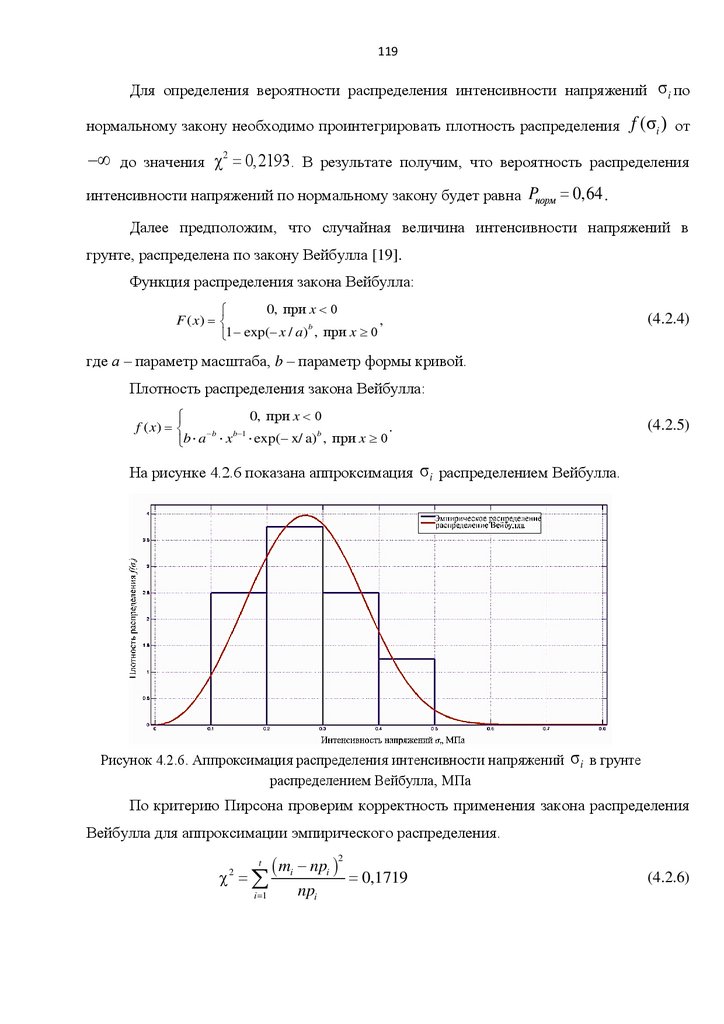

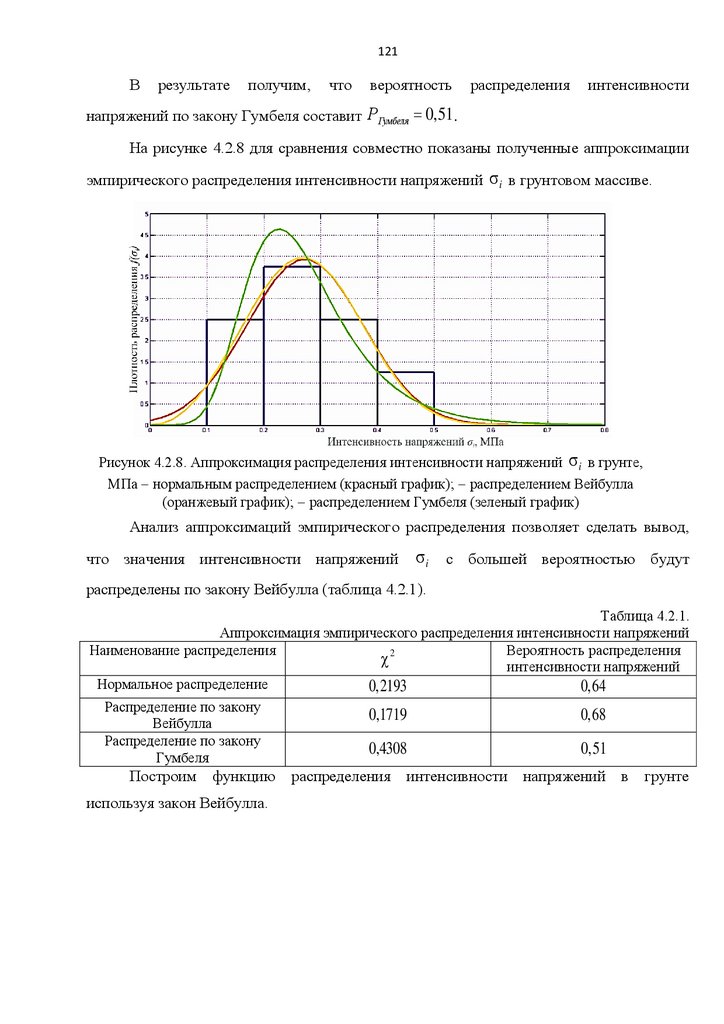

























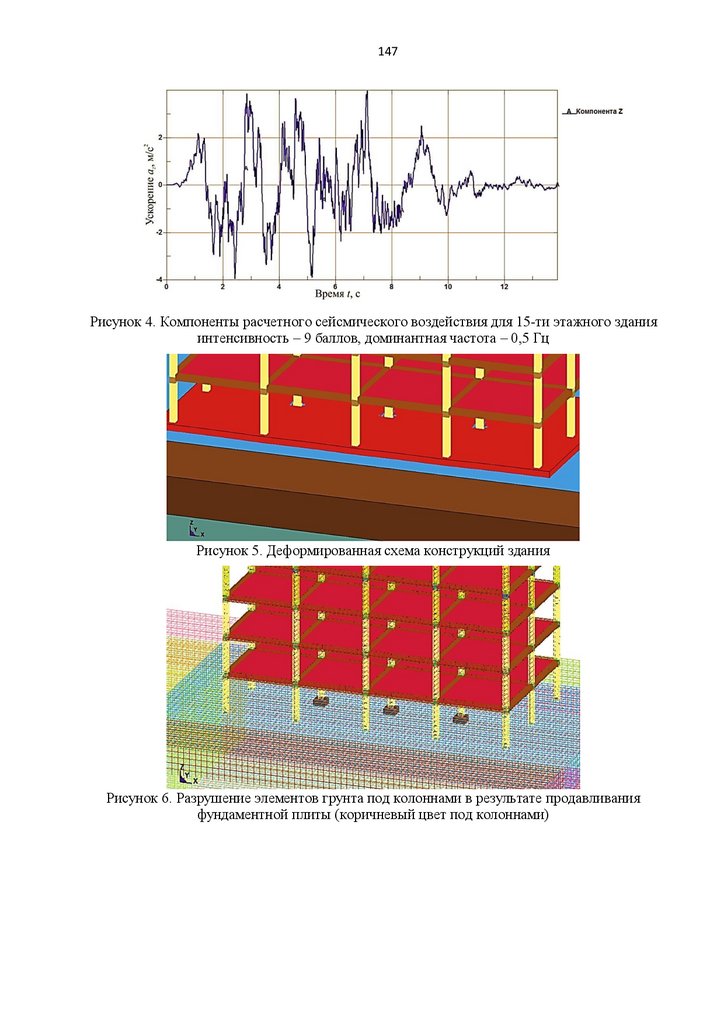
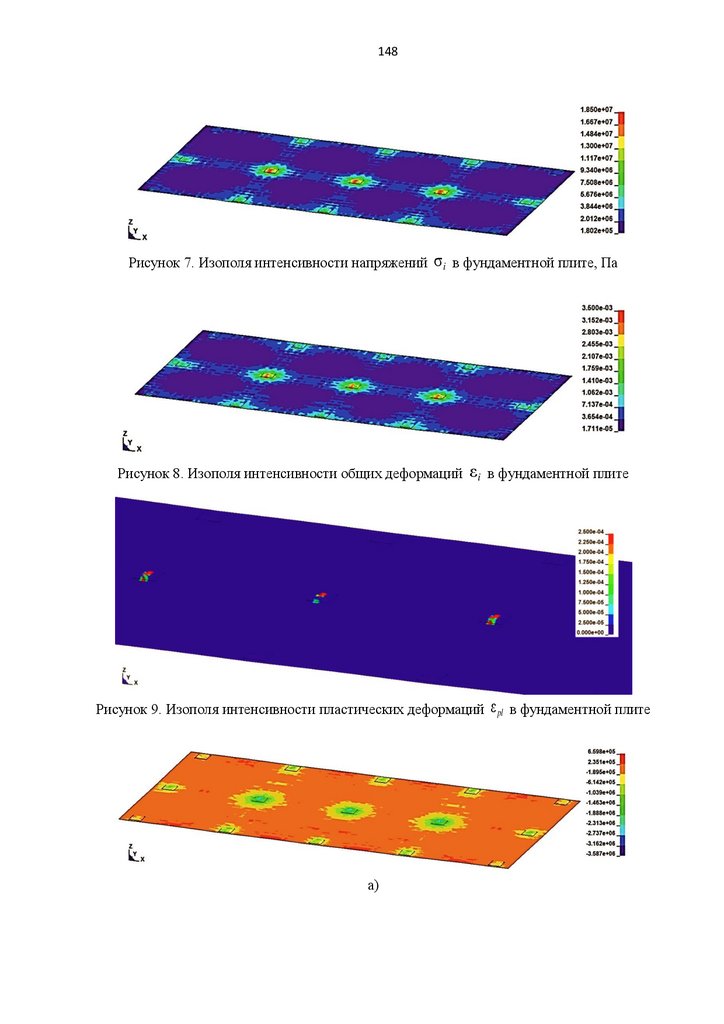


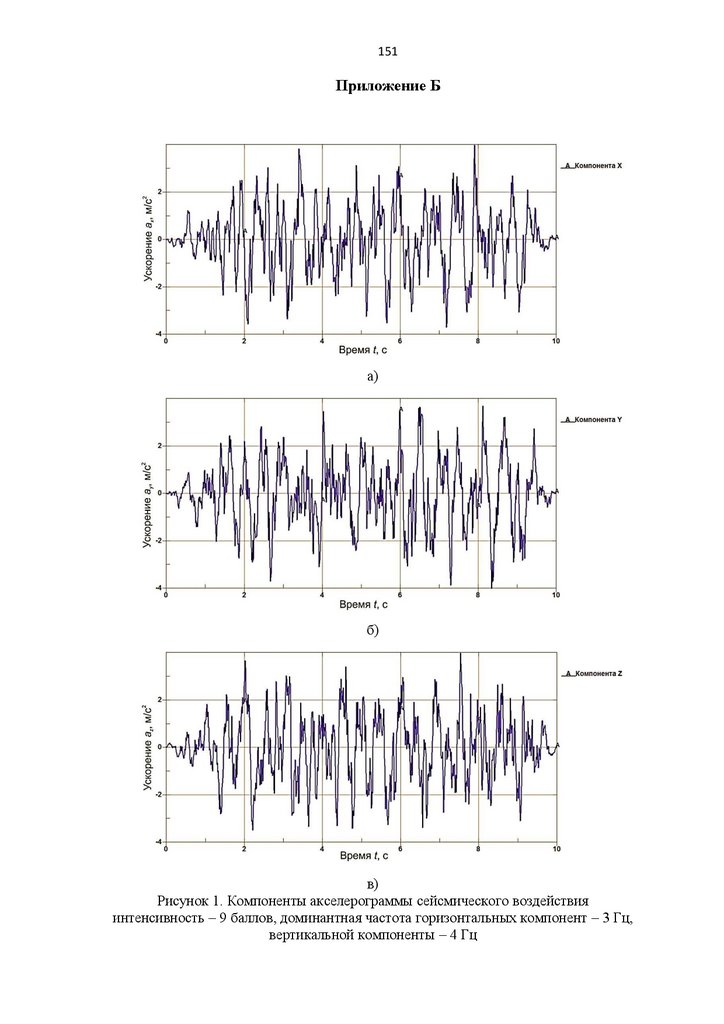
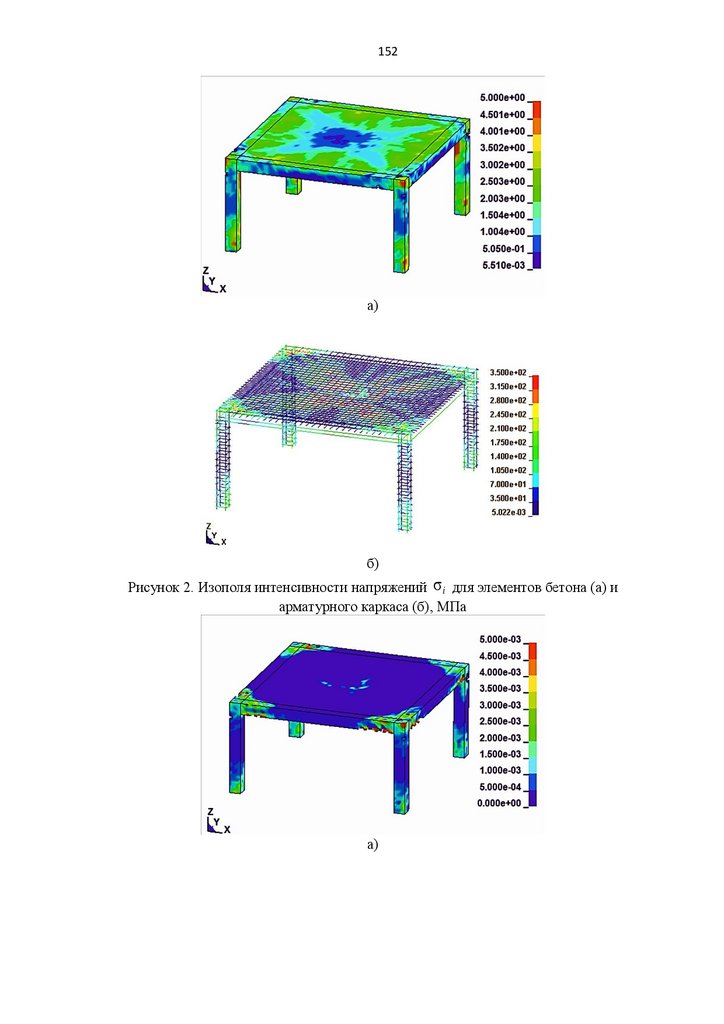






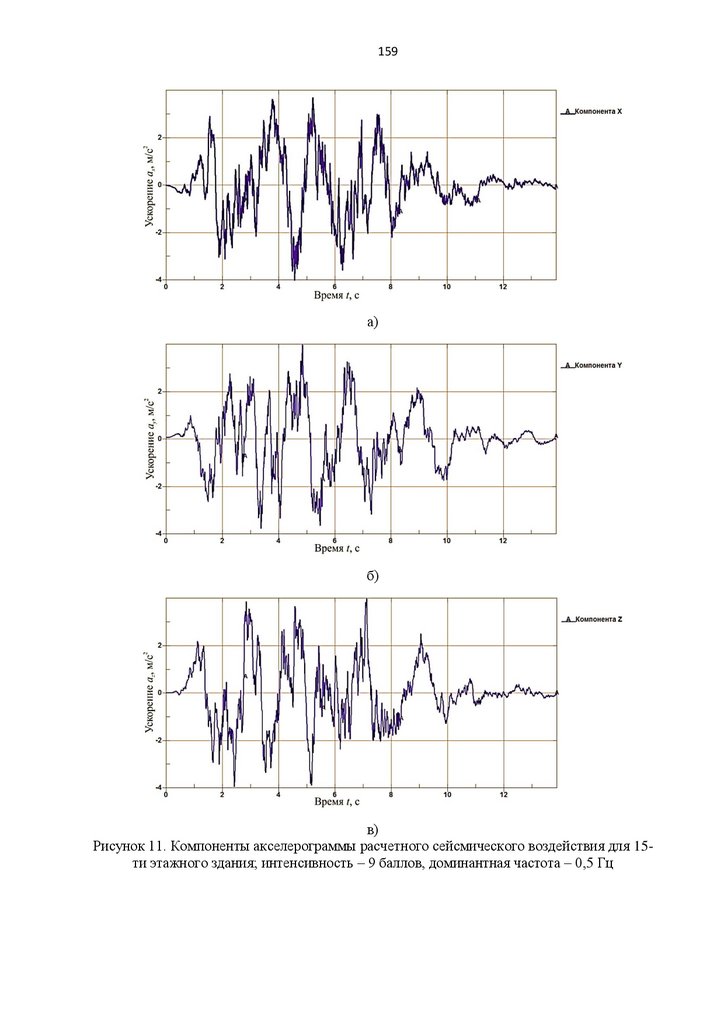




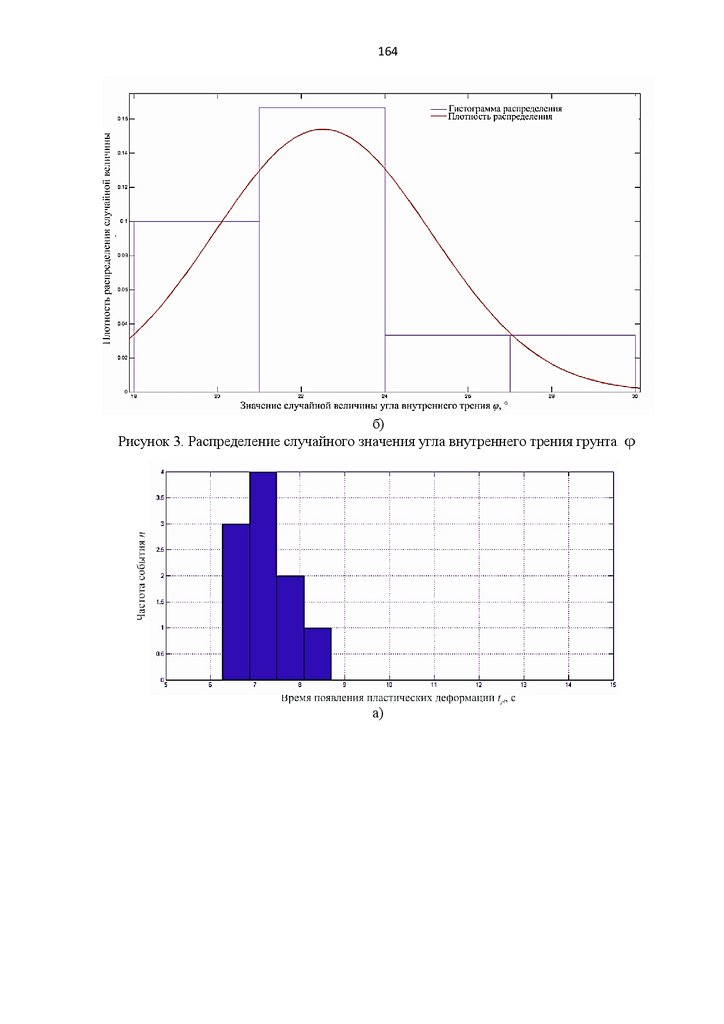












 Строительство
Строительство








