Похожие презентации:
Simple Harmonic Motion
1.
Simple Harmonic MotionWhen a vibration or an oscillation repeats itself over and over,
the motion is called periodic.
A mass on a spring is oscillating on a
frictionless surface. As the mass
moved from the equilibrium position
there is a restoring force applied to it.
The restoring force is directly
proportional to the displacement x.
F = – kx
Every system that has this force exhibits a simple harmonic
motion (SHM) and is called a simple harmonic oscillator.
The amplitude (A) is the maximum value of its displacement on
either side of the equilibrium position.
2.
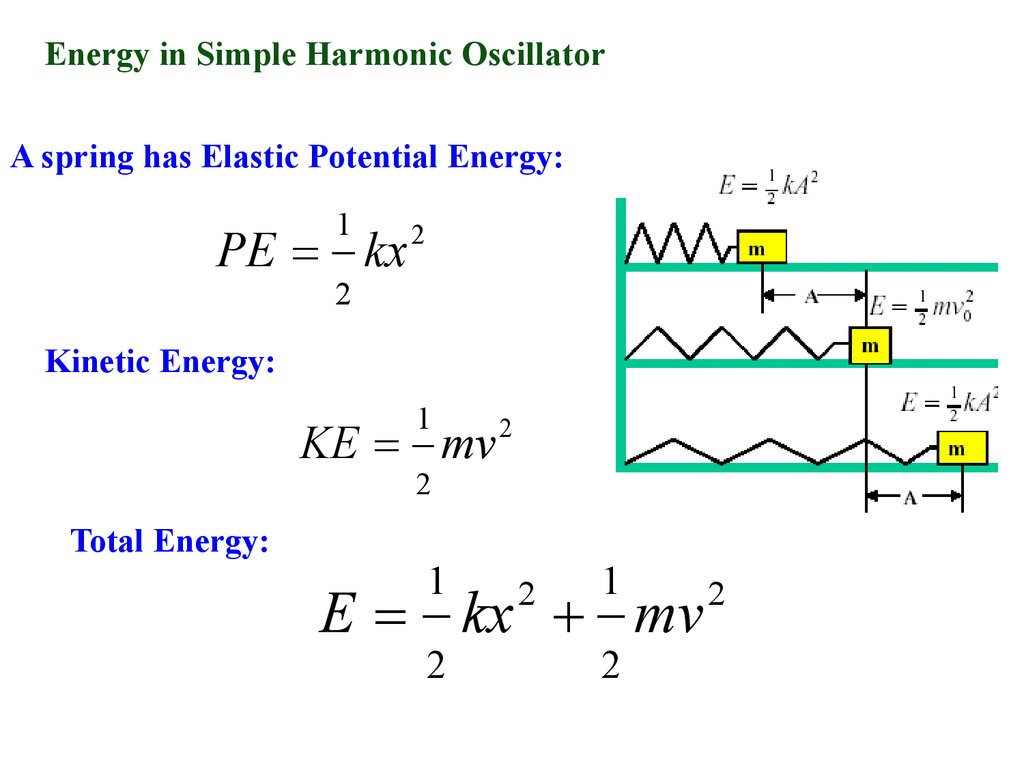
Energy in Simple Harmonic OscillatorA spring has Elastic Potential Energy:
1
PE kx
2
2
Kinetic Energy:
1
KE mv
2
2
Total Energy:
1
1
E kx mv
2
2
2
2
3.
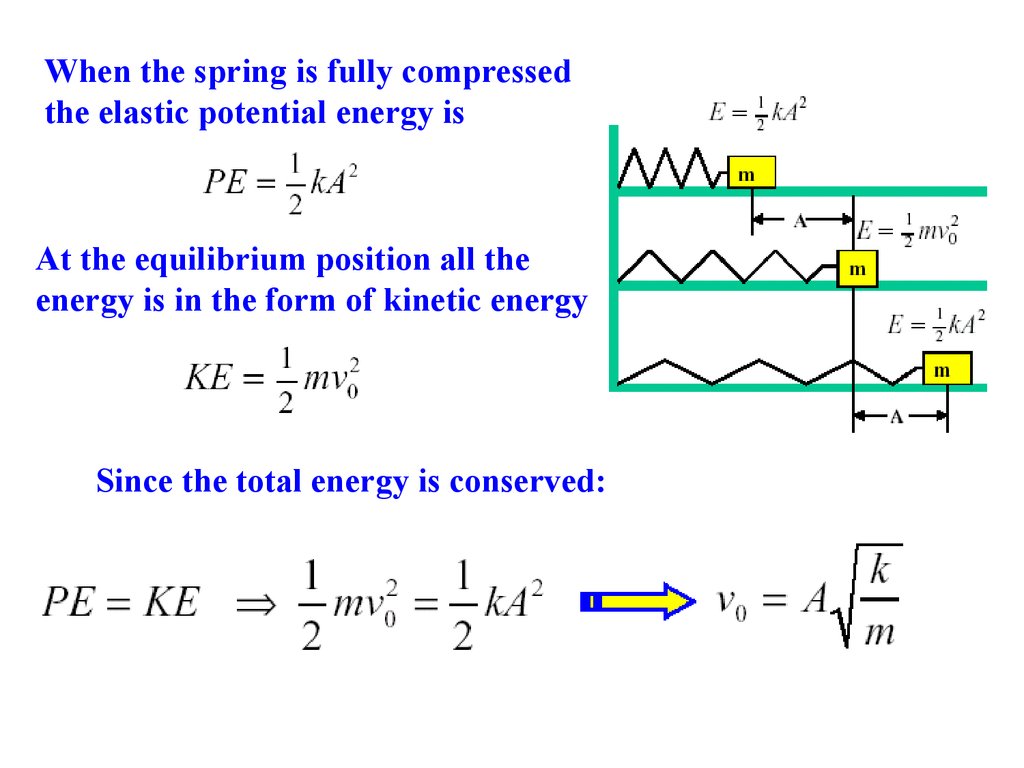
When the spring is fully compressedthe elastic potential energy is
At the equilibrium position all the
energy is in the form of kinetic energy
Since the total energy is conserved:
4.
At any point the velocity is:5.
PERIOD AND FREQUENCYThe period of an object in SHM is the time it takes the
mass to make a complete revolution.
UNITS:
T in seconds
f in Hz (s-1)
6.
Simple PendulumFor small displacements a pendulum obeys SHM.
Its period is:
The period and frequency DO NOT depend on the mass.
7.
11.1 For the motion shown in the figure, find:a. Amplitude
b. Period
c. Frequency
a. Amplitude: maximum displacement from equilibrium
A = 0.75 cm
b. T = time for one complete cycle
T = 0.2 s
c.
f = 1/T = 1/0.2 = 5 Hz
8.
11.2 A spring makes 12 vibrations in 40 s. Find the period and frequencyof the vibration.
f = vibrations/time
= 12/40
= 0.30 Hz
T = 1/f
= 1/0.3
= 3.33 s
9.
11.3 The amplitude of a SH oscillator is doubled. How does this affect:a. The period,
b. The total energy, and
c. The maximum velocity of the oscillator.
a. T is independent of A so it is unchanged
b. TE = 1/2 kx2
x’ = 2x so
TE' = 4TE
c. vmax occurs when x = 0 and all energy (TE) is K
TE' = 4TE then
4 = ½ mv2 therefore vmax must be doubled
10.
11.4 A 200-g mass vibrates horizontally without friction at the end of ahorizontal spring for which k = 7.0 N/m. The mass is displaced 5.0 cm
from equilibrium and released. Find:
a. Maximum speed
m = 0.2 kg
k = 7 N/m
xo = A = 0.05 m
vmax is at x = 0 then
1
2
1
1
kx mv kx 2
2
o
2
2
2
k
7
v A
0.05
m
0.2
v = 0.295 m/s
11.
b. Speed when it is 3.0 cm from equilibrium.x = 0.03 m
1
1
1
kx mv kx 2
2
k 2
v
( A x2 )
m
2
o
2
2
2
7
(0.052 0.032 )
0.2
v = 0.236 m/s
12.
c. What is the acceleration in each of these cases?F = ma = - kx
k
a
x
m
a. x = 0 therefore a = 0
b. x = 0.03 m therefore
7
a
(0.03) = -1.05 m/s2
0.2
13.
11.5 As shown in the figure, a long, light piece of spring steel is clamped atits lower end and a 2.0-kg ball is fastened to its top end. A horizontal force
of 8.0 N is required to displace the ball 20 cm to one side as shown. Assume
the system to undergo SHM when released. Find:
a. The force constant of the spring
F=8N
x = 0.2 m
m = 2 kg
F
8
= 40 N/m
k
x 0.2
b. Find the period with which the ball will vibrate back and forth.
2
m
2p
T 2p
= 1.4 s
40
k
14.
11.6 In a laboratory experiment a student is given a stopwatch, a woodenbob, and a piece of cord. He is then asked to determine the acceleration of
gravity. If he constructs a simple pendulum of length 1 m and measures the
period to be 2 s, what value will he obtain for g?
l=2m
T=2s
l
T 2p
g
4p l 4p 2 (1)
2
g 2
=
9.86
m/s
T
22
2
15.
Wave MotionA wave is, in general, a disturbance that moves through a
medium. It carries energy from one location to another
without transporting the material of the medium.
Examples of mechanical waves include water waves,
waves on a string, and sound waves.
The wave caries energy from one place to the other. It
does not carry the particles.
16.
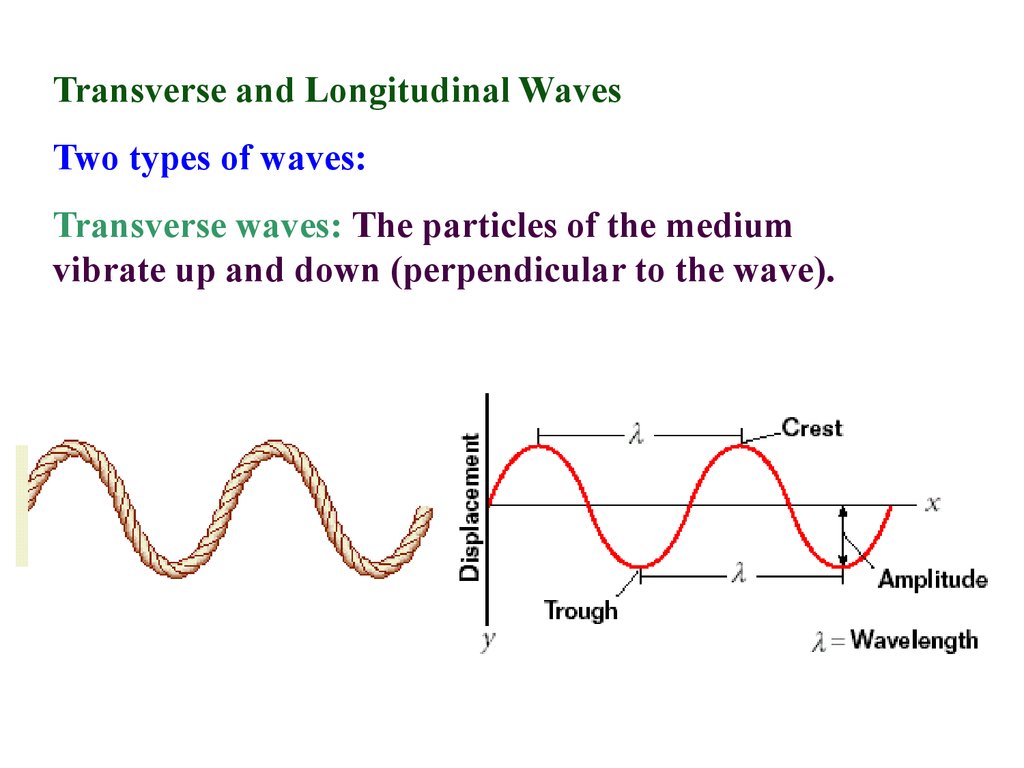
Transverse and Longitudinal WavesTwo types of waves:
Transverse waves: The particles of the medium
vibrate up and down (perpendicular to the wave).
17.
Longitudinal waves: The particles in the medium vibratealong the same direction as the wave (parallel). The medium
undergoes a series of expansion and compressions. The
expansions are when the coils are far apart (momentarily)
and compressions are when they are when the coil is close
together (momentarily).
Expansions and compressions are the analogs of the crests
and troughs of a transverse wave.
18.
Wave MotionWave velocity v is the
velocity with which the
wave crest is propagating.
Wave velocity v depends on
the medium.
A wave crest travels one
wavelength in one period:
On a string with tension
FT and mass per unit length of
the string (linear density) m/L
the velocity (m/s) of the wave is:
19.
11.7 Measurements show that the wavelength of a sound wave in a certainmaterial is 18.0 cm. The frequency of the wave is 1900 Hz. What is the
speed of the sound wave?
λ = 0.18 m
f = 1900 Hz
v=λf
= 0.18 (1900)
= 342 m/s
20.
11.8 A horizontal cord 5.00 m long has a mass of 1.45 g.a.
What must be the tension in the cord if the wavelength of a 120 Hz wave is
60 cm?
L=5m
m = 1.45x10-3 kg
f = 120 Hz
λ = 0.6 m
FT
v
m/ L
m 2 1.45 x10 3
2
FT v
(72) = 1.5 N
5
L
21.
b. How large a mass must be hung from its end to give it this tension?FT = mg
m = FT/g
= 1.5/9.8
= 0.153 kg
22.
11.9 A uniform flexible cable is 20 m long and has a mass of 5.0 kg. It hangsvertically under its own weight and is vibrated from its upper end with a
frequency of 7.0 Hz.
a. Find
the speed of a transverse wave on the cable at its midpoint.
L = 20 m
m = 5 kg
f = 7 Hz
FT =mg = 5 (9.8) = 49 N
At midpoint the cable supports
half the weight so:
FT = 1/2 (49) = 24.5 N
FT
24.5
v
= 9.89 m/s
m/ L
5 / 20
23.
b. What are the frequency and wavelength at the midpoint?f = 7 Hz at all points
v 9.89
= 1.4 m
l
f
7
24.
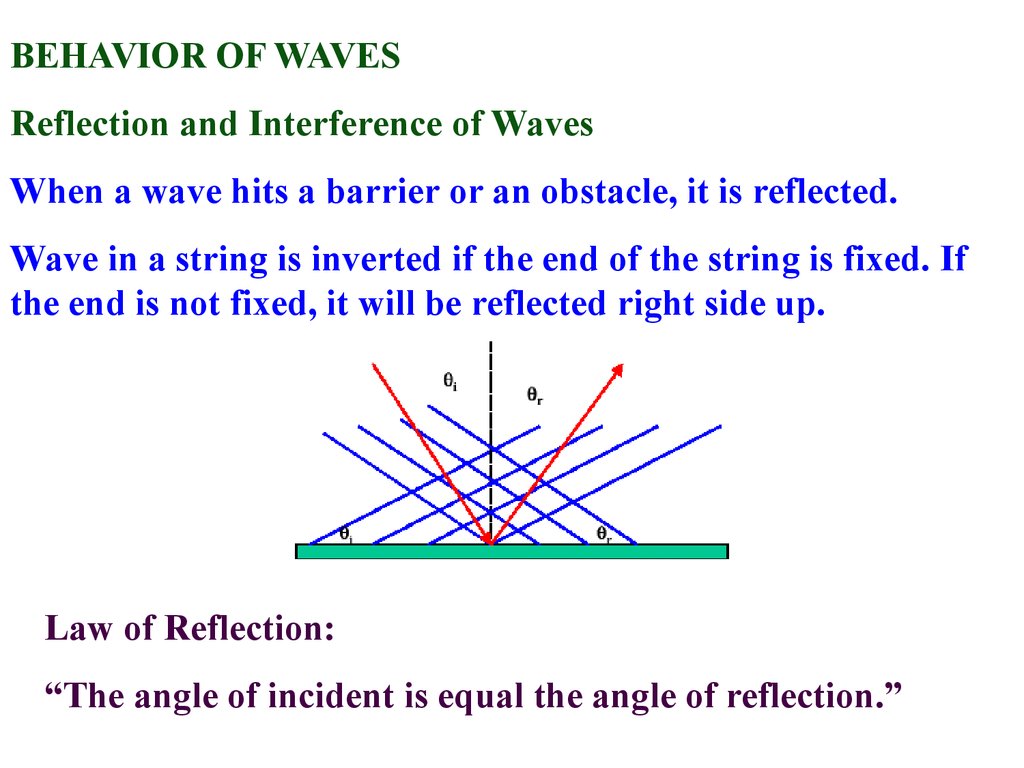
BEHAVIOR OF WAVESReflection and Interference of Waves
When a wave hits a barrier or an obstacle, it is reflected.
Wave in a string is inverted if the end of the string is fixed. If
the end is not fixed, it will be reflected right side up.
Law of Reflection:
“The angle of incident is equal the angle of reflection.”
25.
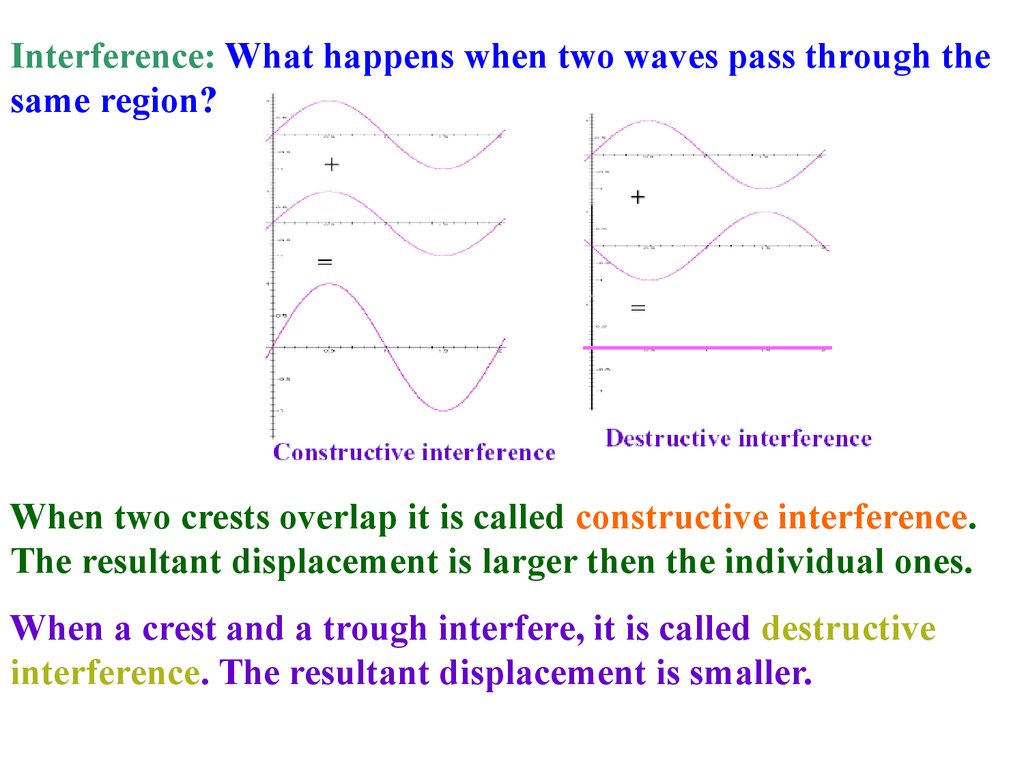
Interference: What happens when two waves pass through thesame region?
When two crests overlap it is called constructive interference.
The resultant displacement is larger then the individual ones.
When a crest and a trough interfere, it is called destructive
interference. The resultant displacement is smaller.
26.
Standing WavesIf a string is fixed on one end and oscillates on the other, the
moving waves will be reflected by the fixed end. If the string
vibrates at the right frequency, a standing wave can be
produced.
The points where there is destructive interference, where the
string is still are called nodes, the points where there are
constructive interference are called antinodes.
The nodes and antinodes remain in a fixed position for a given
frequency.
There can be more than one frequency for standing waves.
Frequencies at which standing waves can be produced are
called the natural (or resonant) frequencies.
27.
Standing WavesA string can be fixed in both sides, like a guitar or piano
string.When the string is plucked, many frequency waves will
travel in both directions. Most will interfere randomly and die
away. Only those with resonant frequencies will persist.
Since the ends are fixed, they will be the nodes.
The wavelengths of the standing waves have a simple relation
to the length of the string.
The lowest frequency called the fundamental frequency has
only one antinode. That corresponds to half a wavelength:
28.
The other natural frequencies are called overtones. They arealso called harmonics and they are integer multiples of the
fundamental.
The fundamental is called the first harmonic.
The next frequency has two antinodes and is called the second
harmonic.
29.
11.10 A metal string is under a tension of 88.2 N. Its length is 50 cm and itsmass is 0.500 g.
a. Find the velocity of the waves on the string.
m = 5x10-4 kg
FT = 88.2 N
L = 0.5 m
FT
88.2
v
m/ L
5 x10 4 / 0.5
= 297 m/s
b. Determine the frequencies of its fundamental, first overtone and second
overtone.
Fundamental:
L = 1/2 λ
λ = 2L
= 2(0.5)
=1m
v 297
f
l 1
= 297 Hz
30.
First overtonefn = n f'
f2 = 2(297)
= 594 Hz
Second overtone
fn = n f'
f3 = 3(297)
= 891 Hz
31.
11.11 A string 2.0 m long is driven by a 240 Hz vibrator at its end. Thestring resonates in four segments. What is the speed of the waves on the
string?
L =2 m
f = 240 Hz
L = 4/2 λ = 2 λ
λ = 1/2 L
= 1/2 (2)
=1m
v=fλ
= 240 (1)
= 240 m/s
32.
11.12 A banjo string 30 cm long resonates in its fundamental to a frequencyof 256 Hz. What is the tension in the string if 80 cm of the string have a
mass of 0.75 g?
L = 0.3 m
f' = 256 Hz
L = 0.8 m
m = 0.75x10-3 kg
L= 1/2 λ
λ = 2 (0.3)
= 0.6 m
v=fλ
= 256(0.6)
= 154 m/s
m 2 0.75 x10 3
2
FT v
(154) = 22.2 N
L
0.8
33.
11.13 A string vibrates in five segments to a frequency of 460 Hz.a. What is its fundamental frequency?
f5 = 460 Hz
fn = n f'
f' = 460/5
= 92 Hz
b. What frequency will cause it to vibrate in three segments?
fn = n f'
f3 = 3(92)
= 276 Hz
34.
DAMPED HARMONIC MOTIONA system undergoing SHM will exhibit damping. Damping is
the loss of mechanical energy as the amplitude of motion
gradually decreases.
In the mechanical systems studied in the previous sections, the
losses are generally due to air resistance and internal friction
and the energy is transformed into heat.
For the amplitude of the motion to remain constant, it is
necessary to add enough energy each second to offset the
energy losses due to damping.
35.
In many instances damping is a desired effect. For example,shock absorbers in a car remove unwanted vibration.
36.
FORCED VIBRATIONS: RESONANCEAn object subjected to an external oscillatory force tends to
vibrate. The vibrations that result are called forced vibrations.
These vibrations have the same frequency as the external force
and not the natural frequency of the object.
If the external forced vibrations have the same frequency as the
natural frequency of the object, the amplitude of vibration
increases and the object exhibits resonance. The natural
frequency (or frequencies) at which resonance occurs is called
the resonant frequency.
EXAMPLES OF RESONANCE































 Музыка
Музыка



