Преобразование сигналов в радиотехнических цепях

1.

1. Преобразование сигналов в
радиотехнических цепях

2.

В процессе своей деятельности при общении с различными предметами, явлениями или
процессами человек получает о них определенные сведения. Совокупность этих сведений о какомлибо объекте или процессе называется информацией. Для передачи или хранения информации
используются различные знаки (слова, рисунки, математические символы и т.п.), которые
позволяют представить информацию в определенной форме (текста, живой речи,
радиолокационного изображения, математических формул и т.д.). Информация, выраженная в
определенной форме и предназначенная для передачи или хранения, называется сообщением.
Передача сообщений на расстояние осуществляется с помощью какого-либо материального
носителя: бумаги, магнитной ленты, звуковых, световых и электромагнитных волн и др.
Последние три носителя являются физическими процессами. Физические процессы, несущие
сообщения, называются сигналами. Несмотря на большое разнообразие сигналов, понятию
"сигнал" можно дать четкое определение.
Сигнал – это некоторый физический процесс, характеристики (параметры) которого
изменяются по закону сообщения, который способен распространяться (т.е. перемещаться во
времени и в пространстве) и предназначен для управления местными источниками энергии или
для воздействия на особые органы специально организованной системы (на органы чувств
человека, магнитную ленту, органы управления летательным аппаратом или оружием и т.п.).
2

3.

Следует подчеркнуть, что физическое явление или процесс может быть сигналом только в
специально организованной системе. В противном случае любое физическое явление, которое
несомненно свидетельствует о процессах в том или ином объекте или субъекте, необходимо было
бы считать сигналом. В радиотехнике в качестве физических процессов – переносчиков
сообщений наибольшее распространение получили электрические и электромагнитные колебания,
параметры которых изменяются по закону передаваемых сообщений. Сигналы, применяемые в
радиотехнике, принято называть радиотехническими сигналами.
Для того, чтобы сделать сигналы объектами теоретического изучения и расчетов, следует
указать способ их математического описания, представляющего реальные сигналы с заданной
точностью, т.е. создать математическую модель.
Математическая модель представляет собой количественную формализацию абстрактных
представлений об изучаемом явлении, процессе или объекте. Она может быть представлена
различными математическими средствами: действительными или комплексными величинами,
матрицами, геометрическими образами, уравнениями, неравенствами, функциями и т.д. Так как
непосредственно в радиоэлектронной аппаратуре используются в основном одномерные
электрические сигналы в виде тока i(t) и напряжения u(t), то в дальнейшем будем пользоваться
одномерными математическими моделями сигналов, которые с равным успехом описывают ток,
напряжение, напряженность и т.д. Знание математических моделей дает возможность сравнивать
сигналы между собой, анализировать их преобразования и проводить классификацию.
3

4.

Для преобразования сообщений в сигнал в радиотехнике применяются специальные
устройства, называемые преобразователями (электрофизическими преобразователями). Они
преобразуют исходную физическую величину (механическую, звуковую, световую, тепловую т.д.)
в другую физическую величину, в частности, в электрическую, которая более удобна для
дальнейшей обработки в радиотехнических устройствах и системах. В качестве преобразователей
в радиотехнике используются: микрофоны – для преобразования звуковых колебаний в
электрический сигнал; терморезисторы – для преобразования тепловых изменений в
электрический сигнал; передающие телевизионные трубки (ортикон, суперортикон и т.п.),
формирователи сигналов изображения на приборах с зарядовой связью – для преобразования
светового сообщения в электрический сигнал и т.д. Основным требованием к преобразованию
является однозначное соответствие между сообщением и сигналом. Только в этом случае
сообщение может быть передано без искажений.
4

5.

Классификация сигналов
В зависимости от возможности точного предсказания мгновенных значений
радиотехнических сигналов в любые моменты времени они делятся на детерминированные и
случайные.
Детерминированные сигналы – сигналы, значения которых в любой момент времени точно
известны, т.е. точно (с вероятностью, равной единице) предсказуемы. Способы задания
детерминированных сигналов могут быть разнообразными – аналитические функции,
вычислительные алгоритмы, графики, таблицы и т.д. Строго говоря, детерминированных сигналов
в природе не существует. Неизбежное и точно не предсказуемое взаимодействие источника
сообщений с окружающими физическими объектами, явлениями и процессами, наличие
хаотических тепловых флуктуаций – все это заставляет рассматривать реальные сигналы как
случайные функции времени и говорить о случайных сигналах.
Случайные сигналы – сигналы, мгновенные значения которых не могут быть точно
предсказаны (с вероятностью, равной единице). Эти сигналы описываются случайными
функциями времени. К случайным сигналам относятся сигналы, описываемые
детерминированными функциями со случайно изменяющимися, неизвестными для получателя
параметрами. В радиотехнике случайные колебания часто проявляют себя как помехи,
препятствующие извлечению нужной информации из принятого сигнала.
5

6.

Практически очень часто бывает, когда уровень помех значительно меньше уровня
полезного сигнала с известной формой. В таком случае для анализа и расчетов обычно
используется детерминированная модель сигнала, которая значительно проще модели случайного
сигнала. Поэтому в учебнике рассматриваются только детерминированные сигналы, которые, в
свою очередь, подразделяются на непрерывные и импульсные.
Непрерывными называются сигналы, существующие непрерывно во времени и
описываемые непрерывной функцией, например, a(t) = = Amcos ot, – < t < + , где Am –
максимальное значение (амплитуда) колебания; o – круговая частота; t – текущее время.
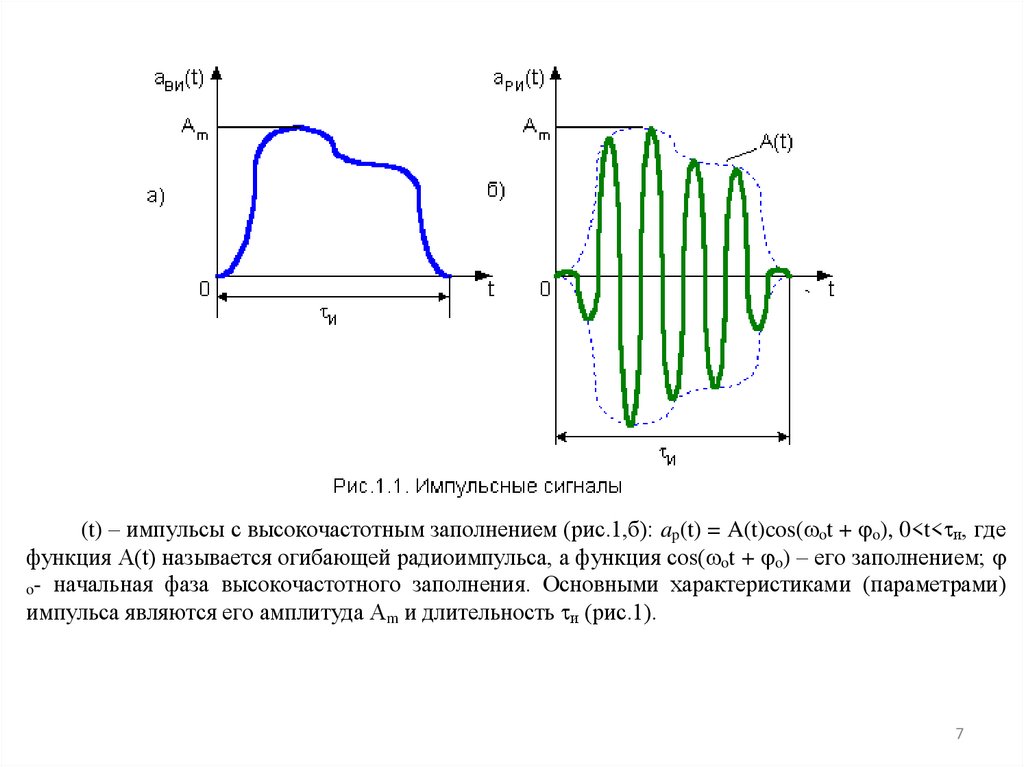
Импульсными называются сигналы, отличные от нуля лишь на конечных (небольших)
отрезках времени. Они разделяются на два класса: видеоимпульсы aв(t) (рис.1,а) и радиоимпульсы
ap
6

7.

(t) – импульсы с высокочастотным заполнением (рис.1,б): ap(t) = A(t)cos( ot + o), 0<t< и, где
функция A(t) называется огибающей радиоимпульса, а функция cos( ot + o) – его заполнением;
o- начальная фаза высокочастотного заполнения. Основными характеристиками (параметрами)
импульса являются его амплитуда Am и длительность и (рис.1).
7

8.

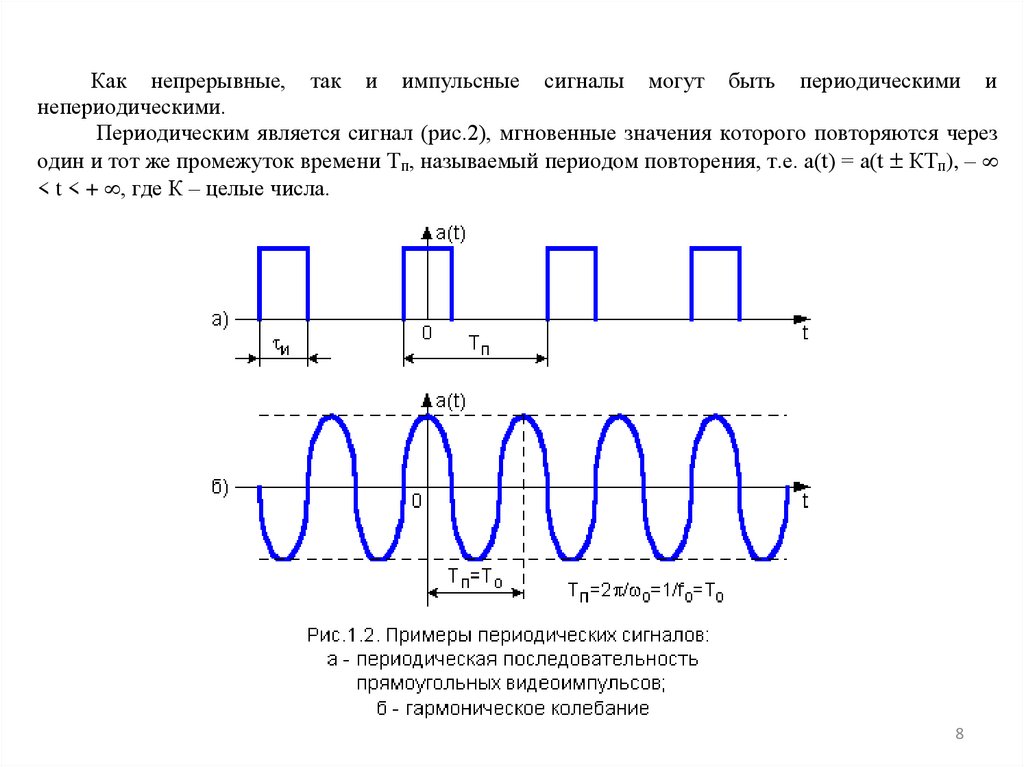
Как непрерывные, так и импульсные сигналы могут быть периодическими и
непериодическими.
Периодическим является сигнал (рис.2), мгновенные значения которого повторяются через
один и тот же промежуток времени Tп, называемый периодом повторения, т.е. a(t) = a(t КTп), –
< t < + , где К – целые числа.
8

9.

Непериодическим называется любой сигнал, не удовлетворяющий условию периодичности,
т.е. a(t) a(t КTп).
В зависимости от своего назначения радиотехнические сигналы подразделяются на
управляющие (модулирующие) и радиосигналы (высокочастотные немодулированные и
модулированные).
Управляющие сигналы – это сравнительно низкочастотные колебания, которые получаются
после преобразования сообщений или первичных сигналов, отображающих сообщения, в
радиотехнические сигналы и предназначены для управления местными источниками энергии. Эти
сигналы делятся на аналоговые, дискретные и
цифровые.
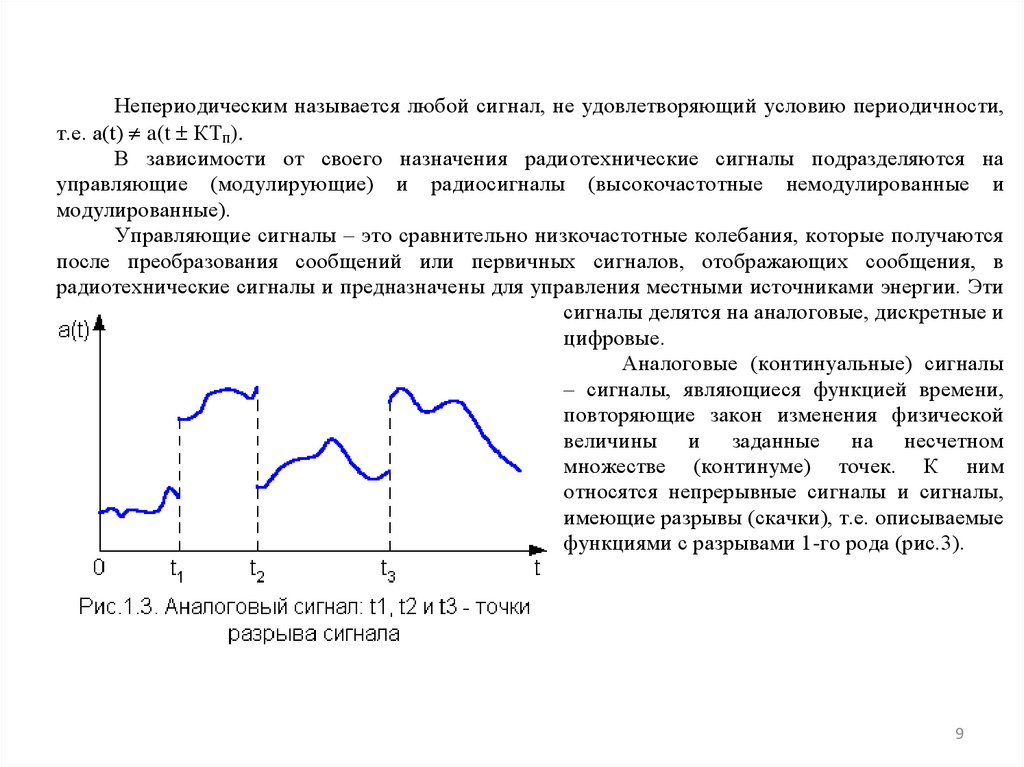
Аналоговые (континуальные) сигналы
– сигналы, являющиеся функцией времени,
повторяющие закон изменения физической
величины и заданные на несчетном
множестве (континуме) точек. К ним
относятся непрерывные сигналы и сигналы,
имеющие разрывы (скачки), т.е. описываемые
функциями с разрывами 1-го рода (рис.3).
9

10.

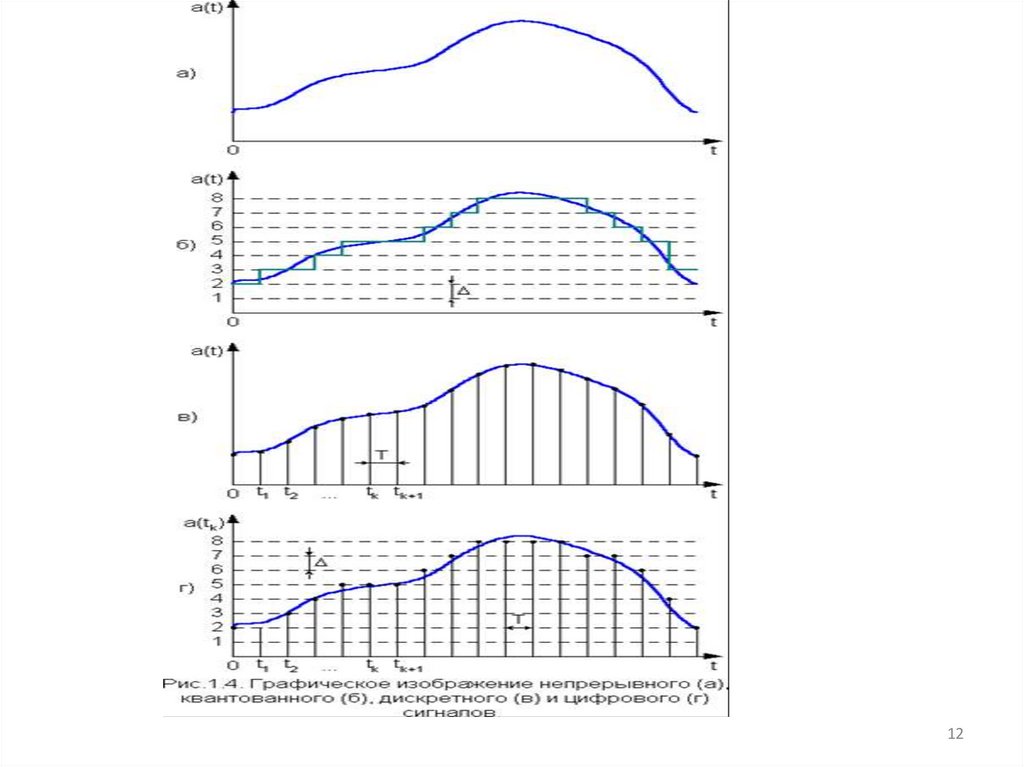
На рис.4,б изображен сигнал, соответствующий тому же сообщению, что на рис.4,а, но его
величина может принимать лишь дискретные значения. Дискретизация сигнала по величине
(уровню) называется квантованием. Интервал дискретизации по уровню называется шагом
квантования. Квантование аналоговых сигналов может проводиться с постоянным или
изменяющимся шагом квантования по диапазону значений сигнала.
Сигналы, квантованные по величине и заданные на несчетном множестве точек по оси
времени, называются квантованными сигналами. Они являются разновидностью аналоговых
сигналов.
Дискретные сигналы – сигналы произ-вольные по величине и дискретные по вре-мени, т.е.
заданные в фиксированные моменты времени tк (рис.4,в ) (на счетном множестве временных
точек). Интервал (T=tк+1- — tк), через который берутся отсчеты сигнала aк, называется периодом
или шагом дискретизации. Как правило, T берется постоянным. Одно из преимуществ дискретных
сигналов по сравнению с аналоговыми заключается в отсутствии необходимости воспроизведения
сигнала непрерывно во все моменты времени, что позволяет по одной и той же радиолинии
передавать сообщения от разных источников различным потребителям, организуя
многоканальную связь с разделением каналов по времени.
10

11.

Особой разновидностью дискретных сигналов являются цифровые сигналы (рис.4,г),
которые характерны тем, что каждый фиксированный уровень в них нумеруется числами с
конечным числом разрядов.
Таким образом, цифровые сигналы – дискретные по времени и квантованные по величине
(уровню) сигналы, представленные цифровыми кодами. Чаще всего цифровые сигналы
представляются с помощью двоичных кодов. Преобразование аналоговых сигналов в цифровые в
аппаратуре осуществляется с помощью специальных устройств, называемых аналого –
цифровыми преобразователями (АЦП). В АЦП аналоговые сигналы подвергаются операциям
дискретизации, квантованию и цифровому кодированию.
11

12.

12

13.

Управляющие сигналы, как правило, не могут быть непосредственно переданы по
радиоканалу. Дело заключается не только в том, что они недостаточно велики по амплитуде.
Гораздо более существенное обстоятельство заложено в их относительной низкочастотности.
Поскольку передающая антенна эффективно излучает электромагнитную энергию только в случае,
когда ее линейные размеры соизмеримы или значительно больше рабочей длины волны, то для
эффективной передачи сигналов с помощью радиоволн необходимо перенести их из
низкочастотной области в диапазон достаточно высоких частот. С этой целью на передающей
стороне формируется вспомогательное высокочастотное колебание, называемое несущим. В
радиотехнике в качестве несущего колебания обычно используется простое гармоническое
колебание
а(t ) Amo sin( o t o ) Amo sin (t ),
(1)
a(t ) Amo cos( o t o ) Amo cos (t ),
в котором амплитуда Amо, частота o и начальная фаза o являются постоянными величинами. В
(1) (t) = ot + o – полная фаза колебания (или просто фаза колебания). Если хотя бы один из
этих параметров в (1) изменяется по закону передаваемого сообщения, то несущее колебание
приобретает новое свойство – оно несет в себе информацию, которая первоначально была
заключена в управляющем сигнале.
13

14.

Процесс изменения параметров высокочастотного колебания по закону передаваемого
сообщения (управляющего сигнала) называется модуляцией.
Высокочастотное колебание, один или несколько параметров которого промодулированы
управляющим сигналом, называется модулированным сигналом или радиосигналом. В
зависимости от того, какой из параметров несущего колебания изменяется при модуляции,
различают амплитудно – модулированные (АМ), частотно – модулированные (ЧМ) и фазо –
модулированные (ФМ) радиосигналы. В последних двух радиосигналах
вместе с изменением частоты изменяется фаза и наоборот, т.к. t
t
(t ) ( )d , a (t} d (t ) / dt ,
(2)
t1
где t1 – начальное значение времени. Поэтому ЧМ и ФМ – радиосигналы называют
радиосигналами с угловой модуляцией (УМ).
Математические выражения (модели) перечисленных выше радиосигналов в общем виде
можно записать следующим образом:
(3)
a АМ (t ) Am (t ) cos( o t o );
t
аЧМ (t ) Amo cos ( )d o
t1
aФМ (t ) Amo cos o t (t ) .
(4)
(5)
14

15.

На практике используются также импульсная модуляция, амплитудно – частотная,
амплитудно – фазовая и ряд других видов модуляции.
При анализе преобразований детерминированных сигналов часто используются некоторые
стандартные (элементарные) сигналы, в качестве которых наиболее широко применяются функция
включения 1(t), прямоугольный единичный импульс (прямоугольная функция) rect(t/ и), функция
Кронекера (единичный импульс) 1(t) и дельта-функция (t). Перечисленные функции относятся к
так называемым обобщенным функциям.
Функция включения или функция единичного скачка, или единичная ступенчатая функция,
или функция Хевисайда (рис.5) в зависимости от решаемых задач описывается одним из
следующих выражений:
1, t 0,
1, t 0,
1, t 0,
(6)
1(t ) 0,5, t 0, 1((t )
1(t )
0, t 0;
0, t 0.
0, t 0;
15

16.

В случае отрицательного аргумента (t < 0, рис.1.5,б)
1, t 0,
1, t 0,
1, t 0,
1(t ) 0,5, t 0, 1(t )
1(t )
0
,
t
0
,
0, t 0.
0, t 0,
(6а)
Если функция включения смещена по оси времени на величину t o (рис.5,а), то в правых
частях равенств (6) вместо 0 следует подставить значение to, например,
1, t to ,
1(t to ) 0,5t , t to ,
(7)
0, t t .
o
Функция включения является безразмерной.
16

17.

Если функцию a(t), существующую при любых значениях t, умножить на функцию
единичного скачка (рис.6), то получится новая функция, которая будет существовать только при
значениях аргумента, определяющих функцию включения, т.е.
t t0 ,
a (t ),
а (t ) 1(t to ) 0,5 a (t ), t t0 ,
(8)
0,
t t0 .
Другими словами, функция включения обладает фильтрующим свойством.
Прямоугольная функция и функция Кронекера. Прямоугольную функцию, описывающую
прямоугольный импульс единичной амплитуды и длительности и (рис.7,а), записывают таким
образом:
1, и / 2 t и / 2,
t
(9)
rect 0,5, t и / 2,
и 0, t / 2иt / 2
т
и
Или
t
rect
и
1, и / 2 t и / 2, ,
0, t т / 2иt и / 2
(9а)
17

18.

В последних выражениях rect – это начальное выражение английского слова rectanguiar –
прямоугольный. Прямоугольную функцию можно представить в виде разности двух функций
включения (рис.7,6):
rect (t / и ) 1(t и / 2) 1(t и / 2).
(10)
При смещении прямоугольной функции на величину t0
1, t0 и / 2 t t0 и / 2,
t t
rect 0 0,5, t t0 и / 2,
и 0, t t t / 2иt t / 2.
0
0
0
0
и
(11)
18

19.

Если в (9) и (11) устремить и к нулю, то получится импульс единичной амплитуды и
нулевой (бесконечно малой) длительности (рис.8), который называется функцией Кронекера или
единичным импульсом:
t
1, t 0,
rect
t
lim
1
и 0
0, t 0,
и
(12)
t t0
1, t t0 ,
rect
t
t
0
lim
1
и 0
0, t t0 .
и
(12a)
Из выражений (9) – (11) для прямоугольного импульса единичной амплитуды и (12), (12а)
для единичного импульса следует, что они также являются безразмерными, как и функция
единичного скачка. Эти функции обладают хорошими фильтрующими свойствами.
19

20.

Умножение функции a(t), определенной при произвольных значениях аргумента, на
прямоугольную функцию, дает значения функции a(t) только при тех значениях аргумента, при
которых существует прямоугольная функция:
t t0
a t при
a t rect
И
И
И
t t0 .
t0
2
2
(13)
При умножении произвольной функции a(t) на единичный импульс получитcя значение этой
функции в момент существования функции Кронекера, т.е.
a t 1 t a 0 , a t 1 t t 0 a t 0 .
(14)
Таким образом, единичный импульс (функция Кронекера) обладает идеальным
фильтрующим свойством.
20

21.

Дельта – функция. Если взять видеоимпульс прямоугольной формы с амплитудой A m =1/ и и
площадью S = Am и = 1, расположенный четным образом на координатной плоскости (рис.1.9), и
устремить и к нулю, то Am устремится к бесконечности, а площадь останется неизменной и
равной
(15)
S и 1/ и 1.
Аналитически полученный импульс выражается функцией
, t t 0 ,
t
0, t t 0 ,
(16)
при одновременном выполнении условия
0
0
S t dt t dt 1.
(17)
Функцию (t),обладающую свойствами (16) и (17), принято называть дельта – функцией ( –
функцией) или функцией Дирака.
Таким образом, – функцией называется такая функция, которая описывает импульс,
имеющий бесконечно большую амплитуду, бесконечно малую длительность и площадь, равную
единице (рис.10).
21

22.

Из приведенного выше доказательства следует, что – функция является четной, т.е. (-t) =
(t), с размерностью, обратной размерности аргумента. В данном случае [ (t)] = 1/C.
При сдвиге – функции по оси времени на величину to
, t t0 ,
t t0
0, t t0 ,
S (t t0 ) dt 1.
(18)
Если известна – функция от аргумента в t, то
S b t d b t 1.
(19)
Здесь множитель (в) взят под знаком дифференциала по абсолютной величине, т.к. площадь
– функции, равная единице, всегда положительна, а множитель может быть отрицательным
числом.
22

23.

Приравняв интегралы из (17) и (19) друг другу, несложно показать, что
bt
1
t .
b
(20)
Так как – функция равна нулю везде, кроме точки своего существования, то ее умножение на
произвольную функцию a(t) будет равно: (t) a(t) = (t) a(0), (t – to) a(t) = (t – to)a(to).
Проинтегрировав полученные равенства, найдем:
t a t dt a 0 t dt a 0 ;
(21)
t t 0 a t dt a t 0 t t 0 dt a t 0 .
и и
b t 2 , - 2 t u
a t
1, и t ,
2
и
1 и
,
t
,
b
da t
2
и 2
a t
dt
0, и t .
2
23

24.

Таким образом, интеграл от произведения любой функции на – функцию равен ее
значению в точке существования – функции. Другими словами, соотношение (21) показывает,
что – функция обладает фильтрующим свойством.
Связь между функциями включения, прямоугольной и Кронекера выражается равенствами (10) и
(12).
Дельта- функцию можно выразить через производную от функции включения:
(22)
(t) = d1(t)/dt.
24

25.

При анализе и преобразованиях сложных сигналов очень часто возникает
необходимость их представления в виде совокупности (суммы) более простых
колебаний (сигналов), которые принимаются за элементарные. В качестве
"элементарных" сигналов в настоящее время используются ступенчатые функции,
прямоугольные видеоимпульсы, гармонические (синусные и косинусные) колебания
с соответствующей амплитудой, частотой и фазой, функции Уолша, Лежандра,
Чебышева, Эрмита и др.
Представление сложного сигнала в виде совокупности "элементарных" сигналов принято называть спектром сигнала. Если "элементарные" сигналы (колебания) являются только функцией времени (функции Уолша, прямоугольные видеоимпульсы, т.д.), то спектр называется временным, а если частоты [cos (к t + к),
где к = 1, 2, 3... – целое число], то спектр сложного сигнала называется частотным.
Слово "спектр" в переводе с латинского "specter" означает "образ" или
"признак". Таким образом, спектр является образом реального сложного сигнала,
который содержит все его признаки.
25

26.

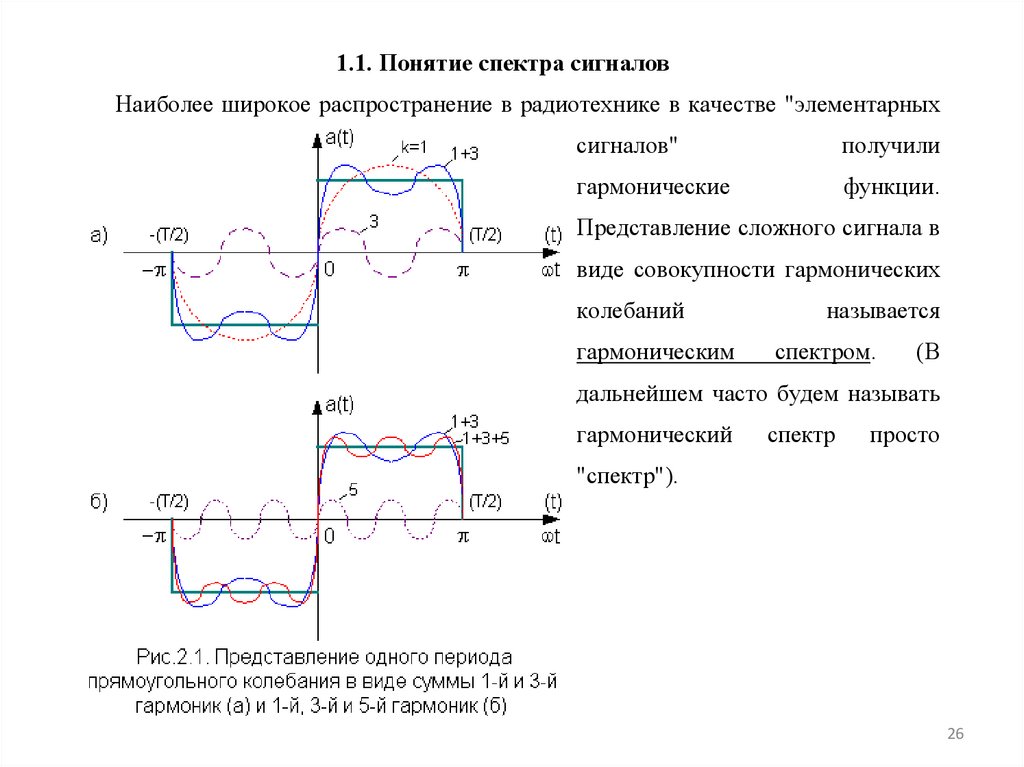
1.1. Понятие спектра сигналов
Наиболее широкое распространение в радиотехнике в качестве "элементарных
сигналов"
получили
гармонические
функции.
Представление сложного сигнала в
виде совокупности гармонических
колебаний
гармоническим
называется
спектром.
(В
дальнейшем часто будем называть
гармонический
спектр
просто
"спектр").
26

27.

На рис.2.1. показано для примера представление одного периода прямоугольного
колебания с помощью суммы двух (а) и трех (б), гармонических колебаний
соответственно.
Впервые идею о том, что сложный сигнал можно представить в виде суммы
простейших гармонических колебаний, высказал академик М.В.Шулейкин еще в
1916 г. Большая заслуга в развитии физических представлений, связанных со
спектральным анализом, разработке спектрального анализа сложных сигналов и их
преобразований принадлежит академикам Л.И.Мандельштаму и А.А.Харкевичу.
Знание спектров сложных сигналов необходимо для настройки и выбора
полосы пропускания приемных и передающих устройств, для правильной
расстановки по частотному диапазону различных радиосредств, для определения
параметров излучаемых сигналов радиотехническими устройствами и системами
противника, для создания электронных помех радиосредствам противника и т.д.
27

28.

Бурное развитие цифровой вычислительной техники значительно расширило
сферу приложения спектральных методов к обработке сигналов, сформировав
направление цифрового спектрального анализа, который, в свою очередь, оказывает
стимулирующее влияние на дальнейший процесс вычислительных методов и
средств их реализации. Появление цифровых алгоритмов быстрого преобразования
Фурье (БПФ) значительно расширило роль спектрального оценивания и превратило
его в средство решения многих практических задач, например: получение
высококачественного изображения земной поверхности в радиолокаторах с
синтезированной апертурой антенны (РСА), определения движущихся целей и
измерения скоростей их движения и т.д.
28

29.

1.2. Спектральный анализ периодических сигналов
Из курса высшей математики известно, что периодическую функцию
aп(t) = aп (t кTп), к = 0,1,2,..., удовлетворяющую условиям Дирихле (функция
на отрезке [-T/2, T/2] ограничена и имеет конечное число разрывов первого рода),
можно представить в виде тригонометрического ряда Фурье:
A 0m
a n (t)
A km cos(k n t k )
2
k 1
(1.1)
где Aom – коэффициент нулевой гармоники (постоянной составляющей); Aкm –
амплитуда к-й гармонической составляющей ряда; п = 2 Fп = = 2 /Tп; Fп = 1/Tп –
частота повторения функции aп(t); к – начальная фаза к-го гармонического
колебания. Поскольку cos(к пt + к) = cos кcosк пt – sin кsinк пt, то, обозначив
Aкmcos к = Aк, – Aкmsin к= Вк, (1.1) можно переписать в другом виде:
A 0m
a n (t)
(A k cos k n t B k sin k n t ).
2
k 1
(1.2)
29

30.

Коэффициенты ряда (1.2) вычисляют по формулам:
A 0m
2
Tn
2
Bk
Tn
Tn / 2
a n ( t )dt;
Tn / 2
Ak
2
Tn
Tn / 2
a n ( t ) cos k n tdt;
Tn / 2
Tn / 2
a n ( t ) sin k n tdt.
(1.3)
Tn / 2
Из сравнения выражений (1.1) и (1.2) следует, что
A km
A 2k B 2k ,
k arctg (B k / A k ).
Так как в соответствии с формулами Эйлера
cos(k n t k )
1 j( k n t k )
e
e j( k n t k ) ,
2
(1.4)
то, подставив (1.4) в (1.1), получим
a n (t)
1
jk n t
A 0 m A
e
A *km e jk n t
km
2
k 1
k 1
1
A km e jk n t ,
2 k
(1.5)
j k
где A
km A km e
A *km A km e j k .
Следовательно,
амплитуды
A-кm=Aкm
являются четными, а фазы -к= – к – нечетными функциями к.
30

31.

В соответствии с формулами (1.3) комплексная амплитуда
2
A
A
cos
jA
sin
km
km
k
km
k
Tn
Tn / 2
a n ( t )e jk n t dt.
(1.6)
Tn / 2
Таким образом, тригонометрический (1.1), (1.2) и комплексный (1.5) ряды
Фурье можно рассматривать как два способа представления одного и того же ряда.
В дальнейшем будем пользоваться той формой записи ряда Фурье, которая лучше
будет подходить для решения конкретной задачи.
Переход от вещественной к комплексной форме ряда Фурье можно
интерпретировать геометрически как замену вещественной величины Aкmcos(К пt +
к) суммой двух вращающихся навстречу друг другу с угловыми скоростями
(круговыми частотами) к п и -к п векторов на комплексной плоскости (рис.2.2).
31

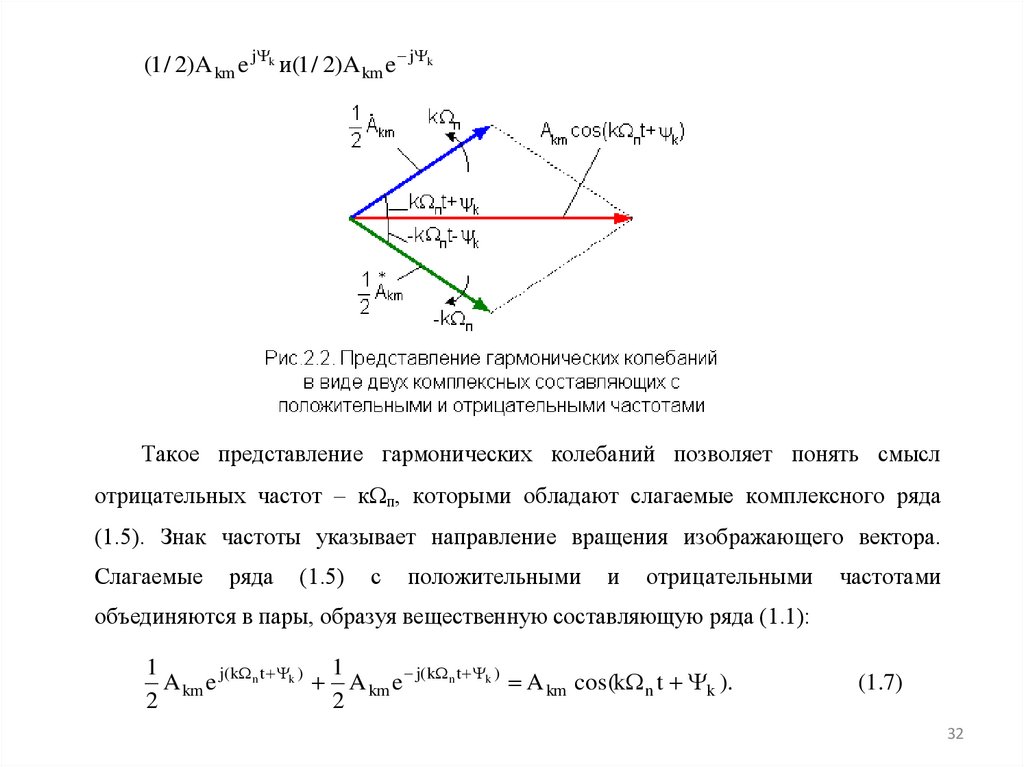
32.

(1 / 2)A km e j k и(1 / 2)A km e j k
Такое представление гармонических колебаний позволяет понять смысл
отрицательных частот – к п, которыми обладают слагаемые комплексного ряда
(1.5). Знак частоты указывает направление вращения изображающего вектора.
Слагаемые
ряда
(1.5)
с
положительными
и
отрицательными
частотами
объединяются в пары, образуя вещественную составляющую ряда (1.1):
1
1
A km e j( k n t k ) A km e j( k n t k ) A km cos(k n t k ).
2
2
(1.7)
32

33.

Следовательно,
отрицательная
частота
–
понятие
не
физическое,
а
математическое, вытекающее из способа представления гармонических колебаний.
Из формул (1.1), (1.2) и (1.5) следует, что спектр периодического сигнала
является дискретным и в общем случае состоит из бесконечного количества
гармонических составляющих с дискретными частотами O, п, 2 п, 3 п,..., к п и
т.д.
Представление сложного сигнала в виде совокупности гармонических
колебаний называется гармоническим спектром. Знание спектров сложных сигналов
необходимо для настройки и выбора полосы пропускания приемных и передающих
устройств, для правильной расстановки по частотному диапазону различных
радиосредств,
для
радиотехническими
определения
устройствами
и
параметров
системами
излучаемых
противника,
для
сигналов
создания
электронных помех радиосредствам противника и т.д.
Таким
образом,
тригонометрический
и
комплексный
ряды
Фурье
можно
рассматривать как два способа представления одного и того же ряда. В дальнейшем
будем пользоваться той формой записи ряда Фурье, которая лучше будет подходить
для решения конкретной задачи.
33

34.

Представление сложного сигнала в виде совокупности "элементарных"
сигналов принято называть спектром сигнала. Наиболее широкое распространение в
радиотехнике в качестве "элементарных сигналов" получили гармонические
функции.
Представление сложного сигнала в виде совокупности гармонических
колебаний называется гармоническим спектром. (В дальнейшем часто будем
называть гармонический спектр просто "спектр"). Знание спектров сложных
сигналов необходимо для настройки и выбора полосы пропускания приемных и
передающих устройств, для правильной расстановки по частотному диапазону
различных радиосредств, для определения параметров излучаемых сигналов
радиотехническими
устройствами
и
системами
противника,
для
создания
электронных помех радиосредствам противника и т.д.
34

35.

1.3. Амплитудно – частотные и фазо – частотные спектры периодических
сигналов
Так как каждая гармоническая составляющая спектра полностью определяется
амплитудой Aкm и начальной фазой к, то графически спектр периодического
сигнала изображается в виде двух спектральных диаграмм, на которых по
горизонтальной оси откладываются частоты гармоник к п, а по вертикальной оси на
одной из диаграмм откладываются амплитуды Aкm, а для другой – начальные фазы
к гармоник. На рис.2.3 первая диаграмма выражает амплитудно – частотный
спектр (АЧС) сигнала (рис.1.3,а,в), а вторая – его фазочастотный спектр (ФЧС)
(рис.1.3,б,г). Совокупность АЧС и ФЧС образует спектр сложного сигнала, т.е. его
представление в частотной области. Причем из выражений (1.1), (1.5) и (1.7)
следует, что вещественный спектр периодического сигнала является односторонним
(рис.1.3,а,б), а комплексный спектр – двусторонним (рис.1.3,в,г), в котором
амплитуды
гармонических
составляющих
в
два
раза
меньше
амплитуд
соответствующих гармоник вещественного АЧС, а ФЧС получается путем
нечетного продолжения одностороннего ФЧС в область отрицательных частот.
35

36.

Под шириной спектра понимается вся полоса частот, занимаемая спектром сигнала.
Большинство сигналов имеют неограниченно широкий спектр, однако амплитуды
гармонических
составляющих
сигнала распределены по частотам
неравномерно. Они, как правило,
сильно
затухают
за
пределами
некоторой конечной полосы частот
и ими пренебрегают. В этом случае
переходят от спектра с бесконечной
шириной к спектру с конечной
шириной,
которую
принято
называть
активной
шириной
спектра. Конечно, пренебрежение
гармониками
даже
с
малой
амплитудой приводит к искажению
формы сигнала. Но это искажение
незначительно и вполне приемлемо
для практики.
36

37.

На основании вышеуказанного можно сказать, что активная ширина спектра
есть интервал частот fс или c = 2 fc, в котором заключены гармонические
составляющие, выражающие сигнал с требуемой точностью.
37

38.

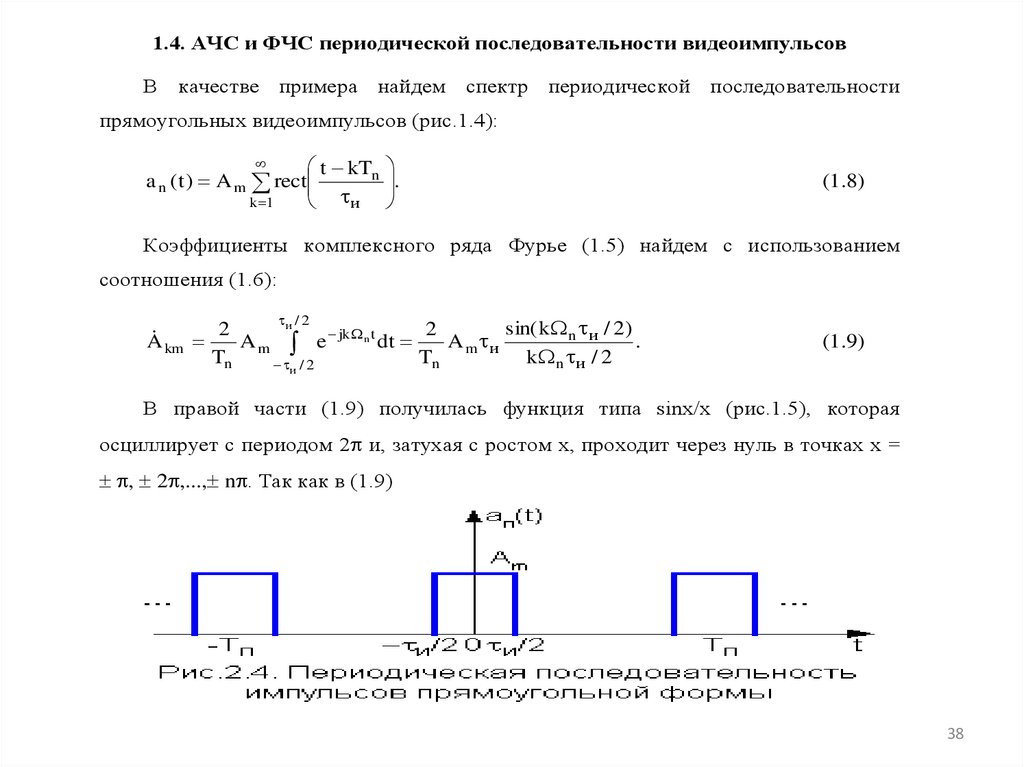
1.4. АЧС и ФЧС периодической последовательности видеоимпульсов
В качестве примера найдем спектр периодической последовательности
прямоугольных видеоимпульсов (рис.1.4):
t kTn
a n ( t ) A m rect
k 1
и
.
(1.8)
Коэффициенты комплексного ряда Фурье (1.5) найдем с использованием
соотношения (1.6):
и / 2
sin( k n и / 2)
2
2
A km
A m e jk n t dt
A m и
.
Tn
T
k
/
2
n
n
и
/ 2
(1.9)
и
В правой части (1.9) получилась функция типа sinx/x (рис.1.5), которая
осциллирует с периодом 2 и, затухая с ростом x, проходит через нуль в точках x =
, 2 ,..., n . Так как в (1.9)
38

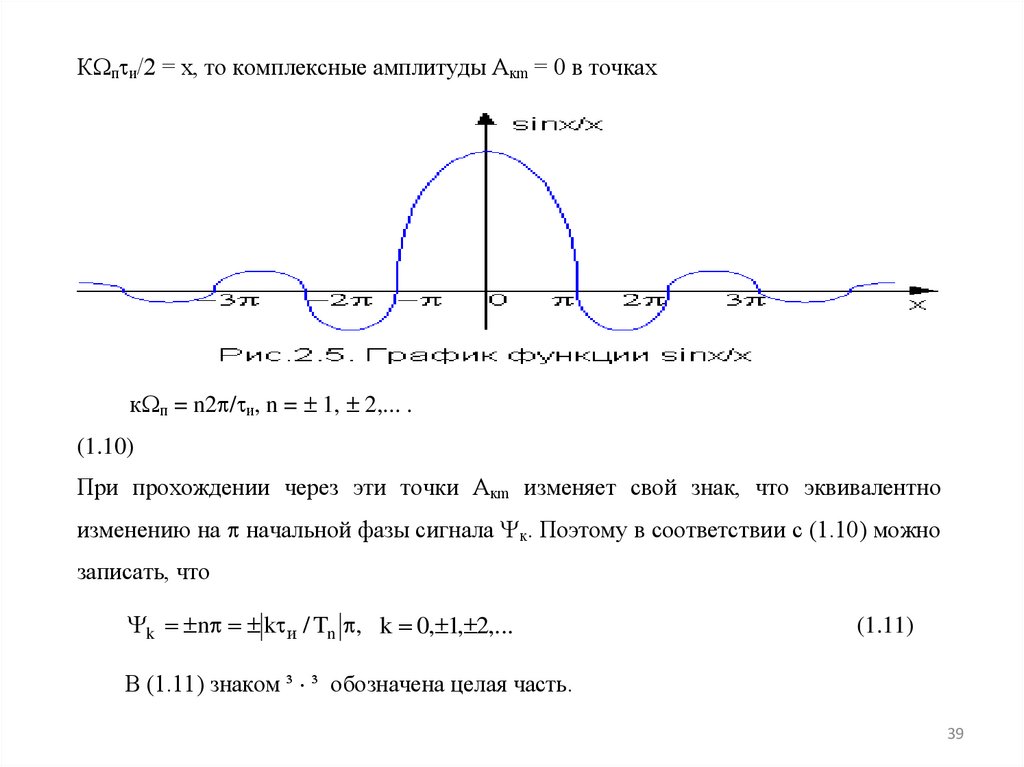
39.

К п и/2 = x, то комплексные амплитуды Aкm = 0 в точках
к п = n2 / и, n = 1, 2,... .
(1.10)
При прохождении через эти точки Aкm изменяет свой знак, что эквивалентно
изменению на начальной фазы сигнала к. Поэтому в соответствии с (1.10) можно
записать, что
k n k и / Tn , k 0, 1, 2,...
(1.11)
В (1.11) знаком ³ ³ обозначена целая часть.
39

40.

Модуль выражения (1.9) определяет амплитуды гармоник
sin( k n и / 2)
2
A km A
A
km
m и
Tn
k n и / 2
(1.12)
С учетом (1.9) комплексный ряд Фурье (1.5) для рассматриваемого сигнала
будет иметь вид:
a n (t) A m и
Tn
sin( k n и / 2) jk n t
e
.
k
/
2
k
n и
(1.13)
На основе полученных соотношений (1.11), (1.12) и (1.13) на рис.1.6 построены
односторонние (рис.1.6,а) и двусторонние (рис.1.6,б) АЧС и ФЧС периодической
последовательности прямоугольных импульсов для Тп/ и = 4.
Из выражений (1.12), (1.13) и рис.1.6 следует, что с увеличением
(уменьшением) и (при постоянном значении Тп) будут соответственно уменьшаться
(увеличиваться) ширина лепестков спектра сигнала и увеличиваться (уменьшаться)
амплитуды спектральных составляющих АЧС. В случае увеличения Тп (при и =
const)
количество
спектральных
составляющих
в
каждом
лепестке
будет
увеличиваться, а амплитуды спектральных составляющих в АЧС уменьшаться. При
уменьшении Тп процесс изменения спектра будет обратным.
40

41.

1.5. Энергетический спектр периодического сигнала
Так как периодический сигнал длится бесконечно долго, то его энергия
является бесконечно большой. Поэтому основной интерес представляет средняя
мощность периодического сигнала и ее распределение между отдельными
гармониками. Очевидно, что средняя мощность рассматриваемого сигнала на всей
временной оси совпадает со средней мощностью за период Тп. Следовательно,
среднюю мощность P периодического сигнала aп(t) (тока или напряжения),
рассеиваемую на единичном сопротивлении (R = 1 Ом) за период, можно
определить по формуле
1
P
Tn
Tn / 2
a 2n ( t )dt
(1.14)
Tn / 2
Поскольку периодический сигнал записывается в виде ряда Фурье (1.1), то
a 2n ( t )
A 0m
A 0m
A km cos(k n t k )
A m cos(l n t l ) .
k 1
l 1
2
2
41

42.

При перемножении правой части этого равенства получаются слагаемые
следующих видов:
A 0m A 0m A 02m
A
A
1)
;2) 0m A lm cos(l n t l ); 0m A km cos(k n t k );
2
2
4
2
2
4) A2кm cos2(к пt + к) при к = l.
Среднее за период Тп значение слагаемых вида 2) и 3) равно нулю, а каждое из
слагаемых 4) в результате усреднения будет равно
1
Tn
Tn / 2
A 2km
cos (k n t k )dt
.
2
(1.15)
A 02m 2
A km cos2 (k n t k ).
4
k 1
(1.16)
Tn / 2
A 2km
2
Значит,
a 2n ( t )
Подставив (1.16) в (1.14), с учетом (1.15) можно получить, что
2
1 2
A 0m
P
A km .
2 k 1
2
(1.17)
42

43.

Итак, средняя мощность периодического сигнала равна сумме средних
мощностей, выделяемых по отдельности гармониками с амплитудами Aкm и
постоянной составляющей Aom/2. Это означает, что средняя мощность не зависит от
фазировки отдельных гармоник.
Формула (1.17) представляет собой аналитическую запись распределения
средней мощности между отдельными составляющими сложного периодического
сигнала, т.е. его энергетический спектр.
Графически спектр периодического сигнала изображается в виде двух
спектральных диаграмм, на которых по горизонтальной оси откладываются частоты
гармоник к п, а по вертикальной оси на одной из диаграмм откладываются
амплитуды Aкm, а для другой – начальные фазы к гармоник. Первая диаграмма
выражает амплитудно – частотный спектр (АЧС) сигнала , а вторая – его
фазочастотный спектр (ФЧС) . Совокупность АЧС и ФЧС образует спектр сложного
сигнала.
Средняя мощность периодического сигнала равна сумме средних мощностей,
выделяемых по отдельности гармониками с амплитудами Aкm и постоянной
составляющей Aom/2. Это означает, что средняя мощность не зависит от фазировки
отдельных гармоник.
43

44.

Активная ширина спектра есть интервал частот fс или c = 2 fc, в котором
заключены гармонические составляющие, мощность которых составляет 90 – 95%
средней мощности сигнала.
44

45.

3.1.Определение дискретных сигналов
Как отмечалось ранее дискретными принято называть сигналы,
рассматриваемые в фиксированные моменты времени tk, т.е. заданные на
счетном множестве временных точек.
45

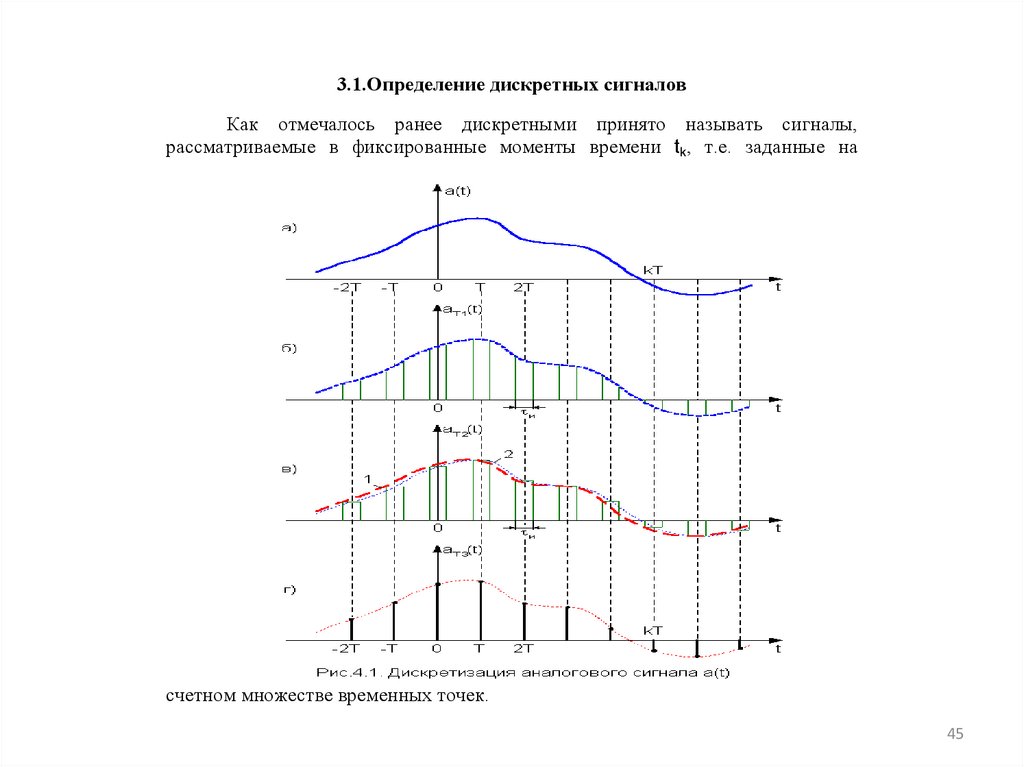
46.

Дискретизировать по времени аналоговый сигнал - значит исключить все
его значения на некоторых заданных интервалах времени, называемых
интервалом (шагом) дискретизации Т. Обычно Т=const и называется периодом
дискретизации. Дискретизация аналоговых сигналов осуществляется, как
правило, с помощью амплитудно - импульсной модуляции (АИМ), при которой
в соответствии с мгновенными значениями аналогового сигнала в точках
отсчета
изменяется
(модулируется)
амплитуда
периодической
последовательности импульсов (рис.4.1). Системы передачи и обработки
информации, радиолокации, радионавигации и автоматического управления,
использующие модулированные сообщения последовательности импульсных
сигналов, называют дискретными или импульсными.
Несмотря на то, что модулированные импульсные последовательности
физически являются аналоговыми, т.е. заданными на несчетном множестве
точек оси времени, передаваемые ими сообщения определены лишь в
отдельных (дискретных) точках (отрезках) времени, чем и обусловлено
название этих сигналов. Все дискретные сигналы можно разделить на три
основных вида: сигналы первого вида (рис.4.1 б), второго вида (второго вида с
запоминанием) (рис.4.1 в) и третьего вида (второго вида без
запоминания)(рис.4.1 г).
Из приведенного рисунка следует, что два первых вида дискретных
сигналов являются обычными сигналами с АИМ. Причем дискретные сигналы
первого вида называют сигналами АИМ-1, а вторые - АИМ-2. В дальнейшем
будем считать, что огибающая дискретных сигналов АИМ-2 проходит через
центры вершин прямоугольных импульсов (кривая 2 на рис.4.1 в), т.е. сдвинута
относительно "истинной огибающей" (кривая 1) во времени на tи/2. Такой сдвиг
огибающей не изменяет АЧХ спектра импульсного сигнала и создает большие
удобства для сравнения между собой аналитических выражений дискретных
сигналов различных видов.
46

47.

Поскольку при АИМ-1 (рис.4.1 б) вершины промодулированных
импульсов повторяют форму аналогового сигнала на отрезках времени
кТ и / 2) t (кТ и / 2) , то дискретные сигналы АИМ-1 можно описать
функцией
a T1 ( t ) a ( t )
t kT
.
rect
k
и
(4.1)
Из рис.4.1 в следует, что k-й импульс дискретного сигнала АИМ-2 будет
равен а (кТ) rect[( t кТ) / и ] , где a(кТ) - значение аналогового сигнала a(t) в
момент времени tk= кТ. В таком случае сигнал АИМ-2
t kT
.
a T 2 ( t ) a (kT ) rect
k
и
Если импульсы дискретизирующей
отличны от прямоугольных, то
a T 2 (t)
a (kT ) U ДП ( t kT ),
(4.2)
последовательности
в
АИМ-2
(4.2,а)
k
где Uдп(t) - функция, описывающая форму импульса единичной амплитуды
дискретизирующей последовательности.
47

48.

Дискретные сигналы третьего вида (рис.4.1 г) аналитически выражаются
как произведение аналогового сигнала (рис.4.1 а) на периодическую
последовательность единичных импульсов (функций Кронекера) (1.12 а):
a T3 ( t ) a ( t )
1 ( t kT ) a (kT ) 1 ( t kT ).
k
(4.3)
k
К математической модели (4.3) сходятся обе выше рассмотренные
модели дискретных сигналов (4.1) и (4.2), (4.2 а) при tи 0.
В теории часто используют идеализированную математическую модель
дискретного сигнала, получаемую на основе применения в качестве
дискретизирующей последовательности периодической последовательности функций:
a T (t) a (t)
( t kT ) a (kT ) ( t kT ).
k
(4.4)
k
Идеализированную математическую модель (4.4) можно получить из (4.1)
и (4.2), (4.2 а), если tи устремить к нулю, одновременно увеличивая амплитуду
прямоугольных импульсов обратно пропорционально tи и оставляя площадь
импульса все время равной 1.
48

49.

При пользовании идеализированной моделью (4.4) следует иметь в виду,
что размерность aT(t) равна размерности аналогового сигнала a(t), деленной на
секунду, т.к. размерность - функции равна 1/с.
Дискретный сигнал, представляющий собой совокупность импульсов
нулевой длительности с амплитудами, равными мгновенным значениям
непрерывной функции, которые отсчитываются через одинаковые промежутки
времени, называется решетчатой функцией. Другими словами, решетчатая
функция представляет собой последовательность (множество) отсчетов {a(kТ)}
аналогового сигнала a(t).
Из данного определения следует, что рассмотренный ранее дискретный
сигнал третьего вида (см. рис. 4.1 г и соотношение (4.3)) является решетчатой
функцией. Ее также можно получить из идеализированной импульсной
последовательности (4.4) путем интегрирования. В обозначении решетчатой
функции фигурные скобки обычно не ставят и часто опускают в записи
аргумента период дискретизации Т, что как бы соответствует нормировке
аргумента к периоду Т:
a(t)
t кТ а (кТ) а (к), к
.
Теория решетчатых функций в настоящее время достаточно глубоко
разработана и широко применяется при анализе и синтезе дискретных и
цифровых систем. Однако использование решетчатых функций в качестве
моделей сигналов в этих системах требует применения специального
математического аппарата, отличного от математического аппарата описания и
анализа аналоговых сигналов и систем.К решетчатым функциям, например, не
применимы операции дифференцирования и интегрирования. Этим операциям
соответствуют определения конечных разностей и конечных сумм от
решетчатых функций.
49

50.

Ранее было показано, что особой разновидностью дискретных сигналов
являются цифровые сигналы, которые широко применяются в цифровых
системах передачи и обработки информации. В этих системах аналоговые
сигналы дискретизируются по времени и квантуются по уровню на конечное
число значений - уровней квантования. Шаг квантования (рис. 1.4 г) обычно
выбирается постоянным, но может и изменяться по какому - либо закону.
Квантованные отсчеты сигнала называются цифровым сигналом. По существу
цифровой сигнал представляет собой последовательность чисел, выраженных в
определенном коде и принимающих только конечное число значений.При
квантовании действует следующее правило: если в момент дискретизации
аналогового сигнала a(t) его величина не равна уровню квантования, то отсчету
цифрового сигнала присваивается значение ближайщего уровня квантования.
Следовательно, квантование сопровождается ошибками, которые называются
шумом квантования. Часто бывает удобно при анализе цифровых систем
рассматривать неквантованные отсчеты a(kТ) аналогового сигнала, а ошибки
квантования учитывать добавлением к дискретному сигналу шума квантования
с соответствующими статистическими характеристиками.
50

51.

3.2. Спектры дискретных сигналов
Применив к (4.1) преобразование Фурье, найдем соотношение для
спектральной плотности дискретного сигнала АИМ-1:
S T1 ( )
t kT j t
e
a
(
t
)
rect
dt.
и
k
(4.5)
Так как выражение в квадратных скобках (4.5) описывает периодическую
последовательность прямоугольных импульсов единичной амплитуды, то его
можно заменить рядом Фурье в комплексной форме (2.13):
t kT 1 и
rect
T
k
и
sin( n и / 2) jn t
n / 2 e .
n
и
(4.6)
где =2 /T; Am=1. Подставив (4.6) в (4.5), получим
S T1 ( ) и
T
sin( n и / 2)
n / 2 S( n ),
n
и
где S ( n )
a ( t )e
j( n ) t
(4.7)
dt - спектральная плотность исходного
непрерывного сигнала a(t).
51

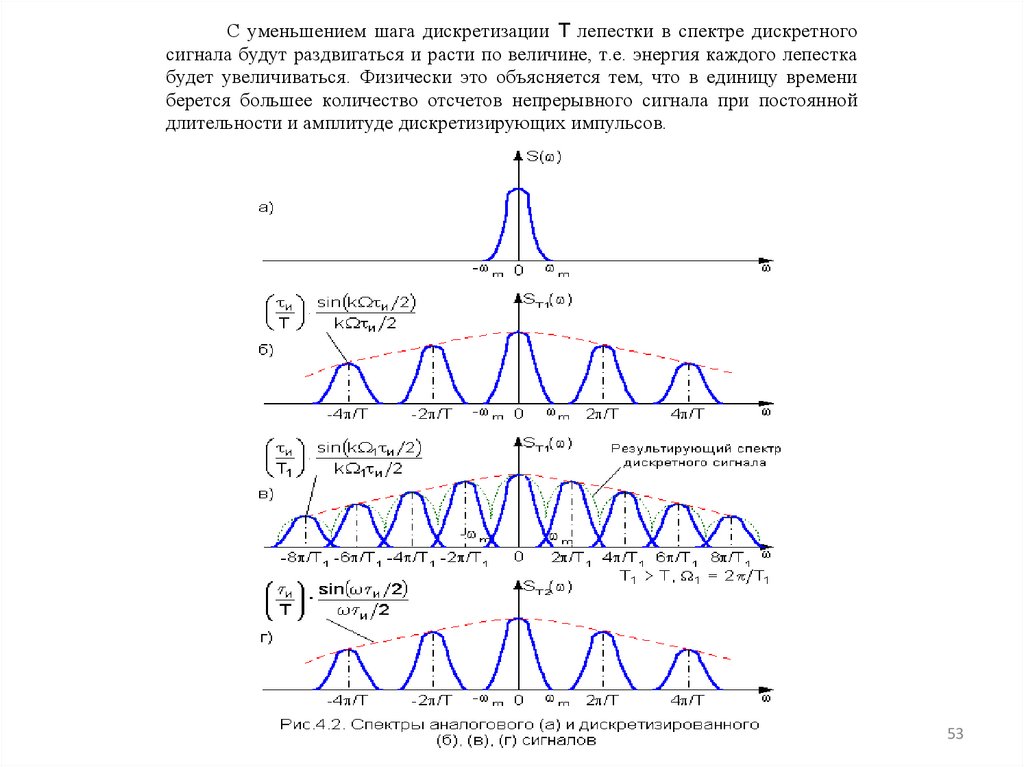
52.

Из (4.7) следует, что спектр дискретного сигнала АИМ-1 представляет
собой с точностью до постоянного множителя и/Т последовательность
спектров исходного сигнала, сдвинутых друг относительно друга на =2 /T,
убывающих по закону sinx/x.
Другими словами, формула (4.7) выражает связь спектральной плотности
дискретного сигнала (АИМ-1) со спектральной плотностью непрерывного
аналога.Графики функций S( ) и ST1( ) представлены на рис.4.2 а, б, в
соответственно.
Из рис.4.2 б видно, что если расстояние по частоте между центрами
соседних лепестков в спектре дискретного сигнала =2 /T 2 m ( m максимальная циклическая частота в спектре непрерывного сигнала), то они не
перекрываются. Следовательно, с помомщью соответствующего фильтра
низких частот с полосой пропускания ф= m можно снова выделить
огибающую дискретного сигнала (АИМ-1). Ее также можно выделить и с
помощью полосового фильтра, настроенного на одну из частот k , с полосой
пропускания ф=2 m. Если же соседние лепестки перекрываются (рис.4.2 в),
то в этом случае восстановить непрерывный сигнал (огибающую дискретного
сигнала) без искажений невозможно, т.к. нельзя выделить отдельно ни один
лепесток,который с точностью до постоянного множителя является спектром
непрерывного аналога.
Таким образом, для неискаженной передачи (представления) аналогового
сигнала с помощью дискретного необходимо интервал дискретизации выбирать
из условия
T 2 /( 2 m ) / m 1 /( 2f m ),
где fm= m/2 - максимальная частота в спектре аналогового сигнала.
(4.8)
52

53.

С уменьшением шага дискретизации Т лепестки в спектре дискретного
сигнала будут раздвигаться и расти по величине, т.е. энергия каждого лепестка
будет увеличиваться. Физически это объясняется тем, что в единицу времени
берется большее количество отсчетов непрерывного сигнала при постоянной
длительности и амплитуде дискретизирующих импульсов.
53

54.

Из соотношения (4.7) и рис.4.2 в следует, что с уменьшением tи
огибающая спектра все более приближается к прямой линии, а лепестки спектра
выравниваются, уменьшаясь по величине. В пределе при и d (к нулю),
спектр
приобретает
строго
периодическую
структуру,
т.к.
lim sin n и / 2 / n и / 2 1, а уровень лепестков стремится к бесконечно
и 0
малой величине (к нулю). Так как в этом случае периодическая
последовательность прямоугольных импульсов единичной амплитуды
преобразуется в периодическую последовательность функций Кронекера, то
спектральная плотность (4.7) дискретного сигнала первого вида преобразуется в
спектральную плотность сигнала третьего вида (4.3):
d
S TЗ ( )
S ( n ).
T n
54

55.

Для того, чтобы уровень лепестков в спектре дискретного сигнала не
снижался при уменьшении и необходимо одновременно с уменьшением
длительности импульса увеличивать его амплитуду так, чтобы площадь
импульса Sи оставалась неизменной. Если взять для упрощения Sи=1, то при
и 0 (d ), от моделей АИМ-1 (4.1) или АИМ-2 (4.2), (4.2 а) переходим к
идеализированной математической модели (4.4) дискретного сигнала,
спектральную плотность которой в соответствии с (4.7) можно представить в
виде:
S ( ) 1 S ( n ).
T
T n
(4.10)
Следует отметить, что энергия сигнала aT(t) (4.4), выраженного через функции, бесконечно велика. Соответственно и энергия спектра (4.10) тоже
бесконечно велика.
55

56.

Для определения спектра дискретного сигнала второго вида (АИМ-2)
применим прямое преобразование Фурье к равенству (4.2):
S T 2 ( )
t kT j t
e
dt
rect
)
kT
(
a
и
kT и / 2
a (kT )
k
e
j t
kT и / 2
e j t ( kT и / 2) e j t ( kT и / 2)
dt a (kT )
j
k
(4.11)
sin( и / 2)
j kT
S r ( ) a (kT ) e j kT .
a (kT ) e
1 и
и / 2
k
k
При произвольной форме Uдп(t) дискретизирующих импульсов с
использованием теоремы запаздывания (2.31) несложно получить, что
S T 2 ( )
j t
a (kT ) U дп ( t kT ) e dt
k
a (kT ) U дп ( t kT )e j t dt
k
S ДП ( )
(4.11 а)
a (kT )e j kT .
k
56

57.

По аналогии с вышерассмотренным случаем примем Sи=1. Тогда при
и 0 дискретный сигнал АИМ-2 (4.2) превращается в идеализированный (4.4),
S r ( ) S ДП ( ) S ( ) 1, , а из (4.11) и (4.11 а) следует, что
S T ( )
a (kT ) e j kT .
(4.12)
k
Приравняв правые части равенств (4.10) и (4.12), получим
a (kT ) e
k
j kT
1
S( n ).
T n
(4.13)
Из (4.13) следует, что спектральную плотность S Т можно определить
непосредственно по совокупности временных отсчетов a(kТ), без обращения к
спектру S исходного непрерывного сигнала, что существенно упрощает
спектральный анализ дискретных сигналов.
57

58.

С учетом (4.13) спектральная плотность (4.11) дискретного сигнала
АИМ-2 с прямоугольным дискретизирующими импульсами будет выражаться
формулой
sin( и / 2) и
S T 2 ( )
и / 2
T
1
S ( n ) S r ( ) T S ( n )
n
n
(4.14)
Для произвольной формы дискретизирующих импульсов
1
S T 2 ( ) S ДП ( )
S ( n ).
T n
(4.14а)
Формулы (4.11), (4.11 а) и (4.14), (4.14 а) выражают связь спектральной
плотности дискретного сигнала АИМ-2 со спектральной плотностью
непрерывного аналога a(t).
Приведенные рассуждения и соотношения (4.14), (4.14 а) показывают,
что в отличие от спектра сигнала АИМ-1, где каждый смещенный спектр S
аналогового сигнала умножался на некоторое постоянное значение спектра
прямоугольного импульса при =n (n=0, ±1, ±2,...) в спектре дискретного
сигнала АИМ-2 каждое значение смещенного спектра умножается на
соответствующее значение непрерывной функции S r [(или S дл ].Поэтому
отдельные лепестки в спектре сигнала АИМ-2 будут несколько несимметричны
относительно вертикальной линии, проводимой через точки =n (рис.4.2 г).
58

59.

Дискретными принято называть сигналы, рассматриваемые в
фиксированные моменты времени tk
Дискретный сигнал, представляющий собой совокупность импульсов
нулевой длительности с амплитудами, равными мгновенным значениям
непрерывной функции, которые отсчитываются через одинаковые промежутки
времени, называется решетчатой функцией.
Спектр дискретного сигнала АИМ-1 представляет собой с точностью до
постоянного множителя и/Т последовательность спектров исходного сигнала,
сдвинутых друг относительно друга на =2 /T, убывающих по закону sinx/x.
С уменьшением tи огибающая спектра все более приближается к прямой
линии, а лепестки спектра выравниваются, уменьшаясь по величине. В пределе
при и d (к нулю), спектр приобретает строго периодическую структуру.
59

60.

3.3. Спектр пачки импульсов
Из соотношений (3.14) и (3.14а) следует, что спектральная плотность
дискретного сигнала АИМ-2 с точностью до постоянного множителя 1/Т равна
произведению
спектральной
плотности
одиночного
импульса
дискретизирующей последовательности на сумму спектральных плотностей
непрерывного аналога (огибающей). Если огибающую ограничить по времени,
то дискретный сигнал будет представлять собой пачку (серию) импульсов с
изменяемой по форме огибающей амплитудой.
В частности, в случае прямоугольной огибающей длительностью Т ог и
амплитудой Am из (3.14,а) найдем, что спектр пачки импульсов
( ) S
( ) A TОГ
S
ПИ
ДИ
m
T
(3.15)
sin[( n )TОГ / 2]
.
(
n
)
T
/
2
n
ОГ
При прямоугольной форме импульсов в пачке
T
sin( и / 2)
S ПИ ( ) и
A m ОГ
и / 2
T
sin[( n )TОГ / 2]
(
n
)
T
/
2
n
ОГ
sin( и / 2) sin[( n )TОГ / 2]
S и nи
,
и / 2 n ( n )TОГ / 2
(3.16)
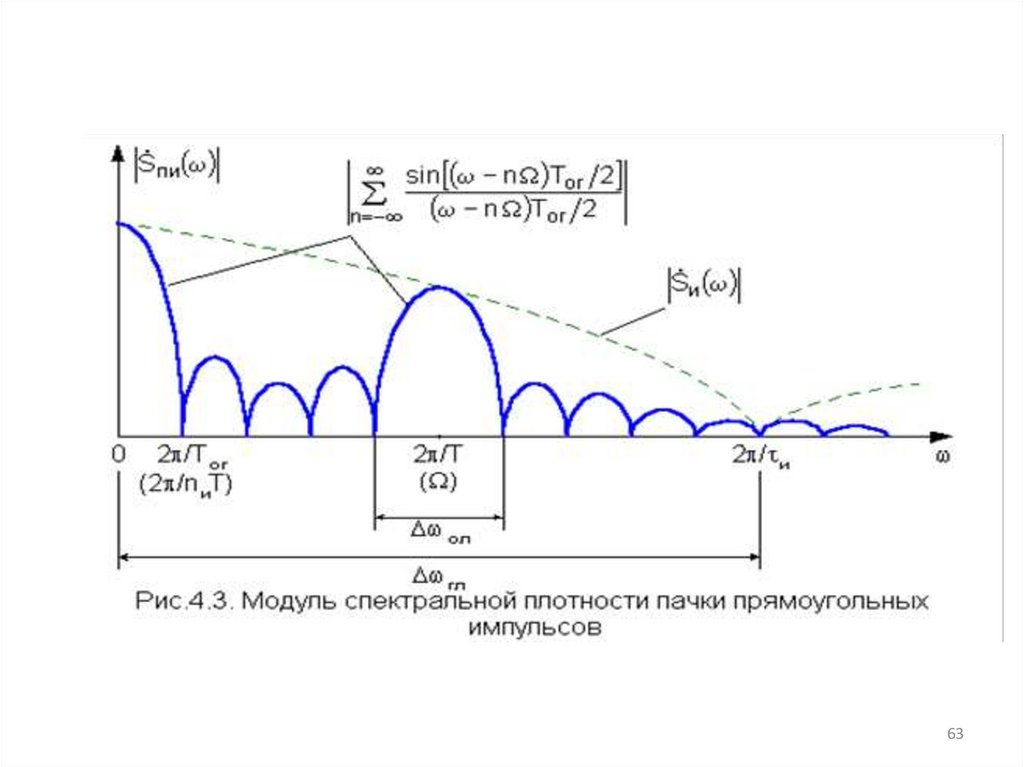
где nu = Тог/Т – количество импульсов в пачке; Su = Am u – площадь импульса,
т.к. амплитуда импульса в данном случае равна амплитуде огибающей. На
рис.4.3. для примера изображен модуль спектра пачки прямоугольных
импульсов для nu = 5 и Т/ u = 2.
60

61.

Из выражений (3.15) и (3.16) следует, что огибающая спектра пачки
импульсов определяется формой спектра одиночного импульса. В эту
огибающую "вписан" периодически повторяющийся с частотой спектр
огибающей пачки импульсов. Таким образом, спектр пачки видеоимпульсов в
общем случае является сплошным и носит лепестковый характер. При = 0 и n
= 0 его значение будет максимальным и равным SuТог/Т Su nu. Центры
основных лепестков располагаются в точках n = n и имеют ширину ол = 4
/Тог = 4 /(nuТ). Следовательно, с увеличением временного расстояния Т между
соседними импульсами (уменьшением частоты ) центры основных лепестков
в спектре пачки сближаются. Если при этом количество импульсов nu в пачке
остается
постоянным (Тог растет), то ширина ол каждого основного лепестка и
максимальное значение спектра уменьшаются. В случае Т , ол 0, а
спектр пачки импульсов стремится по виду к спектру одиночного
видеоимпульса с шириной главного лепестка гл = 2 / u. Однако
распределение энергии между спектральными составляющими в пределах гл
сильно изменится в силу "изрезанности" спектра пачки видеоимпульсов.
61

62.

С другой стороны, чем большее число импульсов будет в пачке при Т = const
(больше длительность пачки Тог), тем больше будет максимальное значение и
уже ширина каждого основного лепестка. Если nu , то ол 0 и
сплошной спектр пачки импульсов стремится к линейчатому, так как пачка
превращается в периодическую последовательность импульсов.
Поэтому, если рассматривать пачку (серию) одинаковых импульсов,
появляющихся через равные промежутки времени Т, начиная с некоторого
момента времени to, то длительность пачки будет расти с течением времени, ее
спектр изменяться во времени в зависимости от числа импульсов, появившихся
в пачке к текущему моменту времени t = nuТ. Спектр такого сигнала получил
название текущего спектра.
Спектр реального процесса, наблюдаемый на анализаторе спектра, является
текущим. Независимо от того, как долго продолжается серия импульсов, в
начальный момент рассмотрения прохождения импульсов через анализатор
спектра спектр серии будет сплошным. С течением времени наблюдения
количество появившихся импульсов увеличивается, а ширина основных
лепестков спектра уменьшается, то есть текущий спектр приближается к
линейчатому, оставаясь в принципе сплошным.
62

63.

63

64.

3.4. Теорема Котельникова
Впервые теорема отсчетов была независимо сформулирована и доказана
русским академиком В.В.Котельниковым (1933 г.) и американским ученым
Р.Найквистом. Эта теорема устанавливает возможность представления
аналогового сигнала с ограниченным спектром в виде отдельных отсчетов и
сколь угодно точного его восстановления по данным отсчетам. Читается
теорема следующим образом.
Сигнал, который описывается непрерывной функцией времени a(t) с
ограниченным спектром, полностью определяется своими значениями,
отсчитываемыми через интервал времени
T=1/(2fm)= m.
(3.17)
Эта теорема полностью согласуется с полученным ранее результатом (3.8) по
выбору периода дискретизации аналогового сигнала.
64

65.

Как было показано в п. 4.2, если период дискретизации выбран в
соответствии с условием (3.18) (или (3.8)), то лепестки спектра дискретного
cигнала не перекрываются (рис.4.2 б, г), и непрерывный сигнал a(t) можно
восстановить, например, по нулевому лепестку. Действительно, поскольку в
пределах m спектральная плотность S( ) совпадает с периодической
функцией (3.12), умноженной на коэффициент Т (см. (3.13)), то, взяв обратное
преобразование Фурье от правой части (3.12), умноженной на Т, в пределах
m, получим
j kT j t
T
a
(
kT
)
e
d .
e
m k
1 m
a( t )
2
С учетом (3.17) последнее соотношение преобразуется к виду
1
a (t)
2 m
m
k
a (kT )
m
e
j ( t kT )
d
k
a (kT )
sin[ m ( t kT )]
. (3.18)
m ( t kT )
Формула (3.18) аналитически выражает теорему отсчетов и называется
рядом Котельникова. На основании этой формулы теорему отсчетов можно
сформулировать так:
Произвольный сигнал, спектр которого не содержит составляющих выше
fm Гц, может быть полностью восстановлен, если известны отсчетные
значения этого сигнала, взятые через равные промежутки времени 1/(2fm)
с.
65

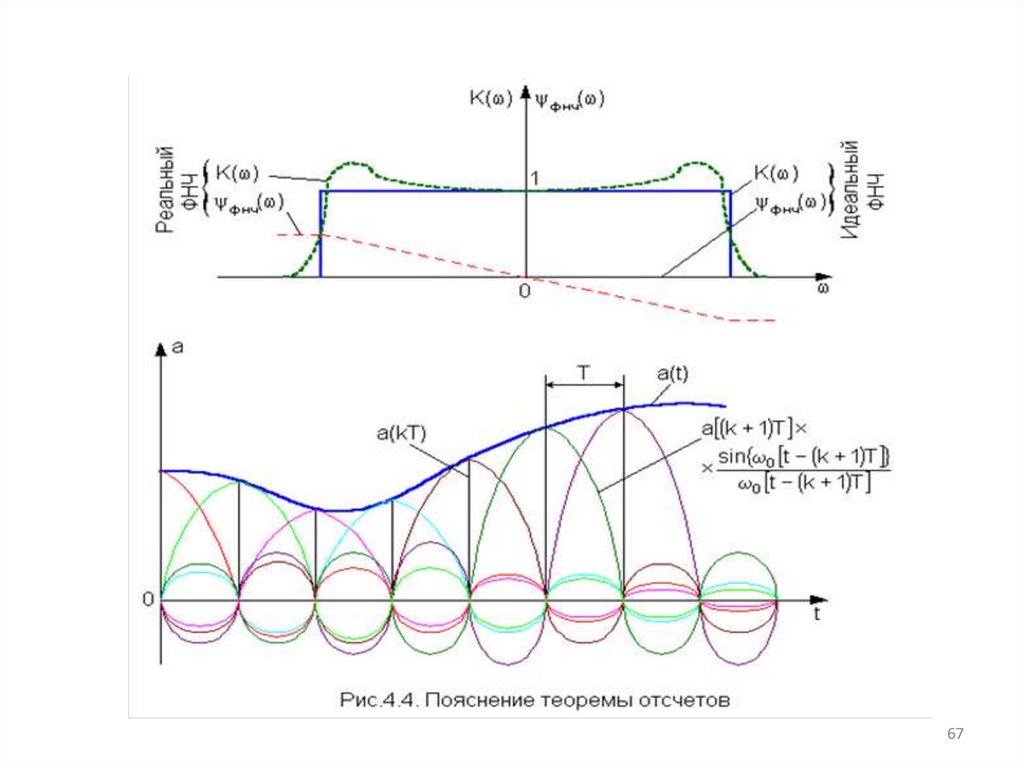
66.

Произведение под знаком суммы в (3.18) выражает реакцию идеального
фильтра нижних частот (ФНЧ) с полосой пропускания от - m до + m на
воздействие k-го одиночного импульса с амплитудой, равной отсчетному
значению a(kТ). Если и T (т.е. и d ), то в пределах полосы пропускания
идеального ФНЧ спектральная плотность будет постоянна и в соответствии
с(2.41) равна
S k ( ) a (kT )e j kT .
(3.19)
Так как передаточная функция К( ) идеального ФНЧ равна 1 (рис.4.4 а),
то спектральная плотность (3.19) передается на его выход без изменения.
Поэтому, взяв обратное преобразование Фурье от (3.19) в пределах m, найдем
сигнал на выходе ФНЧ при воздействии на его вход k-го импульса:
1 m
1 m j ( t kT )
j kT
j T
a k (t)
e d a (kT )
d
a (kT )e
e
2
2
m
sin[ m ( t kT )]
1
a (kT )
T
m ( t kT )
m
(3.20)
66

67.

67

68.

Сравнение соотношений (3.20) и (3.18) показывает, что для точного
соответствия выходного сигнала (реакции) идеального ФНЧ значениям
функции ряда Котельникова его передаточная функция должна быть равна не 1,
а Т.
Если учесть конечную длительность и дискретизирующих импульсов,
то аналогично можно показать, что в пределах полосы пропускания идеального
ФНЧ
sin[ m ( t kT )]
S k ( ) и a (kT )e j kT , a k ( t ) и a (kT )
T
m ( t kT )
Поэтому передаточная функция идеального ФНЧ должна быть равна
Т/ и.
Приведенные выше рассуждения позволили достаточно наглядно
показать, что идеальный ФНЧ преобразует импульсы в непрерывные колебания
вида sin x/x с максимальными значениями, равными отсчетным величинам
непрерывного сигнала в k-ые моменты времени. Сумма этих колебаний
выражает непрерывный сигнал (рис.4.4 б).
Таким образом, с помощью ФНЧ можно восстановить непрерывный
сигнал по его дискретным значениям, взятым в соответствии с теоремой
отсчетов.
68

69.

Следует отметить, что при восстановлении непрерывного сигнала по его
дискретам считалось, что сигнал на выходе идеального ФНЧ появляется при
t 0, т.е. когда на его входе еще не действует импульс дискрета, чего реально не
может быть. Это говорит о том, что нельзя сделать такую цепь, которая бы
только ограничивала АЧХ спектра сигнала и не изменяла его ФЧХ. Любая
реальная избирательная цепь (в том числе и ФНЧ) является инерционной и
задерживает воздействующий на ее вход сигнал на некоторое время tз. В полосе
пропускания ФНЧ можно считать, что tз не зависит от частоты. Тогда фаза
колебания будет пропорциональна его частоте, т.е. фнч tз. Кроме того,
реальные сигналы всегда ограничены не только по частоте, но и во времени.
Поэтому с достаточной степенью точности непрерывный сигнал можно
восстановить
по
конечному
числу
его
дискретных
значений
N=tсигн/T+1=2fmtсигн+1, где tсигн - длительность непрерывного сигнала. С учетом
сделанных замечаний
a(t)
2f m t сигн. 1
a (kT)
k 0
sin[ m ( t kT t 3 )]
.
m ( t kT t 3 )
В заключение необходимо подчеркнуть, что ряд Котельникова (3.19), по
существу, является спектром непрерывного сигнала во временной области, в
котором в качестве элементарных сигналов (базисных функций) взяты функции
вида sinx/x.
69

70.

Таким образом, было показано, что огибающая спектра пачки импульсов
определяется формой спектра одиночного импульса. В эту огибающую
"вписан" периодически повторяющийся с частотой спектр огибающей пачки
импульсов. Спектр пачки видеоимпульсов в общем случае является сплошным
и носит лепестковый характер. При = 0
Котельников показал, что сигнал, который описывается непрерывной
функцией времени a(t) с ограниченным спектром, полностью определяется
своими значениями, отсчитываемыми через интервал времени
T=1/(2fm)= m.
70