Criterii de congruentă a triunghiurilor

1.

2.

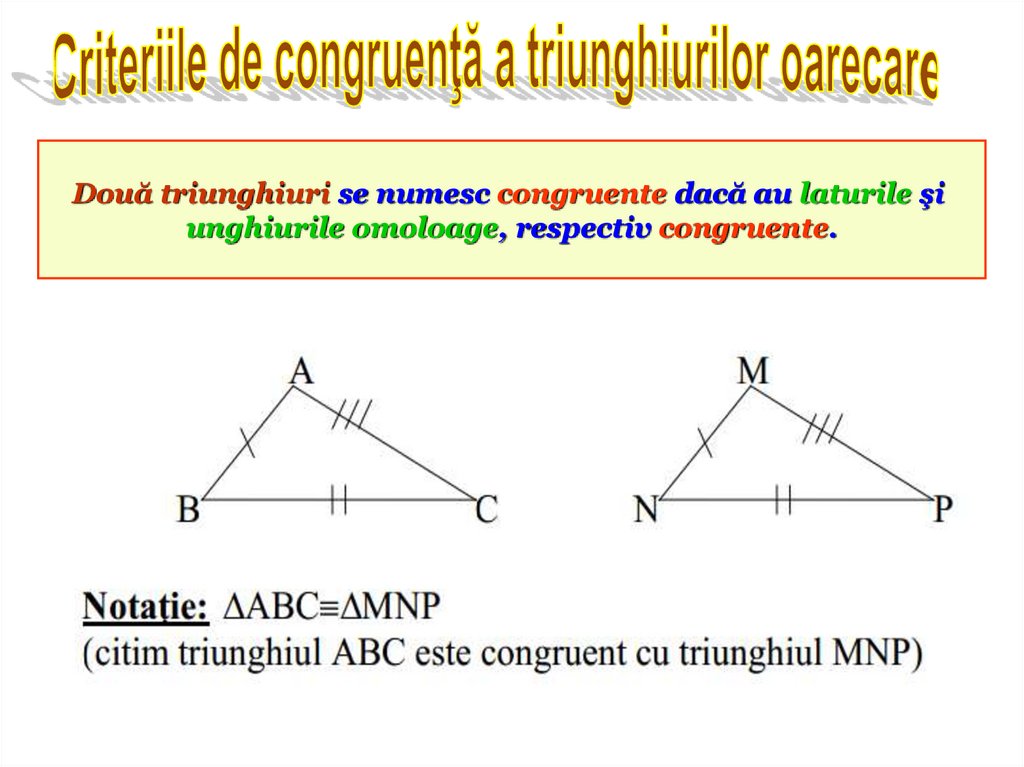
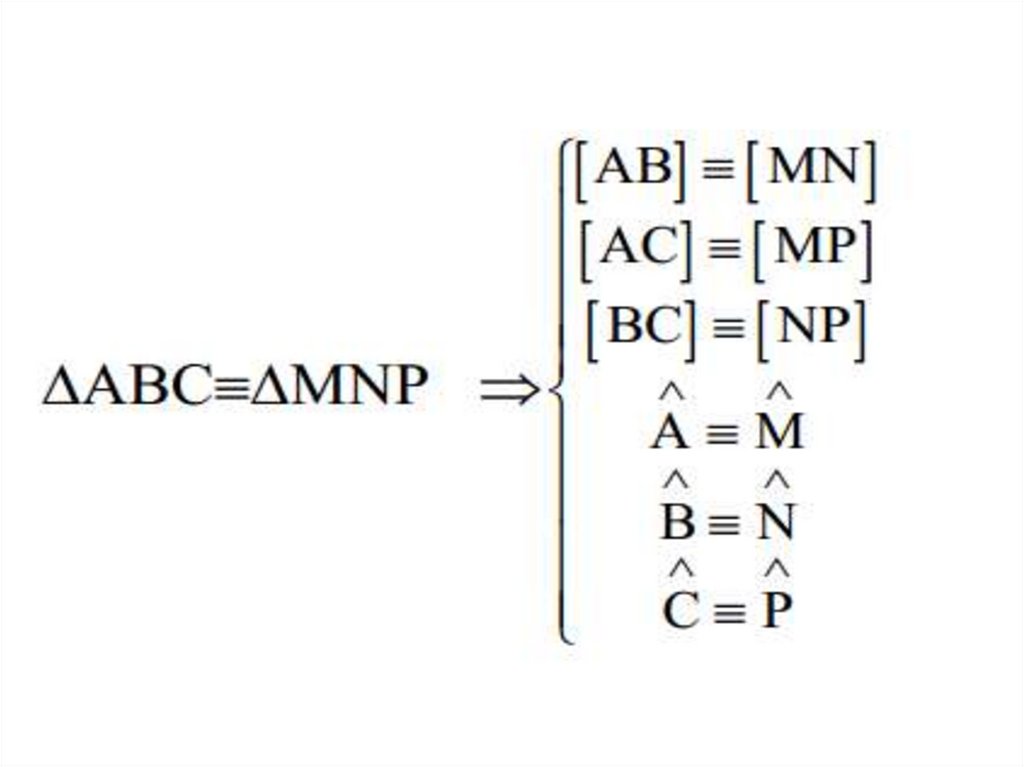
Două triunghiuri se numesc congruente dacă au laturile şi
unghiurile omoloage, respectiv congruente.

3.

4.

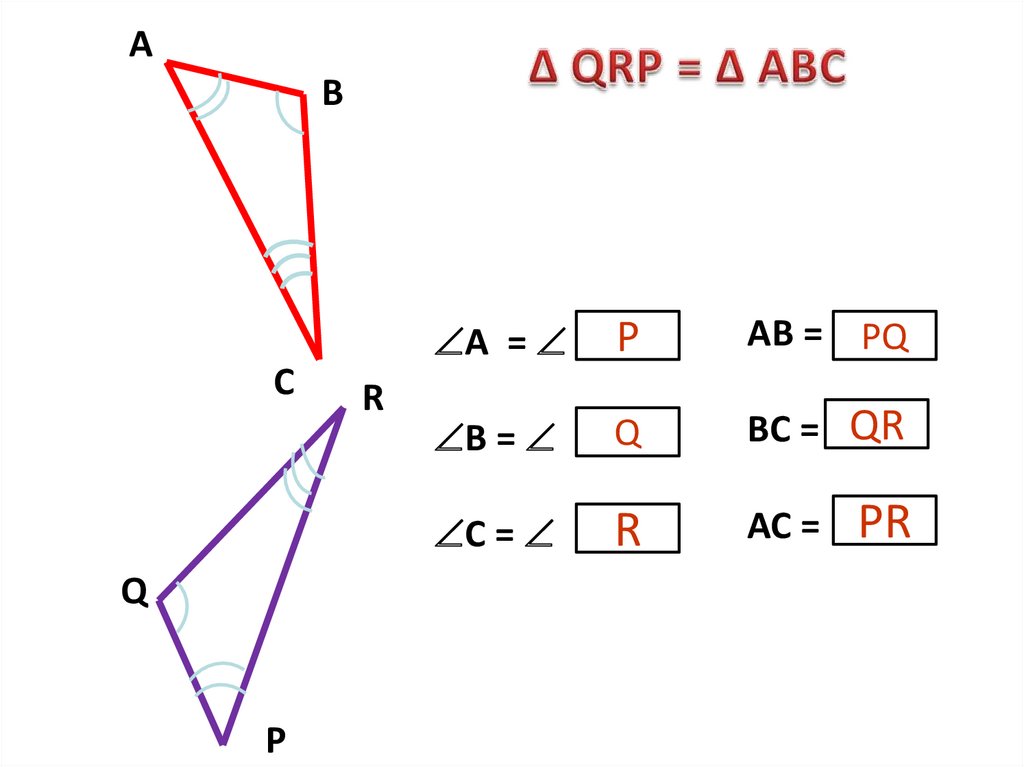
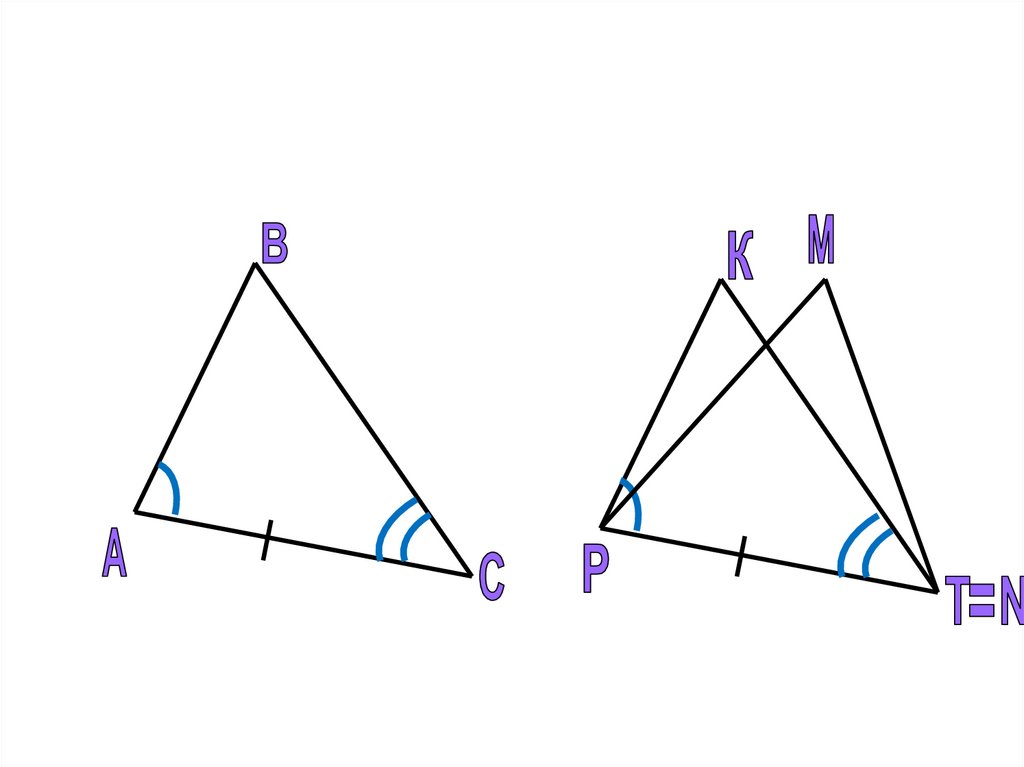
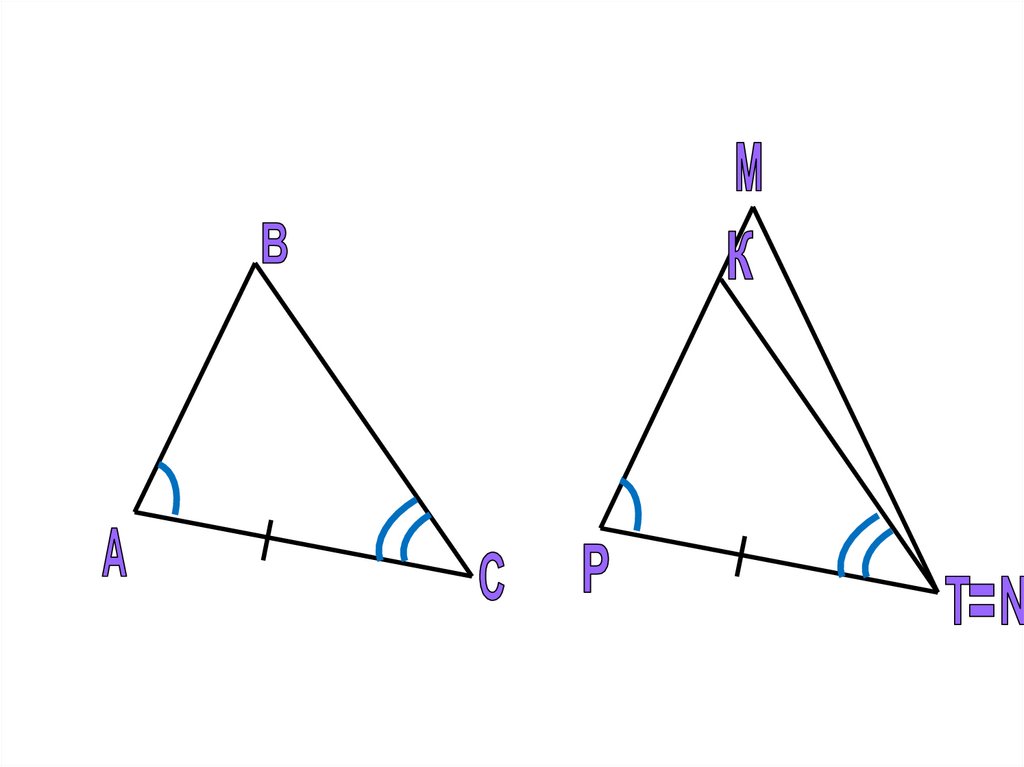
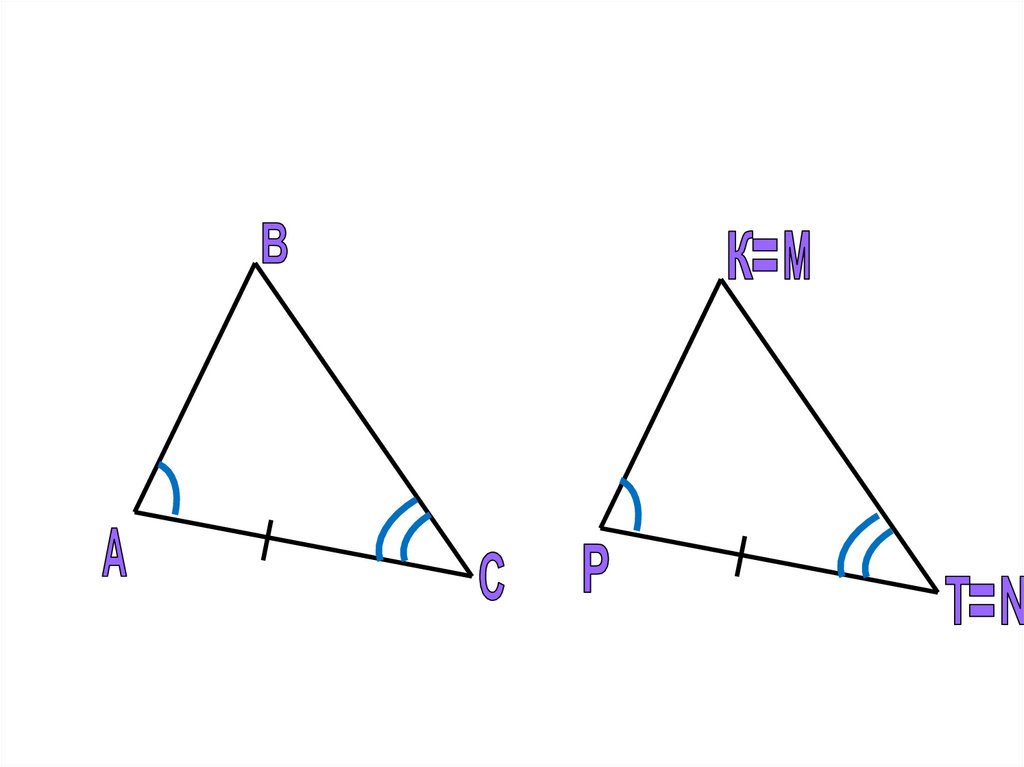
А
В
С
Q
P
R
А =
P
АВ = PQ
В =
Q
ВС = QR
С =
R
АС =
PR

5.

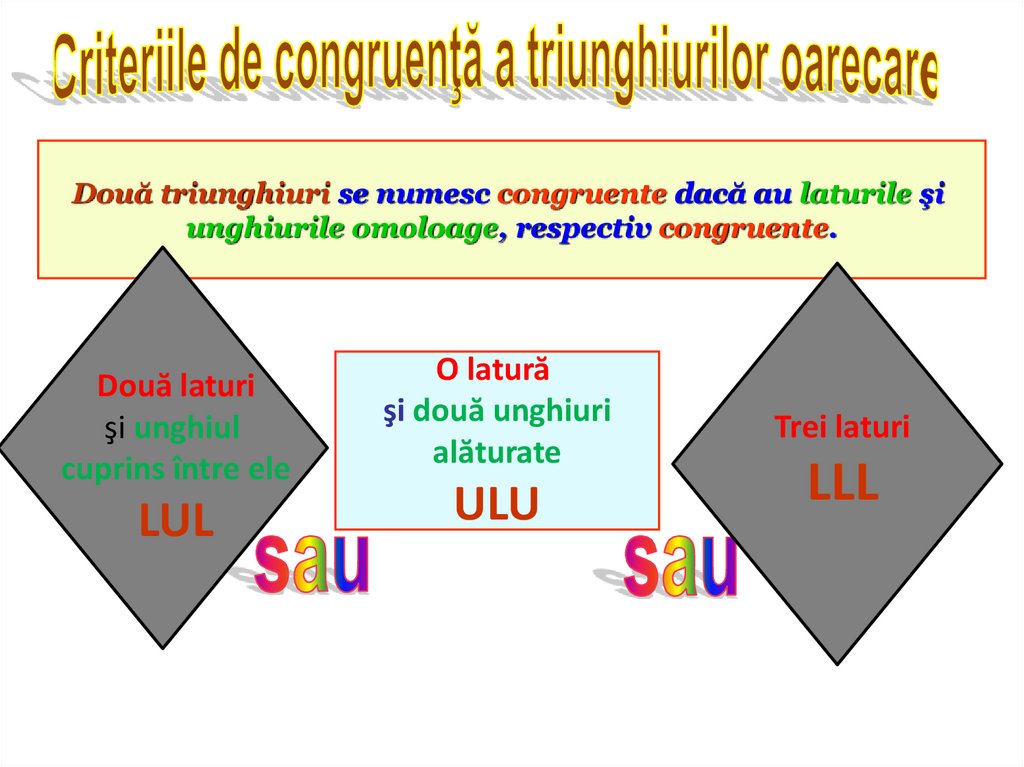
Două triunghiuri se numesc congruente dacă au laturile şi
unghiurile omoloage, respectiv congruente.
Două laturi
şi unghiul
cuprins între ele
LUL
O latură
şi două unghiuri
alăturate
ULU
Trei laturi
LLL

6.

7.

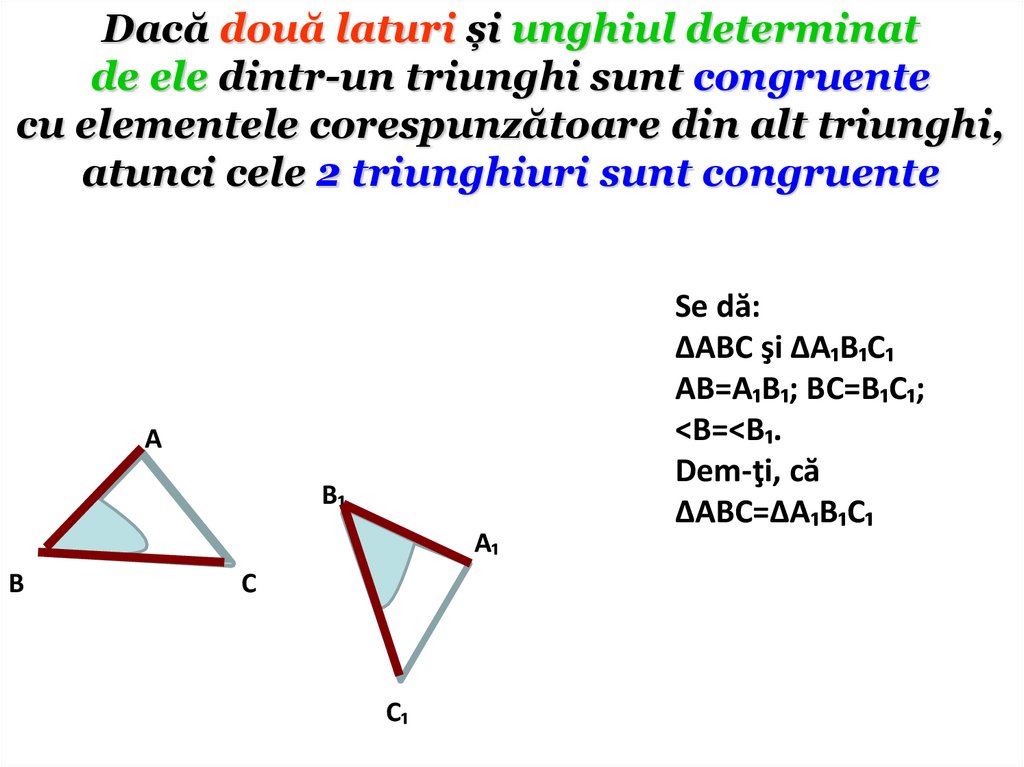
Dacă două laturi și unghiul determinat
de ele dintr-un triunghi sunt congruente
cu elementele corespunzătoare din alt triunghi,
atunci cele 2 triunghiuri sunt congruente
А
В₁
А₁
В
С
С₁
Se dă:
∆АВС şi ∆А₁В₁С₁
АВ=А₁В₁; ВС=В₁С₁;
<В=<В₁.
Dem-ţi, că
∆АВС=∆А₁В₁С₁

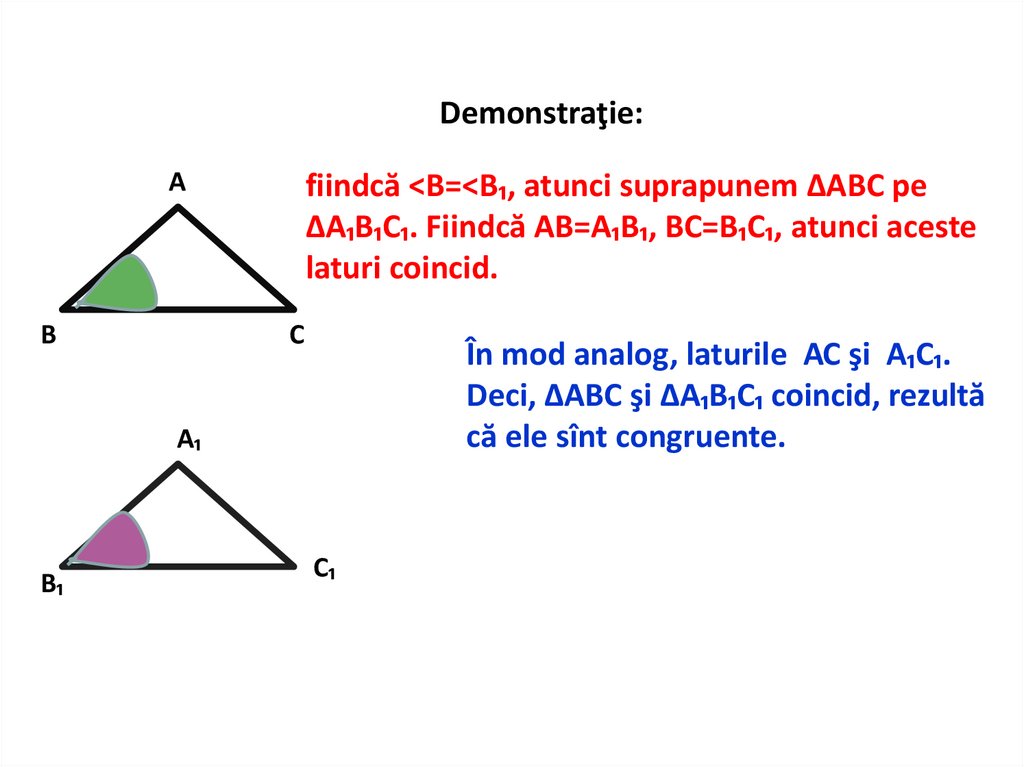
8.

Demonstraţie:
А
В
fiindcă <В=<В₁, atunci suprapunem ∆АВС pe
∆А₁В₁С₁. Fiindcă АВ=А₁В₁, ВС=В₁С₁, atunci aceste
laturi coincid.
С
În mod analog, laturile АС şi А₁С₁.
Deci, ∆АВС şi ∆А₁В₁С₁ coincid, rezultă
că ele sînt congruente.
А₁
В₁
С₁

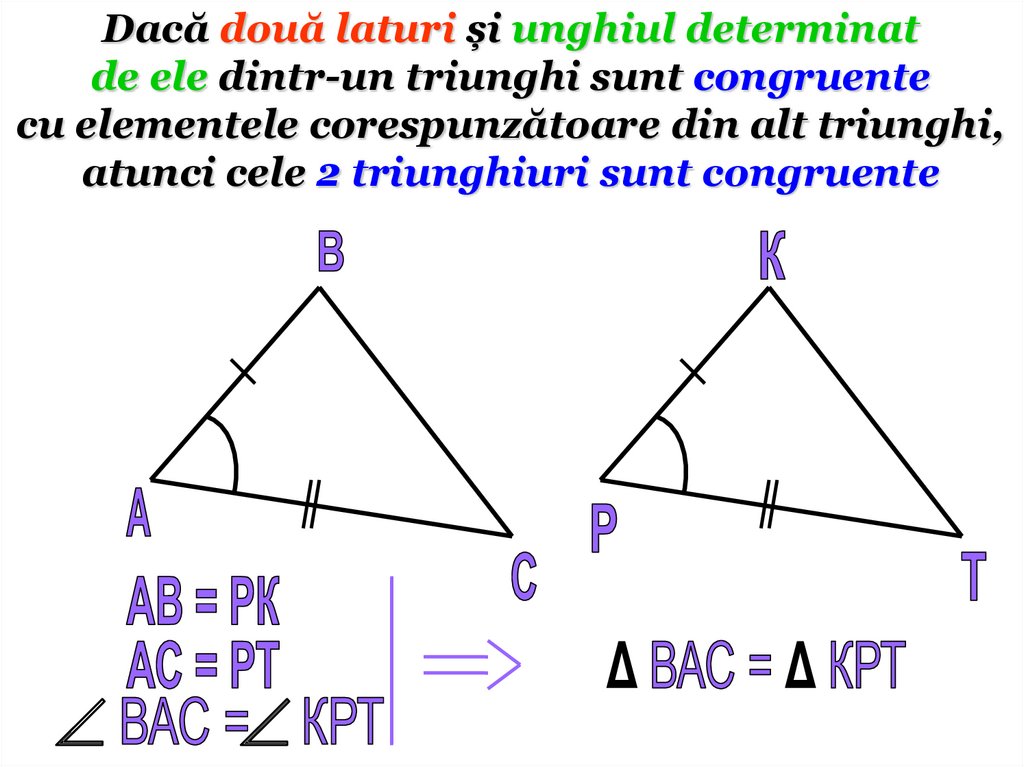
9.

Dacă două laturi și unghiul determinat
de ele dintr-un triunghi sunt congruente
cu elementele corespunzătoare din alt triunghi,
atunci cele 2 triunghiuri sunt congruente

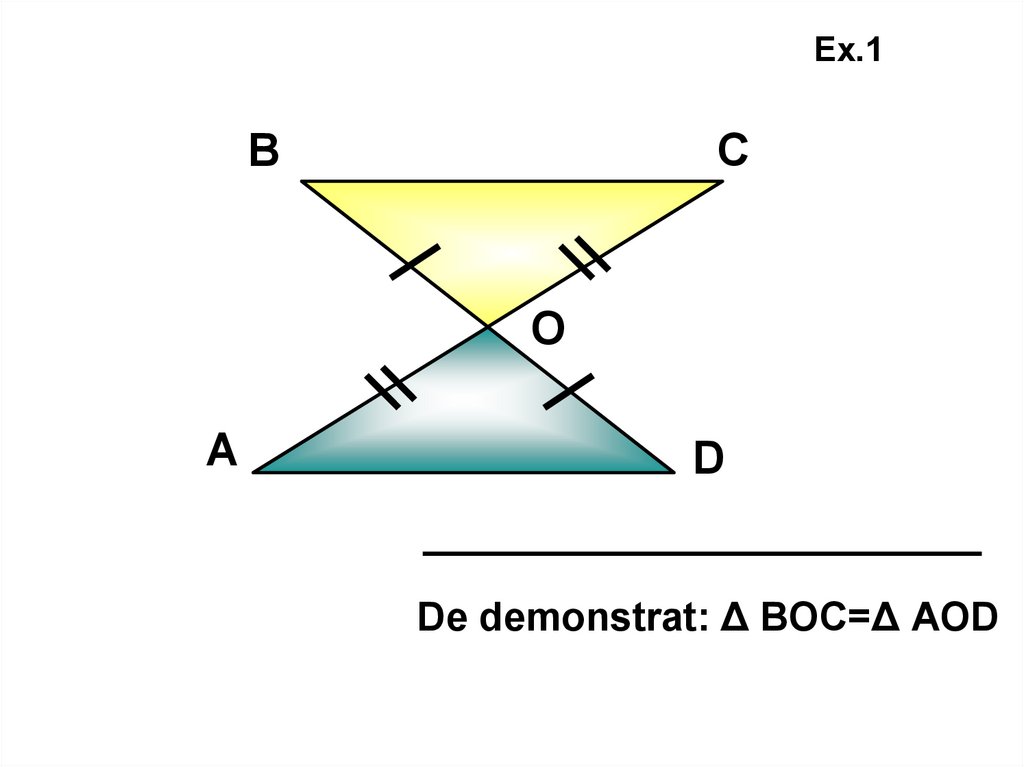
10.

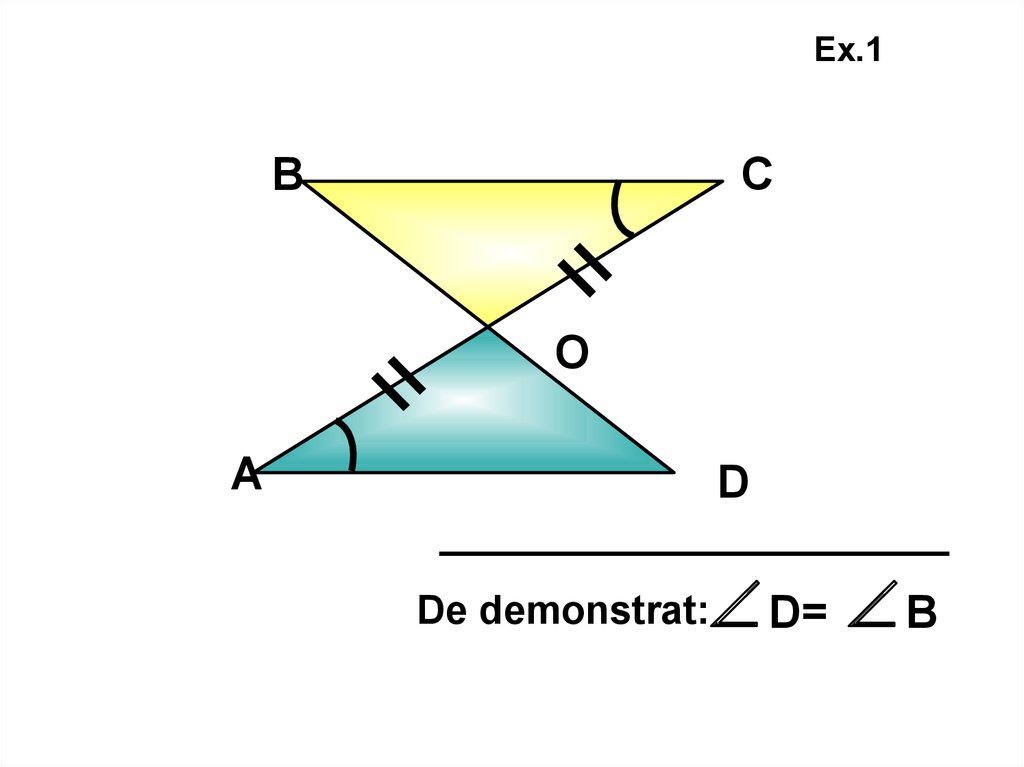
Ex.1
В
С
О
А
D
De demonstrat: Δ ВОС=Δ АОD

11.

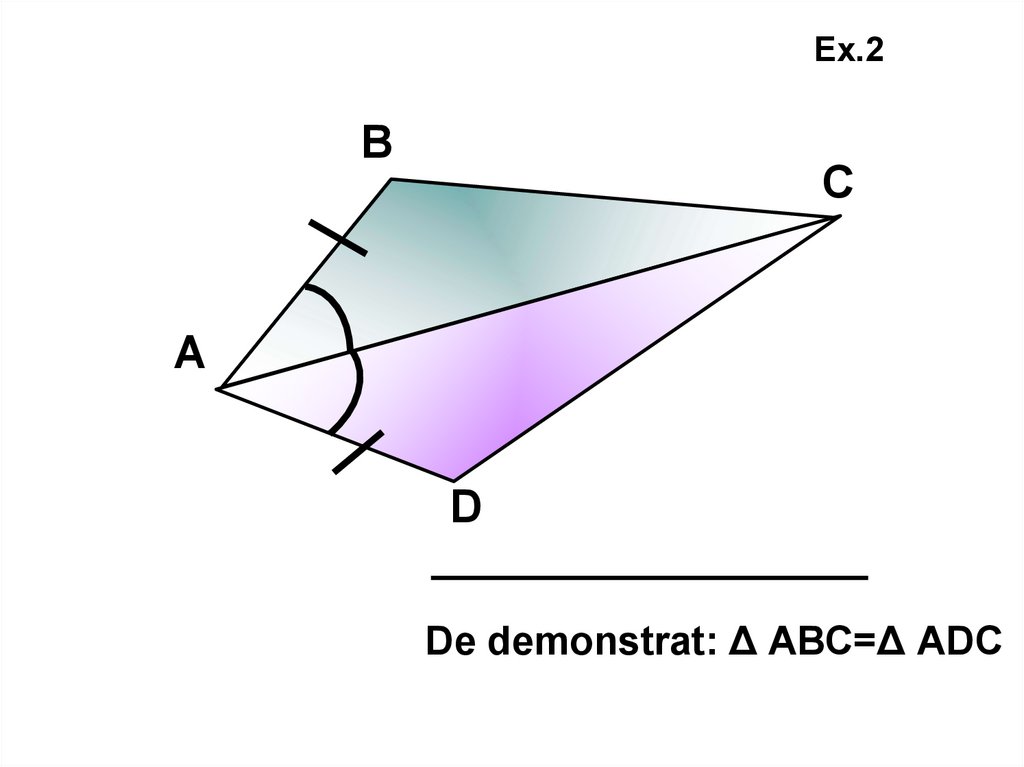
Ex.2
В
С
А
D
De demonstrat: Δ АВС=Δ АDС

12.

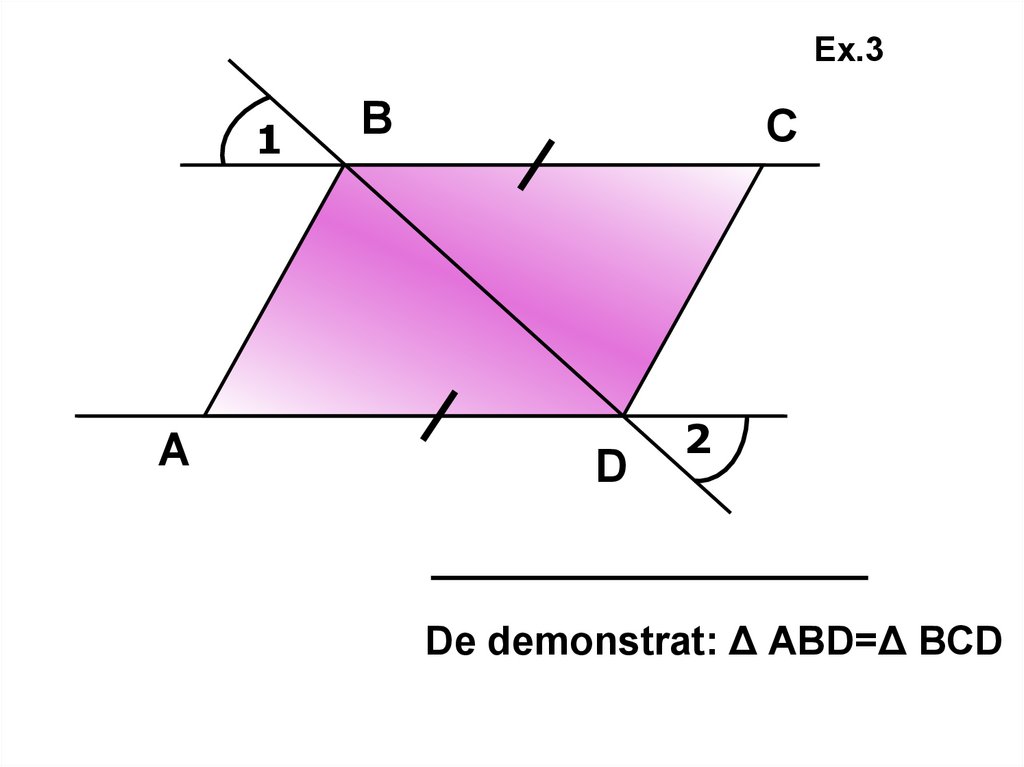
Ex.3
1
А
В
С
D
2
De demonstrat: Δ АВD=Δ ВСD

13.

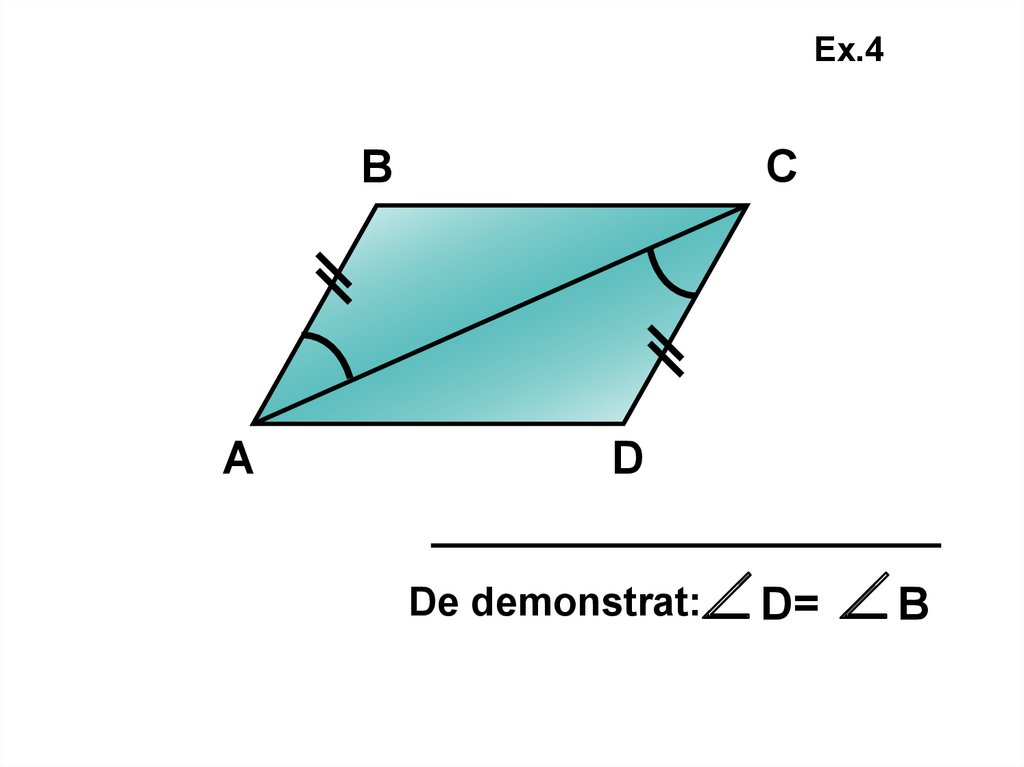
Ex.4
В
А
С
D
D= В
De demonstrat:

14.

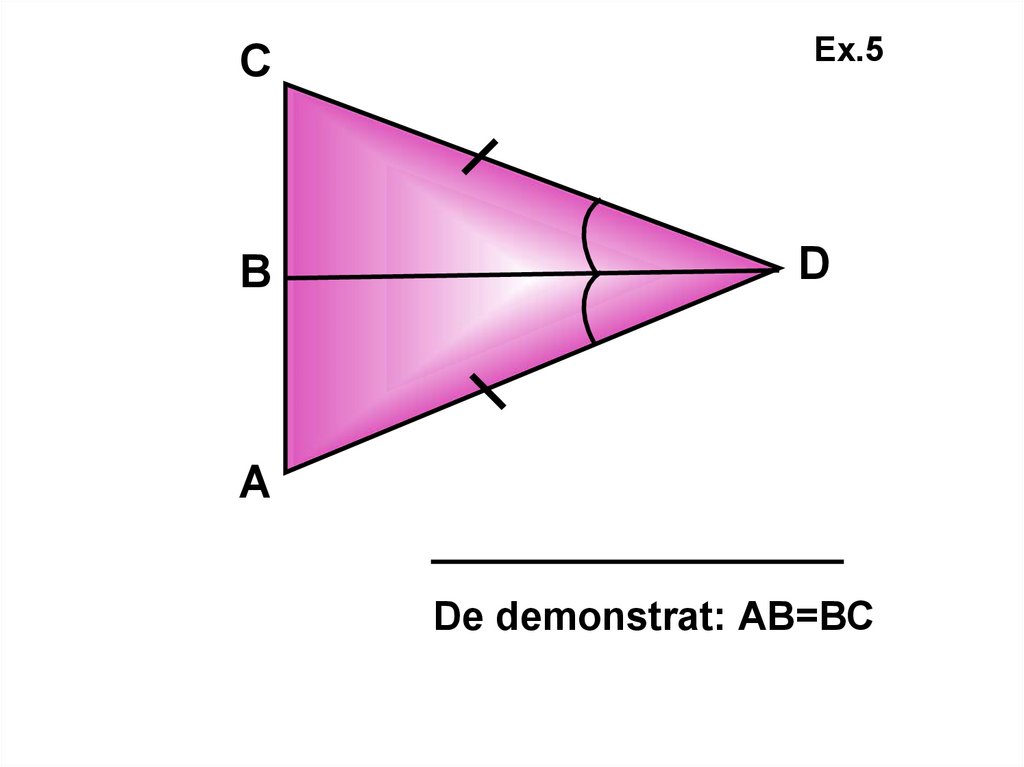
C
В
Ex.5
D
А
De demonstrat: АВ=ВС

15.

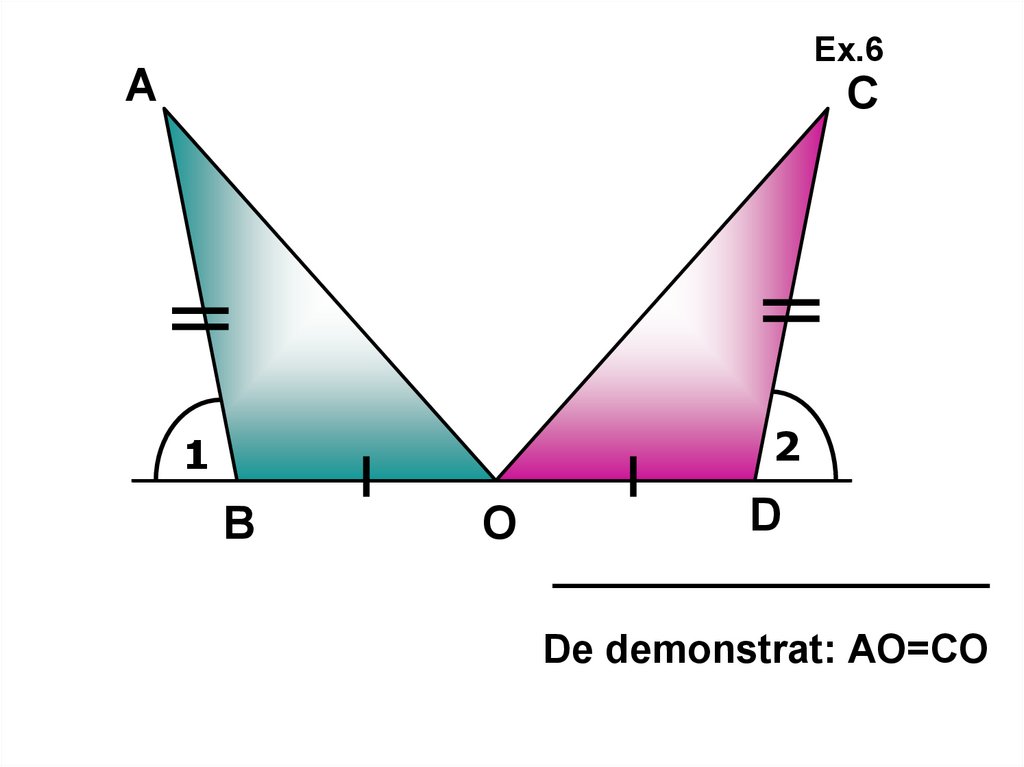
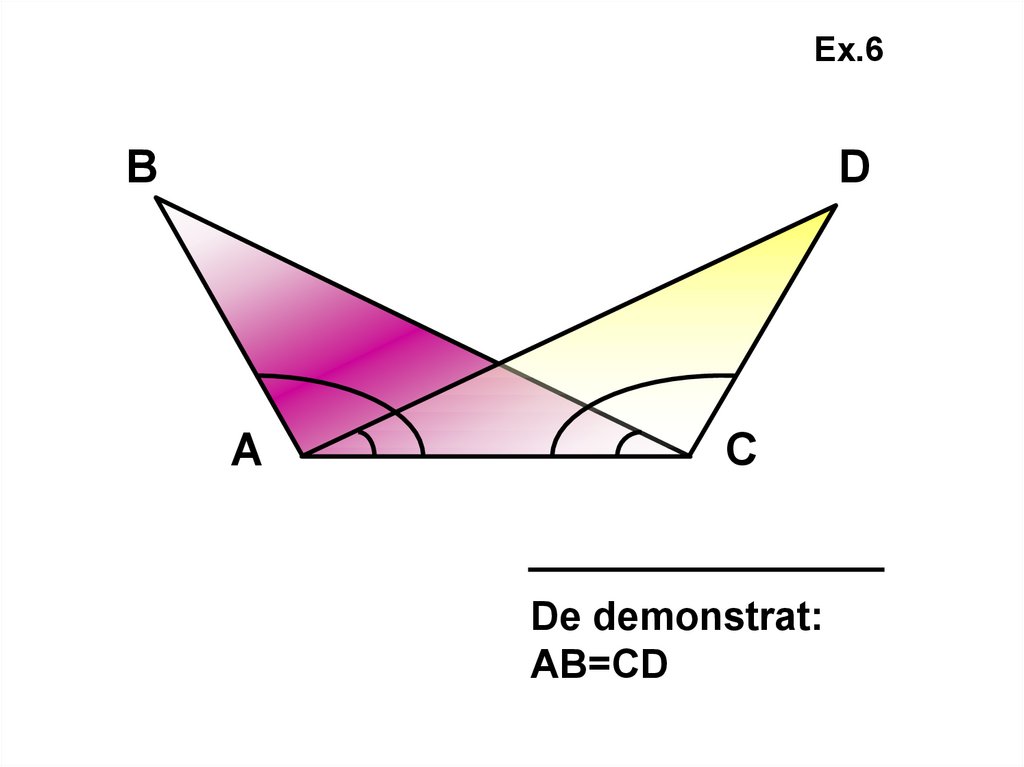
Ex.6
А
С
2
1
В
О
D
De demonstrat: АО=СО

16.

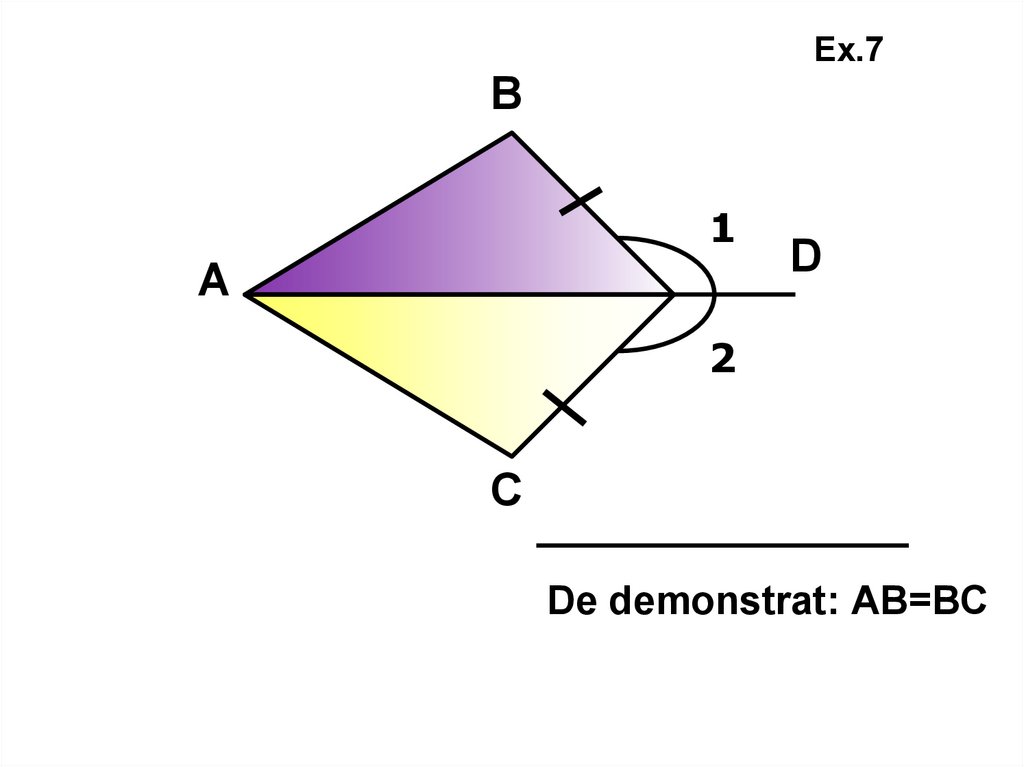
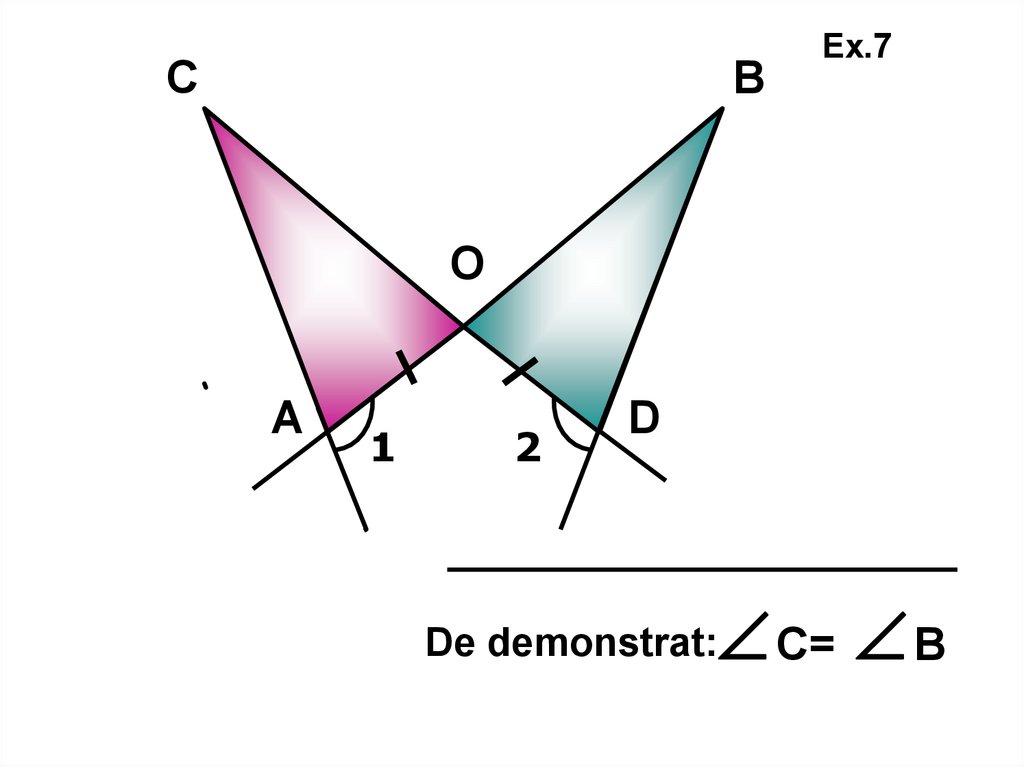
Ex.7
В
1
А
D
2
С
De demonstrat: АВ=ВС

17.

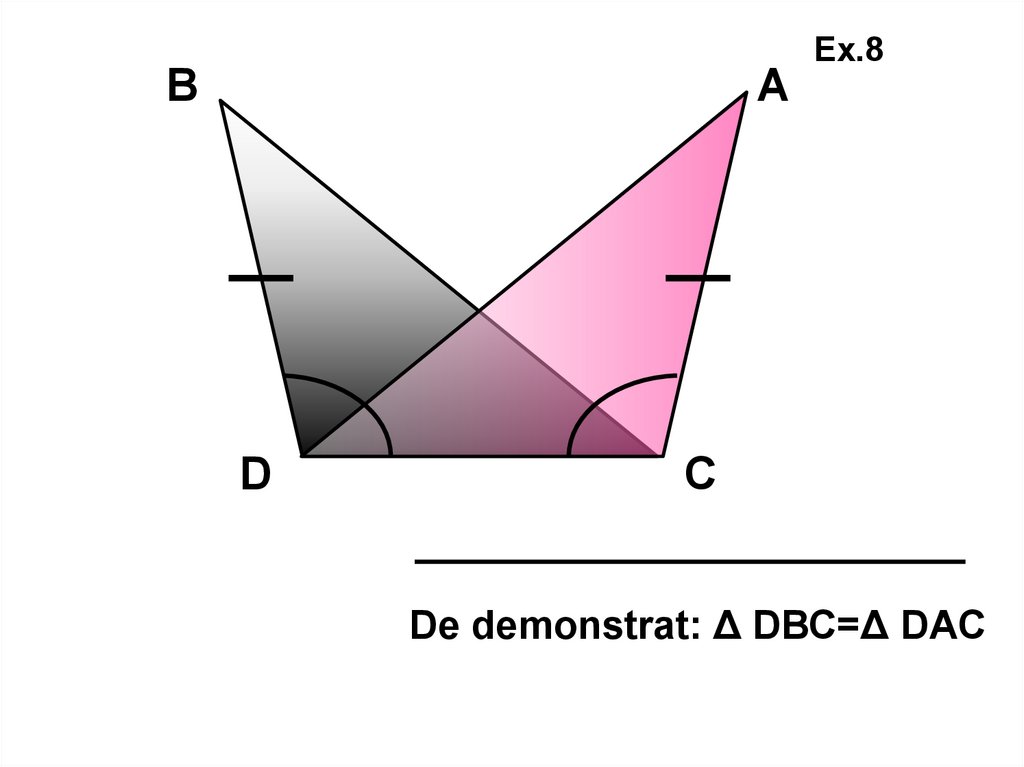
В
А
D
Ex.8
С
De demonstrat: Δ DВС=Δ DАС

18.

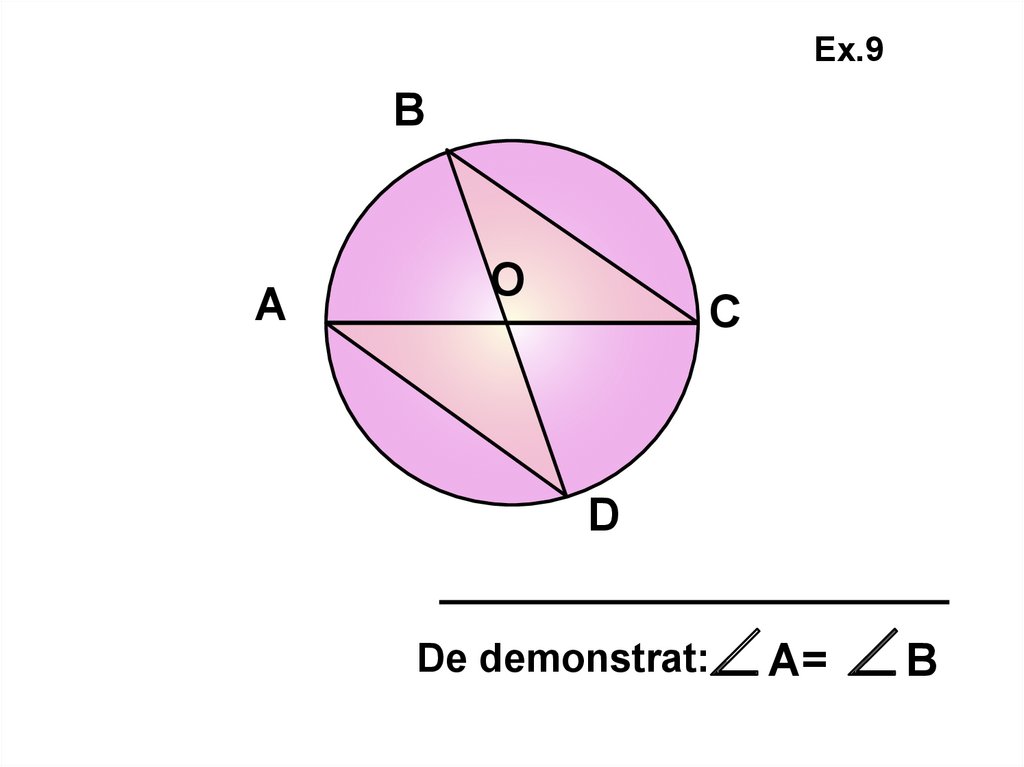
Ex.9
В
А
О
C
D
А= В
De demonstrat:

19.

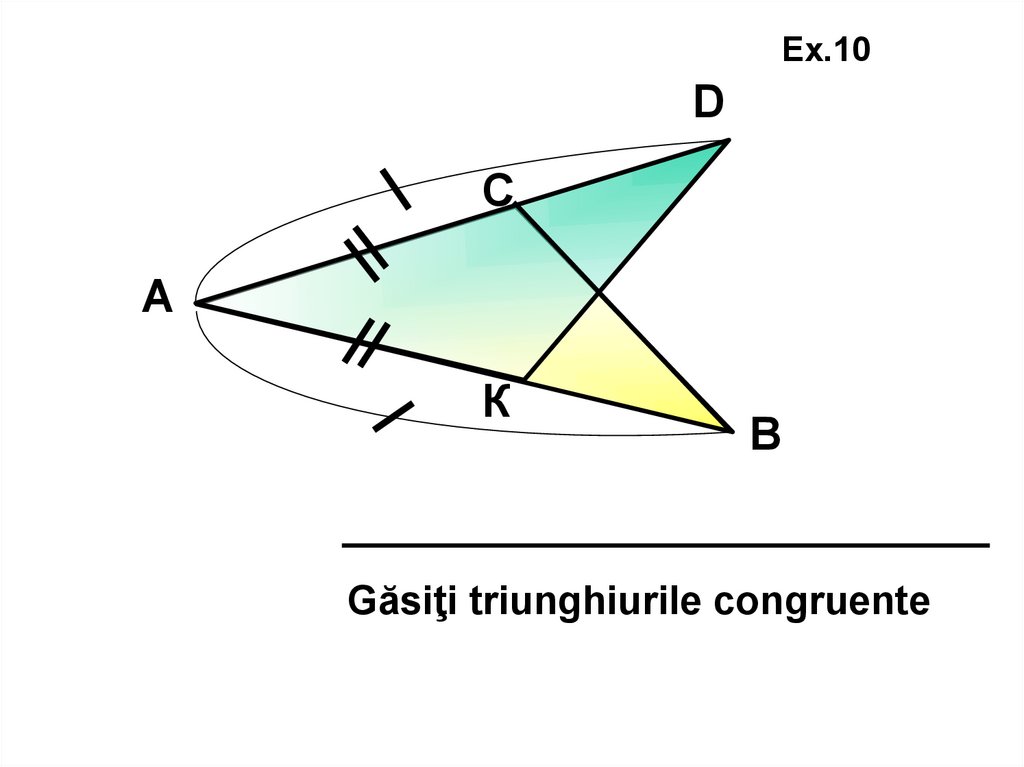
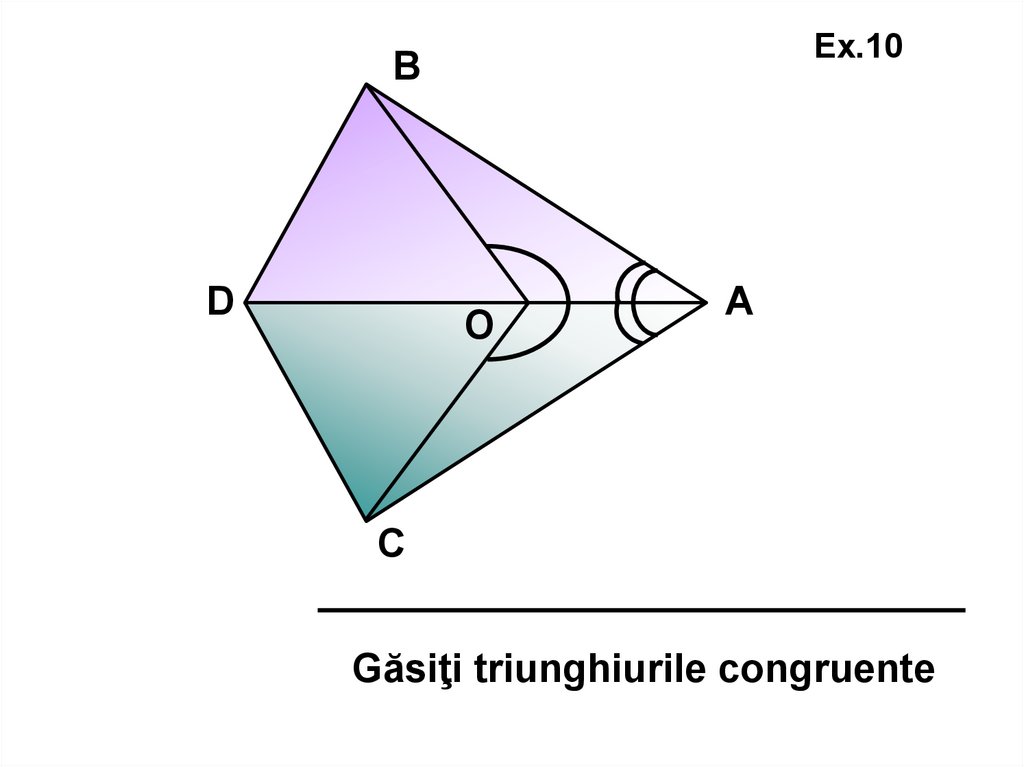
Ex.10
D
С
А
К
В
Găsiţi triunghiurile congruente

20.

21.

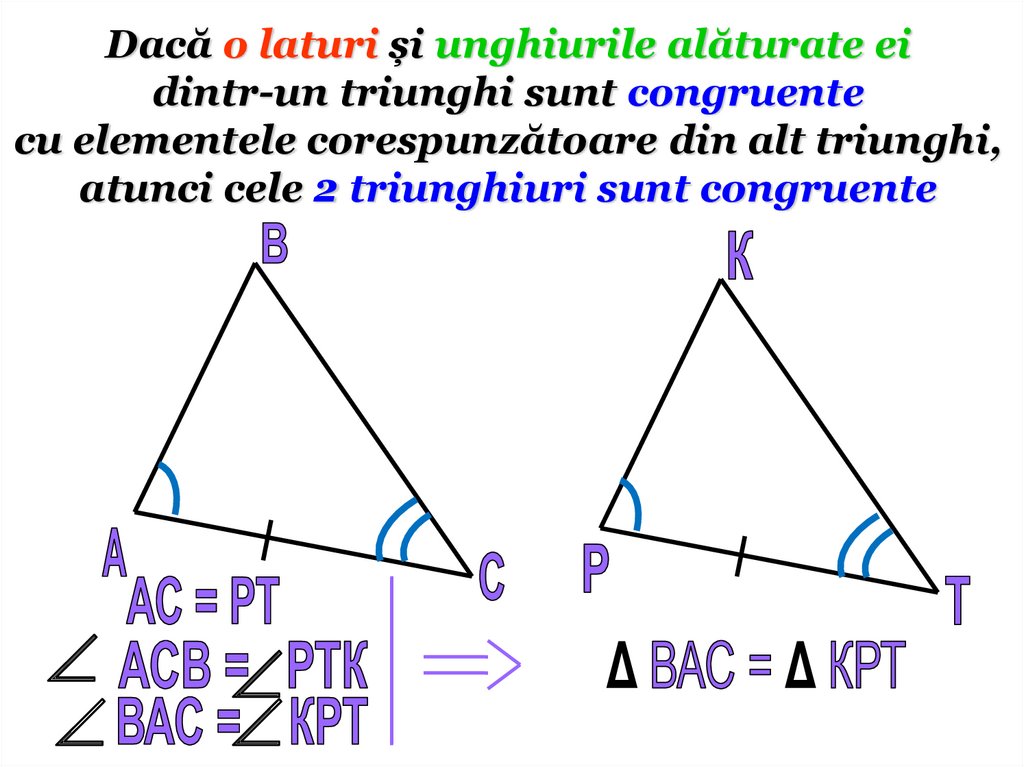
Dacă o laturi și unghiurile alăturate ei
dintr-un triunghi sunt congruente
cu elementele corespunzătoare din alt triunghi,
atunci cele 2 triunghiuri sunt congruente

22.

23.

24.

25.

26.

27.

Ex.1
В
С
О
А
D
D= В
De demonstrat:

28.

В
О
А
Ex.2
С
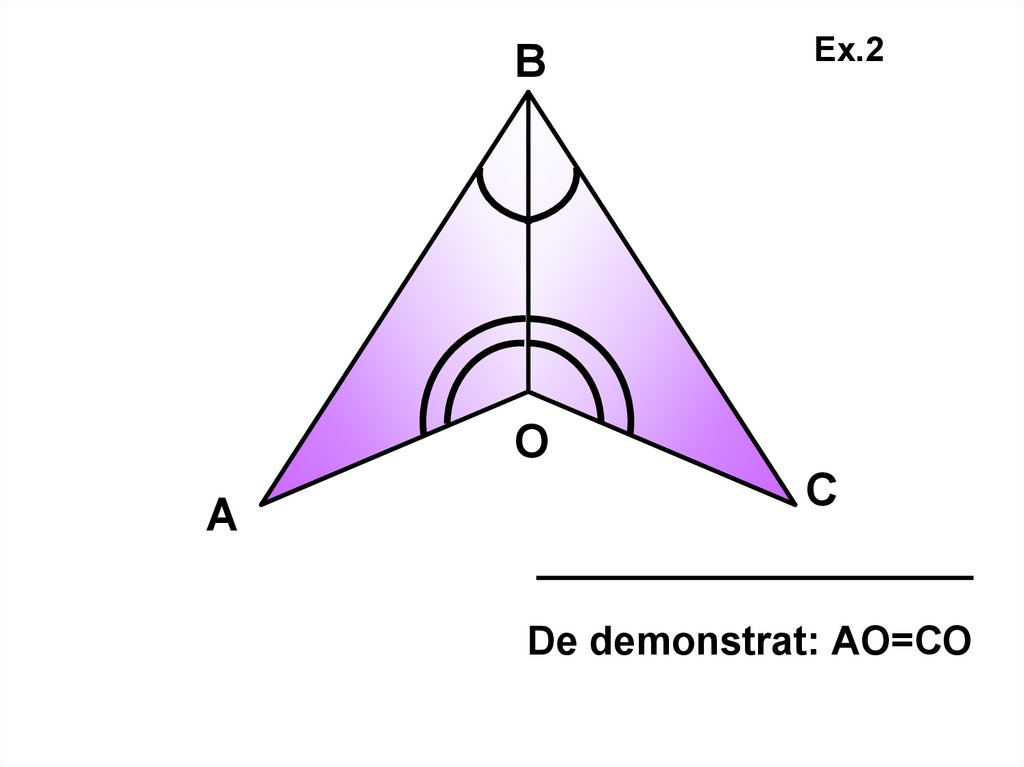
De demonstrat: АО=СО

29.

Ex.3
В
А
С
D
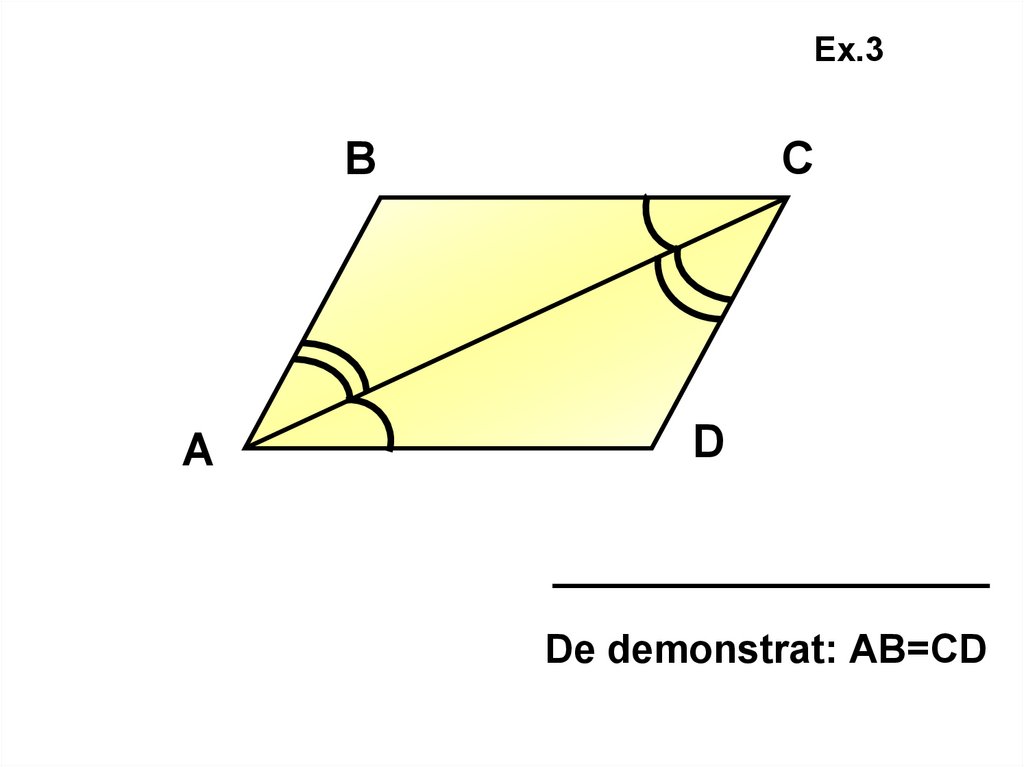
De demonstrat: АВ=СD

30.

Ex.4
В
С
А
D
К
Р
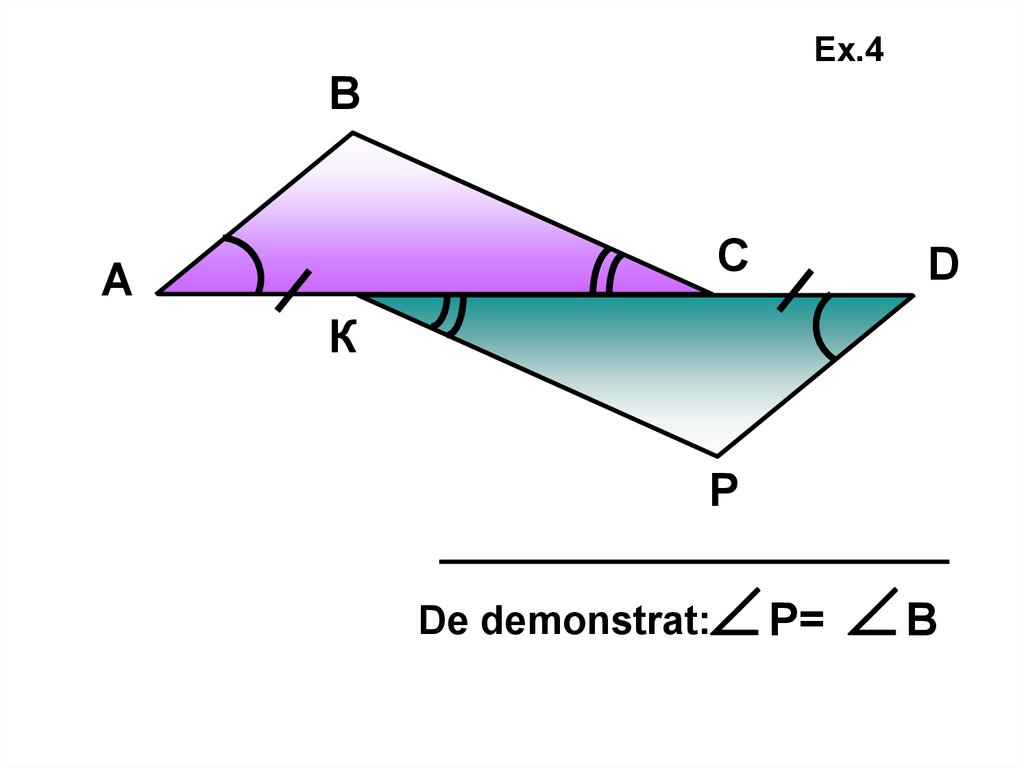
Р= В
De demonstrat:

31.

Ex.5
А
D
В
С
К
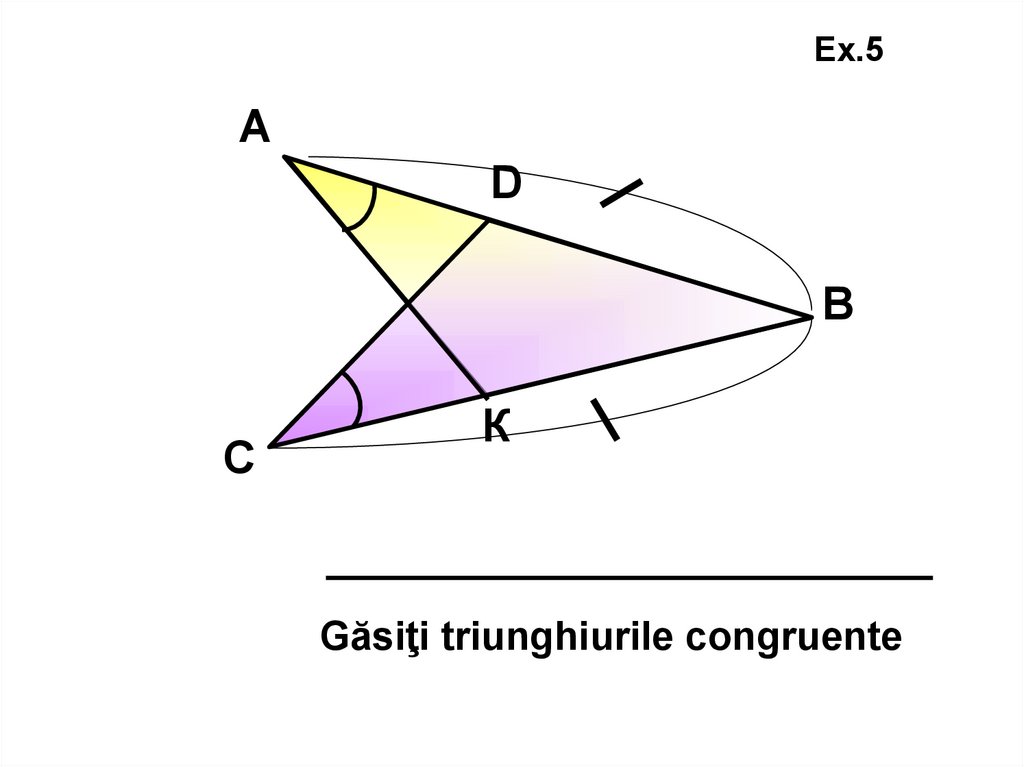
Găsiţi triunghiurile congruente

32.

Ex.6
В
D
А
С
De demonstrat:
АВ=СD

33.

С
В
Ex.7
О
А
1
2
D
С= В
De demonstrat:

34.

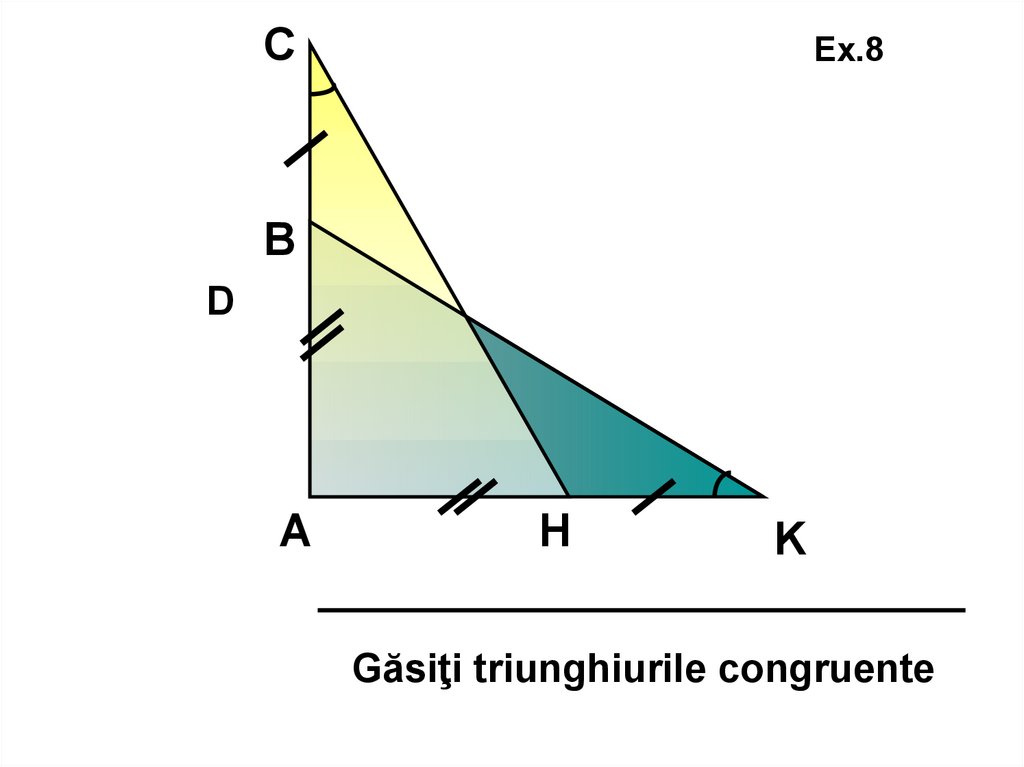
С
Ex.8
В
D
А
H
K
Găsiţi triunghiurile congruente

35.

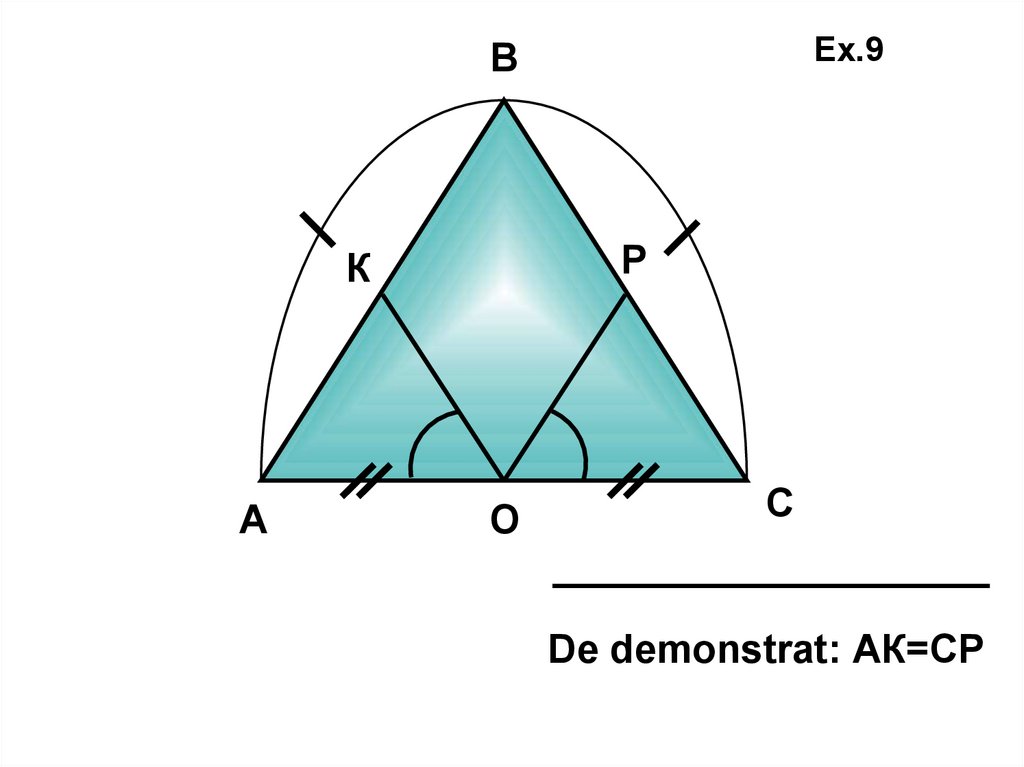
В
Р
К
А
Ex.9
О
С
De demonstrat: АК=СР

36.

Ex.10
В
D
О
А
С
Găsiţi triunghiurile congruente

37.

В
D
Ex.11
С
О
А
Găsiţi triunghiurile congruente

38.

39.

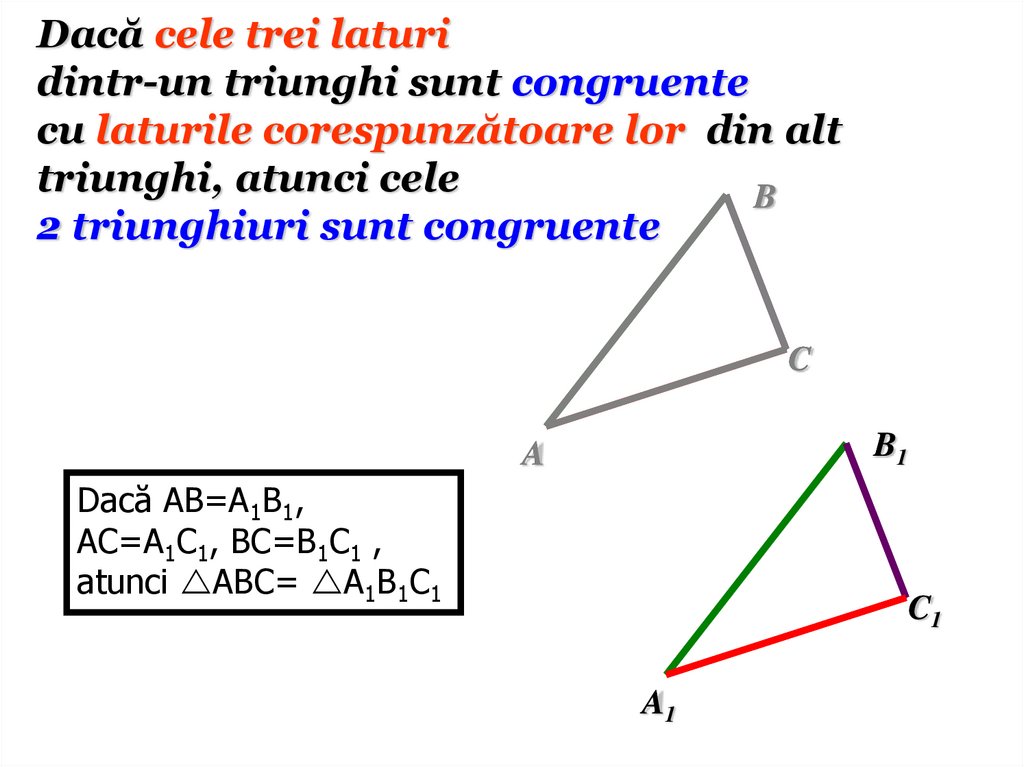
Dacă cele trei laturi
dintr-un triunghi sunt congruente
cu laturile corespunzătoare lor din alt
triunghi, atunci cele
B
2 triunghiuri sunt congruente
C
B1
A
Dacă AB=A1B1,
AC=A1C1, BC=B1C1 ,
atunci ABC= A1B1C1
C1
A1

40.

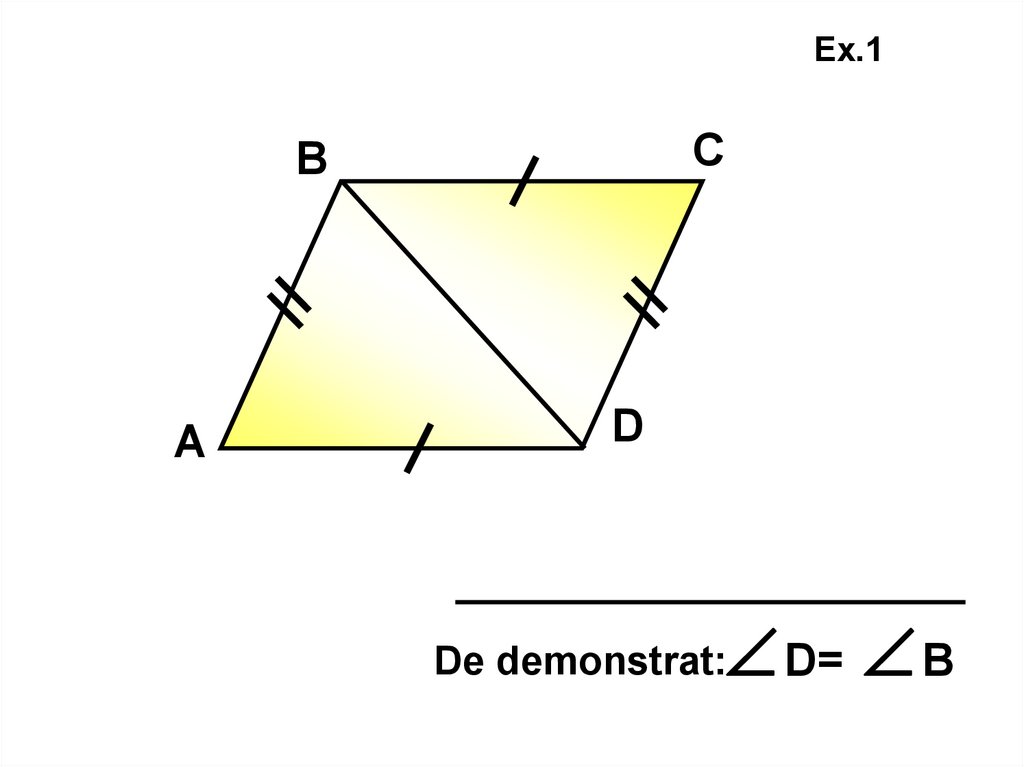
Ex.1
С
В
А
D
D= В
De demonstrat:

41.

В
А
D
Ex.2
С
De demonstrat: Δ АВD=Δ ВСD

42.

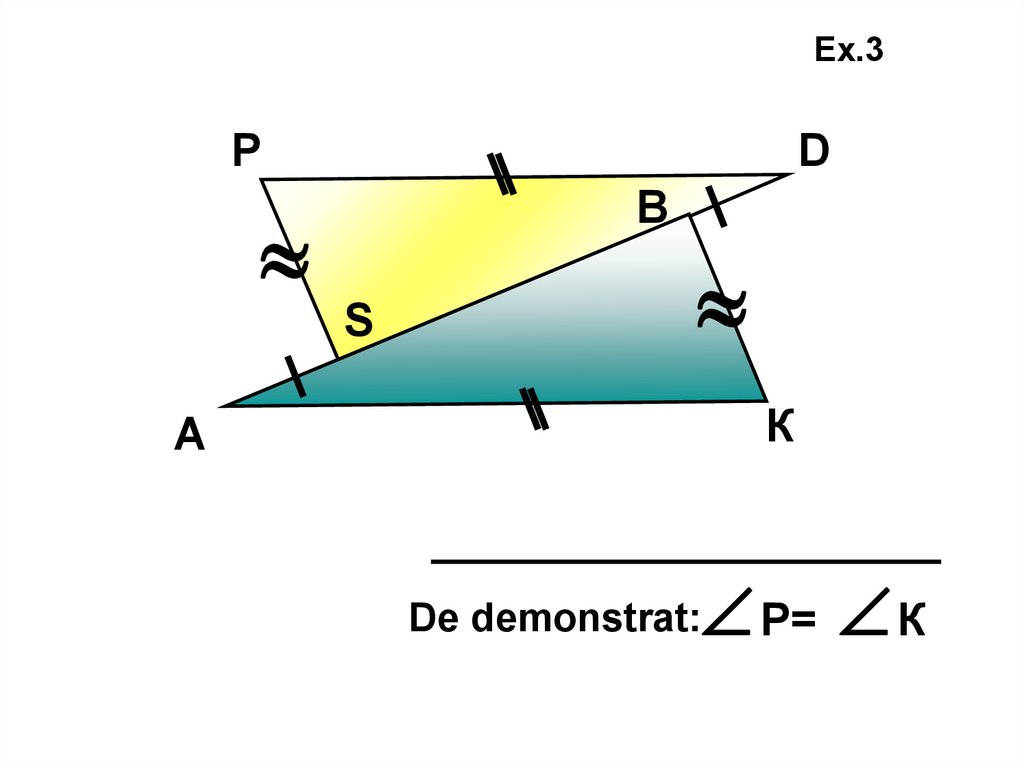
Ex.3
Р
D
В
S
К
А
Р= К
De demonstrat:

43.

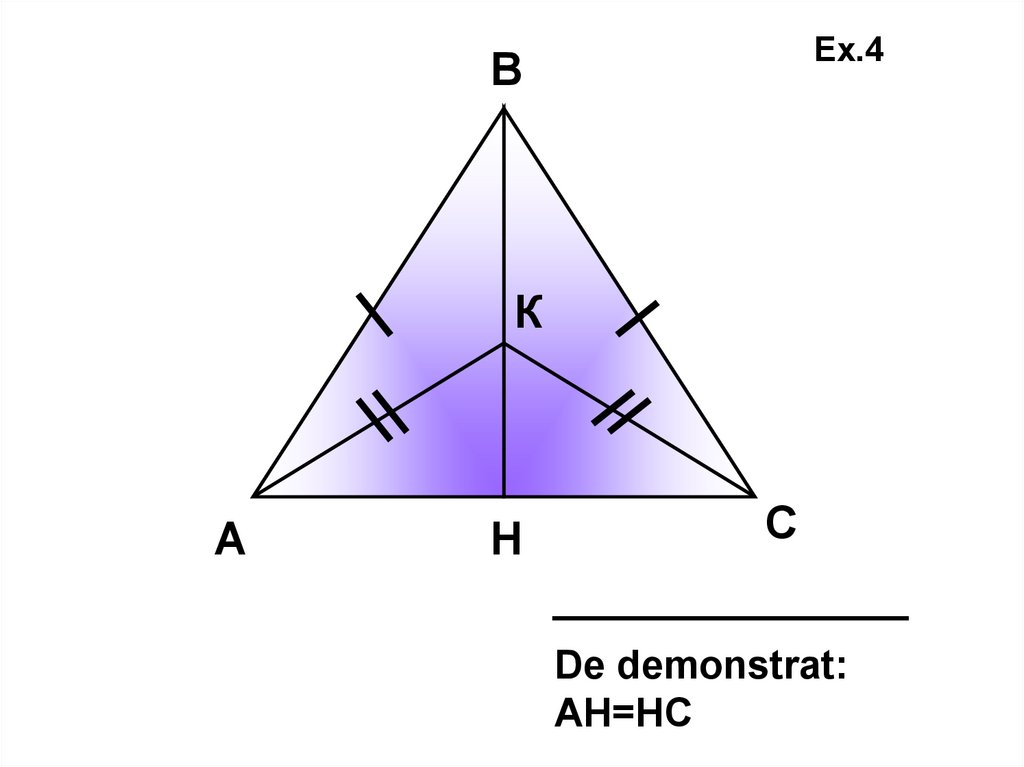
Ex.4
В
К
А
Н
С
De demonstrat:
АН=НС

44.

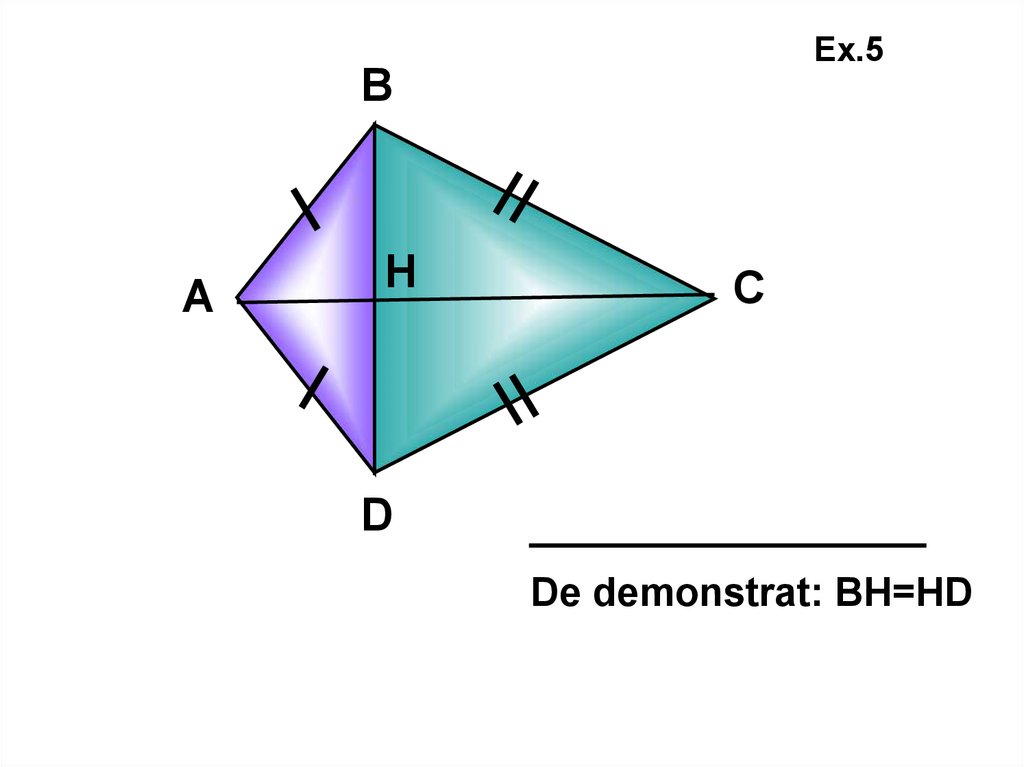
Ex.5
В
А
Н
C
D
De demonstrat: ВН=НD

45.

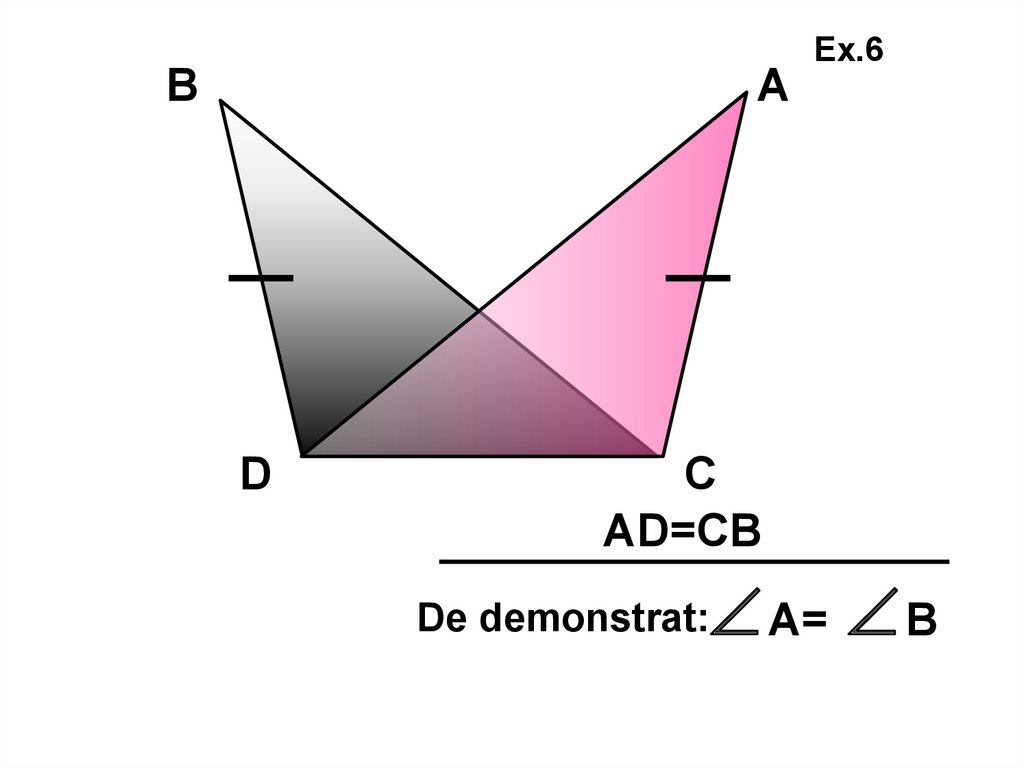
В
А
D
Ex.6
С
АD=СВ
А= В
De demonstrat:

46.

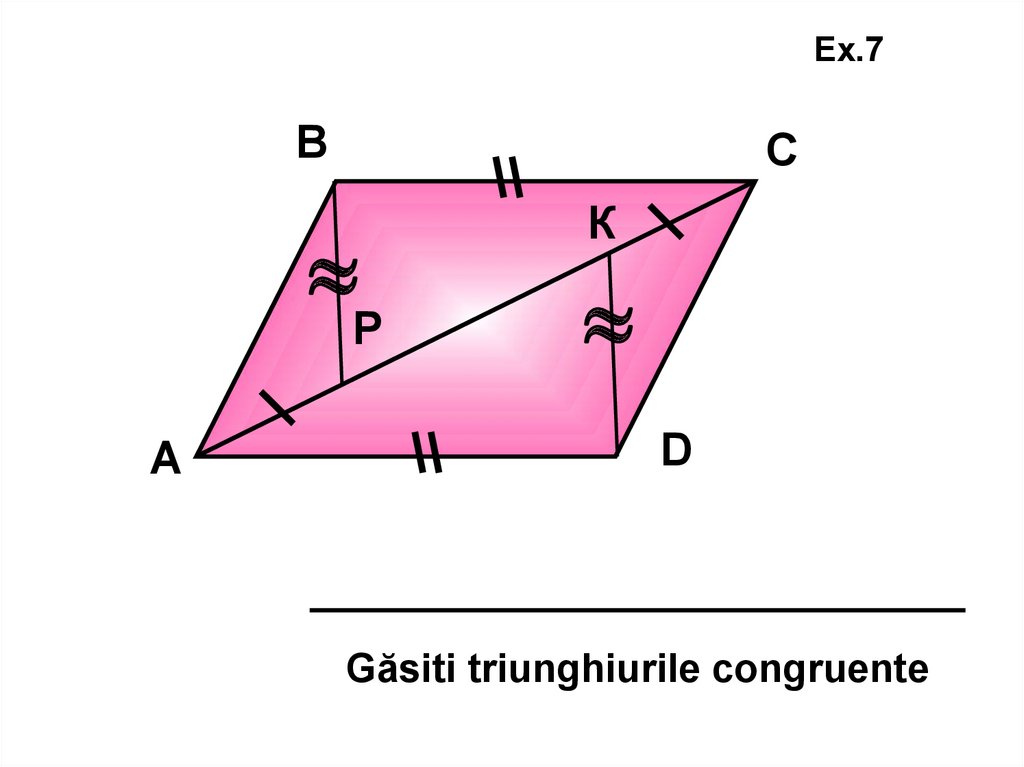
Ex.7
В
С
Р
А
К
D
Găsiti triunghiurile congruente

47.

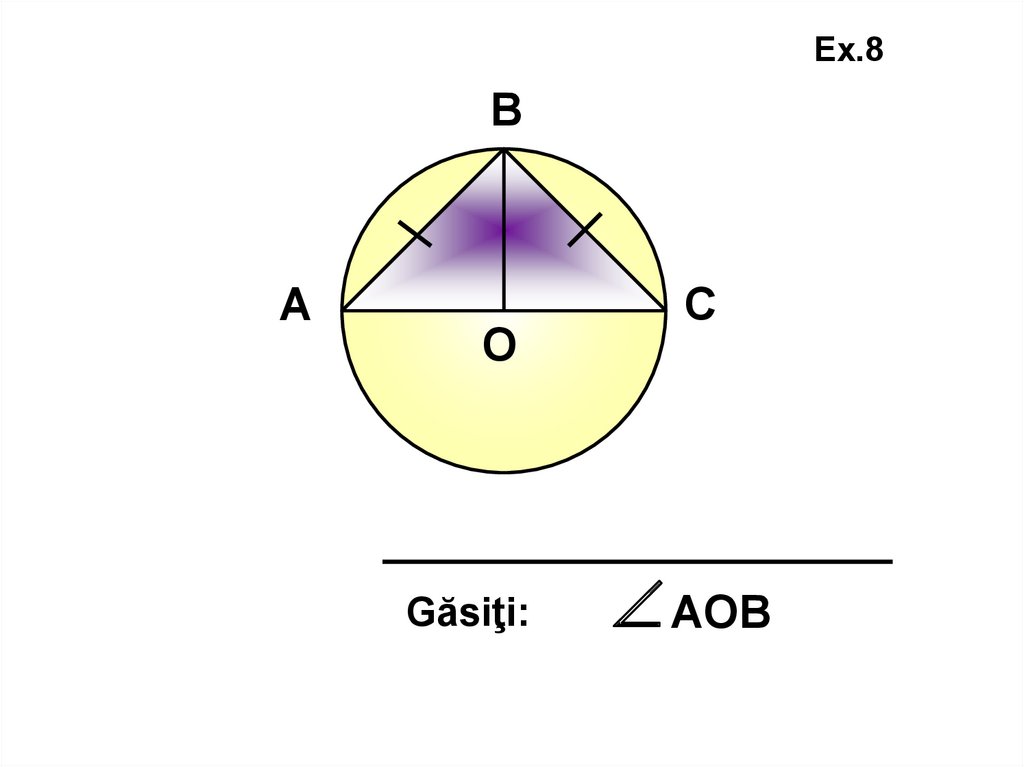
Ex.8
В
А
О
Găsiţi:
С
АОВ

48.

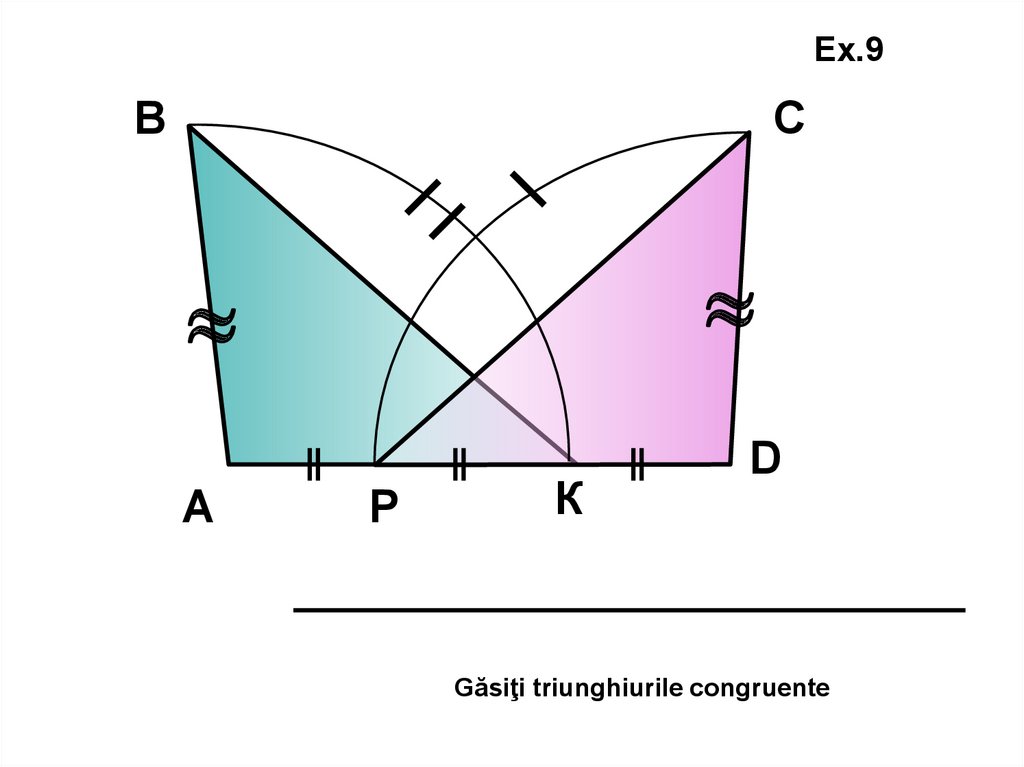
Ex.9
В
С
А
Р
К
D
Găsiţi triunghiurile congruente

49.

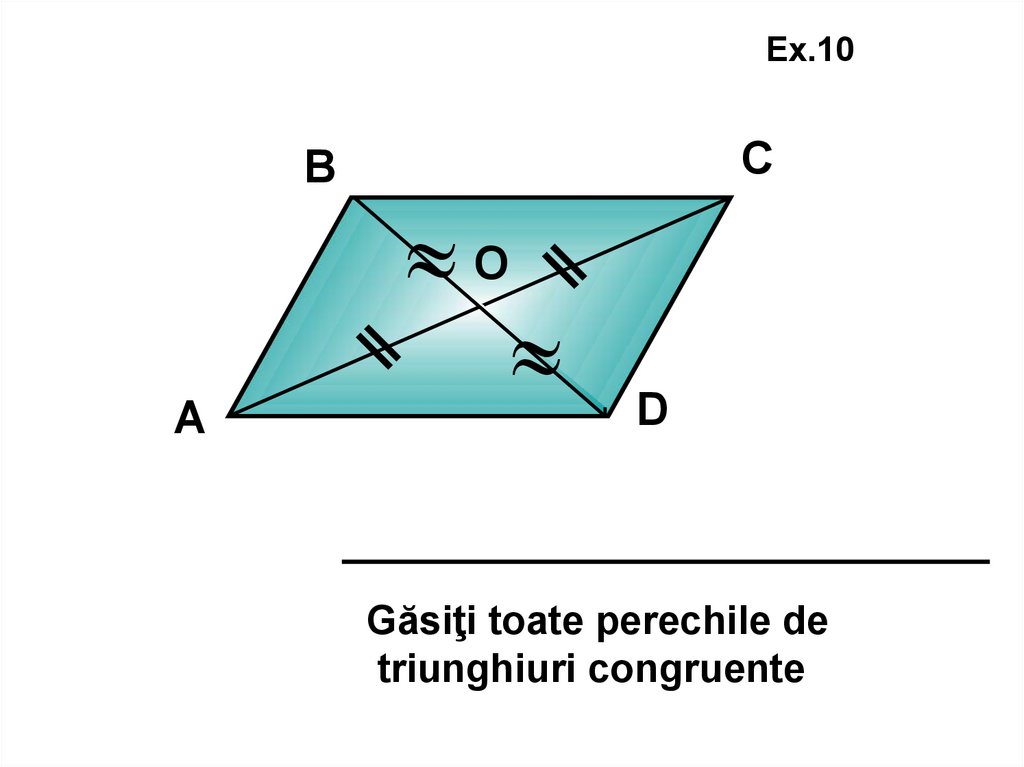
Ex.10
В
А
С
О
D
Găsiţi toate perechile de
triunghiuri congruente