Похожие презентации:
Перпендикулярность прямой и плоскости
1.
Перпендикулярностьпрямой и плоскости
2.
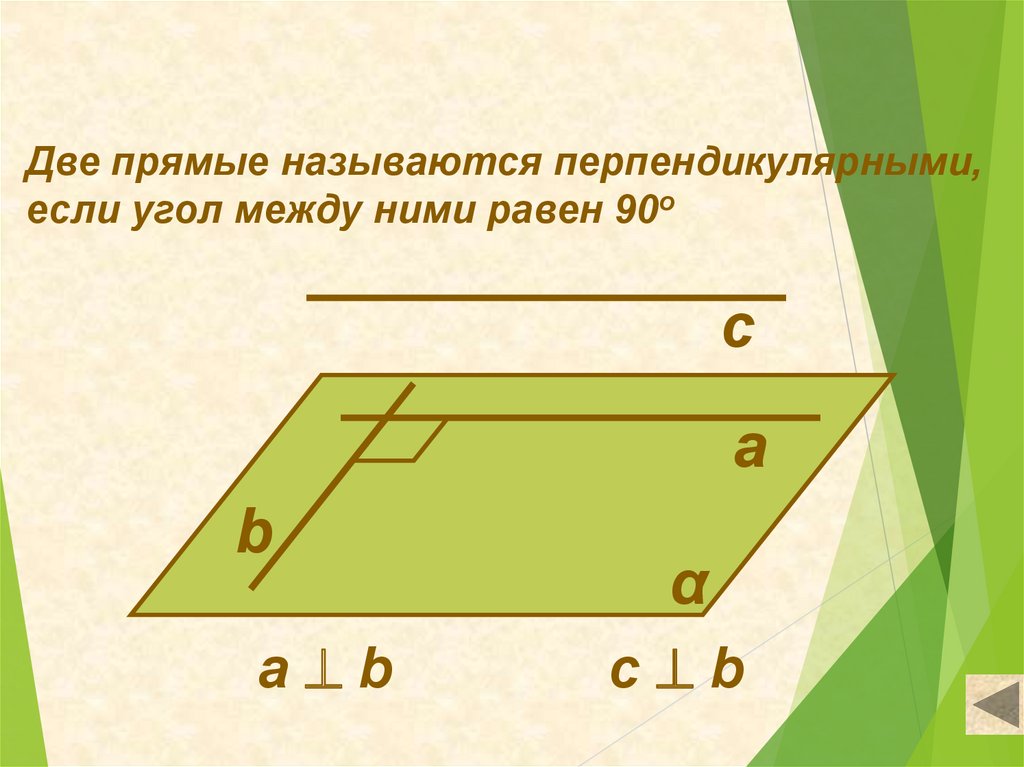
Две прямые называются перпендикулярными,если угол между ними равен 90о
с
а
b
а b
α
c b
3.
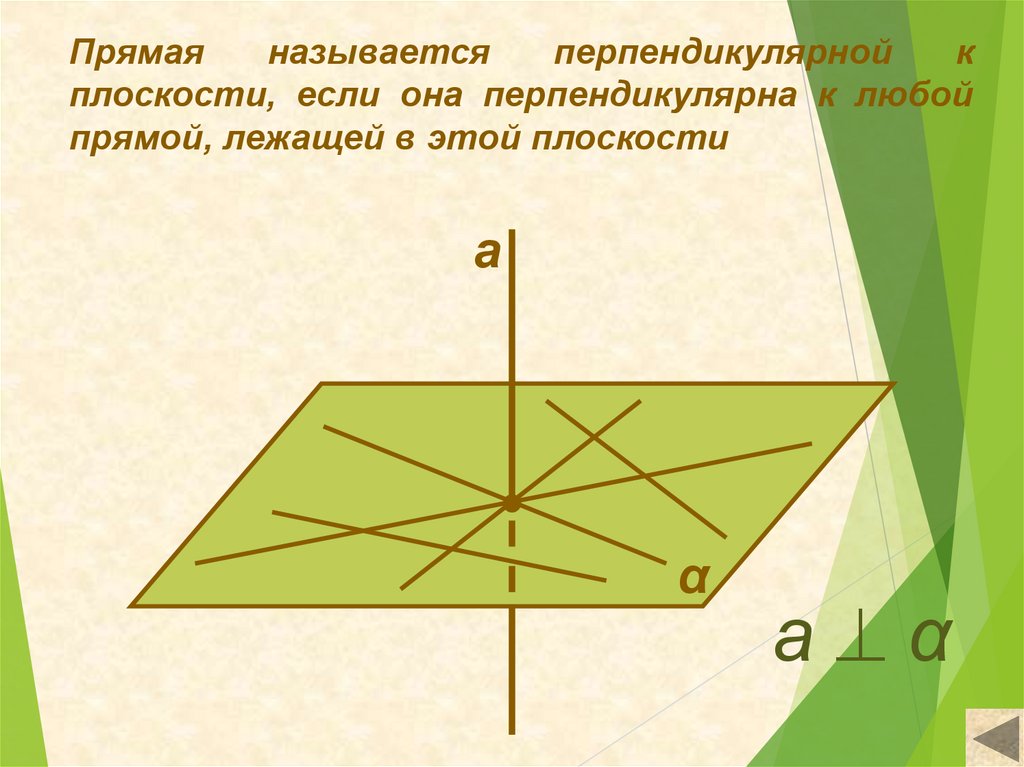
Прямаяназывается
перпендикулярной
к
плоскости, если она перпендикулярна к любой
прямой, лежащей в этой плоскости
а
α
а α
4.
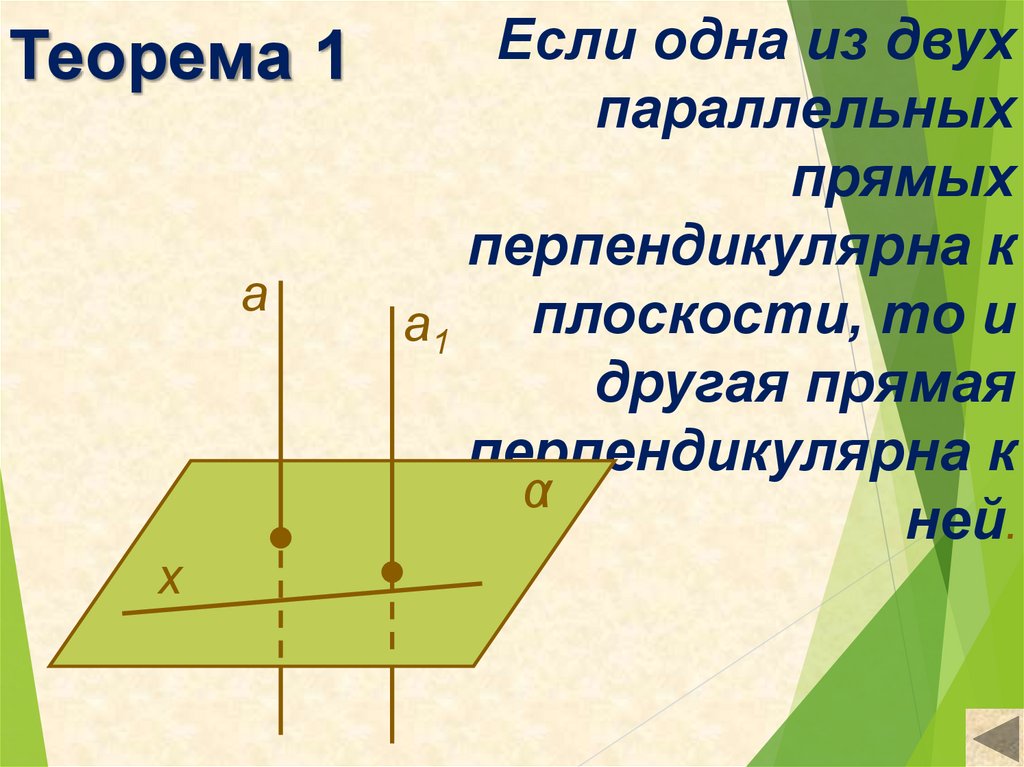
Теорема 1a
х
Если одна из двух
параллельных
прямых
перпендикулярна к
плоскости, то и
а1
другая прямая
перпендикулярна к
α
ней.
5.
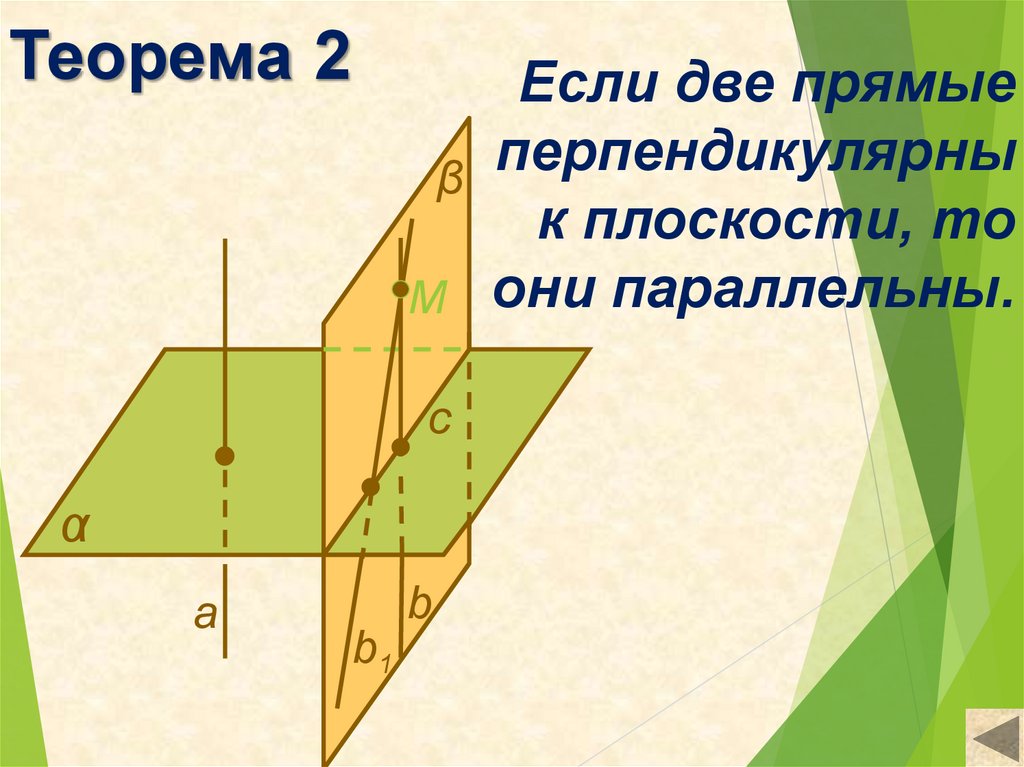
Теорема 2Если две прямые
перпендикулярны
β
к плоскости, то
M они параллельны.
с
α
a
b
b1
6.
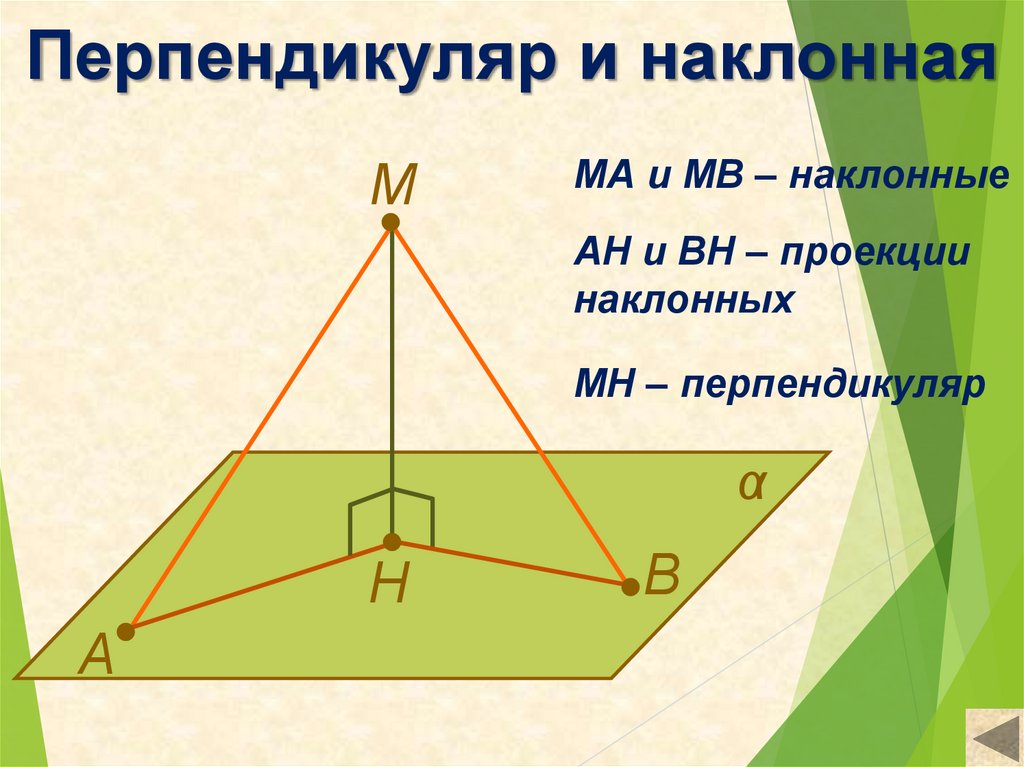
Перпендикуляр и наклоннаяМ
МА и МВ – наклонные
АН и ВН – проекции
наклонных
МН – перпендикуляр
α
Н
А
В
7.
Перпендикуляр, проведенный изданной точки к плоскости, меньше
любой наклонной, проведенной из той
же точки к этой плоскости.
Перпендикуляр- кратчайшее
расстояние от точки до плоскости.
Длина перпендикуляра
называется расстоянием от точки до
плоскости.
8.
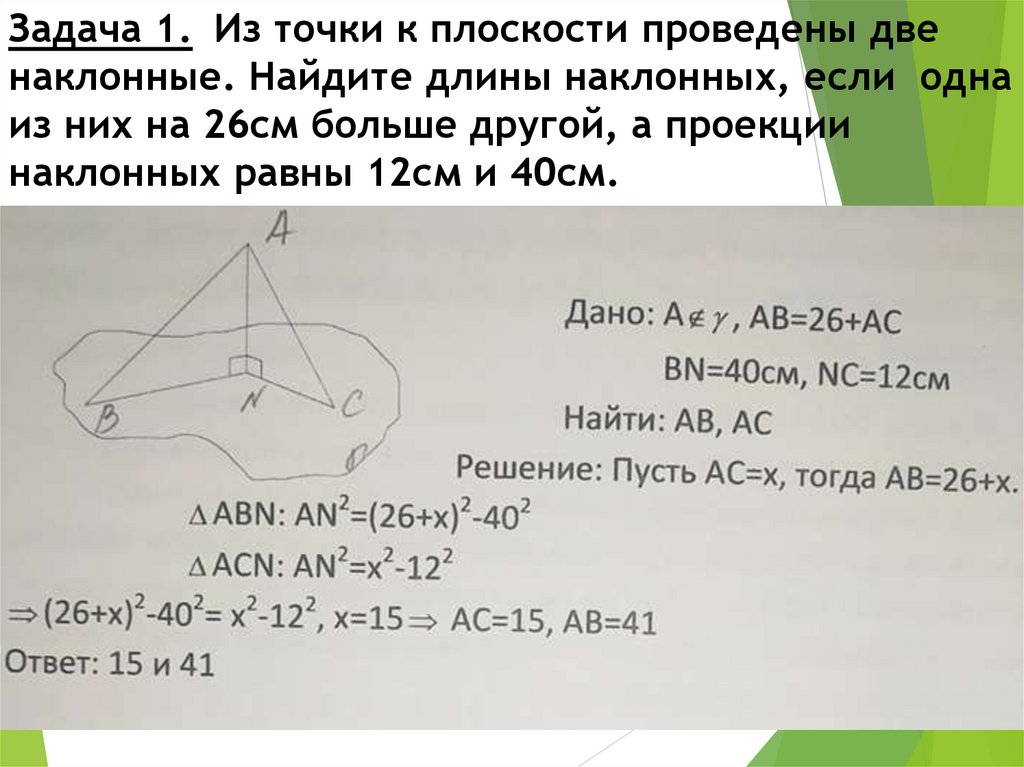
Задача 1. Из точки к плоскости проведены двенаклонные. Найдите длины наклонных, если одна
из них на 26см больше другой, а проекции
наклонных равны 12см и 40см.
9.
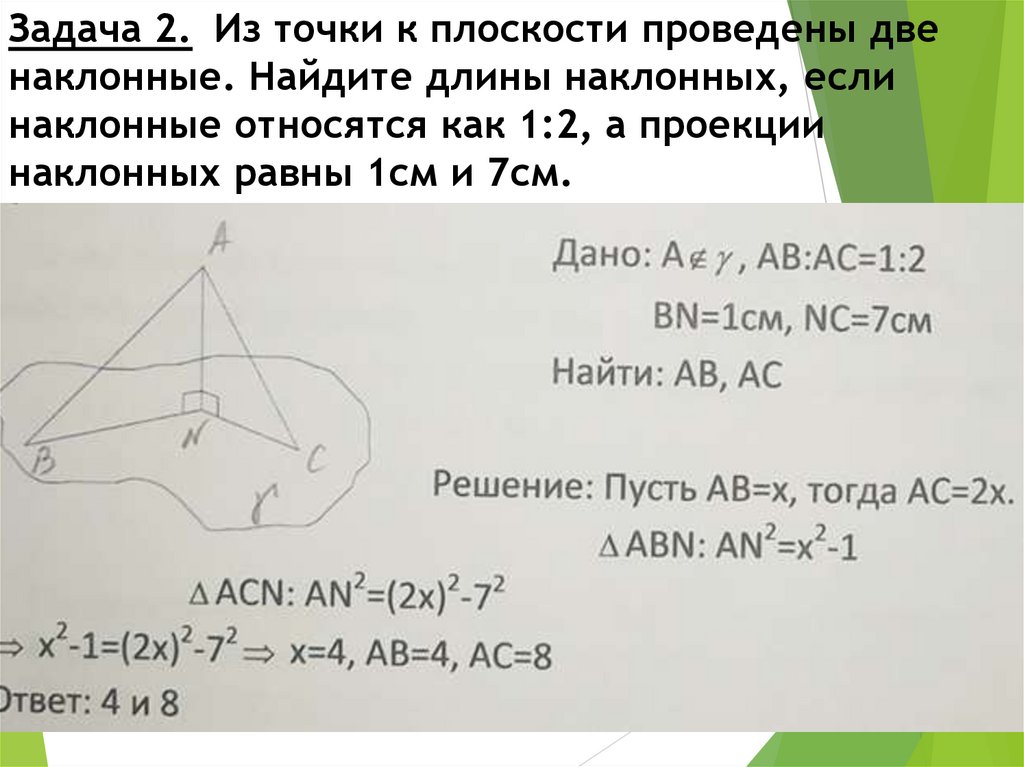
Задача 2. Из точки к плоскости проведены двенаклонные. Найдите длины наклонных, если
наклонные относятся как 1:2, а проекции
наклонных равны 1см и 7см.
10.
Задача 3. Найдите расстояние от середины отрезкаАВ до плоскости, не пересекающей этот отрезок,
если расстояние от точек А и В до плоскости равны
3,2см и 5,3см.
11.
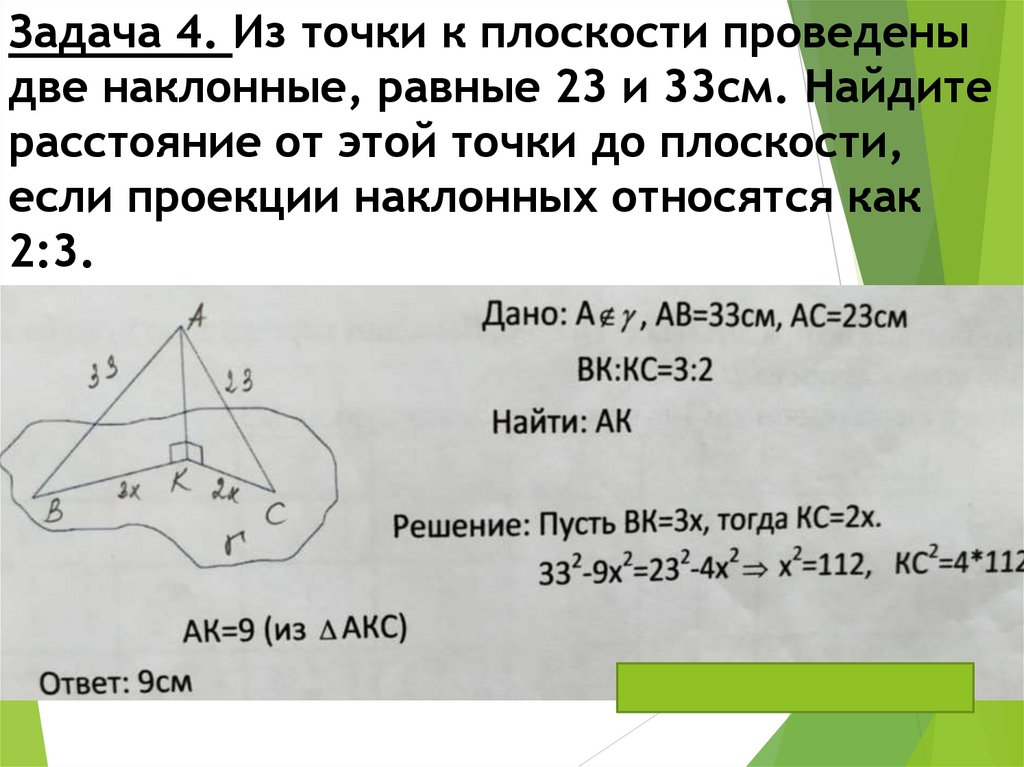
Задача 4. Из точки к плоскости проведеныдве наклонные, равные 23 и 33см. Найдите
расстояние от этой точки до плоскости,
если проекции наклонных относятся как
2:3.
12.
Задача 5. Из точки, непринадлежащей данной плоскости,
проведены к ней две наклонные,
сумма длин которых равна 22 см.
Проекции этих наклонных на
плоскость равны 7см и 10см.
Найдите длины наклонных.
13.
Задача 6. Найдите расстояние отсередины отрезка АВ до плоскости,
не пересекающей этот отрезок, если
расстояния от точек А и В до
плоскости равны
см и
см.
14.
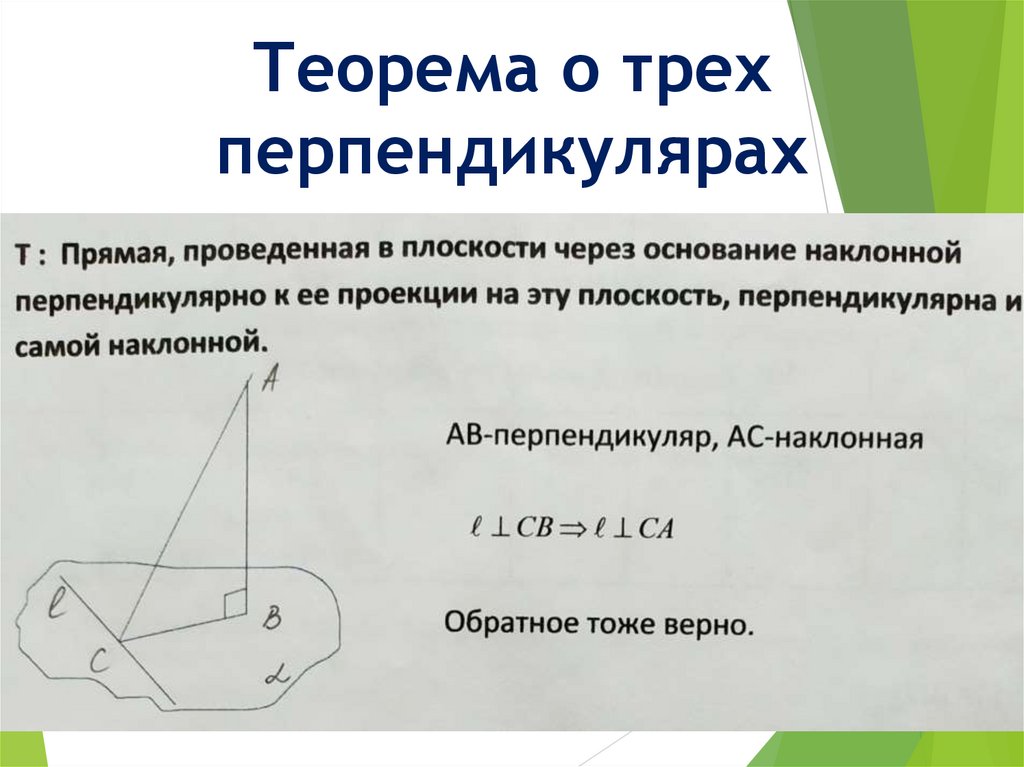
Теорема о трехперпендикулярах
15.
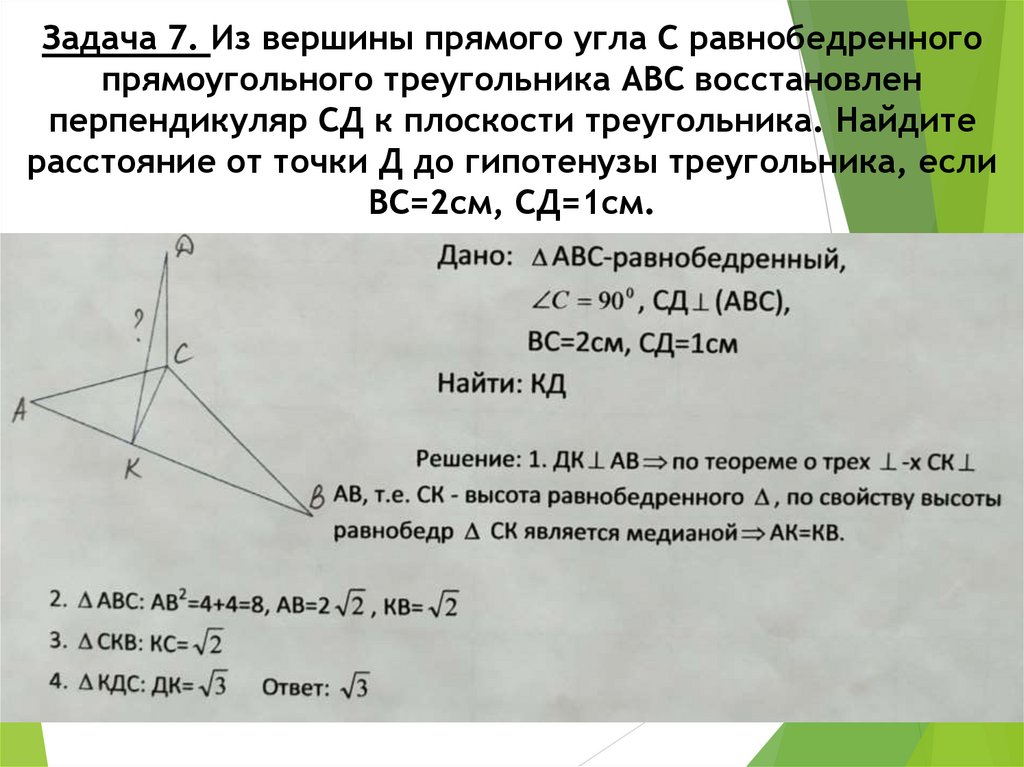
Задача 7. Из вершины прямого угла С равнобедренногопрямоугольного треугольника АВС восстановлен
перпендикуляр СД к плоскости треугольника. Найдите
расстояние от точки Д до гипотенузы треугольника, если
ВС=2см, СД=1см.
16.
Задача 8: В равнобедренном треугольникеАВС основание СВ =12м, боковая сторона
10м. Из вершины А проведен отрезок АД=6м
и перпендикулярный плоскости АВС.
Найдите расстояние от точки Д
до стороны ВС.
17.
Дома:Задачи 5,6 и 8 решить
самостоятельно,
выслать решения в ВК.







 Математика
Математика








