Постановка задачи оптимального управления

1.

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
_______________________________________________________________
Оптимальной называется такая САУ, которой тем или иным способом приданы
наилучшие качества в каком-либо определённом смысле. Существует проблема выбора
наилучшего решения среди возможных в тех или иных условиях. Использование оптимальных систем в
экономике и технике позволяет довести эффективность производства до максимума: увеличить производительность труда, улучшить качество
продукции, экономию электроэнергии, ресурсов, сырья.
Слово “оптимальный” – “optimus” – наилучший, совершенный, иначе говоря
“наиболее оптимальный”.
Для нахождения оптимума – необходимо решить задачи на отыскание экстремума
(max или min) (“exctremum” – крайний).
Примеры оптимальных систем:
- САУ предприятием, обеспечивающим максимальные прибыли при производстве нескольких
видов продукции;
- САУ полётом самолёта, обеспечивающем минимум расхода топлива на заданном
маршруте;
- САУ перемещением тела на заданное расстояние за минимальное t;
- САУ U и f синхронного генератора, обеспечивающем устранение ошибки за минимальное t.
Казалось, что при создании оптимальной САУ логично поставить следующую задачу: должна обеспечивать
максимум быстродействия, наименьшую ошибку, минимальный расход энергии, топлива, стоимости, максимальной
Говорить о быстродействии имеет смысл лишь при
заданной мощности источника энергии, ведь с ↑ P t процесса уменьшаются, но
увеличивается стоимость установки, САУ, и т. д. Поэтому постановка задачи требует
наложении е ограничений на отдельные элементы САУ, то есть говорить о быстродействии
можно лишь тогда, если заданы мощность установки, о максимальной надёжности – при
ограничении массы, стоимости и т. д.
надёжности. Такая постановка в общем случае нелепа.

2.

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
_______________________________________________________________
При решении задач оптимального управления неизвестными, подлежащими
определению, являются не числа, а функции, то есть диаграммы U, M, I, ω, S и т. д. – для
решения таких задач используются вариационные методы. Эти методы позволяют
определить функции, доставляющие наименьшее или наибольшее значение некоторым
величинам (показателям качества), зависящим от этих функций и называемым
функционалами.
Главное требование при проектировании оптимальных САУ – задание
определённой цели управления. Эту цель можно рассматривать как достижение экстремума
некоторой величины. Q – критерий оптимальности.
В качестве критерия выбираются различные экономические или технические
показатели управляемого процесса (минимум времени, расхода топлива, максимальная
надёжность, прибыль). При этом в оптимальных САУ обеспечиваются не просто повышение
того или иного показателя, а достижение его максимального или минимального значения.
Если критерий оптимальности выражает технико-экономические потери (время
переходного процесса, расход горючего, ошибку управления, стоимость установки и т. д.), то
оптимальным будет такое управление, которое обеспечивает минимум этого критерия. Если
же он выражает рентабельность (прибыль предприятия, производительность машины, КПД
установки, дальность полёта), то оптимальной будет САУ при достижении максимума
критерия оптимальности.

3.

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
_______________________________________________________________
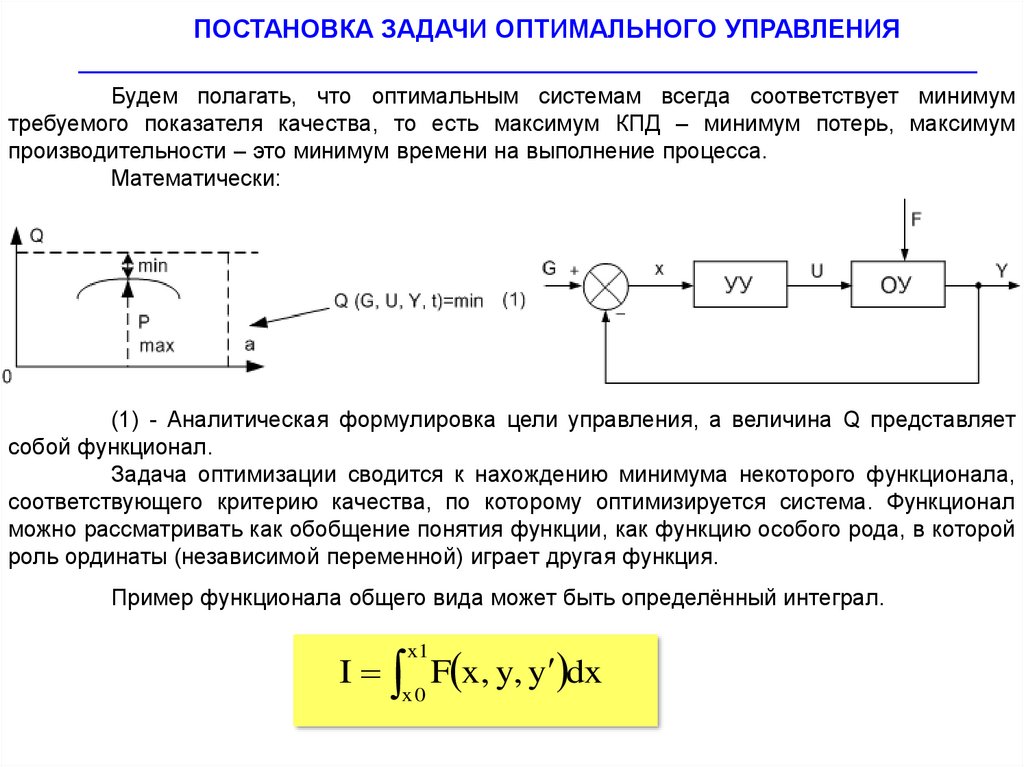
Будем полагать, что оптимальным системам всегда соответствует минимум
требуемого показателя качества, то есть максимум КПД – минимум потерь, максимум
производительности – это минимум времени на выполнение процесса.
Математически:
(1) - Аналитическая формулировка цели управления, а величина Q представляет
собой функционал.
Задача оптимизации сводится к нахождению минимума некоторого функционала,
соответствующего критерию качества, по которому оптимизируется система. Функционал
можно рассматривать как обобщение понятия функции, как функцию особого рода, в которой
роль ординаты (независимой переменной) играет другая функция.
Пример функционала общего вида может быть определённый интеграл.
I F x, y, y dx
x1
x0

4.

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
_______________________________________________________________
В теории оптимального управления получили преимущественное распространение
интегральные функционалы типа:
I F y1 , y 2 ,...ys , u1 , u 2 ,...u r , t1 , t 2 ,...t q dt
t
t0
когда аргументом подынтегральной функции является время t.
Обеспечение минимизации такого функционала и есть задача оптимального
управления, которая разделяется на частные в соответствии с конкретными именами. Дело в том,
что критерии оптимальности, как правило, характеризуют не удельный показатель качества (в определённый момент времени), не текущее
состояние объекта, а изменение его в течение всего времени управления: расход энергии за время движения, интегральная ошибка за время
Поэтому для определения оптимальности требуется интегрировать какуюлибо функцию, которая зависит от текущих значений координат объекта и управляющего
воздействия.
переходного процесса и т. д.

5.

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
_______________________________________________________________
а) Если критерием оптимальности является время (задача на быстродействие), то
F(y,u,t)=1,
а функционал примет вид
t1
I 1dt t1 t0 min;
t0
б) для достижения максимальной точности критерием оптимальности служит минимум
ошибки регулирования:
I x 2 dt min .
t
в) для обеспечения минимума расхода электроэнергии на выполнение определенного
процесса (за данное время Т) функционал можно записать так:
T
I U dt min .
t
2

6.

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
_______________________________________________________________
Часто к системе управления предъявляются противоречивые требования:
минимум расхода и максимум скорости полёта. Поэтому из всех требований выбирают одно
основное, а другие учитываются как ограничение (для этого случая задаётся минимально
возможное значение скорости полёта).
При любой оптимизации какого-либо из качеств САУ фигурируют ограничение в
виде заданной управляющей силы (момента), давления, массы, возможного диапазона
параметров управляющего устройства. При требовании максимальной надёжности САУ
могут ограничиваться стоимость, масса, ошибки управления (максимального быстродействия
– мощность, момент, и т.д.), то есть на условие задачи следует наложить некоторые
ограничения. Эти ограничения (по модулю) могут быть условными и безусловными.
Условные – такие, когда физические величины принципиально могут быть сколь угодно
большой, но по роду соображений её желательно ограничить: ток якоря (коммутация),
скорость двигателя (механическая прочность).
Безусловные – такие, когда физические величины в принципе могут быть больше
определённого значения: момент асинхронного двигателя не может быть больше
критического, ЭДС генератора – максимум значения на кривых холостого хода, и т.д.

7.

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
_______________________________________________________________
Для анализа САУ, описываемой дифференциальными уравнениями n-ного порядка,
его удобно преобразовывать в систему из n уравнений первого порядка то есть запись в
форме уравнений Коши, когда в левой части уравнений – только первые производные
выходной координаты:
dy1
f1 y1 , y 2 ,... ys , u1 , u 2 ,... u r
dt
dy 2
f 2 y1 , y 2 ,... ys , u1 , u 2 ,... u r
dt
(4)
………
dys
f s y1 , y 2 ,... ys , u1 , u 2 ,... u r
dt
Систему (4) можно записать в векторной форме:
F Y, U
Y
При наличии возмущений в более общем виде:
F Y, U, F
Y
(5)

8.

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
_______________________________________________________________
Пример. Если взять систему третьего
порядка, величины y1, y2, y3 можно
рассматривать
как
прямоугольные
координаты некоторой точки М. В реальном
процессе в каждый момент времени
переменные y1, y2, y3 принимают некоторые
значения, то есть точка М во времени
перемещается по определённой траектории,
которая называется фазовой, а трёхмерное
пространство – фазовым пространством.
Движение изображающей точки М в фазовом пространстве – наглядная геометрическая
интерпретация поведения оптимальной системы. Совокупность фазовых траекторий при
различных нормальных условиях образуют фазовый портрет. В установившемся режиме,
когда производные равны нулю, траектория обращается в точку, в частном, в начало
координат.
В принципе число уравнений Коши определяет мерность пространства (n-мерное), однако
для анализа можно применять лишь трёхмерное. Движение изображающей точки на фазовой
плоскости всегда осуществляется по часовой стрелке.

9.

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
_______________________________________________________________
Задача об управлении теперь может быть представлена так:
Пусть в начальный момент времени t0 состояние объекта в фазовом пространстве
соответствует точке М0. Требуется выбрать такое уравнение u(t), которое переводит объект в
заранее заданное конечное фазовое состояние М1 (траектория 1). Знак управляющего
воздействия u можно из СУ (4) или (5) однозначно определить движение объекта при t>t0.
Если управление изменить, то движение изображающей точки будет осуществляться по
другой траектории (2, 3 и т. д.) Поэтому перевод из точки М0→М1 может осуществлять по
разным траекториям в зависимости от уравнения. Среди множества траекторий существует
наилучшие в определённом смысле, то есть оптимальные.
Задача оптимизации − задача вариационного типа, когда
требуется подобрать закон изменения управляющего
воздействия u(t) такими, чтобы обеспечивался минимум
функционала, который в общем случае служит критерием
оптимальности САУ при соблюдении необходимых
ограничений.
Вариационное исчисление − это математический аппарат,
который позволяет определить экстремальные значения
функционалов, а также находить кривые-экстремали, на
которых двигаются эти экстремальные значения.

10.

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
_______________________________________________________________
Методы вариационного исчисления можно условно разделить на классические
и современные. К классическим принадлежат методы, базирующиеся на уравнениях
Эйлера, Якоби, Вейерштрасса, к современным – принцип максимума Понтрягина и
метод динамического программирования Беллмана.
Классические методы целесообразно использовать в задачах, не имеющих
ограничений. Это бывает в тех случаях, когда рассматриваются малые отклонения
переменных состояния и управляющих воздействий от установившихся значений.
Современные методы дают возможность учесть ограничения управляющих
воздействий.
Сформулируем задачу оптимального управления.
Для объекта управления, описываемого уравнениями состояния, найти такое
управление u, которое при соблюдении ограничений переводит объект из начального
состояния x(t0)=x0 в конечное x(tf)=xf так, что при этом функционал достигает минимума, а
уравнение динамики объекта и характеристики внешних воздействий в процессе управления
не изменяются.
Управление, удовлетворяющее этим условиям, называется оптимальным.
Решение задачи программного управления в форме u(t) соответствует
программному управлению, т.е. синтезу задающего устройства, а в форме u(x) −
управлению с обратной связью, т.е. синтезу оптимального регулятора или оптимального
фильтра.
График функции, обеспечивающий экстремум функционалу качества, называют
экстремалью, или оптимальной траекторией.

11.

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
_______________________________________________________________
x(t f ) x f
Условия x(t 0 ) x 0
называют граничными, или краевыми.
Первое из этих условий определяет левый конец оптимальной траектории, а второй
– правый.
По типу граничных условий различают такие задачи оптимального управления:
а) с фиксированными (закрепленными) концами, когда каждая граница задается
одним значением;
б) с подвижным правым концом, с подвижным левым концом и с обеими
подвижными концами, когда соответствующие границы задаются несколькими значениями
или являются функциями времени:
x 0 ρ 0 (t ),
x f ρ f (t )
в) со свободным правым концом, когда на x(tf) не наложено никаких ограничений.
По времени переходного процесса различают:
а) задачи с фиксированным временем, когда t0 и tf фиксированные;
б) задачи с нефиксированным временем, когда хотя бы один из моментов времени
t0 или tf (чаще tf) не фиксированный, т.е. не известный.
По критерию оптимальности различают:
J G(x(t0 ), x(t f ), t0 , t f )
а) задачу Майера
tf
б) задачу Лагранжа
J F (x(t ), u(t ), t )dt,
t0
в) задачу Больца
tf
J G(x(t0 ), x(t f ), t0 , t f ) F (x(t ), u(t ), t )dt,
Отдельные случаи задачи Майера:
t0
а) задача терминального управления:
б) задача максимального быстродействия
J t f t0
J G(x(t f ), t f )

12.

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
_______________________________________________________________
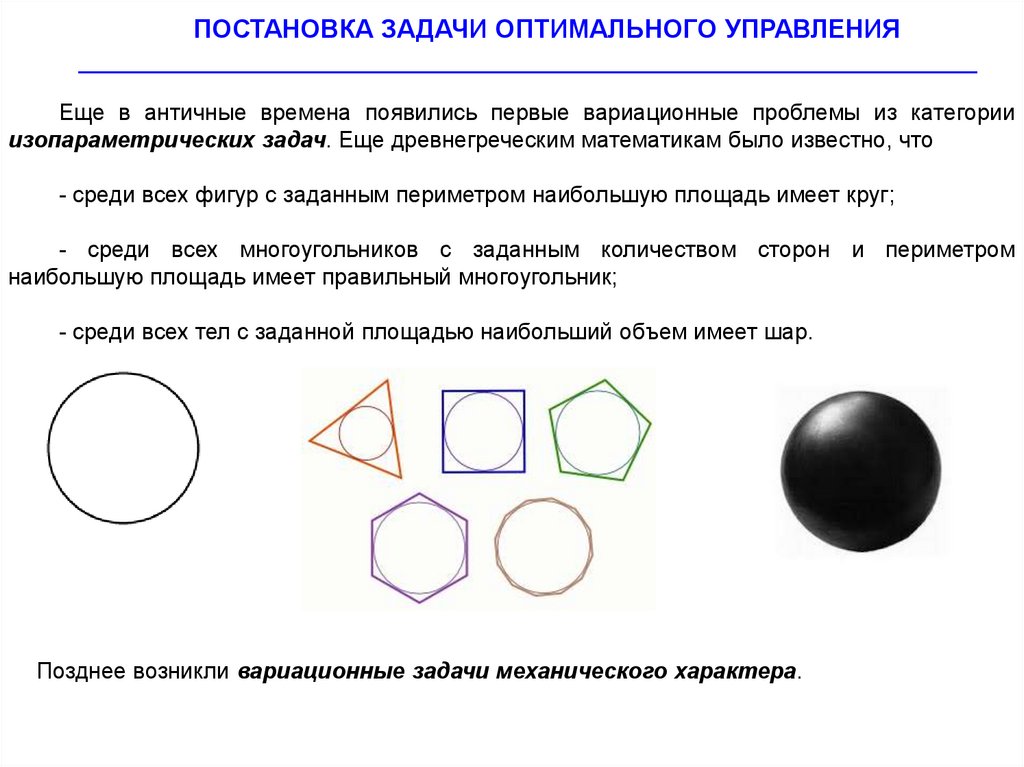
Еще в античные времена появились первые вариационные проблемы из категории
изопараметрических задач. Еще древнегреческим математикам было известно, что
- среди всех фигур с заданным периметром наибольшую площадь имеет круг;
- среди всех многоугольников с заданным количеством сторон и периметром
наибольшую площадь имеет правильный многоугольник;
- среди всех тел с заданной площадью наибольший объем имеет шар.
Позднее возникли вариационные задачи механического характера.

13.

ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
_______________________________________________________________
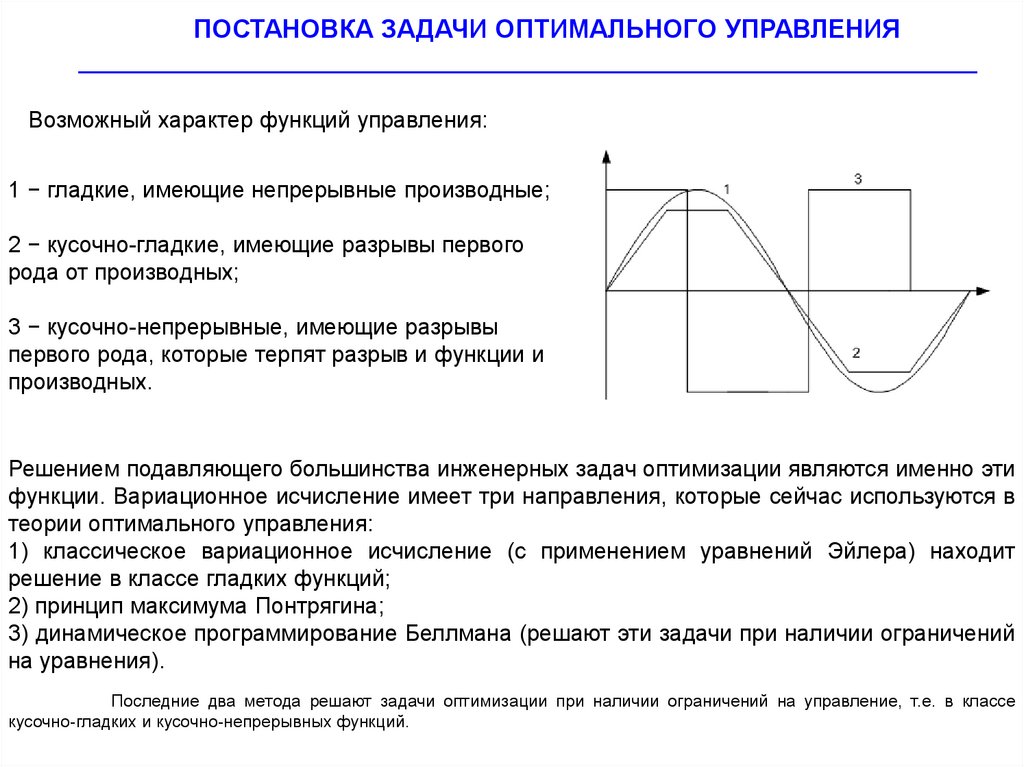
Возможный характер функций управления:
1 − гладкие, имеющие непрерывные производные;
2 − кусочно-гладкие, имеющие разрывы первого
рода от производных;
3 − кусочно-непрерывные, имеющие разрывы
первого рода, которые терпят разрыв и функции и
производных.
Решением подавляющего большинства инженерных задач оптимизации являются именно эти
функции. Вариационное исчисление имеет три направления, которые сейчас используются в
теории оптимального управления:
1) классическое вариационное исчисление (с применением уравнений Эйлера) находит
решение в классе гладких функций;
2) принцип максимума Понтрягина;
3) динамическое программирование Беллмана (решают эти задачи при наличии ограничений
на уравнения).
Последние два метода решают задачи оптимизации при наличии ограничений на управление, т.е. в классе
кусочно-гладких и кусочно-непрерывных функций.

14.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Большая часть ЭП предназначена для перемещения (поворота) исполнительных
механизмов: кранов, поворота экскаваторов, лифтов, манипуляторов и т.д. Их
производительность, приведенная к вращательному движения, оценивается интегралом:
T
dt
0
(8)
т.е. углом поворота за время Т.
Если механизм работает в основном в переходных режимах, то производительность легко
оценивать интегралом:
T
dt
0
(9)
т.е. изменением скорости поворота за время Т.
Задачи оптимального управления ЭП можно сформулировать таким образом:
1. Обеспечить максимальную производительность ЭП, т.е. максимальное значение
интегралов (8) или (9) в заданное время Т. Это управление, оптимальное по
производительности.
2. Обеспечить минимальное время выполнения заданной программы перемещения (α) или
изменения скорости (Δω). Это управление, оптимальное по быстродействию.

15.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Задачи оптимального управления ЭП:
3. Обеспечить минимум потерь в якоре машины постоянного тока, т.е. минимум интеграла
Q
T 2
R0 i dt
0
(10)
при выполнении заданной программы перемещения (α) или изменения скорости (Δω) в
заданное время Т. Это управление, оптимальное по нагреву.
Последняя формулировка важна для тех ЭП, в которых двигатели выбираются по нагреву и где уменьшение потерь в якоре
позволяет снизить мощность, габариты и массу, а также и стоимость двигателя. К ним относятся ЭП длительного режима
работы или повторно-кратковременного с большой частотой включений.
Это наиболее распространенные задачи оптимального управления ЭП.
В частных случаях возможны и другие формулировки этих задач.
4. Управление, обеспечивающее минимум потребления
электрической энергии при выполнении заданной программы
перемещений α.
5. Обеспечить минимум интеграла от тока якоря
(актуально для таких ЭП, питающихся от аккумуляторов).
T
W Ui dt
0
T
q i dt
6. Обеспечить минимум установленной мощности источника питания.
0

16.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Ограничения, которые нельзя не учитывать в ЭП:
Q Qдоп
1.Основное ограничение - по нагреву, т.е. интеграл (10):
Это интегральное ограничение. Очень часто двигатель выбирается по нагреву, и если температура превышает допустимую, наступает быстрое
разрушение изоляции.
2. Ограничение по скорости двигателя, связанное с механической прочностью ротора эд:
3. Ограничение по току якоря
i iдоп
доп
(11)
(12)
4. Ограничение по моменту, определяемое возможностями ад, но
главное - динамическими нагрузками на элементы механизма,
условиями буксования колес механизма, движущегося по рельсам, и т.д.
M M доп (13)
С последним ограничением перекликается ограничение на ускорение:
d
доп
dt
5. Может ограничиваться и рывок, в частности, для
пассажирских лифтов, т.е.
d 2
доп
2
dt
(14)
6. Ограничения мощности при питании от источника ограниченной мощности
Все эти ограничения, за исключением последнего и частично 4, условные.
P Pmax
(15)

17.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
В основные уравнения ЭП и важнейшие ограничения (10)...(13) входят скорость и
ток якоря, но не эти величины являются управляющими. Так, для системы ТП-Д следует
воздействовать на управляющее напряжение преобразователя Uy. Однако удобнее сначала
искать оптимальные диаграммы тока i(t) и скорости ω(t), на которые не влияет, в частности,
индуктивность якоря. А зная эти диаграммы несложно рассчитать и построить зависимость
Uy(t), на которую влияют также свойства самого ТП и инерционность цепи якоря.
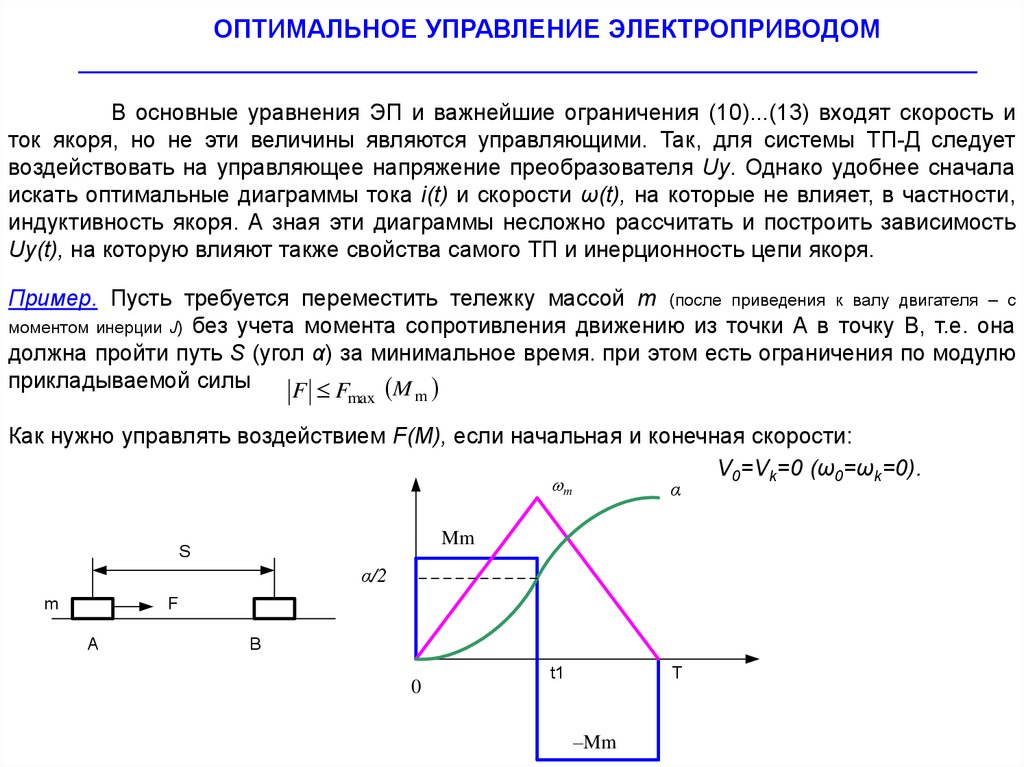
Пример. Пусть требуется переместить тележку массой m (после приведения к валу двигателя – с
моментом инерции J) без учета момента сопротивления движению из точки А в точку В, т.е. она
должна пройти путь S (угол α) за минимальное время. при этом есть ограничения по модулю
прикладываемой силы
M
F F
max
m
Как нужно управлять воздействием F(M), если начальная и конечная скорости:
V0=Vk=0 (ω0=ωk=0).
m
α
t1
T
Mm
S
α/2
m
F
A
B
0
–Mm

18.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Это простейшая задача на быстродействие многих производственных механизмов
и транспортных средств: движение поездов метро между станциями, механизмом поворота
экскаватора, манипулятора и т.д.
Ясно, что следует до середины пути разгонять тело, приложив момент +Mm, а
затем тормозить моментом –Mm. При равноускоренном движении за время t1 будет пройден
путь S/2.
α
m
Mm
J
α/2
m
F
A
Причем
0.5 0.5
Mm
S
B
Mm 2
t1
J
Откуда полное время перемещения (поворота)
t1
0
T
–Mm
T 2t1 2
Максимальная скорость, достигаемая к моменту времени t1:
J
Mm
M m
J

19.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Определить уравнение в функции времени
электромагнитного момента
электродвигателя M(t), который необходимо приложить, чтобы двигатель осуществил поворот
на заданный угол αf за заданное время tf с минимальными тепловыми потерями
электроэнергии от моментообразующего тока I(t), пренебрегая моментом статического
сопротивления на валу двигателя (Mc=0). Определить также оптимальные траектории
изменения угловой скорости ω(t) и углового положения α(t).
Объект управления описывается дифференциальными уравнениями:
M j cI j J
и линейным алгебраическим уравнением
Тепловые потери, подлежащие минимизации, определяются уравнением:
tf
Q j R I j (t )dt
2
0
J 2R
c
2
tf
0
2
(t )dt
J 2R
c
2
' , '
J
Ij
с
Q
Т.е. подынтегральная функция критерия оптимизации имеет вид:
F 2
В сформулированной задаче входной координатой объекта регулирования с вектором
состояния
x можно считать угловое ускорение, пропорциональное вращающему моменту u
(0) 0, (t f ) f , (0) 0, (t f ) 0.
Граничные условия имеют вид:
Кроме того, существуют ограничения на управляющее воздействие: (0 ) 0,
(t t f ) 0.

20.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Составляем функцию Гамильтона:
H 2 1 2
и запишем уравнение Эйлера-Лагранжа:
H
'
0
1
H
1 C1 const
Из первого уравнения
1
2 '
H
2 C1t C 2
из второго –
2 2 0
C1t C2
2
из третьего –
'
2
2
'
Подставляем полученное выражение в последнее дифференциальное уравнение и
интегрируем его. В результате получим:
C1t 2 C 2 t
(t )
C3
4
2
Находим производную и интеграл от угловой скорости:
Ct C
(t ) ' (t ) 1 2
2
2
C1t 3 C 2 t 2
(t ) (t )dt
C3t C 4
12
4
(0) C 4 0,
Используя граничные условия получаем:
C1t f 2 C2t f
C1t f 3 C2t f 2
(t f )
0
(t f )
f
4
2
12
4
(0) C3 0,

21.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
24 f
12 f
Решая систему двух последних уравнений, получаем:
C1
t 3f
,
C2
t 2f
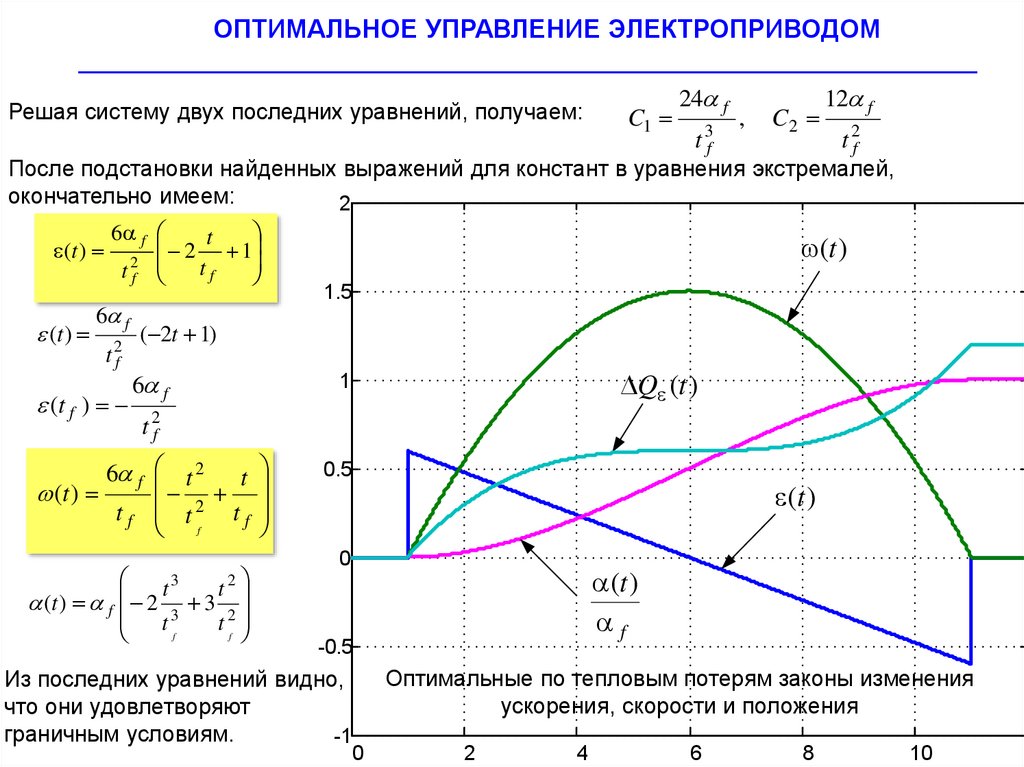
После подстановки найденных выражений для констант в уравнения экстремалей,
окончательно имеем:
2
(t )
(t )
6 f
2 t 1
tf
t 2f
6 f
t 2f
(t f )
(t )
1.5
( 2t 1)
6 f
Q (t )
1
t 2f
6 f t 2 t
(t )
t f t2 t f
f
t3
t 2
(t ) f 2 3 3 2
tf
tf
0.5
(t )
0
(t )
f
-0.5
Из последних уравнений видно,
что они удовлетворяют
граничным условиям.
-1
Оптимальные по тепловым потерям законы изменения
ускорения, скорости и положения
0
2
4
6
8
10
1

22.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
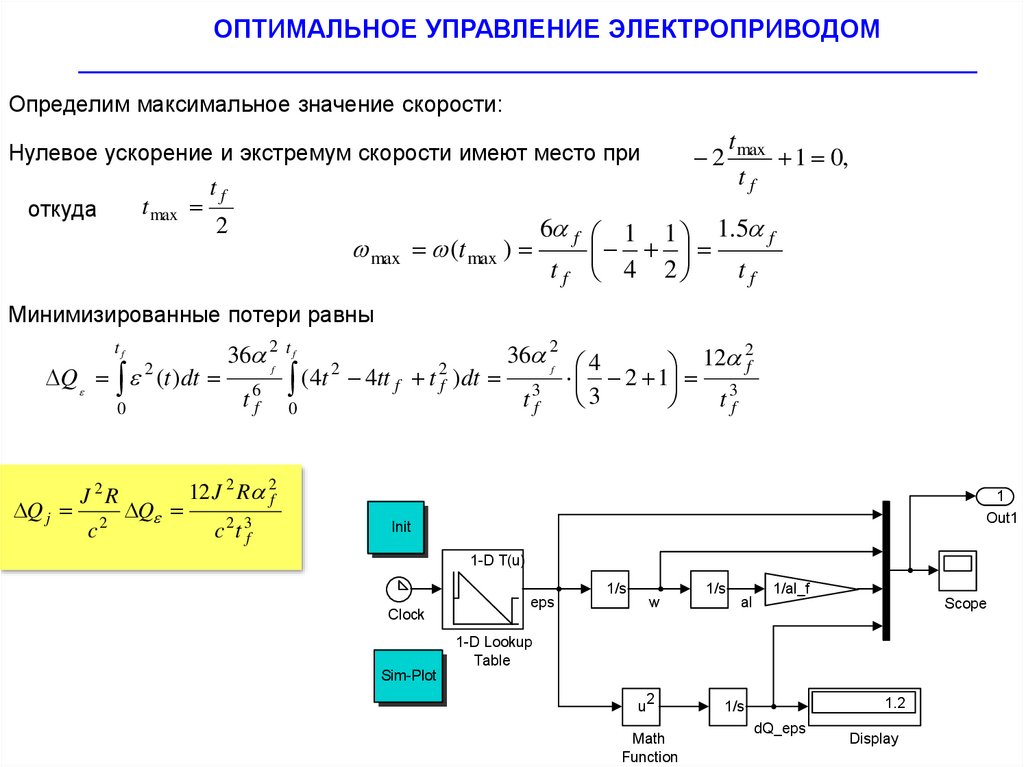
Определим максимальное значение скорости:
Нулевое ускорение и экстремум скорости имеют место при
t max
откуда
2
tf
2
max
t max
1 0,
tf
6 f 1 1 1.5 f
(t max )
t f 4 2
tf
Минимизированные потери равны
tf
Q 2 (t )dt
0
Q j
J 2R
c2
Q
36 2f
t 6f
2
2
36
4
12 f
f
2
2
(4t 4tt f t f )dt t 3 3 2 1 t 3
f
f
0
tf
12 J 2 R 2f
c 2 t 3f
1
Out1
Init
1-D T(u)
Clock
eps
1/s
w
1/s
al
1/al_f
Scope
1-D Lookup
Table
Sim-Plot
u
2
Math
Function
1.2
1/s
dQ_eps
Display

23.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
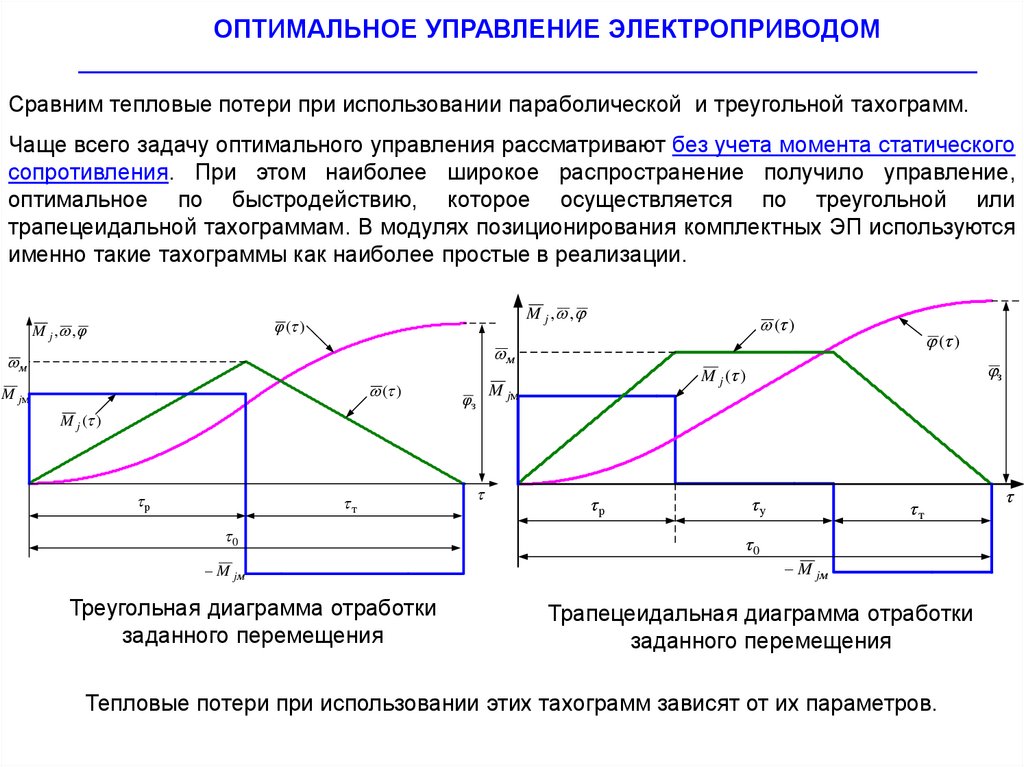
Сравним тепловые потери при использовании параболической и треугольной тахограмм.
Чаще всего задачу оптимального управления рассматривают без учета момента статического
сопротивления. При этом наиболее широкое распространение получило управление,
оптимальное по быстродействию, которое осуществляется по треугольной или
трапецеидальной тахограммам. В модулях позиционирования комплектных ЭП используются
именно такие тахограммы как наиболее простые в реализации.
M j , ,
( )
M j , ,
( )
м
м
( )
M jм
M j ( )
р
т
0
M jм
Треугольная диаграмма отработки
заданного перемещения
з
M j ( )
M jм
з
( )
р
у
т
0
M jм
Трапецеидальная диаграмма отработки
заданного перемещения
Тепловые потери при использовании этих тахограмм зависят от их параметров.

24.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
р
0
т
р
у
0
т
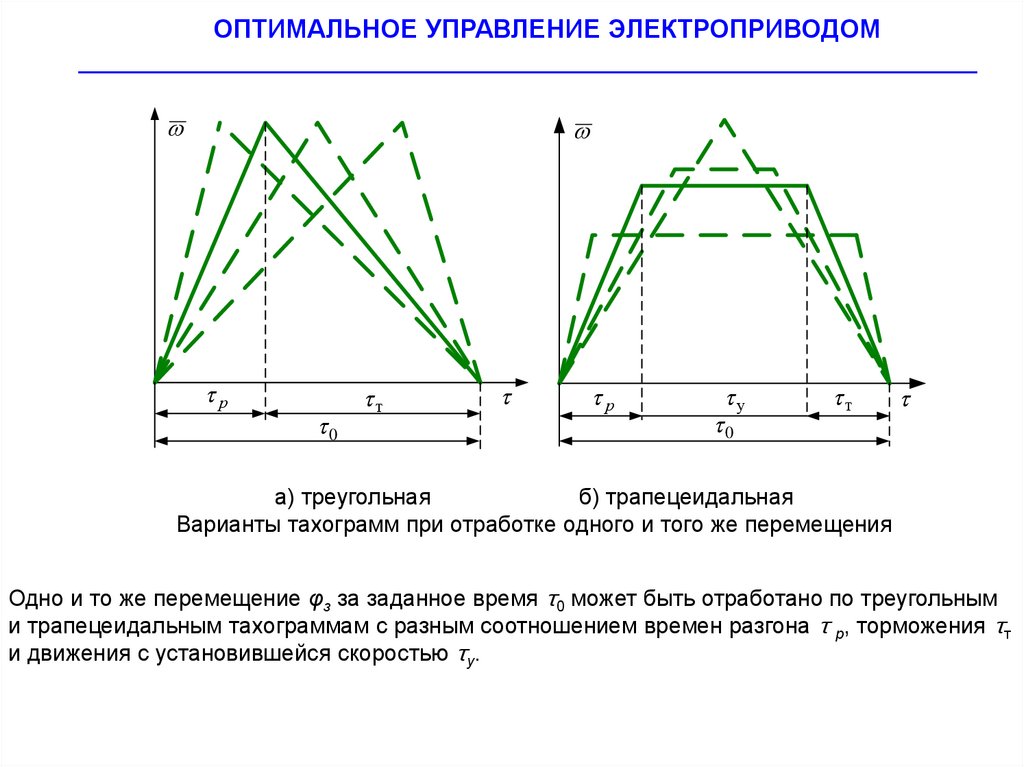
а) треугольная
б) трапецеидальная
Варианты тахограмм при отработке одного и того же перемещения
Одно и то же перемещение φз за заданное время τ0 может быть отработано по треугольным
и трапецеидальным тахограммам с разным соотношением времен разгона τ р, торможения τт
и движения с установившейся скоростью τу.

25.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Q
1
2
0
р
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
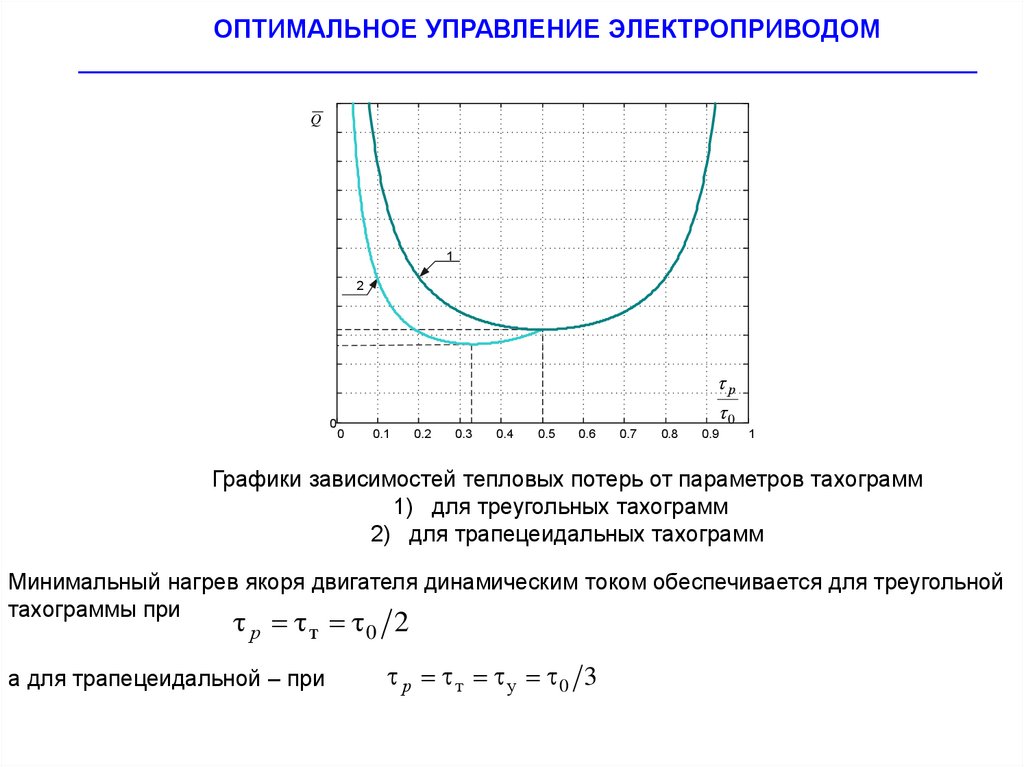
Графики зависимостей тепловых потерь от параметров тахограмм
1) для треугольных тахограмм
2) для трапецеидальных тахограмм
Минимальный нагрев якоря двигателя динамическим током обеспечивается для треугольной
тахограммы при
р т 0 2
а для трапецеидальной – при
р т у 0 3

26.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
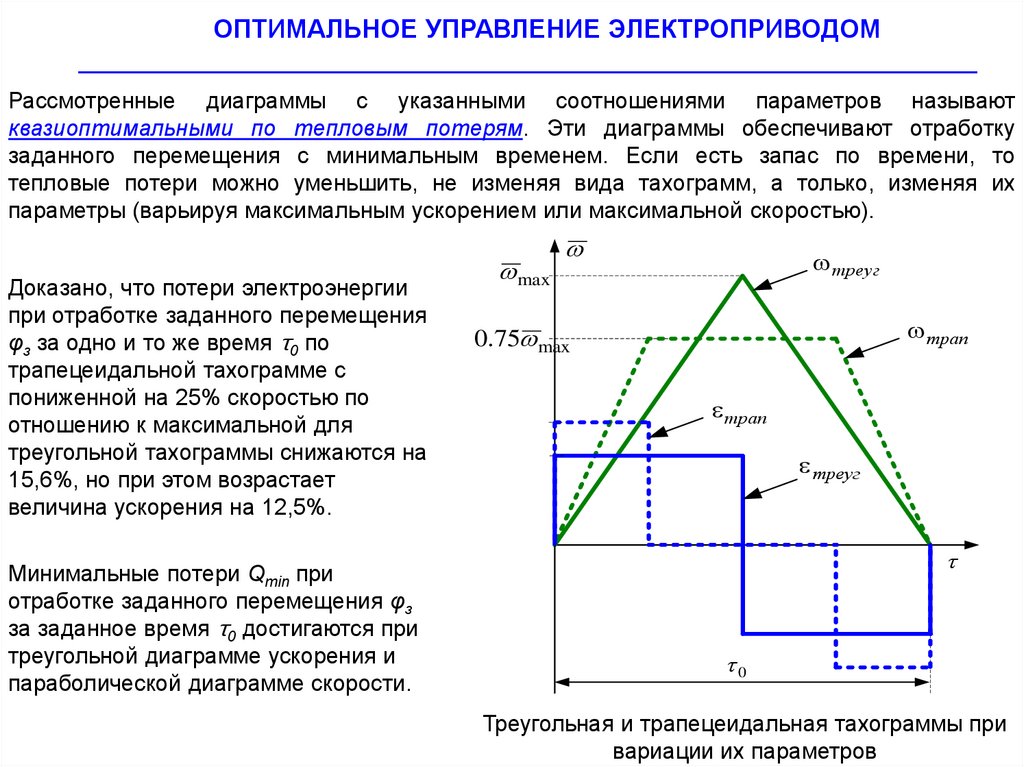
Рассмотренные диаграммы с указанными соотношениями параметров называют
квазиоптимальными по тепловым потерям. Эти диаграммы обеспечивают отработку
заданного перемещения с минимальным временем. Если есть запас по времени, то
тепловые потери можно уменьшить, не изменяя вида тахограмм, а только, изменяя их
параметры (варьируя максимальным ускорением или максимальной скоростью).
Доказано, что потери электроэнергии
при отработке заданного перемещения
φз за одно и то же время τ0 по
трапецеидальной тахограмме с
пониженной на 25% скоростью по
отношению к максимальной для
треугольной тахограммы снижаются на
15,6%, но при этом возрастает
величина ускорения на 12,5%.
Минимальные потери Qmin при
отработке заданного перемещения φз
за заданное время τ0 достигаются при
треугольной диаграмме ускорения и
параболической диаграмме скорости.
max
треуг
трап
0.75 max
трап
треуг
0
Треугольная и трапецеидальная тахограммы при
вариации их параметров

27.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
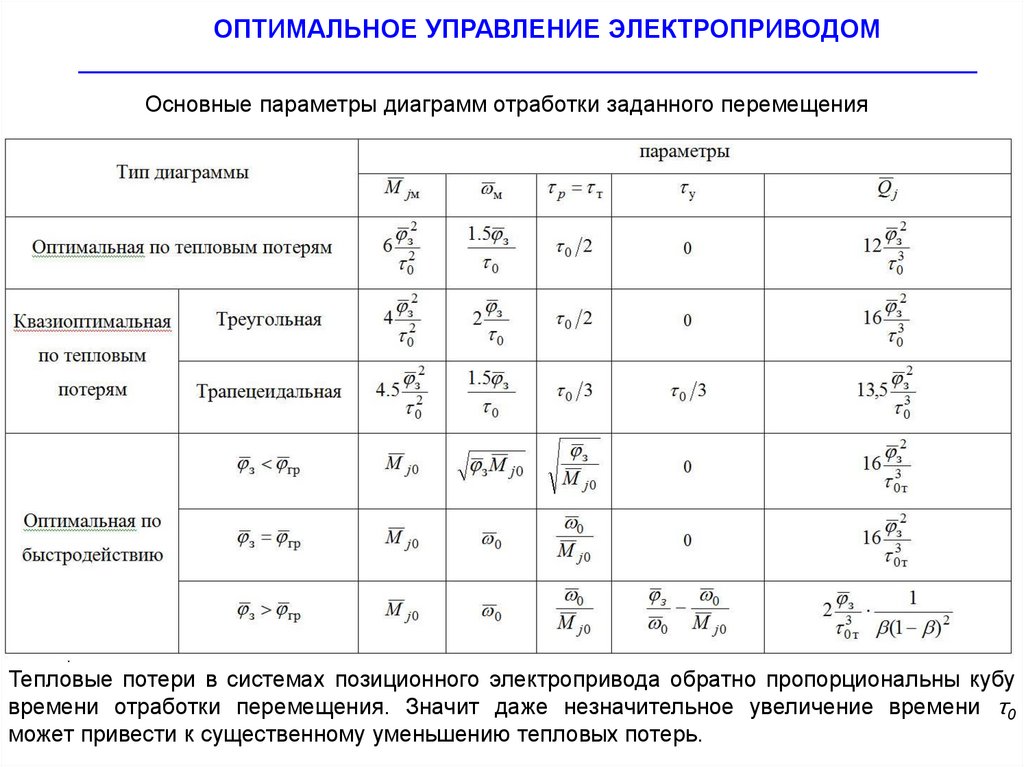
Основные параметры диаграмм отработки заданного перемещения
Тепловые потери в системах позиционного электропривода обратно пропорциональны кубу
времени отработки перемещения. Значит даже незначительное увеличение времени τ0
может привести к существенному уменьшению тепловых потерь.

28.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Известно, что параболическая диаграмма имеет минимальные потери Q, но самое
большое значение максимального ускорения Mjm (в 1,5 раза выше, чем в треугольной и в 1,33
раза выше, чем в трапецеидальной квазиоптимальных диаграммах).
Квазиоптимальная трапецеидальная диаграмма имеет при таком же, как и у оптимальной
диаграммы значение максимальной скорости ωм и меньшем значении максимального
ускорения Mjm, тепловые потери Q, превышающие минимально возможные Qmin на 12,5%.
Треугольная квазиоптимальная диаграмма характеризуется минимальным значениям
ускорения Mjm, но самым большим значением максимальной скорости ωм и потерь Q (на
33% выше, чем Qmin).

29.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Задачу оптимального управления позиционным ЭП, в которой связаны между
собой величины перемещения, время, за которое оно совершается, и тепловые потери,
формулируются в 3-х вариантах:
1. Найти оптимальное управление, обеспечивающее минимальные тепловые потери при
перемещении объекта на заданное расстояние за заданное время – задача на
минимизацию тепловых потерь, решаемая минимизацией функционала
tf
J Q j R I j 2 (t )dt
0
2. Найти оптимальное управление, обеспечивающее минимальное время перемещении
объекта на заданное расстояние при заданных тепловых потерях – терминальная задача
оптимального управления, для решения которой необходимо минимизировать
функционал
tf
J dt t f
0
3. Найти оптимальное управление, обеспечивающее максимальную величину перемещения
объекта за заданное время с заданными тепловыми потерями – задача на максимальную
производительность, в которой необходимо обеспечить максимум функционала
tf
J (t )dt f
0

30.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Терминальную задачу не стоит путать с задачей на максимальное
быстродействие, в которой тепловые потери не ограничиваются, а ограничиваются
величины ускорения и скорости, т.е. ограничения накладываются не только на координаты,
но и на управление.
Последняя задача решается с использованием принципа максимума Понтрягина.
Все 3 задачи связаны между собой, и из решения одной из них можно легко получить
решение двух других.
Для этого достаточно из равенства, связывающего между собой тепловые потери,
перемещение и время
12 J 2 R 2f
J 2R
Q j 2 Q
,
c
c 2 t 3f
во втором случае определить минимальное время, а в третьем – определить максимальное
перемещение.

31.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
2
(t )
1.5
1
0.5
(t )
0
-0.5
-1
0
2
4
6
8
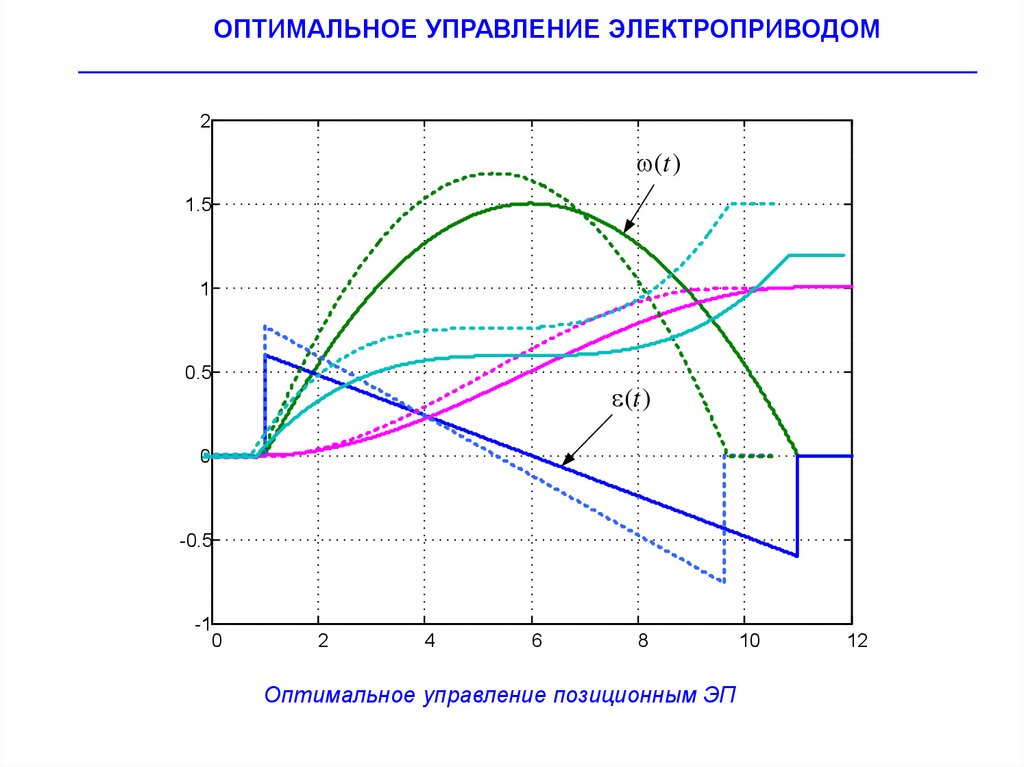
Оптимальное управление позиционным ЭП
10
12

32.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
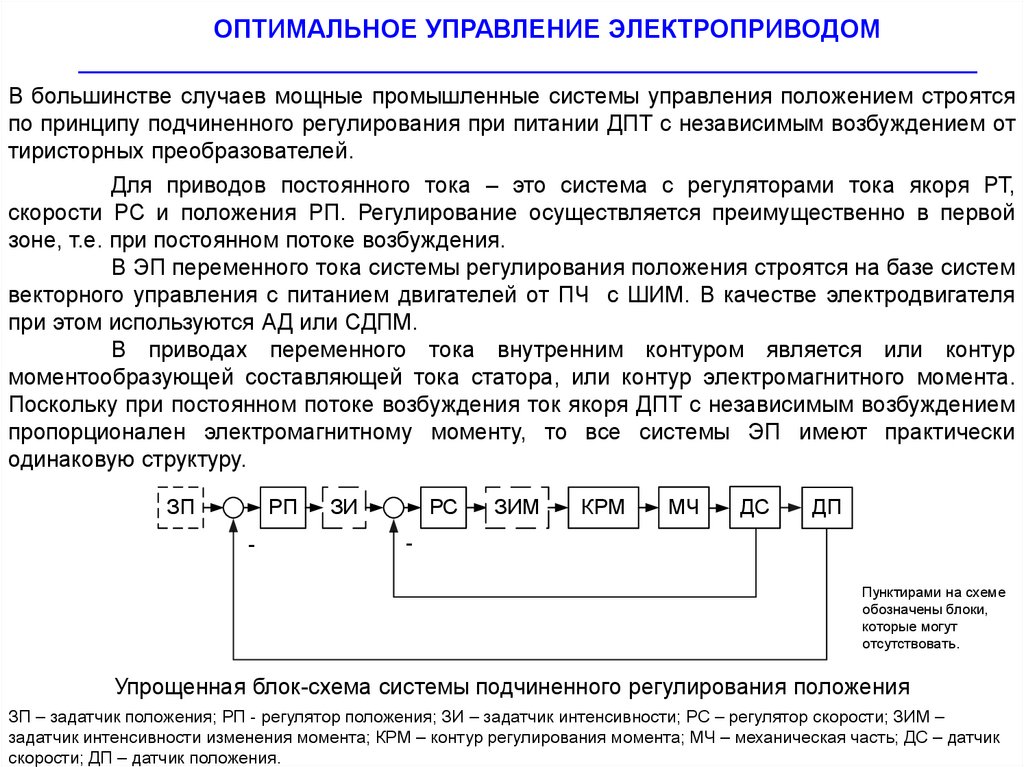
В большинстве случаев мощные промышленные системы управления положением строятся
по принципу подчиненного регулирования при питании ДПТ с независимым возбуждением от
тиристорных преобразователей.
Для приводов постоянного тока – это система с регуляторами тока якоря РТ,
скорости РС и положения РП. Регулирование осуществляется преимущественно в первой
зоне, т.е. при постоянном потоке возбуждения.
В ЭП переменного тока системы регулирования положения строятся на базе систем
векторного управления с питанием двигателей от ПЧ с ШИМ. В качестве электродвигателя
при этом используются АД или СДПМ.
В приводах переменного тока внутренним контуром является или контур
моментообразующей составляющей тока статора, или контур электромагнитного момента.
Поскольку при постоянном потоке возбуждения ток якоря ДПТ с независимым возбуждением
пропорционален электромагнитному моменту, то все системы ЭП имеют практически
одинаковую структуру.
ЗП
РП
-
ЗИ
РС
ЗИМ
КРМ
МЧ
ДС
ДП
Пунктирами на схеме
обозначены блоки,
которые могут
отсутствовать.
Упрощенная блок-схема системы подчиненного регулирования положения
ЗП – задатчик положения; РП - регулятор положения; ЗИ – задатчик интенсивности; РС – регулятор скорости; ЗИМ –
задатчик интенсивности изменения момента; КРМ – контур регулирования момента; МЧ – механическая часть; ДС – датчик
скорости; ДП – датчик положения.

33.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
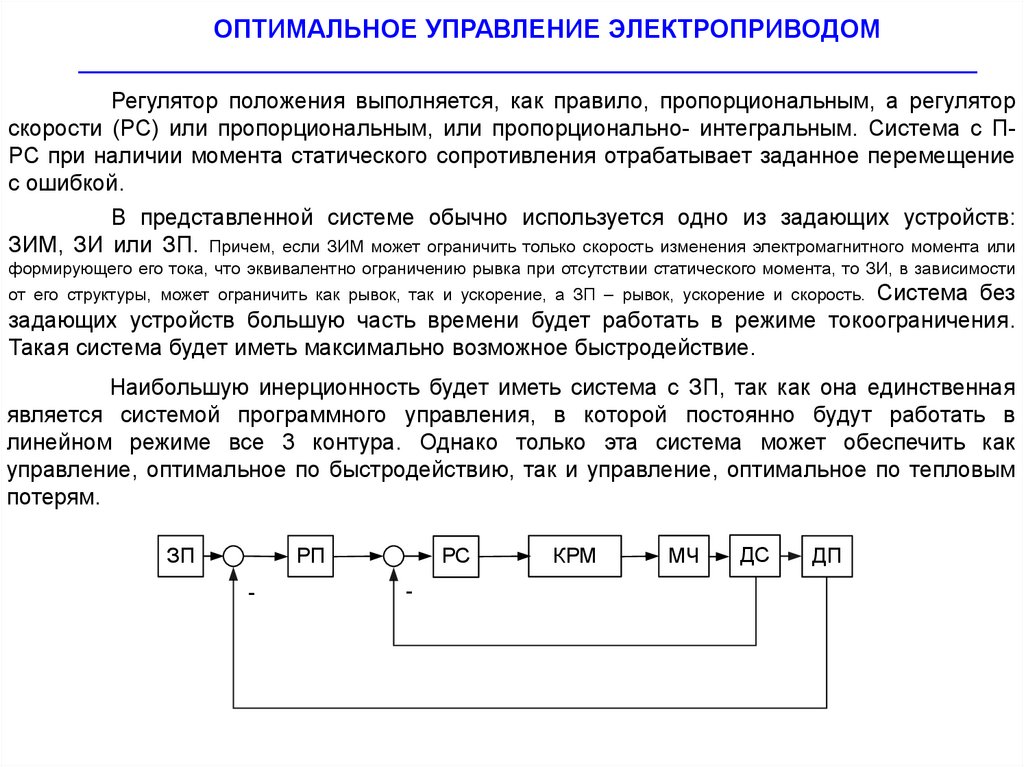
Регулятор положения выполняется, как правило, пропорциональным, а регулятор
скорости (РС) или пропорциональным, или пропорционально- интегральным. Система с ПРС при наличии момента статического сопротивления отрабатывает заданное перемещение
с ошибкой.
В представленной системе обычно используется одно из задающих устройств:
ЗИМ, ЗИ или ЗП. Причем, если ЗИМ может ограничить только скорость изменения электромагнитного момента или
формирующего его тока, что эквивалентно ограничению рывка при отсутствии статического момента, то ЗИ, в зависимости
Система без
задающих устройств большую часть времени будет работать в режиме токоограничения.
Такая система будет иметь максимально возможное быстродействие.
от его структуры, может ограничить как рывок, так и ускорение, а ЗП – рывок, ускорение и скорость.
Наибольшую инерционность будет иметь система с ЗП, так как она единственная
является системой программного управления, в которой постоянно будут работать в
линейном режиме все 3 контура. Однако только эта система может обеспечить как
управление, оптимальное по быстродействию, так и управление, оптимальное по тепловым
потерям.
ЗП
РП
-
РС
-
КРМ
МЧ
ДС
ДП

34.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Система с ЗИ и линейным РП может обеспечить только управление, оптимальное по
быстродействию, при работе по трапецеидальной тахограмме. Чтобы обеспечить
оптимальную отработку как больших, так и средних перемещений (работа по треугольной тахорамме),
необходимо использовать РП с нелинейной характеристикой, наладка которого является
достаточно сложной и ответственной технической задачей. Система с ЗИМ и без задающих устройств
может обеспечить управление оптимальное по быстродействию только в том случае, если величина статического момента
является неизменной и известной. Недостатком этой системы является также отсутствие ограничения по ускорению,
необходимое для многих производственных механизмов.
t0
з
0 , 0 , i0
Формирование
(nT )
Поэтому рассматриваем систему с цифровым ЗП.
(nT )
ЦИC
(nT )
ЦИП
(nT )
Структура задатчика положения, работающего по разомкнутому принципу
ЦИС, ЦИП – цифровые интеграторы, формирующие задание на скорость и положение
ЗП обычно функционируют следующим образом: Вначале они формируют
диаграмму задания на ускорение ε(nT) в виде кусочно-линейной аппроксимации табличной
зависимости, узловые точки которой рассчитываются, исходя из величины отрабатываемого
перемещения φз и желаемого времени его отработки t0 с учетом ограничений на скорость ω0
и ускорение ε0 привода.

35.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
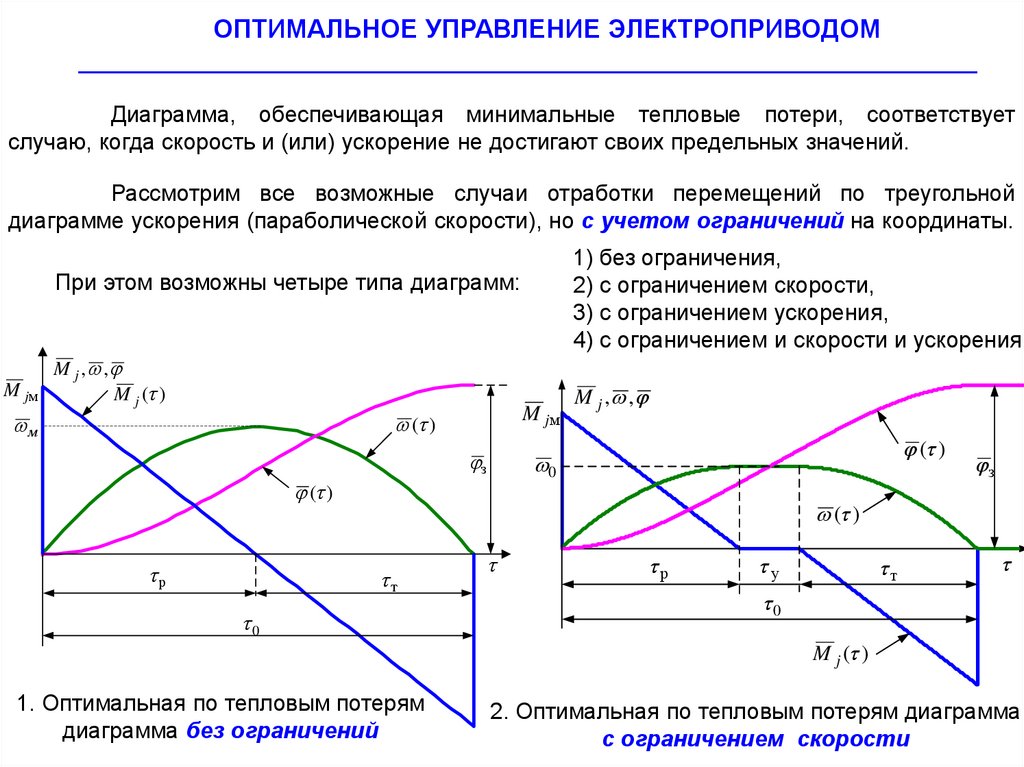
Диаграмма, обеспечивающая минимальные тепловые потери, соответствует
случаю, когда скорость и (или) ускорение не достигают своих предельных значений.
Рассмотрим все возможные случаи отработки перемещений по треугольной
диаграмме ускорения (параболической скорости), но с учетом ограничений на координаты.
1) без ограничения,
2) с ограничением скорости,
3) с ограничением ускорения,
4) с ограничением и скорости и ускорения.
При этом возможны четыре типа диаграмм:
M jм
M j , ,
M j ( )
M jм
( )
м
з
( )
0
( )
р
M j , ,
з
( )
т
0
1. Оптимальная по тепловым потерям
диаграмма без ограничений
р
у
т
0
M j ( )
2. Оптимальная по тепловым потерям диаграмма
с ограничением скорости

36.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
M j , ,
M j , ,
M j ( )
M0
M j ( )
M0
м
( )
з
( )
0
з
( )
( )
1
р
т
0
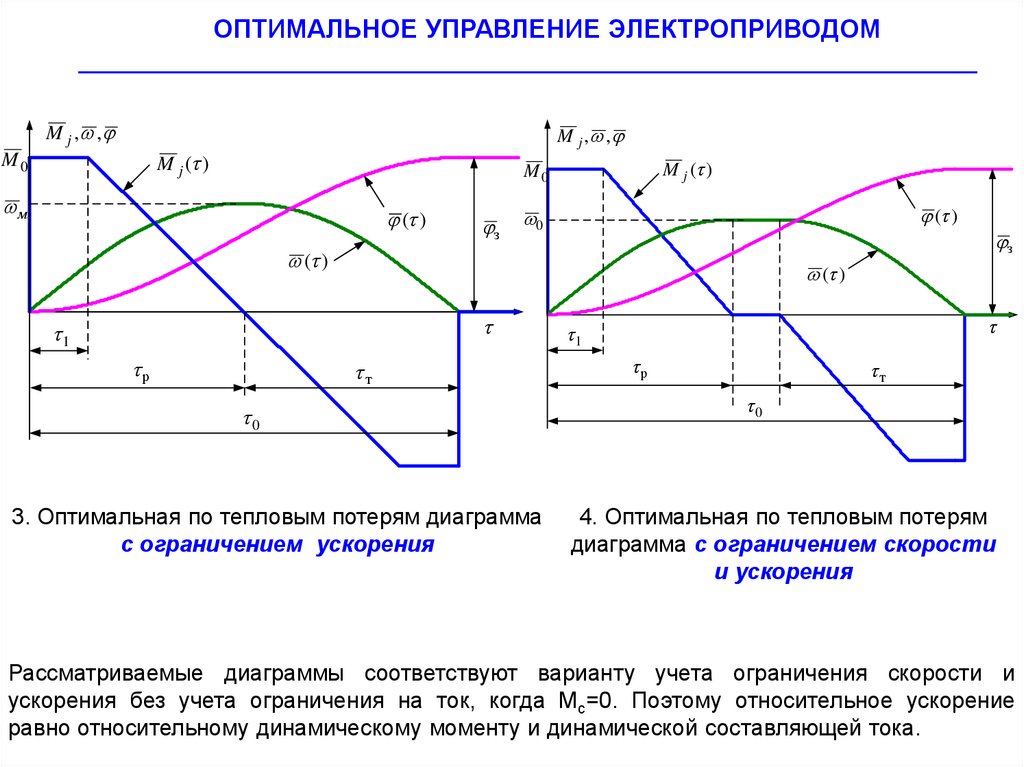
3. Оптимальная по тепловым потерям диаграмма
с ограничением ускорения
1
р
т
0
4. Оптимальная по тепловым потерям
диаграмма с ограничением скорости
и ускорения
Рассматриваемые диаграммы соответствуют варианту учета ограничения скорости и
ускорения без учета ограничения на ток, когда Мс=0. Поэтому относительное ускорение
равно относительному динамическому моменту и динамической составляющей тока.

37.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________

38.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
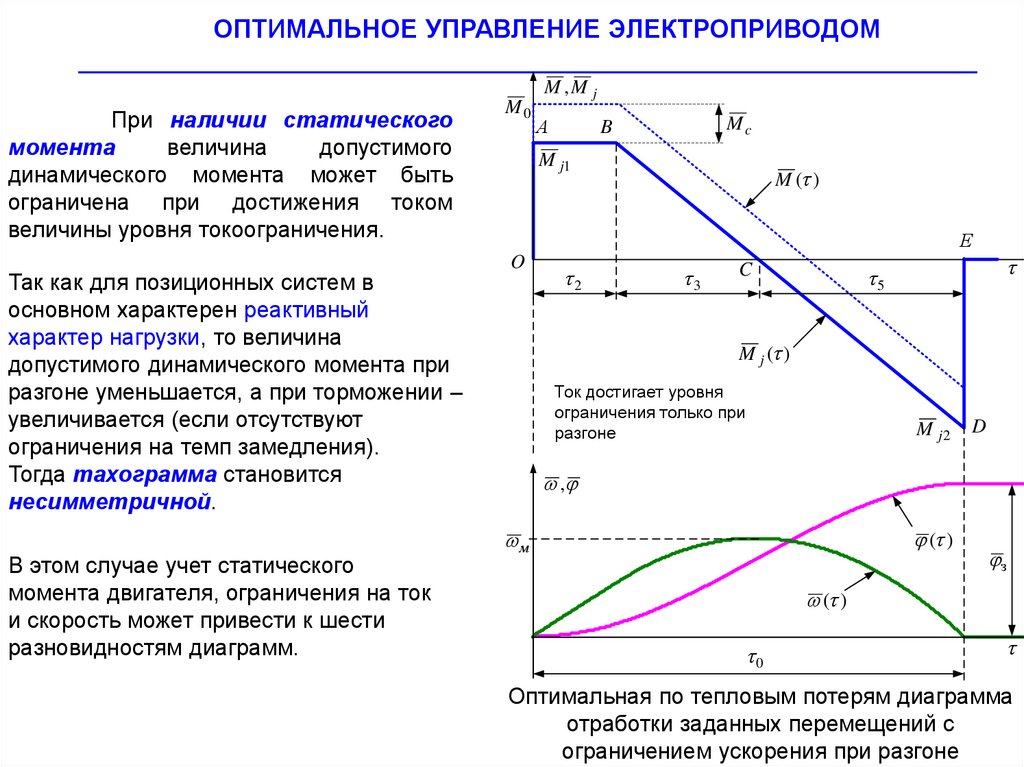
При наличии статического
момента
величина
допустимого
динамического момента может быть
ограничена при достижения током
величины уровня токоограничения.
Так как для позиционных систем в
основном характерен реактивный
характер нагрузки, то величина
допустимого динамического момента при
разгоне уменьшается, а при торможении –
увеличивается (если отсутствуют
ограничения на темп замедления).
Тогда тахограмма становится
несимметричной.
В этом случае учет статического
момента двигателя, ограничения на ток
и скорость может привести к шести
разновидностям диаграмм.
M0
M ,M j
А
Mc
B
M j1
M ( )
Е
O
2
3
C
5
M j ( )
Ток достигает уровня
ограничения только при
разгоне
M j2
D
,
( )
м
з
( )
0
Оптимальная по тепловым потерям диаграмма
отработки заданных перемещений с
ограничением ускорения при разгоне

39.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
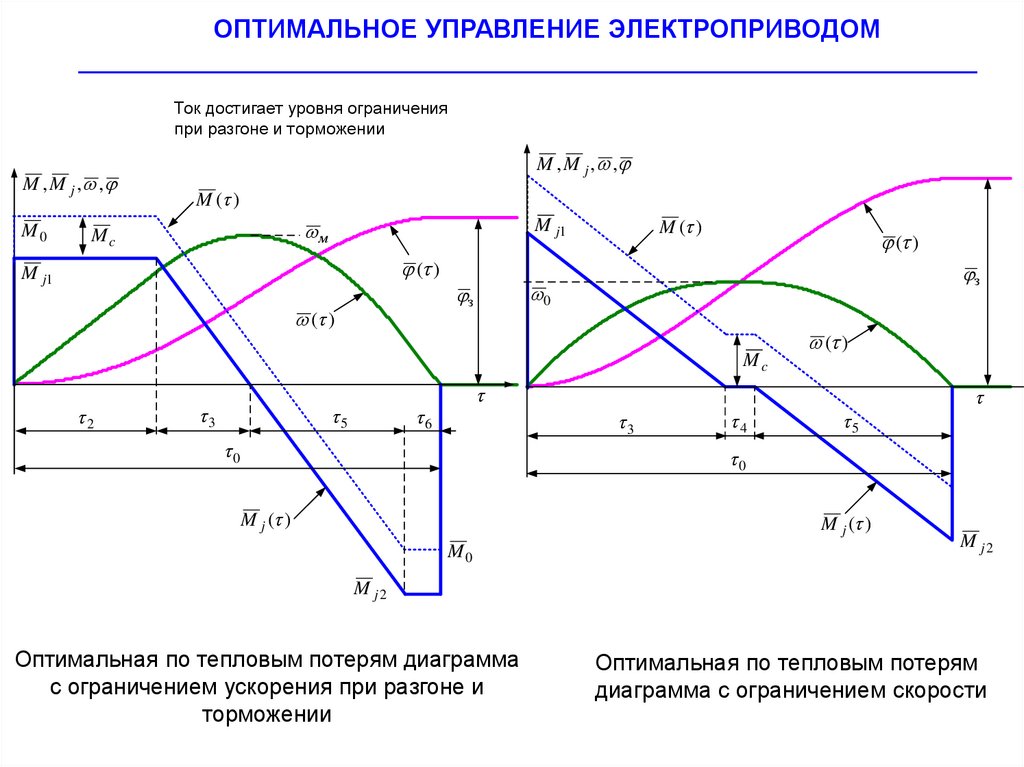
Ток достигает уровня ограничения
при разгоне и торможении
M , M j , ,
M0
M , M j , ,
M ( )
м
Mc
M ( )
M j1
( )
M j1
з
0
з
( )
( )
Mc
2
3
5
( )
6
3
0
4
5
0
M j ( )
M j ( )
M0
M j2
M j2
Оптимальная по тепловым потерям диаграмма
с ограничением ускорения при разгоне и
торможении
Оптимальная по тепловым потерям
диаграмма с ограничением скорости

40.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
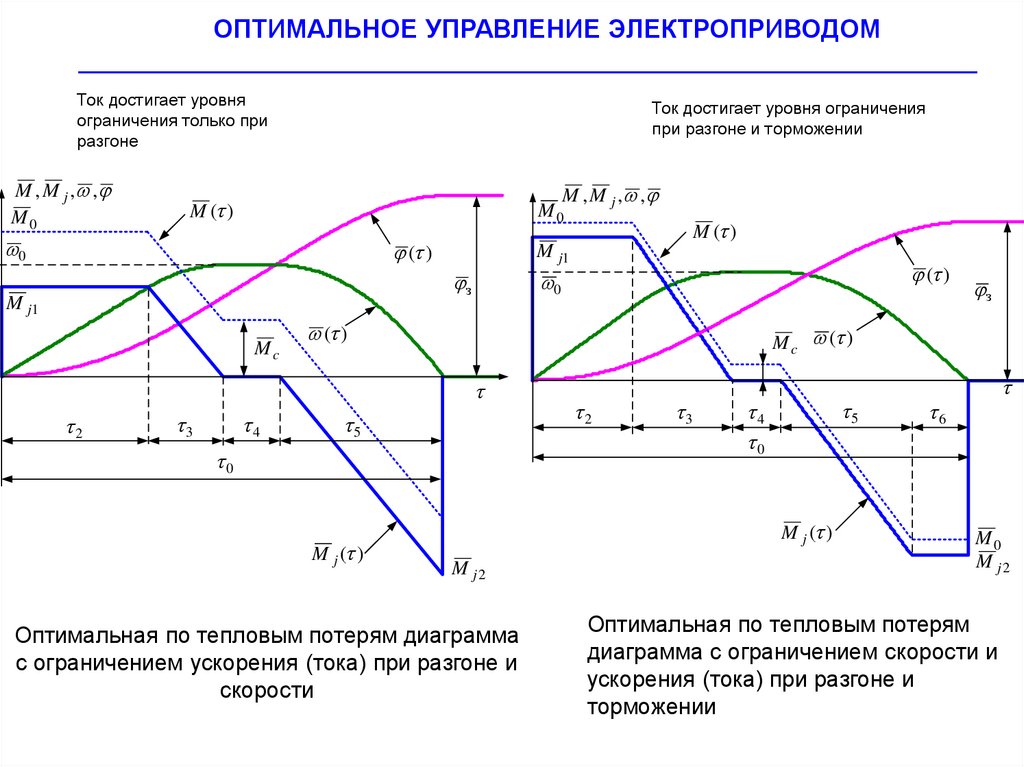
Ток достигает уровня
ограничения только при
разгоне
M , M j , ,
M0
Ток достигает уровня ограничения
при разгоне и торможении
M , M j , ,
M0
M ( )
0
( )
M j1
Mc
( )
4
3
5
0
M j ( )
з
M c ( )
2
( )
0
з
M j1
M ( )
2
3
5
4
0
M j ( )
M j2
Оптимальная по тепловым потерям диаграмма
с ограничением ускорения (тока) при разгоне и
скорости
6
M0
M j2
Оптимальная по тепловым потерям
диаграмма с ограничением скорости и
ускорения (тока) при разгоне и
торможении

41.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
M , M j , ,
M0
M ( )
Mc
M , M j , ,
м
M0
M j1
( )
M j1
M ( )
( )
0
з
з
( )
( )
2
Mc
6
0
M j ( )
2
4
6
0
Mc
M0
M j2
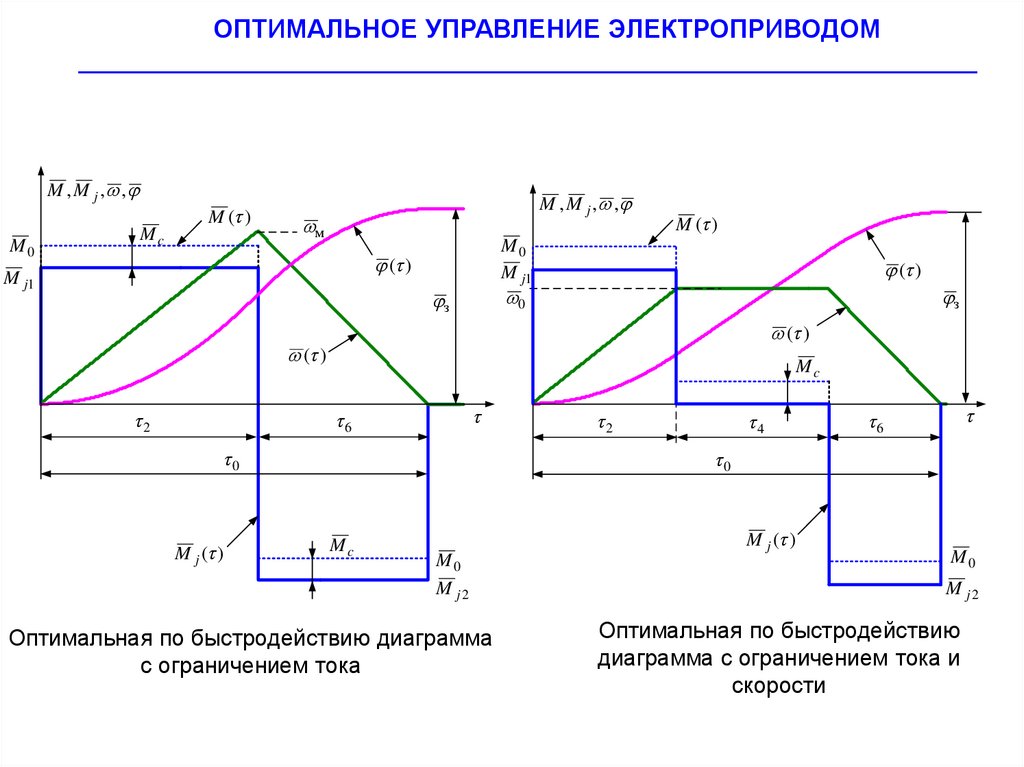
Оптимальная по быстродействию диаграмма
с ограничением тока
M j ( )
M0
M j2
Оптимальная по быстродействию
диаграмма с ограничением тока и
скорости

42.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
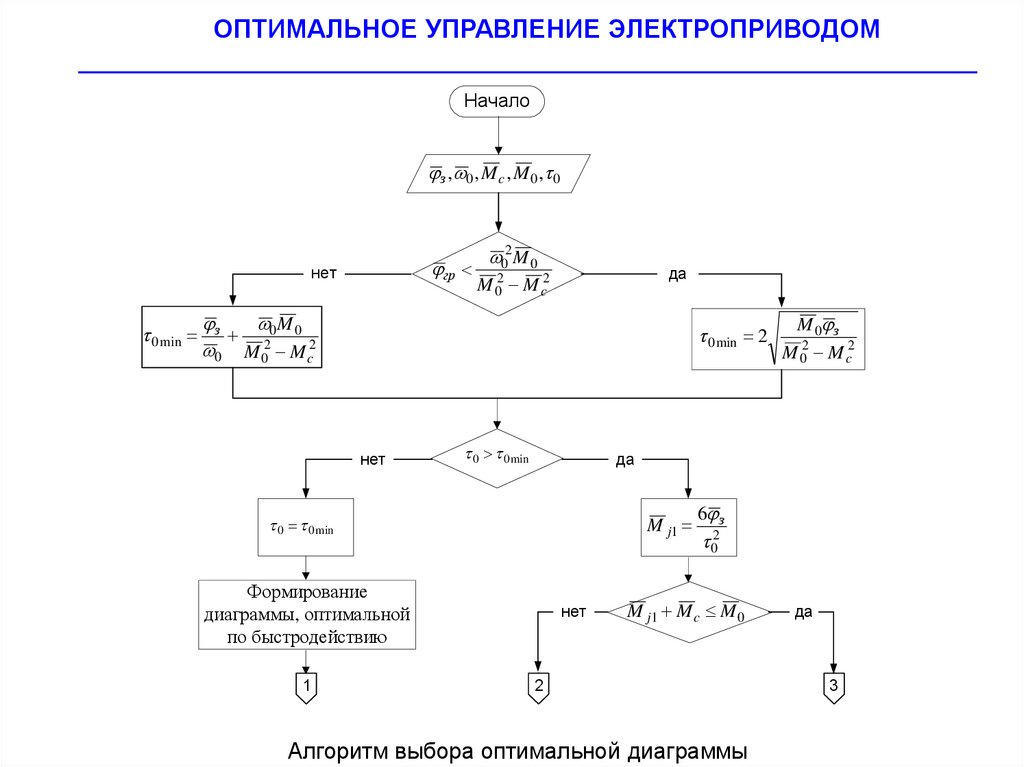
Начало
з , 0 , M c , M 0 , 0
гр
нет
0 min
02 M 0
да
M 02 M c2
з
M
20 0 2
0 M 0 M c
0 min 2
нет
0 0 min
да
M j1
0 0 min
Формирование
диаграммы, оптимальной
по быстродействию
1
M 0 з
M 02 M c2
нет
6 з
02
M j1 M c M 0
2
Алгоритм выбора оптимальной диаграммы
да
3

43.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
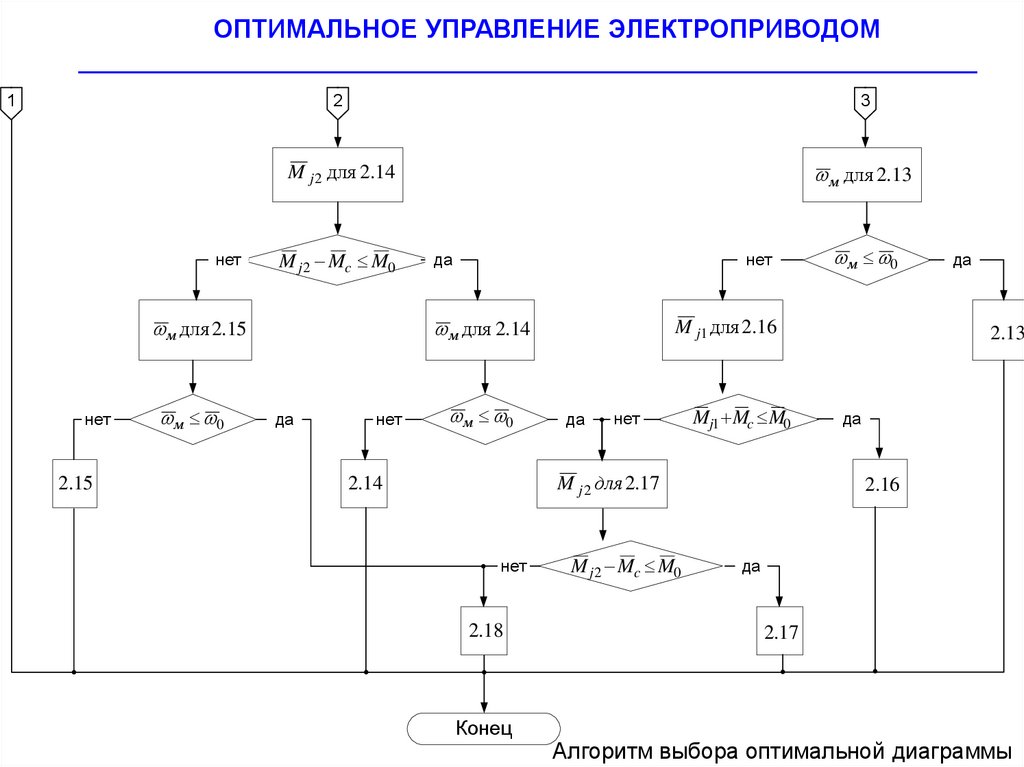
1
нет
2
3
M j 2 для 2.14
м для 2.13
M j 2 Mc M0
2.15
м 0
нет
м для 2.14
м для 2.15
нет
да
да
нет
м 0
M j1 для 2.16
да
нет
Mj1 Mc M0
M j 2 для 2.17
2.14
нет
2.18
Конец
м 0
M j2 Mc M0
да
2.13
да
2.16
да
2.17
Алгоритм выбора оптимальной диаграммы

44.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
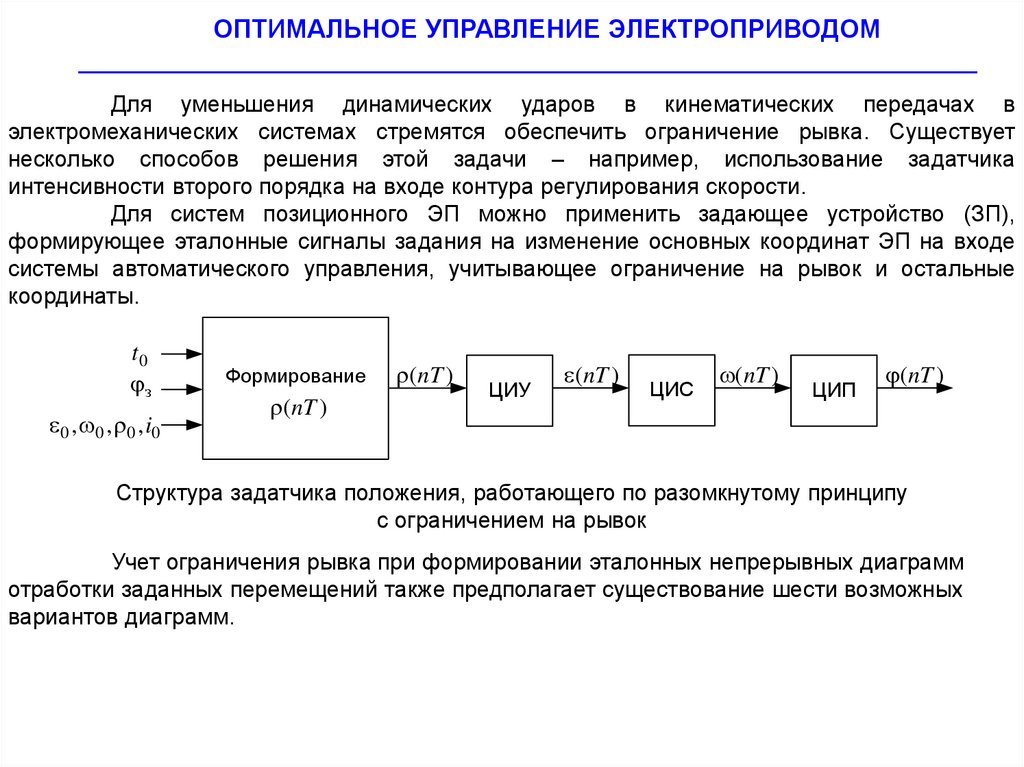
Для уменьшения динамических ударов в кинематических передачах в
электромеханических системах стремятся обеспечить ограничение рывка. Существует
несколько способов решения этой задачи – например, использование задатчика
интенсивности второго порядка на входе контура регулирования скорости.
Для систем позиционного ЭП можно применить задающее устройство (ЗП),
формирующее эталонные сигналы задания на изменение основных координат ЭП на входе
системы автоматического управления, учитывающее ограничение на рывок и остальные
координаты.
t0
з
0 , 0 , 0 , i0
Формирование
(nT )
(nT )
ЦИУ
(nT )
ЦИС
(nT )
ЦИП
(nT )
Структура задатчика положения, работающего по разомкнутому принципу
с ограничением на рывок
Учет ограничения рывка при формировании эталонных непрерывных диаграмм
отработки заданных перемещений также предполагает существование шести возможных
вариантов диаграмм.

45.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
M j , ,
M j , ,
M j ( )
M j1
( )
м
M j ( )
M j1
( )
м
з
( )
1
3
з
( )
5
7
0
3
5
7
0
M j2
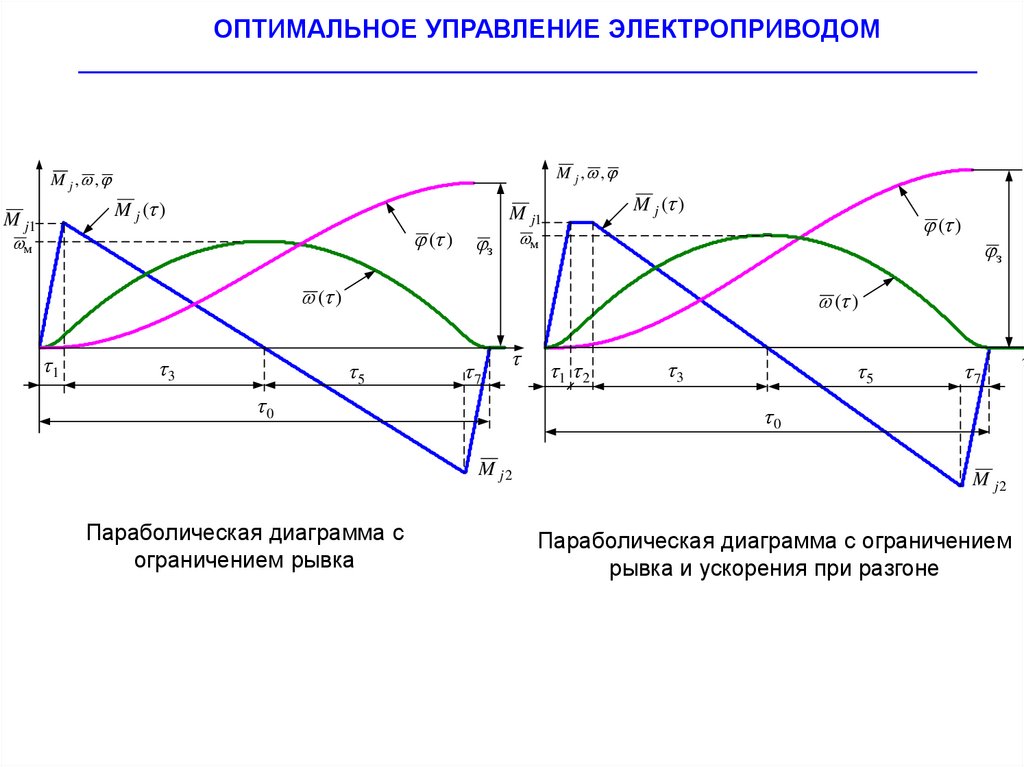
Параболическая диаграмма с
ограничением рывка
1 2
M j2
Параболическая диаграмма с ограничением
рывка и ускорения при разгоне

46.

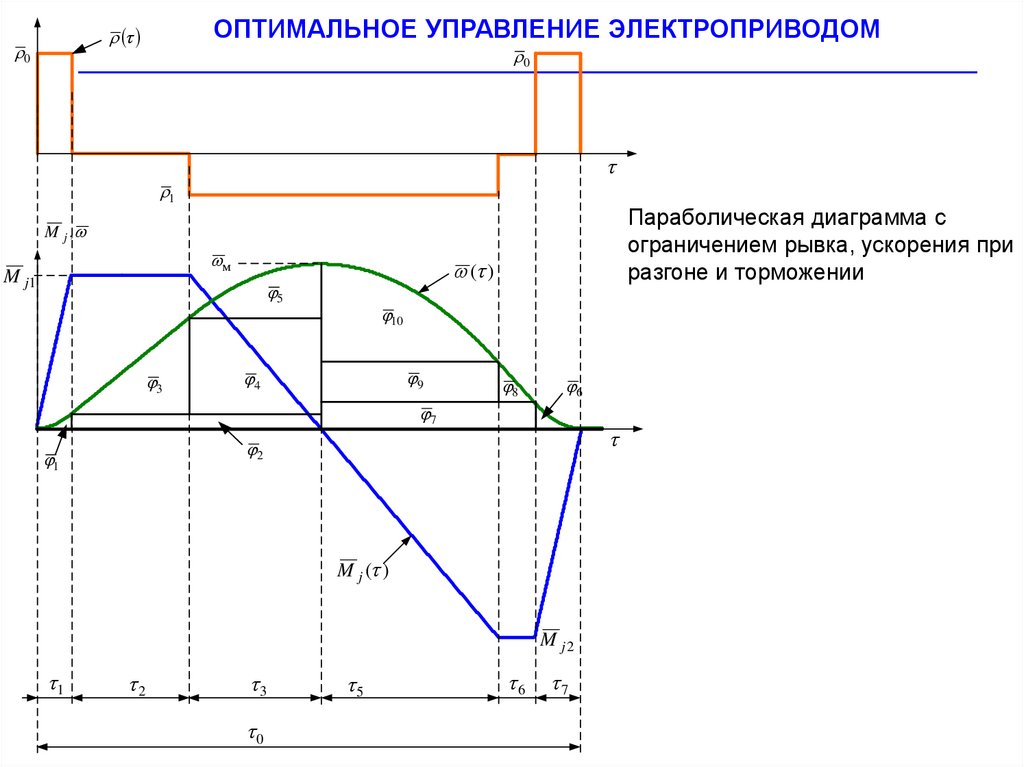
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
0
_______________________________________________________________
0
1
Параболическая диаграмма с
ограничением рывка, ускорения при
разгоне и торможении
M j ,
м
M j1
( )
5
3
10
9
4
8
6
7
2
1
M j ( )
M j2
1
2
3
0
5
6
7

47.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
M j , ,
M j , ,
M j ( )
M j1
M j1
( )
0
M j ( )
( )
з 0
( )
1
3
4
з
( )
5
7
1
2
3
4
5
7
0
0
M j2
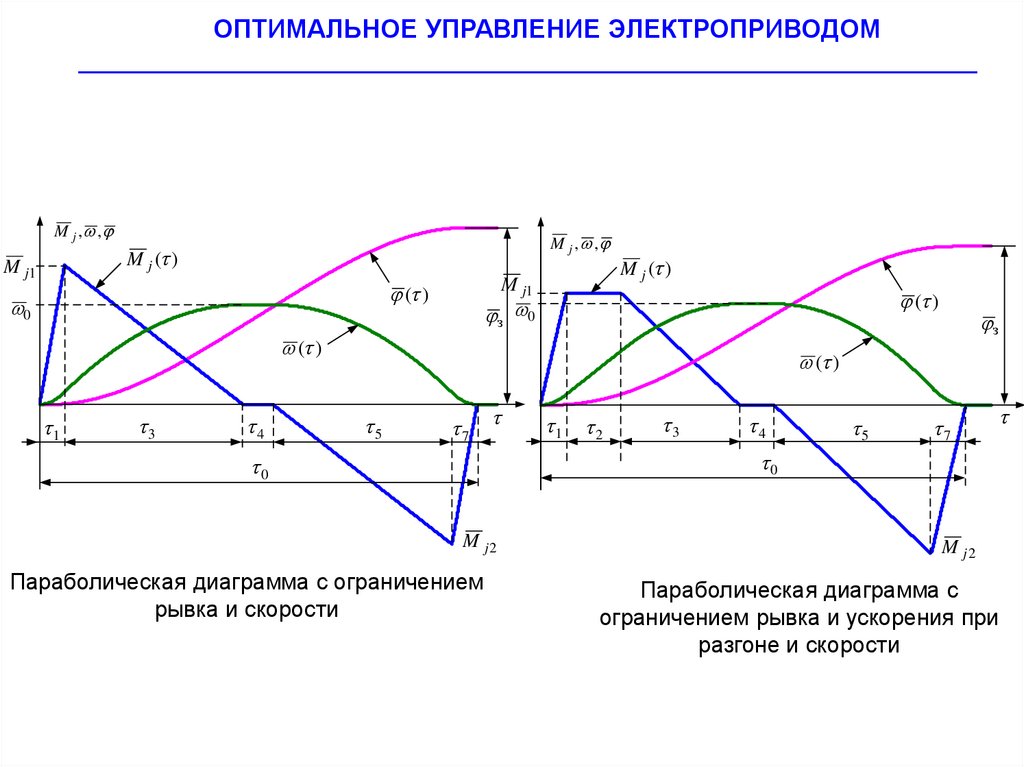
Параболическая диаграмма с ограничением
рывка и скорости
M j2
Параболическая диаграмма с
ограничением рывка и ускорения при
разгоне и скорости

48.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
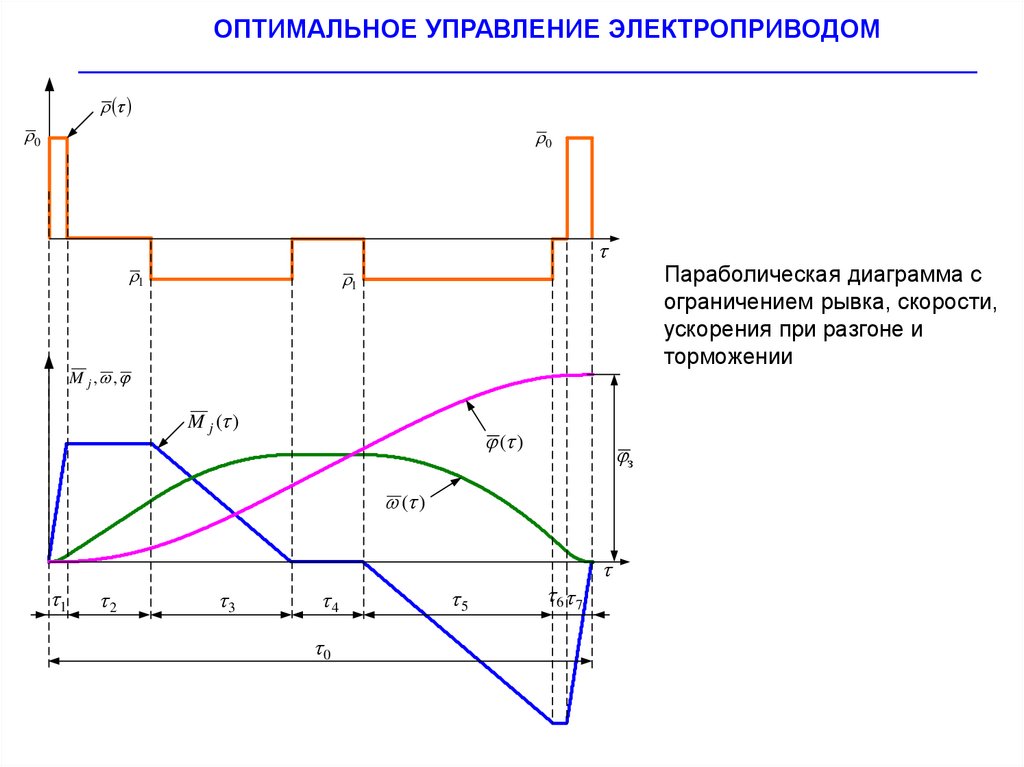
0
0
1
Параболическая диаграмма с
ограничением рывка, скорости,
ускорения при разгоне и
торможении
1
M j , ,
M j ( )
( )
з
( )
1
2
3
4
0
5
6 7

49.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
м
M j ( )
M j , ,
M j , ,
0
( )
M j1
( )
M j1
з
з
( )
1
2
3
5
( )
6
7
1
2
4
3
5
6
7
0
0
M j ( )
M j2
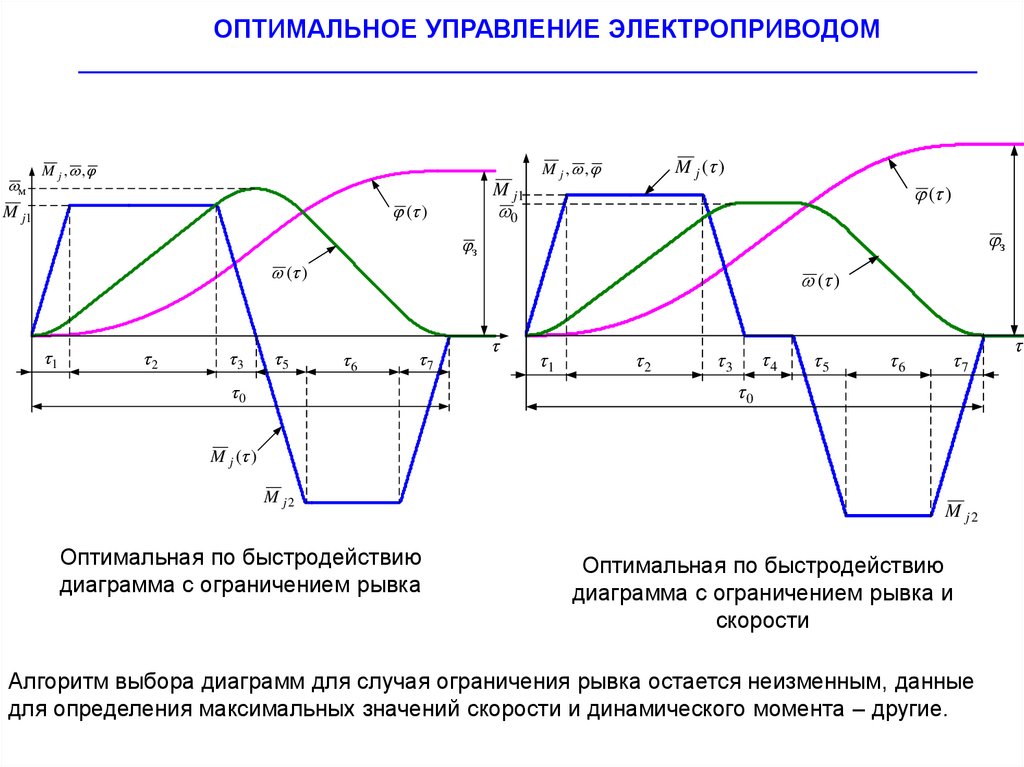
Оптимальная по быстродействию
диаграмма с ограничением рывка
M j2
Оптимальная по быстродействию
диаграмма с ограничением рывка и
скорости
Алгоритм выбора диаграмм для случая ограничения рывка остается неизменным, данные
для определения максимальных значений скорости и динамического момента – другие.

50.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
При сравнении различных законов управления позиционными механизмами чаще
всего анализируют только величину тепловых потерь при нулевом статическом моменте Mс
на валу двигателя. Однако, наряду с тепловыми потерями, необходимо рассчитывать и
анализировать еще и величину механической мощности, затрачиваемой на совершение
полезной работы.
Суммируя оба эти показателя, можно оценить величину энергопотребления
системы и выбрать, если это позволяют технологические условия, время отработки
заданного перемещения из условия минимума потребляемой электроэнергии.
Электроэнергия, потребляемая из сети
t
А U (t )I я (t )dt AМ AТ
(потерями в обмотке
возбуждения
пренебрегаем)
0
расходуется на механическую работу
t
и тепловые потери в цепи якоря
t
t
AМ EД (t ) I я (t )dt (t ) M (t )dt
0
AТ I я2 (t ) Rя dt
0
0
Разложим электромагнитный момент двигателя и пропорциональный ему (при постоянном
потоке возбуждения) ток якоря на статическую и динамическую составляющие:
M (t ) M j (t ) M c
I я (t ) I j (t ) I c

51.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Тогда
t
t
t
AТ
0
0
0
AМ (t ) M j (t )dt M с (t )dt
Учитывая, что
t
t
I j (t )dt (t0 ) 0
(t )dt
0
0
AМ M с
и
t
2 t 2
( I j (t ) I c ) Rя dt Rя I c t I j (t )dt 2 I c I j (t )dt
0
0
0
t
I я2 (t )Rя dt
2
t
(t )M j (t )dt 0 , окончательно имеем:
0
t
2 t 2
2
AТ Rя I c t I j (t )dt AcТ A jТ Rя I c t0 Rя I 2j (t )dt
0
0
Найдем выражения для расчета тепловых
потерь электроэнергии от действия
динамической составляющей тока якоря AjTi
на каждом из участков диаграммы (i – номер
участка), полагая, что механическая
характеристика привода является абсолютно
жесткой.
Cуммарные тепловые потери от
динамического тока для рассматриваемой
диаграммы составляют:
1
A jТ 2 Rя I 2j 0t1 I 2j 0t2
3
Выражения для этих потерь через величину перемещения, время его отработки
и ограничения по скорости и ускорению (динамическому току) выведены
(показаны ранее).
t
0
1
t
0
t
t
2
t1
t2
t3
t4
t5
Диаграмма отработки перемещения

52.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Добавляя к ним составляющие
AcТ Rя I c2t0
и
AМ M с ,
легко переходим к выражениям для полных потерь.
Величина потребленной электроэнергии и время достижения минимума

53.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
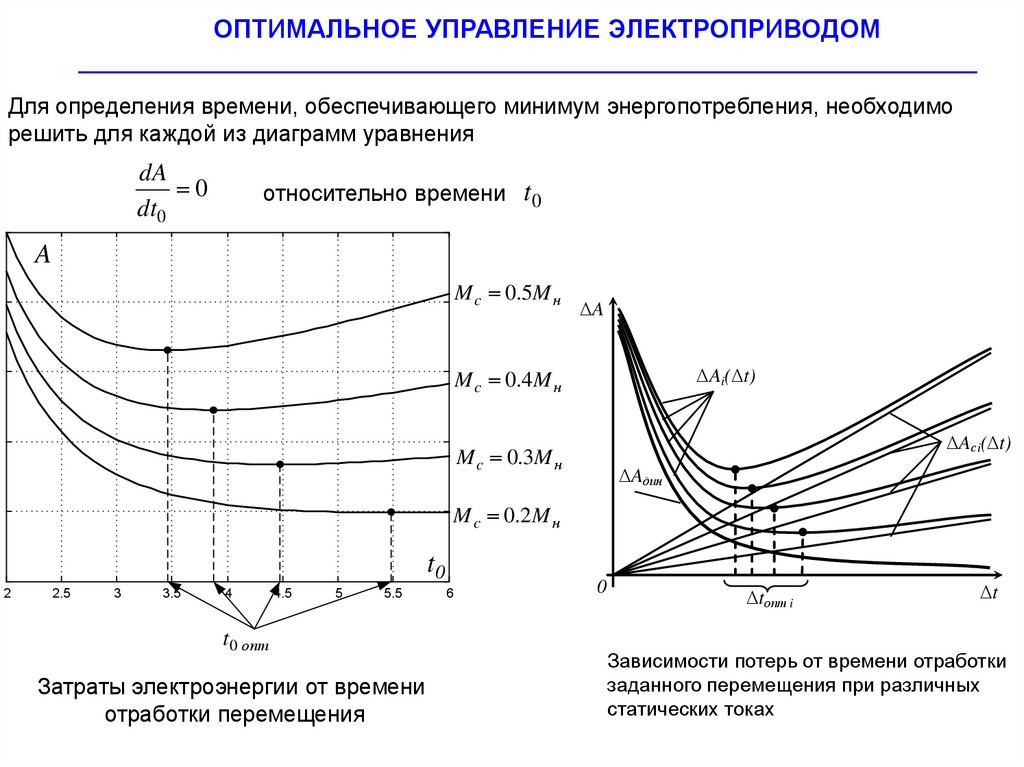
Для определения времени, обеспечивающего минимум энергопотребления, необходимо
решить для каждой из диаграмм уравнения
dA
0
dt0
относительно времени t 0
A
M c 0.5M н
ΔA
M c 0.4M н
ΔAi(Δt)
ΔAсi(Δt)
M c 0.3M н
ΔAдин
M c 0.2M н
t0
2
2.5
3
3.5
4
4.5
5
5.5
t0 опт
Затраты электроэнергии от времени
отработки перемещения
6
0
Δtопт i
Δt
Зависимости потерь от времени отработки
заданного перемещения при различных
статических токах

54.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Оптимизация энергопотребления позиционным электроприводом на основе системы
векторного управления АД
При минимизации тепловых потерь часто пренебрегают некоторыми их
составляющими. Например, в приводах постоянного тока не учитывают потери в обмотке
возбуждения; очень часто для ЭП, у которых момент нагрузки обусловлен только наличием
трения, пренебрегают потерями от статических составляющих токов.
При переносе опыта, полученного при разработке этих систем, на современные
системы векторного управления АД необходимо учитывать некоторые их особенности. В
частности, соотношение между потокообразующей и моментообразующей составляющими
тока статора в АД таково, что потерями, обусловленными необходимостью поддержания
потокосцепления ротора на заданном уровне в процессе перемещения пренебрегать нельзя.
(В АД отношение статических потерь к динамическим выше, чем в ДПТ, т.к. постоянной составляющей потерь в АД нельзя
пренебречь даже в режиме идеального холостого хода.)
Суммарные потери в обмотках 3-хфазного АД:
t
A 3 I s2 Rs I r2 Rr dt
0
В АД с векторным полеориентированным управлением, для мат. описания которого обычно
используют ортогональную систему координат dq, ориентированную по вектору
потокосцепления ротора, пространственный вектор тока статора представляют в виде двух
ортогональных составляющих, одна из которых формирует потокосцепление ротора в
соответствии с передаточной функцией
Lm
r p
,
isd p Tr p 1
а вторая – электромагнитный момент в соответствии с выражением
M 3z p kr r isq / 2 .

55.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Оптимизация энергопотребления позиционным электроприводом на основе системы
векторного управления АД
Электромагнитный момент двигателя можно разделить на 2 составляющие: статическую и
d (t )
динамическую:
M M j Mc
Mj J
dt
Соответственно моментообразующую составляющую тока статора можно представить в виде
Mj
суммы динамической и статической компонент:
2 Mc
isq isqj isqc 2
3 z p kr r 3 z p kr r
Суммарные потери АД можно разделить на следующие составляющие:
- потери от токов, вызывающих изменение скорости ЭП:
t
t
t
3
3
2
2
2
2
A j
Rs isqj (t )dt Rr irqj (t )dt Rs k r Rr isqj
(t )dt
2
2 0
0
0
- потери от токов, уравновешивающих действие момента статического сопротивления и
способствующих поддержанию скорости на заданном уровне, которые при постоянной
нагрузке и при однозонном регулировании скорости являются линейной функцией времени:
Ac
M c2
3
2
2
2
Rs kr Rr isqct Rs kr Rr
t
2
z p kr r 0
- потери от токов, обеспечивающих изменение
потокосцепления ротора
A j
- потери от токов, обеспечивающих поддержание
постоянства потокосцепления ротора
t
t
3
2
2
Rs isd (t )dt Rr ird
(t )dt
2 0
0
Ac
2
3 2
3 rd
Rsisd 0t Rs 2 0 t .
2
2
Lm

56.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Оптимизация энергопотребления позиционным электроприводом на основе системы
векторного управления АД
Тогда суммарные тепловые потери при отработке заданного перемещения с постоянным
потокосцеплением ротора:
t
3
2
2
2
2
2
A Ac Ac A j
Rs kr Rr isqc Rsisd 0 t Rs kr Rr isqj (t )dt
2
0
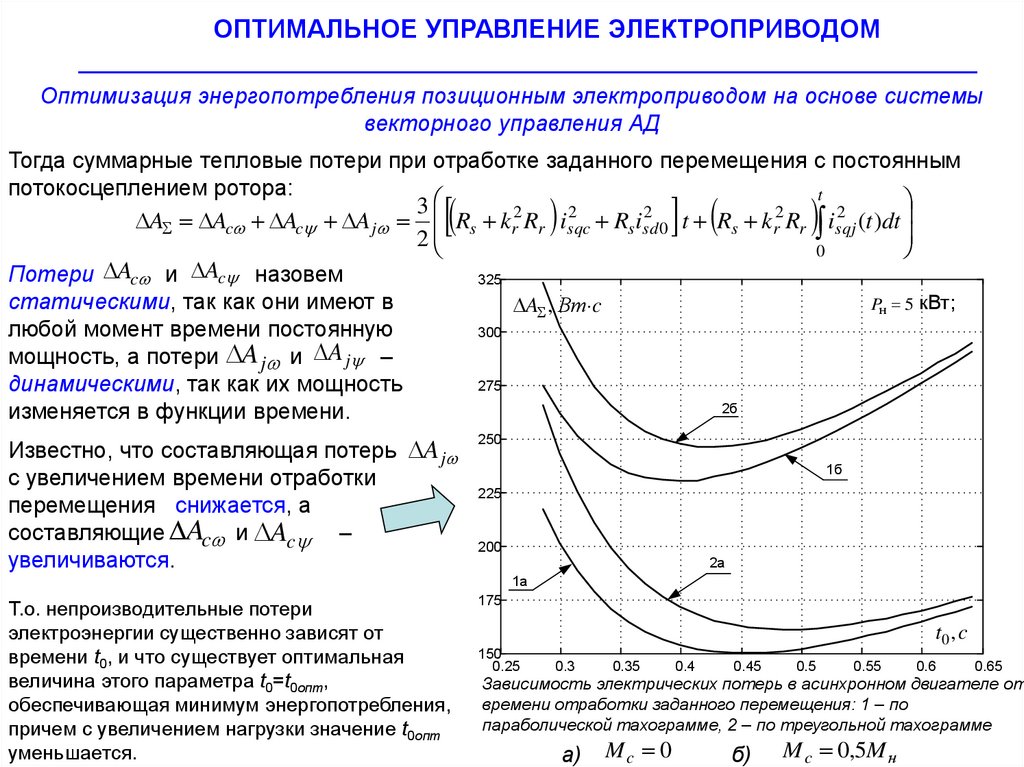
A
Потери Ac и
c назовем
325
статическими, так как они имеют в
Pн 5 кВт;
A , Вт c
любой момент времени постоянную
300
мощность, а потери A j и A j –
275
динамическими, так как их мощность
2б
изменяется в функции времени.
Известно, что составляющая потерь A j
с увеличением времени отработки
перемещения снижается, а
составляющие Ac и Ac –
увеличиваются.
250
1б
225
200
2a
1a
Т.о. непроизводительные потери
электроэнергии существенно зависят от
времени t0, и что существует оптимальная
величина этого параметра t0=t0опт,
обеспечивающая минимум энергопотребления,
причем с увеличением нагрузки значение t0опт
уменьшается.
175
t0 , c
150
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
Зависимость электрических потерь в асинхронном двигателе от
времени отработки заданного перемещения: 1 – по
параболической тахограмме, 2 – по треугольной тахограмме
а)
Mc 0
б)
M c 0,5M н

57.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Оптимизация энергопотребления позиционным электроприводом на основе системы
векторного управления АД
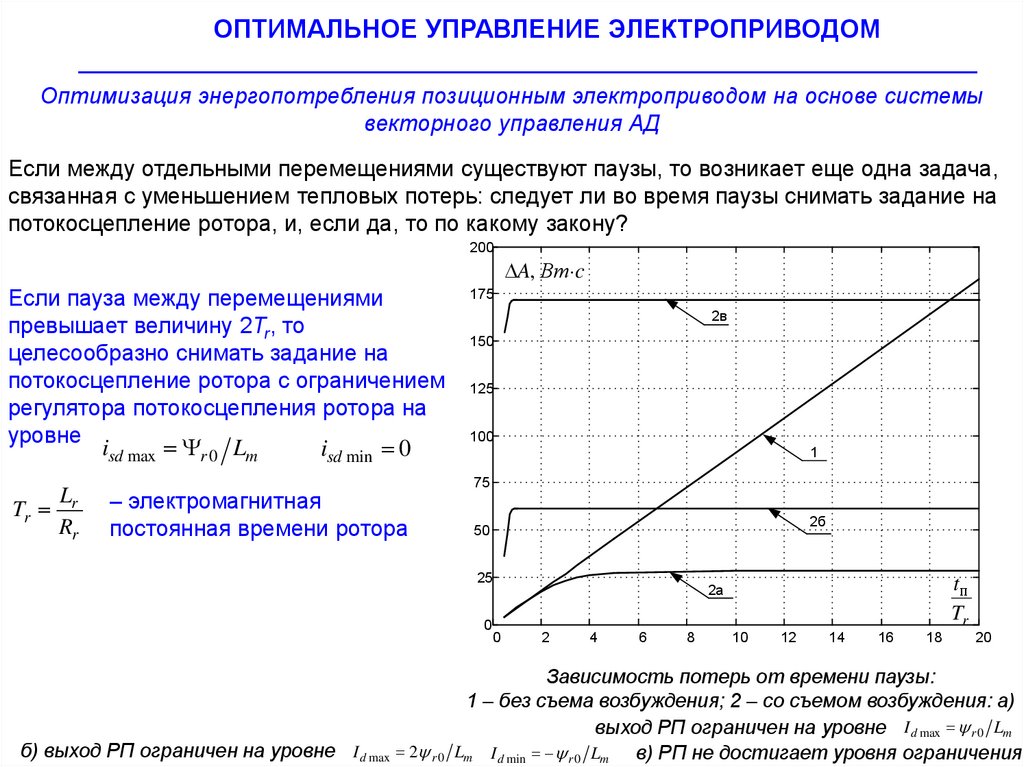
Если между отдельными перемещениями существуют паузы, то возникает еще одна задача,
связанная с уменьшением тепловых потерь: следует ли во время паузы снимать задание на
потокосцепление ротора, и, если да, то по какому закону?
200
A, Вт c
Если пауза между перемещениями
превышает величину 2Tr, то
целесообразно снимать задание на
потокосцепление ротора с ограничением
регулятора потокосцепления ротора на
уровне
isd max r 0 Lm
isd min 0
L
Tr r
Rr
– электромагнитная
постоянная времени ротора
175
2в
150
125
100
1
75
2б
50
25
0
б) выход РП ограничен на уровне I d max 2 r 0
tп
Tr
2a
0
2
4
6
8
10
12
14
16
18
20
Зависимость потерь от времени паузы:
1 – без съема возбуждения; 2 – со съемом возбуждения: а)
выход РП ограничен на уровне I d max r 0 Lm
Lm I d min r 0 Lm
в) РП не достигает уровня ограничения

58.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
ОПТИМИЗАЦИЯ ЭНЕРГОПОТРЕБЛЕНИЯ ПОЗИЦИОННЫМ ЭП ПРИ УЧЕТЕ ЭНЕРГИИ ПОТЕРЬ ОТ
ПОДДЕРЖАНИЯ МАГНИТНОГО ПОЛЯ ДВИГАТЕЛЯ
Суммарные потери энергии можно представить в
виде суммы составляющих:
t0
A Aa A f Ra ia2 (t )dt R f i 2f t0
0
A Aac A f Aaj
Ra
M c2
c2
t0
R f i 2f t0
Ra
J2
c2
t0
2
(t )dt
0
В последней формуле первые два слагаемых определяют статические потери , мощность
которых постоянна, а энергия возрастает пропорционально времени работы привода. Третье
слагаемое определяет динамические потери, мощность и энергия которых зависят от формы
и параметров диаграммы ускорения.

59.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________

60.

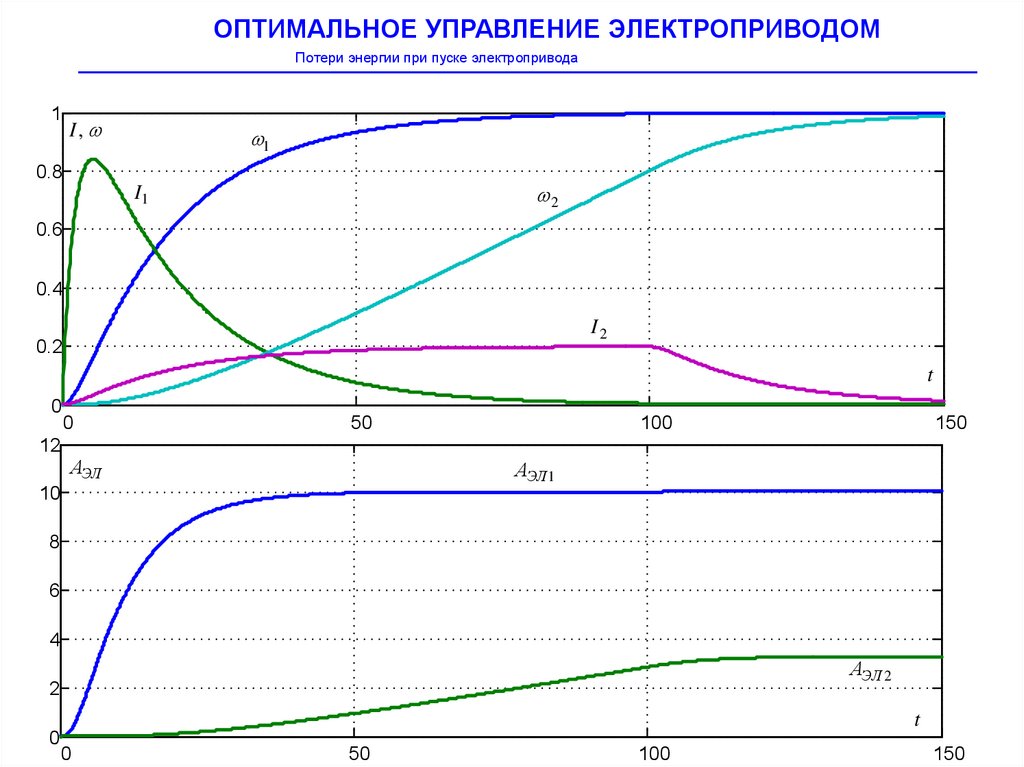
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ Зеленов А.Б.
Потери энергии при пуске электропривода
«Теория электропривода»
_______________________________________________________________
При пуске и торможении ЭП с различными типами ЭД всегда есть потери энергии,
определяющие экономичность ЭП. Рассмотрим расчет потерь в ЭП при пуске и торможении,
зависимость величины потерь от параметров ЭП, способов пуска и торможения.
Потери при пуске ДПТ.
Допущения: пуск двигателя производится без нагрузки; машина разгоняется до скорости идеального холостого хода; потери
энергии на намагничивание (потери в стали), механические потери и возбуждение не учитываются.
Потребляемая из сети мощность расходуется на механическую работу и на потери в цепи
якоря:
Р РМЕХ РЭЛ или U Н I EI I 2 RЯ
(1)
Для выяснения количества энергии, потребляемой из сети и распределяемой при пуске ЭП,
необходимо проинтегрировать выражение (1) в пределах времени пуска (0-tП), за которое
скорость двигателя меняется от 0 до ω0:
А АМЕХ АЭЛ
0
0
0
2
U
Idt
EIdt
I
Н
RЯ dt .
или
0
0
(2)
0
Для перехода под знаком интеграла от dt к dω надо воспользоваться следующими известными соотношениями:
U Н СФН 0
Е СФН
М СФН I J
d
dt
I
J
d
СФН dt
Учтя их, определим энергию, потребляемую из сети А и механическую работу АМЕХ:
0
J
d
А СФН 0
dt
СФ
dt
Н
0
0
J 0 d J 0
2
0
.
(3)

61.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
Потери энергии при пуске электропривода
_______________________________________________________________
Т.о., при пуске двигателя вхолостую из сети потребляется энергия, равная удвоенному запасу
кинетической энергии ЭП. Выражение (2) лучше записать в виде:
А J 0 ( 0 0) ,
(4)
где видна скорость, до которой идет разгон двигателя (ω0) и перепад скорости на ступени пуска (ω0 - 0).
Для определения величины механической работы вычислим
0
АМЕХ
J
d
СФН
dt
СФ
dt
Н
0
0
J d J
0
02
2
.
(5)
Потери энергии при пуске вхолостую в соответствии с (2) равны:
АЭЛ А АМЕХ J
02
J
02
2
J
02
2
.
(6)
Т.о., при пуске ЭП с ДПТ НВ половина потребляемой из сети энергии расходуется на
механическую работу (разгон вращающихся масс с моментом инерции J до скорости ω0), а
половина – на потери в цепи якоря.
Величина этих потерь не зависит от R, то есть пуск двигателя с большим или меньшим
пусковым током (при разных значениях пускового сопротивления в цепи якоря) не изменит
величины потерь при пуске.

62.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
Потери энергии при пуске электропривода
_______________________________________________________________
Уточним приведенный расчет учетом статической нагрузки при пуске.
АЭЛ J
С2
М С С t П J
С2
2
МС
С t П
2
, или А J С М С t . (6а)
ЭЛ
С
П
2
2
2
Второе слагаемое в (6а) по сравнению с (6) увеличивает потери при пуске двигателя, но
незначительно (на 5-10%).
Для ДПТ с последовательным или смешанным возбуждением величина потерь при пуске
также, в основном, определяется запасом кинетической энергии, накапливаемым в ЭП.
При расчете потерь при пуске напряжение на якоре двигателя считалось неизменным, то
есть пуск осуществлялся в одну или несколько ступеней за счет изменения сопротивления в
цепи якоря.
Рассмотрим теперь расчет пусковых потерь при ступенчатом изменении напряжения на
якоре двигателя (допущения те же). В общем случае число пусковых ступеней при
регулируемом напряжении на якоре равно К.
Это значит, что при переходе к очередной ступени пуска напряжение на якоре повышается на
UН
вольт.
Соответственно скорость идеального холостого хода на первой ступени пуска равна
К
2
3 0
, на второй - 0 К
, на третьей - 0 К
и т.д.
К

63.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
Потери энергии при пуске электропривода
_______________________________________________________________
Используя выражение (4) можно записать общую энергию, забираемую из сети при таком
способе пуска, следующим образом:
А J
ω
0 0
2 2
3 3
2
0 J 0 0 0 J 0 0 0 ...
К К
К К
К
К К
К
... J
J
Кω0/K
(К-1)ω0/K
К 0 К 0
( К 1) 0
К К
К
02
02 (1 К ) К
К
К
(1 2 3 ... К ) J
2
АЭЛ А АМЕХ
02 1 К
2
2
02
J
АЭЛ J
2
К
U=(K-1)UН/K
02 1 К
2
К
02 1 К
J
J
J
1, т.е.
2
К
2
2 К
02 1
U=KUН/K
3ω0/K
2ω0/K
ω0/K
U=3UН/K
U=2UН/K
U=UН/K
(7)
М
Т.о., при пуске ступенчатым повышением напряжения на якоре двигателя потери энергии
обратно пропорциональны числу пусковых ступеней К.
Если при принятых допущениях обеспечить идеально плавное повышение напряжения (т.е.
при К ), то пуск будет проходить без потерь энергии в якорной цепи двигателя.
Идеально плавный пуск двигателя изменением напряжения источника питания может
обеспечить нулевые электрические потери лишь при бесконечно медленном увеличении
напряжения, то есть при увеличении скорости ЭП по характеристике ω=f(М), совпадающей с
осью ординат.

64.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
Потери энергии при пуске электропривода
_______________________________________________________________
В реальном ЭП это, конечно же, невозможно, потери в якорной цепи двигателя существуют,
но пуск путем плавного увеличения напряжения на якоре двигателя позволяет существенно
уменьшить эти потери. Соотношение (7) наглядно показывает одно из преимуществ систем
ЭП с регулируемым источником питания якорной цепи (системы Г-Д, ТП-Д и др.).
Потери энергии при пуске АД.
Расчет потерь при пуске АД выполним с допущениями: статическая нагрузка на валу
двигателя отсутствует, потери в статоре (т.е. потери на возбуждение электромагнитного
поля) не учитываются.
Мощность потерь в роторной цепи
Р2 Р1 Р2 М 0 М М ( 0 )
Р1 – электромагнитная мощность, забираемая из сети;
Р2 – полезная мощность на валу двигателя, вращающегося со скоростью ω;
М – электромагнитный момент, равный примерно вращающему моменту на валу двигателя.
При пуске вхолостую М J
d
dt
и поэтому Р2 J
d
( 0 )
dt
Потери при холостом пуске в интервале скоростей 0 0
0
АЭЛ
0
d
Р2 dt J
( 0 ) dt
dt
0
0
0
0
J 0 d J d J
0
0
02
J
02
2
J
02
2
Таким образом, потери в цепи ротора АД при пуске вхолостую, также как и для ДПТ, составляют
величину, равную запасу кинетической энергии, т.е.
02
АЭЛ J
2

65.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
Потери энергии при пуске электропривода
_______________________________________________________________
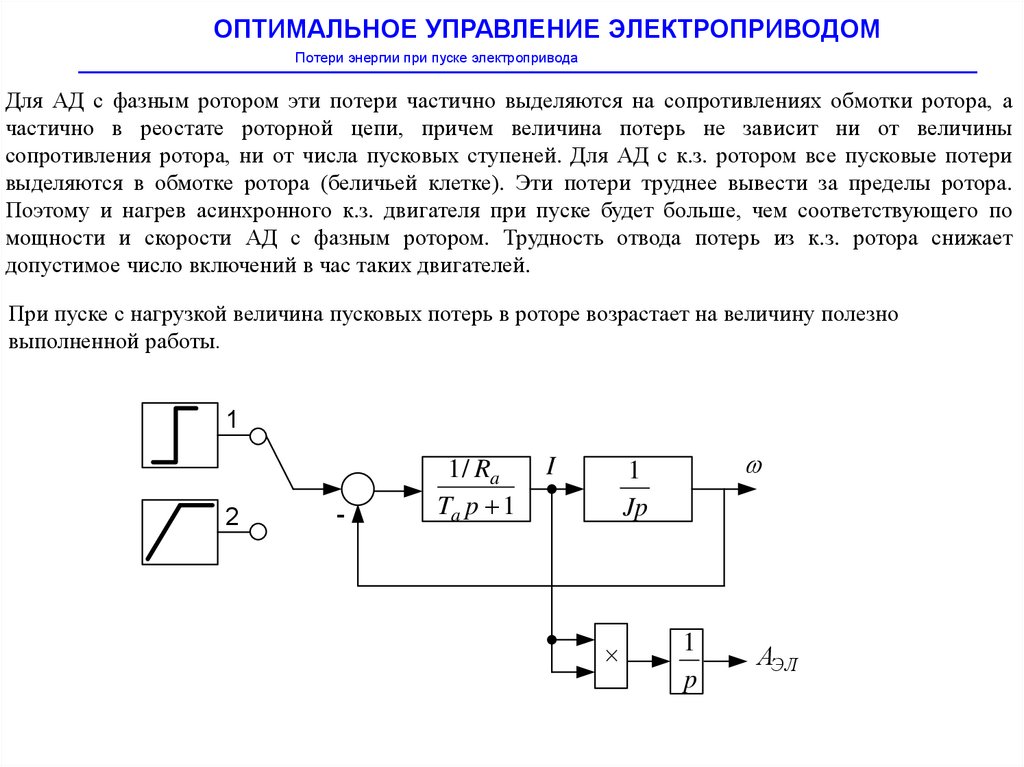
Для АД с фазным ротором эти потери частично выделяются на сопротивлениях обмотки ротора, а
частично в реостате роторной цепи, причем величина потерь не зависит ни от величины
сопротивления ротора, ни от числа пусковых ступеней. Для АД с к.з. ротором все пусковые потери
выделяются в обмотке ротора (беличьей клетке). Эти потери труднее вывести за пределы ротора.
Поэтому и нагрев асинхронного к.з. двигателя при пуске будет больше, чем соответствующего по
мощности и скорости АД с фазным ротором. Трудность отвода потерь из к.з. ротора снижает
допустимое число включений в час таких двигателей.
При пуске с нагрузкой величина пусковых потерь в роторе возрастает на величину полезно
выполненной работы.
1
2
-
1 / Ra
Ta p 1
I
1
Jp
1
p
АЭЛ

66.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
Потери энергии при пуске электропривода
_______________________________________________________________
1
I,
1
0.8
2
I1
0.6
0.4
I2
0.2
t
0
12
0
50
АЭЛ
100
150
АЭЛ 1
10
8
6
4
АЭЛ 2
2
t
0
0
50
100
150

67.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
Оптимальное передаточное число при длительном режиме работы ЭП
_______________________________________________________________
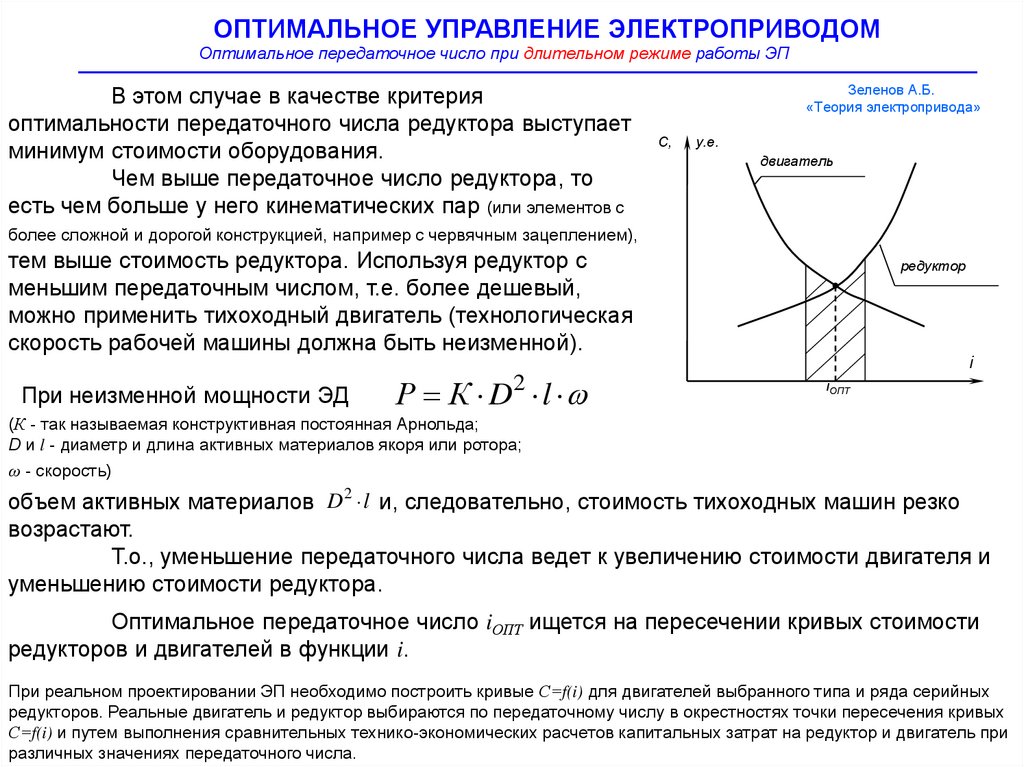
В этом случае в качестве критерия
оптимальности передаточного числа редуктора выступает
минимум стоимости оборудования.
Чем выше передаточное число редуктора, то
есть чем больше у него кинематических пар (или элементов с
Зеленов А.Б.
«Теория электропривода»
С,
у.е.
двигатель
более сложной и дорогой конструкцией, например с червячным зацеплением),
тем выше стоимость редуктора. Используя редуктор с
меньшим передаточным числом, т.е. более дешевый,
можно применить тихоходный двигатель (технологическая
скорость рабочей машины должна быть неизменной).
При неизменной мощности ЭД
Р К D2 l
редуктор
i
iОПТ
(К - так называемая конструктивная постоянная Арнольда;
D и l - диаметр и длина активных материалов якоря или ротора;
ω - скорость)
объем активных материалов D 2 l и, следовательно, стоимость тихоходных машин резко
возрастают.
Т.о., уменьшение передаточного числа ведет к увеличению стоимости двигателя и
уменьшению стоимости редуктора.
Оптимальное передаточное число iОПТ ищется на пересечении кривых стоимости
редукторов и двигателей в функции i.
При реальном проектировании ЭП необходимо построить кривые С=f(i) для двигателей выбранного типа и ряда серийных
редукторов. Реальные двигатель и редуктор выбираются по передаточному числу в окрестностях точки пересечения кривых
С=f(i) и путем выполнения сравнительных технико-экономических расчетов капитальных затрат на редуктор и двигатель при
различных значениях передаточного числа.

68.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
Оптимальное передаточное число при повторно-кратковременном режиме работы ЭП
_______________________________________________________________
В этом случае вопрос выбора скорости двигателя и передаточного числа редуктора
значительно сложнее. Экономическая эффективность ЭП при повторно-кратковременном
режиме определяется не столько стоимостью оборудования (т.е. капитальными затратами),
сколько производительностью рабочей машины, прямо зависящей от быстродействия
пусковых и тормозных режимов работы двигателя.
Продолжительность пуска и торможения ЭП существенно зависит от величины
передаточного числа редуктора.
Рассчитаем время движения при пуске и торможении механизма tМ, в котором все
величины взяты приведенными к валу механизма:
tМ
J
М . ПР М
М М М СМ
JМ.ПР – момент инерции всех вращающихся частей, приведенный к валу механизм
ММ – пусковой или тормозной момент двигателя, приведенный к валу механизма
МСМ – момент статического сопротивления на валу механизма.
Знак (+) - для режима торможения, а знак (-) – для режима пуска рабочей машины.
Выражая JМ.ПР и ММ через i и учтя потери в передачах с помощью КПД η их получим:
tП
J М J Д i 2
М i М СМ
М
(1)
tТ
J М J Д i 2
М i / М СМ
М
(2)
JМ – момент инерции механизма;
J\Д – момент инерции двигателя и элементов на его валу (муфта, датчики, быстроходный вал редуктора);
М – пусковой или тормозной момент двигателя (при ступенчатом пуске – среднее значение момента).
tП=f(i) и tТ=f(i) - экстремальные функции, имеющие минимальное значение при i=iОПТ.
Величина iОПТ.П при пуске или iОПТ.Т при торможении определяется при исследовании
выражений (1) и (2) на экстремум по условию:
dt
di
0

69.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
_______________________________________________________________
Оптимальное передаточное число при повторно-кратковременном режиме работы ЭП
2
2 J Д iОПТ . П ( М iОПТ . П М СМ ) М J М J Д iОПТ
dt П
.П
М
0
2
di
( М iОПТ . П М СМ )
Приравняв нулю числитель, получим после преобразования следующее квадратное уравнение и его решение:
2
iОПТ
.П 2
М СМ
J
iОПТ.П М 0
М
J Д
iОПТ.П
М
М
СМ СМ
М
М
2
JМ
J Д
(3)
Перед корнем надо учитывать при расчетах лишь знак (+). При знаке (-) iОПТ.П не имеет физического смысла (iОПТ.П<0).
Аналогично при торможении:
2
iОПТ .Т
М СМ
J
М
СМ М
М
J Д
М
(4)
iОПТ.П iОПТ.Т , то при реальных расчетах принимают среднее, либо средневзвешенное
Т.к.
значение, т.е.
iОПТ
iОПТ . П iОПТ .Т
2
либо
iОПТ
iОПТ .П t П iОПТ .Т tТ
t П tТ
Если ЭП имеет большие моменты инерции и незначительную статическую нагрузку,
т.е. при М СМ 2 J М величина оптимального передаточного числа приближенно:
J Д
М
iОПТ
JМ
J Д
(5)

70.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
Оптимальное передаточное число при повторно-кратковременном режиме работы ЭП
_______________________________________________________________
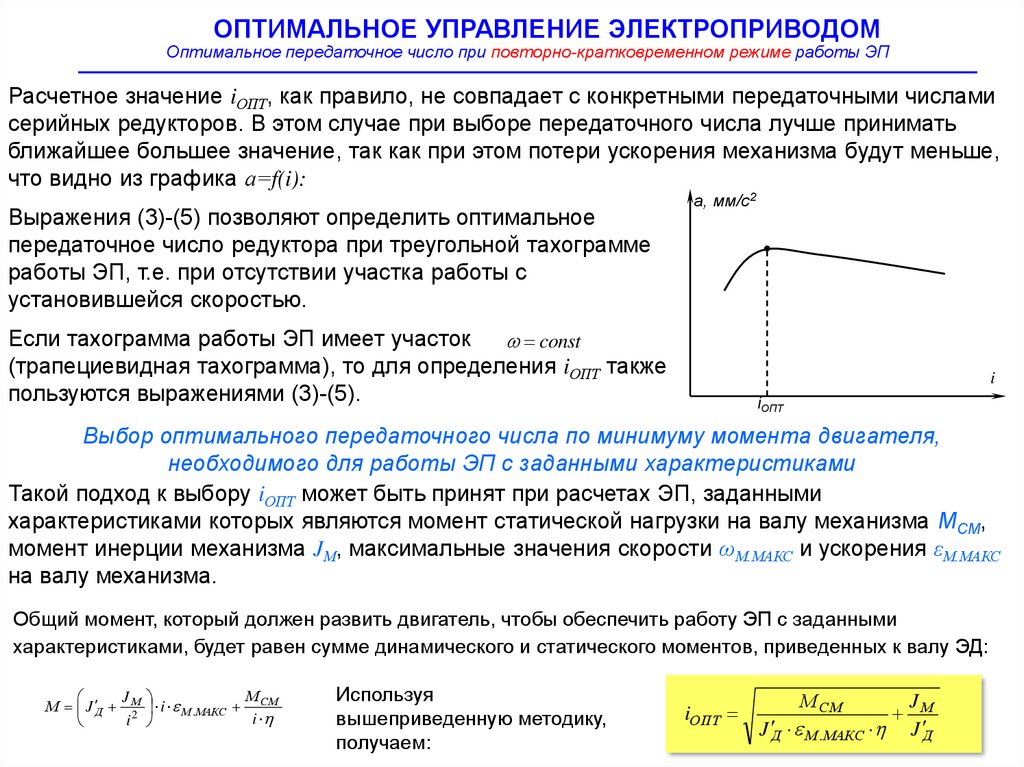
Расчетное значение iОПТ, как правило, не совпадает с конкретными передаточными числами
серийных редукторов. В этом случае при выборе передаточного числа лучше принимать
ближайшее большее значение, так как при этом потери ускорения механизма будут меньше,
что видно из графика а=f(i):
Выражения (3)-(5) позволяют определить оптимальное
передаточное число редуктора при треугольной тахограмме
работы ЭП, т.е. при отсутствии участка работы с
установившейся скоростью.
а, мм/с2
Если тахограмма работы ЭП имеет участок
const
(трапециевидная тахограмма), то для определения iОПТ также
пользуются выражениями (3)-(5).
i
iОПТ
Выбор оптимального передаточного числа по минимуму момента двигателя,
необходимого для работы ЭП с заданными характеристиками
Такой подход к выбору iОПТ может быть принят при расчетах ЭП, заданными
характеристиками которых являются момент статической нагрузки на валу механизма МСМ,
момент инерции механизма JМ, максимальные значения скорости ωМ.МАКС и ускорения εМ.МАКС
на валу механизма.
Общий момент, который должен развить двигатель, чтобы обеспечить работу ЭП с заданными
характеристиками, будет равен сумме динамического и статического моментов, приведенных к валу ЭД:
J
М J Д М
i2
М
i М .МАКС СМ
i
Используя
вышеприведенную методику,
получаем:
iОПТ
М СМ
J Д М .МАКС
JМ
J Д

71.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
Оптимальное передаточное число при длительном режиме работы электропривода
_______________________________________________________________
Оптим. Управление СДПМ

72.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
Оптимальное передаточное число при длительном режиме работы электропривода
_______________________________________________________________

73.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
Оптимальное передаточное число при длительном режиме работы электропривода
_______________________________________________________________

74.

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЭЛЕКТРОПРИВОДОМ
Оптимальное передаточное число при длительном режиме работы электропривода
_______________________________________________________________