Деление отрезка на равные части

1.

Деление
отрезка на равные
части;
Деление
угла и дуги на равные
части;
Деление
окружностей на равные
части;
Нахождение
центра дуги;
1

2. Деление отрезка на равные части

1'
А
2'
3'
4'
В
1
2
3
4
С
[А1']=[1'2']=[2'3']=[3'В]
2

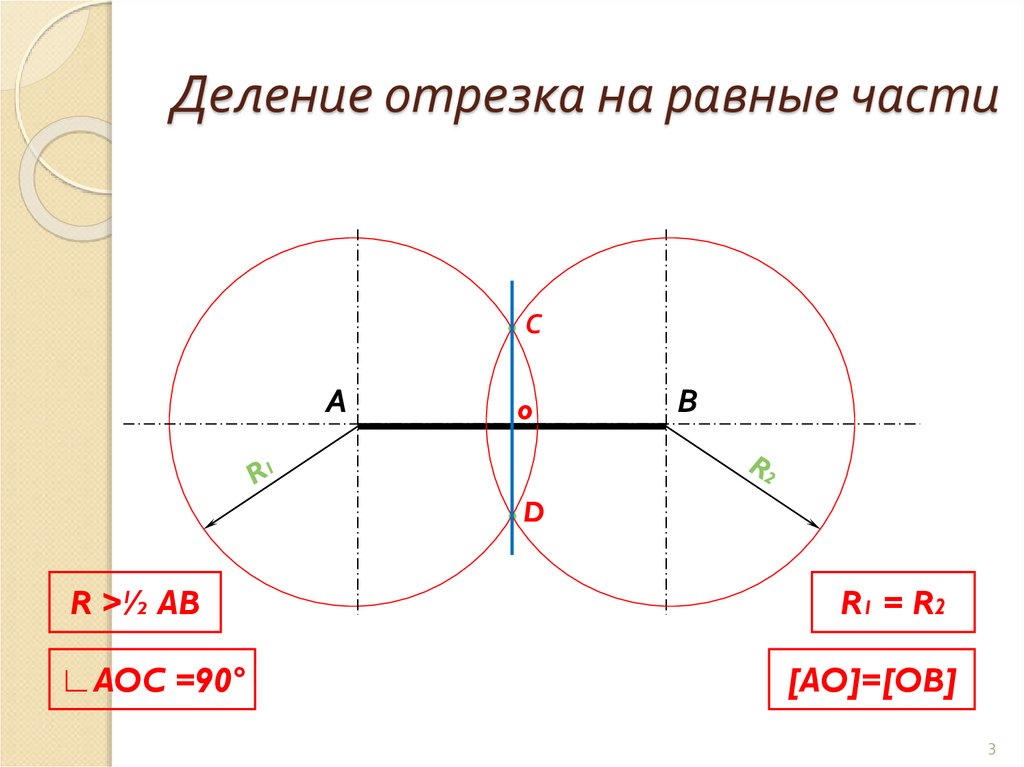
3. Деление отрезка на равные части

•С
А
o
R >½ AB
∟AOC =90°
В
D
R1 = R2
[AO]=[OB]
3

4. Деление угла на равные части

А
•1
R1 = R2 = R3
3
α=β=γ
•4
•2
С
В
4

5. Деление угла на равные части

А
•1
R1 = R2 = R3
3
D
ABD = DBC
•4
•2
С
В
5

6. Нахождение центра дуги

•2
C
E
1
•3
А
•D
O
•4
∟C =∟D=90°
R = [OE]
В
6

7.

2
2
5
6
1
3
О
1
8
3
•7
4
4
7

8.

2
2
7
3
1
5
6
8
3
1
5
6
4
4
8

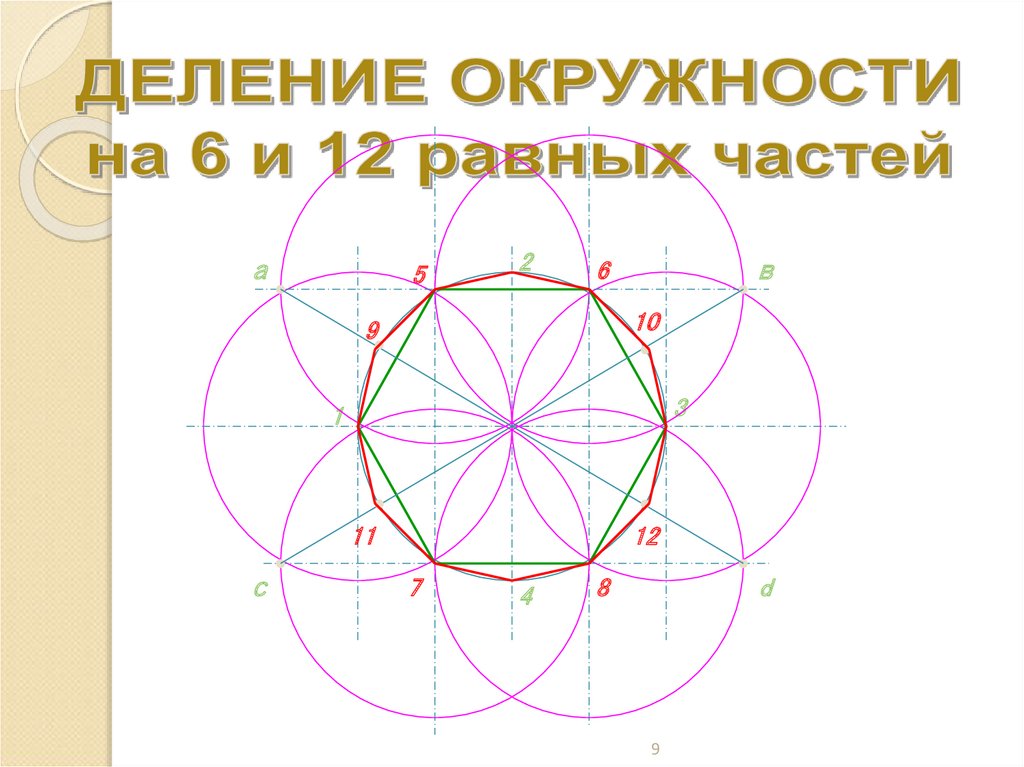
9.

а
5
2
6
10
9
3
1
11
с
в
12
7
4
8
9
d

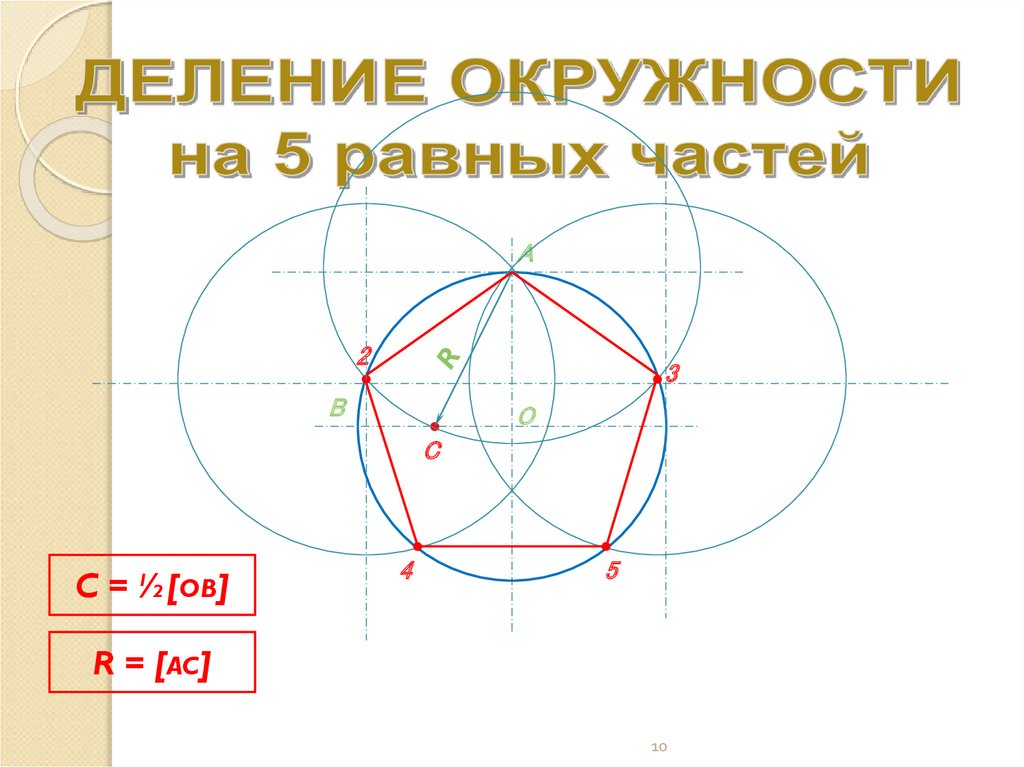
10.

A
2
B
•3
O
C
C = ½[OB]
4
5
R = [AC]
10

11.

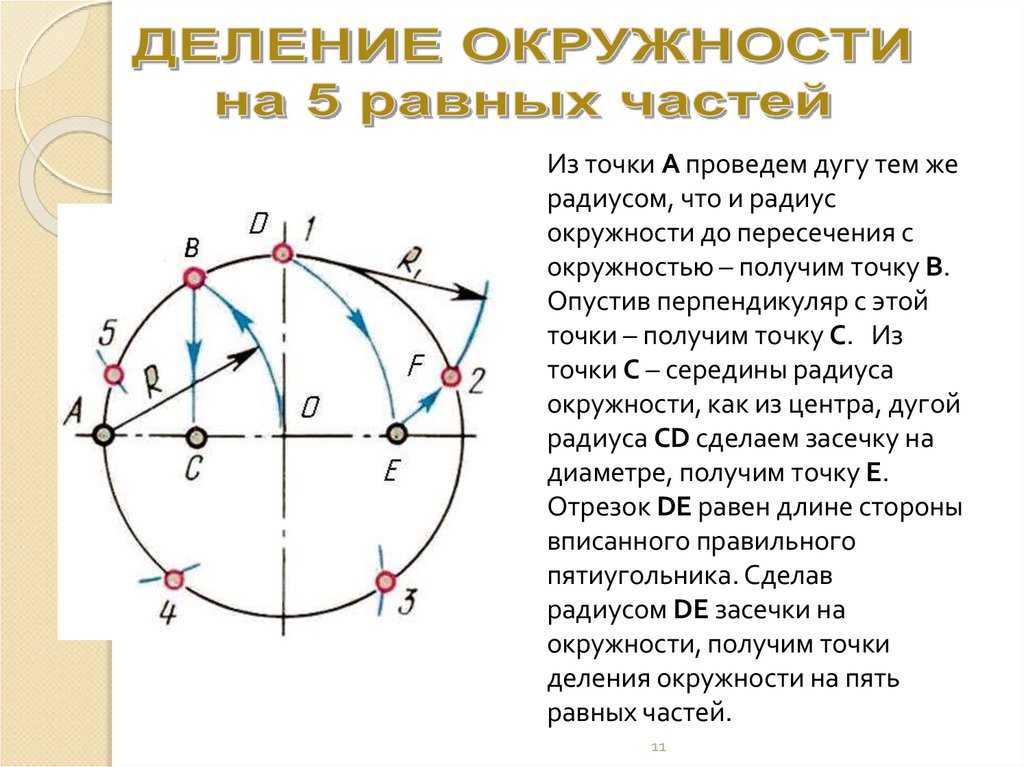
Из точки А проведем дугу тем же
радиусом, что и радиус
окружности до пересечения с
окружностью – получим точку В.
Опустив перпендикуляр с этой
точки – получим точку С. Из
точки С – середины радиуса
окружности, как из центра, дугой
радиуса СD сделаем засечку на
диаметре, получим точку Е.
Отрезок DЕ равен длине стороны
вписанного правильного
пятиугольника. Сделав
радиусом DЕ засечки на
окружности, получим точки
деления окружности на пять
равных частей.
11

12.

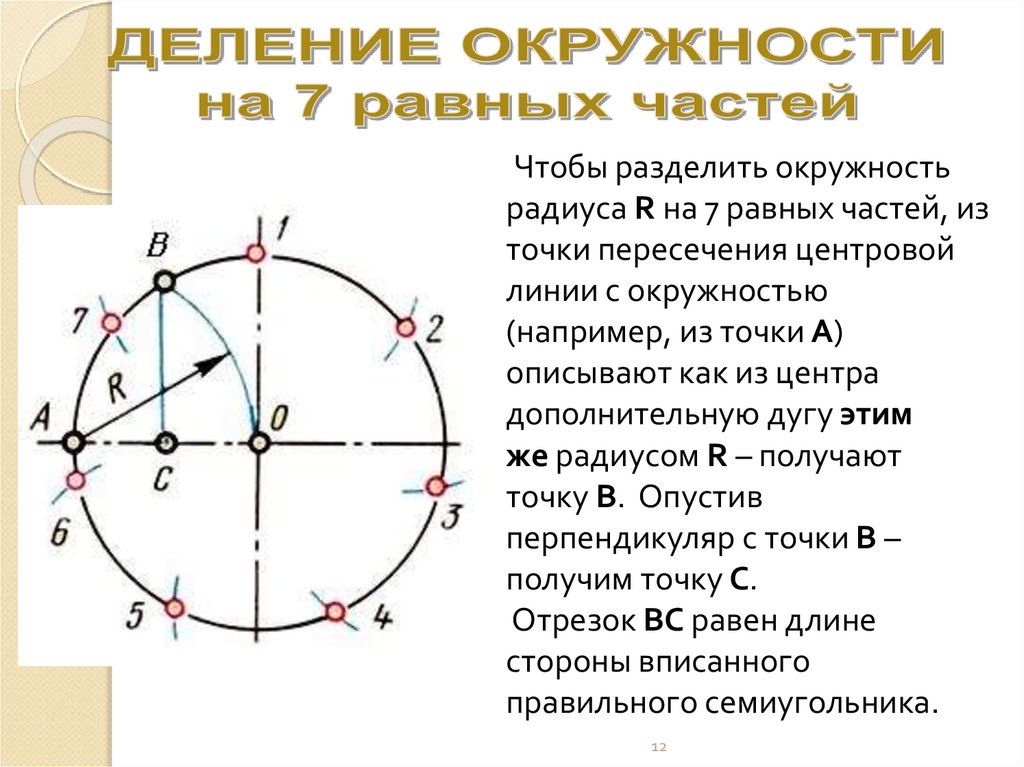
Чтобы разделить окружность
радиуса R на 7 равных частей, из
точки пересечения центровой
линии с окружностью
(например, из точки А)
описывают как из центра
дополнительную дугу этим
же радиусом R – получают
точку В. Опустив
перпендикуляр с точки В –
получим точку С.
Отрезок ВС равен длине
стороны вписанного
правильного семиугольника.
12