Використання програмних засобів для розв’язування системи лінійних рівнянь

1. ВИКОРИСТАННЯ ПРОГРАМНИХ ЗАСОБІВ ДЛЯ РОЗВ’ЯЗУВАННЯ СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ

2.

Робота складається з двох розділів. У першому розділі
викладені основні теоретичні відомості: табличний
процесор Microsoft Exсel, основні поняття про
електронну таблицю та роботу з формулами. В
другому розділі моєї роботи розглянуті основні
уявлення про системи лінійних алгебраїчних рівнянь
та методи їх розв’язку. Наведені приклади
розв’язування СЛР методом Крамера та методом
оберненої матриці, а також реалізація цих методів за
допомогою табличного процесора Microsoft Exсel.
Розроблено програму для знаходження розв’язків СЛР
методом Крамера та методом оберненї матриці.

3.

Метою мого дослідження було ознайомитись з
використанням додаткових функцій (які невизначені
програмою з інформатики), що дозволяють
розв’язувати СЛР засобами табличного процесора
Microsoft Exсel та переконати у необхідності
початкових знань мов програмування (зокрема мовою
Паскаль).

4.

Об’єктом дослідження є табличний процесор
Microsoft Exсel.
Предметом дослідження: використання можливостей
табличного процесора Microsoft Excel для
розв’язування задач з математики у ВНЗ та у
шкільному курсі.

5.

Практичне значення наукового дослідження полягає в
можливості використання його при розв’язуванні
математичних завдань студентами ВНЗ та учнями при
підготовці до уроків математики, економіки та хімії, а
також шкільних факультативів. Теоретичну частину
(Розділ 1) можна використовувати як при підготовці до
семінару, так і вчителем –предметником, складаючи
конспект уроку.

6.

Багато завдань практики приводять до необхідності
розв’язувати системи лінійних рівнянь. При
конструюванні інженерних споруд, обробці
результатів вимірів, вирішенні завдань планування
виробничого процесу і ряду інших завдань техніки,
економіки, наукового експерименту доводиться
вирішувати системи лінійних рівнянь. Багато тем
математики, в яких рішення систем рівнянь є
необхідним елементом при вирішенні задач. Тому,
вміння розв’язувати системи рівнянь є необхідною
умовою успішної реалізації розв’язку задачі.

7.

Способів вирішення систем рівнянь існує багато:
складання, підстановки, графічний, за допомогою
зворотної матриці, методом виключення невідомих,
метод Крамера. Який з них найраціональніший?
Серед невідомих мені методів я зацікавилась
методом Крамера та методом оберненої матриці .

8.

Математична теорія змінюється порівняно повільно,
однак технологія застосування математичних методів
зазнала значних змін. Тому сьогодні спеціаліст, що
добре знає математичні закони, але не вміє
реалізовувати математичні методи на комп'ютері, не
може вважатися спеціалістом сучасного рівня.
Обчислювальні машини можна використовувати
ефективно лише за умови бездоганного знання
можливостей конкретного пакету прикладних
програм.

9.

Застосування комп'ютера для проведення розрахунків
сприяє кращій математичній підготовці спеціаліста.
Якщо раніше основна увага була зосереджена на
математичних методах, які передбачали проведення
розрахунків без застосування обчислювальної техніки,
то тепер, з появою спеціалізованих математичних
програм, необхідно навчитися проводити необхідні
обчислення, застосовуючи спеціалізовані програмні
продукти.

10.

Існує значна кількість спеціалізованих пакетів
програмного забезпечення, таких як MatLab, MathCad,
Mathematica, Maple тощо. Усі вони охоплюють основні
розділи математики і дозволяють робити переважну
більшість необхідних розрахунків, у деяких з них
середовище адаптовано для введення даних у формі,
яка є природною для математики. Однак самостійне
засвоєння цих пакетів – досить складне завдання

11.

Загальновідомо, що в умовах вищих навчальних
закладів та середніх шкіл дуже гостро стоїть питання
про роботу на комп’ютерах тільки з ліцензійними
програмами, що на даному етапі не завжди можливо.
В той же час комп’ютери в навчальних закладах та в
домашніх умовах налагоджені, в основному, на
операційну систему Windows з пакетом програм
Microsoft Office.

12.

Табличний процесор Excel входить до цього пакету
програм, має великі обчислювальні можливості,
зручний та простий в користуванні, має російський
інтерфейс, тому раціонально математичні методи
здійснювати в Excel. На мою думку є доцільним
вивчення можливостей електронної таблиці Excel для
реалізації математичних методів.

13.

З огляду на це, я вирішила розглянути реалізацію
методів розв’язування систем лінійних рівнянь (метод
оберненої матриці, метод Крамера) на мові
програмування Паскаль та в табличному процесорі
Excel.
Ця тема є актуальною на сьогоднішній день, так як
саме поєднання чисельних методів і інформатики дає
можливість значно спростити роботу над
розв’язанням різного типу завдань, удосконалити свої
знання з програмування.

14. Зв’язок даної роботи зі шкільною програмою:

Дана робота щільно пов’язана зі шкільною програмою
тим, що цю тему вивчають в курсі математики. При
вирішенні систем лінійних рівнянь в школі на уроках
алгебри, ми використовували такі способи, як
складання, підстановка і графічний.

15.

Проаналізувавши різні сфери діяльності людини,
можна переконатися, що більшість даних, якими ми
оперуємо, мають табличну структуру. Так, у вигляді
таблиці подають телефонну книгу, опис кулінарного
рецепту, розклад руху транспортного засобу, дані
обліку робочого часу, відомості про учнів класу,
прогноз погоди. Цей перелік можна продовжувати
нескінченно.

16.

Виконувати ці операції допомагають спеціальні
програми — табличні процесори (ТП),
найпопулярнішим з яких вважається Microsoft®Office
Excel. Ця програма дає змогу створювати, редагувати,
форматувати і друкувати таблиці, здійснювати в них
обчислення, сортування та групування даних, будувати
на їх основі графіки та діаграми, імпортувати й
експортувати дані.

17.

Рівняння виду a1 x1 a2 x2 .... an xn b називається
лінійним рівнянням з n невідомими: x1 , x2 ....хn
Слово лінійне означає, що рівняння 1-го степеня.
Розв’язком такого рівняння буде такий упорядкований
набір чисел , ,..., , який перетворює наше рівняння
в числову тотожність.
1
2
n

18.

Рівняння виду можна використати для побудови системи
рівнянь:
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1 22 2
2n n
2
.......................................
an1 x1 an 2 x2 ... ann xn bn
Система називається системою n лінійних рівнянь з n
невідомими x , x ,...x , коефіцієнтами при яких є елементами
матриці А, а вільними членами є числа b , b ,..., b .
Розв’язком системи будемо називати такий набір чисел
, ,..., , який задовольняє кожне рівняння системи.
Це буде перетин множин розв’язків кожного рівняння
даної системи.
1
2
n
1
1
2
n
2
n

19.

Якщо визначник системи, тобто визначник, що
складається з коефіцієнтів при невідомих
A
a11
a12
... a1n
a 21
a 22
... a 2 n
...
a n1
...
an2
... ...
... a nn
0
то система має єдиний розв’язок. Цей розв’язок
можна знайти різними способами.

20.

Метод Крамера (Крамера правило) — спосіб
розв'язання квадратних систем лінійних алгебраїчних
рівнянь із ненульовим визначником основної матриці
(при цьому для таких рівнянь розв'язок існує і є
єдиним).
Метод було створено Габріелем
Крамером у 1750 році.
(швейцарський математик,
один з творців лінійної алгебри.)

21.

Позначимо через 1 визначник, що утворюється з
a
a
... a
(1)
a
a
... a
A
11
12
1n
21
22
2n
...
a n1
...
an2
... ...
... a nn
0
після заміни його першого стовпчика стовпчиком вільних
членів системи
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1 22 2
2n n
2
.......................................
an1 x1 an 2 x2 ... ann xn bn
(2)
аналогічно позначимо через визначник, що утворюється з
(1) після заміни його другого стовпчика стовпчиком вільних
членів системи (2), …, - замінено останній стовпчик
стовпчиком вільних членів.

22.

Тоді розв’язок системи записується у вигляді:
x1
1
, x2 2 ,..., xn n
Формули називаються формулами Крамера.
Якшо 0 , а хоча б один з 1 , 2 , …., відмінний від
нуля, то система розв’язків немає.
Якщо ж 1 = 2=…= n=0, то система має безліч розв’язків.
n

23.

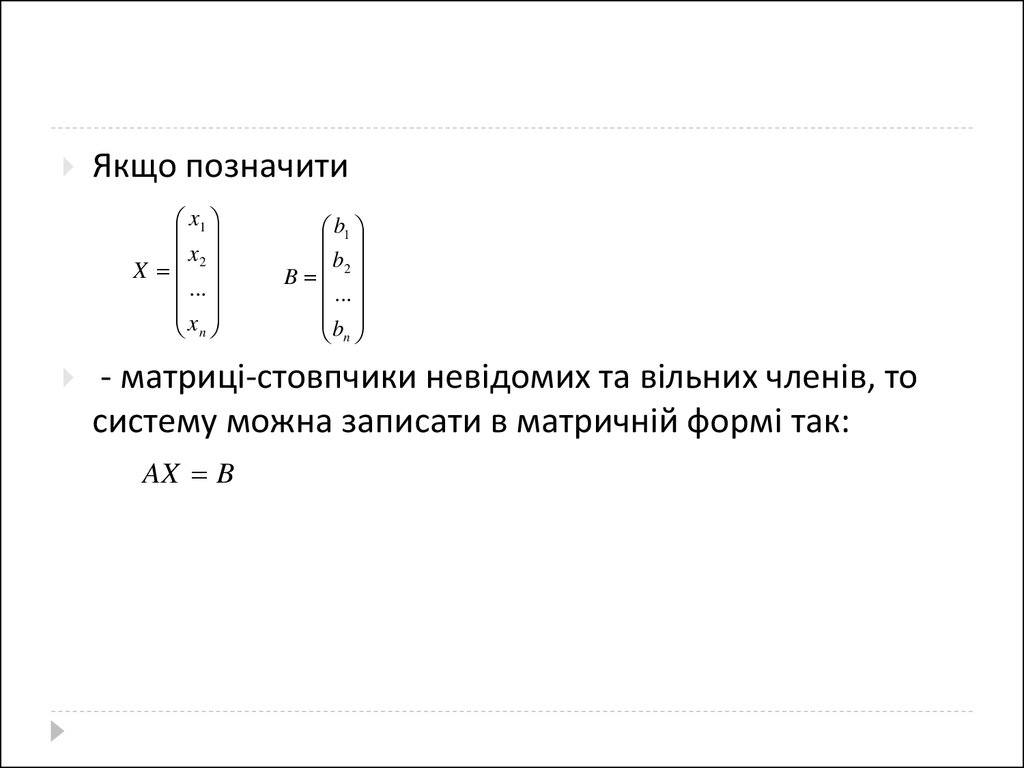
Якщо позначити
x1
x
X 2
...
x
n
b1
b
B 2
...
b
n
- матриці-стовпчики невідомих та вільних членів, то
систему можна записати в матричній формі так:
AX B

24.

Використовуючи властивості оберненої матриці,
маємо:
A 1 AX A 1 B EX A 1 B X A 1 B
З формули випливає твердження: щоб знайти
розв’язок системи, потрібно знайти обернену
матрицю A 1 (це можливо, бо 0 ), а потім
помножити на матрицю В. Результат цієї дії і дає
розв’язок системи.

25.

Результати:
Приклад.
Розв’язати задану систему рівнянь методом Крамера
та за допомогою матричного методу.

26.

І. Матричний спосіб. Матриця А з коефіцієнтів при
невідомих для заданої системи рівнянь має вигляд:
2 1 1
1
2 7 3 1
A
1 5
1 3
1
1
1
1
Шукаємо алгебраїчні доповнення до кожного
елемента матриці:

27.

28.

29.

30.

31.

Щоб отримати обернену матрицю A 1необхідно
алгебраїчні доповнення до елементів рядка записати у
відповідний стовпчик, попередньо поділивши їх на
визначник матриці A .
A 1
1
11
8 20 14 54 2
16
4
6
2
1
11
2
3 43 9
88 36
12 14
22
23
7
3
22
5
22
1
22
1
44
7
44
7
27
44
44
3
1
44
44
3
43
88
88
23
7
88
88
Стовпчик вільних членів
2
23
B
18
4

32.

x
1
X x2 A 1 B
x
3
х4
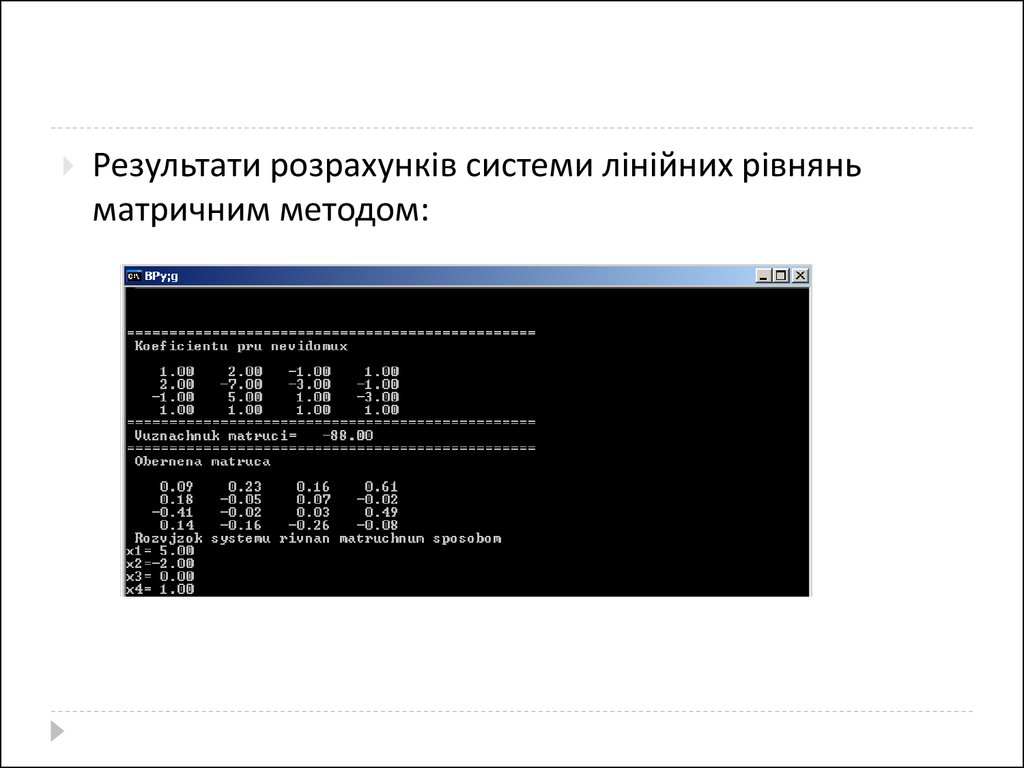
Отже,
x1 5;
x2 2;
x3 0;
x4 1;
0,23
0,16
0,61 2 5
0,09
0
,
18
0
,
05
0
,
07
0
,
02
23
2
0,41 0,02 0,03
0,49 18 0
0,14 0,16 0,26 0,08 4 1

33.

ІІ. Метод Крамера. Знаходимо визначник системи ,
розкладаючи його за елементами першого рядка:
1
2 1 1
7 3 1
2 3 1
2 7 1
2 7 3
2 7 3 1
1 5
1 3 2 1 1 3 ( 1) 1 5 3 1 1 5
1 88
1 5
1 3
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1

34.

Знаходимо визначники
1 , 2 , 3 , 4 :
2
2 1 1
7 3 1
23 3 1
23 7 1
23 7 3
23 7 3 1
1
2 5
1 3 2 18 1 3 ( 1) 18 5 3 1 18 5
1 440
18 5
1 3
1
1
1
4
1
1
4
1
1
4
1
1
4
1
1
1
1
2
1 1
23 3 1
2 3 1
2
23 1
2
23 3
2
23 3 1
2
1 18 1 3 2 1 1 3 ( 1) 1 18 3 1 1 18 1 176
1 18 1 3
4
1
1
1
1
1
1
4
1
1
4
1
1
4
1
1
1
2
2
1
7 23 1
2
23 1
2 7 1
2 7 23
2 7 23 1
3
1 5 18 3 2 1 18 3 2 1 5 3 1 1 5 18 0
1 5 18 3
1
4
1
1
4
1
1
1
1
1
1
4
1
1
4
1
1
2 1 2
7 3 23
2 3 23
2 7 23
2 7 3
2 7 3 23
4
1 5
1 18 2 1 1 18 ( 1) 1 5 18 2 1 5
1 88
1 5
1 18
1
1
4
1
1
4
1
1
4
1
1
1
1
1
1
4

35.

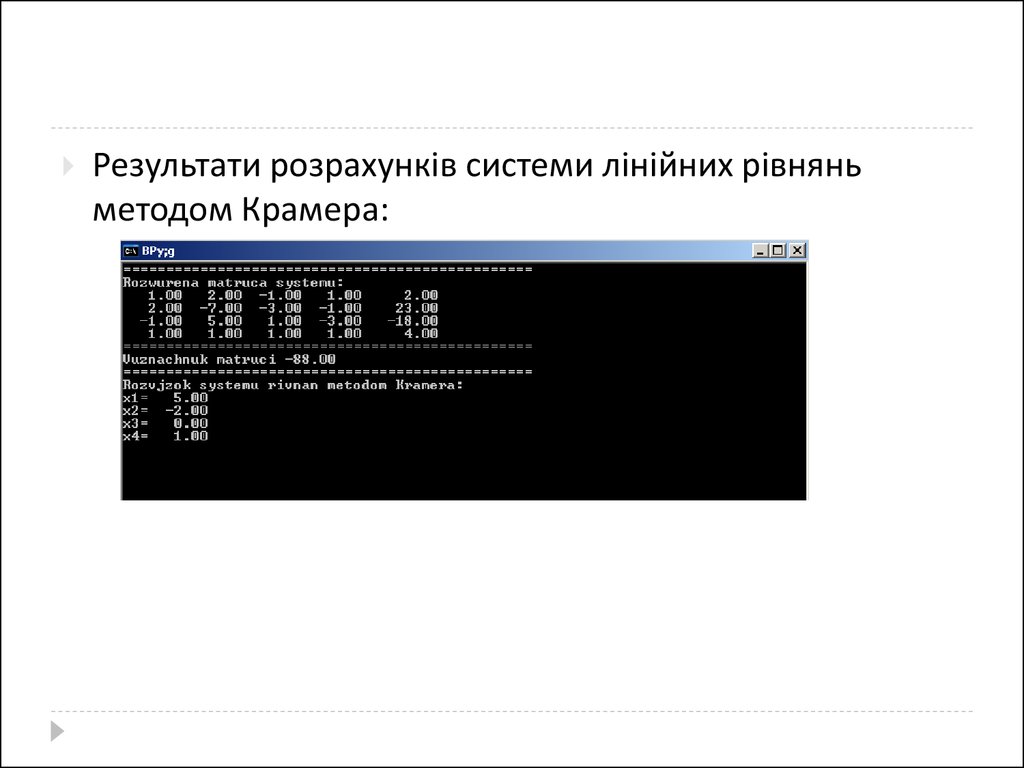
Тоді:
x1
1 440
5;
88
x2
2 176
2;
88
x3
3
0
0;
88
x4
4 88
1;
88

36.

Реалізація методу Крамера на ПК будь-якими
програмними засобами досить проста, оскільки всі
обчислення зводяться до звичайних арифметичних
дій. Що стосується методу оберненої матриці, то
ключовим для його реалізації є обчислення матриці,
оберненої до матриці коефіцієнтів при невідомих.
Метод оберненої матриці доцільніше застосовувати
при розв’язуванні систем лінійних рівнянь в
середовищі MS Excel, оскільки в цих програмах є
„вбудовані” засоби обчислення оберненої матриці. MS
Excel має стандартні функції.

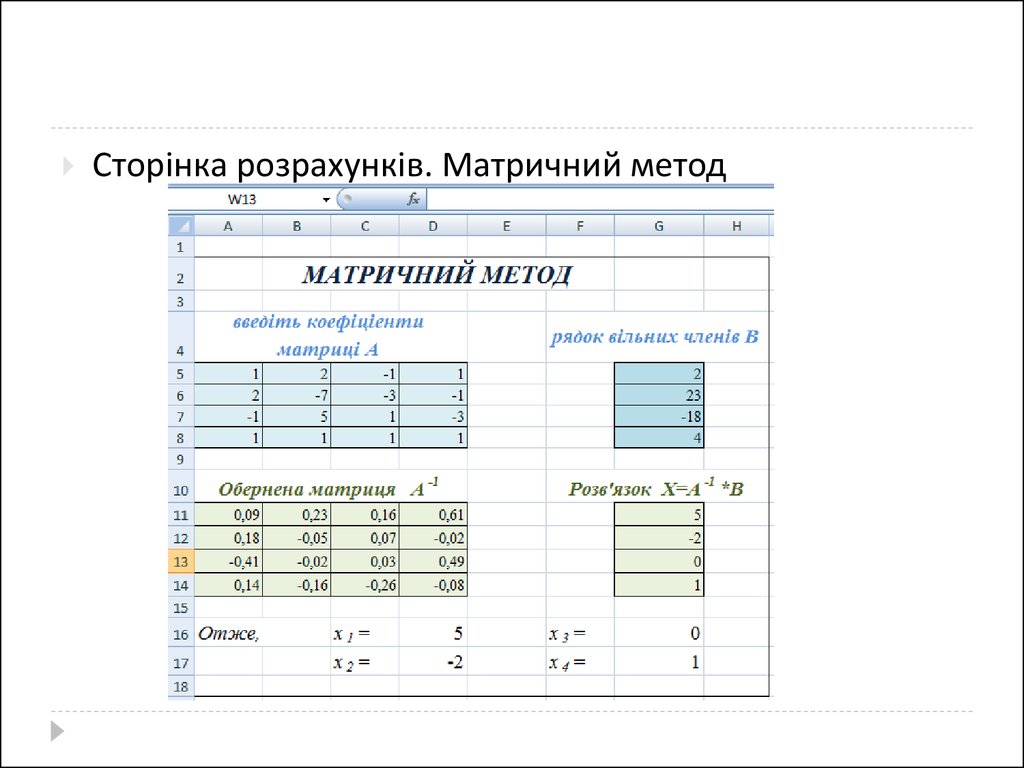
37.

Сторінка розрахунків. Матричний метод

38.

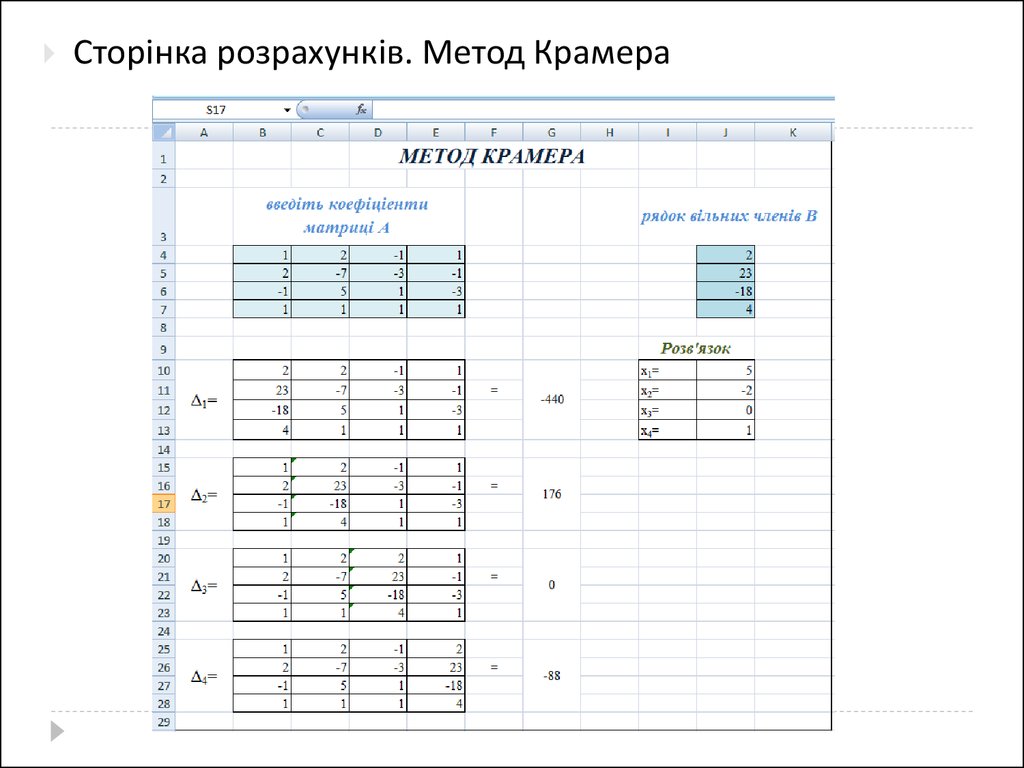
Сторінка розрахунків. Метод Крамера

39.

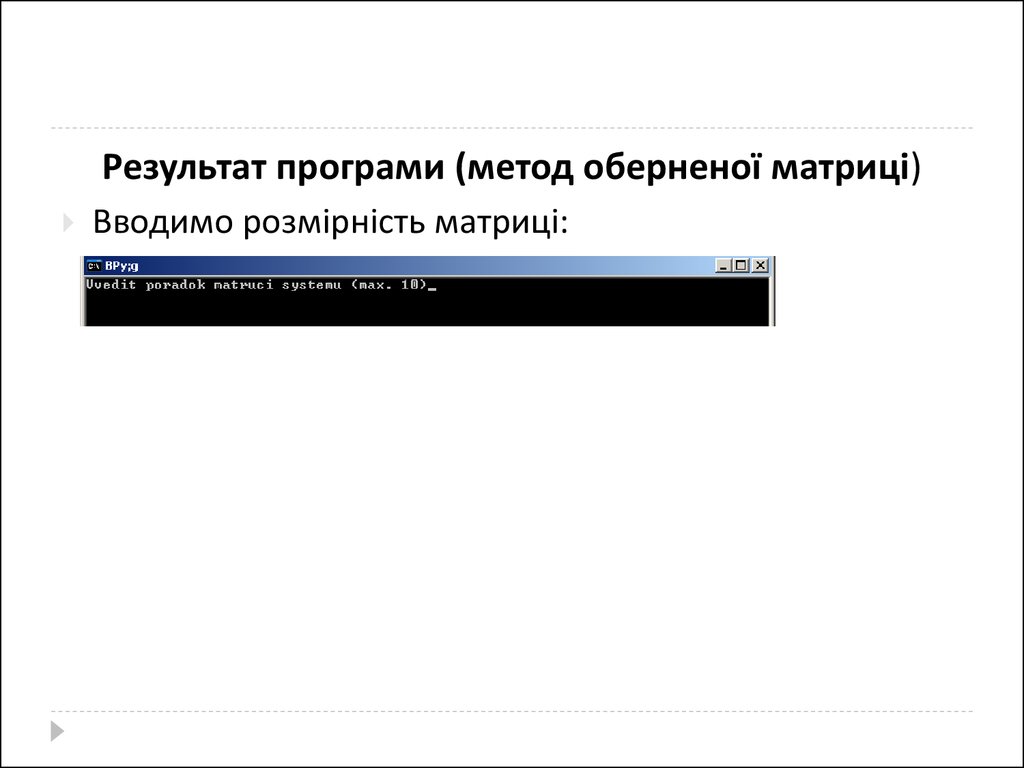
Результат програми (метод оберненої матриці)
Вводимо розмірність матриці:

40.

Вводимо коефіцієнти при невідомих та рядок вільних
членів

41.

Результати розрахунків системи лінійних рівнянь
матричним методом:

42.

Результат програми (метод Крамера)
Вводимо розмірність матриці:

43.

Вводимо коефіцієнти при невідомих та рядок вільних
членів

44.

Результати розрахунків системи лінійних рівнянь
методом Крамера:

45.

Результатом дослідження є економія часу при
обчисленні СЛР за допомою програмних засобів та
переваги використання програм, що входять в пакет
MS Office.

46.

В ході науково дослідницької роботи було
встановлено, що головна особливість електронних
таблиць полягає в можливості застосування формул
для опису зв'язку між значеннями різних осередків.
Розрахунок по заданих формулах автоматичний. Зміна
вмісту якого-небудь осередку приводить до
перерахунку значень всіх осередків, які з нею
пов'язані формульними відносинами і, тим самим, до
оновлення всієї таблиці відповідно до даних, що
змінилися.

47.

Показано, що середовище Microsoft Excel є потужним
інструментом для проведення різноманітних
обчислень. Наведені конретні математичні задачі та їх
розв’язки. Тому учні та студенти отримуючи завдання
розв’язування систем лінійних рівнянь з чотирма
невідомими можуть використовувати вже готовий
шаблон для розрахунків, учень бачить відповідь
відразу після введення останнього коефіцієнта
системи.
Також його можна широко використовувати
вчителями, при підготовці до занять.

48.

Розроблена комп’ютерна програма для розв’язування
СЛР до 10-го порядку методом Крамера та матричним
методом може бути використана в різних областях, де
потрібно рішення систем лінійних рівнянь. Вона
значно скорочує час, дає можливість провести заняття
більш ефективно та, що дуже важливо, формує в учнів
навики, які їм знадобляться як допоміжні при
розв’язуванні задач з фізики, економіки, механіки,
електротехніки та інших дисциплін та зменшує
можливість помилки до нуля.