Похожие презентации:
Проблемы передачи информации (лекция 3)
1.
ЛЕКЦИЯ №3 ПРОБЛЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИЧ.1
Преподаватель: Оцоков Шамиль Алиевич
Москва, 2021 г.
2.
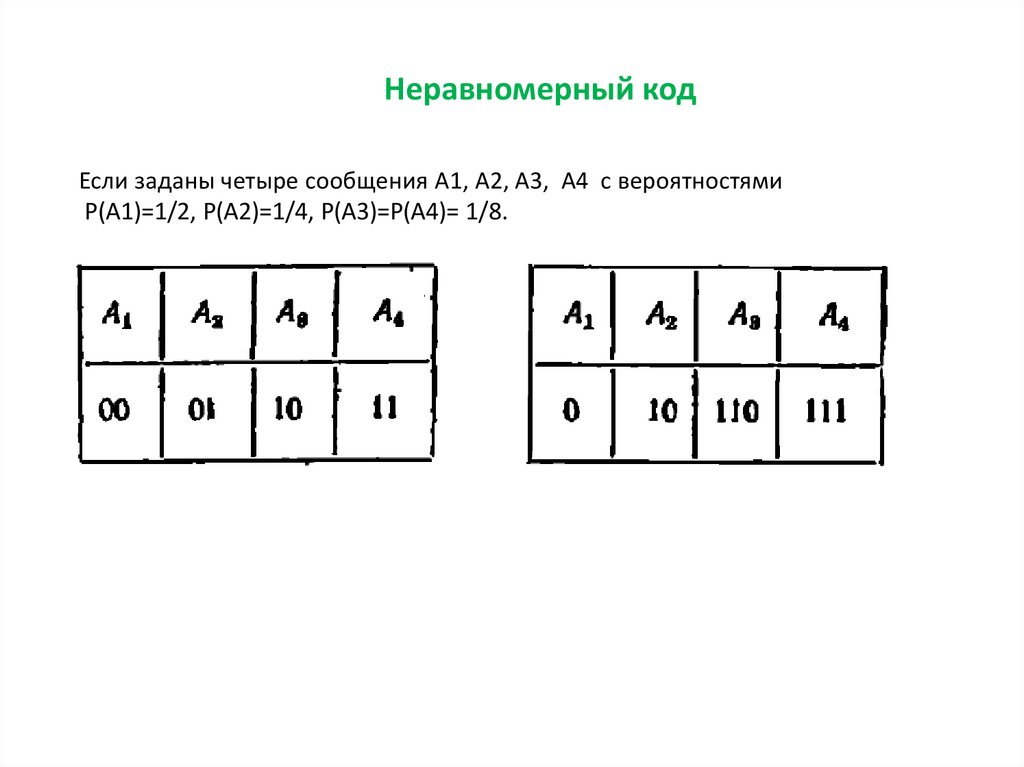
Неравномерный кодЕсли заданы четыре сообщения А1, А2, А3, А4 с вероятностями
Р(А1)=1/2, Р(А2)=1/4, Р(А3)=Р(А4)= 1/8.
3.
Идея метода Шеннона-Фано• Идея этого метода заключалась в том,
чтобы заменить часто встречающиеся
символы более короткими кодами, а редко
встречающиеся последовательности более
длинными кодами.
• Метод Шеннона-Фано относится к
вероятностным методам сжатия
4.
Схема метода Шеннона-Фано5.
Идея метода Шеннона-ФаноЕсли заданы четыре сообщения А1, А2, А3, А4 с вероятностями
Р(А1)=1/2, Р(А2)=1/4, Р(А3)=Р(А4)= 1/8.
6.
Идея метода Шеннона-Фано7.
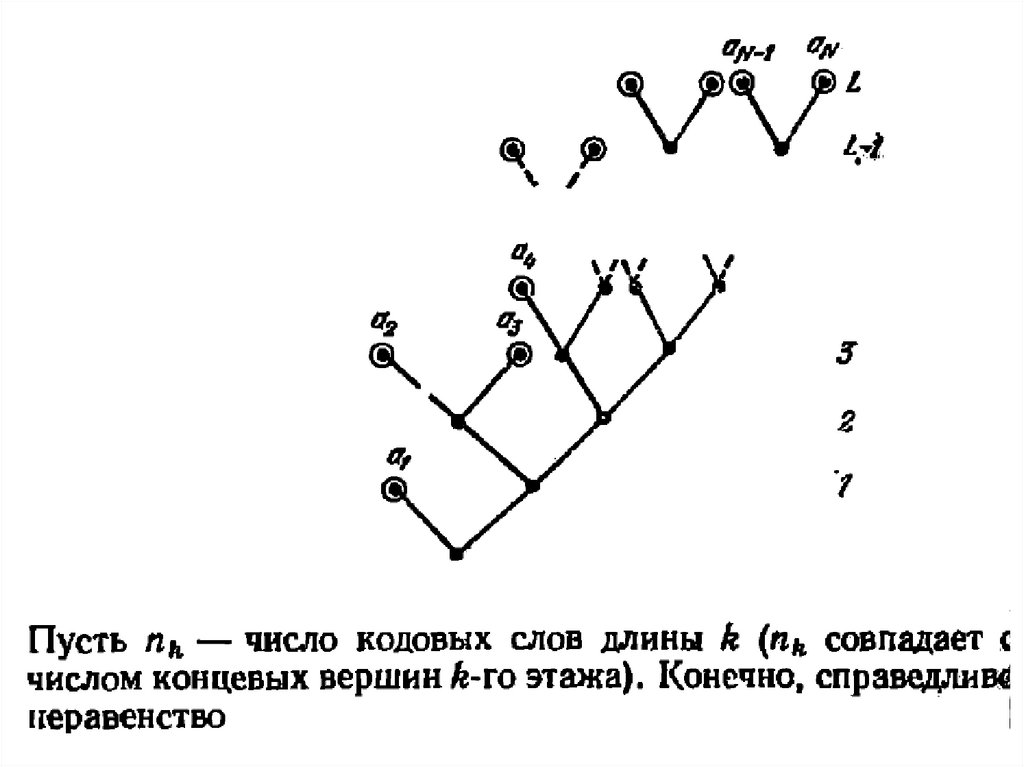
Кодовые деревьяЧем более вероятно сообщение, тем быстрее оно образует «самостоятельную»
группу и тем более коротким словом оно будет закодировано. Эго
обстоятельство обеспечивает высокую экономность кода Фано.
8.
Кодовые деревьяВ любом кодовом тексте выделять отдельные кодовые слова без использования
специальных разделительных знаков.
Чтобы код удовлетворял следующему требованию:
- всякая последовательность кодовых символов может быть единственным
образом разбита на кодовые слова
Коды для которых последнее требование выполнено,
называются однозначно декодируемыми (иногда их называют
кодами без зanятой).
Наиболее простыми и употребимыми кодами без запятой являются так
называемые nрефuкcные коды, обладающие тем свойством. что никакое
кодовое слово не является началом (префиксом) другого кодового слова. Если
код префиксный, то, читая кодовую запись подряд от начала. мы всегда сможем
разобраться, где кончается одно кодовое слово и начинается следующее.
9.
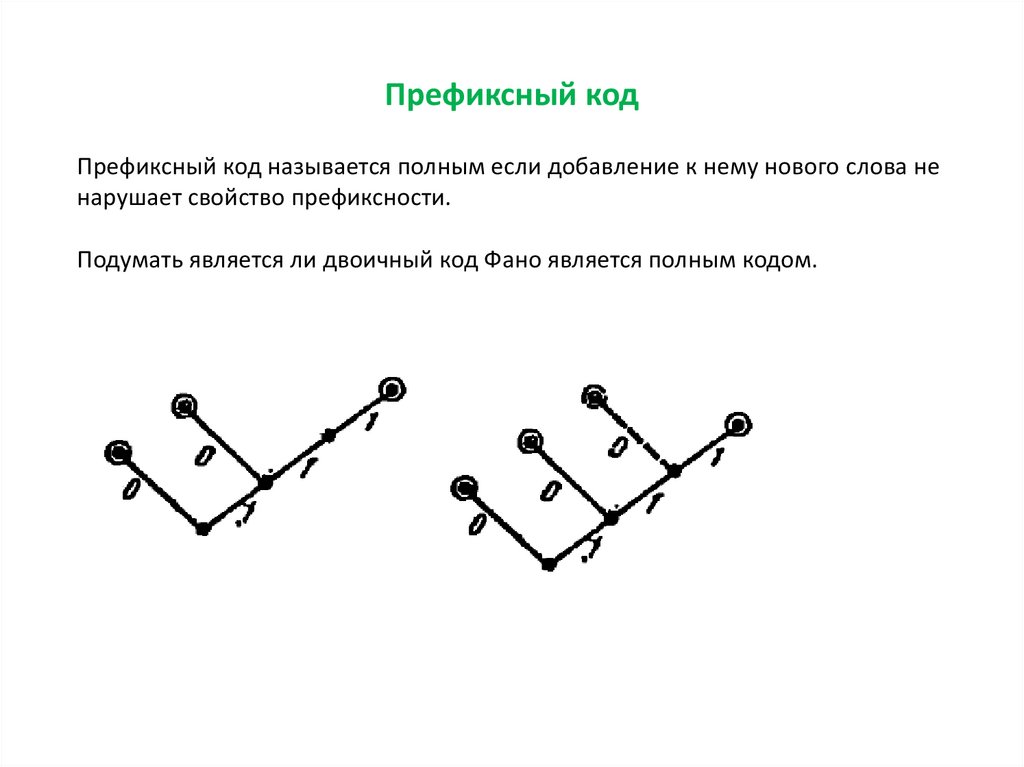
Префиксный кодПрефиксный код называется полным если добавление к нему нового слова не
нарушает свойство префиксности.
Подумать является ли двоичный код Фано является полным кодом.
10.
Однозначно декодируемый код, который не являетсяпрефиксным
{1,10}, {01, 10, 011}
Не существует префиксного кода с длинами кодовых слов 1,1,2.
Существует ли префиксный код с заданными длинами слов?
11.
12.
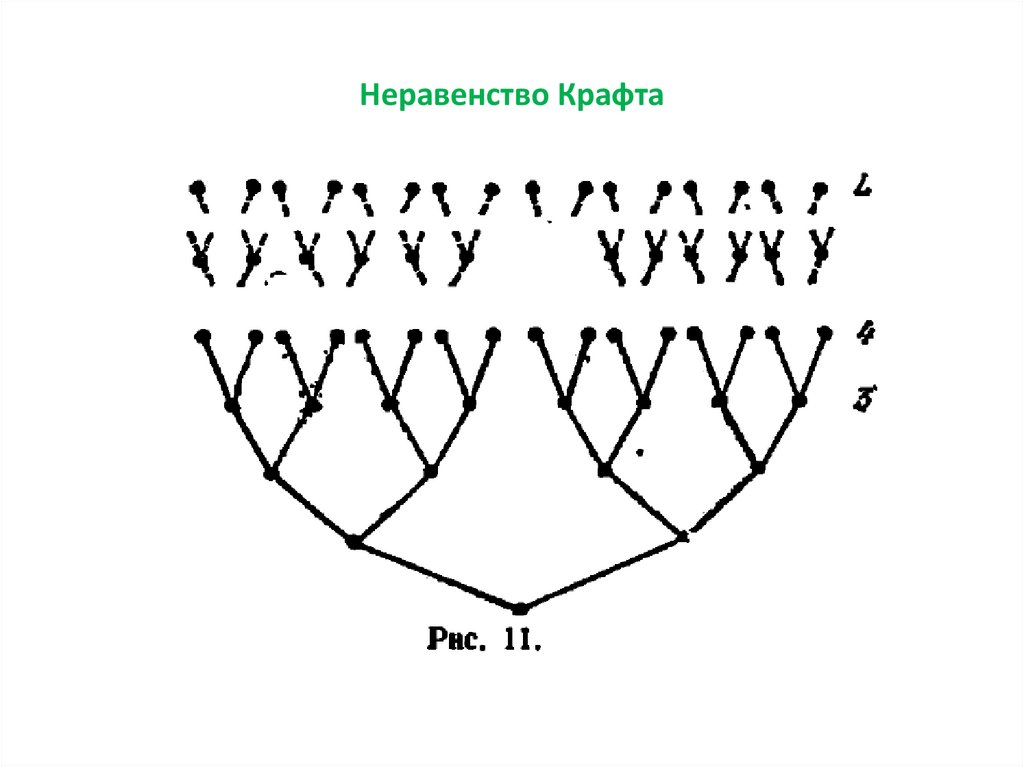
Неравенство Крафта13.
Неравенство Крафта14.
Неравенство Крафта15.
Неравенство Крафта16.
Неравенство Крафта17.
Неравенство Крафта18.
Неравенство Крафта19.
Неравенство Крафта20.
Неравенство Крафта21.
Неравенство Крафта22.
Метод Шеннона построения префиксного кода сзаданными длинами слов
23.
Метод Шеннона построения префиксного кода сзаданными длинами слов
24.
Метод Шеннона построения префиксного кода сзаданными длинами слов
25.
Метод Шеннона построения префиксного кода сзаданными длинами слов

































 Информатика
Информатика








