Силовое действие магнитного поля

1.

Лекция 2
СИЛОВОЕ ДЕЙСТВИЕ
МАГНИТНОГО ПОЛЯ
Вопросы:
1. Проводник с током в магнитном поле.
Сила Ампера.
2. Движение заряженных частиц в
магнитном поле. Сила Лоренца.
Эффект Холла.
3. Вихревой характер магнитного поля.

2.

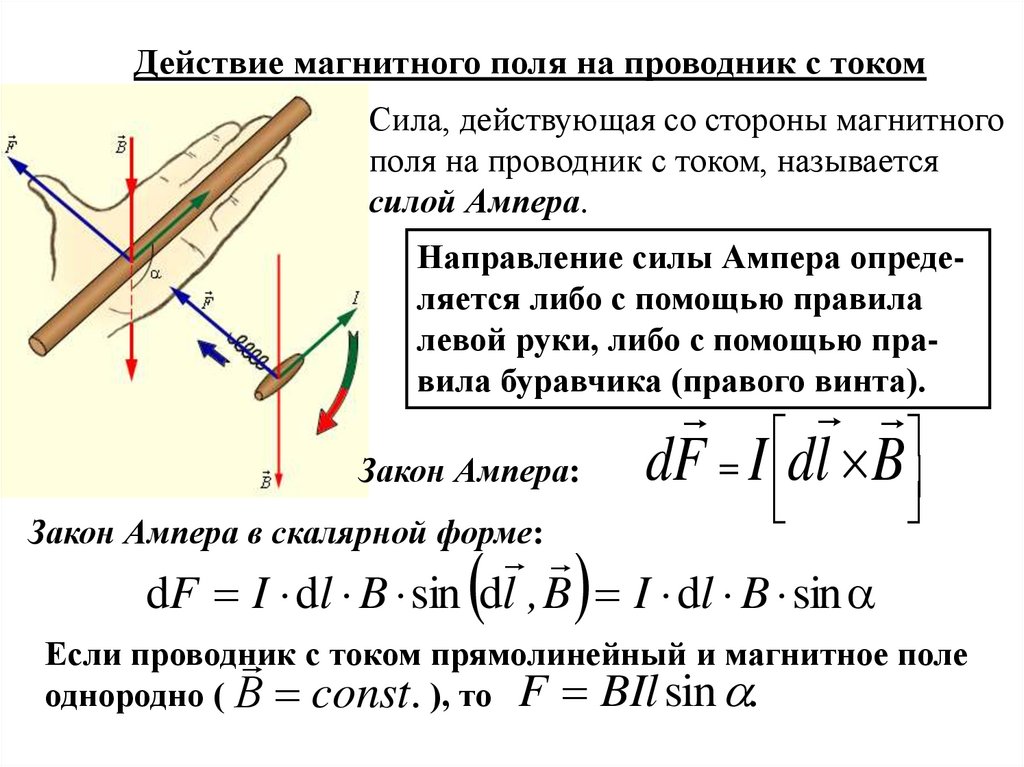
Действие магнитного поля на проводник с током
Сила, действующая со стороны магнитного
поля на проводник с током, называется
силой Ампера.
Направление силы Ампера определяется либо с помощью правила
левой руки, либо с помощью правила буравчика (правого винта).
Закон Ампера:
Закон Ампера в скалярной форме:
dF I dl B
dF I dl B sin dl , B I dl B sin
Если проводник
с током прямолинейный и магнитное поле
однородно ( В const. ), то F BIl sin .

3.

Взаимодействие параллельных проводников с током
I1
B
2
I2
F
F
По закону Био-Савара-Лапласа:
B
1
2
1
d
При
l1 l2 l
F1 F2 F :
0 I1I 2l
F
2
d
l >> d
и
0 I1
B1
2 d
0 I 2
B2
2 d
По закону Ампера:
0 I1I 2 dl
dF2 B1I 2 dl
dF1
2
d
Параллельные проводники с током
взаимодействуют с силами, пропорциональными произведению токов и
обратно пропорциональными расстоянию между ними.

4.

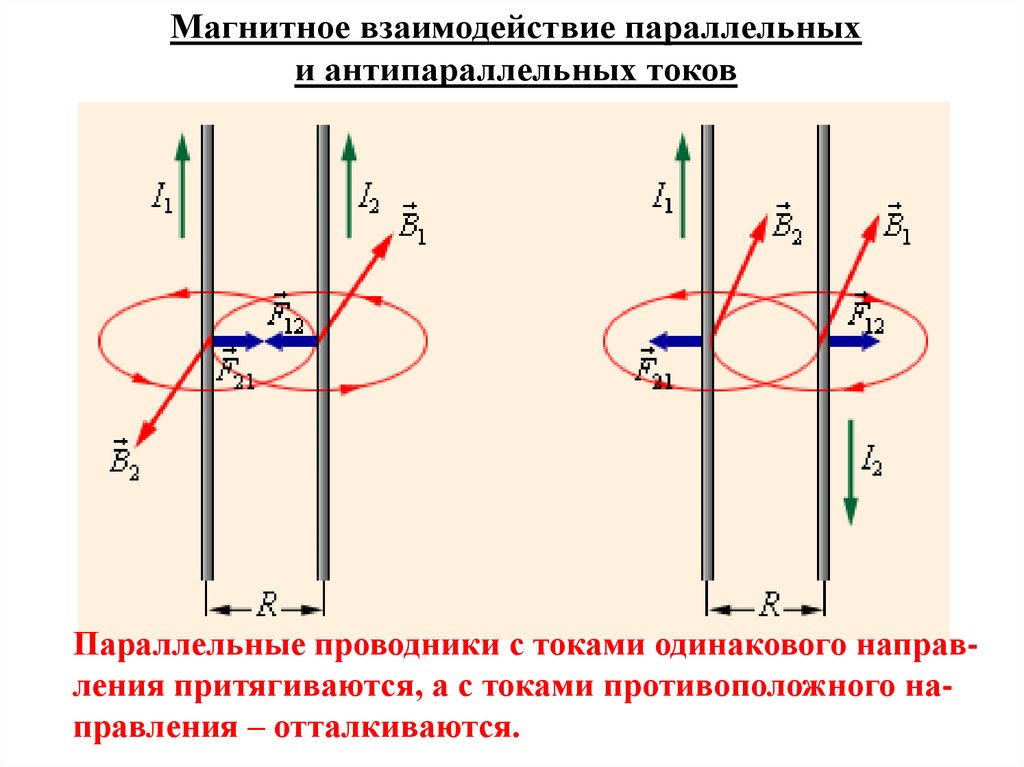
Магнитное взаимодействие параллельных
и антипараллельных токов
Параллельные проводники с токами одинакового направления притягиваются, а с токами противоположного направления – отталкиваются.

5.

Действие магнитного поля на движущийся заряд
B
В
Сила, действующая со стороны магнитного поля
на движущийся заряд, называется силой Лоренца.
Направление силы Лоренца, действующей
на положительно заряженную частицу,
определяется с помощью правила левой
руки.
F
Л
F q B
Л
F q B sin
Л
Сила Лоренца:
• не действует на незаряженную или покоящуюся частицу;
• не действует на частицу, движущуюся вдоль
линий магнитной индукции (α = 0 или π);
• не совершает работы, следовательно, не изме- Хендрик Лоренц
няет модуль скорости (кинетическую энергию). (1853 – 1928)

6.

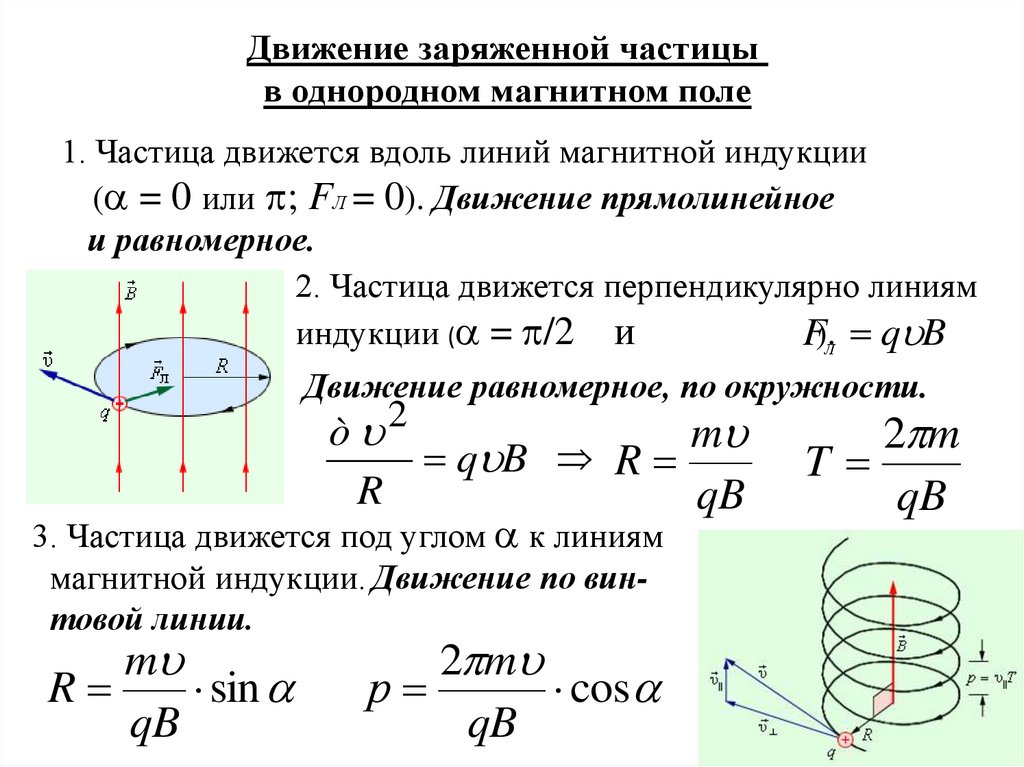
Движение заряженной частицы
в однородном магнитном поле
1. Частица движется вдоль линий магнитной индукции
( = 0 или ; FЛ = 0). Движение прямолинейное
и равномерное.
2. Частица движется перпендикулярно линиям
индукции ( = /2 и
F).Л q B
Движение равномерное, по окружности.
ò 2
m
q B R
R
qB
3. Частица движется под углом к линиям
магнитной индукции. Движение по винтовой линии.
m
R
sin
qB
2 m
р
cos
qB
2 m
T
qB

7.

Если на движущуюся заряженную частицу одновременно
действуют электрическое поле
напряженностью Е и маг
нитное поле с индукцией В , то результирующая сила
равна:
F q( E B )
– обобщенная сила Лоренца.
Электрическая составляющая обобщенной силы Лоренца
изменяет модуль скорости (кинетическую энергию) движущейся заряженной частицы, а магнитная составляющая – только направление ее движения.
Действие силы Лоренца лежит в основе работы масс-спектрографов и управления движением заряженных частиц
в современных ускорителях (циклотронах, синхрофазотронах и т.д.)

8.

Эффект Холла (обнаружен в 1879 г.)
E
B
Эффект Холла – это
возникновение поперечной разности потенциалов в проводнике с током, помещенном в магнитное
поле.
Под действием силы Лоренца возникает разделение зарядов
на противоположных гранях проводника и образуется поперечное электрическое поле.
Fл Fэл
– холловская разность
потенциалов.

9.

Постоянная Холла
где
Эдвин Герберт Холл
(1855 – 1938)
– постоянная
Холла.
Измерив постоянную Холла, можно найти концентрацию
носителей тока в данном металле.
Применение эффекта Холла:
• МГД-генераторы;
• датчики магнитного поля;
• исследование свойств полупроводников.

10.

Циркуляция вектора магнитной индукции
L
B
B B dl
dl
L
– циркуляция вектора
магнитной индукции.
L – произвольный
замкнутый контур.
Если для электростатического поля всегда:
E E dl 0,
L
то для магнитного поля
в общем случае:
B dl 0
B
L
(вихревое поле)

11.

B
Пример: вычислим циркуляцию вектора
для прямолинейного проводника с током в вакууме вдоль контура,
совпадающего с одной из магнитно-силовых линий.
I
r
0 I
B
2 r
d
B
0 I 2 r
B
d
l
d
l
I
0
L
2 r 0
Этот результат справедлив не только для кругового контура,
но и для замкнутого контура любой геометрической формы.

12.

Закон полного тока в вакууме
I1
S
I2
n
I3
Если контур охватывает
несколько токов, то справедлив
принцип суперпозиции:
B
d
l
I
0
i
i
L
Закон полного тока в вакууме:
циркуляция вектора магнитной индукции в вакууме равна произведению
L
магнитной постоянной на алгебраическую сумму токов, охватываемых
этим контуром.
Например, для схемы,
показанной на рисунке:

13.

Магнитный поток
n
dS
ÔB
B
Магнитным потоком через
площадку dS называется
скалярная физическая величина
dÔ B B ndS B cos α dS BndS
B dS B ndS Bn dS
S
S
S
Для однородного поля и плоской площадки
ÔB
S
B dS 0
– магнитный
поток через
конечную площадку.
– теорема Гаусса
для магнитного поля.

14.

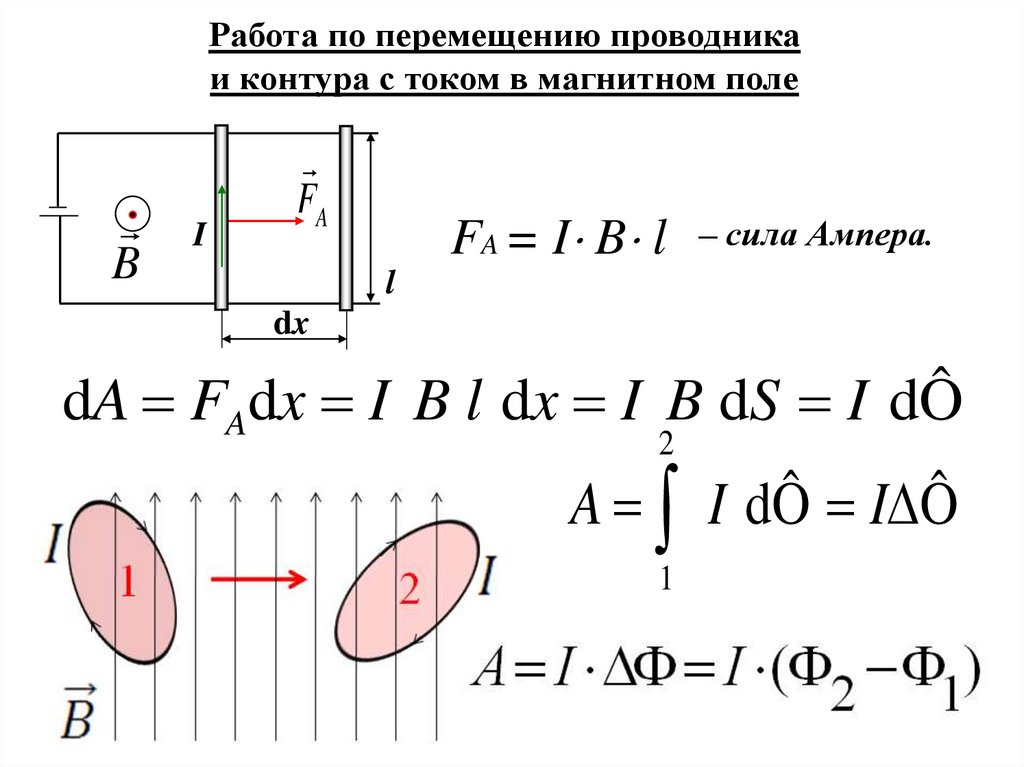
Работа по перемещению проводника
и контура с током в магнитном поле
B
I
FA
FA = I B l
– сила Ампера.
l
dx
dA FAdx I B l dx I B dS I dÔ
2
A I dÔ I Ô
1