Формирование комплектов машин в условиях определенности (лекция 13)

1. Лекция № 13 Тема: Формирование комплектов машин в условиях определенности

Задан некоторый технологический процесс
строительства автомобильной дороги, включающий
множество операций (i = 4). Каждая операция может
быть выполнена различными типами или типоразмерами
машин, имеющимися в парке машин строительной
организации.
1-ая операция - работают три экскаватора с различной
вместимостью ковша;
2-ая операция - транспортировка грунта тремя автомобилямисамосвалами различной грузоподъемности;
3-я операция - планировка грунта двумя автогрейдерами;
4-ая операция - уплотнение грунта катками двух видов.

2.

Известны приведенные затраты на
выполнение каждой операции каждой
машиной С i j.
Требуется сформировать оптимальный
комплект машин для выполнения всего
технологического процесса. Изобразим
графически все возможные комплекты машин
с заданными операциями в виде сетевого
графа
Рис. 1.
Каждая операция в сетевом графе
представляется в виде стрелки с указанием
над ней стоимости машиносмены.
Стрелка означает возможные связи одной
машины с другой или другими.

3.

Кружек означает завершение одной операции одним
типом машин и начало выполнения другой операции
другим типом машин. Число под кружком означает
сквозную нумерацию машин, для выполнения
технологического процесса.
Начальный и конечный кружки сетевого графа
означают соответственно начало и конец
технологического цикла, а номер 0 и 11- номера
фиктивных машин.
Таким образом в нашей задаче есть десять
машин (3 - экскаватора, 3 -самосвала, 2 - автогрейдера
и 2 – катка). Все эти машины по производительности и
другим техническим параметрам увязаны между собой.
Если какая-то машина не увязывается – в графе
должна отсутствовать стрелка (связь) между этими
машинами. Множество таких ограничений часто
упрощает решение задачи. Увеличение операций и
количество машин значительно усложняет задачу.

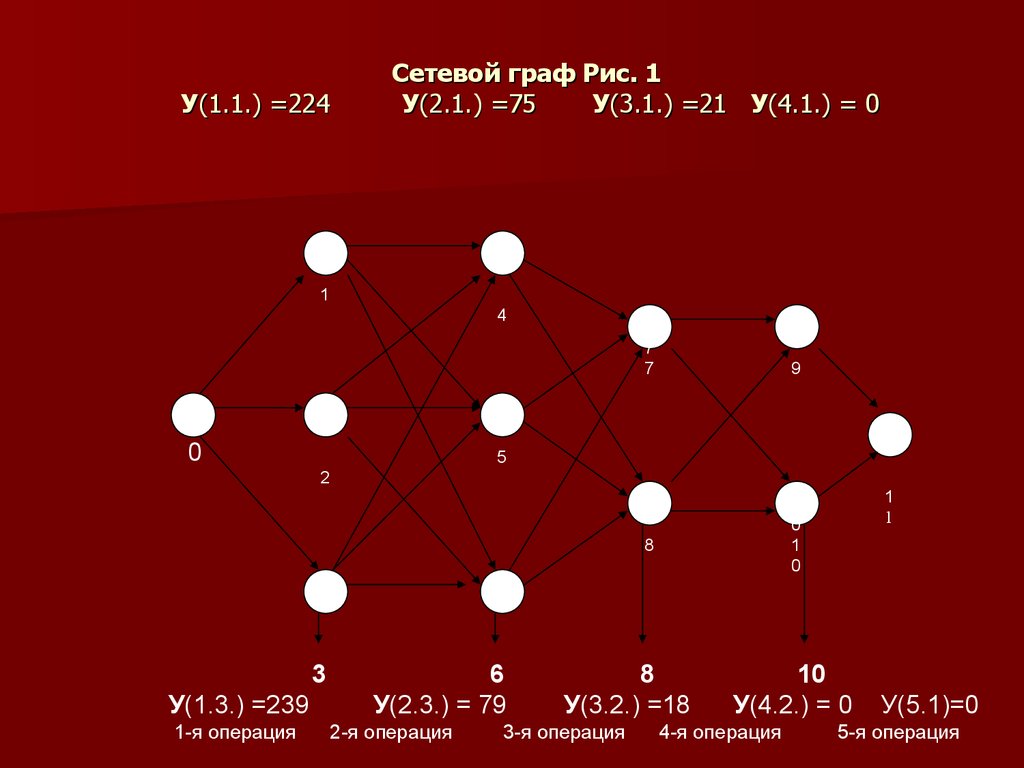
4. Сетевой граф Рис. 1 У(1.1.) =224 У(2.1.) =75 У(3.1.) =21 У(4.1.) = 0

У(1.1.) =224
Сетевой граф Рис. 1
У(2.1.) =75
У(3.1.) =21 У(4.1.) = 0
4
1
1
4
7
7
2
9
5
0
5
2
8
8
У(1.3.) =239
1-я операция
3
3
3
6
У(2.3.) = 79
2-я операция
8
У(3.2.) =18
3-я операция
1
1
1
0
1
0
10
У(4.2.) = 0
4-я операция
У(5.1)=0
5-я операция

5.

*С(1.1.1.) =46; С(1.1.2.) = 48; С(1.1.3.) =
35;
*С(2.1.1.) = 157; С(2.1.2.) = 150;
С(2.1.3.) = 145; С(2.2.1.) =155;
С(2.2.2.) = 150; С( 2.2.3.) = 146;
С(2.3.1.) = 165; С(2.3.2.) = 162;
С(2.3.3.) = 160;
* С(3.1.1.) = 52; С(3.1.2.) = 56;
С(3.2.1.) = 56; С(3.2.2.) = 60;
С(3.3.1.) = 58; С(3.3.2.) = 60;
* С(4.1.1.) = 21; С(41.2.) =24; С(4.2.1)=20;
С(4.2.2.) = 18;
* С(5.1.1) =0; С(5.2.1.) = 0.

6.

Для решения данной задачи воспользуемся
принципом оптимальности Беллмана (метод
динамического программирования), согласно которому
оптимальный выбор обладает тем свойством, что,
каково - бы ни было состояние и решение в
начальный момент, последующие решения должны
быть оптимальными.
Метод динамического программирования дает
возможность заменить перебор всех вариантов
определенной системой действий, при которых
отыскание экстремума многих переменных заменяется
многократным отысканием экстремума одной
переменной.
Оптимизируемый процесс разделяется на ряд
последовательных этапов (шагов) и производится
последовательная оптимизация каждого шага.

7.

В качестве математической модели может быть использовано
функциональное уравнение Беллмана, которое дает ключ для
решения задачи:
Y(( i - 1), j) = min [C i j + Y(( i+1), j)]
где:
Y(( i - 1), j) - минимальная стоимость машиносмены для
комплекта машин, начиная с i операции и j
машины;
Y(( i+1), j) - тоже, начиная с ( i+1) операции и j машины.
Алгоритм оптимизации выбора оптимального комплекта машин
методом динамического программирования состоит из двух
основных этапов.
На первом этапе производят расчет критерия оптимизации для
частичных комплектов машин, начиная его с расчета машин,
выполняющих последнюю операцию. Постепенно переходя к
началу процесса и используя функциональное уравнение
Беллмана, определяют минимальную стоимость машиносмены.

8.

На первом шаге полагаем:
Y (5.1.) = 0
Y (4.1.) = min ( С (5.1.1.) + Y (5.1.) = min (0 + 0) = 0
Y (4.2.) = min ( С (5.2.1.) + Y (5.1.) = min (0 + 0) = 0
На втором шаге добавляем еще одну операцию и
определяем для всех частных комплектов машин тот, который
имеет минимальные затраты:
С (4.1.1.) + Y (4.1.)
21 + 0
Y(3.1.) = min {
} = min {
} = 21
С (4.1.2.) + Y (4.2.)
24 + 0
С (4.2.1.) + Y (4.1.)
20 + 0
Y(3.2.) = min {
} = min {
}
С (4.2.2.) + Y (4.2.)
18 + 0
= 18

9.

На третьем шаге:
С (3.1.1.)+Y (3.1.)
54 + 21
Y(2.1.)=min{
}=min{
}= 75
С (3.1.2.)+Y (3.2.)
58 + 18
С (3.2.1.)+Y (3.1.)
56 + 21
Y(2.2.)=min{
}=min{
}= 77
С (3.2.2.)+Y (3.2.)
60 + 18
С (3.3.1.)+Y (3.1.)
58 + 21
Y(2.3.)=min{
}=min{
}=79
С (3.3.2.)+Y (3.2.)
62 + 18

10.

На четвертом шаге:
С (2.1.1.) + Y (2.1.)
157 + 75
Y(1.1.)=minС (2.1.2.) + Y (2.2.)=min 150 + 77=224
С (2.1.3.) + Y (2.3.)
145 + 79
С (2.2.1.)+ Y (2.1.)
155 + 75
Y(1.2.)=min С(2.2.2.) + Y (2.2.)=min 150 + 77 =225
С (2.2.3.)+ Y (2.3.)
146 + 79
С (2.3.1.) + Y (2.1.)
165 + 75
Y(1.3.)=minС (2.3.2.) + Y (2.2.)=min 162 + 77 =239
С (2.3.3.) + Y (2.3.)
160 + 79

11.

На пятом шаге:
С (1.1.1.) + Y (1.1.)
46 + 224
Y(0.1.)= minС (1.1.2.) +Y (1.2.)=min 48 +225 = 270
С (1.1.3.) + Y (1.3.)
35 + 239
Первый этап закончен, получена минимальная
суммарная стоимость машиносмены Y =270.
Теперь определим машины, какие входят в комплект с
наименьшими затратами.
На втором этапе, который выполняется в
обратной последовательности, на каждом шаге
определяется машина, затраты от которой вошли в
суммарный минимум критерия оптимизации.

12.

На первой операции или на пятом шаге: смотрим строку,
которая дала минимальное значение (46 + 224)=270 по связи
С(1.1.1) = 46 выходим на машину-1.
На второй операции или на четвертом шаге: выходим на
строку, имеющее значение 224 и смотрим, какое значение его
дало (145 + 79) =224. По связи С (2.1.3) = 145 выходим на
машину - 6.
На третьей операции или на третьем шаге: аналогично ранее
отмеченному машина - 7.
На четвертой операции или втором шаге: машина – 9.
Проверка:
(46 + 145 + 58 +21) = 270
Таким образом получен оптимальный комплект
состоящий из машин – 1, 6, 7, 9.