Методы измерения физических величин

1.

2.

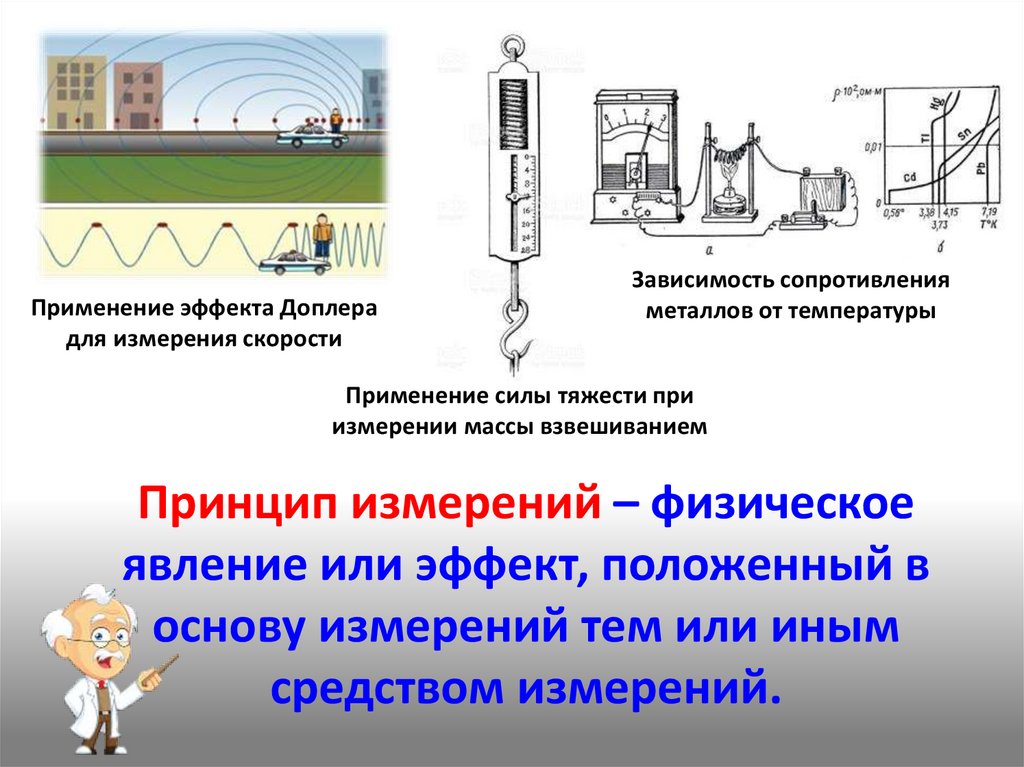
Применение эффекта Доплера
для измерения скорости
Зависимость сопротивления
металлов от температуры
Применение силы тяжести при
измерении массы взвешиванием
Принцип измерений – физическое
явление или эффект, положенный в
основу измерений тем или иным
средством измерений.

3.

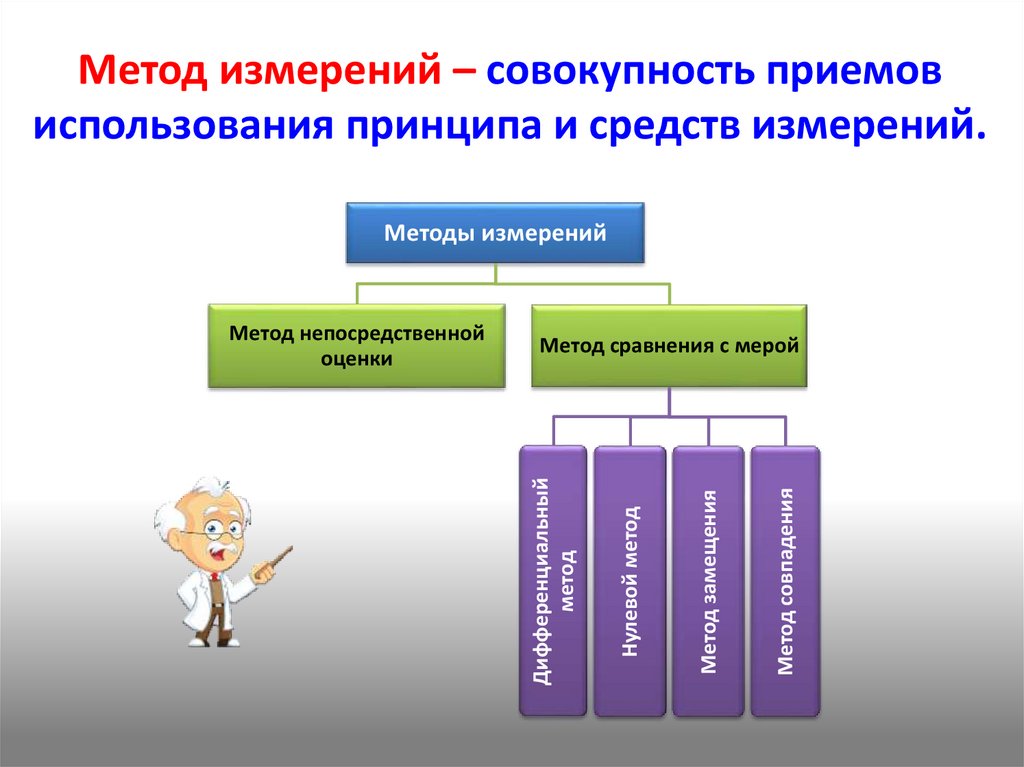
Метод измерений – совокупность приемов
использования принципа и средств измерений.
Методы измерений
Метод совпадения
Метод замещения
Нулевой метод
Метод сравнения с мерой
Дифференциальный
метод
Метод непосредственной
оценки

4.

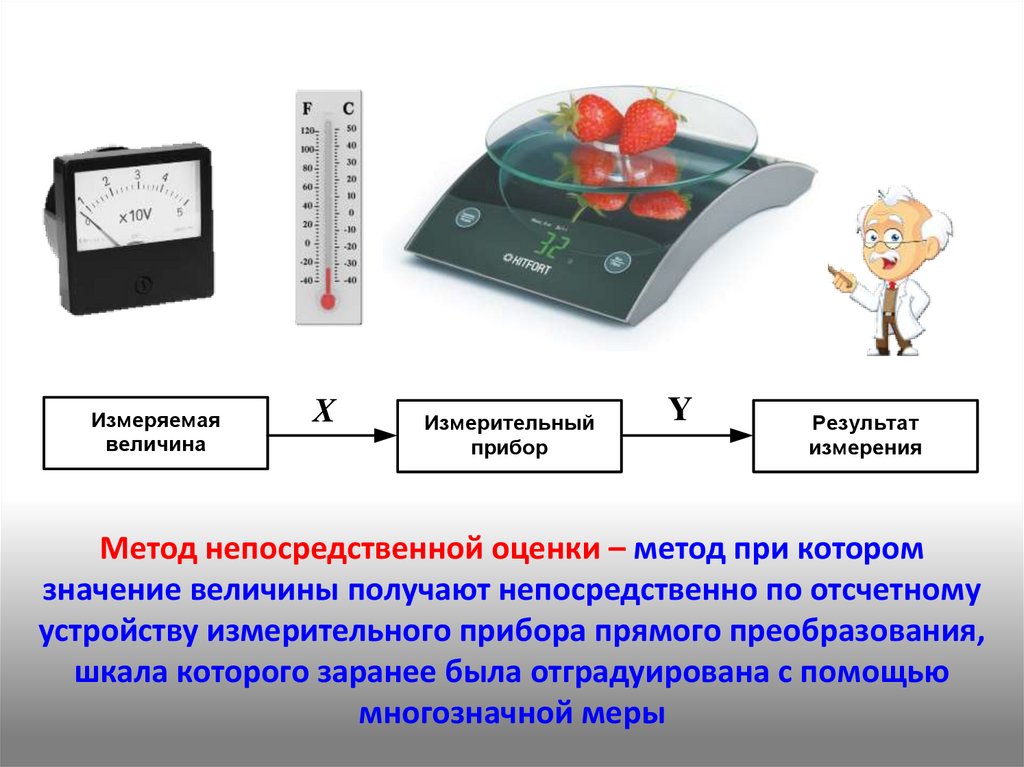
Измеряемая
величина
X
Измерительный
прибор
Y
Результат
измерения
Метод непосредственной оценки – метод при котором
значение величины получают непосредственно по отсчетному
устройству измерительного прибора прямого преобразования,
шкала которого заранее была отградуирована с помощью
многозначной меры

5.

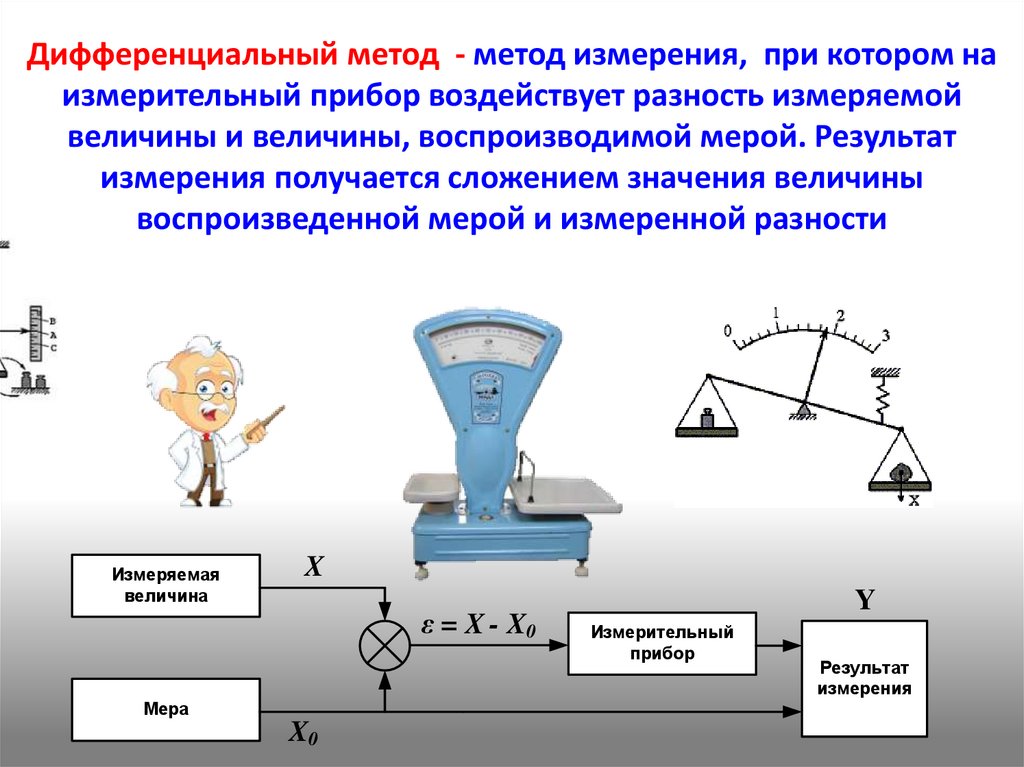
Дифференциальный метод - метод измерения, при котором на
измерительный прибор воздействует разность измеряемой
величины и величины, воспроизводимой мерой. Результат
измерения получается сложением значения величины
воспроизведенной мерой и измеренной разности
Измеряемая
величина
X
ε = X - X0
Мера
X0
Y
Измерительный
прибор
Результат
измерения

6.

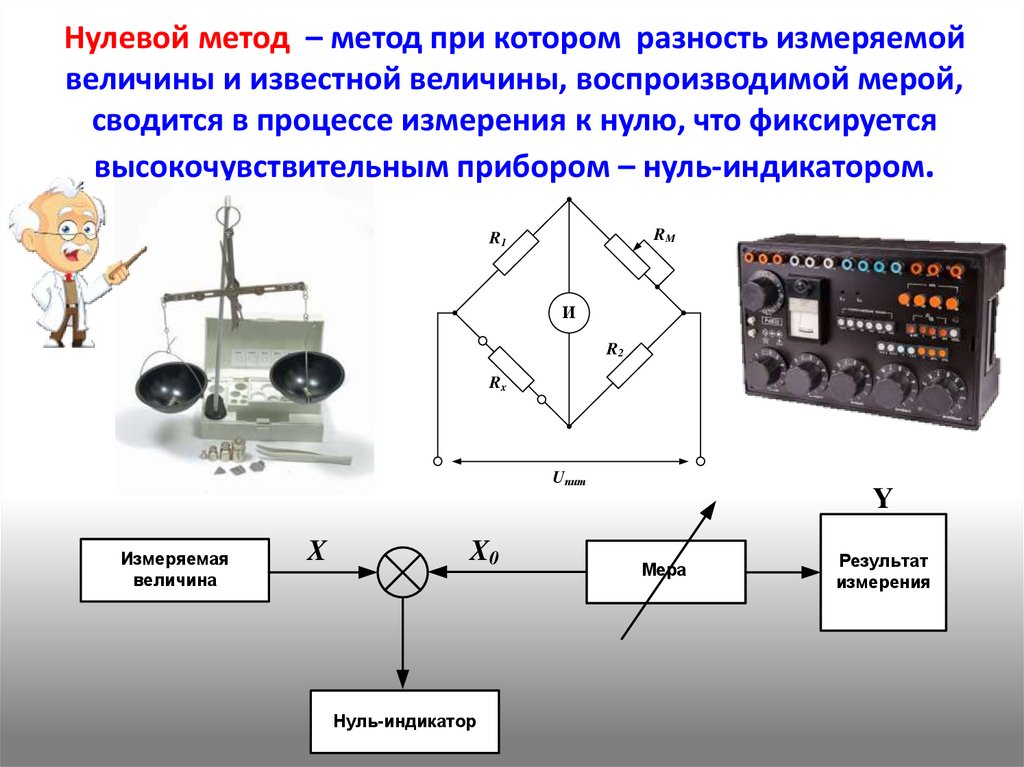
Нулевой метод – метод при котором разность измеряемой
величины и известной величины, воспроизводимой мерой,
сводится в процессе измерения к нулю, что фиксируется
высокочувствительным прибором – нуль-индикатором.
RM
R1
И
R2
Rx
Uпит
Y
Измеряемая
величина
X
X0
Нуль-индикатор
Мера
Результат
измерения

7.

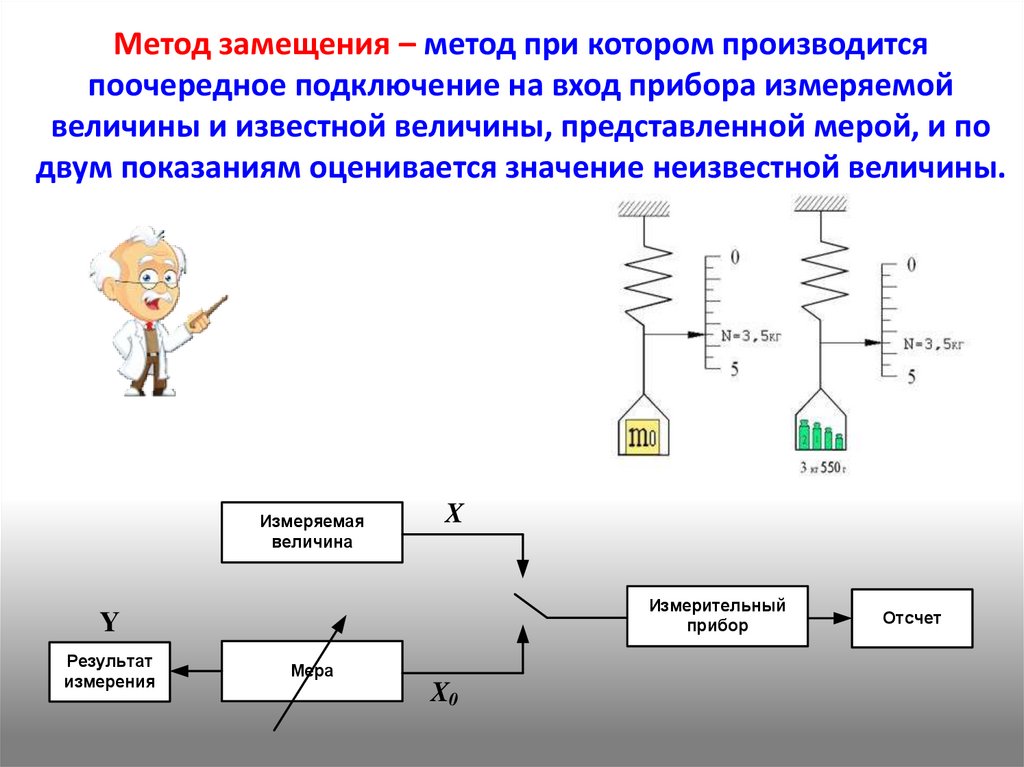
Метод замещения – метод при котором производится
поочередное подключение на вход прибора измеряемой
величины и известной величины, представленной мерой, и по
двум показаниям оценивается значение неизвестной величины.
Измеряемая
величина
X
Измерительный
прибор
Y
Результат
измерения
Мера
X0
Отсчет

8.

Метод совпадений (метод «нониуса») - метод, в котором
измеряют разность между измеряемой величиной и
величиной воспроизводимой мерой, используя совпадение
отметок шкал или периодических сигналов.
1
0
2
3
4
5
6
7
8
9
10
DxК1
Nx DxК1
Вторая мера со ступенями DК2
0
1
Dx
2
3
4
DxК2
5
6
7
8
9
10