Системы принятия решений

1.

НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМ. Н.И.ЛОБАЧЕВСКОГО
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ
ИНСТИТУТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МАТЕМАТИКИ И МЕХАНИКИ
Системы принятия решений
VLADIMIR GRISHAGIN

2.

Оценки экстремума
Рассмотрим следующий простой пример. Пусть класс - класс непрерывных
функций, т.е. априорно известно, что минимизируемая функция ( y ) непрерывна
в области Q . Предположим, что вычислены значения функции в конечном числе
точек y1 , y 2 ,..., y k . Что после этого можно сказать о координате глобального
минимума? Каковы бы ни были точки y1 , y 2 ,..., y k и значения z 1 , z 2 ,..., z k , для
любой точки y * Q ( y * { y1 ,..., y k })
всегда можно построить непрерывную
i
i
функцию, проходящую через точки ( y , z ), 1 i k ,
т.е. принадлежащую классу
( k ) из (1.11), которая имеет глобальный минимум в точке y * с любым наперед
заданным значением
* min z i .
1 i k
Например, в качестве такой функции можно взять интерполяционный
полином k -й степени, проходящий через точки ( y i , z i ), 1 i k , и точку ( y * , * ) .

3.

Оценки экстремума
Все сказанное означает, что по результатам конечного числа испытаний
никаких выводов о расположении координаты глобального минимума сделать
нельзя. Точно так же о величине * глобального минимума можно лишь
сказать, что
* k*
(1.17)
где k* из (1.15), однако оценить величину
k * k*
(1.18)
т.е. погрешность решения задачи, невозможно.
Возможность получения оценок экстремума по конечному числу испытаний
зависит от свойств класса функций, которому принадлежит минимизируемая
функция, или, другими словами, от априорной информации о функции .
Фактически известны лишь два широких класса функций, допускающих
построение таких оценок: класс одномерных унимодальных функций и класс
функций, удовлетворяющих условию Липшица (в общем случае многомерных и
многоэкстремальных).

4.

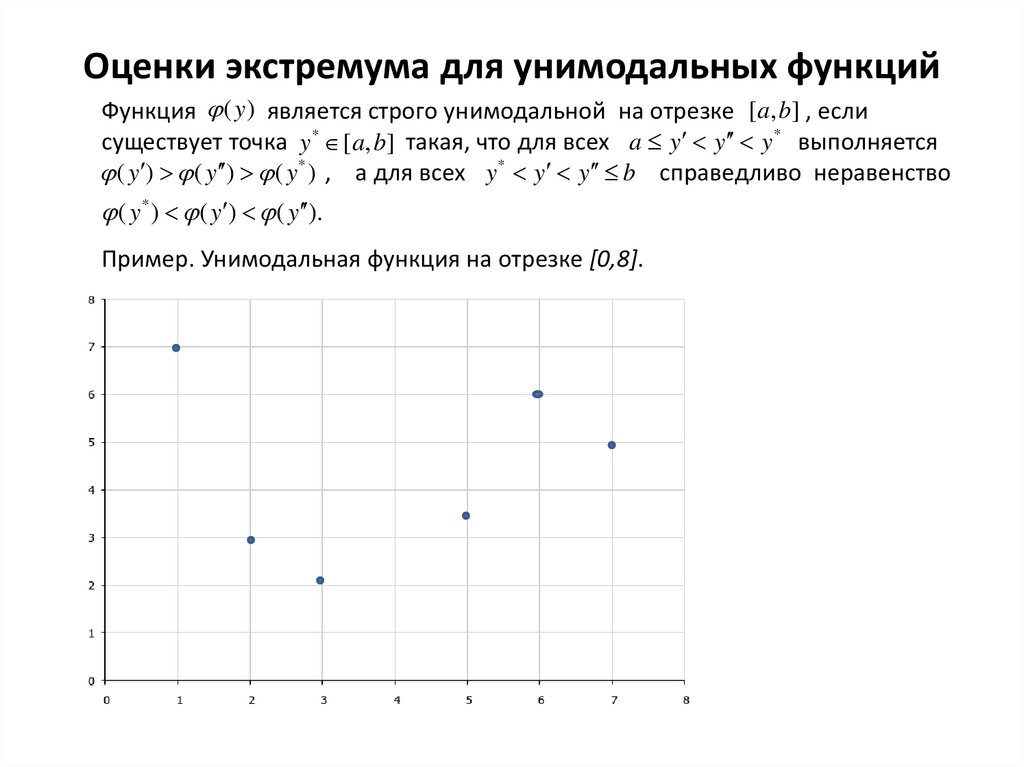
Оценки экстремума для унимодальных функций
Функция ( y ) является строго унимодальной на отрезке [a, b] , если
существует точка y * [a, b] такая, что для всех a y y y * выполняется
( y ) ( y ) ( y * ) , а для всех y * y y b справедливо неравенство
( y * ) ( y ) ( y ).
Пример. Унимодальная функция на отрезке [0,8].

5.

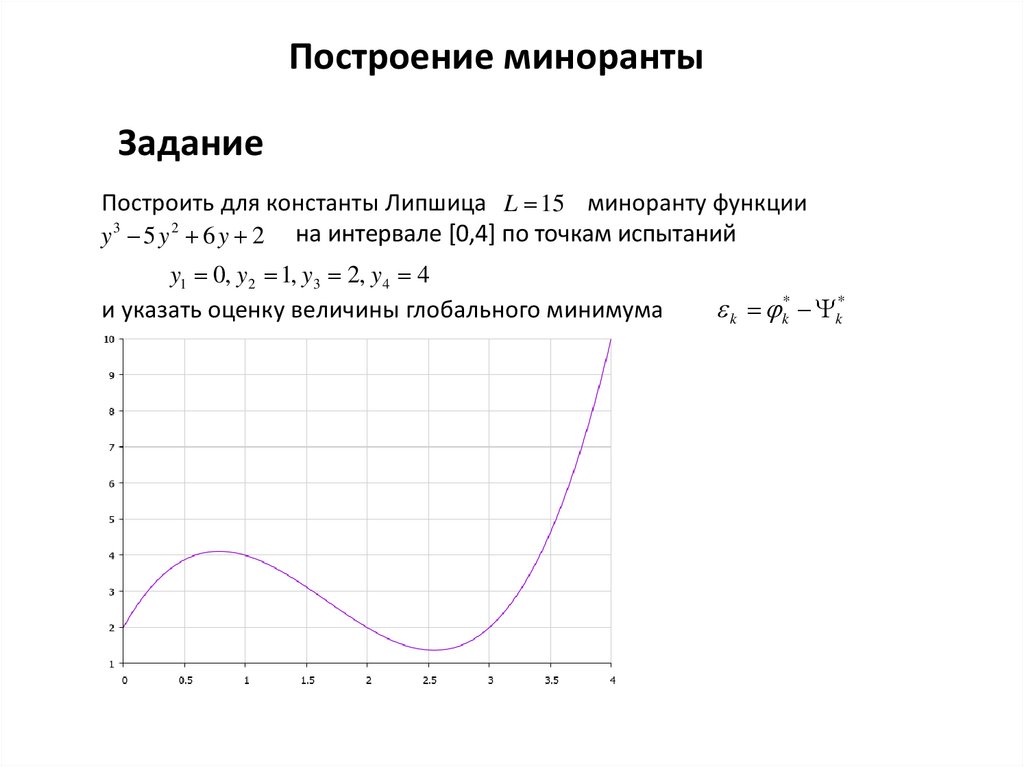
Построение миноранты
Задание
Построить для константы Липшица L 15 миноранту функции
y 3 5 y 2 6 y 2 на интервале [0,4] по точкам испытаний
y1 0, y2 1, y3 2, y4 4
и указать оценку величины глобального минимума
k k* k*

6.

Оптимальность алгоритмов оптимизации
Рассмотрим класс S алгоритмов s S , предназначенных для решения
задач оптимизации функций .
Вводится вещественная функция V( ,s) - критерий эффективность
решения задачи минимизации функции Φ с помощью метода s S
Критерии эффективности метода s на классе Φ
W (s) sup V ( , s)
или
Φ
W ( s) V ( , s)dP( ),
P( ) — некоторое распределение вероятностей, заданных на классе
измеримых подмножеств множества Φ .
*
Оптимальный алгоритм s :
W ( s * ) inf W ( s )
s S
(1.28)

7.

Оптимальность алгоритмов оптимизации
ε-оптимальный алгоритм оптимизации s * ( 0) :
W ( s * ) inf W ( s )
s S
(1.29)
Наилучший (последовательно-оптимальный алгоритм ) оптимизации
(А.Г.Сухарев) - алгоритм, наилучшим образом использующий
апостериорную (поисковую) информацию.

8.

Одношаговая оптимальность
Существуют значительные трудности в создании алгоритмов в соответствии с
принципами оптимальности (1.28) или (1.29). Чтобы преодолеть эти трудности,
можно попытаться упростить понятие оптимальности. Такую возможность
предоставляет принцип одношаговой оптимальности, когда мы требуем
оптимального поведения алгоритма не в течение всего процесса оптимизации,
а только на один шаг вперед, т.е. при выборе точки очередного испытания.
Чтобы кратко описать модель одношагово-оптимального алгоритма,
вспомним ряд обозначений, принятых в общей схеме численного метода
оптимизации (1.9)-(1.14).
1
2
k
После k испытаний, выполненных методом в точках y , y ,..., y с результатами
z1 , z 2 ,..., z k , z i ( y i ), 1 i k , мы имеем в своем распоряжении новую
информацию
k {( y1 , z1 ), ( y 2 , z 2 ),..., ( y k , z k )}
и мы можем утверждать, что целевая функция принадлежит классу
Φ ( k ) { Φ : ( y i ) z i , 1 i k}

9.

Одношаговая оптимальность
k ( k ) S ( k ) S
Vk 1 ( k , y, z ) - эффективность проведения очередного испытания в
точке y с получением результата z ( y )
Модель алгоритма
s {Gk },{Ek ),{H k },{Vk }
Множество таких алгоритмов обозначим через S 0
Wk 1 ( y k 1 )
sup
Vk 1 ( k , y k 1 , ( y k 1 ))
( k )
k 1
~
Wk 1 ( y k 1 ) ~min
W
(
y
) - критерий одношаговой оптимальности
k
k 1
x
Wk 1 ( y k 1 )
Q
k 1
k 1
k 1
k 1
V
(
,
y
,
z
)
dP
(
z
/
,
y
)
k
1
k
k
( k )
P( z k 1 / k , y k 1 ) - условное (по отношению к результатам испытаний)
распределение вероятностей

10.

Асимптотическая оптимальность
S K - множество методов, в которых остановка осуществляется ровно через K
шагов поиска
W ( K ) inf
s SK
W ( s),
Если метод s K* S K - оптимальный, то очевидно, что W (sK* ) W ( K )
Рассмотрим алгоритм s такой, что на каждом шаге K его усечение
sK S K
Алгоритм s называется асимптотически оптимальным, если
lim W ( sK ) / W ( K ) 1
K

11.

Характеристические алгоритмы
оптимизации
( x) min, x Q [a, b]
(*)
Определение. Алгоритм решения задачи (*) называется характеристическим,
k 1
если, начиная с некоторого шага поиска k0 1 , выбор координаты x
очередного испытания (k k0 ) заключается в выполнении следующих
действий.
1. Задать множество
k {x0 , x1 ,..., x }
конечного числа 1 (k ) 1 точек области Q [a, b] , полагая, что
i
a k , b k , все координаты предшествующих испытаний x k , 1 i k ,
множество k упорядочено (нижним индексом) по возрастанию координаты,
т.е.
a x0 x1 ... x 1 x b.
и сопоставить точкам множества значения zi ( xi ), 0 i .

12.

Характеристические алгоритмы
оптимизации
2. Каждому интервалу ( xi 1 , xi ) , 1 i , поставить в соответствие число R (i ) ,
называемое характеристикой этого интервала.
3. Определить интервал ( xt 1 , xt ) , которому соответствует максимальная
характеристика R (t ) , т.е.
R(t ) max{ R(i ) : 1 i }
4. Провести очередное испытание в точке
x k 1 d (t ) ( xt 1 , xt )
и вычислить значение z
k 1
( x k 1 ).

13.

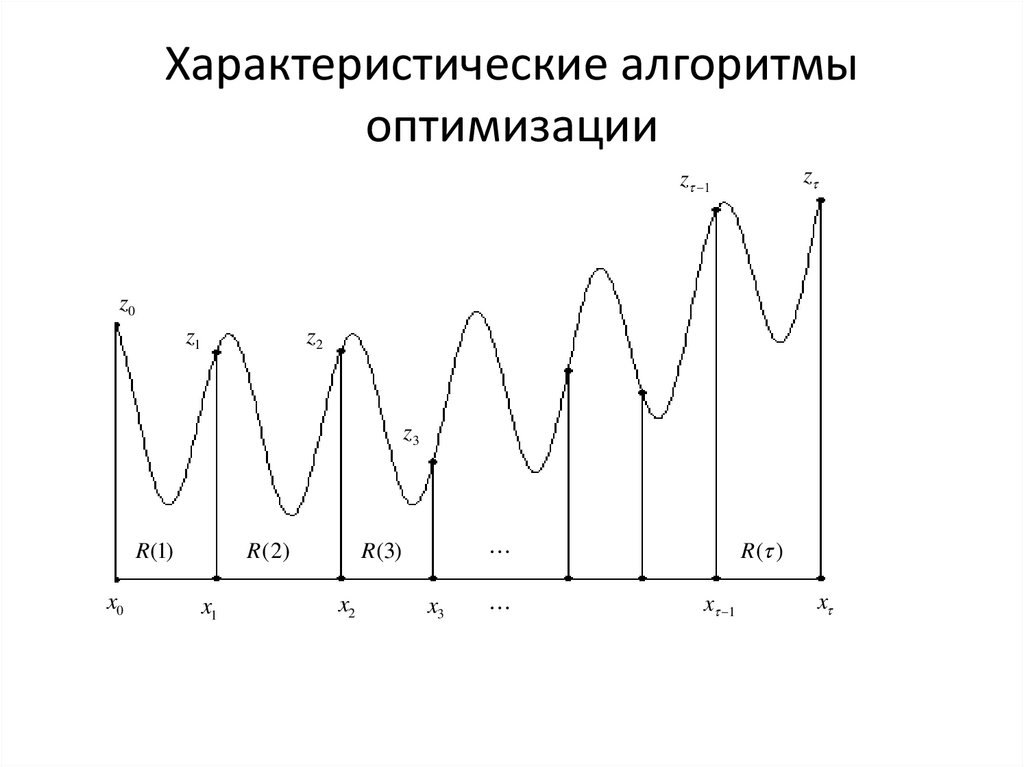
Характеристические алгоритмы
оптимизации
z
z 1
z0
z1
z2
z3
R ( 2)
R (1)
x0
x1
x2
R ( )
R(3)
x3
x 1
x

14.

Примеры характеристических алгоритмов
Два первых испытания проводятся в точках x1 a и x 2 b ,
характеристическое правило вступает в действие, начиная с k=2, при этом
множество k (k 2) состоит только из точек испытаний, т.е.
k {x1 , x 2 ,..., x k ) и, следовательно,
k 1.
Метод последовательного сканирования (перебор).
R(i) xi xi 1
x k 1 0.5( xt 1 xt ).

15.

Методы Пиявского и Стронгина
Метод Пиявского (метод ломаных)
R(i) 0.5m( xi xi 1 ) ( zi zi 1 ) / 2,
x k 1 0.5( xt xt 1 ) ( zt zt 1 ) /( 2m),
Алгоритм глобального поиска – АГП (метод Стронгина)
( zi zi 1 ) 2
R(i) m( xi xi 1 )
2( zi zi 1 ),
m( xi xi 1 )
rM , M 0
m
1, M 0
M max
1 i
zi zi 1
xi xi 1
r 1 - параметр метода

16.

Метод Кушнера
Характеристика подынтервала ( xi 1 , xi )
4( k* k zi )( k* k zi 1 )
R(i)
xi xi 1
Точка очередного испытания
x
k 1
( xt xt 1 )( k* k zt )
xt 1
2( k* k ) zt zt 1
k 0 - параметр метода, зависящий в общем случае от номера испытания k
k* min zi
0 i
- минимальное вычисленное значение после k испытаний

17.

Алгоритм глобального поиска без
вычислений на концах интервала
Согласно алгоритму одно или несколько начальных испытаний выполняются
в произвольных внутренних точках отрезка [a, b] и только потом вступает в
действие характеристическое правило. Множество k включает в себя
координаты проведенных испытаний и дополнительно концы отрезка.
Как и ранее, z j ( x j ) , однако, только для 1 j k . Значения z0 ( x0 ) (a )
и z ( x ) (b) не определены, поскольку точки x0 a, x b не
являются точками испытаний и, следовательно, значения целевой функции в
них не вычисляются.
Характеристика подынтервала ( xi 1 , xi ) вычисляется согласно выражению
r ( zi zi 1 ) 2
2( zi zi 1 ), 1 i ,
m( xi xi 1 )
M ( xi xi 1 )
R (i ) m( x1 x0 ) 4 z1 , i 1,
m ( x x ) 4 z , i ,
1
1

18.

Алгоритм глобального поиска без
вычислений на концах интервала
Точка очередного испытания
0, t 1 or t ,
x k 1 0.5( xt xt 1 )
( zt zt 1 ) /( 2m), 2 t 1,
rM , M 0
m
1, M 0
M max
2 i 1
zi zi 1
xi xi 1
r 1 - параметр метода

19.

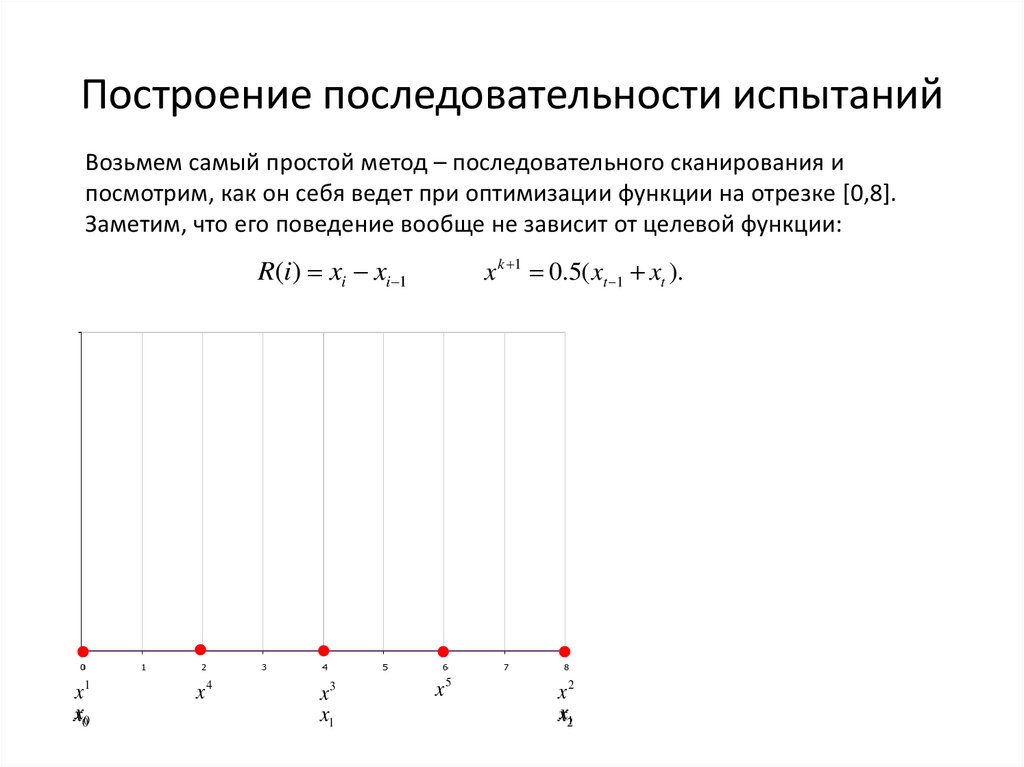
Построение последовательности испытаний
Возьмем самый простой метод – последовательного сканирования и
посмотрим, как он себя ведет при оптимизации функции на отрезке [0,8].
Заметим, что его поведение вообще не зависит от целевой функции:
R(i) xi xi 1
x1
x00
x4
x3
x1
x k 1 0.5( xt 1 xt ).
x5
x2
x21

20.

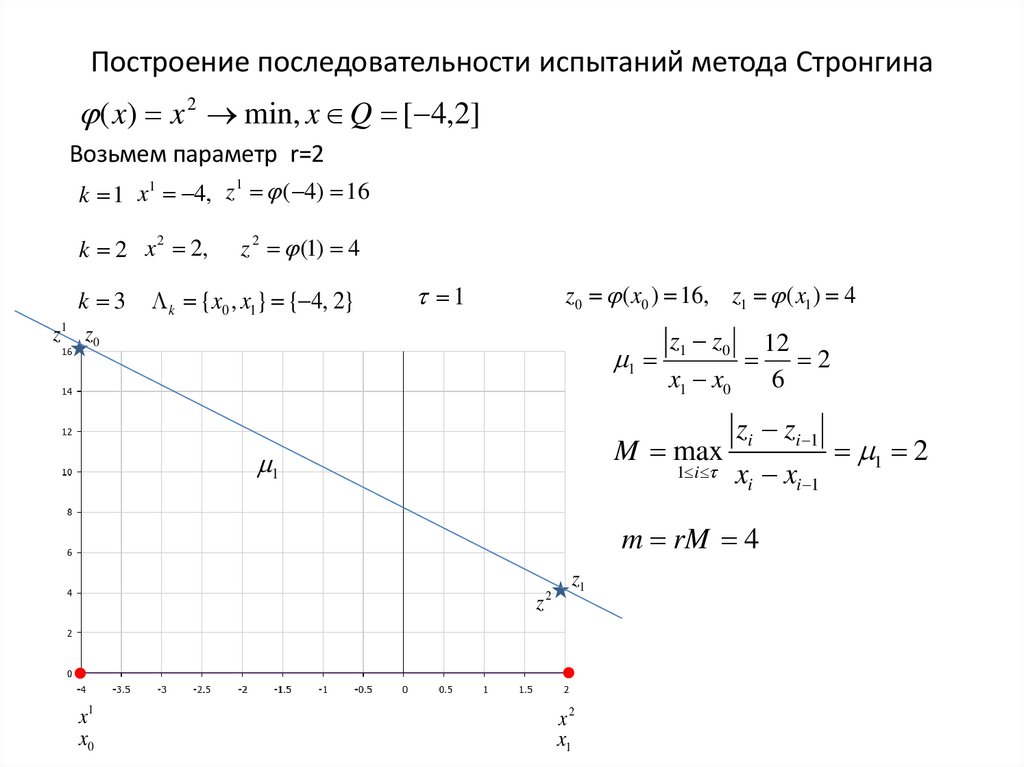
Построение последовательности испытаний метода Стронгина
( x) x 2 min, x Q [ 4,2]
Возьмем параметр r=2
1
k 1 x1 4, z ( 4) 16
k 2 x 2 2,
k 3
z 2 (1) 4
k {x0 , x1} { 4, 2}
z0 ( x0 ) 16, z1 ( x1 ) 4
1
z 1 z0
1
z1 z0
x1 x0
M max
1
1 i
zi zi 1
xi xi 1
m rM 4
z
x1
x0
2
z1
x2
x1
12
2
6
1 2

21.

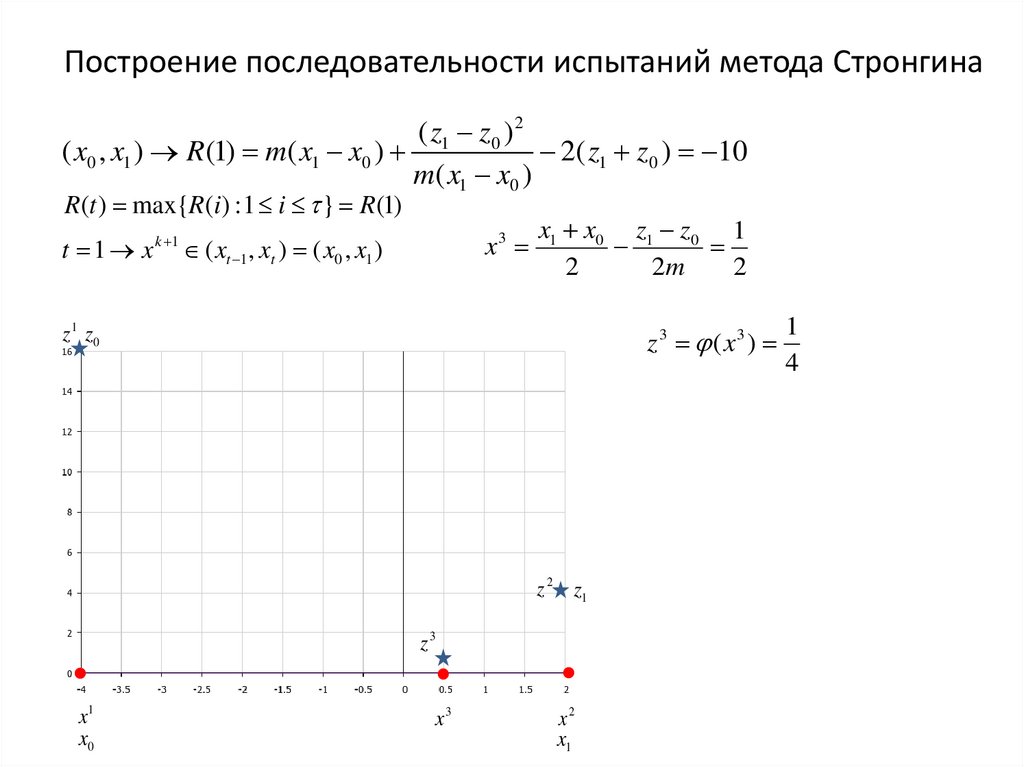
Построение последовательности испытаний метода Стронгина
( z1 z0 ) 2
( x0 , x1 ) R (1) m( x1 x0 )
2( z1 z0 ) 10
m( x1 x0 )
R (t ) max{R (i ) : 1 i } R(1)
x3
t 1 x k 1 ( xt 1 , xt ) ( x0 , x1 )
x1 x0 z1 z0 1
2
2m
2
z 1 z0
z 3 ( x3 )
z 2 z1
z3
x1
x0
x3
x2
x1
1
4

22.

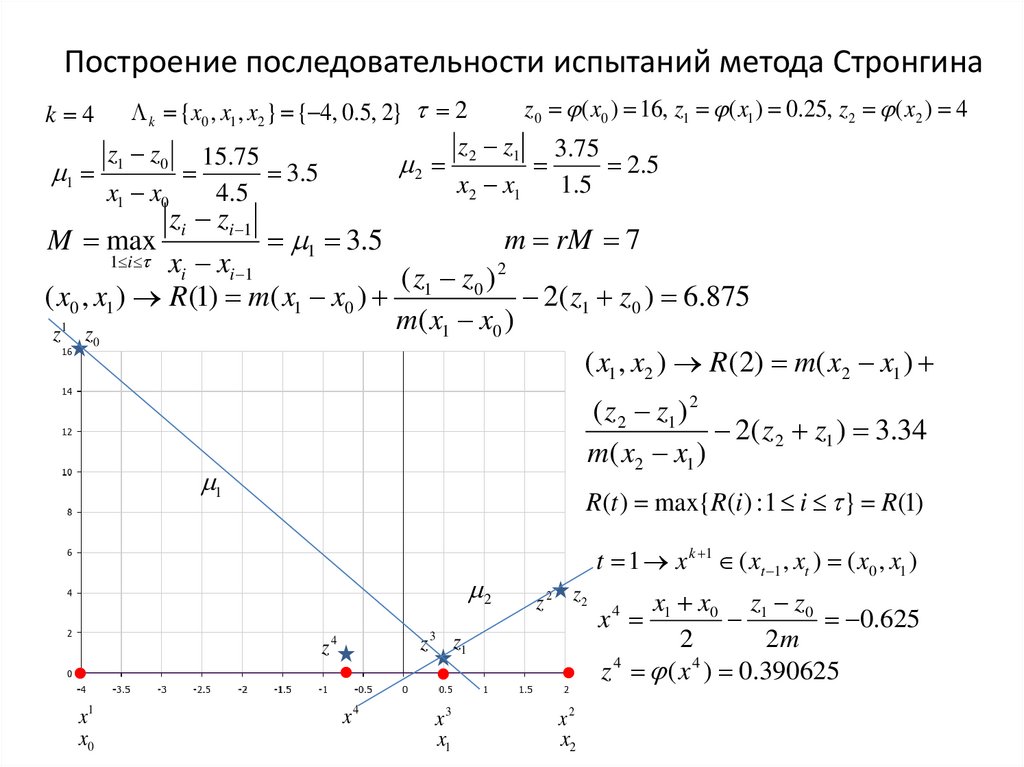
Построение последовательности испытаний метода Стронгина
z0 ( x0 ) 16, z1 ( x1 ) 0.25, z 2 ( x2 ) 4
k {x0 , x1 , x2 } { 4, 0.5, 2} 2
z 2 z1 3.75
z1 z0 15.75
2 .5
2
1
3 .5
x2 x1
1 .5
x1 x0
4 .5
k 4
M max
zi zi 1
1 3.5
m rM 7
xi xi 1
( z1 z0 ) 2
( x0 , x1 ) R (1) m( x1 x0 )
2( z1 z0 ) 6.875
m( x1 x0 )
z 1 z0
( x1 , x2 ) R (2) m( x2 x1 )
1 i
( z 2 z1 ) 2
2( z 2 z1 ) 3.34
m( x2 x1 )
1
R(t ) max{R(i ) : 1 i } R(1)
2
z 2 z2
z 3 z1
z4
x1
x0
t 1 x k 1 ( xt 1 , xt ) ( x0 , x1 )
x4
x3
x1
x2
x2
x1 x0 z1 z0
0.625
2
2m
z 4 ( x 4 ) 0.390625
x4