Кодирование информации

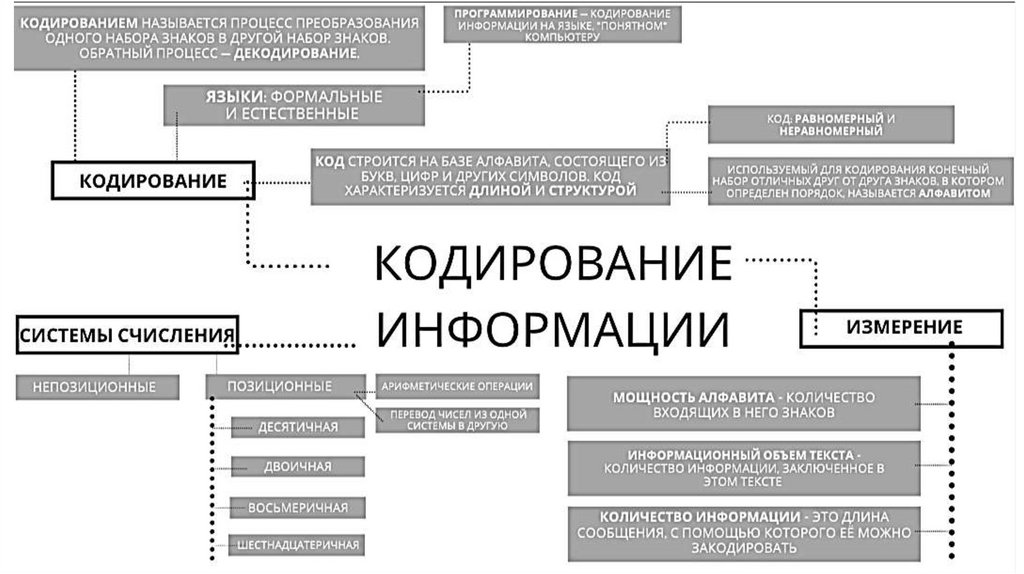
1. КОДИРОВАНИЕ ИНФОРМАЦИИ

2.

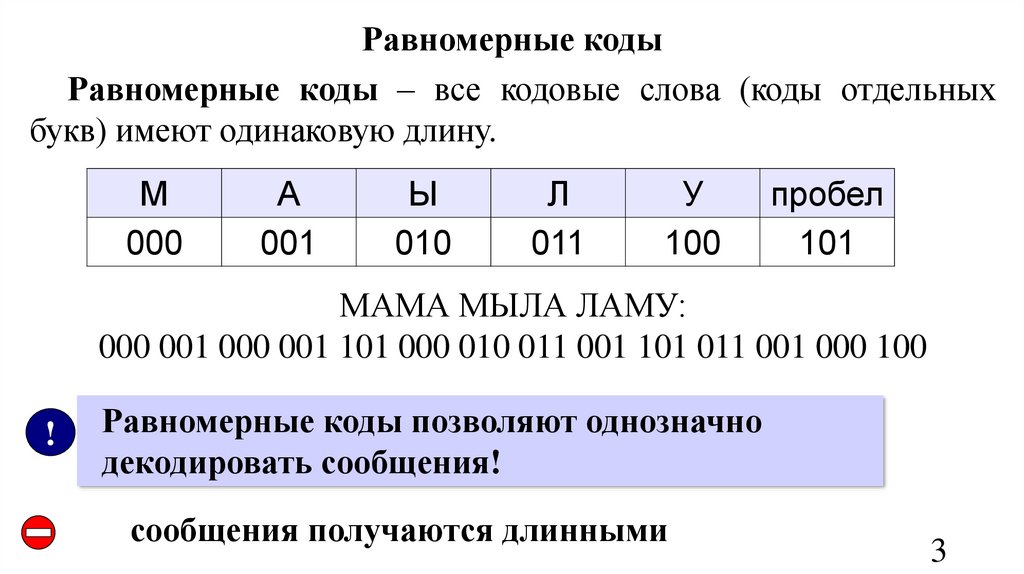
3. Равномерные коды

Равномерные коды – все кодовые слова (коды отдельных
букв) имеют одинаковую длину.
М
000
А
001
Ы
010
Л
011
У
100
пробел
101
МАМА МЫЛА ЛАМУ:
000 001 000 001 101 000 010 011 001 101 011 001 000 100
!
Равномерные коды позволяют однозначно
декодировать сообщения!
сообщения получаются длинными
3

4.

Закодируйте свое имя с помощью кодовой таблицы (Windows1251):
0 1 2 3 4 5 6 7 8 9 A B C D E F
C А Б В Г Д Е Ж З И Й К Л М Н О П
D Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я
ВАСЯ
В А С Я
С2 С0 D1 DF
! Код равномерный, разделитель НЕ нужен!

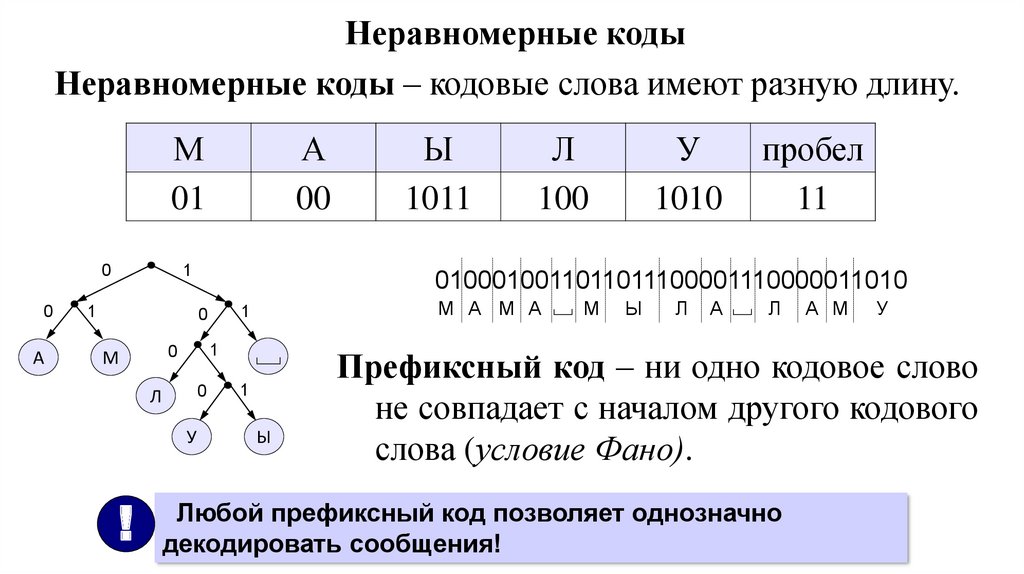
5. Неравномерные коды

Неравномерные коды – кодовые слова имеют разную длину.
М
01
0
0
А
А
00
1
1
0
У
!
М А М А
1
1
0
Л
Л
100
У
1010
пробел
11
0100010011011011100001110000011010
0
М
Ы
1011
1
Ы
М
Ы
Л
А
Л
А М
У
Префиксный код – ни одно кодовое слово
не совпадает с началом другого кодового
слова (условие Фано).
Любой префиксный код позволяет однозначно
декодировать сообщения!

6.

Закодируйте свое имя с помощью азбуки Морзе.
ВАСЯ
!
Код неравномерный, нужен разделитель!

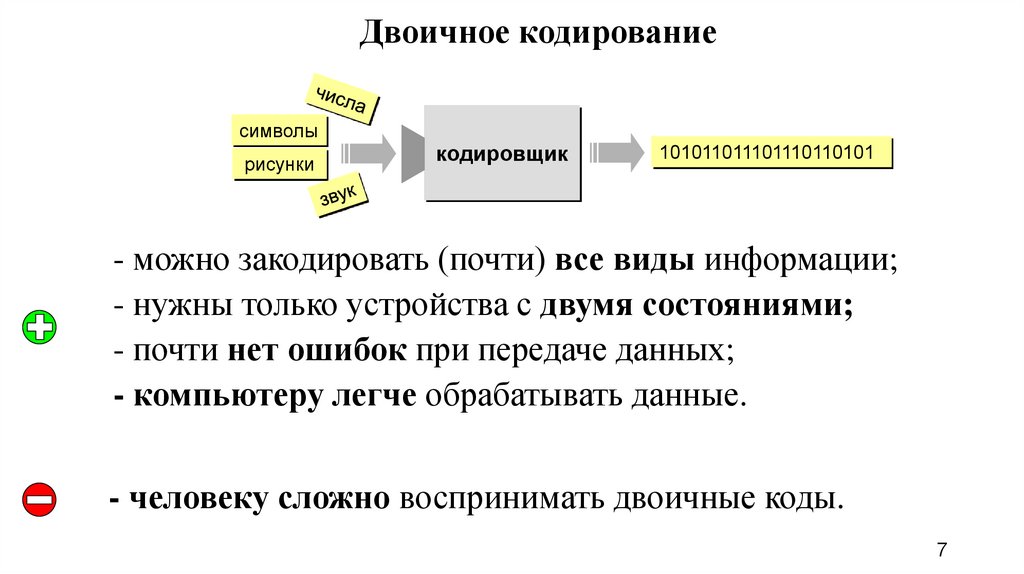
7. Двоичное кодирование

символы
рисунки
кодировщик
101011011101110110101
- можно закодировать (почти) все виды информации;
- нужны только устройства с двумя состояниями;
- почти нет ошибок при передаче данных;
- компьютеру легче обрабатывать данные.
- человеку сложно воспринимать двоичные коды.
7

8.

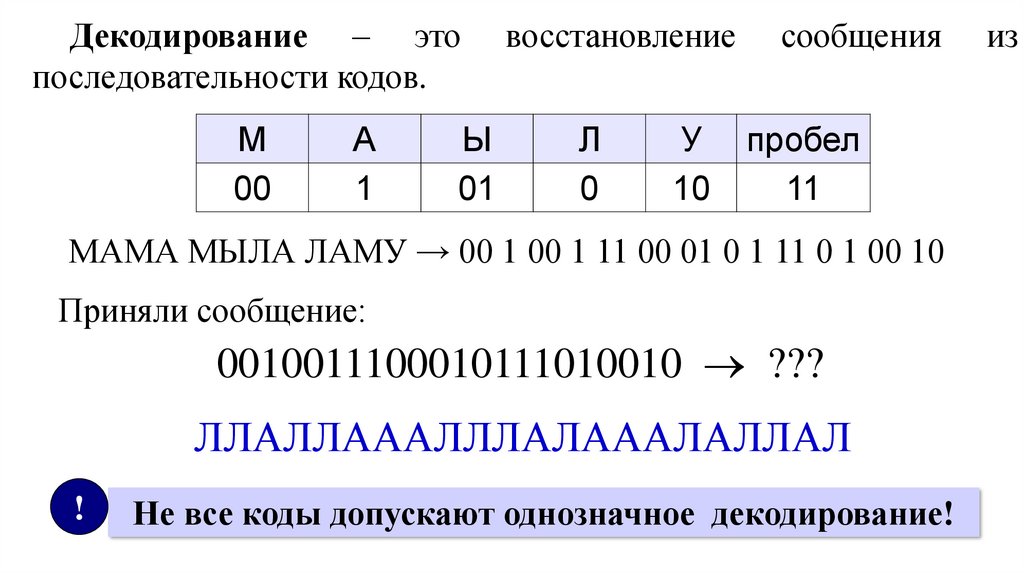
Декодирование – это
последовательности кодов.
М
00
А
1
Ы
01
восстановление
Л
0
У
10
сообщения
пробел
11
МАМА МЫЛА ЛАМУ → 00 1 00 1 11 00 01 0 1 11 0 1 00 10
Приняли сообщение:
0010011100010111010010 ???
ЛЛАЛЛАААЛЛЛАЛАААЛАЛЛАЛ
!
Не все коды допускают однозначное декодирование!
из

9.

Помехоустойчивое
кодирование
кодирование,
предназначенное для передачи данных по каналам с помехами,
обеспечивающее исправление возможных ошибок передачи
вследствие помех.
Для обнаружения ошибок используют коды обнаружения
ошибок, для исправления - помехоустойчивые коды.
Помехоустойчивое кодирование предполагает введение в
передаваемое сообщение, наряду с информационными, так
называемых
проверочных
разрядов,
формируемых
в
устройствах защиты от ошибок (кодерах - на передающем конце,
декодерах - на приемном).

10.

Лабораторная работа №5
ПОМЕХОУСТОЙЧИВЫЙ КОД ХЭММИНГА
Цель работы: изучение принципов помехоустойчивого
кодирования,
получение
навыков
моделирования
помехоустойчивых кодов с помощью ElectronicsWorkbench.

11.

ЗАДАНИЕ 1.
Формирование бита чётности
Простейший код, предназначенный для обнаружения одной
ошибки (точнее – для обнаружения нечётного числа ошибок),
основан на добавлении к информационным битам одного
контрольного бита.
При этом контрольный бит должен быть таким, чтобы
суммарное число единиц в образованном машинном слове
было чётным.
Добавляемый бит называется битом паритета.

12.

Проверочный бит k для n-битного двоичного слова b1b2...bn
вычисляется по формуле:

13.

Пример.
Пусть дан байт
10111100.
тогда k=1 и кодовая комбинация равна
101111001

14.

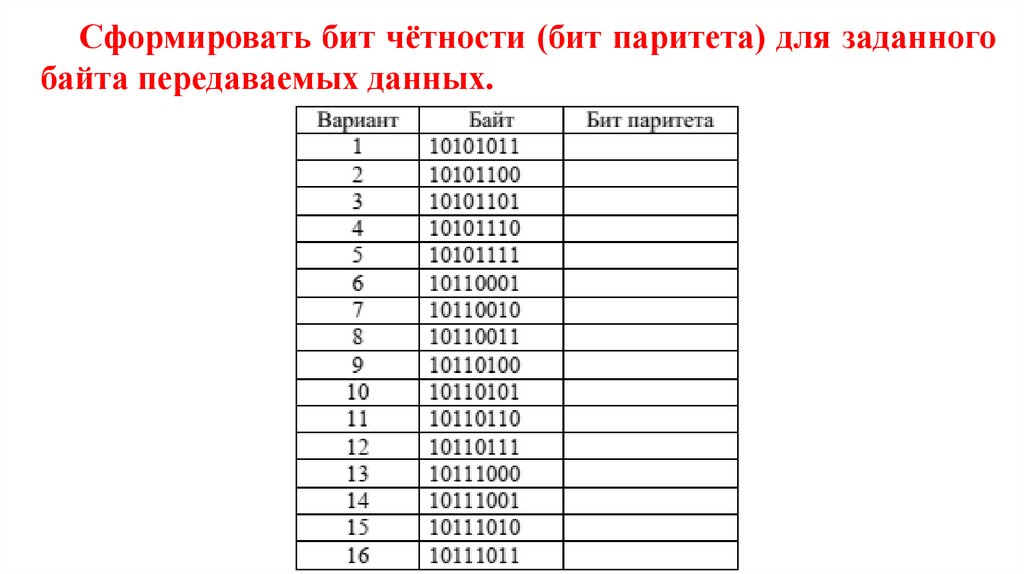
Сформировать бит чётности (бит паритета) для заданного
байта передаваемых данных.

15.

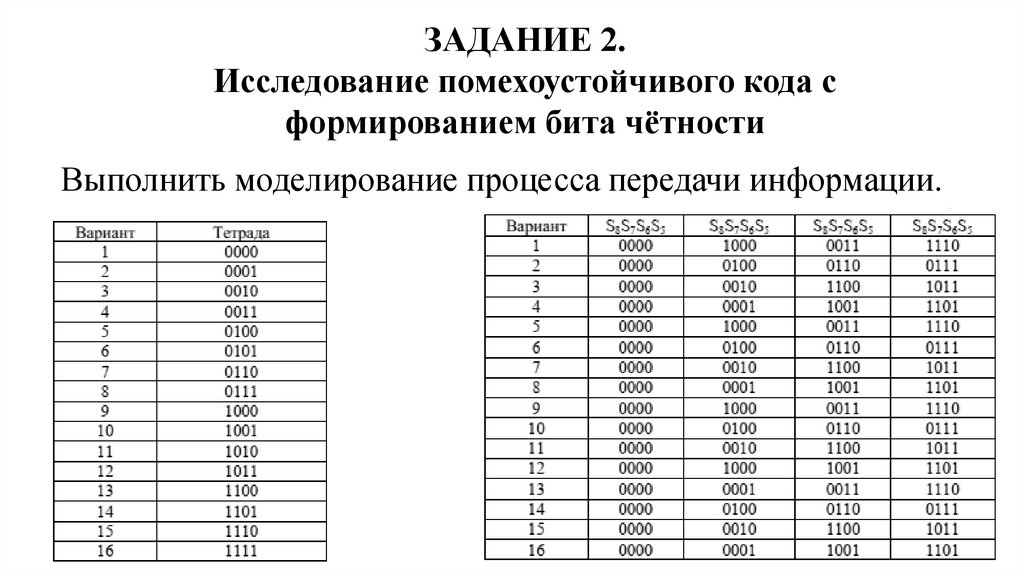
ЗАДАНИЕ 2.
Исследование помехоустойчивого кода с
формированием бита чётности
Выполнить моделирование процесса передачи информации.

16.

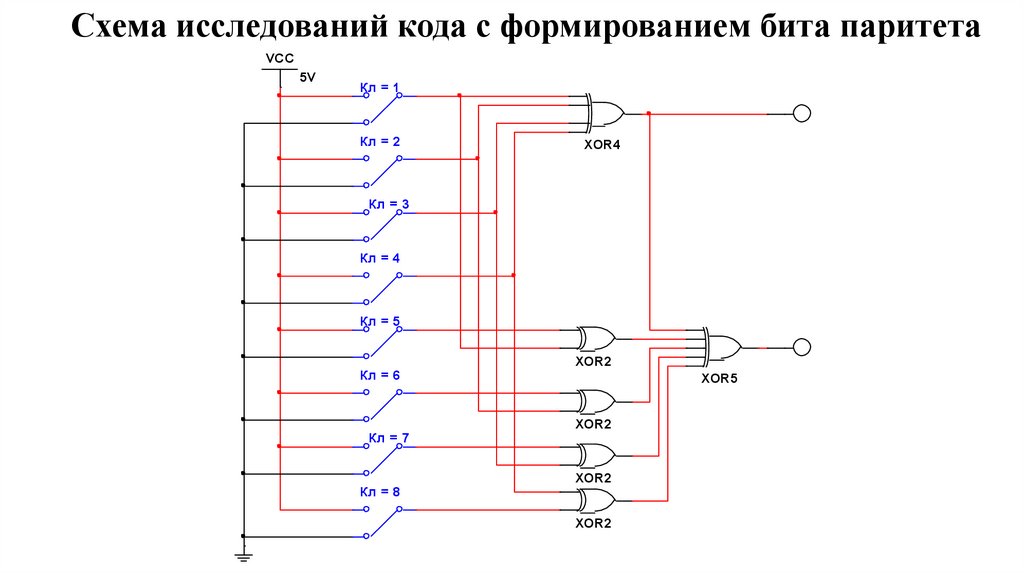
Схема исследований кода с формированием бита паритета
VCC
5V
Кл = 1
Кл = 2
XOR4
Кл = 3
Кл = 4
Кл = 5
Кл = 6
Кл = 7
Кл = 8
XOR2
XOR5
XOR2
XOR2
XOR2

17.

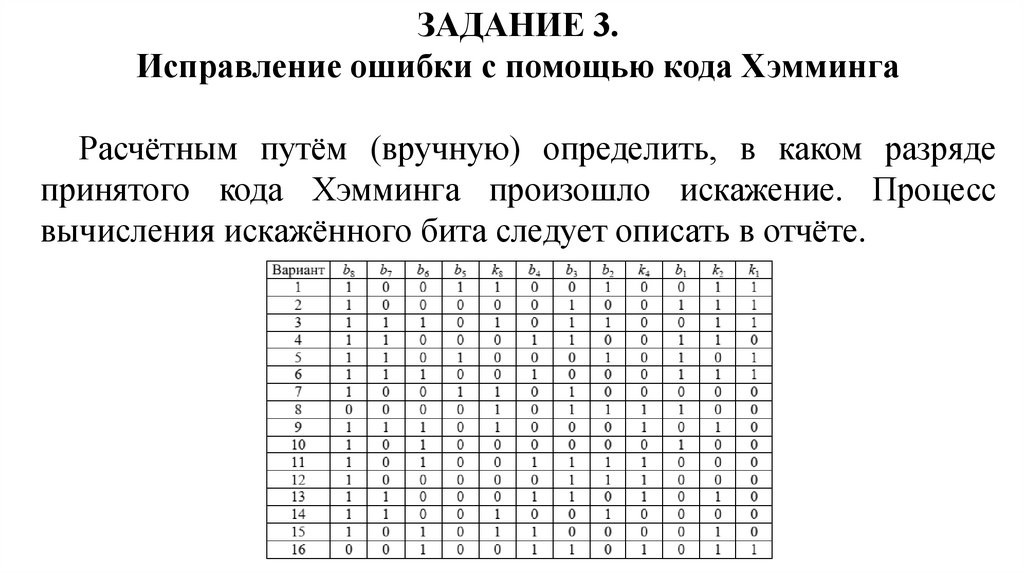
ЗАДАНИЕ 3.
Исправление ошибки с помощью кода Хэмминга
Расчётным путём (вручную) определить, в каком разряде
принятого кода Хэмминга произошло искажение. Процесс
вычисления искажённого бита следует описать в отчёте.

18.

Код Хемминга – это блочный код, позволяющий исправлять
одиночные и фиксировать двойные ошибки, разработанный
Ричардом Хеммингом в 40-х годах прошлого столетия.

19.

В это время он работал в лаборатории Bell Labs на
электромеханической счетной машине Bell Model V.

20.

Идея кода Хемминга заключается в разбиении данных на
блоки фиксированной длины и вводе в эти блоки
контрольных бит, дополняющих до четности несколько
пересекающихся групп, охватывающих все биты блока.
Ричард Хемминг рассчитал минимальное
проверочных бит, позволяющих однозначно
однократные ошибки.
k
k=2
–m–1
m - длина информационного блока;
k - количество контрольных бит.
количество
исправлять

21.

Рассмотрим пример кодирования бинарной последовательности
данных, состоящей из 8 элементов: 10101101.
1. Определим необходимое количество контрольных разрядов.
k
k=2
–m–1
m - длина информационного блока;
k - количество контрольных бит.
k=3
3=23 – 8 – 1, 3>– 1
k=4
4=24 – 8 – 1, 4<7

22.

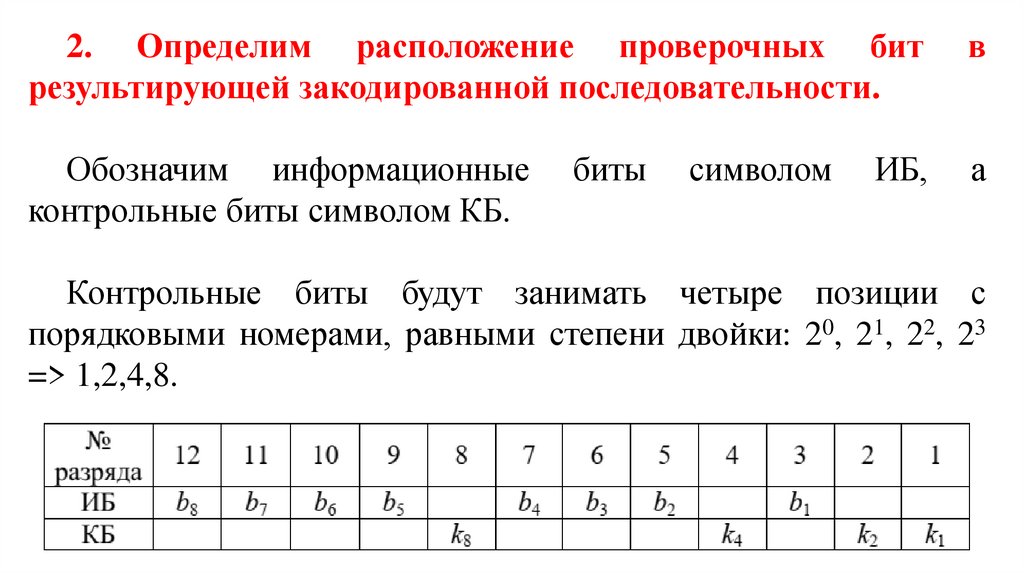
2. Определим расположение проверочных бит
результирующей закодированной последовательности.
в
Обозначим информационные
контрольные биты символом КБ.
а
биты
символом
ИБ,
Контрольные биты будут занимать четыре позиции с
порядковыми номерами, равными степени двойки: 20, 21, 22, 23
=> 1,2,4,8.

23.

3. Определим, какие группы контролируют проверочные
биты.
ИБ3: 3 = 20 + 21 = 1 + 2 => информационный бит проверяется
контрольными битами 1 и 2.
ИБ5: 5 = 20 + 22 = 1 + 4 => Информационный бит проверяется
контрольными битами 1 и 4.
ИБ6: 6 = 21 + 22 = 2 + 4 => Информационный бит проверяется
контрольными битами 2 и 4.

24.

ИБ7: 7 = 20 + 21 + 22 = 1 + 2 + 4 => Информационный бит
проверяется контрольными битами 1, 2 и 4.
ИБ9: 9 = 20 + 23 = 1 + 8 => Информационный бит проверяется
контрольными битами 1 и 8.
ИБ10: 10 = 21 + 23 = 2 + 8 => Информационный бит
проверяется контрольными битами 2 и 8.
ИБ11: 11 = 20 + 21 + 23 = 1 + 2 + 8 => Информационный бит
проверяется контрольными битами 1, 2 и 8.
ИБ12: 12 = 22 + 23 = 4 + 8 => Информационный бит
проверяется контрольными битами 4 и 8.

25.

4. Рассчитаем значения контрольных бит.
Для этого определим группы для всех контрольных бит, а
результат запишем в соответствующие контрольные биты:
KБ1 = ИБ3 ⊕ ИБ5 ⊕ ИБ7 ⊕ ИБ9 ⊕ ИБ11 =
=1⊕0⊕1⊕0⊕0=0
КБ2 = ИБ3 ⊕ ИБ6 ⊕ ИБ7 ⊕ ИБ10 ⊕ ИБ11=
=1⊕1⊕1⊕1⊕0=0
КБ4 = ИБ5 ⊕ ИБ6 ⊕ ИБ7 ⊕ ИБ12 = 0 ⊕ 1 ⊕ 1 ⊕ 1 = 1
КБ8 = ИБ9 ⊕ ИБ10 ⊕ ИБ11 ⊕ ИБ12 = 0 ⊕ 1 ⊕ 0 ⊕ 1 = 0

26.

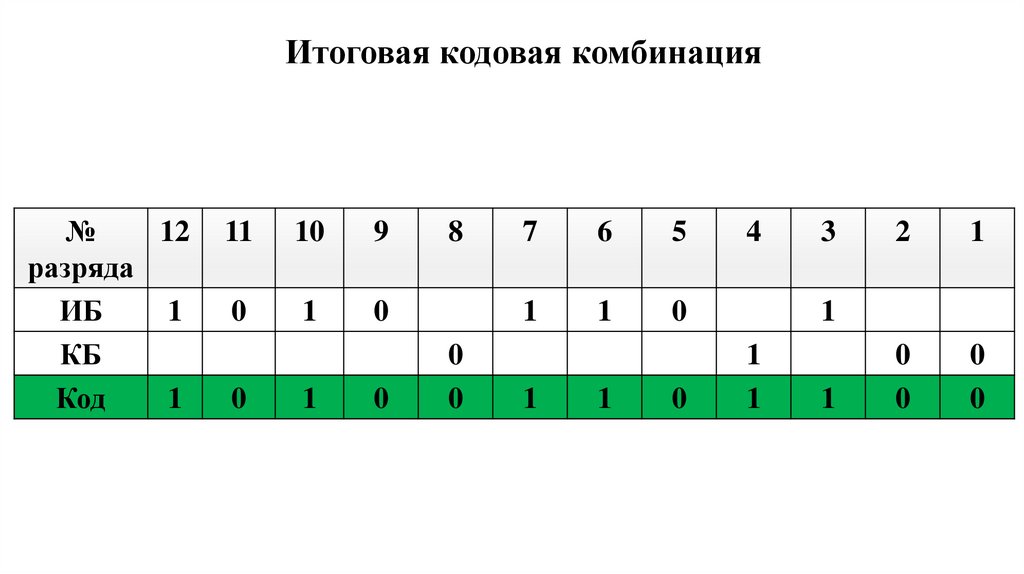
Итоговая кодовая комбинация
№
12
разряда
ИБ
1
КБ
Код
1
11
10
9
0
1
0
0
1
0
8
0
0
7
6
5
1
1
0
1
1
0
4
3
2
1
0
0
0
0
1
1
1
1

27.

Рассмотрим пример нахождения искажённого бита с
помощью кода Хэмминга.
Места расположения информационных битов (ИБ) и
контрольных битов (КБ) в передаваемых данных указаны в
таблице.

28.

Пример.
Предположим, что в процессе передачи некоторых данных
произошло искажение одного информационного бита и на
приёме получены указанные в таблице данные. Требуется найти
и исправить искажённый информационный бит.

29.

Вычислим значения контрольных битов на приёме.
Расчёт производится по формулам:
KБ’1 = ИБ3 ⊕ ИБ5 ⊕ ИБ7 ⊕ ИБ9 ⊕ ИБ11 =
=1⊕0⊕1⊕0⊕0=0
КБ’2 = ИБ3 ⊕ ИБ6 ⊕ ИБ7 ⊕ ИБ10 ⊕ ИБ11=
=1⊕1⊕1⊕0⊕0=1
КБ’4 = ИБ5 ⊕ ИБ6 ⊕ ИБ7 ⊕ ИБ12 = 0 ⊕ 1 ⊕ 1 ⊕ 1 = 1
КБ’8 = ИБ9 ⊕ ИБ10 ⊕ ИБ11 ⊕ ИБ12 = 0 ⊕ 0 ⊕ 0 ⊕ 1 = 1

30.

Контрольные биты, сформированные на передающей и
приёмной сторонах, различаются:
КБ1 = КБ’1 = 0 = 0, КБ2 = КБ’2 = 0 ≠ 1,
КБ4 = КБ’4 = 1 = 1, КБ8 = КБ’8 = 0 ≠ 1,
Для определения неверно принятого бита требуется вычислить
так называемый синдром S=s8s4s2s1, где
s1= ИБ1 ⊕ ИБ’1= 0 ⊕ 0 = 0,
s2= ИБ2 ⊕ ИБ’2= 0 ⊕ 1 = 1,
s4= ИБ4 ⊕ ИБ’4= 1 ⊕ 1 = 0,
s8= ИБ8 ⊕ ИБ’8= 0 ⊕ 1 = 1.

31.

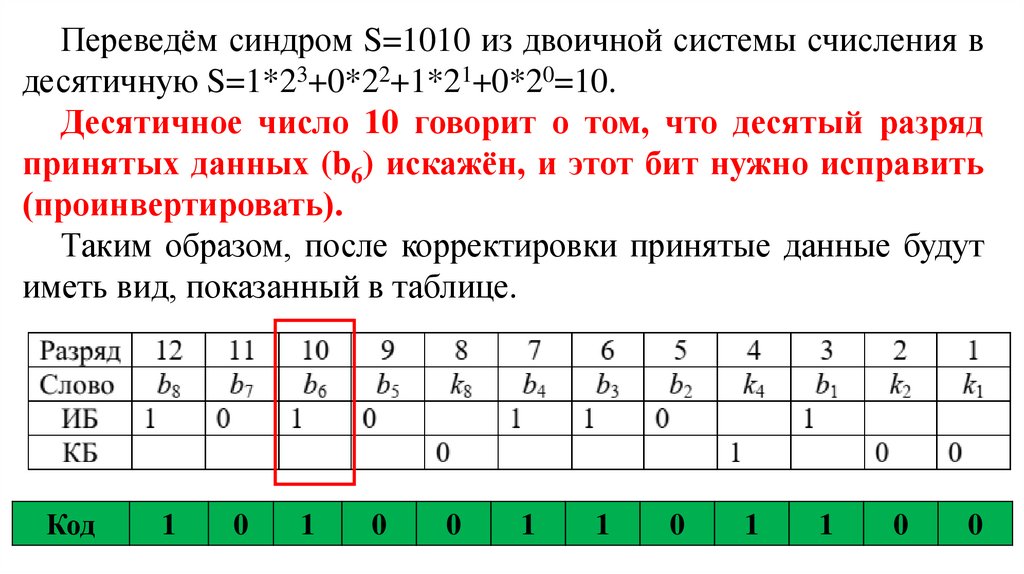
Переведём синдром S=1010 из двоичной системы счисления в
десятичную S=1*23+0*22+1*21+0*20=10.
Десятичное число 10 говорит о том, что десятый разряд
принятых данных (b6) искажён, и этот бит нужно исправить
(проинвертировать).
Таким образом, после корректировки принятые данные будут
иметь вид, показанный в таблице.
Код
1
0
1
0
0
1
1
0
1
1
0
0

32.

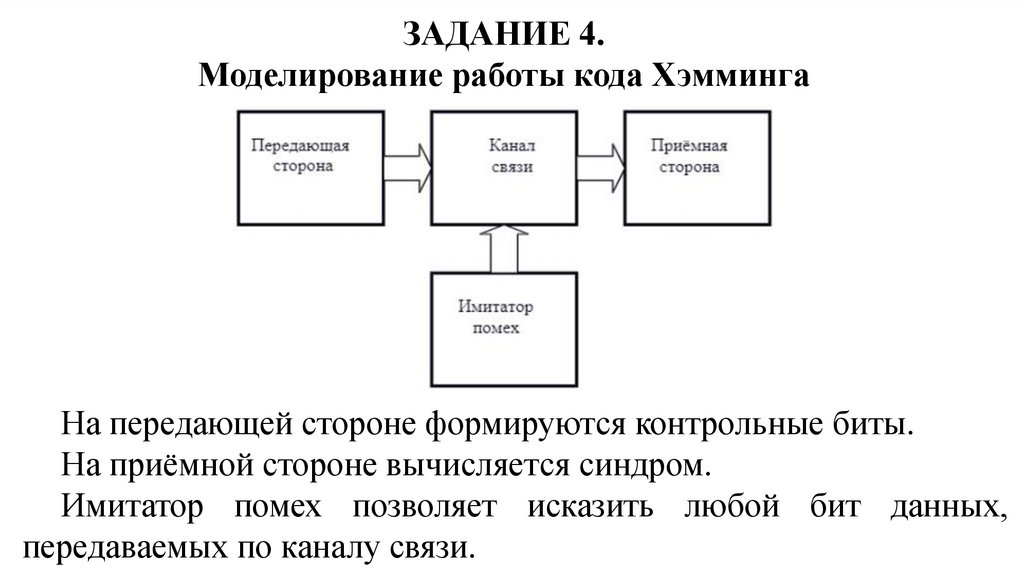
ЗАДАНИЕ 4.
Моделирование работы кода Хэмминга
На передающей стороне формируются контрольные биты.
На приёмной стороне вычисляется синдром.
Имитатор помех позволяет исказить любой бит данных,
передаваемых по каналу связи.

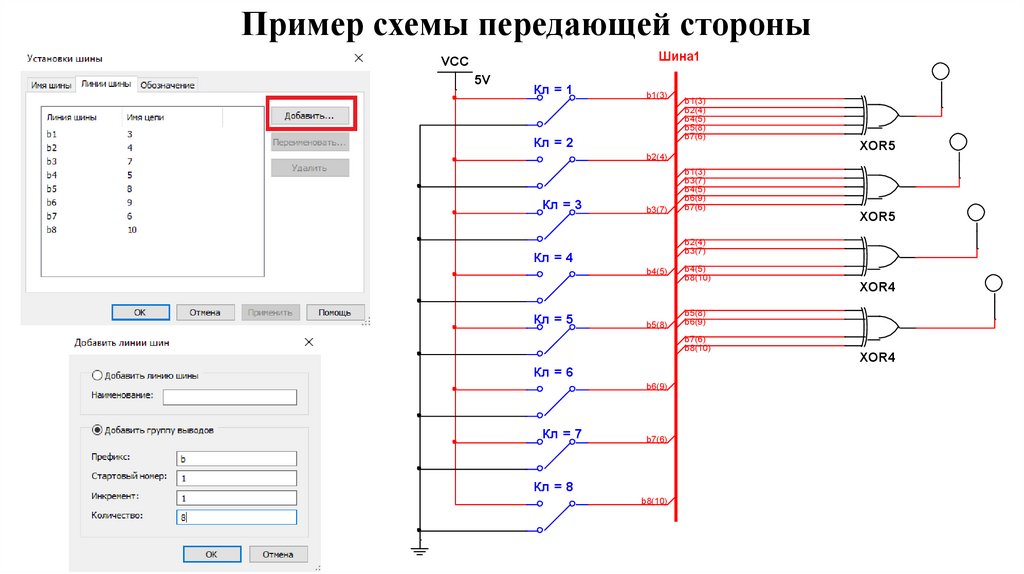
33.

Пример схемы передающей стороны
Шина1
VCC
5V
Кл = 1
b1(‎3)‎
Кл = 2
b1(‎3)‎
b2(‎4)‎
b4(‎5)‎
b5(‎8)‎
b7(‎6)‎
b2(‎4)‎
Кл = 3
b3(‎7)‎
b4(‎5)‎
b5(‎8)‎
b4(‎5)‎
b8(‎10)‎
Кл = 6
b6(‎9)‎
b7(‎6)‎
Кл = 8
b8(‎10)‎
XOR4
b5(‎8)‎
b6(‎9)‎
b7(‎6)‎
b8(‎10)‎
Кл = 7
XOR5
b2(‎4)‎
b3(‎7)‎
Кл = 4
Кл = 5
b1(‎3)‎
b3(‎7)‎
b4(‎5)‎
b6(‎9)‎
b7(‎6)‎
XOR5
XOR4

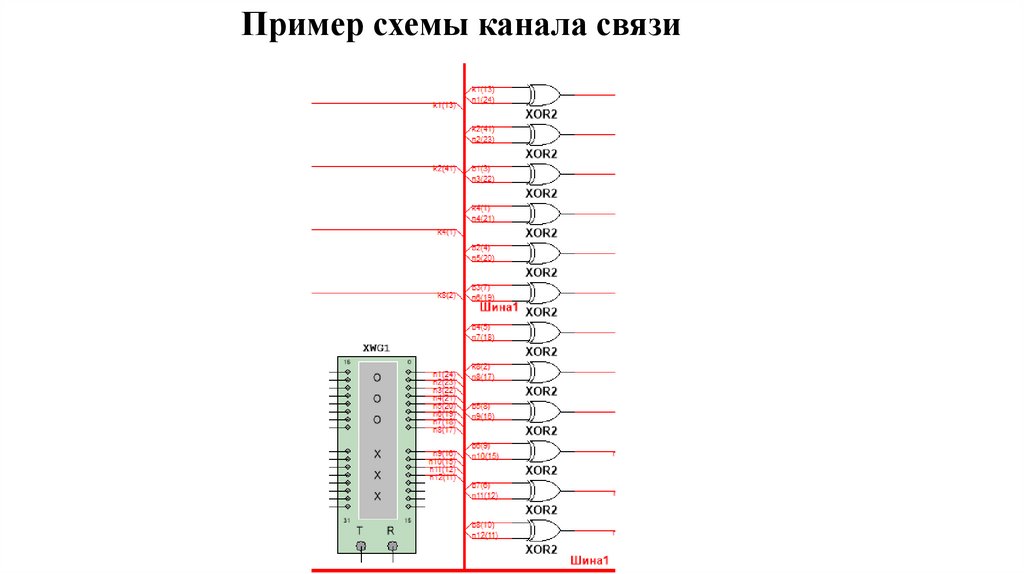
34.

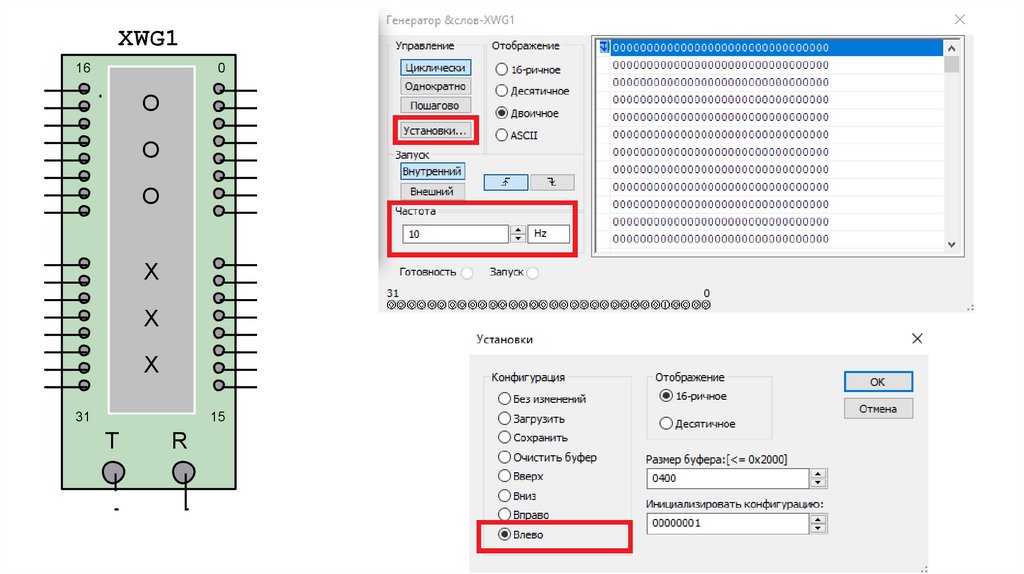
Пример схемы канала связи

35.

XWG1
16
0
O
O
O
X
X
X
31
15
T
R

36.

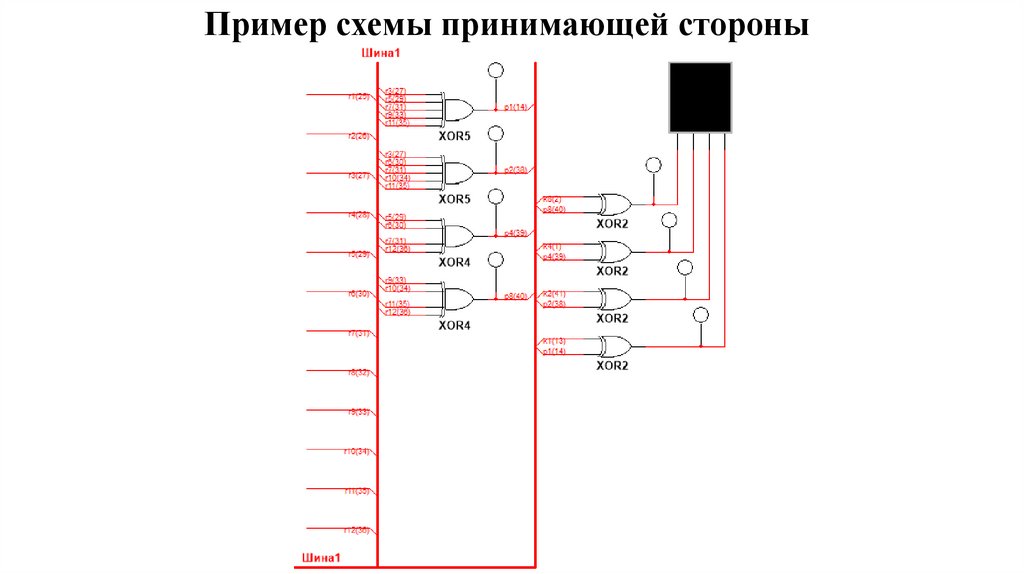
Пример схемы принимающей стороны

37.

Семисегментный
индикатор

38.

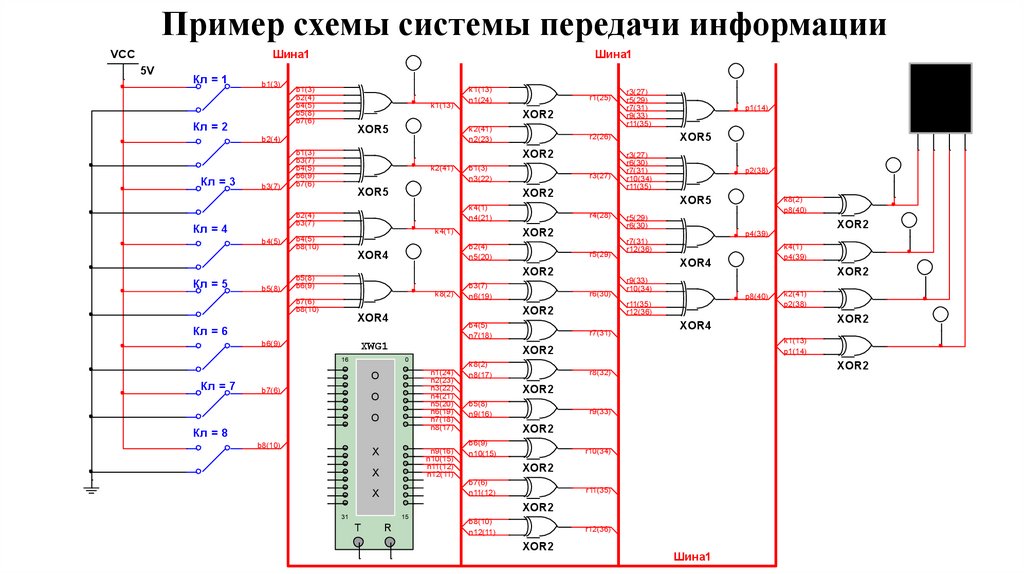
Пример схемы системы передачи информации
Шина1
VCC
5V
Кл = 1
b1(‎3)‎
Кл = 2
Шина1
b1(‎3)‎
b2(‎4)‎
b4(‎5)‎
b5(‎8)‎
b7(‎6)‎
k1(‎13)‎
b3(‎7)‎
b4(‎5)‎
Кл = 5
k2(‎41)‎
n2(‎23)‎
XOR5
b1(‎3)‎
b3(‎7)‎
b4(‎5)‎
b6(‎9)‎
b7(‎6)‎
b5(‎8)‎
r3(‎27)‎
XOR2
k4(‎1)‎
n4(‎21)‎
k4(‎1)‎
b4(‎5)‎
b8(‎10)‎
XOR2
r5(‎29)‎
XOR2
b5(‎8)‎
b6(‎9)‎
k8(‎2)‎
b4(‎5)‎
n7(‎18)‎
Кл = 6
XWG1
16
n1(‎24)‎
n2(‎23)‎
n3(‎22)‎
n4(‎21)‎
n5(‎20)‎
n6(‎19)‎
n7(‎18)‎
n8(‎17)‎
O
O
O
Кл = 8
b8(‎10)‎
XOR5
r3(‎27)‎
r6(‎30)‎
r7(‎31)‎
r10(‎34)‎
r11(‎35)‎
p2(‎38)‎
r5(‎29)‎
r6(‎30)‎
r7(‎31)‎
r12(‎36)‎
r9(‎33)‎
r10(‎34)‎
n9(‎16)‎
n10(‎15)‎
n11(‎12)‎
n12(‎11)‎
X
X
X
XOR2
XOR2
r10(‎34)‎
XOR2
r11(‎35)‎
XOR2
31
15
T
R
b8(‎10)‎
n12(‎11)‎
r12(‎36)‎
XOR2
XOR2
k1(‎13)‎
p1(‎14)‎
r9(‎33)‎
b7(‎6)‎
n11(‎12)‎
k2(‎41)‎
p2(‎38)‎
XOR4
XOR2
b6(‎9)‎
n10(‎15)‎
XOR2
p8(‎40)‎
r8(‎32)‎
b5(‎8)‎
n9(‎16)‎
XOR2
k4(‎1)‎
p4(‎39)‎
XOR4
r11(‎35)‎
r12(‎36)‎
r7(‎31)‎
k8(‎2)‎
n8(‎17)‎
k8(‎2)‎
p8(‎40)‎
p4(‎39)‎
XOR2
0
b7(‎6)‎
r6(‎30)‎
XOR2
XOR4
b6(‎9)‎
b3(‎7)‎
n6(‎19)‎
p1(‎14)‎
XOR5
r4(‎28)‎
b2(‎4)‎
n5(‎20)‎
XOR4
b7(‎6)‎
b8(‎10)‎
Кл = 7
b1(‎3)‎
n3(‎22)‎
XOR5
r3(‎27)‎
r5(‎29)‎
r7(‎31)‎
r9(‎33)‎
r11(‎35)‎
r2(‎26)‎
XOR2
k2(‎41)‎
b2(‎4)‎
b3(‎7)‎
Кл = 4
r1(‎25)‎
XOR2
b2(‎4)‎
Кл = 3
k1(‎13)‎
n1(‎24)‎
Шина1