Геометрические тела и поверхности. Пирамида

1. ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ПОВЕРХНОСТИ

Пирамида

2.

1. Многогранник, составленный из двух
равных многоугольников и ,
расположенных в параллельных
плоскостях, и n параллелограммов …, ,
называется:
А) параллелепипед;
Б) призма;
В) пирамида;
Г) многогранник;
Д) конус.

3.

2. Перпендикуляр, проведенный из какойнибудь точки одного основания к плоскости
другого основания, называется…
А) высотой призмы;
Б) ребром призмы;
В) медианой призмы;
Г) диагональю призмы;
Д) стороной призмы.

4.

3. Прямая призма называется
правильной, если ее основания…
А) равнобедренные треугольники;
Б) не правильные многоугольники;
В) параллелограммы;
Г) окружности;
Д) правильные многоугольники.

5.

4. Чему равен квадрат
диагонали прямоугольного
параллелепипеда?
А) сумме квадратов трех его
измерений;
Б) сумме ребер;
В) сумме трех его измерений;
Г) сумме квадратов ребер;
Д) корню из суммы трех его
измерений.

6.

5. У параллелепипеда
противолежащие грани равны
и…
А) параллельны;
Б) лежат в одной плоскости;
В) перпендикулярны;
Г) лежат в разных плоскостях;
Д) образуют между собой угол

7. Классификация

ГЕОМЕТРИЧЕСКИЕ ТЕЛА
МНОГОГРАННИКИ
ТЕЛА ВРАЩЕНИЯ
КОНУС
ЦИЛИНДР
ПРИЗМА
ПИРАМИДА
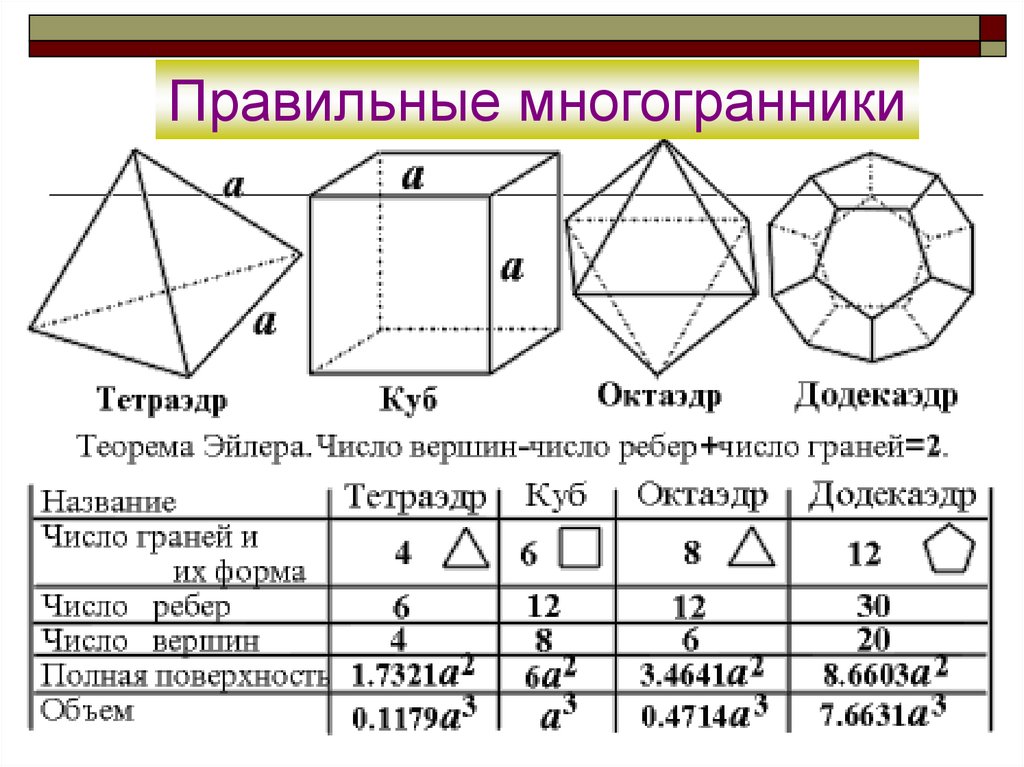
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
ШАР

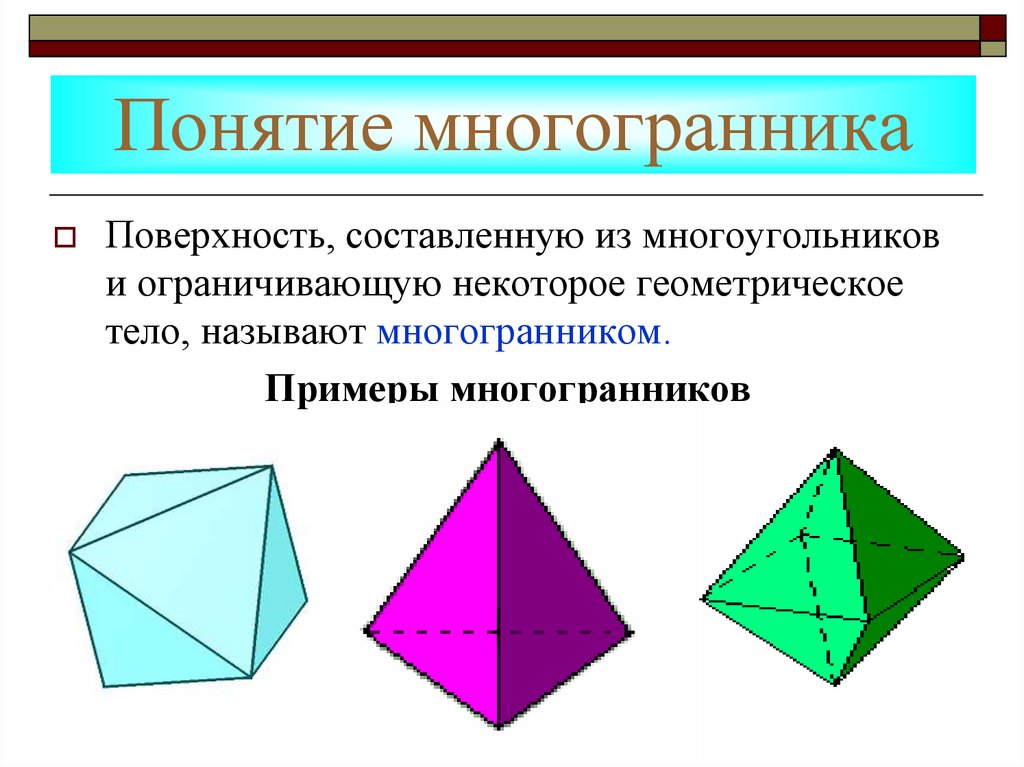
8. Понятие многогранника

Поверхность, составленную из многоугольников
и ограничивающую некоторое геометрическое
тело, называют многогранником.
Примеры многогранников

9.

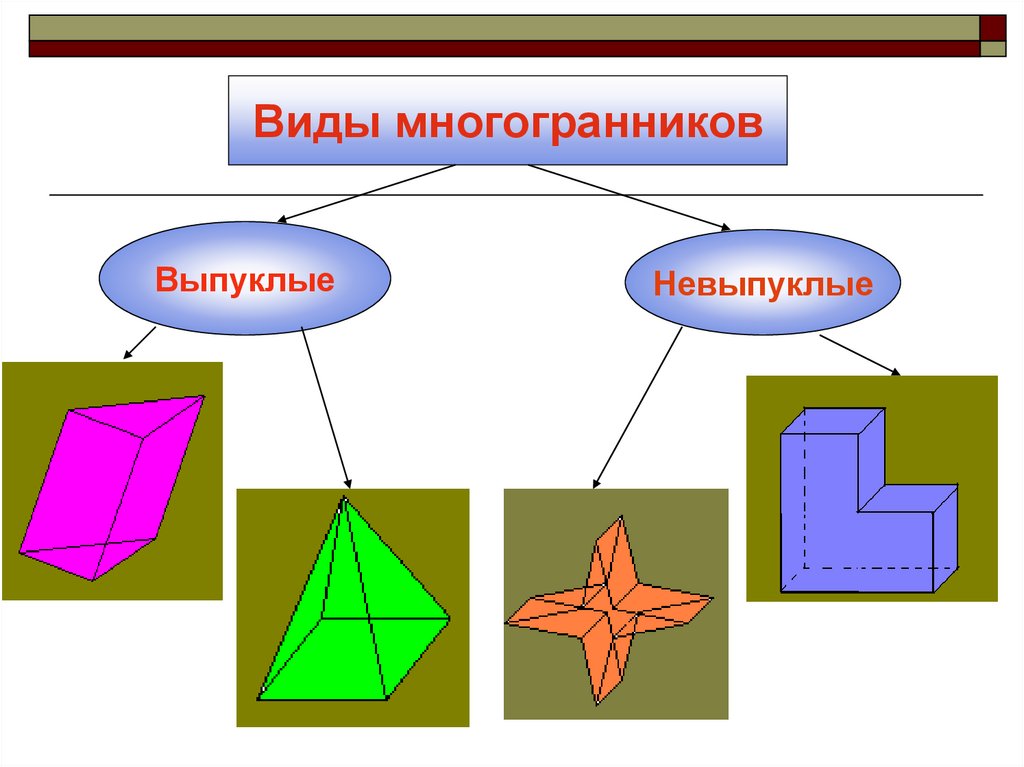
Виды многогранников
Выпуклые
Невыпуклые

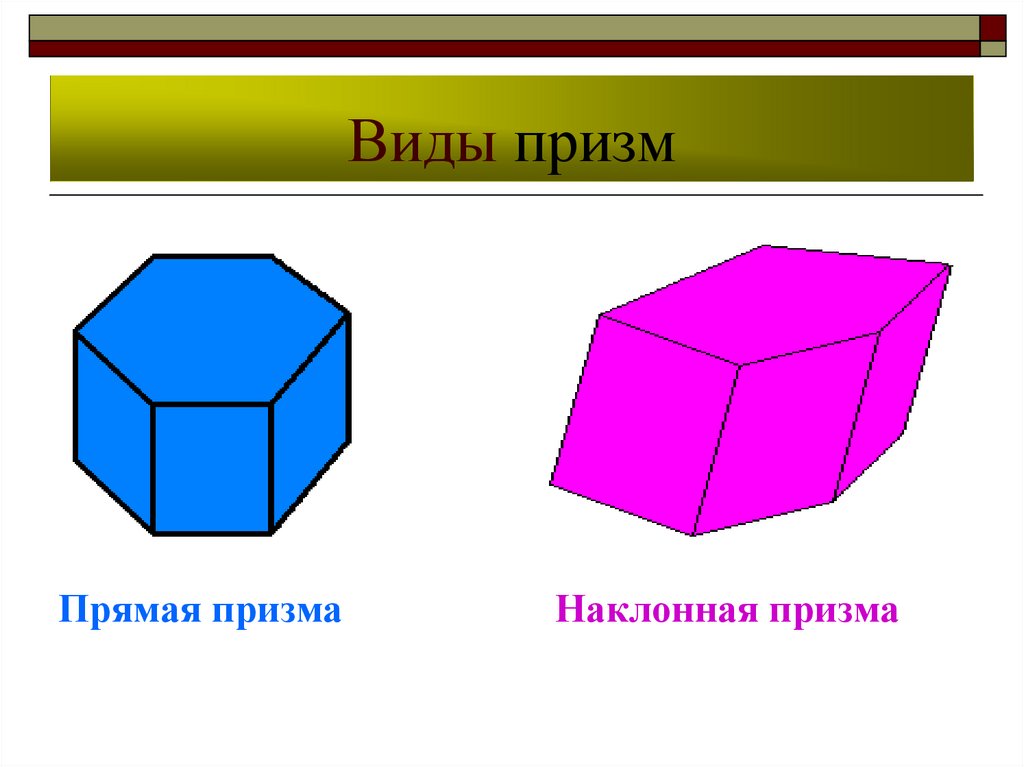
10. Виды призм

Прямая призма
Наклонная призма

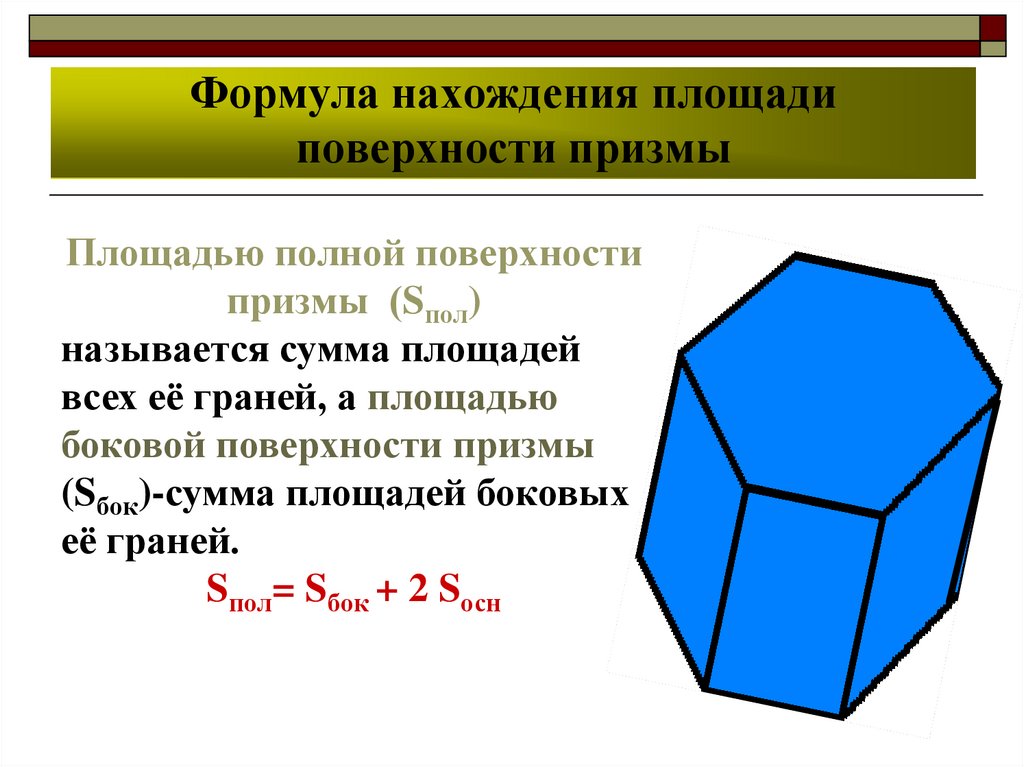
11. Формула нахождения площади поверхности призмы

Площадью полной поверхности
призмы (Sпол)
называется сумма площадей
всех её граней, а площадью
боковой поверхности призмы
(Sбок)-сумма площадей боковых
её граней.
Sпол= Sбок + 2 Sосн

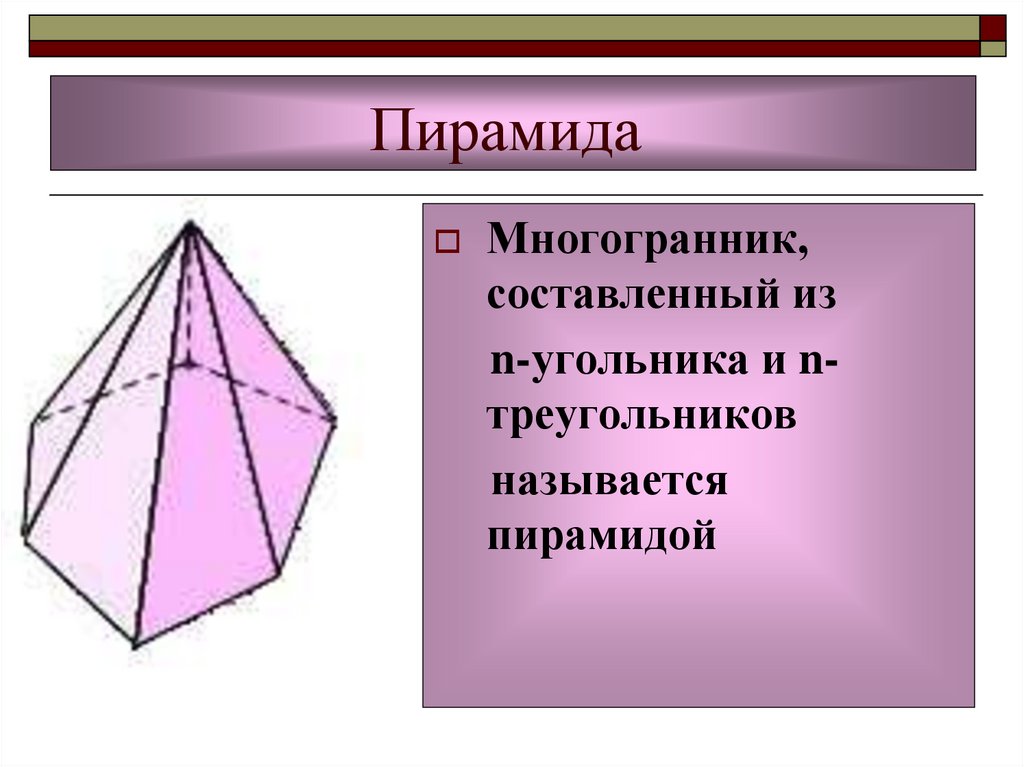
12. Пирамида

Многогранник,
составленный из
n-угольника и nтреугольников
называется
пирамидой

13.

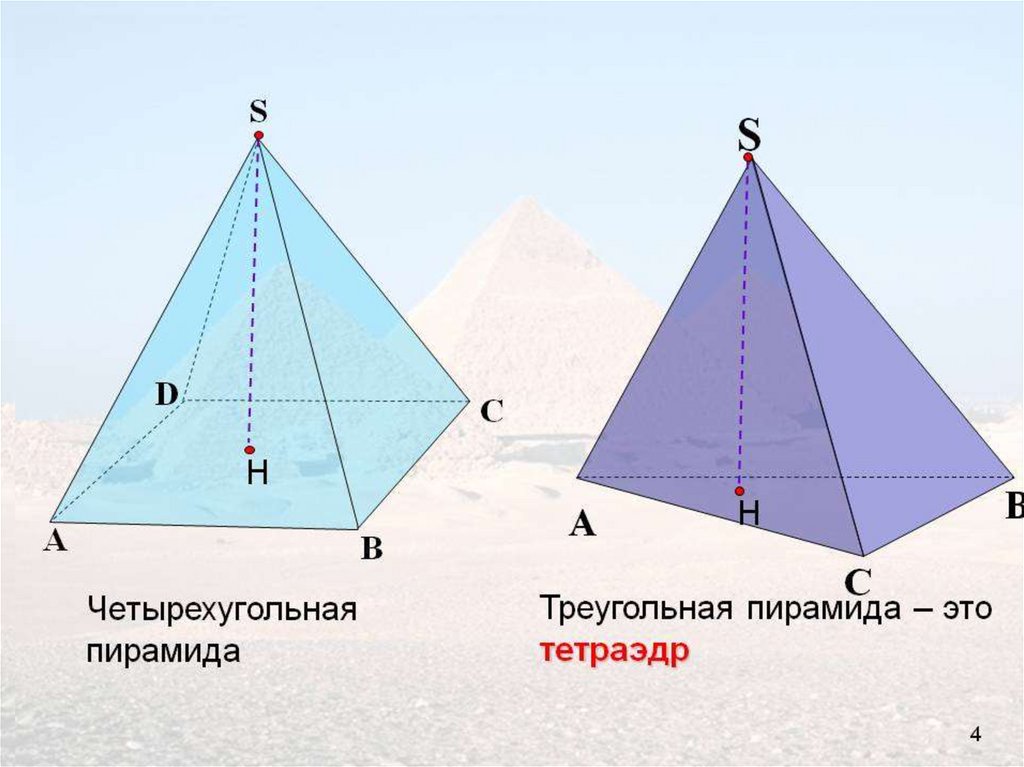
Пирами́да (др.-греч. πυραμίς, род. п.
πυραμίδος) — многогранник, одна из
граней которого (называемая
основанием) — произвольный
многоугольник, а остальные грани
(называемые боковыми гранями) —
треугольники, имеющие общую
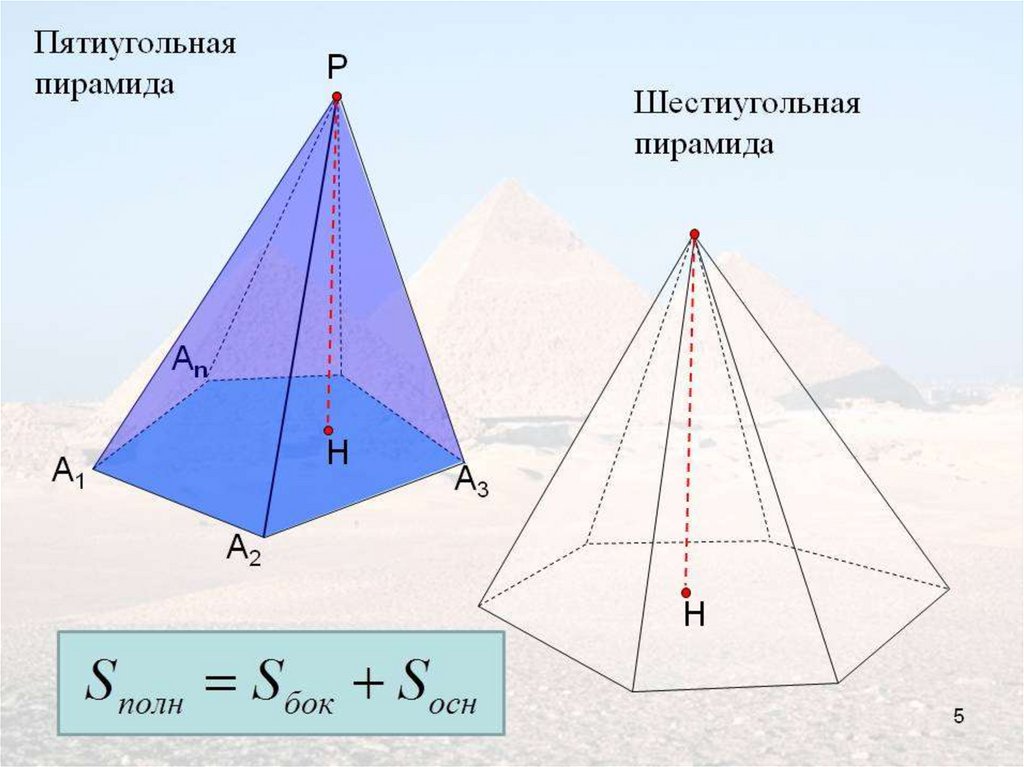
вершину[1]. По числу углов основания
различают пирамиды треугольные
(тетраэдр), четырёхугольные и т. д.

14. История развития пирамиды в геометрии

Начало геометрии пирамиды было положено в Древнем
Египте и Вавилоне, однако активное развитие получило в
Древней Греции. Объем пирамиды был известен древним
египтянам. Первым греческим математиком, кто установил,
чему равен объём пирамиды, был Демокрит, а доказал Евдокс
Книдский. Древнегреческий математик Евклид
систематизировал знания о пирамиде в XII томе своих
«Начал», а также вывел первое определение пирамиды:
телесная фигура, ограниченная плоскостями, которые от
одной плоскости сходятся в одной точке (книга XI,
определение 12).

15.

16. Свойства пирамиды

Если все боковые рёбра равны, то:
вокруг основания пирамиды можно описать окружность, причём
вершина пирамиды проецируется в её центр;
боковые рёбра образуют с плоскостью основания равные углы;
также верно и обратное, то есть если боковые рёбра образуют с
плоскостью основания равные углы, или если около основания
пирамиды можно описать окружность, причём вершина пирамиды
проецируется в её центр, то все боковые рёбра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним
углом, то:
в основание пирамиды можно вписать окружность, причём вершина
пирамиды проецируется в её центр;
высоты боковых граней равны;
площадь боковой поверхности равна половине произведения
периметра основания на высоту боковой грани.

17. Элементы пирамиды

1-высота пирамиды
1
2-боковая грань
пирамиды
2
3
3-основание
пирамиды

18.

19.

20. Гексаэдр

Куб составлен из
шести квадратов.
Каждая его вершина
является вершиной
трех квадратов.
Сумма плоских углов
при каждой вершине
равна 270 градусов.
Таким образом, куб
имеет 6 граней, 8
вершин и 12 ребер

21.

Правильные многогранники