Черчение геометрических фигур не отрывая карандаш от бумаги

1.

5.04.2021г.
« Фигуры одним росчерком пера».

2.

Если можно, то с какой точки
Для
решения
задач,вычерчивание?
подобных
следует
начинать
этой,
существуют
признаки,
Изучением
этих
Попробуйте,
непризнаков
отрывая и их
пообоснованием
которым заранее
не сложно
карандаш отзанимается
бумаги и ненаука
установить,
можно ли данную
топология
.
проводя
по одной линии
фигуру начертить одним
дважды, начертить
росчерком или нет.
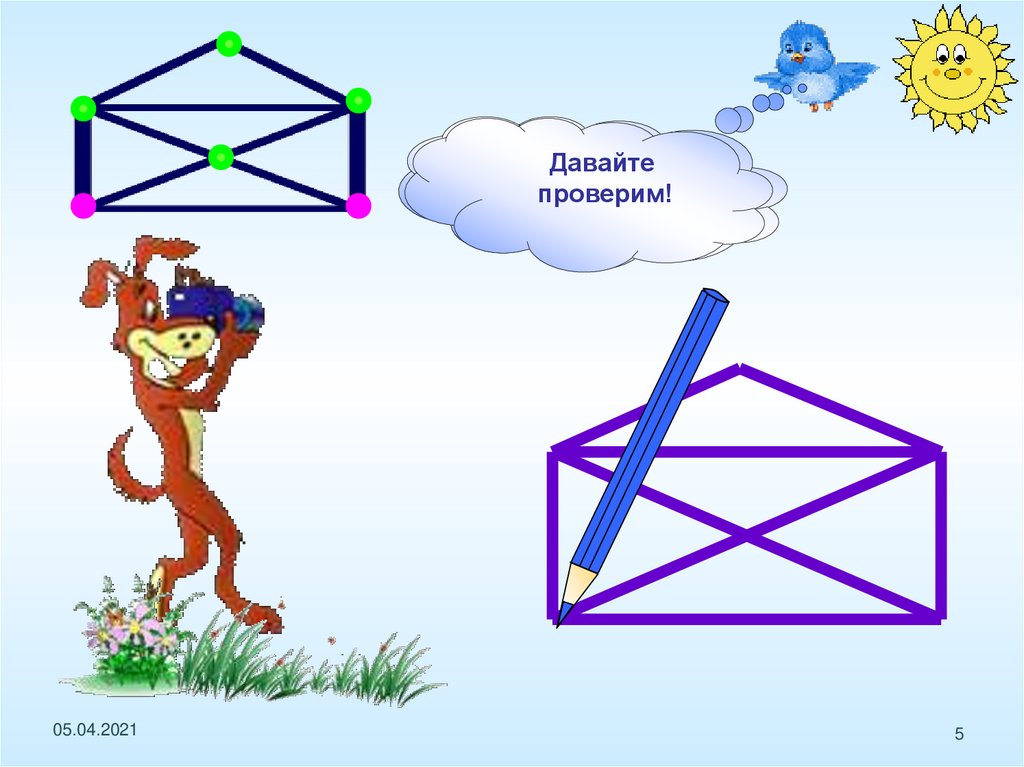
«открытый конверт».
05.04.2021
2

3.

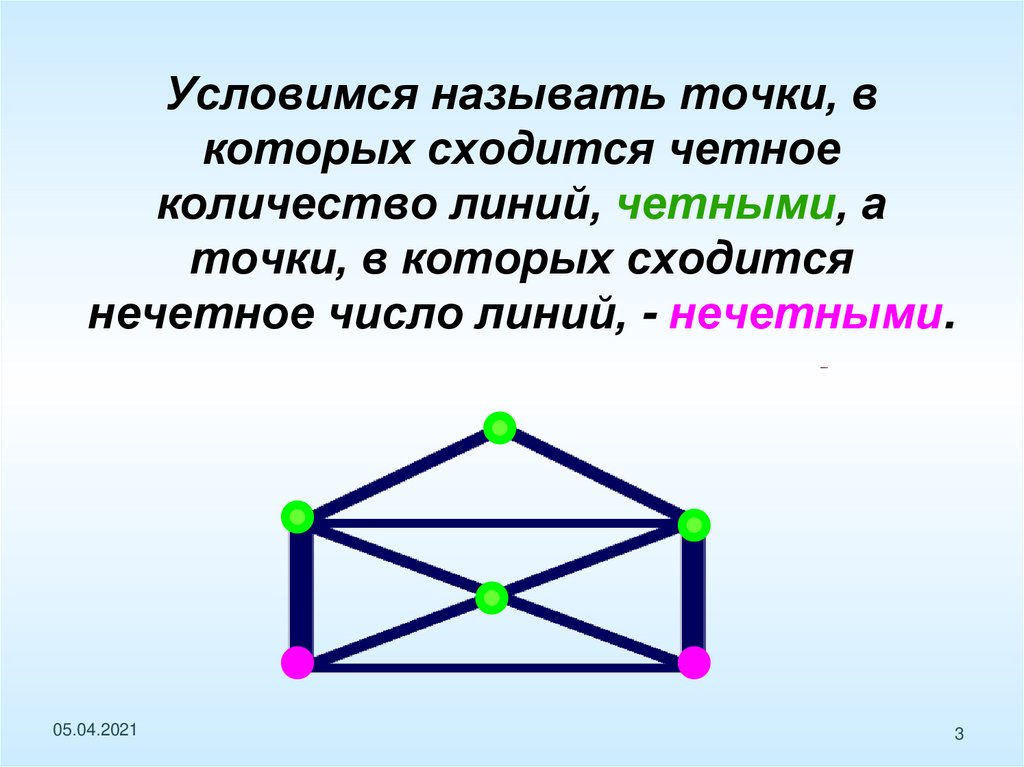
Условимся называть точки, в
которых сходится четное
количество линий, четными, а
точки, в которых сходится
нечетное число линий, - нечетными.
05.04.2021
3

4.

Признаки вычерчивания
фигур одним росчерком:
• если нечетных точек в фигуре нет, то ее
можно начертить одним росчерком, начиная
вычерчивать с любого места;
• если в фигуре две нечетные точки (если
фигура имеет нечетную точку, то она всегда
имеет и вторую нечетную точку), то ее можно
начертить одним росчерком, начав
вычерчивание в одной из нечетных точек и
закончив в другой;
• если в фигуре более двух нечетных точек, то
ее нельзя вычертить одним росчерком.
05.04.2021
4

5.

Попробуйте
Давайте
начертить
проверим!
самостоятельно
05.04.2021
5

6.

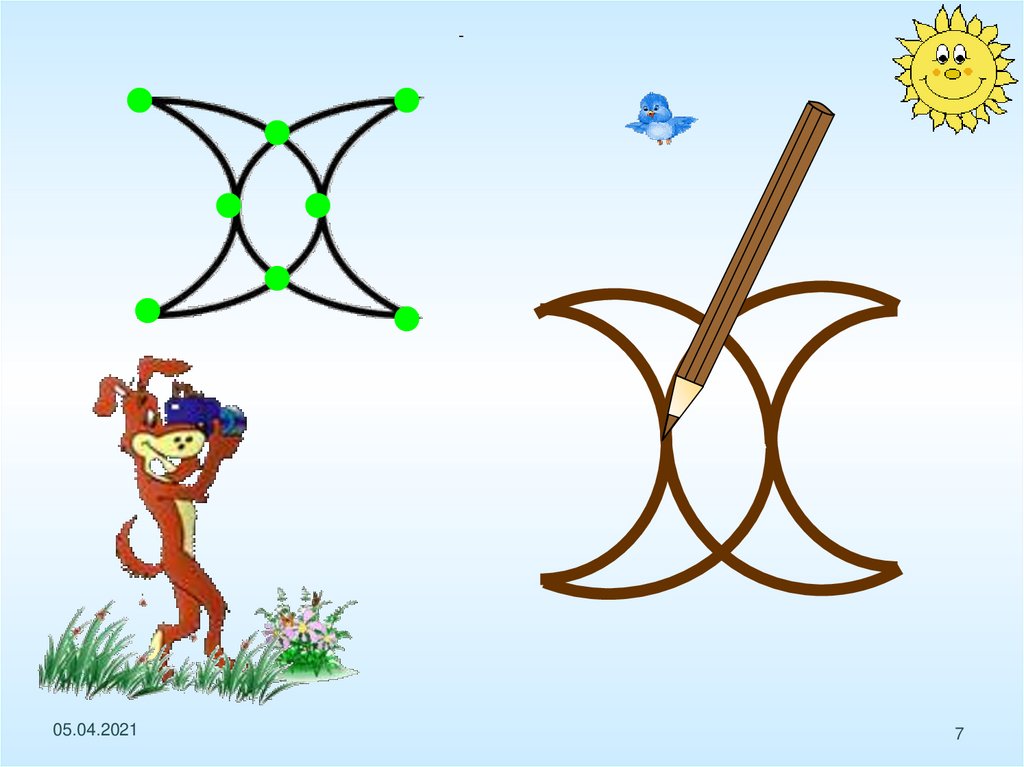
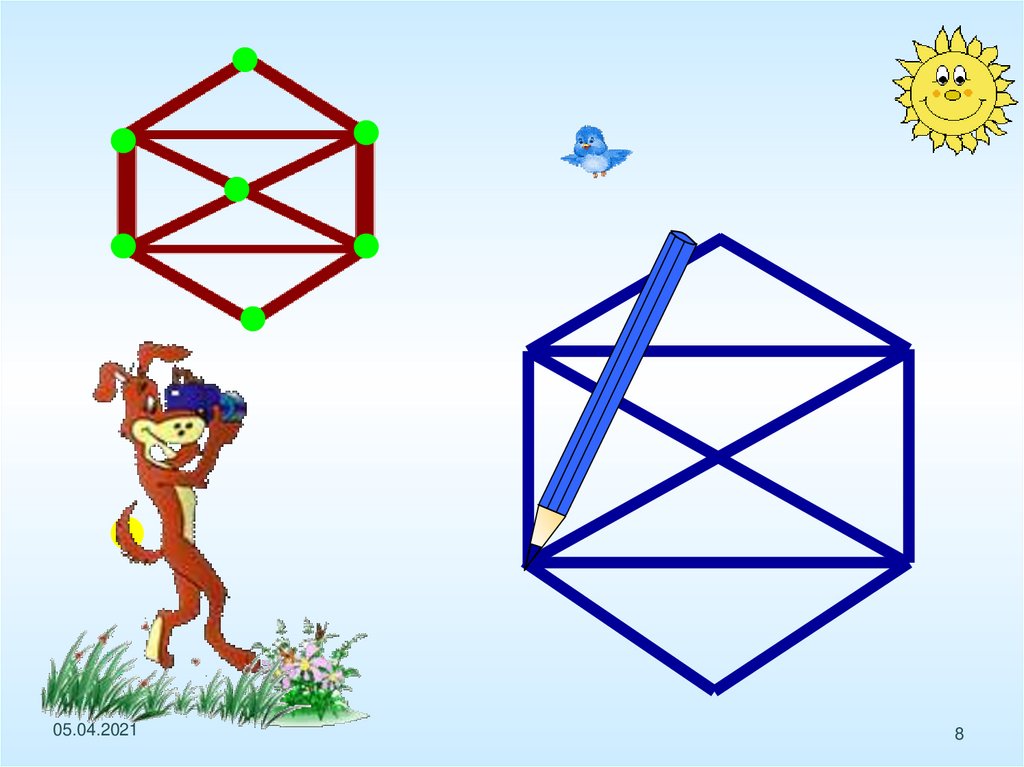
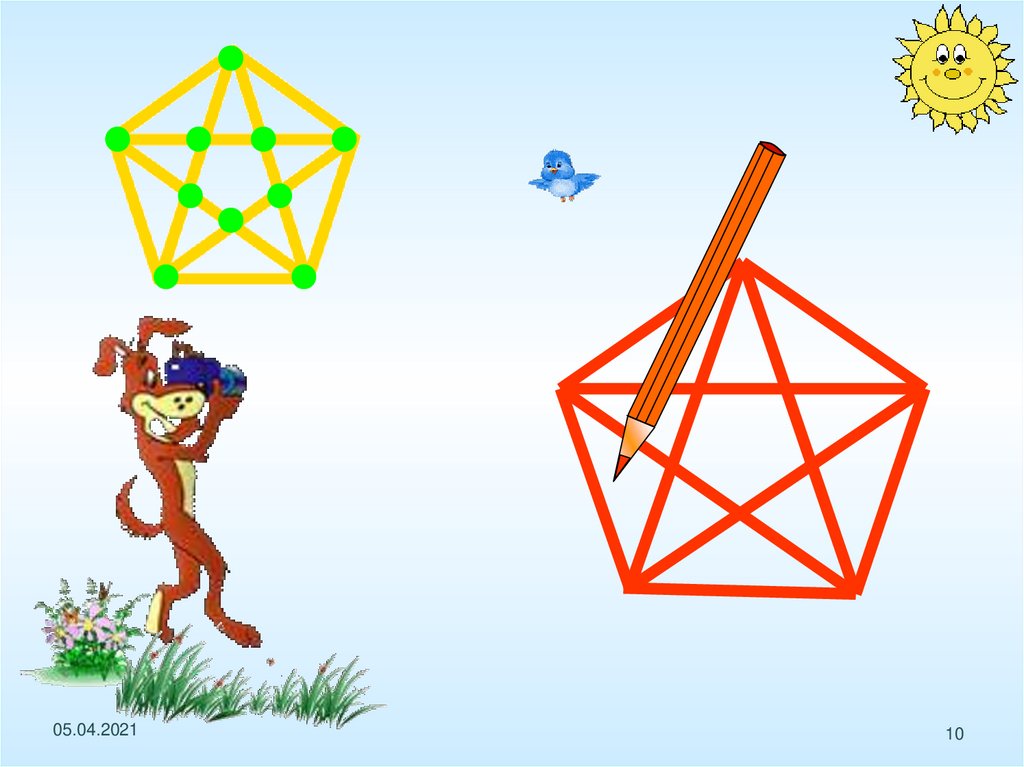
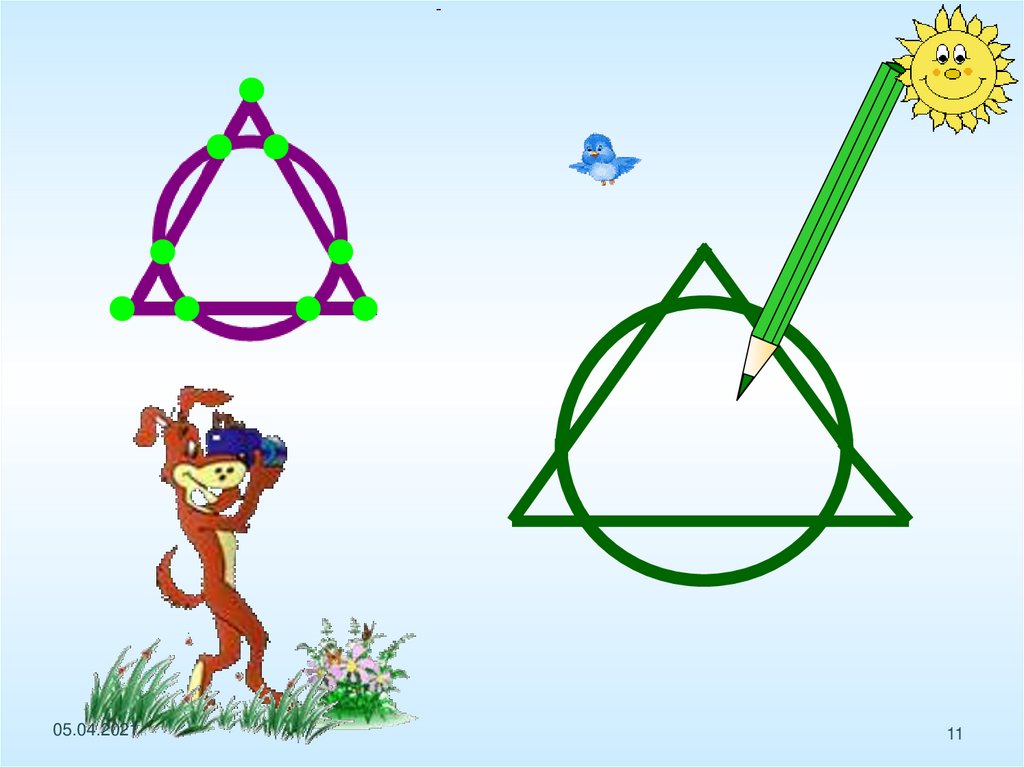
Определите, какие из фигур
можно начертить не отрывая
карандаш от бумаги
(и не проводя по одной линии
дважды).
05.04.2021
6

7.

05.04.2021
7

8.

05.04.2021
8

9.

05.04.2021
9

10.

05.04.2021
10

11.

05.04.2021
11

12.

05.04.2021
12

13.

05.04.2021
13

14.

Только что приобретенные
вами знания имеют порой
любопытное применение.
Великий математик Л. Эйлер в 1736 г.
занимался решением такой
своеобразной
задачи:
05.04.2021
14

15.

№1
05.04.2021
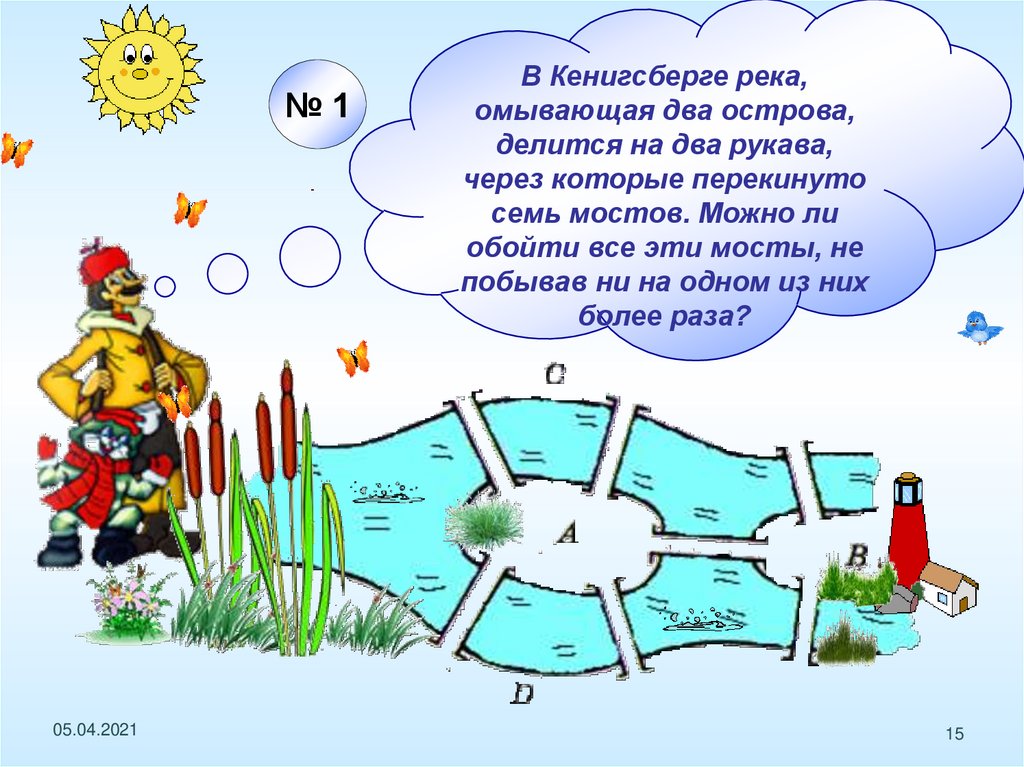
В Кенигсберге река,
омывающая два острова,
делится на два рукава,
через которые перекинуто
семь мостов. Можно ли
обойти все эти мосты, не
побывав ни на одном из них
более раза?
15

16.

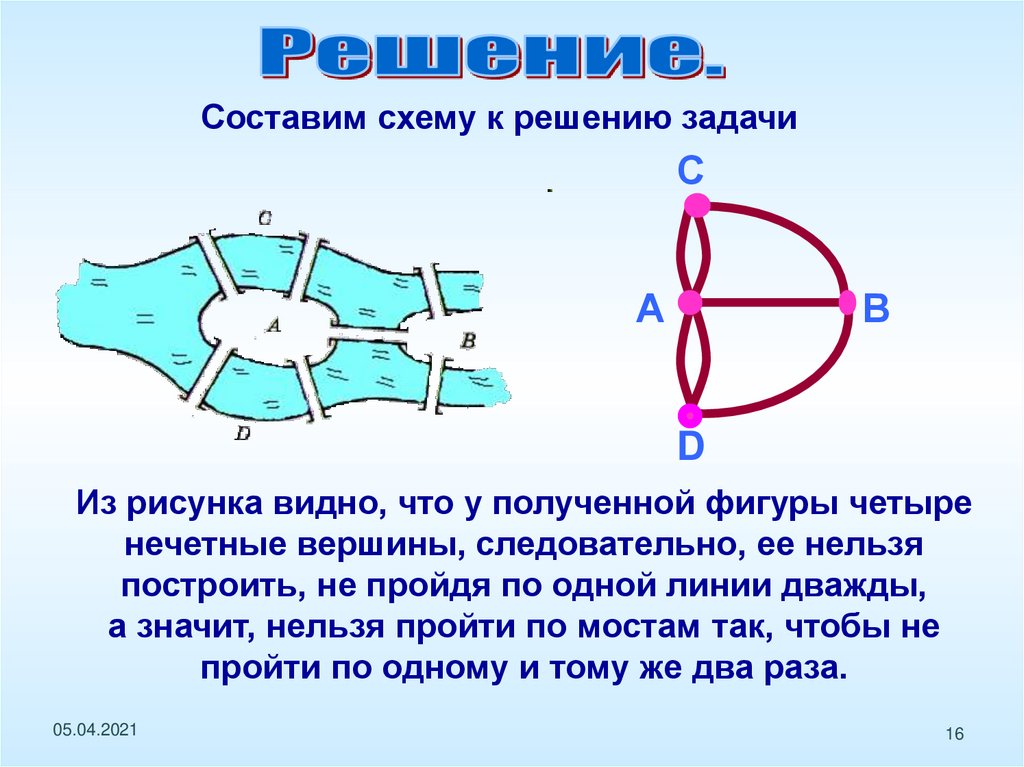
Составим схему к решению задачи
С
А
В
D
Из рисунка видно, что у полученной фигуры четыре
нечетные вершины, следовательно, ее нельзя
построить, не пройдя по одной линии дважды,
а значит, нельзя пройти по мостам так, чтобы не
пройти по одному и тому же два раза.
05.04.2021
16

17.

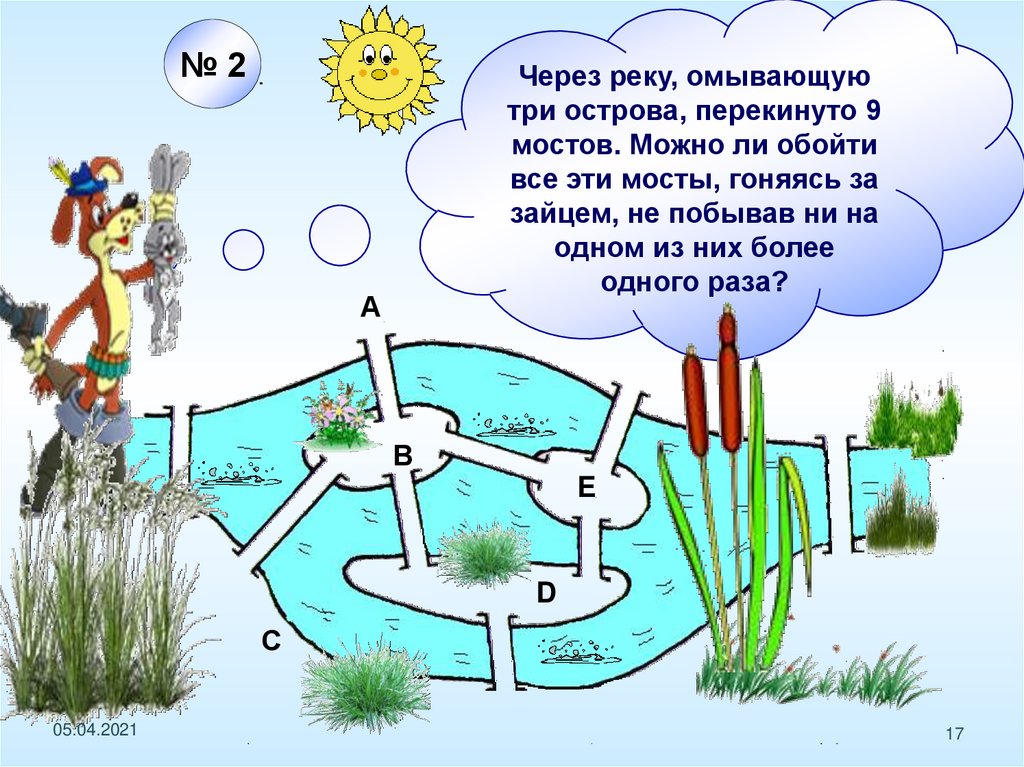
№2
Через реку, омывающую
три острова, перекинуто 9
мостов. Можно ли обойти
все эти мосты, гоняясь за
зайцем, не побывав ни на
одном из них более
одного раза?
А
В
E
D
С
05.04.2021
17

18.

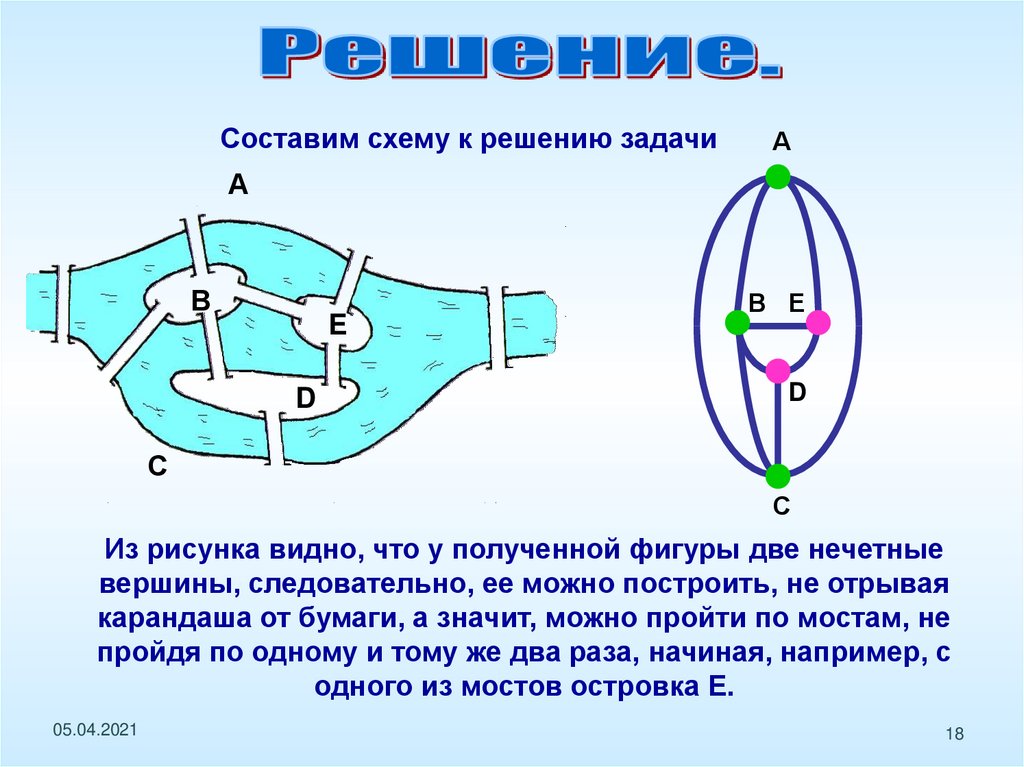
Составим схему к решению задачи
А
А
В
E
D
В Е
D
С
С
Из рисунка видно, что у полученной фигуры две нечетные
вершины, следовательно, ее можно построить, не отрывая
карандаша от бумаги, а значит, можно пройти по мостам, не
пройдя по одному и тому же два раза, начиная, например, с
одного из мостов островка Е.
05.04.2021
18

19.

05.04.2021
19