Похожие презентации:
Применение производной к исследованию функции и построению графика функции
1.
ПРИМЕНЕНИЕПРОИЗВОДНОЙ
к исследованию функции и
построению графика функции
Разработано преподавателем
математики Кольтиновой С.В.
2. Цели урока
• Ввести понятие касательной к графикуфункции в точке и выяснить в чем
состоит геометрический смысл
производной
• Научиться находить уравнение
касательной для конкретных функций
• Научиться определять промежутки
возрастания и убывания функции
(исследовать функции на
монотонность)
• Научиться находить точки экстремума
функции
• Научиться применять производную к
исследованию функции и построению
графика
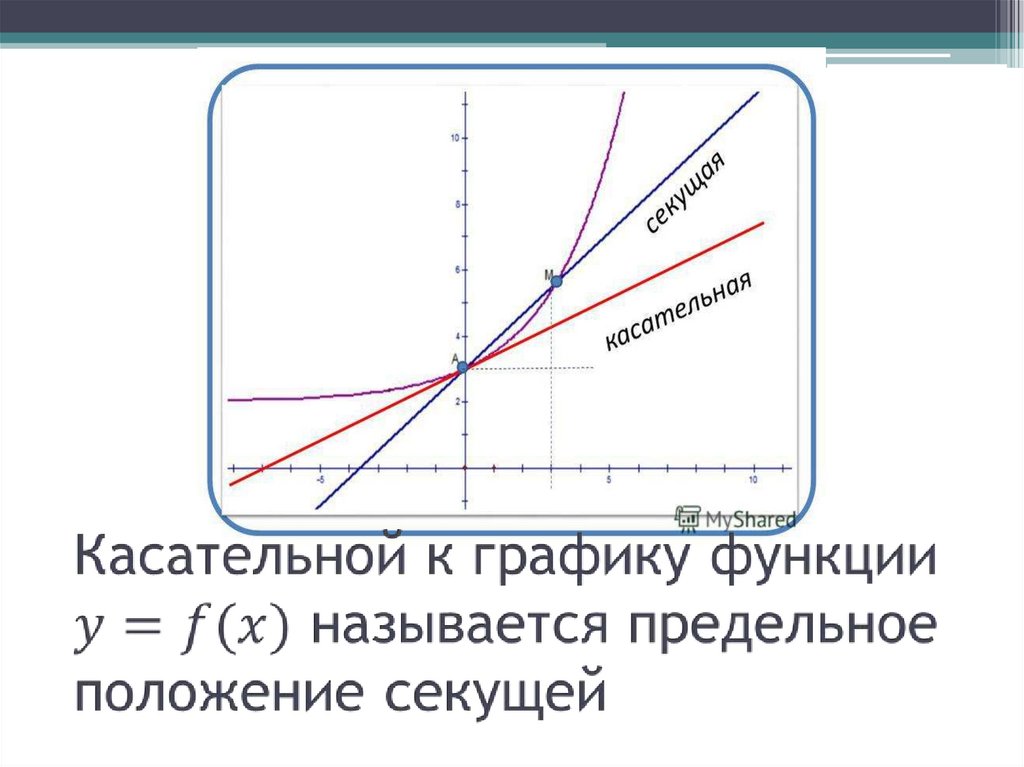
3. Касательной к графику функции y=f(x) называется предельное положение секущей
4.
5.
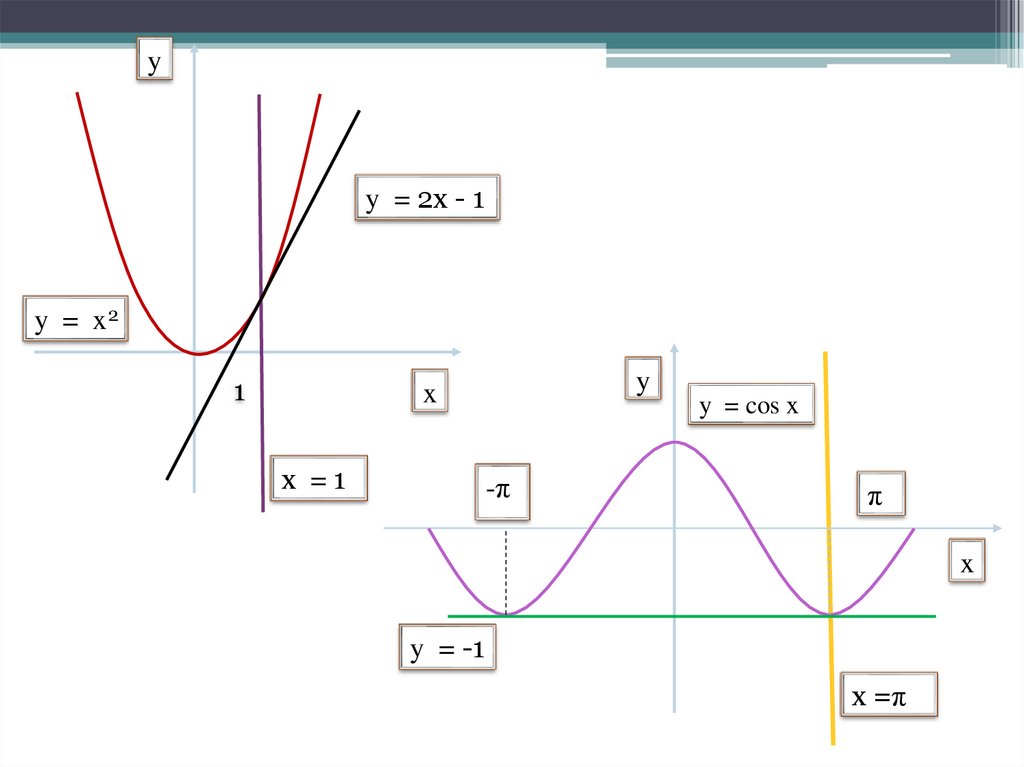
yy = 2х - 1
y = x2
1
y
x
х =1
y = cos x
-π
π
x
y = -1
х =π
6.
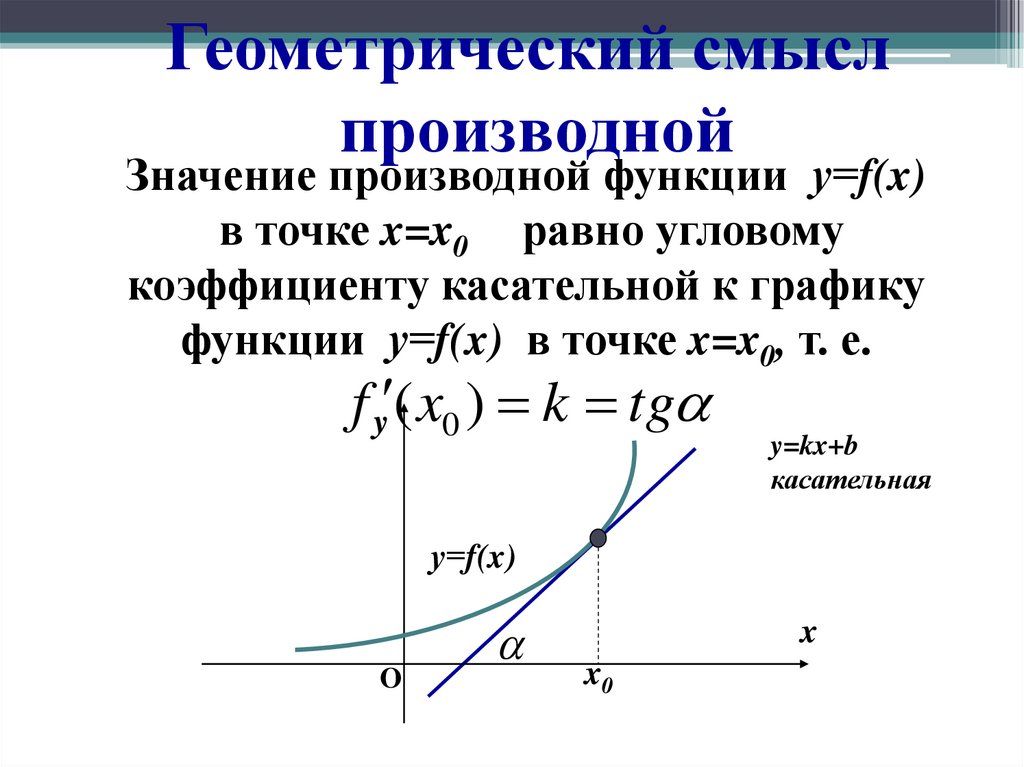
Геометрический смыслпроизводной
Значение производной функции у=f(x)
в точке x=x0 равно угловому
коэффициенту касательной к графику
функции у=f(x) в точке x=x0, т. е.
f y ( x0 ) k tg
y=kx+b
касательная
у=f(x)
O
x
x0
7.
f ( x0 ) tg'
Причем, если :
.
1. f ' ( x0 ) tg 0, то острый
2. f ' ( x0 ) tg 0, то развернутый
3. f ' ( x0 ) tg 0, то тупой
8. Уравнение касательной
9. Алгоритм
• Найти значение функции в точке хо• Вычислить производную функции
• Найти значение производной функции в
точке хо
• Подставить полученные числа в формулу
y = f(xo) + f `(xo)( x – xo)
• Привести уравнение к стандартному виду
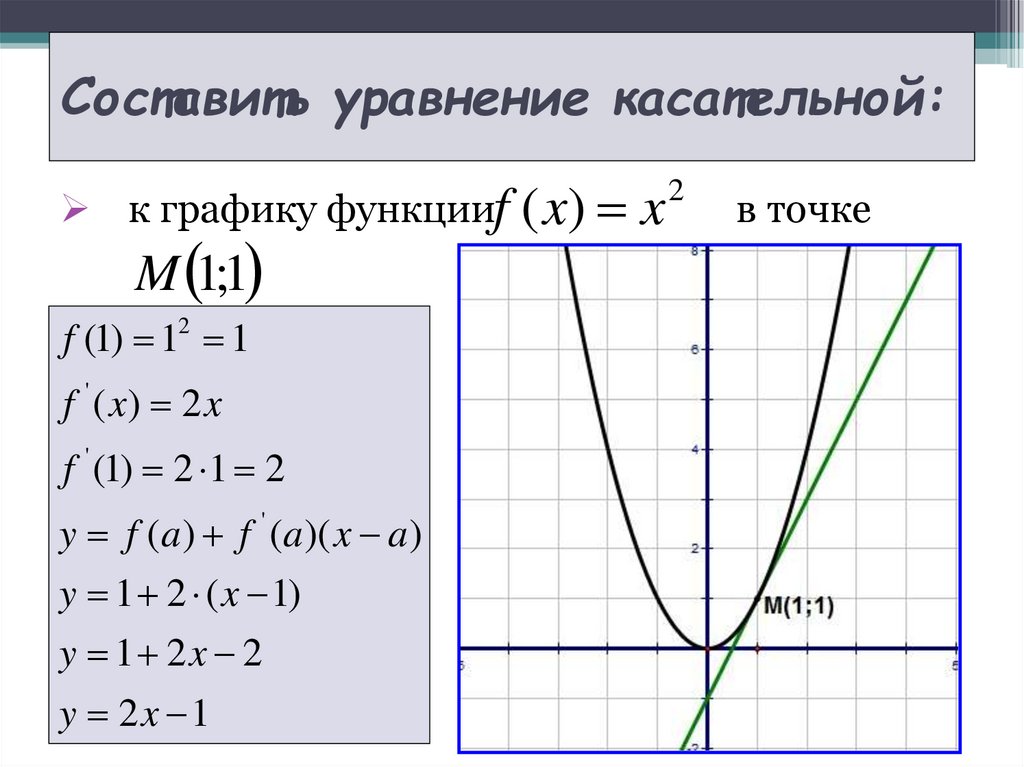
10. Составить уравнение касательной:
к графику функцииfM 1;1
f (1) 12 1
f ' ( x) 2 x
f ' (1) 2 1 2
y f (a ) f ' (a )( x a )
y 1 2 ( x 1)
y 1 2x 2
y 2x 1
( x) x
2
в точке
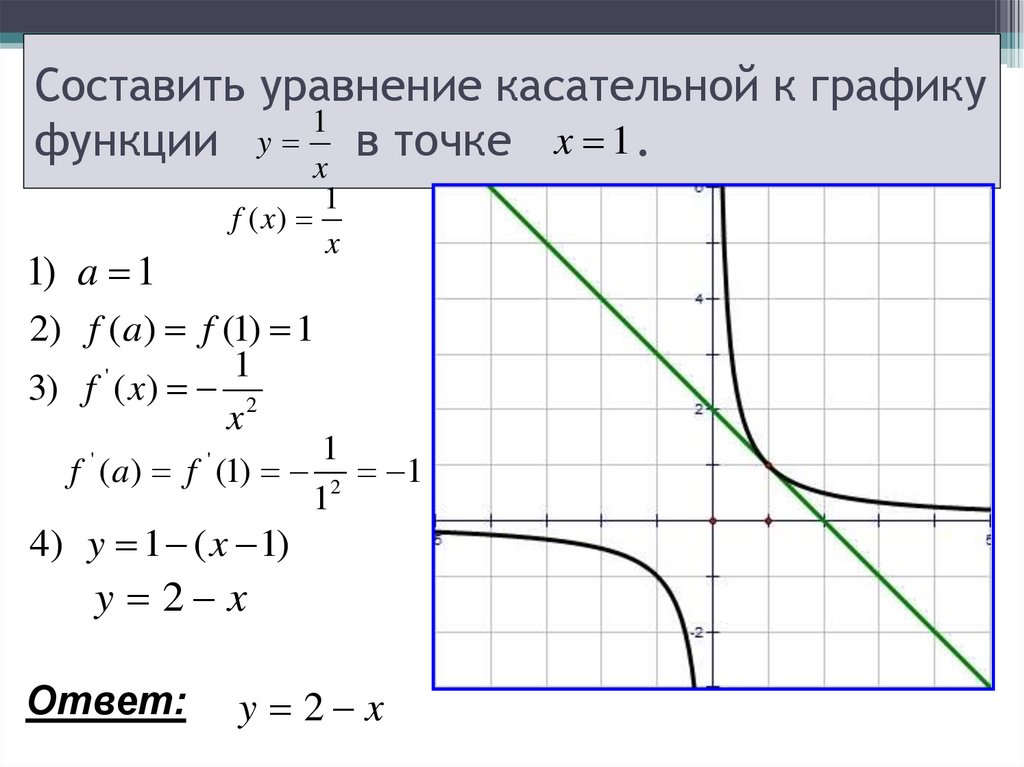
11. Составить уравнение касательной к графику функции в точке .
Составить уравнение касательной к графику1
y
x 1.
функции
в
точке
x
1
f ( x)
x
1) a 1
2) f (a) f (1) 1
1
'
3) f ( x) 2
x
1
f (a ) f (1) 2 1
1
'
'
4) y 1 ( x 1)
y 2 x
Ответ:
y 2 x
12.
Исследованиефункции на
монотонность
13.
Исследовать функциюна монотонность – это
значит выяснить, на каких
промежутках из области
определения
функция возрастает,
а на каких –
убывает.
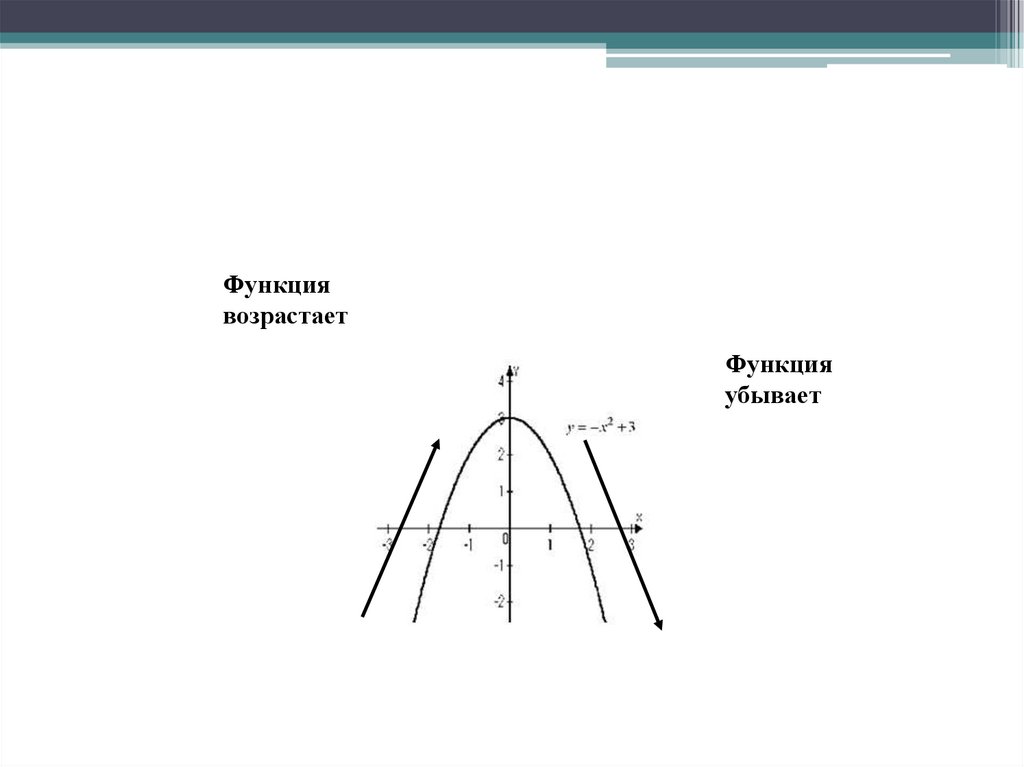
14.
Функциявозрастает
Функция
убывает
15. Возрастание и убывание функции можно изобразить так
Иду под гору. Функцияубывает на
промежутке[a;с]
Иду в гору. Функция
возрастает на
промежутке[b;a]
y
a
b
0
c
x
16. Для определения промежутков возрастания и убывания функции можно использовать и производную .
17.
Теорема:Если f(x) – непрерывна на промежутке и
имеет f´(x), то
а) если f´(x) > 0, то f(x) – возрастает
б) если f´(x) < 0, то f(x) – убывает
f´(x)
f (x)
+
-
18. Алгоритм исследования функции на монотонность
1) Найти производную функции f ΄(х)2) Найти стационарные (f ΄(х) = 0) и
критические (f ΄(х) не существует)
точки функции у= f(х)
3) Отметить стационарные и критические
точки на числовой прямой
4) Определить знаки производной на
получившихся промежутках
5) По знаку производной определить
промежутки монотонности функции
(если f ΄(х) > 0 – функция возрастает; если f ΄(х) <
0
функция убывает; если f ΄(х) =0 – функция
постоянна)
19. Определения
• Внутренние точки области определенияфункции, в которых производная
функции равна нулю, называются
стационарными.
• Внутренние точки области определения
функции, в которых функция
непрерывна, но производная не
существует, называются критическими
20.
Например: найти промежуткимонотонности функции f(x) = x³ - 6x² + 9x – 1
1) f´(x) = 3x² - 12x + 9
2) Найдем стационарные точки:
f´(x) = 0, 3x² - 12x + 9 = 0
x² - 4x + 3 = 0
x=1их=3
f ´(x)
+
+
3)
х
1
3
f(x)
4)
5) f ´(x) > 0, при x ϵ (-∞; 1) и (3; + ∞)
f ´(x) < 0, при х ϵ (1; 3)
Ответ: при x ϵ (-∞; 1) и (3; + ∞) функция возрастает, а
при х ϵ (1; 3) - убывает
21.
Нахождениеточек экстремума
функции
22.
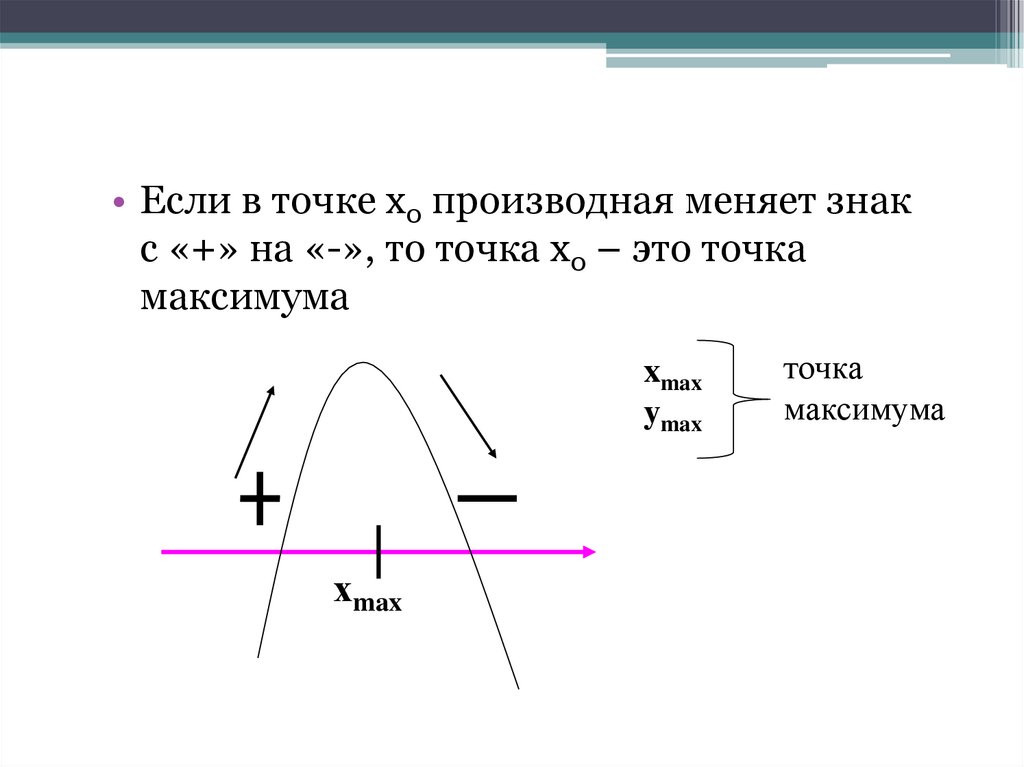
• Если в точке х0 производная меняет знакс «+» на «-», то точка х0 – это точка
максимума
xmax
ymax
хmax
точка
максимума
23.
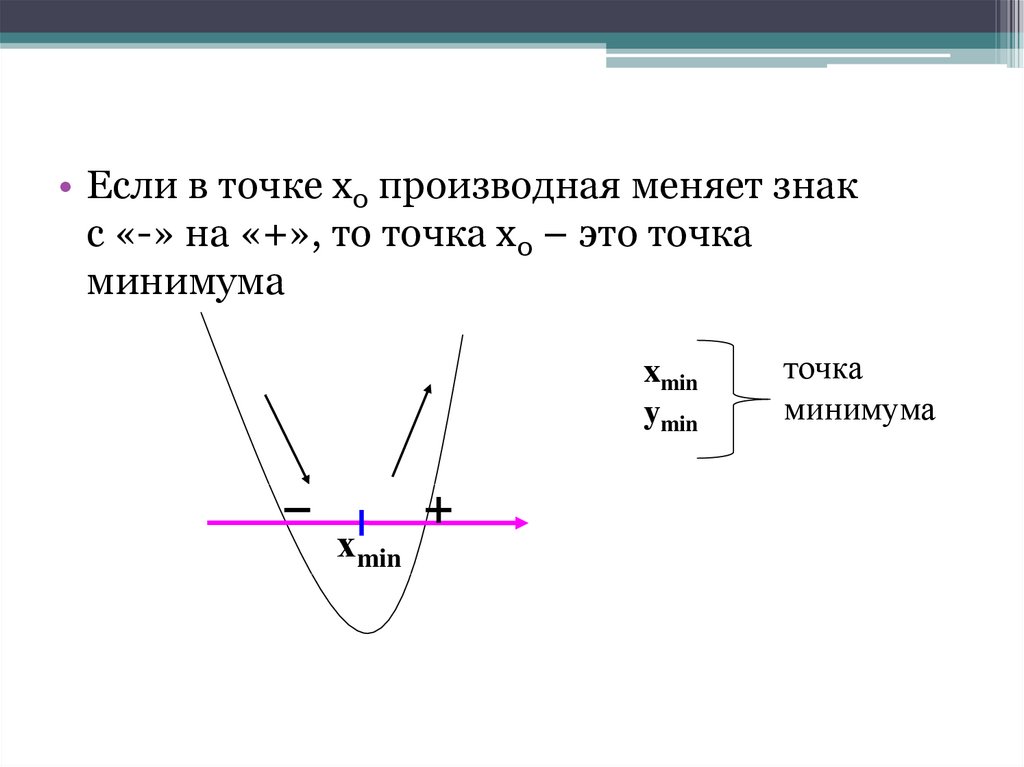
• Если в точке х0 производная меняет знакс «-» на «+», то точка х0 – это точка
минимума
xmin
ymin
хmin
точка
минимума
24.
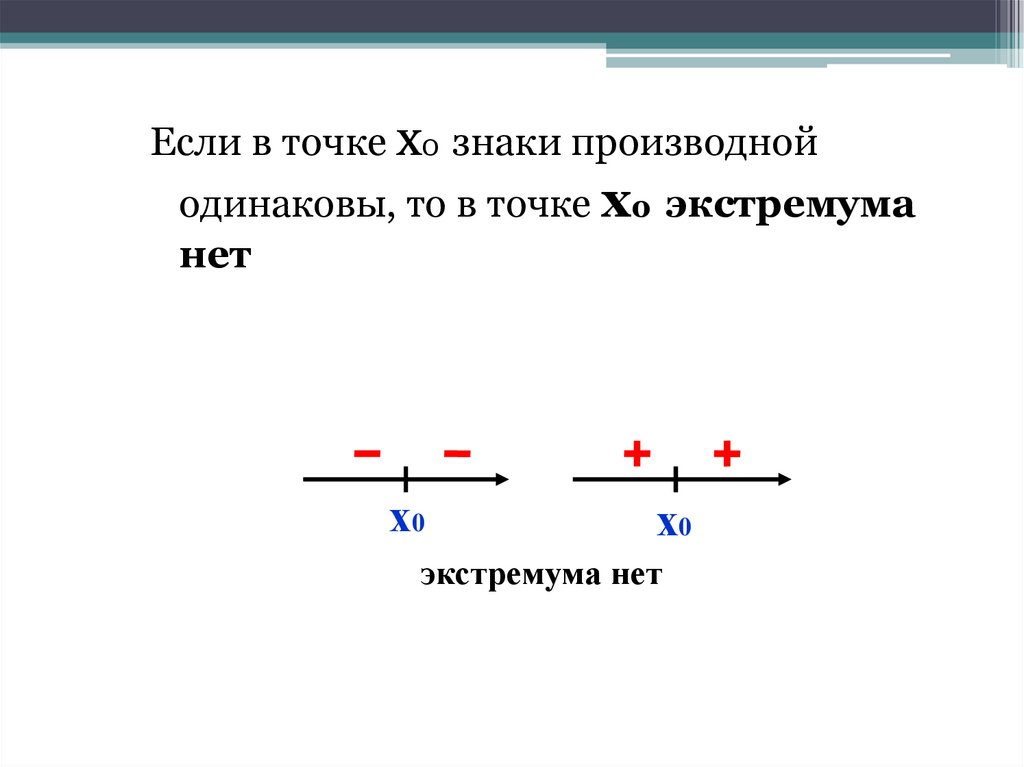
Если в точке х0 знаки производнойодинаковы, то в точке х0 экстремума
нет
х0
х0
экстремума нет
25. Алгоритм нахождения точек экстремума функции
1) Найти производную функции f ΄(х)2) Найти стационарные и критические
точки функции у = f(х)
3) Отметить стационарные и критические
точки на числовой прямой
4) Определить знаки производной на
получившихся промежутках
5) Если f ′(х0) при переходе через точку
меняет знак с «+» на «-», то эта точка –
точка максимума. Если f ′(х0) при
переходе через точку меняет знак с «-»
на «+», то эта точка – точка минимума.
Если f ′(Х0) не меняет знак, то в этой
точке экстремума нет (это точка
перегиба).
26. Например: найти точки экстремума функции
у 3х 16 х 24 х 114
3
2
Решение. 1) у΄=12 х³ - 48х² + 48х =
= 12х(х²-4х+4) = 12х (х - 2)²
2) у΄=0 при х =0 и х =2 (стационарные
точки)
3) f ´(x)
+
+
4)
х
0
2
5) Значит: х = 0 – точка минимума,
27.
у 3х 16 х 24 х 114
3
2
х = 0 – точка минимума,
хmin = 0
уmin 3 0 16 0 24 0 11 11
4
3
2
(0;-11) точка минимума (экстремума)
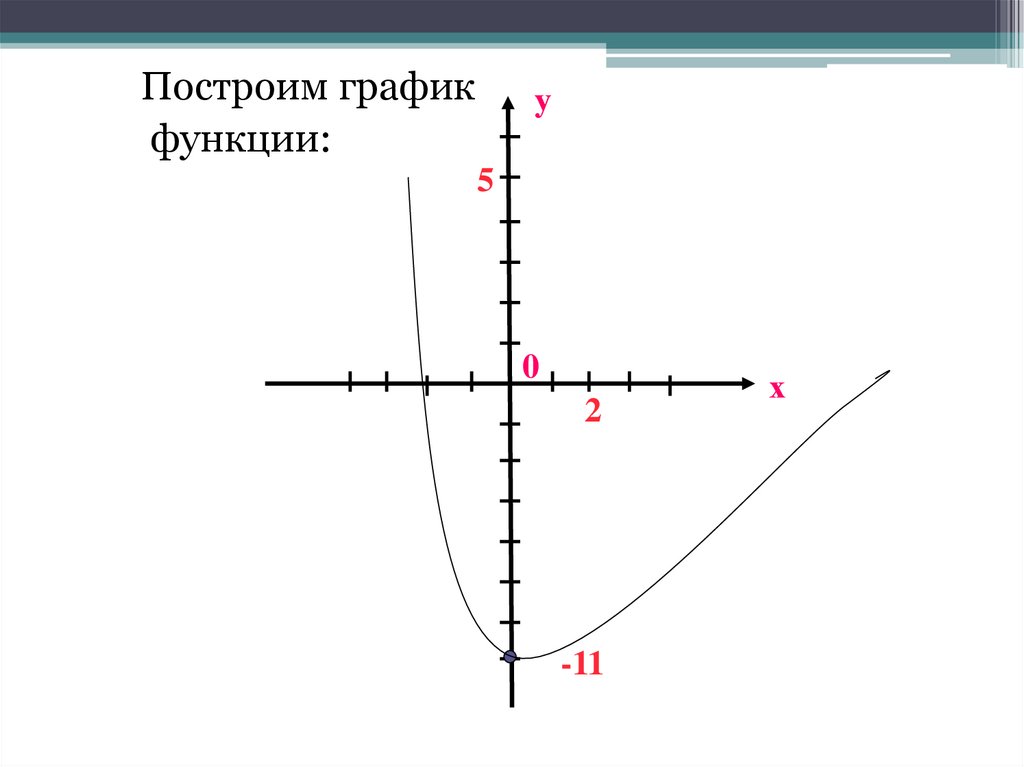
28.
Построим графикфункции:
у
5
0
2
-11
х
29. Например: исследовать функцию у = 2х³+3х² -1 и построить её график
Решение. D(у)= (-∞; +∞), четность неопределена
Найдем стационарные точки:
т.к. у΄=6х²+6х=6х(х+1) => 6х(х+1)=0
тогда х=0 и х=-1 стационарные точки
Найдем точки экстремума:
т.к.
f´(x)
-
+
f(x)
-1
+
0
и х=-1 – точка максимума
х= 0 – точка минимума
х
30.
Найдем промежутки монотонности:при x ϵ (-∞; -1] и [0; + ∞) - функция
возрастает
при x ϵ [-1; 0] - функция убывает
т.к. х=-1 – точка максимума, то уmax=0 т.к.
х= 0 – точка минимума, уmin=-1
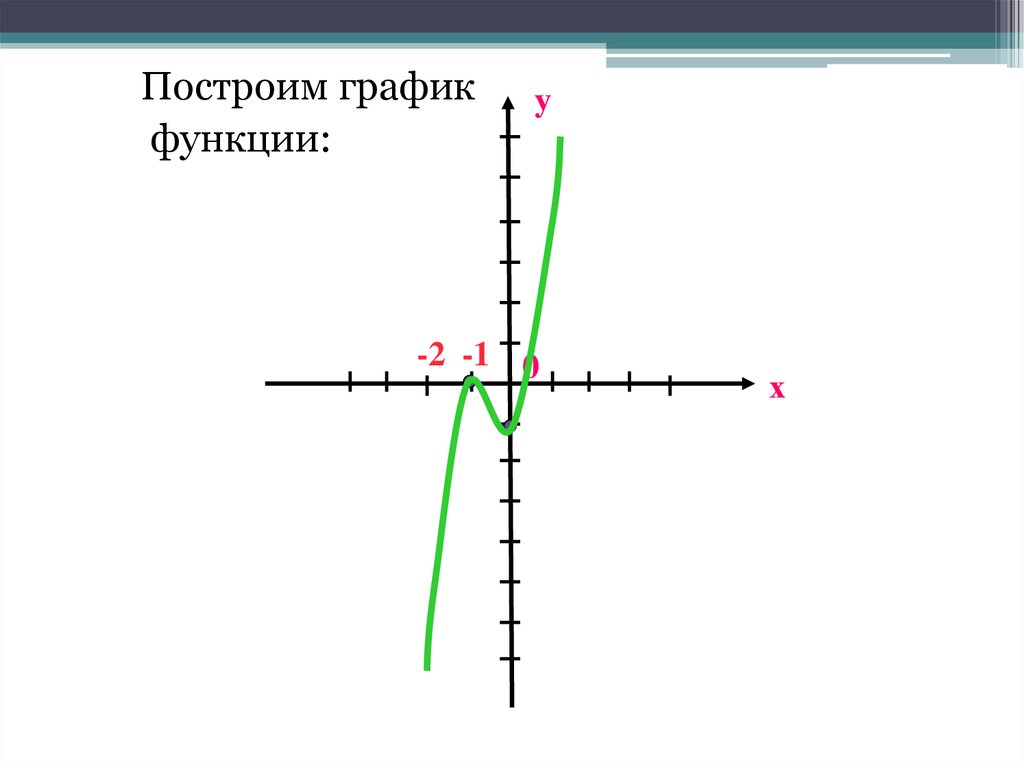
31.
Построим графикфункции:
у
-2 -1 0
х



















 Математика
Математика








